Multiobjective Reactive Power Optimization Planning for Medium Voltage Distribution Networks Based on Improved Genetic Algorithm
Abstract
The medium voltage distribution network is a key bridge between the power sector and electricity users. In the process of increasing user demand for electricity, the medium voltage distribution network system has encountered problems such as insufficient reactive power, unreasonable distribution, and insufficient voltage at the end nodes of the line, which have affected the power supply quality and stability of the power system. Therefore, a multiobjective reactive power optimization planning method for medium voltage distribution networks based on an improved genetic algorithm is studied. Establish a mathematical model for medium voltage distribution network planning based on the multiobjective functions of active power loss, total voltage deviation of system nodes, and minimum total compensation amount of system compensation devices. The balance equation between active and reactive power of power nodes and power absorption losses is taken as the equality constraint, and the maximum and minimum constraints of variables such as voltage at the generator end and tap position of the on-load tap changer are taken as the constraints of the model. By combining the advantages of the standard genetic algorithm and simulated annealing algorithm, an improved genetic algorithm is formed to effectively solve the constructed mathematical model. After countless iterations, the effective solution of the model is obtained to achieve multiobjective reactive power optimization planning for medium voltage distribution networks. The experimental results show that this method can achieve multiobjective reactive power optimization in medium voltage distribution networks and improve the stability of the power system.
1. Introduction
The medium voltage distribution network is a key component of the power system. As a hub link connecting the transmission network with end users, its operational reliability directly affects the quality of power supply and the safety of user electricity consumption [1]. The power industry is developing rapidly, the scale of medium voltage distribution networks is expanding, and the combination of lines is becoming more complex [2]. Multiple factors such as demand growth have led to reactive power shortage, distribution imbalance, and low terminal voltage in medium voltage distribution systems, posing a threat to safe operation [3]. Reactive power optimization planning for medium voltage distribution networks is crucial for ensuring safe operation.
Many scholars have conducted in-depth research on this issue, and Abdelmoumene et al. have also made contributions [4], and Abdelhady et al. [5] showed that the research on reactive power optimization in voltage distribution networks focuses on minimizing active power losses. Abdelmoumene used the enhanced cosine algorithm, while Nagarajan solved based on the standard genetic algorithm, both achieving the objective optimization [6]. Reactive power optimization in medium voltage distribution networks aims to reduce losses and stabilize voltage. The Levy internal search algorithm is used to solve the model and achieve multiobjective optimization. Shojaei et al. [7] research on reactive power optimization in medium voltage distribution networks, balancing load and wind power uncertainty, minimizing active power loss and total load, applying information gap decision-making and particle swarm optimization algorithm to solve, and achieving target optimization planning. Htay et al. [8] construct a reactive power optimization model for medium voltage distribution networks with the goal of minimizing transmission losses, solve it using particle swarm optimization algorithm, and optimize the compensator output. However, the overall optimization effect needs to be improved.
Although genetic algorithms improve efficiency by parallelizing search and reducing the risk of getting stuck in local optima, for large medium voltage distribution networks, their control variables are numerous and computational complexity is still high. This paper establishes a mathematical model for medium voltage distribution network planning using multiobjective functions of active power loss, total voltage deviation of system nodes, and minimum total compensation amount of system compensation devices. Through sensitivity analysis, candidate positions for reactive power compensation are determined, thereby reducing computational burden. Therefore, to propose a multiobjective reactive power optimization method for medium voltage distribution networks based on improved genetic algorithm, a mathematical model for medium voltage distribution network planning was established with the multiobjective function of minimizing active power loss, total voltage deviation of system nodes, and total compensation amount of system compensation devices. The balance equation between active and reactive power of power nodes and power absorption losses is used as an equality constraint, which not only considers the minimization of active network losses, but also considers the minimization of the total voltage deviation of system nodes and the total compensation amount of system compensation devices, achieving multiobjective optimization and improving the comprehensiveness of the planning scheme. By combining the advantages of the standard genetic algorithm and simulated annealing algorithm, an improved genetic algorithm has been developed to effectively solve the constructed mathematical model. Through countless iterative operations, the effective solution of the model can be obtained, achieving multiobjective reactive power optimization planning for medium voltage distribution networks. This method can cope with the problems of insufficient reactive power, unreasonable distribution, and insufficient voltage at the end nodes of the line in the medium voltage distribution network system and improve the power supply quality and stability of the power system.
2. Multiobjective Reactive Power Optimization Planning Method for Medium Voltage Distribution Networks
2.1. Constructing a Mathematical Model for MV Distribution Network Planning
2.1.1. Modeling and Objective Function Design
- 1.
Objective: To reduce active power loss and improve voltage quality, expressed as follows:
() -
Gij is the conductivity between the i and j power nodes; Ui and Uj are the power node identifiers for the voltage and power of nodes i and j; θij is the phase difference in voltage between the power supply nodes i and j; f1 is the minimum value of the active network loss; n is the total number of power nodes; and f‴ for the introduced penalty function is used to impose effective restrictions on f1. Uilim and Qjlim are PQ node voltage limit value and generator reactive output limit value, respectively; Uimax and Uimin represent the upper and lower limits of the PQ node voltage; Qjmax and Qjmin are the upper and lower limits of the reactive power output of the generator. λu is the node voltage crossing penalty factor; λQ is the reactive power penalty factor for the generator node.
- 2.
Objective: Minimize the total compensation amount of the network compensation device, expressed as follows:
() -
Among them, f2 is the minimum of the total compensation of the compensating device. αi is the power node i for its annual consumption of the reactive power compensation factor. NC is the number of compensating nodes, ECi is the compensation amount for node i, β is the loss coefficient, and Ploss is the active power loss of the system.
- 3.
Goal: Minimize node voltage deviation and expression as follows:
() -
dU is the voltage deviation and UN is the rated voltage; x is the control variable; ΔUij is the vertical component of node i, and j is the branch; and is the lateral component of nodes i and j.
2.1.2. Multiobjective Reactive Power Optimization Planning Mathematical Model Constraints for MV Distribution Networks
2.2. Mathematical Model Solution for Multiobjective Reactive Power Optimization Planning of MV Distribution Network Based on Improved Genetic Algorithm
The core of genetic algorithm lies in analyzing genes and optimizing chromosomes carrying optimal genes to solve problems [11], simulate biological genetics, analyze chromosomal genes, and select individuals with high fitness for inheritance to offspring [12]. Genetic algorithm is used for multiobjective optimization of the power grid, non–single-point search, cluster parallel processing, reducing computational complexity, avoiding local optima, and strong robustness [13].
The genetic algorithm for optimizing the power grid starts with encoding variables and finding the optimal solution through reasonable encoding to speed up and improve accuracy [14]. Common encoding forms binary, real, decimal, and decimal real [15]. Based on the advantage of decimal integer real number encoding [16], this paper adopts its variable encoding for multiobjective reactive power optimization model of a medium voltage distribution network.
Among them, t1, qC1, and ugt are the values of transformer ratio, capacitor reactive power compensation, and generator terminal voltage obtained after decoding, respectively. Δt1, ΔqC1, and Δugt are the standardized values when the three control variables are regulated, respectively.
The basic genetic operations of genetic algorithms mainly refer to selection, crossover, and mutation [17]. Select the optimal candidate based on fitness for genetic selection; cross-operation pairs chromosome exchange genes to generate new organisms, leading global search; and mutation operation involves gene mutation to generate new organisms and enhance local search. The genetic algorithm process for reactive power optimization in medium voltage distribution networks is shown in Figure 1.
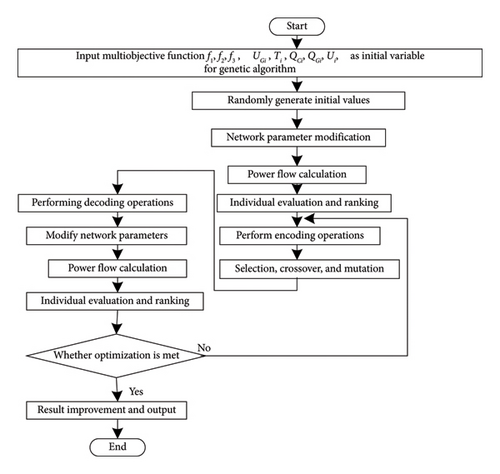
- 1.
Sensitivity analysis: For medium voltage distribution networks with multiple nodes [18] and complex control variables [19], sensitivity analysis is used to select compensation nodes [20]. Based on the sensitivity of reactive power changes to network losses, the computational burden of genetic algorithms is reduced:
() -
Among them, ξ is the system network loss sensitivity. ∂ is the derivation. The fitness function is a key factor used in genetic algorithms to evaluate individual performance. When designing the fitness function, the evaluation results of loss sensitivity or other techniques can be considered as one of the important indicators. A composite fitness function containing loss sensitivity indicators can be designed to prioritize solutions that have a significant impact on system performance during the evolution process. After setting the sensitivity, select the two to three most sensitive nodes on the branch as compensation candidates, focus on efficient nodes in the initial calculation, and reduce the computational complexity and time of the genetic algorithm.
- 2.
Tail mutation is dominant. When the control variable code is mutated, if the individual mutates a little at the high position, the mutated variable is likely to exceed the specified range, thus limiting its value to the boundary. Even if the variable does not exceed the boundary, its change will be more intense, resulting in irregular jumps of the operating point in the solution space. This will have a very adverse impact on the local search of genetic algorithm. In view of this situation, the rule that the tail of the code string is dominant is proposed, so that the mutation operation only occurs in the last or two bits of the code string. In actual work, it needs to be determined according to the type of variables. After such operation, the probability of out-of-bounds behavior of variables after the reasonable mutation operation is performed will be very low, which can fully ensure that the operating point is still around the original operating point. Thus, the local optimization ability of variables is significantly improved. The process is as follows:
- 1.
Randomize the individuals about to undergo mutation, the location of the control variables, and the direction of mutation.
- 2.
Range of variation for a fixed variable: If it changes upward, the upper limit minus the current value; if it changes downward, the current lower limit will be reduced.
- 3.
Mutation: Add a random number up, subtract a random number down, and fine tune the variable around its current value. When the mutated variable exceeds the limit value, then the boundary value is taken. In this paper, the variable coding is varied so that it changes within a range of −3 to +3 around the current value.
- 1.
- 3.
Voltage and reactive power overrun penalty coefficient adjustment. In this paper, the two through the linear dynamic value to make reasonable adjustment, λu max. Upper and lower limits of λu min set voltage crossing penalty coefficient. λu step is the step amount in the adjustment of the voltage crossing penalty factor; and λQ max and λQ min are the upper limit and the lower limit of the generator reactive power overrun penalty coefficient. λQstep is the step amount in the adjustment of the generator reactive power crossing penalty factor, and t‴ is the evolutionary algebra, and then, the node voltage crossing penalty factor λu and the principle of dynamic taking of changes follow t‴ for the generator node reactive power crossing penalty factor λQ that can be described by the equation as follows:
()() - 4.
Combining simulated annealing and genetic algorithm to solve reactive power optimization in medium voltage distribution networks, continuously correcting individual fitness:
() -
F‴ is the fitness, F is the target value; T0 is the initial temperature, at the same level as F; k is the evolution coefficient < 1; exp(·) is language functions.
-
In the initial stage, genetic algorithms are used to optimize reactive power in medium voltage distribution networks and after calibration operations. usually be larger, with little difference in fitness between individuals, more favorable to individual diversification; with the increasing of t‴ and decreasing of , the greater the replication adaptation, the greater the compulsion of the individual, which is conducive to the convergence of the algorithm.
- 5.
Crossover rate as well as variation rate improvement. Pc, cross rate, and Pm, change rate, improved equation involving Pc and Pm:
()() -
Among them, fmax is the maximum fitness value in the population; favg has an average fitness value, and f′ has a high fitness, Pc1. The upper and lower limits of Pc2 crossover probability; the Pm1 and Pm2 are the maximum and minimum values of the probability of variation. Pc1 = 0.9, Pc2 = 0.7, Pm1 = 0.1, and Pm2 = 0.001.
- 6.
Optimal individual preservation and improvement of termination criteria. In order to effectively prevent the optimal individuals obtained in the evolutionary process from being lost in the future process, an optimal individual that is better than the previous one in a certain generation is recorded and is not involved in the competitive selection of the next generation; in the improvement of the termination criterion, a combination of the number of termination generations and the optimization criterion is used to determine whether the program should be terminated or not. The optimization standard is an average target of ≤ 0.001 for the 10th generation.
3. Experimentation and Analysis
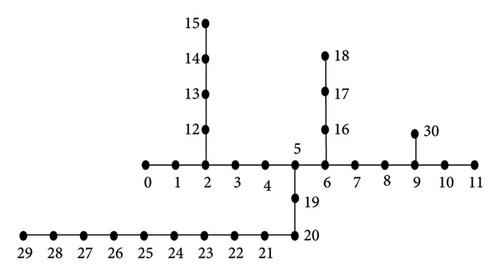
Simulate the multiobjective reactive power optimization of IEEE 30 node medium voltage distribution network using MATLAB in the experiment to verify its advantages. The system consists of 22 35 kV stations, with main transformers and on-load tap changers having capacities of 180.69MVA and 466.85MVA, respectively. There are 29 35 kV lines with a length of approximately 235.69 km. There are 6 generator nodes, 6 adjustable transformer branches, 6 compensation nodes, and a compensation capacity of 6 × 50 kvar. There is one balanced node, and the rest are photovoltaic nodes and also include 5 connecting wires. The wiring diagram is shown in Figure 2, and the load parameters are shown in Table 1.
| Node number | Load |
|---|---|
| 0 | — |
| 1 | 90 + j60 |
| 2 | 90 + j40 |
| 3 | 100 + j80 |
| 4 | 60 + j20 |
| 5 | 60 + j30 |
| 6 | 40 + j30 |
| 7 | 20 + j10 |
| 8 | 60 + j20 |
| 9 | 40 + j30 |
| 10 | 120 + j80 |
| 11 | 60 + j40 |
| 12 | 60 + j10 |
| 13 | 60 + j20 |
| 14 | 60 + j30 |
| 15 | 90 + j50 |
| 16 | 120 + j80 |
| 17 | 150 + j70 |
| 18 | 60 + j40 |
| 19 | 60 + j30 |
| 20 | 60 + j30 |
| 21 | 210 + j100 |
| 22 | 60 + j30 |
| 23 | 420 + j200 |
| 24 | 420 + j200 |
| 25 | 60 + j20 |
| 26 | 100 + j80 |
| 27 | 60 + j40 |
| 28 | 60 + j10 |
| 39 | 40 + j30 |
| 20 | 60 + j30 |
| 21 | 210 + j100 |
| 22 | 60 + j30 |
| 23 | 420 + j200 |
| 24 | 420 + j200 |
| 25 | 60 + j20 |
| 26 | 100 + j80 |
| 27 | 60 + j40 |
| 28 | 60 + j10 |
| 39 | 40 + j30 |
Based on MATLAB, we develop standards and improve genetic algorithms to optimize reactive power in medium voltage distribution networks. In terms of parameter settings, set the population size of both algorithms to 50 and the termination algebra to 100. The standard GA crossover rate is 0.7, and the variation rate is 0.05; we improve GA crossover rate by 0.7–0.9 and the mutation rate by 0.1–0.001 and refer to the empirical literature, the λu min taking a value of 1, the λu max taking a value of 20, the λu step taking the value of 0.2, the λQ min taking the value of 0.5, the λQ max taking a value of 10, and the λQ step taking the value of 0.1, and in the process of writing the program to improve the genetic algorithm, the improvement strategy is implemented in strict accordance with the method of this paper to write a reasonable program.
3.1. Comparative Analysis of the Effect of Multiobjective Reactive Power Optimization Planning for MV Distribution Networks
The verification grammar is superior to the multiobjective reactive power optimization results in reference [4], enhanced sine and cosine [5], Levy search [6], and particle swarm optimization [8]. Table 2 shows the comparison results.
| Method | Minimum active power loss of the optimized system (MW) | Total deviation of optimized node voltage (%) | The total compensation amount of the optimized system compensation device (Mvar) |
|---|---|---|---|
| Proposed method | 6.075 | 1 | 62.47810 |
| Reference [4] method | 6.976 | 3 | 72.47811 |
| Reference [5] method | 6.876 | 7 | 69.47812 |
| Reference [6] method | 6.654 | 5 | 62.97813 |
| Reference [7] method | 6.979 | 4 | 64.47814 |
| Reference [8] method | 6.980 | 2 | 65.47819 |
Table 2 shows that the method proposed in this paper optimizes the multiobjective reactive power planning of medium voltage distribution networks, resulting in better performance, reducing active power losses, voltage deviations, and compensation amounts, improving economy and safety, and meeting practical needs.
3.2. Multiobjective Reactive Power Optimization Planning Capability Analysis for MV Distribution Networks
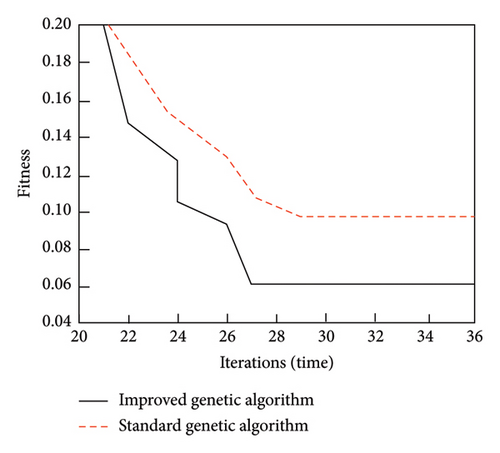
The standard and improved genetic algorithm are used to solve the reactive power optimization of medium voltage distribution networks, and the results are shown in Figure 3 and Table 3.
| State | Not optimized | Standard genetic algorithm optimization | Improved geneticalgorithm optimization |
|---|---|---|---|
| Network loss (MW) | 10.36 | 8.362 | 6.075 |
| Total deviation of node voltage (%) | 7 | 5 | 1 |
| Total compensation amount of system compensation device (Mvar) | 93.03921 | 72.50145 | 62.47810 |
| Convergent algebra | — | 29 times | 27 times |
As shown in Figure 3 and Table 3, the modified algorithm has fast iteration and excellent convergence. The network loss, voltage deviation, and compensation amount are all lower than those of the standard algorithm. When applied to multiobjective reactive power optimization in medium voltage distribution networks, the effect is more ideal.
3.3. Voltage State Analysis After Optimal Planning of MV Distribution Networks
The changes in node voltage and control variables before and after optimization are shown in Tables 4 and 5.
| Node number | Voltage before optimization (pu) | Optimized voltage |
|---|---|---|
| 0 | 1.049 | 1.097 |
| 1 | 0.998 | 1.088 |
| 2 | 1.004 | 1.076 |
| 3 | 0.993 | 1.070 |
| 4 | 0.998 | 1.062 |
| 5 | 0.990 | 1.068 |
| 6 | 0.985 | 1.059 |
| 7 | 0.998 | 1.072 |
| 8 | 0.974 | 1.033 |
| 9 | 0.954 | 1.006 |
| 10 | 0.998 | 1.088 |
| 11 | 0.974 | 1.013 |
| 12 | 0.098 | 1.030 |
| 13 | 0.956 | 0.998 |
| 14 | 0.951 | 1.003 |
| 15 | 0.957 | 0.999 |
| 16 | 0.949 | 0.985 |
| 17 | 0.938 | 0.984 |
| 18 | 0.935 | 0.984 |
| 19 | 0.920 | 0.888 |
| 20 | 0.940 | 0.992 |
| 21 | 0.941 | 0.993 |
| 22 | 0.937 | 0.983 |
| 23 | 0.928 | 0.977 |
| 24 | 0.917 | 0.983 |
| 25 | 0.951 | 0.965 |
| 26 | 0.986 | 0.995 |
| 27 | 0.930 | 1.065 |
| 28 | 0.918 | 0.975 |
| 29 | 0.924 | 0.963 |
| Transformer tap position | Transformation ratio before optimization | Optimized transformation ratio | Number of capacitor input groups | Capacity before optimization | Optimized capacity |
|---|---|---|---|---|---|
| 6–9 | 8 | 5 | 17 | 0 | 32.47810 Mvar |
| 6–10 | 8 | 5 | 18 | 0 | 0 |
| 4–12 | 8 | 5 | 23 | 0 | 0 |
| 5–17 | 8 | 5 | 25 | 0 | 30.00000 Mvar |
| 27–28 | 8 | 5 | 27 | 0 | 0 |
| 26–29 | 8 | 5 | 29 | 0 | 0 |
The lower limit of node voltage is 0.95 pu. Table 4 shows that after optimization, the voltage of nodes 17–25 has increased to above 0.95 pu. Table 5 shows the control variable over limit correction to ensure system safety and economy.
4. Conclusion
- 1.
Compared with the other five methods, this method is used for multiobjective reactive power optimization in medium voltage distribution networks, with low network loss, voltage deviation, and compensation, meeting demand, reducing risk, and improving economy.
- 2.
Compared to traditional methods, the modified algorithm has fewer iterations and better optimization, especially suitable for complex medium voltage distribution networks, proving the feasibility of multiobjective reactive power optimization.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
No funding was received for this research.
Open Research
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.




