To address the economic challenges posed by the integration of a large number of electric vehicles (EVs) into microgrids, while leveraging their mobile energy storage (MES) capabilities and accounting for the impact of EV users’ travel patterns on charging and discharging behaviors, a microgrid scheduling model is proposed that incorporates the MES characteristics of EVs under user travel habits. Firstly, based on the spatial and temporal characteristics of the EV travel chain, the upper and lower bounds of the state of charge (SOC) that EVs must maintain at specific moments during their driving process are determined. Secondly, a mathematical model of a microgrid operation incorporating EV mobile storage batteries, wind power, photovoltaic systems, stationary batteries, and micro-gas turbines is developed. This model considers the costs of electricity purchase and sale, wind and solar curtailment, and natural gas consumption, with the objective of minimizing the total operating cost. To validate the effectiveness of the proposed approach, the optimal scheduling model is implemented and solved using YALMIP and GUROBI. Simulation results demonstrate that the proposed model significantly reduces the total operating cost of the microgrid compared to traditional methods. It also improves the profitability of EV users to a certain extent, promoting new energy consumption when new energy resources are abundant.

1. Introduction

Under the “dual carbon” goal, fully leveraging the mobile energy storage (MES) capabilities of electric vehicles (EVs) is crucial for enhancing the flexibility of microgrids [1–3]. As large-scale MES devices, EVs possess significant potential for flexible scheduling. When effectively controlled in alignment with specific objectives and integrated into microgrid scheduling, they can substantially improve the economic performance of microgrids. Consequently, there is an urgent need for in-depth research on optimal scheduling methods for microgrids that incorporate EVs.

Currently, scholars have conducted various studies on the participation of EV MES in microgrid scheduling. The authors of [4] studied the impact of using EVs as MES on the energy cost and greenhouse gas emissions of commercial buildings, revealing the potential economic and environmental impacts of EVs. In [5], the authors analyzed the demand-side response potential of EV as MES according to the charging characteristics and proposed a dispatch operation model. In [6], the authors took into account the spatiotemporal energy transfer characteristics of MES and constructed a multiscenario, multiobjective dispatch model, which improves the consumption capacity of PV power generation and improves the voltage limitation problem. In [7], based on the different departure and arrival times of EVs, a clustering algorithm is proposed to set the boundaries of the parking time periods of clustered EVs, which takes full advantage of the EV’s MES characteristics and improves the performance of the multi-microgrid system. Based on the microgrid system, the authors in [8] integrated and analyzed different types of distributed generation with the utility grid to reduce its operating costs to a large extent. Mobile storage can provide various auxiliary services and the authors proposed a day-ahead energy management system for mobile storage that minimizes the cost of importing power from the grid in [9]. However, the load calculations for EV charging in the above studies are relatively simplistic or focus solely on the temporal distribution, failing to incorporate EV users’ travel habits into the forecasting process. This limitation reduces the accuracy of the load predictions.

Regarding the impact of EV orderly charging and discharging strategies on microgrids, in [10], in order to evaluate the effectiveness of vehicle-to-grid (V2G) scheduling results, this study systematically evaluates EV charging behaviors through a comprehensive assessment framework spanning five critical dimensions: renewable energy accommodation ratio, schedulable capacity, dispatch response efficiency, load stability, and economic benefits of dispatch operations. Based on the analysis of EV users′ travel patterns, distinct load forecasting models were developed for two operational scenarios: uncoordinated charging versus coordinated charging–discharging strategies. Furthermore, building upon prior research in [11], we propose an optimized microgrid energy dispatch model that strategically integrates EV charging–discharging protocols. This innovative framework achieves dual optimization objectives by simultaneously minimizing operational costs and environmental remediation expenditures, thereby addressing both economic efficiency and ecological sustainability imperatives. In [12], the authors made full use of distributed energy in microgrids, considered the satisfaction of EV users, and proposed a collaborative optimal scheduling method based on the participation of EVs in multiple microgrids and distribution grids. In [13], the authors formulated two charging and discharging strategies and established a load model respectively according to the characteristics of EVs and then included new energy sources in the economic scheduling model of microgrids by using the priority method for hierarchical subarea scheduling. And in [14], in order to be able to achieve the simultaneous suppression of load fluctuation and reduction of the operating cost of EVs, the authors have developed a multiobjective optimization model for V2G in distributed systems, and through validation, the results can balance the load fluctuation and the operating cost of EVs in distributed systems. The authors developed a multiobjective scheduling model containing multiple flexibility resources from distributed generation, battery storage, EV clusters, and VSC converters, controlled by an EV charging and discharging model, with the aim of minimizing the system operating costs and maximizing the flexibility adequacy in [15]. The state of charge (SOC) constraints during charging and discharging of EVs in the above literature are not accurate enough and little consideration is given to EV user requirements.

In response to the limitations of previous studies, this paper comprehensively considers the travel habits of EV users by integrating the EV travel chain to impose constraints on the charging and discharging domains of EVs. Additionally, the subjective preferences of EV users are incorporated to ensure that their desired SOC levels are met during participation in the scheduling process. The study divides the distribution network into three distinct regions, each with unique base load characteristics and EV charging and discharging power requirements. Corresponding constraints are established for these regions. A microgrid scheduling model is proposed with the objective of minimizing the total operating cost while leveraging the MES characteristics of EVs, tailored to align with the travel habits of EV users.

2. MES Capacity Domain of EV Based on Travel Chains

2.1. User Travel Chains

The spatial and temporal distribution characteristics of EV charging loads are strongly influenced by users’ charging behaviors, which are closely tied to their travel patterns. Therefore, analyzing these relationships is essential. Travel destinations are categorized into three types: H (home), W (work), and O (other affairs). The following assumptions are made:

1.
The users’ initial and final travel locations are both in the H zone.
2.
The impact of other factors (e.g., route considerations between different functional areas) on EV charging is disregarded.
3.
The entire travel process is confined to the time range of 00:00–24:00.

Based on these assumptions, the spatial and temporal structure of the travel chain is depicted in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Structure of spatiotemporal characteristics of the traveling chain.

According to Figure 1, the whole traveling chain is divided into two parts: the external time chain and the internal space chain. In the internal space chain, d represents the driving mileage between the two destinations. In the external time chain, t represents the moment, which indicates the starting and ending moments of each section of the journey, respectively.

2.2. Time-Invariant Probability Distribution

2.2.1. The First Driving Start and Duration Moment

The distribution of the first driving start moment T_s1 can be regarded as a gamma distribution with a probability density function [16]:

()

In daily life, the travel time of EVs is limited. It is assumed that a single trip cannot exceed 150 min. The travel process is categorized into three cases: Class I, travel from a point in the H region to a point in a non-H region; Class II, travel between two points in non-H regions; and Class III, travel from a point in a non-H region to a point in the H region. The travel times for these three classes are modeled as lognormal distributions, with their respective probability density functions given as follows:

()

Based on the three different types of trips, the fitting parameters for each type of case are [16]:

()

2.2.2. Duration of Stationing

The duration of dwell time influences the charging time of EV. The length of EV dwell time Δt_stay,i is closely related to the type of dwelling location. Since there is no consensus on the distribution of EV dwell time in existing studies, this paper synthesizes the data into several common distribution patterns. Specifically, the probability density of the stopping time duration in the visible W region follows a generalized extreme value distribution:

()

The probability density function for the duration of stopping time in region H is modeled using a Weibull distribution:

()

The probability density of the length of stopping time in region O follows a generalized extreme value distribution [14]:

()

2.3. Probability Distribution of Miles Traveled

There are some gaps in journeys at different moments, and based on existing research, it can be assumed that the conditional probability density of EV miles traveled d_i in the ith time window obeys the following normal distribution:

()

In the above equation, Δt_i denotes the ith time window of traveling time; μ_i is the average value of mileage traveled under this time window; and σ_i is the standard deviation of mileage traveled under this time window.

Given the limited duration of single trips, it is assumed that the driving distance for a single trip does not exceed 130 km, and the corresponding driving time is primarily concentrated within 100 min. Considering the significant variation in the number of samples across different time periods, this paper discretizes the three types of driving times to enhance the accuracy of the fitted data. The statistical results of the fitting process are presented in Table 1.

Table 1. μ and σ of mileage in time windows.

(min)	Class I traveling time		Class II traveling time		Class III traveling time
(min)	μ_i (km)	σ_i (km)	μ_i (km)	σ_i (km)	μ_i (km)	σ_i (km)
(0,10)	2.20	1.02	2.49	1.91	2.77	1.94
[10,19]	7.28	3.73	6.47	3.79	6.76	3.77
[20,29]	13.32	6.14	11.75	6.15	11.95	6.25
[30,39]	18.71	8.10	16.79	8.99	16.97	8.31
[40,49]	24.65	10.69	21.80	10.94	23.00	10.81
[50,59]	32.14	14.51	28.64	14.67	25.01	12.05
[60,79]	36.87	16.95	33.48	17.31	32.57	17.40
[80,99]	48.41	24.72	47.26	23.60	45.82	23.42
[100,150]	68.31	27.11	71.51	28.62	72.72	26.81

2.4. Space Transfer Probability

A travel chain can be seen as a special kind of Markov. At a certain point in time, the current trip destination D_EST(i) is only related to the previous trip destination D_EST(i − 1) and is independent of earlier destinations, indicating a lack of posteriority. If each of D_EST(i + 1) and D_EST(i) is considered as a state, according to the theory of Markov chain, the next state of the EV is determined by the current state, counting the current state as E_i and the next state as E_j, and there are:

()

where p_ij is the probability of transferring the current state to the next state, which is defined as the EV spatial transfer probability in this paper.

There are three main categories of travel trajectory chains involved, and the percentage of daily activity trips made by private vehicles was counted as shown in Table 2.

Table 2. Share of different travel chains.

Travel chain	Percentage (%)
H-W-H	52.1
H-O-H	23.1
H-W-O-H	24.1

2.5. MES Capacity Domain Constraints of EVs

The SOC is utilized as a real-time quantitative characterization of MES capacity, which relates the EVs’ SOC between different time instances, as shown as:

()

where

denote the charging and discharging power of the nth EV at time t, respectively;

denote the charging and discharging efficiency of the nth EV, respectively.

To maintain the battery health of EVs and prevent potential damage caused by overcharging or over-discharging, the SOC of the EV must remain within a specified range at all times. This requirement can be expressed as

()

In the above equation, denotes the charging state of the nth EV at time t and SOC_max and SOC_min denote the upper and lower bounds of the range in which the SOC of the EV is located, respectively.

Meanwhile, when the EV departs from its current area and travels to the next area, its SOC must be sufficient to ensure the completion of the upcoming journey. This requirement imposes the following constraints:

()

In the above equation, represents the SOC value that the EV needs to satisfy a moment before traveling to the next region, and represents the value selected by the EV owner before departure; represents the distance that the nth EV traveled to the next destination, and E₁₀₀ represents the 100 km power consumption of the EV; Q_n represents the rated capacity of the nth EV; and represents the SOC of the nth EV when it left the current region. Equation (12) shows the minimum value of SOC that an EV should satisfy before the occurrence of the ith leg of the journey, and equation (13) takes into account the battery life of the EV to avoid irreversible damage to the battery caused by excessive charging and discharging of the battery.

2.6. MES Capacity Domain Determination

Based on the travel chain, the conditions that the SOC must satisfy at any moment during the EVs’ driving process can be determined. This provides a foundation for analyzing the subsequent charging and discharging behaviors of EVs. The specific steps are as follows:

1.
Determine the total number of EVs as N and number them 1, 2, 3, …n. Assume that the SOC at the departure moment of all EVs is 0.9, and start calculating from the first EV.
2.
Determine the situation of the traveling chain of the EVs.
3.
Extract the travel start time of the EVs, determine the duration of the first segment of the trip, and based on the trip duration, identify the first segment of the journey. Then, calculate the power consumption of the EV during the first leg of the journey.
4.
Extract the stopping time of the EV, calculate the time when it leaves the current location, and determine the next travel distance based on the travel chain.
5.
Calculate the SOC to be met by the EV, and continue to perform Step 4 until the end of the journey.

The specific steps are shown in Figure 2.

3. Economic Dispatch Models for Microgrids

3.1. Structural Models

3.1.1. Photovoltaic (PV) Power Generation

The power generation of PV systems is influenced by factors such as solar irradiance, temperature, and environmental conditions. Under standard test conditions (STCs), which include a temperature of 25°C and a light intensity of 1000 W/m², the output power model of a PV cell can be approximated as

()

In the above equation, P_PV(t) denotes the PV output force at time t; P_STC is the maximum output power under the STCs; G_STC denotes the light intensity under the STCs; and G(t) and T(t) denote the light intensity and surface temperature at the test time, respectively.

3.1.2. Wind Power

Given the specific value of wind speed, the corresponding output power of wind power generation can be calculated. The relationship between the wind turbine’s output power and wind speed is typically characterized as

()

where P_WT is the output power of the WT, P_r is the rated output power of the WT, v is the actual wind speed, v_in is the cut-in wind speed of the WT, v_r is the rated wind speed of the WT, and v_out is the cut-out wind speed of the WT.

3.1.3. Storage Battery

Energy storage batteries, as critical components of a microgrid, play an essential role in maintaining system stability. They supplement demand when other power sources are insufficient, store excess power during periods of low demand, and provide peak shaving to balance load variations. The operational state of the energy storage battery can be described by the following mathematical model:

()

where SOC_BA(t) represents the charging state of the storage battery at time t;

represent the charging and discharging power of the storage battery at time t;

represent the charging and discharging efficiency of the storage battery; E represents the rated capacity of the storage battery; and Δt represents the interval time.

3.1.4. EVs

The range conditions governing the charging state of the EV have been provided in Section 2.

3.2. Economic Dispatch Model

3.2.1. Objective Function

To enhance the economic performance of the microgrid and increase the consumption capacity of RE, the objective function for microgrid operational costs, considering wind and solar curtailment, is established as follows [17]:

()

where C_fule, C_om, C_grid, and C_cur are the natural gas fuel cost, maintenance cost, the cost of purchasing and selling electricity to the upper level, and the cost of abandoning wind and light, respectively. k denotes the price of natural gas; P_MT(t) denotes the power issued by the gas turbine at the moment t; LHV denotes the low calorific value; η_MT denotes the power generation efficiency of the gas turbine; γ₁, γ₂, γ₃, τ, ρ are the corresponding fitting coefficients; θ_BA, θ_MT denote the charging and discharging power of the storage battery at time t;

denote the maintenance coefficient of the storage battery and the maintenance coefficient of the gas turbine, respectively; C_pri,buy(t), C_pri,sell(t) denote the purchase and sale price of electricity to the higher grid at time t; ϕ(t) denotes the price of abandoned wind and light at time t; and P_{WT_cur}(t), P_{PV_cur}(t) denote the power of abandoned wind and light at time t, respectively.

3.2.2. Condition

3.2.2.1. Microgrid Power Balance Constraints

()

where

denotes the charging load of EV at time t; P_load,des(t) denotes the base load in the microgrid at time t; and des represents the location information of the area where it is currently located and can take W, H, and O.

3.2.2.2. Micro-Gas Turbine Constraints

Output constraints:

()

Climbing constraints:

()

where

are the upper and lower limits of the gas turbine output and r is the maximum climb of the micro-gas turbine.

3.2.2.3. Energy Storage Battery Constraints

()

In the above equation, , are the upper and lower limits of the charging and discharging power of the energy storage battery and , are the upper and lower limits of the SOC of the energy storage battery.

3.2.2.4. EV Constraints [18]

The range of SOC constraints for EVs has been outlined in Chapter 1. Additionally, the following constraints are also considered.

The charging and discharging power constraints for EVs are shown in equation (31). In the charging and discharging process, charging and discharging cannot occur simultaneously, so the state constraints for charging and discharging are given in equation (32).

()

where

denote the maximum values of charging and discharging power of EV, respectively.

and

are both binary variables, where a value of 1 indicates that the EV is in the charging state at time t, and a value of 0 indicates that the EV is in the discharging state.

4. Calculus Analysis

4.1. Microgrid Data and Parameters

4.1.1. Wind Energy Output Curve

Using a 15 min time step, a 24 h period is selected as a cycle, divided into 96 segments. The following parameters are used: P_rt = 200 kW, v_rt = 3 m/s, v_out = 25 m/s, c = 4.8, and k = 3.5. According to the formula in Section 2, the Monte Carlo method is used to predict the wind power output, and the results are shown in Figure 3.

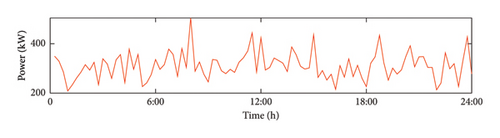
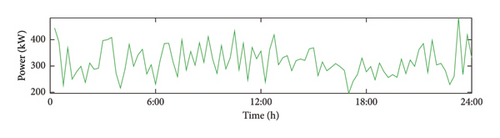
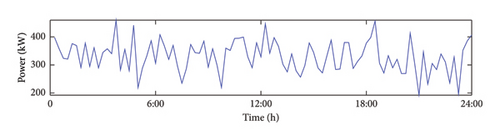
4.1.2. PV Output Curve

Using the same method to predict the PV output, the first step is to obtain the variation in ambient temperature in the region over one cycle. Based on this, the final PV output curve is shown in Figure 4.

4.1.3. Load Curves

The daily load curves vary across different areas. In residential areas, where there are a higher number of users during the night, the load tends to be higher. In contrast, the load decreases in the other two areas due to off-duty periods and breaks. A set of data curves illustrating these variations is presented in Figure 5.

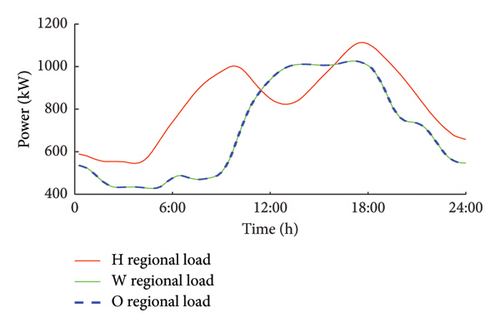
4.1.4. Price and Operating Parameters

Price and operating parameters are shown in Tables 3 and 4, respectively, where the unit of the price parameters is in Chinese Yuan (CHN).

Table 3. Price parameters.

Time	Period	Electricity purchasing price (CHN)	Electricity selling price (CHN)	Abandoned WT and PV power prices (CHN)	Natural gas purchasing price (CHN)
11:00–15:00 19:00–21:00	Peak	1.18	1	0.5	2.9
8:00–10:00 16:00–18:00 22:00–24:00	Plain	0.68	0.55	0.2	2.9
1:00–7:00	Valley	0.35	0.28	0.1	2.9

Table 4. Other parameters.

Parameter	Value
SOC_max/SOC_min	0.9/0.2
///	0.9/0.9
/ (kW)	5/5
N	100
γ₁/γ₂/γ₃	0.075/0.4/0.417
/ (kW)	45
θ_BA	0.0018
LHV (kW/m³)	10.1
Q (kWh)	30
E₁₀₀ (kWh)	15
E (kWh)	250
/ (kW)	65/0
r (kW/h)	20
τ/ρ	65/0.1
θ_MT	0.0648
/	0.95/0.2

From the table, it can be seen that 11:00–15:00 and 19:00–21:00 belong to the load peak hours, 1:00–7:00 belongs to the load valley hours, and the rest of the time belongs to the load flat hours.

4.2. Analysis of Simulation Results

4.2.1. Results of the Proposed Model

Figure 6 illustrates the variation in SOC for a single EV across the three travel chains, along with the corresponding charging and discharging data.

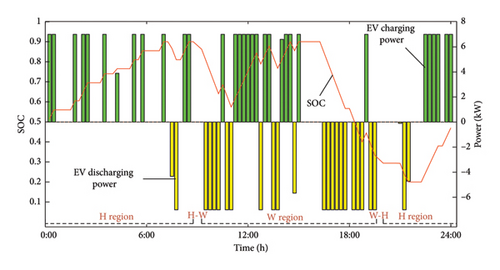
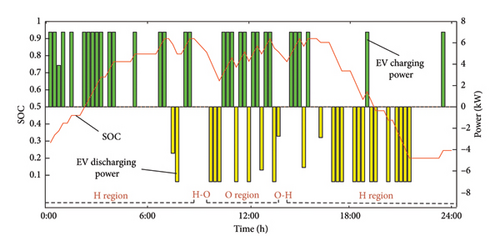
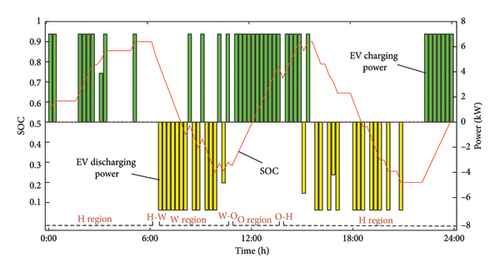
Figure 6 selects three categories based on the travel chain status from 100 EVs participating in the dispatch, showing their respective charging and discharging states as well as SOC trends. It can be observed that the three types of EVs charge and discharge during roughly the same time periods. A notable feature is that the EVs predominantly charge during the nighttime (the load trough period) and discharge during the two load peaks to help alleviate the pressure on the power grid.

Figure 7 presents the charging and discharging patterns of 100 EVs over the course of a day in different regions: W, H, and O.

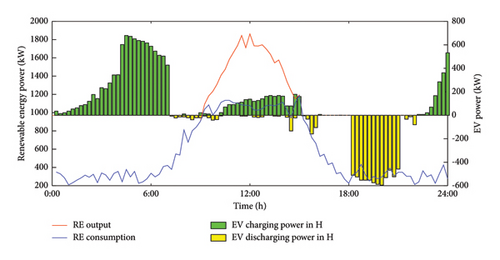
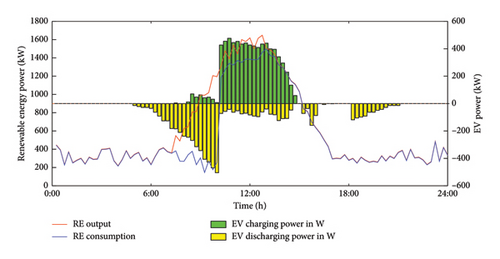
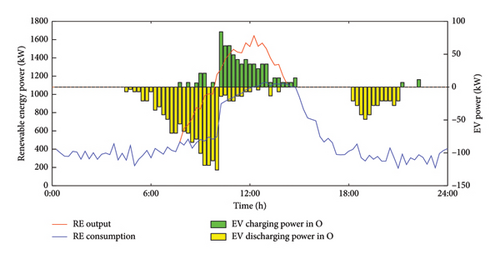
Based on the travel chain state of each EV, their charging and discharging power in each region is accumulated to produce Figure 7. Due to variations in the locations and times of travel stops, the EVs initially remain in the H region from early morning until departure, where the electricity price is low, and charge to meet their driving requirements. After departure, depending on the type of travel chain, the EVs either stay in the W region or the O region. In these regions, the charging and discharging behavior is adjusted according to the electricity price, ensuring that the EVs can satisfy the requirements for subsequent trips while optimizing their charging and discharging behavior. And we found that between 10:00 and 14:00, the new energy output value reaches the peak of the day, and at the same time, the EV charging power also increases, which can achieve the new energy consumption to a greater extent.

4.2.2. Comparative Results and Analysis

To verify the economic performance of the method proposed in this paper, economic data under two alternative scenarios are provided for comparison.

Scenario 1: It is assumed that EV users must charge when they arrive in the H region until they meet their travel requirements. Additionally, only 30% of the users who arrive at non-H regions opt to charge.

Scenario 2: In this scenario, EV users make charging decisions based solely on their own interests, choosing charging times that minimize their own costs, while ensuring they meet the necessary travel requirements.

Scenario 3: This scenario involves the EVs participating in V2G charging and discharging scheduling as proposed in this paper.

The total operating cost of the microgrid, the charging cost of EVs, and the consumption of new energy under the three scenarios are shown in Table 5.

Table 5. Cost comparison.

Term	Total operating costs of microgrids (CHN)	Charging costs for EV users (CHN)	New energy consumption (kWh)
Scenario 1	62,549	1682.9	36,495
Scenario 2	62,415.7	664.4761	36,316
Scenario 3	41,029	−486.78	46,170

Based on the above calculations, it can be seen that in Scenario 1 and Scenario 3 (neither EV participates in V2G scheduling), the amount of RE consumption is lower than the point in Scenario 3. At the same time, Scenario 2 carries out orderly charging, which effectively reduces the cost of charging and discharging for the EV user. And there is a negative cost in Scenario 3, which shows that the gain achieved in the process of EV participation in the V2G scheduling process can help to promote the participation of the EV in the scheduling plan. On the total cost of grid operation, the method proposed in this paper makes full use of the MES characteristics of EVs, and the cost is reduced by 34.4% compared with the other two scenarios.

5. Conclusion

In this paper, a V2G dispatch model is proposed based on the travel habits of EV users, incorporating microgrid operating costs and the MES characteristics of EVs. An example analysis is conducted to validate the feasibility and effectiveness of the proposed strategy. The specific conclusions are as follows:

1.
Based on data on EV users’ travel patterns, the locations and durations of EV stopping times throughout the day are calculated. By considering user preferences and the battery’s upper and lower limits, the regional SOC ranges that EVs must satisfy at different times of the day are determined.
2.
Under a time-of-use tariff framework, leveraging the MES characteristics of EVs, a V2G scheduling model is developed with the goal of minimizing microgrid operating costs. The simulation example demonstrates that the charging and discharging behaviors of EVs across different travel chains are similar: EVs discharge during periods of high tariffs and loads to alleviate grid pressure and charge during periods of low tariffs and loads to reduce operating costs.
3.
The comparison of different scenarios demonstrates that the proposed scheduling model effectively promotes RE consumption. The consumption rate is increased by more than 26.5% compared to the other scenarios. Additionally, through the value attributes of MES, users can realize tangible benefits even when their EVs are expected to charge and consume energy, thereby enhancing user willingness to participate in V2G scheduling.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research was supported by the Science and Technology Project of State Grid Jibei Integrated Energy Service Co., Ltd., Grant/Award Number: SGJBZN00AJJS2400078.

Acknowledgments

This research was supported by the Science and Technology Project of State Grid Jibei Integrated Energy Service Co., Ltd. (SGJBZN00AJJS2400078).

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author, upon reasonable request.

References

1 Wang J., Huang K., Wu L., and Xu X., Adaptive Carbon-Electricity Dual Pricing Mechanism for EVs Orderly Charging, 2022 IEEE 6th Conference on Energy Internet and Energy System Integration (EI2), April 2022, 3052–3057, https://doi.org/10.1109/EI256261.2022.10116947.
10.1109/EI256261.2022.10116947
Google Scholar
2 Yang L. and Wang G., Carbon Emissions in a Dual-Channel Closed-Loop Supply Chain with Consumer’s Preference, 2017 International Conference on Service Systems and Service Management, June 2017, 1–6, https://doi.org/10.1109/ICSSSM.2017.7996182, 2-s2.0-85028619732.
10.1109/ICSSSM.2017.7996182
Google Scholar
3 Rui L., Analysis and Research on the Adjustment of Energy Consumption Structure Based on the “Dual Carbon” Target, 2022 21st International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), May 2022, 10–14, https://doi.org/10.1109/DCABES57229.2022.00016.
10.1109/DCABES57229.2022.00016
Google Scholar
4 Bozchalui M. C. and Sharma R., Analysis of Electric Vehicles as Mobile Energy Storage in Commercial Buildings: Economic and Environmental Impacts, 2012 IEEE Power and Energy Society General Meeting, April 2012, 1–8, https://doi.org/10.1109/PESGM.2012.6345703, 2-s2.0-84870577298.
10.1109/PESGM.2012.6345703
Google Scholar
5 Yi F., Yongxiang L., Xiaomei Z., and Lin G., Power Demand Side Response Potential and Operating Model Based on EV Mobile Energy Storage, 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), July 2017, 1–6, https://doi.org/10.1109/EI2.2017.8245418, 2-s2.0-85049350867.
10.1109/EI2.2017.8245418
Google Scholar
6 Tong L., Zhao S., Jiang H., Zhou J., and Xu B., Multi-Scenario and Multi-Objective Collaborative Optimization of Distribution Network Considering Electric Vehicles and Mobile Energy Storage Systems, IEEE Access. (2021) 9, 55690–55697, https://doi.org/10.1109/ACCESS.2020.3026204.
10.1109/ACCESS.2020.3026204
Google Scholar
7 Wu C., Han H., Gao S., and Liu Y., Coordinated Scheduling for Multimicrogrid Systems Considering Mobile Energy Storage Characteristics of Electric Vehicles, IEEE Transactions on Transportation Electrification. (2023) 9, no. 1, 1775–1783, https://doi.org/10.1109/TTE.2022.3201033.
10.1109/TTE.2022.3201033
Google Scholar
8 Shehzad M., Jamal N., Muqeet H. A., Mirsaeidi S., and Muttaqi K. M., Cost Effective Analysis of Stationary and Mobile Energy Storage Systems in Prosumer Microgrid Considering System Reliability and Real-Time Pricing Scheme, 2023 IEEE International Conference on Energy Technologies for Future Grids (ETFG), August 2023, 1–5, https://doi.org/10.1109/ETFG55873.2023.10407514.
10.1109/ETFG55873.2023.10407514
Google Scholar
9 Abdeltawab H. H. and Mohamed Y. A.-R. I., Mobile Energy Storage Scheduling and Operation in Active Distribution Systems, IEEE Transactions on Industrial Electronics. (2017) 64, no. 9, 6828–6840, https://doi.org/10.1109/TIE.2017.2682779, 2-s2.0-85029537019.
10.1109/TIE.2017.2682779
Google Scholar
10 Omara A. M., Shalabi A. A., and Islam M. R., Voltage Stability Analysis of Grid-Connected Microgrid Incorporating Plug-In Electric Vehicles, 2021 IEEE 6th International Conference on Computing, Communication and Automation (ICCCA), October 2021, 813–818, https://doi.org/10.1109/ICCCA52192.2021.9666440.
10.1109/ICCCA52192.2021.9666440
Google Scholar
11 Xu K., Wang S., Zhao J., Dou X., and Zhang P., Research on Microgrid Dispatch Considering the Charge and Discharge Strategy of Electric Vehicles, 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference, July 2020, 1–5, https://doi.org/10.1109/APPEEC48164.2020.9220487.
10.1109/APPEEC48164.2020.9220487
Google Scholar
12 Tang W. and Qin H., Multi-Microgrid Optimal Scheduling Considering Electric Vehicle Participation, 2019 IEEE 3rd Conference on Energy Internet and Energy System Integration (EI2), August 2019, 2026–2031, https://doi.org/10.1109/EI247390.2019.9061789.
10.1109/EI247390.2019.9061789
Google Scholar
13 Yan S., Li B., Zhang Y., Ye J., and Yin W., A Multi-Objective Optimization Strategy for V2G-Based Scaled Electric Vehicles in Distribution System with Various PV Penetration, 2024 IEEE PES 16th Asia-Pacific Power and Energy Engineering Conference, April 2024, 1–5, https://doi.org/10.1109/APPEEC61255.2024.10922597.
10.1109/APPEEC61255.2024.10922597
Google Scholar
14 Qiu H., Zhang X., Zhao Q., and Zu G., Enhancing Flexibility in Distribution Networks and Charging Stations through Coordinated Optimization with EV Cluster Integration, IET Conference Proceedings. (2025) 2024, no. 33, 1127–1133, https://doi.org/10.1049/icp.2025.0681.
10.1049/icp.2025.0681
Google Scholar
15 Raju B. A., Mohan Reddy P. K., and Vuddanti S., Decentralized Coordination of Electric Vehicle Charging in Microgrids Using Game Theory, 2024 IEEE 3rd International Conference on Electrical Power and Energy Systems (ICEPES), July 2024, 1–5, https://doi.org/10.1109/ICEPES60647.2024.10653600.
10.1109/ICEPES60647.2024.10653600
Google Scholar
16 Zhao S., Zhou J., and Li Z., EV Charging Demand Analysis Based on Trip Chain Theory Electric Power Automation Equipment, 2017, https://doi.org/10.16081/j.issn.1006-6047.2017.08.014, 2-s2.0-85028704762.
10.16081/j.issn.1006-6047.2017.08.014
Google Scholar
17 Meng C., Huang Y., and Cong D., Optimal Scheduling Strategy for Electric Vehicles Considering User Defaults, 2024 IEEE 7th Information Technology, Networking, Electronic and Automation Control Conference, May 2024, 1395–1399, https://doi.org/10.1109/ITNEC60942.2024.10733066.
10.1109/ITNEC60942.2024.10733066
Google Scholar
18 Lu X., Liu N., Chen Q., and Zhang J., Multi-objective Optimal Scheduling of a DC Micro-grid Consisted of PV System and EV Charging Station, 2014 IEEE Innovative Smart Grid Technologies-Asia (ISGT ASIA), October 2014, 487–491, https://doi.org/10.1109/ISGT-Asia.2014.6873840, 2-s2.0-84906699810.
10.1109/ISGT-Asia.2014.6873840
Google Scholar

All articles

Multi-Microgrid Optimization With Electric Vehicle Mobile Energy Storage Considering Travel Characteristics

Abstract

1. Introduction

2. MES Capacity Domain of EV Based on Travel Chains

2.1. User Travel Chains

2.2. Time-Invariant Probability Distribution

2.2.1. The First Driving Start and Duration Moment

2.2.2. Duration of Stationing

2.3. Probability Distribution of Miles Traveled

2.4. Space Transfer Probability

2.5. MES Capacity Domain Constraints of EVs

2.6. MES Capacity Domain Determination

3. Economic Dispatch Models for Microgrids

3.1. Structural Models

3.1.1. Photovoltaic (PV) Power Generation

3.1.2. Wind Power

3.1.3. Storage Battery

3.1.4. EVs

3.2. Economic Dispatch Model

3.2.1. Objective Function

3.2.2. Condition

3.2.2.1. Microgrid Power Balance Constraints

3.2.2.2. Micro-Gas Turbine Constraints

3.2.2.3. Energy Storage Battery Constraints

3.2.2.4. EV Constraints [18]

4. Calculus Analysis

4.1. Microgrid Data and Parameters

4.1.1. Wind Energy Output Curve

4.1.2. PV Output Curve

4.1.3. Load Curves

4.1.4. Price and Operating Parameters

4.2. Analysis of Simulation Results

4.2.1. Results of the Proposed Model

4.2.2. Comparative Results and Analysis

5. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information