Machine Learning-Driven Band Gap Prediction/Classification and Feature Importance Analysis of Inorganic Perovskites
Abstract
Perovskites are a class of materials, known for their diverse structural, electronic, and optical properties. Band gap in perovskites is crucial in determining their suitability for applications such as solar cells, light-emitting diodes, and photodetectors. By tuning the band gap through composition and structural modifications, perovskites can be optimized for specific optoelectronic and energy-related applications, making them a versatile material in modern technology. Machine learning (ML) provides an efficient approach to predicting material band gaps by analyzing atomic and structural features, facilitating the discovery of materials with tailored electronic properties. This study employs adaptive boosting regression (ABR), random forest regression (RFR), and gradient boosting regression (GBR) for band gap prediction, alongside support vector machine (SVM), random forest classifier (RFC), and multilayer perceptron (MLP) for classifying compounds with zero and nonzero band gaps. Regression models are assessed using mean absolute error (MAE), mean squared error (MSE), and R2, while classification performance is evaluated based on accuracy, precision, recall, and F1-score. ABR excels in predicting band gaps of inorganic perovskites, while RFC is the most effective model for classification. Feature analysis identifies the standard deviation of valence charges as the key predictor. This study underscores ML’s potential to accelerate perovskite discovery through accurate band gap predictions.
1. Introduction
The study of perovskites is not a new subject, as research on these materials dates back to 1839 when the calcium titanate (CaTiO3) mineral was discovered [1, 2]. The mineral was discovered in the Ural. Named for Russian mineralogist Lev Perovski, Mountains of Russia was written by Gustav Rose [3]. Perovskite’s exceptional qualities and wide range of uses in innovative technology make it significant. The attractive electrical and magnetic properties of perovskites with the ABX3 structure have made them usable in fields including solar cells [4–6], photodetectors [7–9], high-temperature superconductivity [10–12], ferroelectricity [13–15], artificial synapses devices [16–18], and so on.
Ceramics (processed inorganic materials) are among the most widely produced materials by humankind. However, there are still a few specific ceramic phases that, due to their benefits in terms of weight, volume, and especially their technological significance, maintain their dominance over human-made products [19]. Examination of lists of ternary crystal structures highlights the significance of 12 key structures in the world of ceramics [20]. One of the most important of these mentioned structures is the ABX3 structure, or perovskites, which, with chemical modifications, can offer a diverse set of phases with highly varied functionalities.
The general formula of perovskites is ABX3, where the A cation (usually much larger than the B cation) is 12-fold coordinated with the X anions. The B cations are also 6-fold coordinated with the X anions. In this structure, the A cation consists of alkali metals, alkaline earth metals, or rare earth elements, while the B cation is typically a transition metal. The X anions are often elements. The anion X elements consist of Cl, Br, O, I, and F elements [21].
The ionic radii RA, RB, and RX represent the radii of the A, B, and X ions, respectively. When the tolerance factor (t) equals 1, perovskite compounds exhibit an optimal cubic close-packed structure. Deviations from t = 1 introduce geometric strain and crystal distortions. As t diverges further from unity, the crystal transitions to lower-symmetry structures. By calculating t the crystalline structure can be predicted, and its geometric strain and stability can be assessed. A cubic structure is expected for perovskites when the tolerance factor is close to 1. For t < 0.96, the structure is typically orthorhombic, while 0.96 < t < 1 corresponds to a rhombohedral structure. Larger deviations, where t > 1, lead to hexagonal structures. On a qualitative level, perovskite formation is impeded if the A-site cation is excessively large (t > 1). Similarly, if t < 0.8, the A-site cation is too small, potentially resulting in alternative structures [24–26].
Actually, we are speaking about a number of different perovskite branches, each with distinct properties of its own, when we discuss inorganic perovskites. Apart from oxygen (O) occupying the X site exclusively, oxide perovskites have the same overall structure as inorganic perovskites. Although double and layered perovskites are subclasses of inorganic perovskites, halide perovskites have Cl, Br, and I positioned in the X site [27–30].
Band gap is essential to understanding how various materials react to light and electricity in the material science. The magnitude of the band gap determines a material’s electrical conductivity, light absorption capacity, and ultimate categorization as an insulator, conductor, or semiconductor [31]. Perovskites have the potential to be classified as semiconductors, making them suitable materials for use in photovoltaic (solar cells). In recent times, their exceptional qualities and potential applications in various technologies have made them extremely favorable [32–35]. Both computational and experimental techniques can be used to calculate electronic parameters like the band gap. Despite generally offering increased reliability, experimental procedures have drawbacks [36–38]. Density functional theory (DFT), a popular computational technique used in condensed matter physics for many computations, including band gap estimation, is one of the well-known computational techniques [39–42]. Although the generalized gradient approximation (GGA) and the local density approximation (LDA), two popular techniques for estimating the ground state electronic features of materials, are based on uniform and non-uniform electron density distributions, respectively, they are unable to produce accurate results for excited state DFT calculations [43–45]. On the other hand, hybrid approaches seek to include aspects of first principles approaches, such as Hartree-Fock techniques, with improved DFT mathematics and computer codes. According to Many-Body Perturbation Theory, the GW approach is reliable and accurate when used, especially when analyzing the electrical and optical properties [46, 47]. In DFT computations, the hybrid functional, or HSE06, is employed. The GGA is combined with a component of precise exchange from Hartree–Fock theory to increase the precision of electronic structure calculations, especially for band gap predictions in semiconductors and insulators [48, 49].
Moreover, machine learning (ML) is a computational technique to predict the electronic characteristics of materials. ML techniques offer a powerful means to accelerate the discovery of materials while significantly reducing computational costs, all without compromising accuracy compared to traditional first-principles methods. The seamless integration of big data, artificial intelligence, and materials modeling has ushered in a transformative era in materials design [50–53]. These include the ML approaches that have been described by the statistical learning community, which are currently steering research in the direction of a brand-new data-driven science paradigm. Additionally, ML has demonstrated remarkable efficacy in forecasting the band gap of various perovskites [54–58]. Extracting certain features through experimental studies or DFT calculations can be both costly and time intensive. However, features for ML can be effectively generated by means of the properties of the constituent elements of a compound. Feature engineering, encompassing both feature construction and feature selection, plays a key role in the ML workflow. In many ML processes, the model’s maximum performance is largely influenced by the validity of the features, the sample size, and the quality of feature dimensionality within the dataset [59, 60]. The potential of undiscovered perovskite materials for solar energy applications is investigated by Keisuke Takahashi et al. [61] To find materials with promising photovoltaic qualities, the research combines data science and first-principle computations. The work analyzes a dataset of 15,000 perovskite compounds using ML, more precisely a random forest (RF) model, to predict their band gaps—a crucial component for solar energy absorption. The band gap is mostly influenced by 18 physical characteristics, according to the model. Following training, the algorithm predicted 9328 candidate materials with possible uses in solar cell applications. Among these, first-principles calculations were used to analyze a subset of materials further based on lithium (Li) and sodium (Na). Of them, it was discovered that 11 novel materials had the proper band gaps and formation energy for efficient photovoltaic application [61]. ABO3-Perovskites’ band gap predictions can be significantly enhanced by integrating structural information (such as bond-valence vector sums) and formation energy in a progressive learning model, as shown by Li et al. [62] work. The structural diversity of perovskites presents a difficulty that their method effectively overcomes, offering a strong foundation for material discovery in industries such as photovoltaics. Increased precision in predictions was achieved by the model’s effective mapping of the link between structural properties and band gap values [62]. Huang et al. have selected 8 elemental features for wurtzite nitride semiconductors: covalent radius, melting point, valence, atomic weight, atomic number, periodic number, and first ionization energy. The models were trained and evaluated using a feature space derived from the 58-dimensional space, representing all possible combinations of the 8 elemental characteristics. From a physically naturally inclined perspective, covalent radius, and valence have been demonstrated to be the element’s most significant electronic qualities. These characteristics are believed to be the most applicable and effective descriptors for electronic band gap and alignment predictions [63]. Shun Feng et al. explore the prediction of organic–inorganic hybrid perovskites’ band gaps using ML approaches, which are essential for their optical characteristics and utilization in optoelectronic devices. A dataset of 1208 entries and 30 feature descriptors pertaining to the A, B, and X components of perovskites was assembled by the study. Four algorithms were used to create prediction models: XGBoost, RF, LightGBM, and Gradient Boosting Regression (GBR). With a mean absolute error (MAE) of 0.0901, mean squared error (MSE) of 0.0173, and an R2 value of 0.9913, the XGBoost model outperformed the others, demonstrating remarkable accuracy in band gap prediction. The predictions made by the XGBoost model were interpreted using the SHAP (SHapley Additive exPlanations) approach. The results showed that the band gap is strongly influenced by the, A-site ion’s occupancy rate, which has a negative correlation with the expected values [64].
The association between the elemental features of component ions and the band gap of ABX3 perovskites has been described by Vladislav Gladkikh et al. [65] using ML algorithms. The nonlinear mappings between the predictors and band gap were discovered through data analysis using atomic cluster expansion (ACE), a small-scale, semi-parametric ML technique. This approach avoids the curse of dimensionality, does not assume anything about the functional form of the descriptors beforehand, and does not require a lot of processing power. The atomic radii, ionization energies, and electron affinities of the constituent elements are shown to predominantly influence the band gap. This relationship is nonlinear with respect to these descriptors. Further research is required to unravel the molecular mechanisms underlying this dependence [65]. Zhang et al. [66] utilized a set of 20 physical attributes to model and predict the band gaps of double perovskite materials. Their findings revealed that properties such as bulk modulus, superconducting transition temperature, and cation electronegativity play the most significant roles, reflecting their strong connection to the material’s electronic structure [66]. Zhuo et al. [67] have employed 5 distinct ML models, each with features derived only from the elemental characteristics of the constituent elements, to predict the band gap of inorganic solids. These attributes comprise, among other things, the atom’s physical properties, electrical structure, and relative position on the periodic table [67]. The utilization of ML approaches to the prediction of ABX3 perovskites’ electronic band gaps is investigated by Obada et al. [68] In order to create predictive models and give interpretability—a critical component of material science—the study makes use of explainable AI (XAI) tools. This helps researchers better understand the fundamental causes of band gap features. The authors employed a range of ML models, such as SVM and decision trees, and utilized techniques such as SHAP to elucidate the findings and determine the significance of features such as atomic number, valence electrons ionic radius, first ionization energy, and so forth. This explainability trait helps researchers better understand the connections between the band gaps and structural and chemical characteristics of perovskites, which will inform future efforts in material design [68]. Yang et al. [69] aim to expedite the search for stable hybrid perovskites with ideal band gaps for solar cells and optoelectronic applications, while also being free of lead and harmful to the environment. To anticipate band gaps, the authors used ML models such as neural networks (NN) and RF. The predictions were interpreted in terms of how different elemental properties, such as atomic radii and ionization energy, influence them using Explainable AI (XAI) techniques such as SHAP. The model determined important parameters that affect the band gap, including the organic cation in the structure and the halide (X-site) selection. It effectively forecasted novel perovskite materials with the intended band gaps, proving the usefulness of interpretable ML in directing research endeavors [69]. In order to maximize the material’s efficiency for electronic applications, Eti Mahal et al. want to utilize ML to forecast the kind of band adjustment (type-I, type-II, or type-III) in 2D hybrid perovskites. A dataset of well-known 2D perovskite materials including details on band adjustment was assembled by the authors. Predictive models were trained using a variety of ML algorithms, such as SVM and RF, based on the structural and electrical characteristics of the perovskites. Electronic properties, lattice parameters, and elemental qualities were important factors impacting the band alignment prediction. This research demonstrates that properties like band gap levels and variations in component electronegativity have a significant impact on the alignment predictions, according to feature importance analysis [70].
In this study, our data are derived from the paper by Chenebuah and Chenebuah [71] who extracted 16,323 data points from the Open Quantum Materials Database (OQMD). By compiling tens of thousands, or even hundreds of thousands, of DFT simulations into extensive databases, high-throughput DFT (HT-DFT) is rapidly becoming a powerful tool for accelerating materials design and discovery. Due to the extensive variety of structures and chemistries present in these databases, complex material challenges can be addressed in a much more thorough and efficient manner. The OQMD has over a million DFT-calculated crystal structures [71, 72]. Our aim is to classify inorganic perovskites into two categories with zero and nonzero band gaps (Eg) and then to predict the band gap of these materials using ML. For this purpose, in band gap prediction, we used 14 different ML models and for classification we used 7 different ML models with various test-to-train ratios (5/95, 10/90, 15/85, 20/80, 25/75, 30/70) and applied Grid Search Cross-Validation (GridSearchCV) for all models. Among them, three models—MLP, SVM, and RFC—proved to be the best for classification, while three models—ABR, RFR, and GBR—were the best machines for predicting the band gap. For the classification and regression of band gaps, we selected 41 features. Our approach uses less computationally costly features than Tetteh Chenebuah et al.’s work, and the results we get are better than what they have presented.
In the classification, The RFC model outperformed SVM and MLP, achieving a best cross-validation score exceeding 90% and highlighting the most effective values for F1-score among the models. In the band gap prediction, the ABR model outperformed RFR, and GBR for attaining a prediction accuracy above 88% and presenting the best results for mean absolute error (MAE) and mean squared error (MSE) among the models. This work is in line with our previous study on the feature importance of low-symmetry perovskites [73], once again highlighting the importance of valence (std) and valence (mean), and their impact on band gap prediction.
2. Data and Features
The OQMD provided the dataset, which was extracted and included 16,323 strong samples of ABX3 inorganic perovskite structures [71, 72]. 11,316 (or about 80%) of the 16,323 potential data points have a zero-band gap, whereas 5,007 (or about 20%) have a non-zero band gap. The common chemical formula for inorganic perovskites is ABX3, where A is usually a large cation, B is a smaller metal cation, and X is an anion, frequently a halide (Te, I, H, N, Se, Br, S, F, Cl, and O). Except for space group, crystal structure, and formation energy, every attribute of perovskite is determined by the features of its constituent atoms. There are no specific perovskite features that need to be measured. Each significant atomic property, like mass, covalent radius,and valence, has its mean and standard deviation (std) determined; these values are reported as features. Every compound is guaranteed to have an equal number of characteristics by computing all elemental data’s mean and standard deviation. Our goal in this study was to employ the fewest possible computational features. By computing the mean and standard deviation of the elements that make up the perovskite, we can determine our elemental features. These data, however, show perovskites with the same formula but distinct space groups, crystal structures, or formation energy. Therefore, the machine will not be able to discriminate between perovskites with the same formula if we do not add these three computational features to the overall set of features with which the machine learns. We must therefore make use of these three computational features. For this study, two main aims have been established. First, we want to classify inorganic perovskites into two groups: those with zero and nonzero band gaps, utilizing novel features and several ML algorithms. After that, we will forecast the band gap using all of the data.
3. ML Models
4. Criteria
4.1. Band Gap Prediction Criteria
In equations (3) –(5), represents the actual band gap value randomly selected from the test set. is the average value of , is the predicted value of the corresponding regression model, and i = 1, 2, …, N, where N = number of inorganic perovskites.
4.2. Classification Criteria
We will validate the classification results by using four additional metrics, accuracy, precision, recall, and F1-score. These four criteria in classification are essential.
Obviously, a high precision means that when the model predicts a positive class, it is likely correct.
A high recall means that the model is effective in identifying positive instances.
When the distribution of classes is unbalanced (one class is more frequent than the other), the F1-score is very helpful. In many situations, an F1-score is a more revealing metric than accuracy since it shows that both precision and recall are rather good [80, 81].
5. Results
Our data were gathered entirely from publications [71] that are also extracted from OQMD, which includes the dataset of 16,323 inorganic perovskites. Feature selection is an important phase in ML models. ML model performance can also be improved by using a sufficient dataset. Three computational and 38 elemental datasets were initially chosen for this study. Selected properties taken from OQMD and the periodic table are included in Table 1 [72, 82]. For all features except the space group, crystal structure, and formation energy, the mean and standard deviation (std) taken into account. Thus, 41 features ought to be made available. RFC, SVM, and MLP are 3 ML models for classification. Three models—ABR, RFR, and GBR—were to predict the band gap. The range of hyperparameters tested and the best hyperparameters in band gap classification (C) and prediction (P) are found using the Grid-Search tool, as indicated in Table 2.
| Features | Unit |
|---|---|
| Space group | — |
| Crystal structure | — |
| Formation energy | eV/atom |
| Atomic mass | amu |
| Boiling point | K |
| Density | g/L |
| Static average electric dipole polarizability | Ȧ3 |
| Period | — |
| Electron affinity | KJ/mol |
| Villars modified mendeleev number | — |
| Group | — |
| Pettifor mendeleev number | — |
| Atomic radius | Ȧ |
| First ionization energy | KJ/mol |
| Specific heat capacity | J/Kg°C |
| Atomic number | — |
| Heat of fusion | J/g |
| Heat of vaporization | KJ/mol |
| Thermal conductivity | W/m.k |
| Molar volume | Cc |
| Valence | — |
| Covalent radius | Ȧ |
- Note: All values, except the first three, have their means and standard deviations computed.
| Models | Range of hyperparameters tested | Best hyperparameters |
|---|---|---|
| SVM (C) |
|
|
| RFC (C) |
|
|
| MLP (C) |
|
|
| ABR (P) |
|
|
| RFR (P) |
|
|
| GBR (P) |
|
|
5.1. Band Gap Prediction
The 41-dimensional feature is used to compare the performances of the 3 ML models for the predicted band gap of inorganic perovskites and obtained results shown in Table 3. One of the objectives was to identify the optimal test/train ratio for each of the three models—ABR, RFR, and GBR. The RFR and GBR models were shown to perform best with a test/train ratio of 15/85, whereas the ABR model performed best with a ratio of 10/90. With a value of 0.19 eV MAE, 0.18 eV MSE, and 88% R2 on the test set, we found that the ABR model produced the best results when compared to the other two models, regardless of whether R2, MSE, or MAE were used as the assessment criteria. The best-performing ML model (LGB) –MAE ~ 0.21 and R2 ~ 87%—in the study by Chenebuah and Chenebuah [71], from which we obtained the data, yielded results in our study that were approximately equal to the ML model (GBR)— MAE ~ 0.22 and R2 ~ 87%—as the worst outcomes in our study. The 41-dimensional feature set is used in Figure 1 to compare the performance of the 3 ML models in predicting the band gap of ABX3 perovskites. The data in both researches are identical, and comparing with other studies in the field of inorganic perovskites necessitates at least the same dataset, hence this comparison is completely valid. Therefore, it might not be acceptable to compare our findings with others that might have different data. However, the ML models that were employed and the features that the machine was trained with are the two reasons that contributed to the improvement in our outcomes in this comparison. One of the advantages of our work is that we tried to use as few computational features as feasible during this process. The machine learns more efficiently and can distinguish between different things better when it uses more computational features. In this study, we made progress toward our objective of lowering computing costs through the use of ML, while still attaining marginally improved outcomes.
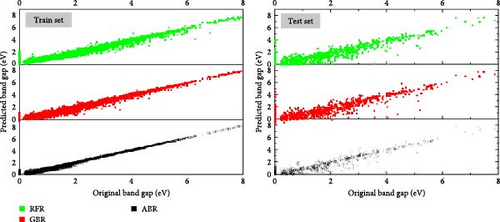
| Band gap prediction model | R2 train % | R2 test % | MSE (eV) | MAE (eV) | Test/train (%) | Cross validation R2 (%) | |
|---|---|---|---|---|---|---|---|
| CV = 5 | CV = 10 | ||||||
| ABR | 99 | 88 | 0.18 | 0.18 | 10/90 | 86 | 85 |
| RFR | 98 | 88 | 0.19 | 0.21 | 15/85 | 86 | 85 |
| GBR | 98 | 87 | 0.19 | 0.22 | 15/85 | 85 | 84 |
The cross-validation (CV) R2 scores are slightly lower than the test scores, which is expected. However, if CV = 10 has lower R2 than CV = 5, this might indicate variance sensitivity. We are responsible for investigating the extent of the difference in reported errors between CV = 5 and CV = 10. Therefore, Table 4 reports the MSE and MAE criteria for both CV = 5 and CV = 10. As shown in Table 4, the approximate difference between these two cases is around 0.02–0.03 eV, which, as expected, was predictable given the observed differences in R2. This result does not indicate any unexpected deviation.
| Band gap prediction model | MSE (eV) CV = 5 |
MAE (eV) CV = 5 |
MSE (eV) CV = 10 |
MAE (eV) CV = 10 |
Test/train % |
|---|---|---|---|---|---|
| ABR | 0.18 | 0.18 | 0.20 | 0.22 | 10/90 |
| RFR | 0.19 | 0.21 | 0.22 | 0.23 | 15/85 |
| GBR | 0.19 | 0.22 | 0.22 | 0.24 | 15/85 |
5.2. Classification
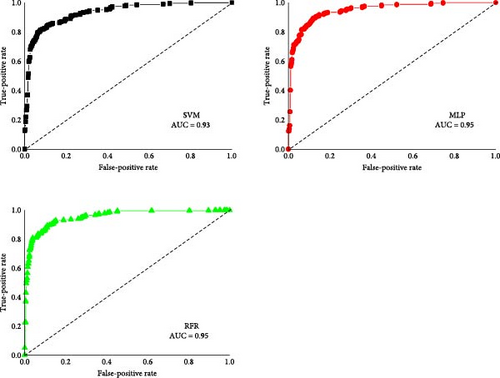
To classify inorganic perovskites based on the previously used dataset and selected features, 3 ML models are employed: RFC, SVM, and MLP. The optimal test/train ratio for all three models was determined to be 5/95, which is acceptable given the substantial size of the dataset. Since our dataset is imbalanced, we tried to address this issue by using CV = 5 and CV = 10. During model evaluation, cross-validation with CV = 5 and CV = 10 was performed to reduce the variance caused by random sampling and to ensure consistent generalization. We used four metrics—accuracy, precision (Pre), recall (Rec), and F1-score (F1)—to validate our models. The accuracy of all models is 90%, and despite 80% of the data having a zero-band gap, they have provided satisfactory results. The last four metrics and confusion matrix are shown in Table 5, and receiver operating characteristic (ROC) is plotted in Figure 2 for each of the learning machines. The confusion matrix is essentially a 2 × 2 matrix that simply displays the efficiency of the model. In the main diagonal of this matrix, the correctly predicted zero and nonzero band gaps are placed, while the off-diagonal elements represent the incorrectly predicted values. The first column shows the correct and incorrect predictions for the zero-band gap, and the second column similarly shows the correct predictions for the nonzero band gap. A graphical depiction called an ROC curve is used to evaluate the performance of a binary classification model. At various threshold values, it displays the interchange between the truepositive rate (TPR) and the false-positive rate (FPR). The percentage of true positives that the model correctly detects is called the TPR, sometimes referred to as recall or sensitivity. The percentage of true negatives that the model incorrectly classifies as positive is known as the FPR. With a TPR of 1 and an FPR of 0, a perfect classifier would have a curve that passes through the ideal point, which is the upper-left corner of the plot. The model’s ability to differentiate between positive and negative classes increases with the ROC curve’s proximity to the upper-left corner. Area under the ROC curve (AUC) is commonly regarded as a measure of the model’s performance. If AUC = 1, we have a perfect classifier and AUC = 0.5 indicates such a random classifier (equivalent to flipping a coin). For AUC < 0.5, the model performs worse than random guessing. The closer the AUC value gets to one, the better the machine we have chosen for the classification [83, 84]. AUC value obtained for two machines, MLP and RFC, is 0.95, and for the SVM learning machine of the value of 0.93 is achieved, which also indicates good results.
| Band gap | MLP | RFC | SVM | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pre | Rec | F1 | Pre | Rec | F1 | Pre | Rec | F1 | ||
| Zero | 0.93 | 0.94 | 0.93 | 0.92 | 0.96 | 0.94 | 0.91 | 0.95 | 0.93 | |
| Non-zero | 0.86 | 0.82 | 0.84 | 0.90 | 0.82 | 0.86 | 0.88 | 0.81 | 0.84 | |
| Accuracy | 0.90 | 0.91 | 0.90 | |||||||
| Accuracy (CV = 5) | 0.89 | 0.90 | 0.89 | |||||||
| Accuracy (CV = 10) | 0.86 | 0.88 | 0.86 | |||||||
| Confusion matrix | ||||||||||
6. Feature Importance
Several feature-ranking approaches, such as Permutation Importance (PI) [74, 85] and Local Interpretable Model-Agnosti Explanations (LIME) [86], are used to evaluate the significance of the features. LIME uses a more straightforward, interpretable model, like linear regression, to locally approximate the complicated model surrounding a given data point in order to clarify the reasons behind a data point’s specific prediction. By looking at the LIME explanations for various data points and predictions, you can have a better understanding of how the model is performing with the existing hyperparameters. We now need to change the hyperparameter if the explanations are unclear or align with our understanding of the data [87]. By rearranging the values of a single feature in the data, PI dissociates the feature from the target variable. The drop in model performance after shuffling indicates the feature’s importance. Features are ranked by PI according to their impact on model performance. Features that consistently result in significant performance decline upon shuffling are likely to be more influential. Conversely, features that exhibit minimal or no impact on performance after rearrangement may be considered redundant or noninformative. These could be suitable candidates to be removed, which would lead to a more limited selection of characteristics for further examination [88]. While our prior work leveraged [73] SHAP for feature ranking, this approach was not feasible for the present work. The previous work was conducted on two datasets consisting of 1493 double perovskites and 491 layered perovskites, respectively. However, in this work, a dataset with 16,323 data points was utilized. While SHAP values are a powerful tool for feature importance, their computational cost was prohibitive for this study and for this scale of data. Therefore, we employed PI and LIME to analyze feature importance and model behavior. Our goal in this work is to utilize the fastest, most cost-effective, and most accurate tool for investigating the band gap and ranking features. These two models are used to identify the top 10 most important input features for band gap and classification. The total number of potential cases for identifying the top 10 is 12. This is because we have two different targets (band gap prediction and classification) × one dataset (inorganic perovskite) × three different ML models and × two methods for finding the top 10 features. The ranking method involves initially examining the frequency with which a feature appears in the top 10. However, this alone is not a sufficient criterion for decision-making. Next, we assess the ranking of the feature (position from 1 to 10). Therefore, in interpreting the importance of this ranking, both the number of times the feature appears in the top 10 and its final ranking score are important. Thus, to find the average score, we need to calculate the total score/number of appearances. Evaluating the feature importance data clearly shows that the “Formation energy” plays a critical role in predicting band gaps and classification. Its significant presence in 9 of the 12 possible cases underscores its high impact across various scenarios. Its importance is further emphasized by its average score of 1, as lower values indicate higher relevance (a score of “1” signifies the highest importance, while “10” denotes the least importance). Since other features do not exhibit a clear order of importance like “Formation energy,” it is challenging to draw a precise conclusion about the determining role of those features. As illustrated in Figure 3, the next four most important features include “Space group,” appearing 8 times with an average score of 2, “Valence (std)” appearing 6 times with an average score of 4, “Valence (mean)” appearing 6 times with an average score of 3.6, and “Crystal structure” appearing 7 times with an average score of 4.5. As mentioned in this study, due to the repetition of perovskite formulas, we are unable to rely solely on elemental features in these calculations. When calculating the mean and standard deviation of features, if the formulas are the same, our features will also be identical. To enhance the model’s ability to differentiate between perovskites with the same formula, we incorporated computational features such as formation energy, space group, and crystal structure into our feature set wherever possible. However, the important point in this study is that, as expected, formation energy, space group, and crystal structure should have had the greatest impact on the calculations. It is noticeable that two features, Valence (std) and Valence (mean), not only showed results very close to the Space group but also performed even better than the Crystal structure.
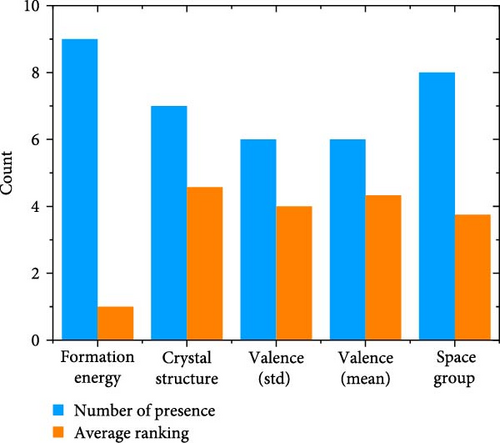
This work, like our previous study [73], once again confirmed that the Valence (std) and Valence (mean) have the greatest impact on band gap prediction and the classification of zero band gaps from nonzero ones. Such repeated evidence of the importance of Valence (std) and Valence (mean) could be an intriguing subject for future studies on their effect on band gaps.
Naturally, the relationship between elemental features and the band gap is by no means straightforward, and we expect the presence of complex correlations. Aside from the significant importance of computational features, the elemental features have had a relatively important impact on the predictions. However, the noteworthy point is that ML, without any knowledge of the features and only receiving a few numerical values, was able to predict this issue effectively. This was achieved by providing only the average and standard deviation of the constituent elements’ features in inorganic perovskites. This certainly deserves more attention in future research.
7. Conclusion
This study demonstrates that ABR outperforms RFR and GBR in predicting band gaps of inorganic perovskites, while RFC surpasses SVM and MLP in classifying zero and nonzero band gaps. By utilizing 38 generalized input features, supplemented with computationally derived descriptors, the models effectively capture critical relationships. Feature analysis using LIME and PI identifies the standard deviation of atomic valence as a key predictor, revealing its strong correlation with band gaps. These findings underscore the potential of ML to enhance the design and optimization of perovskite materials for advanced solar cell applications.
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
Alireza Sabagh Moeini: Data curation, formal analysis, investigation, methodology, software, validation, and writing–original draft. Fatemeh Shariatmadar Tehrani: Conceptualization, funding acquisition, project administration, supervision, visualization, and writing–review and editing. Alireza Naeimi-Sadigh: Conceptualization, methodology, supervision, validation, and writing–review and editing.
Funding
The research has not received any fund or grant.
Open Research
Data Availability Statement
The data supporting this article are available upon request by contact to the corresponding author.




