Aggregated Demand Flexibility Prediction of Residential Thermostatically Controlled Loads and Participation in Electricity Balance Markets
Abstract
The aggregate demand flexibility of a set of residential thermostatically controlled loads (TCLs) can be represented by a virtual battery (VB) in order to manage their participation in the electricity markets. For this purpose, it is necessary to know in advance and with a high level of reliability the maximum power that can be supplied by the aggregation of TCLs. A probability function of the power that can be supplied by a VB is introduced in this paper. This probability function is used to predict the demand flexibility using a rigorous experimental probabilistic method based on a combination of Monte Carlo simulation and extremum search by bisection (MC&ESB) algorithm. As a result, the maximum flexibility power that a VB can provide is obtained. MC&ESB performs the demand flexibility prediction with a given confidence level and taking into account TCLs and users’ real-time constraints, which is a novel contribution. The performance and validity of the proposed method are demonstrated and discussed in three different case studies where a VB bids its aggregate power in the Spanish electricity balancing markets (SEBMs).
1. Introduction
Electricity systems are undergoing a huge transformation due to the need to switch from fossil energy sources to variable renewable energy sources (RESs). At the same time, increasing energy prices are challenging the current structure of electricity markets. The need to adapt the demand curve to mitigate price peaks requires managing demand flexibility. To achieve the desired transformation of the energy system, net metering and self-consumption must be encouraged, and regulation is beginning to change accordingly [1, 2]. At the same time, demand is allowed to participate in new power markets and others traditionally reserved for generation [3, 4].
In the residential sector, heating and cooling account for a large percentage of energy demand [5, 6]. Most of the appliances used for these purposes have a thermal inertia providing flexibility, that is, their electricity demand can be shifted over time without loss of utility. This is the case for thermostatically controlled loads (TCLs), such as refrigerators, electric water heaters, and heat pumps. The aggregation of demand flexibility provided by many TCLs exhibits properties that resemble those of batteries, hence, this aggregation is referred to as a virtual battery (VB). They have been extensively studied [7–9].
VBs can be used to provide ancillary services [10] and to participate in appropriate electricity markets [11]. This requires accurate aggregate demand flexibility forecasting mechanisms. Several approaches have been proposed to forecast demand flexibility. In [12], an evolutionary particle swarm optimization combined with support vector data description is used to find feasible trajectories for residential loads. In [13], a combinatorial optimization is proposed for flexibility prediction using nonintrusive load monitoring in the residential sector. Artificial neural networks are the main method employed in [14–16]. In [17], a genetic-based heuristic is used to predict energy demand and flexibility from data centers for participation in demand response programs. A method utilizing a radial basis function neural network to predict flexibility is proposed in [18]. In [19], a temporal convolution network was applied to predict the flexibility of electric vehicle and domestic hot water systems. Furthermore, the use of regression models based on machine learning is discussed in [20]. Finally, a comprehensive review of flexibility prediction methodologies is given in [21, 22].
Most of the approaches found in the literature do not take into account the actual state of the loads when predicting the flexibility they can provide as a whole, which can lead to inaccurate predictions. In addition, physical and user-imposed constraints must also be taken into account to improve the accuracy of predictions.
The primary contribution of this work is the development of a novel probabilistic method that combines Monte Carlo simulation and extremum search by bisection (MC&ESB) method to accurately predict the flexibility potential of a TCL aggregation modeled as a VB. The cornerstone of this method is Theorem 1, which provides a framework to estimate the probability of successfully delivering a given constant power demand response with a specified confidence level. This contribution addresses a critical gap with respect to other demand flexibility prediction methods by providing a reliable measure of probabilistic confidence. Moreover, it is compatible with load controllers that do take into account user constraints and the real-time status of flexible loads. These are the characteristics of the method for controlling VBs and the variability of their behavior that is also studied in this work. To validate the effectiveness of the proposed methods, the Spanish electricity balancing markets (SEBMs) are used as a test bed, demonstrating the potential for demand flexibility aggregators to leverage the MC&ESB for making competitive market offers.
To enable precise flexibility prediction, the work introduces a flexibility function that quantifies the probability of a VB meeting a specified power demand over a time period. This function is estimated and optimized through MC&ESB. A key innovation of the approach is determining the minimum number of Monte Carlo trials required to achieve a probabilistic guarantee for the power that can be delivered.
The paper is organized as follows: Section 2 explains the materials an methods, specifically the TCLs and VBs models and their management and control methodology. Besides, the electrical markets and the necessary requirements for demand participation are also explained. Additionally in this section, the flexibility prediction is characterized by introducing a probability function of the supply power of a VB. The probability of successfully supplying a given constant power during a demand response event with a measure of confidence is obtained by applying the key result stated by Theorem 1. Based on this theoretical result, the MC&ESB method is developed, which can be easily applied by aggregators and energy service providers based on demand response to make energy bids in the electricity market with high confidence in their supply. In Section 3, three case studies are discussed: the first one estimates the likelihood function of a sample VB, the second one tests the MC&ESB method in three different scenarios in which VBs could participate in SEBM, and the third one evaluates the response of the VB controller to a requested power signal based on the SEBM results. Finally, Section 4 concludes the paper.
2. Materials and Methods
The aggregate flexibility of a set of TCLs can be represented by a VB. The management of the VB is enabled by the existence of a demand flexibility control system that manages the operation of each of the TCLs in the aggregation. In this work, the models and controller reported in [9] are used due to the accuracy with which they are able to satisfy the power requirements of the system operator by measuring the current state of the appliances in real time. But, as explained below, some improvements have been implemented in the control system that allow better demand prediction and more flexibility in the aggregation response. The monitoring and communication system between TCLs and the controller is done using the architecture proposed in [23].
2.1. The TCL Model
A TCL refers to a device or system that, through a thermostat, automatically adjusts its operation based on temperature changes. The purpose of such a load is to regulate and maintain a desired temperature within a specific range. TCLs are commonly used in heating, ventilation, and air conditioning (HVAC) systems, as well as various appliances and industrial processes, such as refrigerators and chemical reactors.
In the context of electrical systems, aggregations of TCLs can play a significant role in optimizing energy consumption, demand response, and grid stability. They can provide regulation services and mitigate power imbalances resulting from fluctuating distributed renewable generation.
The larger the safety band, the more flexibility the TCL will provide.
The model must also include several constraints that affect TCLs, such as short-cycling prevention and availability. Short-cycling prevention avoids the TCL to change its status too frequently, which could cause damage in the device components. The minimum status changing frequency is specified by τi. In addition, availability prevents the TCL from leaving the safety band and ensures that the TCL does not operate when the ambient temperature is above the safety band in heating appliances or below the safety band in cooling appliances.
2.2. The VB Model
A VB models the aggregated demand flexibility of a set of TCLs at each time instant k. The charging and discharging processes have different dynamics. Consequently, two different variables are introduced in the model for the evolution of energy and power magnitudes. Charging magnitudes are considered positive, while discharging magnitudes are considered negative.
2.3. The Demand Flexibility Control
The demand flexibility control developed for a VB operates in a cyclic process with two basic operations: aggregation of TCLs and priority-based dissagregation, as shown in Figure 1. The controller operates with a time step h. As stated before, this control system is used in this paper because of its precision, checking the status of TCLs in real time.
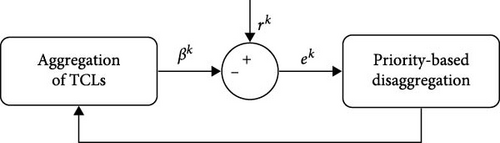
At aggregation of TCLs, all the variables describing the current situation of all TCLs are calculated, preventing their inner temperature from leaving the comfort band. Then, all the information of TCLs is gathered. As a result, a deviation power signal βk is obtained, which is the difference between the power consumed by the VB, its expected base consumption and the amount of power to be switched on or off in the next time instant because of TCLs constraints. Then, βk is compared with the system operator power signal rk, which sets the power requirement. This calculates the regulation power signal ek.
The priority-based dissagregation decides which TCLs must change their status from on to off, or vice versa, in order to cope with the regulation power signal ek. The TCLs chosen first are the available ones that are far in time from being switched on or off due to device constraints.
Additional improvements in the demand flexibility controller of Martín-Crespo, Saludes-Rodil, and Baeyens [9] have been included in this article. First, the absolute error when tracking rk is reduced, as the power difference between switching on or off the last TCL selected in priority-based dissagregation is checked. In addition, the number of changes are examined, and thus, the activations of the short-cycle prevention constraint are reduced. Second, the controller allows to configure periods of time without demand management, which means that only aggregation of TCLs step is executed. This is the case when no rk is required.
2.4. Demand-Side Participation in SEBM
Several European countries have opened their markets to consumers participation, such us United Kingdom, Belgium, Germany, or Sweden [3, 24]. Here, we focus on SEBM, managed by Red Eléctrica de España (REE). In these markets, active power bids can be either upward or downward (from the generation point of view). This is equivalent to a VB discharging, reducing consumption (negative flexibility) or charging, demanding more power (positive flexibility), respectively.
There are currently three SEBM: secondary regulation (SR), tertiary regulation (TR), and replacement reserves (RR) [25].
SR is an optional ancillary service whose purpose is to maintain the balance between generation and demand, correcting the unintentional deviations. Its temporal working horizon ranges from 30 s to 15 min.
TR is an optional ancillary service that, if subscribed to, is accompanied by the obligation to bid and is managed and compensated by market mechanisms. Its objective is to resolve the deviations between generation and consumption and the restitution of the secondary control reserve which has been used.
RR is an optional service managed and remunerated by market mechanisms. The objective is to resolve the deviations between generation and demand which could appear in the period between the end of one intraday market and the beginning of the next intraday market horizon.
All of them focus on maintaining the balance between generation and demand and operate in 15-min periods. The bids submitted to the markets consist mainly of the active power offered, the price, and some possible complex constraints, such as indivisibility. Once the bids are submitted, a matching algorithm is executed. The SEBM comply with the European Commission Regulation [26] and ENTSO-E [27] nomenclature. The main characteristics of the three SEBM are given in Table 1.
| Market name | Secondary regulation (SR) | Tertiary regulation (TR) | Replacement reserves (RR) |
|---|---|---|---|
| ENTSO-E nomenclature | Automatic frequency restoration reserves (aFRR) | Manual frequency restoration reserves (mFRR) | Replacement reserves (RR) |
| European platform | PICASSO | MARI | TERRE |
| Mode of activation | Automatic | Manual | Manual |
| Maximum ramping period | Real-time | 15 min | 30 min |
| Minimum time in advance for submission of bids | 16:00 D-1 | 25 min | 55 min |
All the requirements that demand aggregators need to participate in SEBM are gathered in [29]. According to this, the minimum power bid must be 1 MW.
The method developed in this paper encourages demand-side participation because it provides demand aggregators with a rigourous tool to calculate how much power they could offer in electricity markets.
2.5. The VB Power Supply Probability Function
The control strategy explained previously allows a one-step ahead prediction of the VB parameters, as and are obtained before rk. However, this forecasting horizon is not enough for sophisticated demand flexibility management, including participation in electricity balancing markets, where the demand flexibility must be accurately predicted before the actual provision of the service and for longer prediction horizons. The novel MC&ESB method presented in this paper solves this issue, as the predictions of the method can be calculated several hours in advance.
Predicting the flexibility of VBs requires studying how the temperatures of TCLs are expected to change over time. However, this is not an easy task. The evolution of TCL temperatures is influenced by errors in ambient temperature forecasting, model inaccuracy, and other disturbances related to the operation of the devices (e.g., when a refrigerator is opened). Representing these inaccuracies and perturbations requires the use of random models. The TCLs used in this work encapsulate all of this uncertainty in the perturbation parameter . Usually, is considered to be distributed as a Gaussian random variable of zero expectation and constant variance σ2 [30].
The randomness in the temperature evolution of TCLs is a consequence of random disturbances and uncertainty in the knowledge of the initial conditions. Consequently, the ability of a VB to respond to a given flexibility demand, that is, to satisfy a given power deviation from the reference consumption during a given period of time t, is a random variable characterized by a given probability distribution.
The VB is composed of a set of TCLs. The number of elements in this set, NTCL, is considered large enough to achieve generality and reduce the influence of .
Let x be a real-valued variable representing a candidate deviation power that the VB could provide during a given time period t. In order to characterize the capability of VB to provide a power deviation during certain time period, a power supply probability function Φ(x) is defined.
Let S be a binary random variable representing whether a constant power can be successfully provided by the VB for a certain period of time. The binary random variable takes the value S = 1 if the VB successfully provides the demanded power. Otherwise, S = 0.
In spite of the random nature of the VBs system behavior, we can assume that the probability function Φ(x) is monotonic when the number of TCLs in the VB is large. In other words, the larger the absolute value of the demanded power to a VB for a given duration, the lower the probability of actually supplying it.
2.6. The MC&ESB Method for Estimating a VB Power Supply Probability Function
The monotonicity property of the power supply probability function Φ(x) can be used to estimate the maximum power (positive or negative) that a given VB could supply to an aggregator or other market actor with a probabilistic guarantee measure. This estimate is a prediction of the demand flexibility that can be provided by a TCL aggregate that is modeled as a VB.
To find the maximum flexible demand power that a VB can supply, a new method, named MC&ESB, is designed in this paper. It is based on the combination of Monte Carlo simulation techniques and extremum search using the bisection algorithm.
Monte Carlo simulation is a probabilistic method useful for estimating a value under uncertainty, especially for complex systems [31]. It consists of evaluating a function a large number of times, so it finally converges to the most probable solution (the mean value) despite of the existing uncertainty [32]. The accuracy of the method increases as the number of evaluations of the function increases [33].
We consider that a VB can provide the requested flexibility when the probability of supplying the aggregate power target for a given time period t is equal to 1 with a certain accuracy ε and confidence δ. A VB supplies the power target whenever |rk| is less than or equal to for positive flexibility or for negative flexibility.
Let p be the probability that the VB provides a power target of value x, then, . This probability p is constant but unknown, but can be estimated by performing a sequence of experiments. The confidence measure of the estimate can also be obtained from experiments using Bayesian inference.
Using the above expression, we are interested in obtaining the number of trials to estimate the interval of power range [xmin, xmax] that can be supplied during the demand response event of duration t with a given confidence.
Theorem 1. Let ε and δ be scalars in the open unit interval (0, 1), then,
Proof. If Ξ = N, then, the a posteriori density function of p is given by f(p | Ξ = N) = (N + 1)pN. Then,
The above theorem allows us to estimate the probability of successfully supplying a given constant power during the demand response event with a measure of confidence. Let xmax be the maximum value of x, such that Ξ = N, then, p ≥ 1 − ε with probability greater that 1 − δ if no trial fails for a number of trials satisfying . In a similar way, let xmin be the minimum value of X such that Ξ = N, then, p ≥ 1 − ε with probability greater that 1 − δ if no trial fails for a number of trial satisfying .
In the Monte Carlo simulation stage of the MC&ESB method, the time evolution of the VB is simulated for each candidate value of power x. An estimate of the probability p is given by Equation (11), where N is obtained using Equation (14).
A schematic graphical description of the method is shown in Figure 2. The stage of the extremum search using the bisection algorithm in the MC&ESB method consists of searching for the maximum value of the power x in absolute value that the VB can supply with probability 1. The method starts by defining a search interval, which must be between [0, +∞], when searching for flexibility in charging and between [−∞, 0], when searching for flexibility in discharging. Next, the bisection algorithm computes a first value of x and the estimate of the probability p is computed by Equation (11). The bisection interval bounds a and b are updated at each iteration. The bisection algorithm terminates when |a − b| < γ, with γ being a given tolerance. The solution found x is the maximum flexible demand power that the VB can supply with probability greater than 1 − ε and confidence 1 − δ.
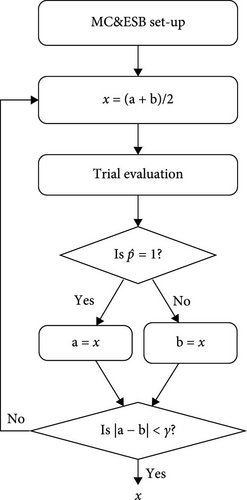
In this paper, the TCL and VB modeling and control, presented in Section 2, has been used as evaluation function for MC&ESB, but any other could be used as long as the effect of TCLs disturbances are considered.
3. Results
This section discusses three case studies. The first case estimates the power supply probability function describing the behavior of a VB composed of a set of TCLs. The second case tests the performance of the MC&ESB method for participating in SEBM in different scenarios. The third case shows how the control of a VB manages the aggregated set of TCLs to supply the power needed to bid in SEBM.
3.1. Case Study 1: Estimation of VB Supply Probability Function
In this case study, the power supply probability function Φ is experimentally estimated along with confidence intervals for a certain VB composed of 3000 TCLs.
The TCLs participating in the VB are 1000 refrigerators, 1000 electric water heaters, and 1000 reversible heat pumps, which are considered as heating pumps in winter and cooling pumps in summer. Their characteristics are shown in Table 2. The location of the VB is Madrid, in Spain, and the season is summer. Thus, the forecast ambient temperature of every device i, , is considered constant and equal to 24°C for refrigerators and electric water heaters, whereas for reversible heat pumps is the temperature of August 10th at 15:00 UTC of the typical meteorological year, obtained with PVGIS [36].
| TCL type | Rth (°C/kW) | Cth (kWh/°C) | P (kW) | η | θs (°C) | Δ (°C) |
|---|---|---|---|---|---|---|
| Heating pumps | 2 | 2.0 | −5.6 | 3.5 | 22.0 | 0.5 |
| Cooling pumps | 2 | 2.0 | 5.6 | 2.5 | 24.0 | 0.5 |
| Electric water heater | 120 | 0.4 | −4.5 | 1.0 | 48.5 | 3.0 |
| Refrigerator | 90 | 0.6 | 0.3 | 2.0 | 2.5 | 1.5 |
The VB aims to modulate its consumption with a constant rk, and the demand response event t is equal to 15 min, which is the time period in which SEBM operates.
The initial status of each devices, , has been randomized, the variance, σ2, is set to 0.05, the minimum status changing frequency, τi, is 1, and the control time step, h, is 1 min (1/60 h).
The accuracy and confidence parameters ε and δ have been set to 0.02 and 0.005, respectively. Then, applying Theorem 1, the number of trials is N = 262. The MC&ESB method is applied to obtain xmin and xmax, where xmin (respectively, xmax) is the minimum (respectively, maximum) value of power that the VB can always supply for N = 262 experiments. Therefore, the probability of supplying power x for any x ∈ [xmin, xmax] is greater that 0.98 with confidence at least of 0.995. For this VB, xmin = −1138.3 kW and xmax = 5841.8 kW. By analogy, the MC&ESB method is also applied to obtain and , where (respectively, ) is the limit value of power such that if (respectively, ), the VB can never supply the power x for N = 262 experiments. Therefore, the probability of not supplying power x for any is greater that 0.98 with confidence at least of 0.995. For this VB, kW and kW. For (respectively, ), the probability function Φ and their bounds for a confidence of at least 0.995 are depicted in Figure 3. The curves have been obtained for 50 equally spaced supply powers x. At each power x, the probability is estimated as , where n is the number of experiments where the power x is successfully supplied and N = 262. The lower and upper bounds, and , have been obtained using Equation (12), such that . The bounds ε1 and ε2 have been selected to be equal, whenever possible. However, this is not possible when approaches 0 or 1. Consequently, nonsymmetric bounds are considered for these cases. The estimated demand probability function Φ and its confidence bounds can be used to characterize the capability of a VB. For example, for the VB of this study, we can state that it can supply a power x ∈ [−1138.3, 5841.8] during 15 min with probability greater than 0.98 and confidence 0.995. Moreover, we can also state from the data represented in Figure 3 that the VB can supply a power x = 5900 kW during 15 min with probability p ∈ [0.7021, 0.8322] and confidence 0.995. Thus, the knowledge of the power supply probability function Φ for a given VB is crucial to decide about participating in electrical markets.

3.2. Case Study 2: Demand Flexibility Prediction
The second case study aims to forecast the maximum flexibility power that the same VB of Case 1 can supply at different times of the year to participate in the different SEBM markets using the MC&ESB method. Three scenarios have been considered. In all of them, the simulation is divided into two periods.
The duration of the first period is the sum of the time taken by the algorithm to calculate the prediction (e.g., 5 min) and the minimum time required for the submission of bids in the corresponding SEBM. The duration of the second period corresponds to the demand management horizon, t equal to 15 min. The first period simulates the TCL evolution without any requested rk power signal, while in the second period demand management is activated.
The MC&ESB method is configured to search for the maximum flexibility power with probability greater than 0.98 and confidence 0.995, as explained in Section 2.6. The remaining variables, parameters, and VB characteristics, if not mentioned below, are the same as in case study 1.
In Scenario 1, the aggregator wants the VB to participate in SR from 01:00 to 01:15 UTC on 7th February. At those hours, only refrigerators and electric water heaters operate. The requested flexibility power is positive because low power consumption is expected at night. The ambient temperature is considered constant and equal to 22°C. The bounds of the bisection algorithm a and b are 0 and 5000, respectively.
Scenario 2 takes place in a summer afternoon. The VB is expected to participate in TR from 16:00 to 16:15 UTC on 19th July. In this case, all the reversible heat pumps operate as cooling pumps. The requested flexibility power is negative to achieve peak saving, as the power consumption on the grid is expected to be high. The ambient temperature is considered constant and equal to 24 °C for refrigerators and electric water heaters, while that of the cooling pumps is obtained from the typical PVGIS weather year. The bounds of the bisection algorithm a and b are 0 and −3500, respectively.
Finally, Scenario 3 considers the morning of a winter day. The VB is intended to participate in RR from 10:00 to 10:15 UTC on 5th January. The requested flexibility power is negative, as in Scenario 2. The ambient temperature is considered constant and equal to 22 °C for refrigerators and electric water heaters, while for heating pumps it is obtained from the typical PVGIS weather year. The bounds a and b are 0 and −3500, respectively.
The resulting flexibility power at each scenario is showed in Table 3. The highest amount of power flexibility is obtained in Scenario 1, followed by Scenario 2 and Scenario 3. Usually, the VB can provide more positive than negative power flexibility because TCLs take longer to increase or decrease their temperature when this change is not caused by an electromechanical element [9]. All calculated powers are above 1 MW in absolute value, which allows the aggregator to make bids in the SEBMs. These results demonstrate that the MC&ESB method is useful to calculate the availability of flexible power to participate in SEBMs and other similar markets in a short period of time, depending on the computational capabilities.
| Scenario 1 | Scenario 2 | Scenario 3 |
|---|---|---|
| 3608.0 | −1482.9 | −1250.1 |
3.3. Case Study 3: Demand Flexibility Control
This case study shows how flexibility is managed once the aggregator’s offer has been accepted in the market and it is time to supply the energy. The flexibility power obtained in Scenario 2 of the previous case study (−1482.9 kW) must now be supplied to the grid. For this purpose, the demand flexibility control system discussed in Section 2.3 is activated. The VB has been simulated with the same conditions as in Scenario 2 during 45 min. During the first 30 min, the TCLs are not managed by the controller, while in the last 15 min the controller comes into operation to supply the requested power. The operation is shown in Figures 4 and 5.
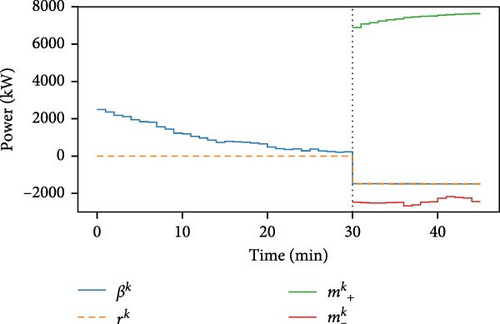
The VB tracks the rk power signal as soon as the controller is activated, that is, from the 30th min onwards. Before that, the TCLs consume the electrical power they need to satisfy the users’ comfort needs without any restriction. This comfort band is also maintained at all times during the 15 min of controller operation, but the coordination in the state of the TCLs makes it possible to supply the requested power flexibility. The VB consumption during the first 30 min was higher than the expected baseline consumption. For this reason, βk is greater than 0 during this period. Deviations from the consumption baseline could occur in real time, so it is important to know the current state of the devices when managing flexibility.
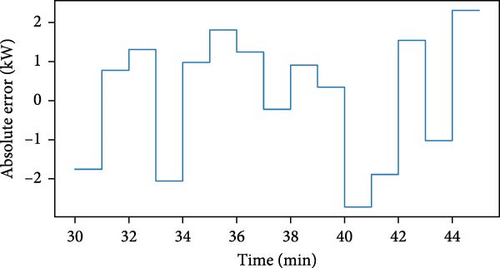
Two aspects are worth noting. The first one is that βk is always between and during controller operation, which means that the VB responds appropriately to the control signal rk. The second one is illustrated in Figure 5 and refers to the fact that the absolute error of the controller is never larger than half of the maximum Pi of the TCLs participating in the VB, provided that rk is always feasible.
4. Conclusion
Demand-side participation in the electricity system is key to reducing the use of fossil fuels and increasing the penetration of renewables in the system. In this paper, a new method for predicting demand flexibility, called MC&ESB, has been developed. The predictability provided by MC&ESB allows an aggregator to participate in electricity markets where demand flexibility can be traded. The method obtains accurate predictions as it can be used with a controller which takes into account the actual state of the loads, as in this paper. Nevertheless, any other control system could be utilized, provided that load disturbances are taken into consideration. The results of demand management with the newly developed approach have been illustrated in three case studies in the Spanish ancillary services electricity market. As a result, the flexibility power above 1 MW has been predicted and the control of the VBs has been simulated.
The VBs used in this work are composed of TCLs, but other sources of residential flexibility, such as electric vehicles and household batteries, could be considered. In addition, the VBs are not limited to residential loads. The MC&ESB method could be used in the industrial sector. Future work will focus on improving the TCL models and testing the methodology in a real environment.
Nomenclature
-
- βk:
-
- Deviation power signal (kW)
-
- δ:
-
- Probability confidence
-
- Δi:
-
- Temperature dead band of i ( °C)
-
- ε, ε1, ε2:
-
- Probability bounds
-
- ηi:
-
- Coefficient of performance of i
-
- γ:
-
- Tolerance of the bisection search algorithm (kW)
-
- :
-
- Forecast ambient temperature of i at k ( °C)
-
- :
-
- Disturbance of i at k ( °C)
-
- :
-
- Supply power probability function and its estimate
-
- ϕi:
-
- Device type of i (0: cooling, 1: heating)
-
- σ2:
-
- Variance of Gaussian disturbance ( °C)
-
- τi:
-
- Minimum status changing frequency of i (h)
-
- :
-
- Internal temperature of i at k ( °C)
-
- :
-
- Set point temperature ( °C)
-
- Ξ:
-
- Sum of Ξj
-
- Ξj:
-
- Result of j (0: no, 1: yes)
-
- a, b:
-
- Bounds of the bisection search algorithm (kW)
-
- :
-
- Thermal capacitance of i (kWh/ °C)
-
- ek:
-
- Regulation power signal (kW)
-
- h:
-
- Control time step (h)
-
- i:
-
- A thermostatically controlled load
-
- j:
-
- A Bernouilli trial
-
- k:
-
- A time instant (h)
-
- L(⋅):
-
- Likelihood function
-
- :
-
- Maximum available charging power at k (kW)
-
- :
-
- Maximum available discharging power at k (kW)
-
- N:
-
- Number of Bernouilli trials
-
- n:
-
- Number of successful Bernouilli trials
-
- NTCL:
-
- Number of aggregated thermostatically controlled load
-
- :
-
- Supply power probability value and its estimate
-
- Pi:
-
- Nominal power of i (+: cooling, −: heating) (kW)
-
- :
-
- Power unavailable for charging at k (kW)
-
- :
-
- Power unavailable for discharging at k (kW)
-
- :
-
- Average expected demanded power of i at k (kW)
-
- rk:
-
- System operator power signal (kW)
-
- :
-
- Thermal resistance of i ( °C/kW)
-
- S:
-
- Capability to supply certain power (0: no, 1: yes)
-
- t:
-
- Demand management event duration (h)
-
- :
-
- Status of i at k (0: off, 1: on)
-
- x:
-
- A value of supply power (kW)
-
- :
-
- Maximum power with nonzero probability (kW)
-
- :
-
- Minimum power with nonzero probability (kW)
-
- xmax:
-
- Maximum power with guaranteed probability (kW)
-
- xmin:
-
- Minimum power with guaranteed probability (kW).
Disclosure
A preprint has previously been published [37].
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This research received funding from the European Union’s Horizon 2020 LocalRES project under the Grant Agreement no. 957819.
Open Research
Data Availability Statement
The data will be made available on request.




