Numerical Investigation of Mass and Heat Transfer in Ternary Hybrid Nanofluid Flow With Activation Energy
Abstract
Ternary hybrid nanofluids (THNFs) are modern fluids introduced to enhance the performance of conventional hybrid nanofluids (HNFs). Their unique properties make them suitable for diverse applications, ranging from heat exchangers to advanced industrial and medical treatments. Due to the practical applications and innovative features of THNFs, this paper aims to analyze the performance of these fluids to improve the efficiency of modern devices. The THNF is formulated by adding nanoparticles of three different kinds of aluminum oxide (Al2O3), silicon dioxide (SiO2), and copper (Cu) into water (H2O) based ethylene glycol (C2H6O2). The momentum equation is formulated considering the influences of Darcy Forchheimer, permeability, and magnetic field. Thermal radiation, intermolecular friction force, and Joule heating effects are accounted in the thermal field equation. Mass concentration relation is acquired considering binary chemical reaction and activation energy (AE). Additionally, the influence of stratifications (thermal and solutal) at the boundary of the cylinder is considered. The physical phenomenon representing partial differential equations is reduced into ordinary ones utilizing the transformations and then solved via Runge–Kutta Fehlberg (RKF-45) numerical scheme in Mathematics. Influence of involved sundry variables on HNF and THNF velocity, thermal field, mass concentration, surface drag force (skin friction coefficient), mass, and heat transfer rates were examined. The results showed that the velocity fields of THNF and HNF decay through variables Darcy Forchheimer, porosity, and Hartman number. Thermal field of THNF and HNF improves via radiation parameter, Eckert number, and Hartman number. Local heat transfer rate upsurges versus curvature variable and Prandtl number.
1. Introduction
Ternary hybrid nanofluids (THNFs) are contemporary fluids used to improve the performance of conventional nanofluids. THNFs consist of three different types of nanoparticles disseminated in a base fluid like ethylene glycol (C2H6O2), water (H2O), or oil. These nanoparticles can be oxides, metals, carbides, carbon-based materials like graphene, or even combinations of these. These fluids have a range of applications across various industries, due to their superior heat transfer capabilities and other enhanced properties. To enhance heat transfer in various systems such as power generation, chemical processing, electronic device cooling, radiator performance, and manufacturing, THNFs are used. Recently several researchers examined diverse aspects of THNFs considering different flow assumptions. Nasir et al. [1] presented a mathematical model for THNF considering the flow caused by extending the sheet with magnetic dipole and thermal radiation. A mathematical analysis for cross bio-nanofluid flow near stagnation point submerged three different sort of nanoparticles was presented by Alraddadi et al. [2]. Kumar et al. [3] elaborated significance of mixed and forced convection in THNF flow along a nonpermeable elongating sheet with magnetic dipole. Gul et al. [4] inspected the characteristics of THNF flow by a stretchable cylinder accounting the features of the magnetic field and homogeneous/heterogeneous reactions. The behavior of radiative and magnetized trihybrid nanofluid flow with stagnation point was described by Al-Kouz et al. [5]. Hussain et al. [6] discovered the improvement of thermal performance in the convective flow of kerosene oil immersed in three different kinds of nanoparticles. Mahmood et al. [7], Jan et al. [8], Bafe, Firdi, and Enyadene [9], and Rajesh and Oztop[10] highlight the performance of THNF flows accounting diverse assumptions.
In industries such as solar energy systems, nuclear reactors, and space technology, the heat generated can be extremely intense. In these cases, thermal radiation becomes a primary mode of heat transfer. Using nanofluids in these environments enables more efficient heat management. Nanoparticles enhance radiative heat transfer due to their ability to absorb and emit radiation effectively. Thermal radiation impact is crucial in high-temperature applications, where conventional heat transfer mechanisms (conduction and convection) are inadequate to meet thermal demands. Dynamics of MHD nanofluid flow and heat transfer under the influence of thermal radiation are explored using a two-phase model by Sheikholeslami et al. [11]. Rashad, Nafe, and Eisa [12] examined the combined impact of thermal radiation and heat generation in Eyring–Powell hybrid nanofluid (HNF) flow by a porous stretched sheet. Heat transfer enhancement in nanofluid flow over an absorbent channel under the influence of thermal radiation is probed by Waqas et al. [13]. Considering heat conduction with dissipation, Marin, Öchsner, and Bhatti [14] investigated the thermoelasticity of dipolar bodies. Entropy creation in Prandtl nanofluid flow in the presence of thermal radiation and cubic autocatalytic chemical reactions is reported by Rehman et al. [15]. Valse et al. [16], Marine, Valse, and Abbas [17], Haq, Rahman, and Hussain [18], Lv et al. [19], Kumar et al. [20], Haq et al. [21], and Poornima, Sreenivasulu, and Souayeh [22] covers diverse aspects of thermal radiation in nanofluid flows.
The Arrhenius energy, also known as the activation energy (AE), is the threshold amount of energy required for a chemical reaction to occur. AE is the energy fence that the reactants must overcome for a reaction to proceed. The higher the AE, the slower the reaction at a given temperature. The AE plays a crucial role in understanding and modeling nanofluid flows, particularly when thermal reactions are involved. Mass transportation analysis in nanofluid flows together with chemical reactions and AE gained the focus of researchers and scientists due to their diverse applications in geothermal reservoirs, cooling of nuclear reactors, recovery of thermal oil, and various fields of chemical engineering. Bestman [23] presented an analysis for boundary layer fluid flow by a permeable wall considering Arrhenius energy and mixed convection. An analysis for mixed convection magneto-nanofluid flow by impermeable surface with binary reaction and AE is conducted by Mustafa et al. [24]. Sensitivity analysis for two-phase nanofluid flow within a circular segment with nonporous walls in the presence of AE and convective edge restrictions was probed by Panda et al. [25]. Raju et al. [26] investigated the impact of reversible and irreversible reactions with AE in non-Newtonian Maxwell fluid flow through a rotating surface. Dynamics of bioconvection and AE in Carreau nanofluid flow by implementing Buongiorno’s model were reported by Varatharaj, Tamizharasi, and Vajravelu [27]. Several researchers investigated the impact of AE with various fluid topographies like thermal radiation [28], Joule heating [29], thermal nonequilibrium [30], mixed convection [31], and irreversibility analysis [32].
- •
A mathematical model for Darcy–Forchheimer flow of HNF and THNF is developed.
- •
Thermal and solutal stratification phenomena are considered at the boundary of the surface.
- •
Impact of Arrhenius’s kinetics linked with chemical reaction are accounted.
- •
This study will provide a comparison between dihybrid nanofluid and THNF.
- •
Graphical and numerical solutions are acquired utilizing the Runge–Kutta Fehlberg (RKF-45) numerical method.
2. Problem Formulation
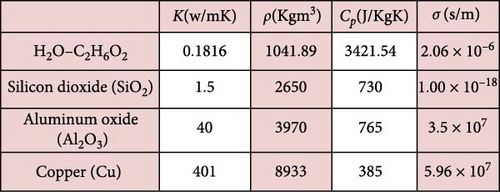
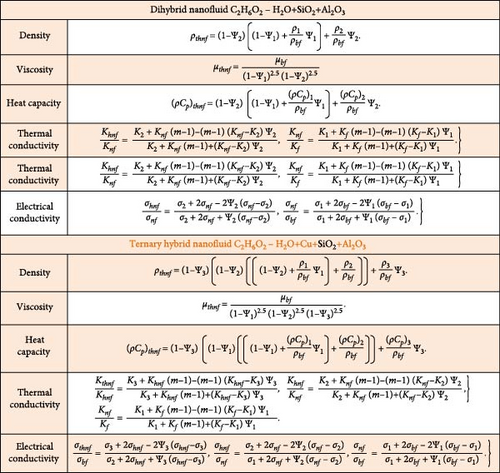
Here, magnetized and stratified Darcy–Forchheimer flow of ternary and dihybrid nanofluid flow by absorbent stretched cylinder is considered. The coordinate system (x, r) is used to analyze the flow. The permeable cylinder is supposed to be stretched along a horizontal axis with velocity , generating the flow. A schematic flow diagram is depicted in Figure 1. C2H6O2 + H2O is considered a carrier liquid. Silicon dioxide (SiO2), aluminum oxide (Al2O3), and copper (Cu) nanoparticles are taken into account for the formation of dihybrid/THNF. A uniform intensity of magnetic field is imposed along the vertical direction. Assume that and are the temperature and concentration stratifications at the surface and ambient, respectively. The impacts of internal friction forces, radiation, and Joule heating are considered in energy relation. Arrhenius’s kinetics linked with chemical reaction is further executed in the mass concentration equation. Thermophysical values of nanoparticles and based fluid are reflected in Figure 2. The flow governing mathematical model is obtained with the implementation of boundary layer assumptions as follows [2–4]:
2.1. Physical Quantities
3. Results and Discussion
After successfully formulating the physical phenomenon in the form of nondimensional Equations (7–9) with edge restrictions Equation (10) in the previous section. The aim of this section is to inspect the significance of sundry involved parameters on HNF and THNF velocity, mass concentration, and thermal field. RKF-45 shooting method in Mathematics is utilized to obtain the computational and graphical results. The RKF-45 is an adaptive numerical method used for solving ODEs. The RKF-45 method is appreciated for its adaptive control, high accuracy, error estimation, and efficiency, making it a go-to method for solving ODEs when computational resources and accuracy need to be balanced. In computational simulations, the empirical relations defined in Figure 3 are utilized. Due to theoretical assumptions, the constant values are assigned to variables as K∗ = Rd = 0.5, Pr = 8.0, m = 4.9.Fr = Ha = K1 = S1 = S2 = 0.2, ϕ1 = ϕ2 = ϕ3 = 0.05, and Ec = 0.3.
3.1. Velocity Field
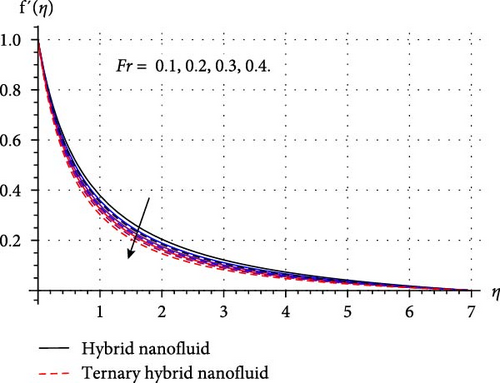
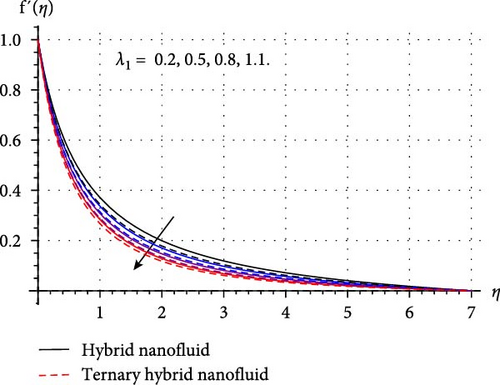
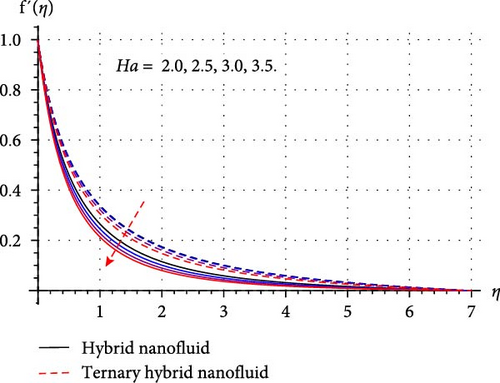
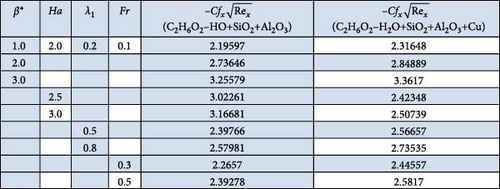
Physical impact of Darcy–Forchheimer (Fr), porosity variable (λ1), curvature parameter (β∗), and Hartmann number (Ha) on HNF and THNF velocity (f′(η)) is illustrated through Figures 4a–d. The performance of f′(η) for intensifying Fr is depicted in Figure 4a. The reduction in velocity rate for both HNF and THNF was justified in light of the increasing fluctuations of Fr was observed. As higher Fr boost the inertial forces which offer resistance to the flow and velocity field diminished. The physical impact of λ1 on f′(η) is probed in Figure 4b. Here, f′(η) and associated layer width decays for both HNF and THNF. Physically, for higher λ1 size of holes of porous surface enhances and more resistance is applied to the flow. Subsequently, f′(η) and correlated layer contracted. Figure 5c reveals variation in f′(η) through higher cylinder curvature variable. Here, fluid velocity decays near the surface, while it escalates when β∗ enhances. Since higher β∗ reduces the radius of the cylinder, and thus, fluid contact region among nanofluid and surface of cylinder minimizes. Consequently, the velocity of fluid near the surface retards while at the ambient its effect is negligible, and thus, fluid velocity away from the surface enhances. Figure 4d shows that the HNF and THNF velocity field retards via the rising magnetic force variable. Since more Lorentz force is generated when the magnetic field strength is increased, it affects the flow in a way that causes a delay. Consequently, THNF and HNF velocity field diminished versus higher Ha.

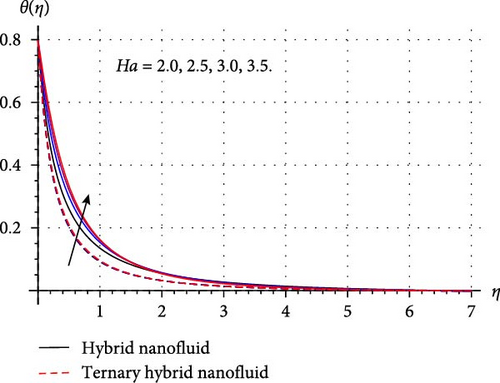

3.2. Temperature Field
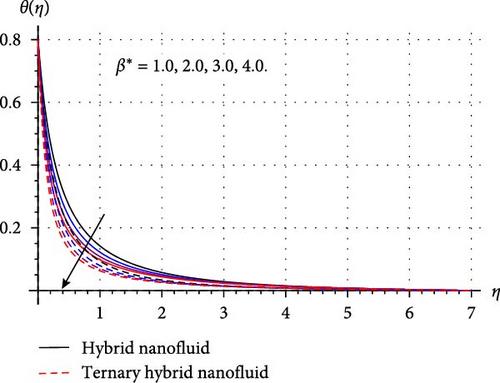
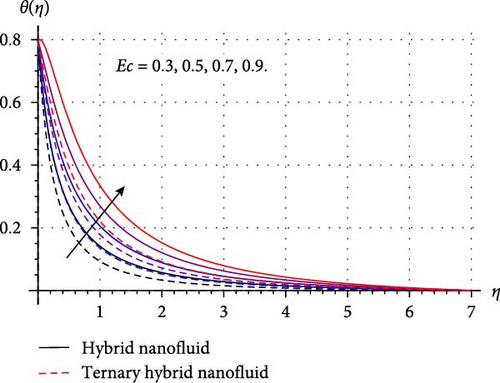
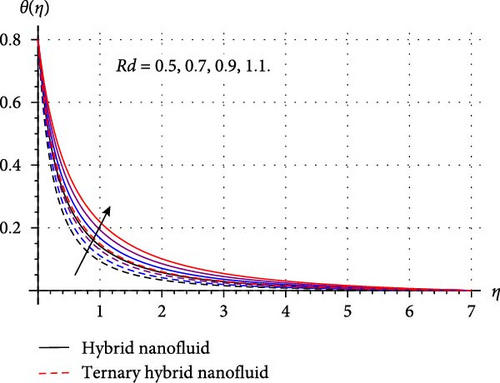
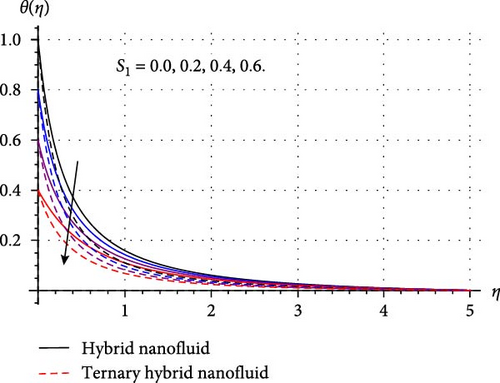
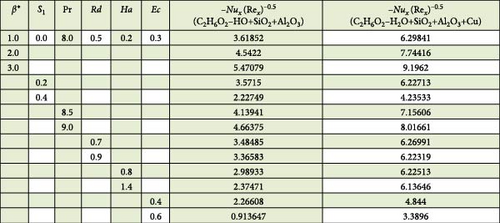
Implications of diverse variables like curvature (β∗), radiation (Rd), thermal stratification (S1), Prandtl number (Pr), Eckert number (Ec), and Hartmann number (Ha) in thermal transport profile (θ(η)) are displayed in Figure 5a–f. Figure 5a shows that thermal field decays through rising β∗ estimations. Since higher β∗ decreases the contact area among HNF and THNF by reducing the radius of the cylinder, thus, temperature field for both HNF and THNF falls. Influence of Eckert number on HNF and THNF is depicted in Figure 5b. Here, the thermal field for both HNF and THNF improves versus higher Ec. Physically, a substantial amount of kinetic energy transfers into the system’s internal energy through work done, and thus, nanofluid temperature field accelerates for higher Ec. Figure 5c clarifies that advancement in Hartmann number enhances the thermal profile for both HNF and THNF. Since improvement in Hartmann number offers more heat to the fluid by increasing the resistive Lorentz force, and hence, thermal field improves for HNF as well as THNF. Consequences of the Prandtl number on the thermal field of HNF/THNF are displayed in Figure 5d. Since higher Pr accelerates the thermal diffusion phenomenon within fluid, and thus, θ(η) decays for HNF/THNF. Figure 5e explores the fluctuation in the thermal field versus advanced radiation variable estimations. Clearly, a direct relation between the thermal field of THNF/HNF and the radiation variable is perceived in this figure. Physically, for higher radiation variable surface heat flux upsurges by reducing the mean absorption coefficient which in turn accelerates the thermal field of THNF/HNF. Characteristics of the thermal field because of the higher stratified thermal parameter is visualized in Figure 5f. Here, θ(η) reduces against rising S1. Physically, thermal field decays against thermal stratification because natural processes like heat conduction, external disturbances, and mixing tend to equalize temperature differences, reducing the degree of stratification over time.
3.3. Concentration Field
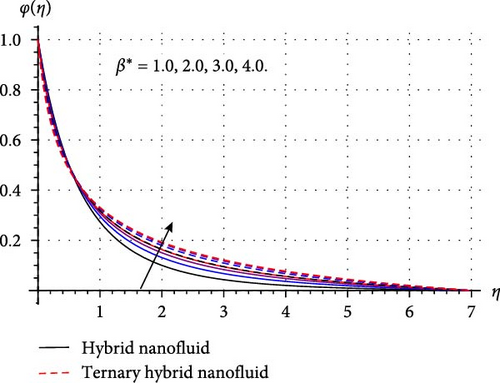
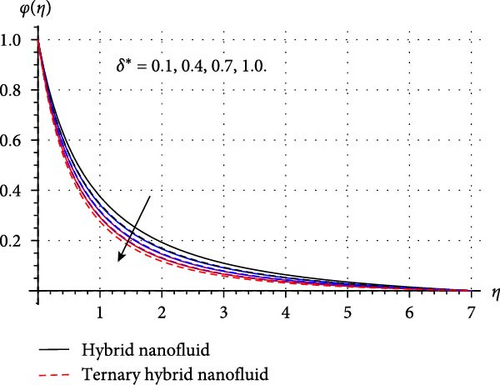
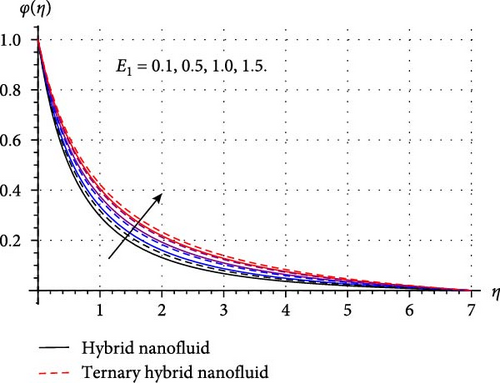
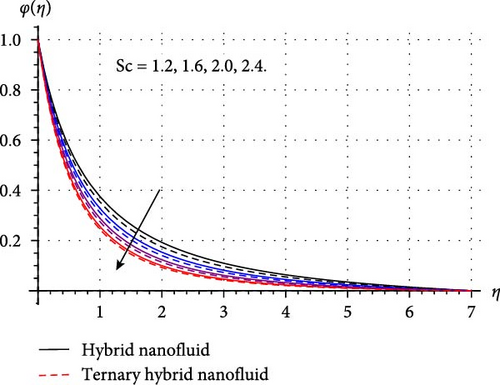
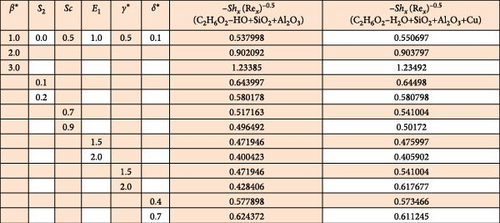
Variation in mass concentration (φ(η)) of THNF/HNF versus improved estimations of sundry variables like chemical reaction (γ∗), surface curvature (β∗), temperature ratio (δ∗), AE (E1), mass stratification (S2), and Schmidt number (Sc) explored in Figure 6a–e. Figure 6 a shows how mass concentration varies through higher chemical reaction variable. Here, an inverse relation between γ∗ and φ(η) is observed. Physically, a higher reaction variable enhances the rate of chemical reaction, and thus, reactive species in HNF and THNF dissolves more rapidly. Therefore, mass concentration falls for both HNF and THNF. FromFigure 6b, a positive change in φ(η) is noticed against the curvature variable. Since improvement in surface curvature augments the resistive force near the surface while at the ambient its effect is negligible. Consequently, the concentration profile decays slightly near the surface while away from the surface it is enhanced. Figure 6c,d are prepared to portray the significance of temperature ratio and AE variables on the concentration of THNF and HNF. Here an opposite trend in curves of mass concentration versus δ∗ and E1 is noticed. As higher δ∗ enhances the surface temperature (Tw), and thus, φ(η) decays. Improved E1 reduces the destructive reaction within HNF and THNF by up surging modified Arrhenius function and consequently φ(η) escalates. Figure 6 (e) portrays that curves of mass concentration diminished through higher Schmidt number. Since improved Sc accelerates the random movement of tiny particles in HNF and THNF, and thus, concentration field retards through Sc. Figure 6 f depicts that φ(η) is decreasing function of the stratified variable. Physically, enhancement in S2 reduces the difference of concentration between the ambient and the surface of the cylinder, thus, mass concentration of HNF and THNF diminished.
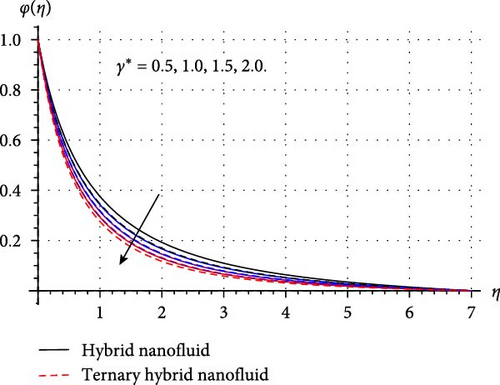
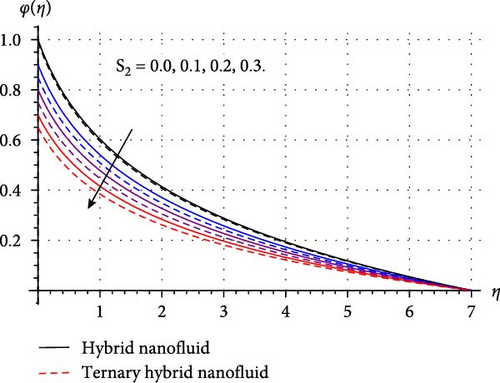
3.4. Skin Friction, Nusselt, and Sherwood Numbers
Consequences of diverse dimensionless variables in skin friction coefficient , Nusselt , and Sherwood numbers of HNF and THNF are portrayed in Figures 7–9. Variation in skin friction force versus the variables curvature, porosity, magnetic, and Darcy–Forchheimer are depicted in Figure 7. This table reveals that the intensity of improves for both HNF and THNF through β∗, Ha, λ1, and Fr. Figure 8 is prepared to observe the heat transfer rate of HNF and THNF via improved estimations of β∗, Ec, Ha, Rd, Pr, and S1. Here, intensity of upsurges through β∗ and Pr, while it decays for S1, Rd, Ha, and Ec. It is further noticed from Figure 8 that the heat transfer rate for THNF is higher than that of HNF. Figure 9 explores the consequences of β∗, Sc, E1, S2, γ∗, and δ∗ on the local mass transfer rate of THNF and HNF. From Figure 9, we observe that retards via rising Sc and E1, whereas enhances through β∗, S2, γ∗, and δ∗.
4. Closing Remarks
- •
Decreasing trend in velocity curves for both dihybrid and THNF versus Fr, Ha, and λ1 is noticed.
- •
Improvement in thermal field of HNF and THNF is observed through Rd, Ec, and Ha, while an opposite impact of β∗, Pr, and S1 is perceived.
- •
For higher approximations of γ∗, δ∗, Sc, and S2 mass concertation of THNF and HNF decreased, whereas it enhances for β∗ and E1.
- •
Intensity of upsurges through β∗ and Pr, while it decays for S1, Rd, Ha, and Ec.
- •
It is noticed that the heat transfer rate of THNF is higher as compared to the HNF.
- •
Magnitude of retards via rising Sc and E1, whereas enhances through β∗, S2, γ∗, and δ∗.
- •
Intensity of improves for both HNF and THNF through β∗, Ha, λ1 and Fr.
Nomenclature
-
- (x, r):
-
- Cartesian coordinates (m)
-
- :
-
- Magnetic field strength (kg s−2A−1)
-
- Kp:
-
- Permeability of porous medium (m2)
-
- ρ:
-
- Density (kgm−3)
-
- Cp:
-
- Specific heat (Jkg−1K−1)
-
- K∗∗:
-
- Mean absorption coefficient (m−1)
-
- uw:
-
- Stretching velocity (ms−1)
-
- n2:
-
- Fitted rate constant
-
- l:
-
- Characteristic length of the cylinder (m)
-
- R
-
- Radius of the cylinder (m)
-
- (C∞, Cw):
-
- Ambient and surface concentration of nanoparticles
-
- (T∞, Tw):
-
- Ambient and surface temperature (K)
-
- (a1, b1, a2, b2):
-
- Constants
-
- C2H6O2:
-
- Ethylene glycol
-
- (f′, θ, φ):
-
- Dimensionless velocity, temperature, and concentration
-
- λ1:
-
- Porosity parameter
-
- β∗:
-
- Curvature variable
-
- Fr:
-
- Inertia parameter
-
- Cu:
-
- Copper
-
- γ∗:
-
- Chemical reaction variable
-
- SiO2
-
- Silicon dioxide
-
- Shx:
-
- Sherwood number
-
- jw:
-
- Mass flux (ms−1)
-
- τw:
-
- Surface shear stress (Wm−2)
-
- qw:
-
- Surface heat flux (Js−2)
-
- ν:
-
- Fluid kinematic viscosity (m2s−1)
-
- Ea:
-
- Activation energy (kgm2s−2)
-
- μ:
-
- Dynamic viscosity (kgm−1s−1)
-
- Kr2:
-
- Rate of reaction (s−1)
-
- Fe:
-
- Inertia coefficient (kgm2)
-
- (S1, S2):
-
- Thermal and concentration stratifications
-
- T0:
-
- Reference temperature (K)
-
- (u, v):
-
- Velocity components (ms−1)
-
- σ:
-
- Electrical conductivity (kg−1m−3s3A2)
-
- C0:
-
- Reference concentration
-
- H2O:
-
- Water
-
- (T, C):
-
- Temperature and concentration
-
- σ∗:
-
- Stefan–Boltzmann constant (Js−1m−2K−4)
-
- Pr:
-
- Prandtl number
-
- Al2O3
-
- Aluminum oxide
-
- Ha:
-
- Hartmann number
-
- Ec:
-
- Eckert number
-
- Rd:
-
- Radiation parameter
-
- k:
-
- Thermal conductivity (Wm−1K)
-
- E1:
-
- Activation energy parameter
-
- ρ:
-
- Density of fluid
-
- Cfx:
-
- Skin friction coefficient
-
- η:
-
- Dimensionless variable
-
- Nux:
-
- Nusselt number
-
- ϕ2:
-
- Volume fraction of Al2O3 nanoparticles
-
- δ∗:
-
- Temperature difference ratio parameter
Subscripts
-
- bf:
-
- Base fluid
-
- hnf:
-
- Hybrid nanofluid
-
- thnf:
-
- Ternary hybrid nanofluid
-
- s2:
-
- Volume fraction of Al2O3
-
- (1, 2, 3):
-
- (SiO2, Al2O3, Cu)
-
- nf:
-
- Nanofluid.
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
Fazal Haq and Jihad Younis: conceived, designed the analysis, and wrote the text paper. Mofareh Hassan Ghazwani and Ali Alnujaie: interpreted and analyzed the data. Hassan Ali Ghazwani: supervised overall activities.
Funding
The authors gratefully acknowledge the funding of the Deanship of Graduate Studies and Scientific Research, Jazan University, Saudi Arabia, through project number: RG24-L09.
Acknowledgments
The authors gratefully acknowledge the funding of the Deanship of Graduate Studies and Scientific Research, Jazan University, Saudi Arabia, through project number: RG24-L09.
Open Research
Data Availability Statement
All data generated or analyzed during this study are included in this published article.




