International Journal of Energy Research

Volume 2024, Issue 1 5577647

Research Article

Open Access

Numerical Investigation of Heat Transfer and Flow Patterns of Supercritical CO₂ in Six-Start Spirally Fluted Tubes

Hanghui Wu

Vehicle Energy and Safety Laboratory , Department of Mechanical Engineering , Ningbo University of Technology , Ningbo , 315336 , China , nbut.cn

Search for more papers by this author

Shanshan Chen,

Corresponding Author

Shanshan Chen

[email protected]

orcid.org/0009-0009-6614-7447

Vehicle Energy and Safety Laboratory , Department of Mechanical Engineering , Ningbo University of Technology , Ningbo , 315336 , China , nbut.cn

Search for more papers by this author

Zhoulin Chen,

Zhoulin Chen

Institute of Refrigeration and Cryogenics Engineering , University of Shanghai for Science and Technology , Shanghai , 200093 , China , usst.edu.cn

Search for more papers by this author

Xiaoping Chen,

Corresponding Author

Xiaoping Chen

[email protected]

orcid.org/0000-0001-9319-1261

Vehicle Energy and Safety Laboratory , Department of Mechanical Engineering , Ningbo University of Technology , Ningbo , 315336 , China , nbut.cn

Search for more papers by this author

Weidong Wu,

Weidong Wu

Institute of Refrigeration and Cryogenics Engineering , University of Shanghai for Science and Technology , Shanghai , 200093 , China , usst.edu.cn

Search for more papers by this author

Hanghui Wu,

Hanghui Wu

Vehicle Energy and Safety Laboratory , Department of Mechanical Engineering , Ningbo University of Technology , Ningbo , 315336 , China , nbut.cn

Search for more papers by this author

Shanshan Chen,

Corresponding Author

Shanshan Chen

[email protected]

orcid.org/0009-0009-6614-7447

Vehicle Energy and Safety Laboratory , Department of Mechanical Engineering , Ningbo University of Technology , Ningbo , 315336 , China , nbut.cn

Search for more papers by this author

Zhoulin Chen,

Zhoulin Chen

Institute of Refrigeration and Cryogenics Engineering , University of Shanghai for Science and Technology , Shanghai , 200093 , China , usst.edu.cn

Search for more papers by this author

Xiaoping Chen,

Corresponding Author

Xiaoping Chen

[email protected]

orcid.org/0000-0001-9319-1261

Vehicle Energy and Safety Laboratory , Department of Mechanical Engineering , Ningbo University of Technology , Ningbo , 315336 , China , nbut.cn

Search for more papers by this author

Weidong Wu,

Weidong Wu

Institute of Refrigeration and Cryogenics Engineering , University of Shanghai for Science and Technology , Shanghai , 200093 , China , usst.edu.cn

Search for more papers by this author

First published: 02 December 2024

https://doi.org/10.1155/er/5577647

Academic Editor: Mumtaz Qaisrani

Share a link

Email
Wechat
Bluesky

Abstract

This research numerically investigates the heat transfer and flow patterns of supercritical carbon dioxide (sCO₂) in a six-start spirally fluted tube. The research focuses on the geometrical optimization of the tube based on three key parameters: the groove depth (e₁), the gap between the main tube and the outer sleeve (e₂), and the thread pitch (p). The influence of these parameters on the heat transfer coefficient (h) and friction factor (f) was also investigated and analyzed. Furthermore, the study examined the overall impact of the gravity inclination angle (δ) on the thermal performance and flow velocity of the spirally fluted tube. The results indicated that the optimal geometrical parameters are as follows: e₁/D = 0.33, e₂/D = 0.04, and p/D = 8.33, yielding the highest values of h/h₈/(f/f₈) in the spirally fluted tub. The change in e₂ has a more significant effect on turbulent kinetic energy (TKE) and thermal performance than the change in e₁. The p value showed a more substantial effect on the f value compared with the h value. Furthermore, the h value was positively correlated with the gravity inclination angle δ in the region where T_b < T_pc. In the region where T_b > T_pc, increasing the gravity inclination angle δ led to a reduction in h value. When δ < 0°, the h value experienced a slight increase. However, the h value showed a substantial variation when δ > 0°, and the near-wall fluid experienced a reduced flow velocity because of the combined effects of gravity and buoyancy, leading to a decrease in heat transfer. Larger gravity inclination angles led to a more pronounced deterioration in heat transfer. This study is anticipated to provide a theoretical basis for the optimized design of heat exchangers and the enhancement of energy conversion efficiency.

1. Introduction

Following the implementation of the Montreal Protocol, there has been a phased out transition from the conventional hydrochlorofluorocarbons and chlorofluorocarbons (HFCs) refrigerants. Increasing concerns about global warming have accelerated the search for alternative solutions. Recently, carbon dioxide (CO₂) has garnered attention from researchers for its excellent refrigeration properties, including being nonflammable, odorless, and nontoxic. More specifically, it is extensively employed in refrigeration systems and warmth pumps. Furthermore, CO₂ is an economical, safe, and environmentally friendly refrigerant, with an ozone depletion potential (ODP) of 0 and a global warming potential (GWP) of 1. Therefore, the collection and utilization of CO₂ are crucial for energy conservation and reducing emissions [1].

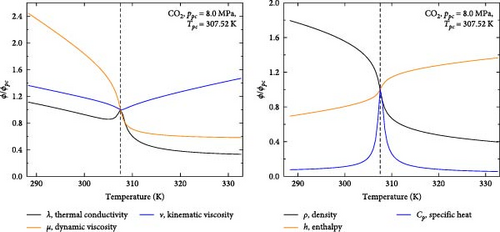
Due to the critical temperature of CO₂ being lower (304.25 K at 7.39 MPa [2], far below the critical point of water), the supercritical CO₂ (sCO₂) state can be reached close to room temperature, which is an ideal working medium for thermal cycles [3]. Figure 1 illustrates the thermophysical curves of sCO₂ at 8.0 MPa in the transcritical cycle, which can be calculated using the National Institute of Standards and Technology (NIST) standard reference database REFPROP version 9. In the subcritical region, the specific heat capacity (C_p) increased gradually with rising bulk temperature, then experienced a sharp rise near the critical point, followed by a sudden drop, and finally returned to its initial value in the supercritical region. The thermal conductivity (λ) followed a pattern similar to that of the specific heat capacity in both the subcritical and supercritical regions. Near the critical point, the kinematic viscosity (v) initially decreased to a minimum, then increased significantly to a maximum, and eventually stabilized. The bulk temperature was negatively correlated with the dynamic viscosity (µ) and density (ρ), with the steepest slopes observed near the quasicritical point. In other words, when the temperature is near the critical point (T_pc), CO₂ has good flow performance, strong heat transfer effect, and small compressibility, which makes the sCO₂ very efficient in the process of mass and heat transfer [4]. Hence, studying the thermal properties of sCO₂ in the transcritical cycle holds great importance.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Thermophysical curves of supercritical carbon dioxide (sCO₂) at 8.0 MPa.

Recently, various gas cooler designs have been proposed to enhance the thermal performance of sCO₂, including twisted structures [5], conical horizontal tubes [6], spiral [7–9], bellows, and so on, which have been proposed to enhance the thermal performance of sCO₂. For instance, Khoshvaght-Aliabadi et al. [5] explored the flow and heat transfer of sCO₂ in a precooler with both twisted tubes and twisted tapes. Their results indicated that the twisted tubes were more effective for sCO₂ in a gas-like state, while the twisted tapes were better suited for sCO₂ in a liquid-like state. Twisted configurations exhibited displayed a heat transfer coefficient ranging from 1.11 to 1.48 times higher than that of the straight mini tube. Zhu et al. [10] conducted experiments to investigate the thermal properties of sCO₂ cooling in two types of grooved tube heat exchangers and one smooth tube heat exchanger. The results showed that the total heat transfer coefficient (h) of the spirally fluted tube was two to three times higher than that of the smooth tube, indicating a substantial improvement in heat transfer efficiency due to the implementation of the spirally fluted design. Yu et al. [11, 12] investigated the heat transfer of sCO₂ cooling in a four-start spirally fluted tube, evaluating the influence of various geometrical parameters on thermal performance. Furthermore, Balla et al. [13] conducted simulations to illustrate that the heat transfer efficiency of a six-head spirally fluted tube is considerably enhanced compared to nonbellows tubes, with a 2.4–3.7 times higher efficiency than a round tube. However, the friction coefficient (f) was found to be 1.7–2.4 times higher than that of a nonbellows tube. Jin et al. [14] conducted simulations on six-start spirally fluted tubes, demonstrating that their thermal performance exceeded that of circular tubes and quadrangle spiral bellows, with flow resistance intermediate between the two. It is worth noting that these studies primarily used water as the working fluid, and there is limited research on the thermal properties of sCO₂ in six-head spirally fluted tubes.

To sum up, the heat transfer performance of spirally fluted tubes is superior to that of conventional tube [15, 16], but there is a lack of research on the flow and heat transfer characteristics of sCO₂ in spirally fluted tubes, particularly those with the six-start spirals. Therefore, this study is the first to numerically explore the thermal properties of sCO₂ cooling in a six-start spirally fluted tube. The research is organized as follows: First, the heat transfers and friction coefficients were optimized with respect to groove depth (e₁), the gap between the main tube and the outer sleeve (e₂), and the thread pitch (p). The thermal efficacy was then investigated with regard to these parameters. The research investigated the overall effects of gravity inclination angles on thermal performance and examined the role of buoyancy under these different inclinations. The research findings are anticipated to provide a theoretical basis for the optimized design of heat exchangers and the enhancement of energy conversion efficiency, which holds significant importance for energy-intensive industries such as power generation, refrigeration, and heat pump systems.

2. Mathematical Description

2.1. Numerical Model

Figure 2a presents the three-dimensional model of the spirally fluted tube, with the flow of CO₂ between the outer and inner walls. The inner wall served as the heat transfer surface, while the outer wall was a uniform cylinder. The symbols L and δ represent the length and inclination angles of the tube, respectively. To simplify the model, only the fluid domain on the CO₂ side was considered, with the test section having a length of 500 mm. To ensure that the fluid entering the test section was fully developed and to eliminate outlet disturbance effects, two adiabatic smooth tubes, each 200 mm in length (27 d_e ~ 37 d_e, depending on the geometric parameters in the cross-section), were connected to the upstream and downstream ends of the test section [12].

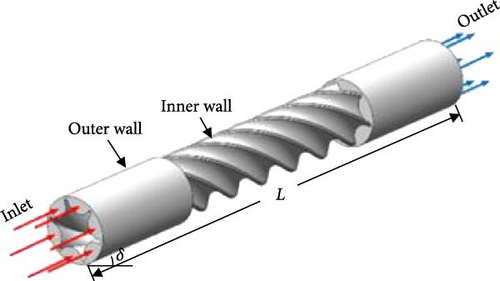
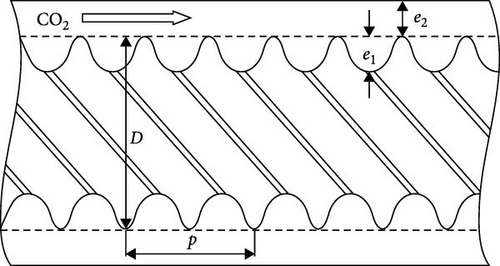
Figure 2b provides a longitudinal section of the threaded tube, where D denotes the diameter of the main tube. For consistency with the experiments, D and L were set to 12 mm and 1 m, respectively, while various designs were considered to optimize the geometry and enhance heat transfer. The study employed single-factor variation parameters based on existing geometrical shapes of six-start spirally fluted tubes. To make the results more universal, the dimensionless parameters were employed in the analysis, and the parameters for each scenario were detailed in Table 1. Moreover, Table 2 provides the gravity components along the x and y axes for various gravity inclinations.

Table 1. Settings of geometrical parameters in different scenarios.

Case	e₁/D	e₂/D	p/D
1	0.33	0.08	8.33
2	0.38	0.08	8.33
3	0.42	0.08	8.33
4	0.46	0.08	8.33
5	0.42	0.04	8.33
6	0.42	0.13	8.33
7	0.42	0.17	8.33
8	0.42	0.08	3.33
9	0.42	0.08	5.00
10	0.42	0.08	6.67

Table 2. Parameters of the gravity inclination angle.

Angle

−90°

−60°

−30°

0°

30°

60°

90°

Flow

direction

Vertical

downward

Inclined

downward

Inclined

downward

Horizontal

Inclined

upward

Inclined

upward

Vertical

upward

g_x (m/s²)

9.81

8.50

4.91

−4.91

−8.50

−9.81

g_y (m/s²)

−4.91

−8.50

−9.81

−8.50

−4.91

Previous studies [17–19] have indicated that the renormalization group (RNG) k-ε model can simulate the turbulent heat transfer in the spiral pipes effectively, as it includes an additional term in its equations that enhances accuracy for rapidly strained flows, such as those found in spiral pipes. Therefore, this study employs the RNG k-ε turbulence model, which delivers accurate results for medium-complexity flows such as jet impingement, separation flow, secondary flow, and swirl flow. The governing equations of this model are as follows [20, 21]:

The continuity is as follows:

(1)

The momentum is as follows:

(2)

The energy is as follows:

(3)

The turbulent kinetic energy (TKE) is as follows:

(4)

The turbulence dissipation rate is as follows:

(5)

where G_k and G_b are the generation of TKE caused by the mean velocity gradients and buoyancy, respectively. These terms are mathematically defined as follows [22]:

(6)

(7)

where the coefficient of thermal expansion β is defined in the form as follows [23]:

(8)

The empirical constants of the model are reported in [24].

2.2. Numerical Strategies and Boundary Condition

The model was implemented using Ansys Fluent 2021. The SIMPLE Consistent (SIMPLIC) algorithm was implemented to accomplish the semi-implicit solution of the coupled pressure and velocity, while the standard wall function method was applied for calculation. The second-order upwind scheme was used for momentum, TKE, turbulent dissipation rate, and energy equations. The thermophysical properties of CO₂ were obtained from the NIST real-gas model provided by the Refprop database. Since the thermal properties of sCO₂ were influenced by heat transfer, an under-relaxation factor of 0.8 was used for the energy term. The convergence criteria were set to achieve precision up to the sixth decimal point [23]. Convergence was determined when the absolute residuals of all equations were consistently less than 1 × 10⁻⁶ and the residuals in inlet and outlet mass flow were below 0.1%.

For simplicity, the flow was assumed to be steady state, with only the flow field on the CO₂ side simulated. Additionally, a no-slip condition was applied to the wall, and both turbulent flow and heat transfer were assumed to be in a steady state. To ensure rational comparison, the inlet conditions were fixed for each inclination angle. To highlight the range of significant changes in thermodynamic properties, the following boundary condition were set: T_in = 320.15 K, inlet pressure P_in = 8.0 MPa, and inlet Reynolds number Re_in = 21,000. Accordingly, the required flow parameters and structure parameters can be obtained. The equivalent diameter, d_e, can be defined as follows:

(9)

where A_c represents the cross-section area and L_p is the wetted perimeter. Both values were obtained by measuring the tool of Solidworks. G denotes the mass flux, which can be calculated as follows:

(10)

(11)

where μ_in is the dynamic viscosity of the inlet.

The acceleration of gravity was established in accordance with Table 2, and the mass-flow-inlet and the pressure-outlet boundaries were applied. For the test section, a constant heat flux of Q = 4500 W was applied to the inner wall, while the outer wall was maintained under adiabatic conditions.

2.3. Data Processing

The experimental section was divided into segments, and the local heat transfer coefficient h_i for each segment i was calculated based on the relationship between the subsection temperature and the wall temperature. The subsection temperature can be defined as the average of the inlet and outlet temperature, as described previously [11].

The subsection temperature is as follows:

(12)

The convective heat transfer coefficient of the subsection is as follows:

(13)

The total h value can be calculated using the following expressions:

(14)

(15)

The flow resistance associated with various structures was analyzed using the Darcy friction coefficient:

(16)

where ∆p represents the pressure drop, u denotes the average velocity, and ρ is the density of sCO₂ at average temperature.

2.4. Model Validation

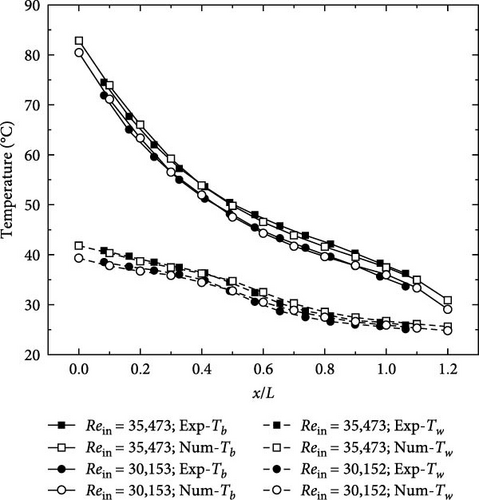
The experimental data were compared with the results to validate the turbulence model [10]. The dimensions of the simulated spirally fluted tube can be specified as follows: L = 1200 mm, R = 11.06 mm, e₁ = 5.5 mm, and e₂ = 4.00 mm. Furthermore, the boundary conditions for the spirally fluted tube that was simulated are as per the following: T_in = 356.15 K, P_in = 11.2 MPa, and Re_in = 35,473. The heat flux q varied with the x-coordinate value and was incorporated into the software for analysis.

To ensure that the results were independent of mesh size, a grid independence test was conducted using four grids with resolutions of 2.3, 3.4, 5.0, and 6.8 million meshes. It was noted that while finer mesh resolutions provided more accurate results, they also resulted in higher computational costs. The dimensionless distance y⁺ of the wall surface reached 1.0 in all scenarios. The grid structure and results are presented in Figures 3 and 4, respectively. It was observed that the meshes with 2.3 and 3.4 million grids displayed a 19.28% difference in the calculation results. In contrast, the results from finer meshes differed by less than 2%. Therefore, a compromise was reached by selecting 5.0 million grids to balance accuracy and computational cost.

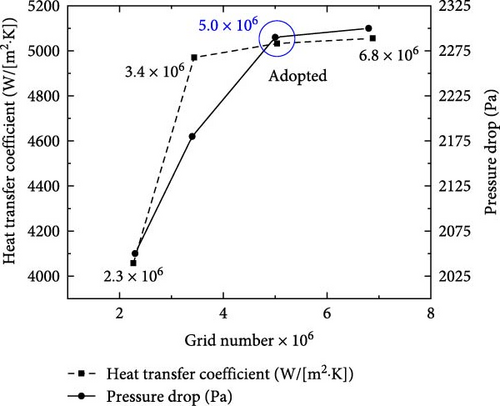
The simulation results were validated against experimental data [10], demonstrating a high degree of accuracy with a deviation of 2.4%. Consequently, the mesh with 5.0 million grids was found to accurately capture the turbulence phenomena in the threaded tubes (as shown in Figure 5).

3. Results and Discussions

3.1. Optimization of Geometrical Parameters

Three scenarios were examined for the geometric factors. The first scenario analyzed the effects of varying groove depth (e₁) on the heat exchange and cross-sectional areas. The second scenario assessed the impact of changing the gap between the main tube and outer sleeve (e₂) on the cross-sectional area while keeping the heat transfer area constant. The third scenario investigated how variations in thread pitch (p) affected the heat transfer surface area, with the cross-sectional area held constant. The results of these scenarios are discussed in the following sections. This study examined the total heat transfer and friction coefficients to assess how geometric variations influenced thermal performance and pressure drop in the spirally fluted tubes. The terms h/h₈ and f/f₈ were employed to optimize the geometry, where h₈ and f₈ represent reference values of h and f in Case 8, respectively.

3.1.1. Influence of e₁ on h Value

Figure 6 illustrates the total heat transfer coefficient h for spirally fluted tubes under the same inlet conditions, with e₁/D of 0.33, 0.38, 0.42, and 0.46, corresponding to Case 1 through Case 4, respectively. The results indicate that as e₁ increases, the total h gradually decreased, while the f increased. In Case 1, the spirally fluted tube showed the highest value of h/h₈/(f/f₈) indicating the smallest friction coefficient and the greatest total h. This observation primarily stemmed from the increase in cross-sectional area as e₁ increased and the resulting decrease in mass flow rate, which led to a reduction in h. As can be seen from Formula (16), there was a close relationship between f and density, pressure drop, average velocity, equivalent radius, and other factors. With the increase of e₁, the cross-sectional area and equivalent radius increased, and the average flow velocity decreased, so the f gradually increased.

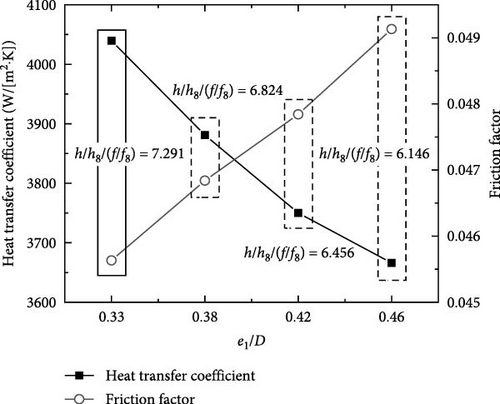
Figure 7 illustrates the relationship between bulk temperature and convective h. T_pc represents the critical temperature of sCO₂, which was 307.5 K at a pressure of 8.0 MPa. The graph revealed the initial increase followed by the decrease in convective h with increasing bulk temperature. There was a remarkable enhancement in h as sCO₂ passes through the pseudocritical point, and the h reached its maximum value when the temperature was slightly above T_pc. These were because that the fluid near the heat transfer wall had a lower temperature compared with the average fluid temperature, causing the near-wall fluid to reach T_pc earlier than the mainstream fluid and resulting in the maximum heat transfer coefficient occurring above T_pc [12]. This pattern also indicated that the region with the most significant difference in the convective h value was observed at the highest point. The temperature corresponding to the max h value remained relatively stable, indicating the limited influence of e₁ on the radial turbulence intensity.

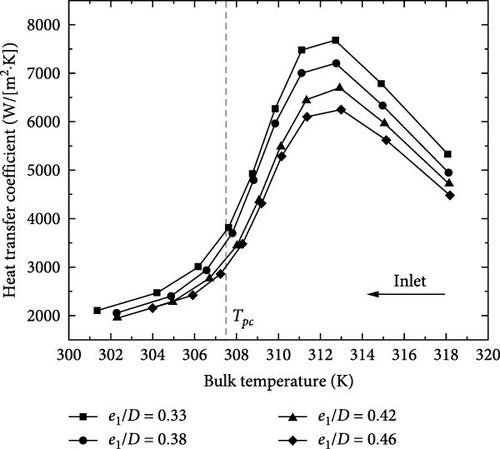
Throughout the entire test section, the spirally fluted tube with a smaller e₁ consistently demonstrated a higher h value compared to the tube with a larger e₁, both for the gas-like and liquid-like sCO₂. Therefore, the optimal e₁/D was 0.33, which would improve the flow heat transfer performance of the six-start spirally fluted tubes.

3.1.2. Influence of e₂ on h Value

Figure 8 illustrates the distribution of total h for a constant inlet condition in spirally fluted tubes with varying values of e₂/D, including 0.04, 0.08, 0.13, and 0.17, corresponding to Case 5, Case 3, Case 6, and Case 7, respectively. It was observed that the h value decreased rapidly with an increase in e₂, which may be primarily due to the increase in cross-sectional area, which resulted in a reduction in mass flow and the spoiler effect between walls. Furthermore, the friction coefficient demonstrated a negative correlation with e₂. This occurred because the change in pressure drops associated with a higher e₂ was more significant than the change caused by e₁, resulting in a lower friction coefficient. The spirally fluted tube with e₂/D of 0.04 demonstrated the highest value of h/h₈/(f/f₈), indicating that the decline rate of the h value was faster than the rate of increase in the friction coefficient with an increase in e₂.

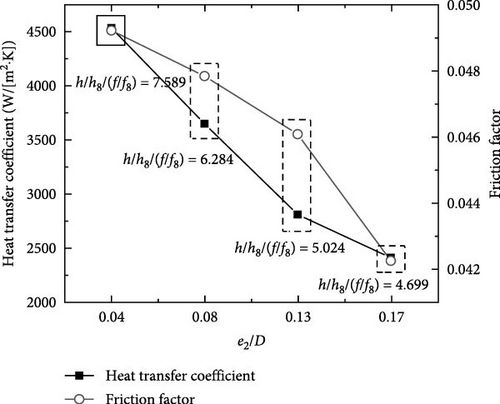
Figure 9 shows the correlation between the bulk temperature and h value. It suggested that the h value initially increased and then decreased as the bulk temperature decreased. It is important to note that the h values for the four distinct e₂/D values exhibited substantial differences, all of which exceeded 10.4%. This observation demonstrates the importance of e₂ as a critical parameter that affects the h value of spirally fluted tubes. The temperature corresponding to the peak h value increases as the wall spacing increases and the h value changes gradually. This phenomenon may primarily originate from the decrease in mass flow rate and turbulence intensity between the walls with increasing e₂, thereby reducing the h value and increasing the temperature difference between the fluid near the wall and the mainstream fluid. Based on the results, it was inferred that the impact of e₂ on the h value was primarily due to the change in fluid turbulence, which was agreement with Yang et al. [9].

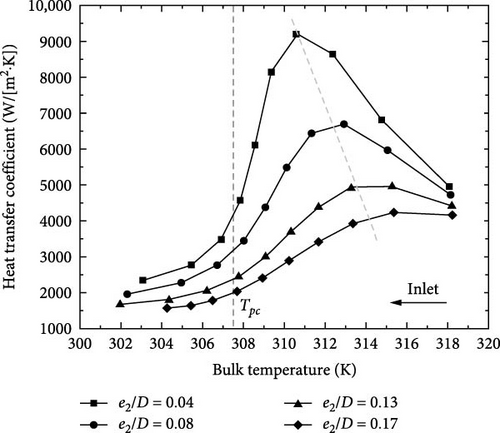
Figure 10 illustrates the variations in TKE for various values of e₁ and e₂. Similar to the pattern observed for the h value, TKE showed a negative correlation with both e₁ and e₂. On the high-temperature side, TKE gradually increased due to the progressive development of the flow boundary layer in the inlet section. However, TKE decreased with lower temperatures, primarily due to the changing physical properties of CO₂. As the temperature dropped, CO₂ density decreased, leading to a reduction in fluid velocity within the spirally fluted tube and consequently, a decrease in TKE. Moreover, Figure 10 reveals that changes in TKE due to variations in e₂ have a more pronounced impact than those caused by e₁, particularly in the temperature range exceeding T_pc. This finding illustrates that a more substantial variation in TKE was associated with a larger variation in heat transfer coefficient caused by wall spacing.

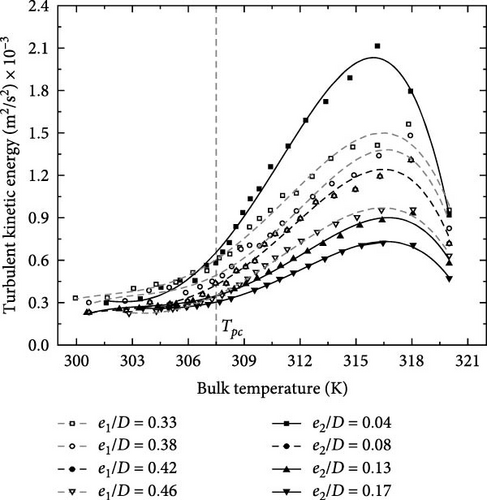
Therefore, it can be concluded that when e₂/D = 0.04, the flow thermal performance of spirally fluted cylinders was more effectively improved and e₂ demonstrated a relatively more significant effect on the h value compared with the e₁.

3.1.3. Influence of the Thread Pitch (p) on the h Value

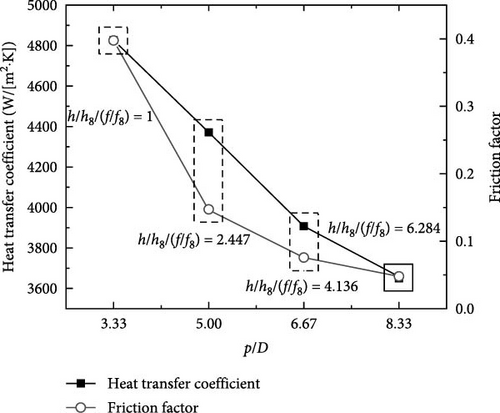
Figure 11 shows the distribution of the h value and friction coefficient of spirally fluted tubes with different p/D, 3.33, 5.00, 6.67, and 8.33, corresponding to Case 8, Case 9, Case 10, and Case 3, respectively. It illustrates the concurrent decrease in both the h and f values with an increase in p. Notably, the value of h/h₈/(f/f₈) was the highest in the spirally fluted tube with p/D = 8.33 (Case 3). This result confirms the idea that the p has a greater influence on the friction coefficient compared to its effect on the h value.

The distribution of the h value in the spirally fluted tube for various p/D and temperatures is depicted in Figure 12. It reveals a pattern similar to the results observed for the first two geometric factors, where the h value initially increased and then decreased. In contrast to the total h value, larger p values in the inlet section of the spirally fluted tube were associated with lower heat transfer coefficients. When the mainstream fluid’s h value reaches its maximum, lesser p values lead to higher h values as the fluid continues to cool. To further analyze the cause, the tangential velocity distribution in the spirally fluted tube for various p/D values and temperatures is displayed in Figure 13. The points positioned at r/r₀ = 0.4 can be defined as follows:

(17)

where r_t is the distance from the testing point to the center of the main tube. The point is in close proximity to the heat exchange surface as r/r0 approaches zero.

Figure 13 shows the initial increase followed by the subsequent decrease in the tangential velocity. When the bulk temperature was higher than T_pc, the tangential velocity decreased rapidly. This phenomenon may be attributed to the transition of CO₂ from a gas-like state to a liquid-like state during the cooling process, resulting in increased density and dynamic viscosity. Therefore, at the same mass flow rate, the tangential velocity gradually decreased, with the reduction being particularly pronounced in the transcritical region. This was consistent with the research result of Yu et al. [11]. The figure also revealed that the smaller p values resulted in higher tangential velocities, which explained the observations in Figure 12. Laminar flow was the predominant flow in the inlet section, as fluid turbulence had not yet completely developed. The radial heat transmission was hindered by the higher tangential velocity in this region, resulting in a substantial temperature disparity between the mainstream fluid and the fluid near the wall. Therefore, larger p values led to a lower heat transfer coefficient. Smaller pitch values led to a stronger TKE and higher h values as the turbulent boundary layer developed.

In conclusion, the section above explores the influence of change in the value of e₁/D, e₂/D, and p/D on the h value. The optimal geometric parameters were determined to be the following: e₁/D = 0.33, e₂/D = 0.04, and p/D = 8.33. Among these parameters, e₁ had the lowest influence on the h value, while primarily influencing heat transfer via alteration in the cross-sectional structure. Moreover, e₂ significantly affected the h value by altering the TKE of the fluid. Compared to e₁, smaller e₂ values were observed to notably increase TKE, which subsequently led to a higher h value. Meanwhile, it was found that p affected the h value by altering the degree of tangential swirl in the fluid. Specifically, smaller p values resulted in a greater degree of swirl and, consequently, a higher h value. However, p showed a more substantial impact on the f value than on the h value. Although a decreased p value increased the h value, it also resulted in a significant increase in the f value, which could potentially compromise flow efficiency. Consequently, the performance of the spirally fluted tube was dependent on a larger p value (p/D = 8.33, p = 100 mm).

3.2. Influence of the Gravity Inclination Angle on the h Value

This section examines the overall effect of varying inclination angles on the h value in the spirally fluted tube. Figure 14 shows that the variation in the h value when considering the gravity factor aligns with the changes observed in the previous section where gravity was not considered. Furthermore, the h value reached its maximum in the region where the fluid temperature was slightly higher than that of T_pc. The reasons were that the primary heat transfer resistance was located in the near-wall fluid, while the change in the value of h was influenced by TKE and mainly determined by the velocity gradient. In the region where T_b > T_pc, the mainstream of sCO₂ was in a gas-like state, and the velocity of the mainstream fluid was much higher than that of the fluid near the heat transfer surface. Where T_b was in close proximity to T_pc, the mainstream fluid experienced a significant increase in fluid density as the phase of the fluid transformed from gas to liquid in the region. The fluid velocity decreased, and the difference of velocity between the mainstream fluid and the near-wall fluid also decreased. Therefore, the h value reached its maximum in the region where the fluid temperature was slightly higher than that of T_pc.

It can also be seen that in the region where T_b < T_pc, the h value was positively correlated with δ, which may be primarily associated with the fact that the key factors influencing heat transfer performance depend on multiple variables. In the region where T_b > T_pc, the h value decreased with increasing δ. When δ was less than 0°, the h value varied slightly, while the changes were significant when δ was greater than 0°. The reasons were that as the δ decreased, the velocity gradient of the fluid increased under the action of gravity, and the heat transfer coefficient increased. Therefore, the h value showed a negative correlation with δ.

To further evaluate the influence of velocity gradients at various inclination angles in the region where T_b > T_pc, Figure 15 illustrates the velocity vector and magnitude in a section of the spirally fluted tube. In this section, the h value reached its maximum (T_b/T_pc = 1.01). Three scenarios were considered with δ values of −60°, 0°, and 60°. The cross-section velocity remained nearly unaltered when δ = −60°, as shown in Figure 15a. A low-speed fluid region was observed near the wall at δ = 0°, and at δ = 60°, this low-speed region was substantially enhanced and occurred in each groove. The observed phenomenon may be attributed to two factors: Firstly, the sCO₂ density increased significantly during the cooling process and phase transition from gas to liquid. The fluid phase increased when δ > 0°, and the velocity was decreased by gravity. Secondly, the buoyancy effect led to the accumulation of quasi-liquid fluid near the wall surface, which substantially decreased the flow rate near the wall surface and may even induce countercurrent phenomena. These results are consistent with the findings in Fan et al. [25].

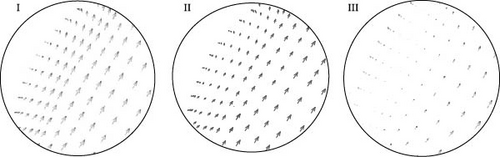
Figure 15b displays the velocity vector of the near-wall fluid in a single groove. The fluid velocity decreased and approached zero when δ exceeded 0°. The results indicate that heat transfer experienced a decrease in the region where T_b > T_pc when δ > 0°. The deteriorating effect was more pronounced as the inclination angle increased. This occurred because the influence of the gravity factor and buoyancy effect led to a low flow rate of the near-wall fluid, explaining the dominance of the velocity gradient in altering the heat transfer coefficient observed in Figure 14.

In addition, the buoyancy in the spirally fluted tube with various gravity inclination angles was analyzed to further investigate the influence of buoyancy on sCO₂ cooling (as illustrated in Figure 16). The ratio of buoyancy to viscous force is represented by the Grashof number in the current study, which can be defined as follows:

(18)

It is important to mention that Bu can also be employed to quantify the effect of buoyancy on heat transfer, which can be defined as follows:

(19)

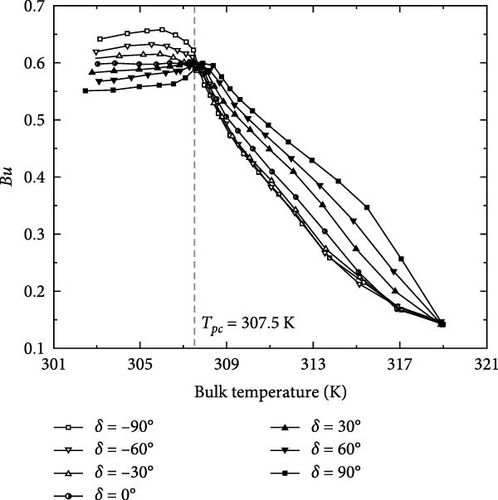
Figure 16 demonstrates that the buoyancy variation trends were fundamentally comparable and reached a turning point at T_pc. In the region where T_b > T_pc, Bu increased gradually with the cooling process. The observed phenomenon primarily originated from the increase in fluid density and the decrease in mainstream flow velocity, leading to lower Re. In the area where T_b < T_pc, Bu remained high with minimal changes. Therefore, the h value in this region was greatly influenced by buoyancy and increased with higher gravity inclination angles, which was consistent with the result of Yu et al. [12].

4. Conclusions

This study conducted numerical simulations to analyze the heat transfer coefficient (h) and flow patterns during cooling in a six-head spirally fluted tube using sCO₂. Initially, the six-start spirally fluted tube was optimized for the heat transfer coefficient (h) value and friction coefficient (f) based on three geometric parameters: depth of the groove (e₁), distance between the main tube and the outer sleeve (e₂), and pitch of thread (p). Subsequently, the effect of these parameters was investigated on the h value. Furthermore, the overall effects of various gravity inclination angles were investigated on the h value and flow patterns in the six-start spirally fluted tube, with an emphasis on comprehending the mechanisms of buoyancy’s influence. The key findings of the study can be summarized as follows:

1.
The optimal parameters for the six-start spirally fluted tube were determined to be e₁/D = 0.33, e₂/D = 0.04, and p/D = 8.33 under specific conditions, including an inlet temperature of 320.15 K, an operating pressure of 8.0 MPa, an inlet Reynolds number of 21,000, and a constant heat flux of 4500 W.
2.
In this study, a smaller e₁ led to improved flow heat transfer performance under the specified working conditions, despite the relatively minor impact on heat transfer. In comparison, e₂ demonstrated a relatively more pronounced effect on the h value, while p showed a more substantial impact on the f value than on the h value. Although a decreased p value increased the h value, it also resulted in a significant increase in the f value, which could potentially compromise flow efficiency. Consequently, the performance of the spirally fluted tube was dependent on a larger p value.
3.
The h value was positively correlated with δ in the temperature range where T_b < T_pc. While in the temperature range of T_b > T_pc, the h value increased with the decrease in gravity inclination angle δ. This phenomenon occurred because the primary heat transfer resistance was located in the near-wall fluid, while the change in the value of h was mainly determined by the velocity gradient, which can be accelerated due to gravity, thereby enhancing heat transfer.
4.
The h value was found to be increased with decreasing δ. When δ < 0°, variations in the h value were negligible. However, for δ > 0°, there was a significant variation in the h value. This was because the flow velocity in the near-wall fluid was reduced and the countercurrent phenomena might even be induced due to the combined effect of gravity and buoyancy, leading to a deterioration in heat transfer. A larger gravity inclination angle δ was associated with a more serious heat transfer deterioration.

In the subsequent stages of our research, based on the geometric optimization of six-head spirally fluted tube, we will further investigate and discuss the detailed effects of gravity inclination δ on the flow and heat transfer behavior of sCO₂.

Nomenclature

A:: Area (mm²)
Bu:: Buoyancy parameter
C_p:: Specific heat (J/[kg·K])
A_c:: The area of cross-section (mm²)
D:: The diameter of inner tube (mm)
d_e:: Equivalent diameter (mm)
e₁:: The depth of the groove (mm)
e₂:: The distance between the main tube and the outer sleeve (mm)
f:: Friction factor
h:: Heat transfer coefficient (W/[m²·K])
g:: Gravitational acceleration (m/s²)
G:: Mass flux (kg/m²·s)
Gr:: Grashof number
k:: Turbulent kinetic energy (m²/s²)
L:: Length (m)
p:: Pitch of thread (mm)
P:: Pressure (Pa)
Pr:: Prandtl number
q:: Heat flux (W/m²)
r:: The radius of the main tube (mm)
Re:: Reynolds number
T:: Temperature (K)
u:: Velocity (m/s)
L_p:: Wetted perimeter (mm).

Greek Symbol

δ:: Inclination angle (°)
ρ:: Density (kg/m³)
ε:: Dissipation rate of turbulent energy (m²/s²)
λ:: Thermal conductivity (W/m K)
μ:: Dynamic viscosity (kg/[m·s]).

Subscripts

avg:: Average
b:: Bulk fluids
h:: Cooling surface
i:: Subsection
in:: Inlet
out:: Outlet
pc:: Pseudocritical
t:: Testing point
w:: Inner wall.

Ethics Statement

The authors declare no ethical issue in relation to this study.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research is funded by the National Natural Science Foundation of China (51971113), the Inter-Governmental S&T Cooperation Project (Research Personnel Exchange Program Between China and Serbia, China and North Macedonian), the Natural Science Foundation of Zhejiang Province (LY20A020004, LY21A020002, and LQ23A020001), the Higher Education Scientific Research Planning Project of China Association of Higher Education (24KC0419), the General Project of Zhejiang Provincial Department of Education (Y202250294 and Y202456499), the Natural Science Foundation of Liaoning Province/Joint Open Fund (2022-KF-24-04), the Foundation of State Key Laboratory of Automotive Simulation and Control (20210235), the Natural Science Foundation of Ningbo Municipality (2023J179 and 2023J389), the Ningbo Major Special Project of the Plan “Science and technology innovation 2025” (2022Z11 and 2023Z036), the Scientific Cultivation Project of Ningbo University of Technology (2022TS15 and 2022TS17), and the National Innovative Training Program for College Students (202411058047). The project is also inseparable from the technical and financial support of Ningbo Liangye Electric Appliance Co., Ltd.

Acknowledgments

This research is funded by the National Natural Science Foundation of China (51971113), the Inter-Governmental S&T Cooperation Project (Research Personnel Exchange Program Between China and Serbia, China and North Macedonian), the Natural Science Foundation of Zhejiang Province (LY20A020004, LY21A020002, and LQ23A020001), the Higher Education Scientific Research Planning Project of China Association of Higher Education (24KC0419), the General Project of Zhejiang Provincial Department of Education (Y202250294 and Y202456499), the Natural Science Foundation of Liaoning Province/Joint Open Fund (2022-KF-24-04), the Foundation of State Key Laboratory of Automotive Simulation and Control (20210235), the Natural Science Foundation of Ningbo Municipality (2023J179 and 2023J389), the Ningbo Major Special Project of the Plan “Science and technology innovation 2025” (2022Z11 and 2023Z036), the Scientific Cultivation Project of Ningbo University of Technology (2022TS15 and 2022TS17), the National Innovative Training Program for College Students (202411058047). The project is also inseparable from the technical and financial support of Ningbo Liangye Electric Appliance Co., Ltd.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Liaw K. L., Kurnia J. C., and Sasmito A. P., Enhancing Supercritical Carbon Dioxide Heat Transfer in Helical Tube Heat Exchangers With Twisted Tape Inserts: A Computational Investigation, International Journal of Heat and Mass Transfer. (2024) 227, https://doi.org/10.1016/j.ijheatmasstransfer.2024.125598, 125598.
10.1016/j.ijheatmasstransfer.2024.125598
CAS Web of Science® Google Scholar
2 Ali H. A. H., Jaddoa A. A., and Daif J. M., Comparison and Analysis of Heat Transfer and Inflow Rate for Supercritical Carbon Dioxide Based on Different Tubes, Frontiers in Heat and Mass Transfer. (2023) 21, no. 1, 443–465, https://doi.org/10.32604/fhmt.2023.042288.
10.32604/fhmt.2023.042288
Web of Science® Google Scholar
3 Duan H., Xie G., Ma Y., Li S., and Sunden B., Mitigation of Heat Transfer Deterioration of Supercritical CO₂ Vertical Tube Upward Flows by Introducing Truncated-Ribs in Helical-Like Distribution, ASME Journal of Heat and Mass Transfer. (2023) 145, no. 5, https://doi.org/10.1115/1.4055858, 0051901.
10.1115/1.4055858
Google Scholar
4 Wang W., Ye Z., Yin X., Song Y., Cui C., and Cao F., Theoretical and Experimental Studies for a Transcritical CO₂ Heat Pump With Spirally Fluted Tube Gas Cooler, Applied Thermal Engineering. (2024) 236, https://doi.org/10.1016/j.applthermaleng.2023.121414, 121414.
10.1016/j.applthermaleng.2023.121414
CAS Web of Science® Google Scholar
5 Khoshvaght-Aliabadi M., Ghodrati P., Mahian O., and Kang Y. T., Performance Evaluation of Non-Uniform Twisted Designs in Precooler of Supercritical CO₂ Power Cycle, Energy. (2024) 292, https://doi.org/10.1016/j.energy.2024.130447, 130447.
10.1016/j.energy.2024.130447
CAS Web of Science® Google Scholar
6 Khoshvaght-Aliabadi M., Ghodrati P., Khaligh S. F., and Kang Y. T., Improving Supercritical CO₂ Cooling Using Conical Tubes Equipped With Non-Uniform Twisted Inserts, International Communications in Heat and Mass Transfer. (2024) 150, https://doi.org/10.1016/j.icheatmasstransfer.2023.107171, 107171.
10.1016/j.icheatmasstransfer.2023.107171
CAS Web of Science® Google Scholar
7 Cai H., Jiang N., Bai Y., An H., and Yao G., Numerical Research on the Heat Transfer and Pressure Drop of Supercritical CO₂ in Spiral Wound Tubes, Numerical Heat Transfer, Part A: Applications. (2024) 1–19, https://doi.org/10.1080/10407782.2024.2314234.
10.1080/10407782.2024.2314234
Web of Science® Google Scholar
8 Chen J., Chen H., Zhao R., Song J.-L., Nian Y.-L., and Cheng W.-L., Experimental Study on the Heat Transfer Characteristics of Supercritical Carbon Dioxide in Spiral Tube With High Pitch to Spiral Diameter Ratio, International Journal of Heat and Mass Transfer. (2023) 217, https://doi.org/10.1016/j.ijheatmasstransfer.2023.124694, 124694.
10.1016/j.ijheatmasstransfer.2023.124694
CAS Web of Science® Google Scholar
9 Yang M., Li G., Liao F., Li J., and Zhou X., Numerical Study of Characteristic Influence on Heat Transfer of Supercritical CO₂ in Helically Coiled Tube With Non-Circular Cross Section, International Journal of Heat and Mass Transfer. (2021) 176, https://doi.org/10.1016/j.ijheatmasstransfer.2021.121511, 121511.
10.1016/j.ijheatmasstransfer.2021.121511
CAS Web of Science® Google Scholar
10 Zhu Y., Huang Y., Lin S., Li C., and Jiang P., Study of Convection Heat Transfer of CO₂ at Supercritical Pressures During Cooling in Fluted Tube-in-Tube Heat Exchangers, International Journal of Refrigeration. (2019) 104, 161–170, https://doi.org/10.1016/j.ijrefrig.2019.03.033, 2-s2.0-85067440669.
10.1016/j.ijrefrig.2019.03.033
CAS Web of Science® Google Scholar
11 Yu Z., Tao L., Huang L., and Wang D., Numerical Investigation on Cooling Heat Transfer and Flow Characteristic of Supercritical CO₂ in Spirally Fluted Tubes, International Journal of Heat and Mass Transfer. (2020) 163, https://doi.org/10.1016/j.ijheatmasstransfer.2020.120399, 120399.
10.1016/j.ijheatmasstransfer.2020.120399
CAS Web of Science® Google Scholar
12 Yu Z., Tao L., and Huang L., et al.Numerical Investigation on Cooling Heat Transfer and Flow Characteristics of Supercritical CO₂ in Spirally Fluted Tube at Various Inclination Angles, International Journal of Thermal Sciences. (2021) 166, https://doi.org/10.1016/j.ijthermalsci.2021.106916, 106916.
10.1016/j.ijthermalsci.2021.106916
CAS Web of Science® Google Scholar
13 Balla H. H., Enhancement of Heat Transfer in Six-Start Spirally Corrugated Tubes, Case Studies in Thermal Engineering. (2017) 9, 79–89, https://doi.org/10.1016/j.csite.2017.01.001, 2-s2.0-85008462096.
10.1016/j.csite.2017.01.001
Web of Science® Google Scholar
14 Jin Z.-J., Liu B.-Z., Chen F.-Q., Gao Z.-X., Gao X.-F., and Qian J.-Y., CFD Analysis on Flow Resistance Characteristics of Six-Start Spirally Corrugated Tube, International Journal of Heat and Mass Transfer. (2016) 103, 1198–1207, https://doi.org/10.1016/j.ijheatmasstransfer.2016.08.070, 2-s2.0-84989862563.
10.1016/j.ijheatmasstransfer.2016.08.070
Web of Science® Google Scholar
15 Jiang Y.-R., Hu P., Jia C.-Q., Zhao P.-P., and Jia L., Analysis of Supercritical Heat Transfer in Horizontal Helical Tube With Internal Roughness, Applied Thermal Engineering. (2022) 211, https://doi.org/10.1016/j.applthermaleng.2022.118463, 118463.
10.1016/j.applthermaleng.2022.118463
CAS Web of Science® Google Scholar
16 Lei X., Zhang J., Gou L., Zhang Q., and Li H., Experimental Study on Convection Heat Transfer of Supercritical CO₂ in Small Upward Channels, Energy. (2019) 176, 119–130, https://doi.org/10.1016/j.energy.2019.03.109, 2-s2.0-85064166396.
10.1016/j.energy.2019.03.109
CAS Web of Science® Google Scholar
17 Hao X., Du S., Yang Q., Zhang S., and Zhang Q., Flow and Heat Transfer Characteristics of S-CO₂ in a Vertically Rising Y-Tube, Energies. (2022) 15, no. 9, https://doi.org/10.3390/en15093312, 3312.
10.3390/en15093312
CAS Web of Science® Google Scholar
18 K S R. P., V K., Bharadwaj M S., and Ponangi B. R., Turbulent Heat Transfer Characteristics of Supercritical Carbon Dioxide for a Vertically Upward Flow in a Pipe Using Computational Fluid Dynamic and Artificial Neural Network, Journal of Heat Transfer. (2022) 144, no. 1, https://doi.org/10.1115/1.4052687.
10.1115/1.4052687
Google Scholar
19 Xu J., Yang C., Zhang W., and Sun D., Turbulent Convective Heat Transfer of CO₂ in a Helical Tube at Near-Critical Pressure, International Journal of Heat and Mass Transfer. (2015) 80, 748–758, https://doi.org/10.1016/j.ijheatmasstransfer.2014.09.066, 2-s2.0-84908518162.
10.1016/j.ijheatmasstransfer.2014.09.066
CAS Web of Science® Google Scholar
20 Maraj E. N., Shah S. I., Akbar N. S., and Muhammad T., Thermally Progressive Particle-Cu/Blood Peristaltic Transport With Mass Transfer in a Non-Uniform Wavy Channel: Closed-Form Exact Solutions, Alexandria Engineering Journal. (2023) 74, 453–466, https://doi.org/10.1016/j.aej.2023.05.056.
10.1016/j.aej.2023.05.056
Web of Science® Google Scholar
21 Akbar N. S., Rafiq M., Muhammad T., and Alghamdi M., Electro Osmotically Interactive Biological Study of Thermally Stratified Micropolar Nanofluid Flow for Copper and Silver Nanoparticles in a Microchannel, Scientific Reports. (2024) 14, no. 1, https://doi.org/10.1038/s41598-023-51017-z, 518.
10.1038/s41598-023-51017-z
CAS PubMed Web of Science® Google Scholar
22 Akbar N. S., Mehrizi A. A., Rafiq M., Habib M. B., and Muhammad T., Peristaltic Flow Analysis of Thermal Engineering Nano Model With Effective Thermal Conductivity of Different Shape Nanomaterials Assessing Variable Fluid Properties, Alexandria Engineering Journal. (2023) 81, 395–404, https://doi.org/10.1016/j.aej.2023.09.027.
10.1016/j.aej.2023.09.027
Web of Science® Google Scholar
23 Akram J. and Akbar N. S., Electroosmotically Actuated Peristaltic-Ciliary Flow of Propylene Glycol+water Conveying Titania Nanoparticles, Scientific Reports. (2023) 13, no. 1, https://doi.org/10.1038/s41598-023-38820-4, 11801.
10.1038/s41598-023-38820-4
CAS PubMed Web of Science® Google Scholar
24 Wang K., Zhang Z.-D., Zhang X.-Y., and Min C.-H., Buoyancy Effects on Convective Heat Transfer of Supercritical CO₂ and Thermal Stress in Parabolic Trough Receivers Under Non-Uniform Solar Flux Distribution, International Journal of Heat and Mass Transfer. (2021) 175, https://doi.org/10.1016/j.ijheatmasstransfer.2021.121130, 121130.
10.1016/j.ijheatmasstransfer.2021.121130
CAS Web of Science® Google Scholar
25 Fan Y. H., Tang G. H., Li X. L., Yang D. L., and Wang S. Q., Correlation Evaluation on Circumferentially Average Heat Transfer for Supercritical Carbon Dioxide in Nonuniform Heating Vertical Tubes, Energy. (2019) 170, 480–496, https://doi.org/10.1016/j.energy.2018.12.151, 2-s2.0-85059589415.
10.1016/j.energy.2018.12.151
CAS Google Scholar

All articles

Numerical Investigation of Heat Transfer and Flow Patterns of Supercritical CO₂ in Six-Start Spirally Fluted Tubes

Abstract

1. Introduction