Thermal Analysis of Magnetized Bioconvective Flow of a Casson Nanofluid With Temperature Dependent Thermal Conductivity: A Numerical Study
Abstract
The current study has applications in various technical fields, including energy generation, fluid dynamics, geophysical fluid mechanics, and biomedical and industrial engineering. This study aims to investigate the explicit solution of a two-dimensional Casson nanofluid flow model incorporating an exponential heat exchanger and activation energy. The fluid motion is induced by an exponentially stretching surface under a convective boundary condition and variable thermal conductivity. Additionally, the influence of microorganisms and magnetohydrodynamics (MHDs) is examined. The governing system of coupled partial differential equations (PDEs) is transformed into a set of ordinary differential equations (ODEs) and numerically solved using the bvp4c solver in MATLAB. A comprehensive graphical and tabulated analysis is conducted for various governing parameters. The findings reveal that an increase in the Casson fluid and porosity parameters leads to a reduction in fluid velocity. Moreover, the microorganism density profile declines with increasing bioconvection Lewis number and Peclet number.
1. Introduction
Non-Newtonian fluids are broadly classified into three primary categories: viscoelastic, time-dependent, and time-independent fluids. For non-Newtonian fluids exhibiting time-invariant behavior, the strain rate at a specific location is exclusively governed by the exerted force at that point, independent of any prior deformation effects or the duration of fluid motion. Instances include Pseudo-plastic, Bingham, Casson, and Dilatant fluids. The equations that explain the behavior of non-Newtonian fluids are far away intricate and nonlinear in contrast to those governing Newtonian fluids. The Casson model, genuinely investigated by Casson [1] to discuss the rheological phenomena of pigment-oil suspensions in printing inks, has since been extensively considered in many fluid dynamics applications. Bird et al. [2] consider a plastic fluid model in term of yield stress, shear-thinning properties, and enhanced viscosity at higher shear rates. Venkatesan et al. [3] interrogated that while blood behaves as a Newtonian fluid in larger arteries with a high shear rate, it exhibits non-Newtonian properties in smaller arteries with low shear rates. The partially ionized Casson nanofluid flow with Cattaneo-Chrsitov heat flux and catalyzed reactions over a bidirectional porous stretching surface was numerically deliberated by Ramzan et al. [4]. Khan [5] premeditated the dynamics of ferromagnetic nanoparticles on non-Newtonian nanofluid flow upon a stretching sheet, employing the Bvp4c technique to solve the transformed ordinary differential equations (ODEs). Similarly, Rehman et al. [6] discussed the transient nature of Casson hybrid nanofluid flow upon a stretching surface under the impact of magnetohydrodynamics (MHDs) and couple-stress theory. They explored the effects of viscous dissipation and thermal regulation in their investigation using a homotopy based analytical methodology to get solutions. Saleem et al. [7] discussed Casson ternary nanofluid flow upon a stretching sheet under EMHD effects, taking radiation, thermal slip, and Joule heating. They used RKF-45 for the solution of transformed ODEs and confirmed that increasing Ag-Cu-TiO2 nanoparticle concentration increase the temperature, while velocity goes down with lower density.
The activation energy or threshold energy, an important parameter in molecular transformations, defines the lowest energy required to start a reaction. This basic factor highly impacts reaction kinetics and has extensive applications in domains like geothermal heat utilization, thermal regulation in nuclear systems, advanced oil extraction techniques, and process optimization in chemical industries. Several studies have investegated the effects of energy threshold on reactive systems and fluid dynamics. Bestman [8] belongs to the pioneer who investigate how activation energy impacts mass transfer within boundary layers during convective processes. Makinde et al. [9] investigated the relationship between chemical reactions and activation energy in unsteady convective flows near heated surfaces. Wang et al. [10] modeled the activation energy and chemical reactions effects with Casson nanofluid flow over an elastic sheet by using MATLAB and RKF-45, revealing 28% mass transfer and 35% heat transfer rates. Aboel-Magd et al. [11] examined the mass and heat transfer in a magnetized flow of Casson nanofluid with bioconvection over a disk. They highlight the influence of gyrotactic microorganisms, activation energy, and magnetization on velocity and microbial density. Jayaprakash et al. [12] studied the magnetized flow of a Casson–Maxwell fluid with activation energy and suction/blowing. Priya and Bala Anki Reddy [13] explored the enhancement of energy dissipation in the steady-state motion of Casson-type nanofluids across three distinct geometric configurations. Their study employed computational and statistical techniques while integrating innovative aspects such as Arrhenius energy threshold and radiative heat transfer. The Results of this study showed the increase in entropy with higher magnetic fields and radiation, with low error metrics confirming high precision, also offered applications in solar energy systems, material processing, and heat exchangers. Raza et al. [14] examined the Casson nanofluid flow over a stretching surface with activation energy, incorporating magnetic fields and slip effects.
Bio-convection is an interesting phenomenon seen in the movement of small organisms. In this process, these microorganisms, which are denser than the surrounding liquid, rise toward the surface. Particularly, gyrotactic microorganisms like algae accumulate near the upper layer of a fluid, making the top layer denser than the bottom, leading to fluid motion known as convection. Researchers have investigated the interactions between nanoparticles and microorganisms at different scales, from nanoscale to macroscale. Bio-convection, a macroscale event, involves the visible movement of fluid driven by motile microorganisms. In the context of nanofluid bio-convection, the behavior of both nanoparticles and microorganisms has been extensively studied. Denser microorganisms can propel themselves, influencing the buoyancy of the system. Various studies have examined the effects of microorganism behavior including gyrotaxis, gravitaxis, and oxytaxis in the context of nanofluid dynamics. Alharabi et al. [15] conducted a study on the unsteady flow of Casson nanofluid between two concentric stretching cylinders, taking into account temperature-dependent viscosity, thermal conductivity, and nonlinear radiation. They also incorporated swimming microorganisms to analyze the stability of the system. Zhao et al. [16] conducted an in-depth analysis of Darcy–Forchheimer Casson nanofluid flow around a vertically stretching cylinder, incorporating convective boundary conditions, activation energy, gyrotactic microorganisms, and magnetic field effects. Similarly, Ramzan et al. [17] conducted an analysis of the transport dynamics of a Sutterby-type nanofluid over an expanding disc, incorporating the influences of Hall current and ion drift effects, Cattaneo–Christov dual-phase diffusion, and the movement of motile microorganisms exhibiting directed locomotion. Their study provided insights into the thermal and concentration distributions influenced by these complex physical mechanisms. Shateri et al. [18] performed a numerical investigation on microorganism-driven convection in a magnetically responsive non-Newtonian hybrid nanofluid containing motile microorganisms with directed movement, employing the Buongiorno framework. Sagadevan et al. [19] analyzed the microorganism-induced convective transport of a nano-enhanced fluid surrounding a rotating disk, integrating motile microbial activity, radiative heat transfer, and reversible chemical interactions. They analyze heat and mass transfer, reaction kinetics, and fluid dynamics, offering insights for applications in biotechnology and thermal engineering. See the references [20–23] for the more recent development in the field.
From the novelty point, this work investigates the explicit solution of the porous magnetized flow of a Casson nanofluid along variable thermal conductivity and exponential heat generation. The mass transport is studied to examine the effect of exponential activation energy at different level. The microorganism phenomena with convective boundary conditions are also considered in the current problem. The governing flow model PDEs are converted into ODEs with the help of similarity transformation. Results are derived using the MATLAB Bvp4c technique to study the effects of different emerging parameters. Moreover, comparison table is drawn to see the great harmony with previous published work.
2. Formulation of Flow Mechanism
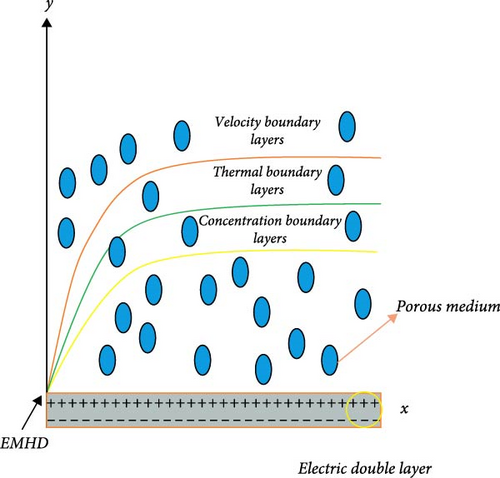
In this work, we consider the steady l Casson nanofluid flow 2D model in the presence of exponentially stretchable surface with bio-convection phenomena driven by microorganisms. A perpendicular magnetic field is imposed on the stretching sheet surface, influencing the fluid dynamics. Additionally, the study incorporates an exponential heat exchanger and activation energy, subject to convective boundary conditions, to comprehensively analyze the thermal and transport phenomena. The geometry of the flow is shown in Figure 1, with stretching velocity is . By incorporating the specified assumptions and employing the boundary layer theory, the key equations that describe the behavior of the fluid flow system are established as follows.
2.1. Flow Equations
2.2. Explicit Solutions
Here, β and λ are the Casson fluid parameter and the convergence parameter, respectively, is the magnetic parameter, is the porosity parameter, γ is the variable thermal conductivity parameter, is the Prandtl number, n is the index number, is the thermophorisis parameter, is the Brownian motion parameter, is the chemical reaction parameter, is the activation energy parameter, is the temperature ratio parameter, is the peclet number, and is the micro-organism ratio parameter.
2.3. Physical Quantities
Here, is a local Reynolds number.
2.4. Solution Methodology
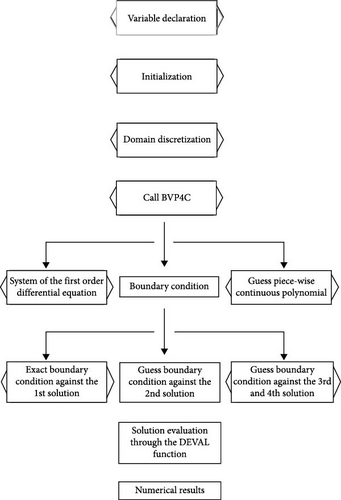
The numerical chart is presented in the Figure 1b.
3. Findings and Analysis
This study investigates the impact of key parameters on Casson nanofluid dynamics over an exponentially stretching surface, emphasizing their role in flow behavior and thermal characteristics. The parameters under investigation include Casson fluid parameter (β), Prandtl and magnetic number, suction/injection and thermal variation parameters, exponential heat source parameter, Brownian motion, thermophoresis effect, stretching ratio parameter, Schmidt number, and Peclet number.
3.1. Graphical Discussion
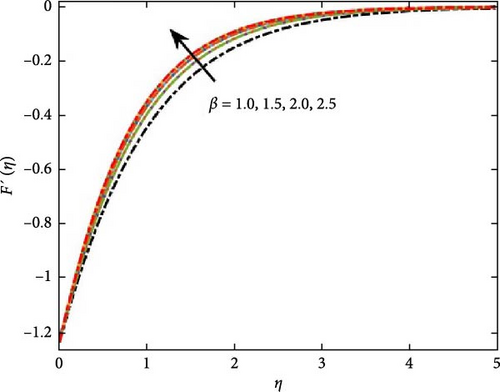
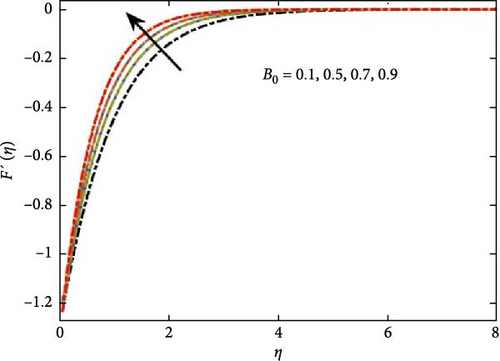
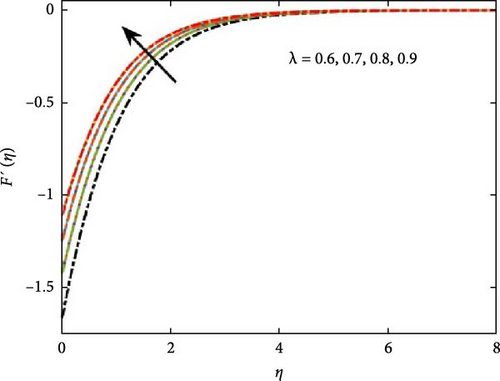
Here we discuss the graphical investigation of the evolving parameters. Figure 2a illustrates the influence of the Casson fluid parameter (β) on the velocity profile in Casson nanofluid flow over an exponentially stretching surface, highlighting its effect on fluid motion dynamics. Increasing β leads to decreased velocity and behavior closer to that of a Newtonian fluid as β approaches infinity. These observations are consistent with the expected behavior of Casson fluids in non-Newtonian fluid dynamics. Porosity plays a significant impact in shaping the velocity profile of Casson nanofluids within porous media. The unique rheological properties of Casson nanofluids, including yield stress and non-linear viscosity, add complexity to the relationship between porosity and velocity. Figure 2b shows that as the porous parameter (B0) increases. A higher porosity level generally enhances fluid viscosity, as increased interaction between the fluid and the porous structure imposes greater resistance to flow. In electrically conductive fluids, an externally applied electromagnetic field interacts with charged particles, producing a MHD force. This force, aligned at a right angle to both the fluid flow and the imposed magnetic influence, opposes the motion of the fluid, thereby altering its dynamic behavior.
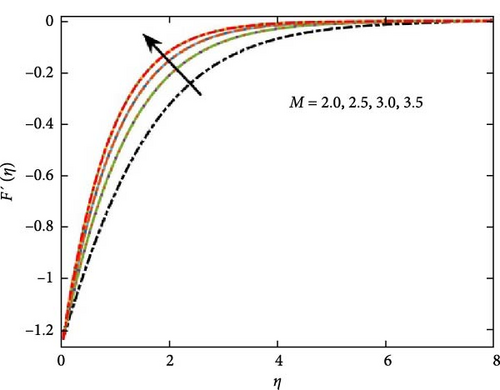
Furthermore, Figure 3a depicts that an increase in the intensity of the applied magnetic field influences (M) has the effect of decreasing the velocity profile of the fluid. This suppression occurs because the magnetic field exerts a force (Lorentz force) that opposes the fluid’s motion. The change at solution of velocity profile is explained in Figure 3b. As the Prandtl number increases, the temperature gradient within the fluid steepens, signifying reduced thermal diffusivity. This results in slower thermal mixing and a prolonged retention of temperature variations within the fluid. A higher Pr can reduce convective heat transfer, leading to less efficient cooling or heating processes.
These characteristics of the Pr number against the temperature profile are depicted in Figure 4a, which shows a decrease in temperature. Increasing Nt results in stronger thermophoretic forces, which lead to deeper migration of nanoparticles and more pronounced temperature variations. Figure 4b is the simulated output of this phenomena which explains the rise in the temperature profile. Brownian motion in Casson nanofluids enhances the dispersion of nanoparticles, contributes to higher effective thermal conductivity, and promotes heat transfer by reducing temperature gradients.
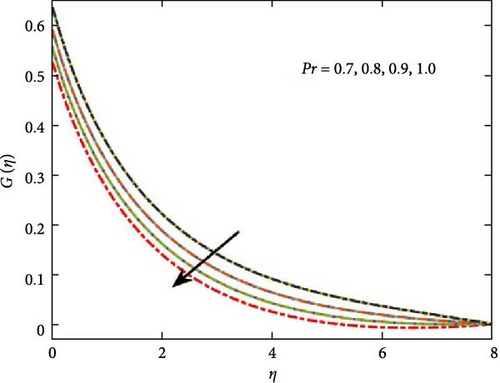
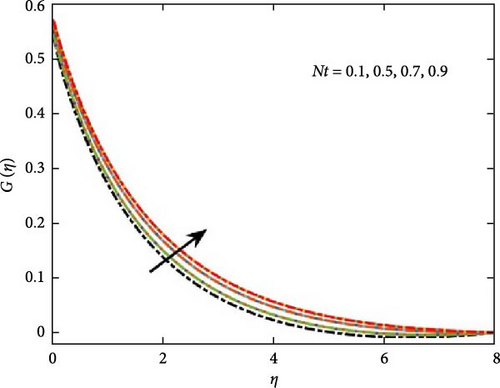
Figure 5 illustrates the declining trend of the temperature profile. With an increase in thermal conductivity, the temperature gradient diminishes, leading to a more uniform temperature distribution. This enhancement in thermal conductivity facilitates more efficient heat transfer throughout the nanofluid. Figure 5b graphically interprets that the temperature profile goes up due to the accelerating conduction rate.
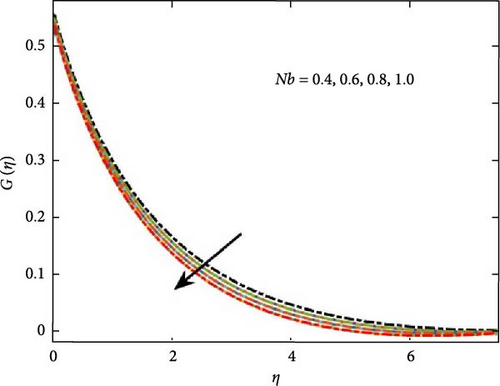

Figure 6 shows the influence of internal heat generation on the temperature profile. It is evident that as the heat source parameter intensifies, the temperature increases accordingly. Meanwhile, Figure 7 depicts the influence of the thermal gradient parameter, demonstrating a decrease in temperature as its magnitude increases. Additionally, an enhancement in the chemical reaction rate accelerates interactions between nanoparticles and the surrounding fluid. This heightened reaction rate facilitates a faster conversion of nanoparticles, leading to a reduction in the mass concentration profile, as graphically represented in Figure 7.
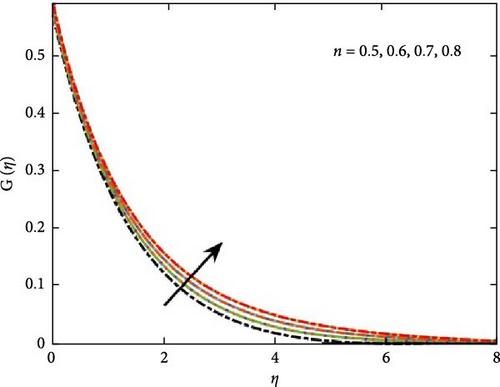
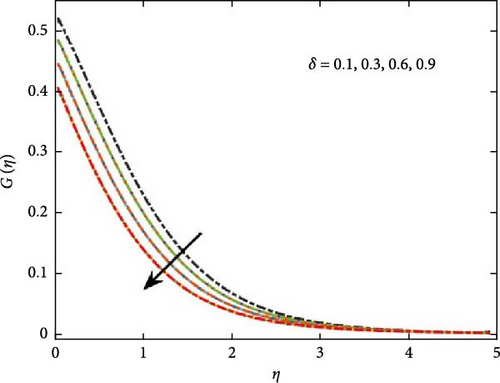
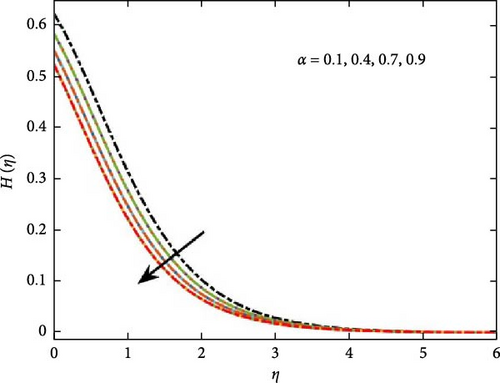
Figure 8 illustrates the influence of internal mass generation intensity, revealing a decline in concentration as the heat exchange index number parameter increases. Furthermore, a rise in the activation energy parameter signifies a higher energy barrier for chemical reactions, thereby slowing reaction rates. Consequently, nanoparticles undergo a more gradual transformation into chemical species, as depicted in Figure 8.
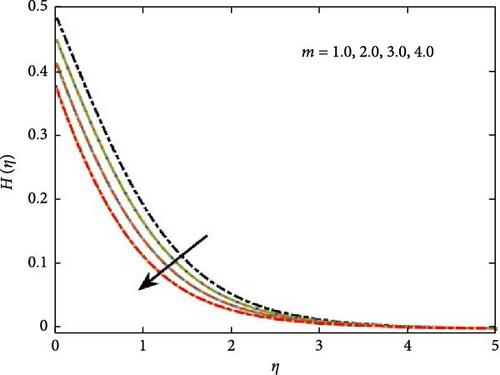

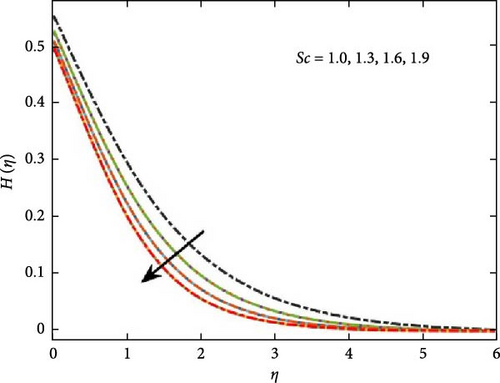
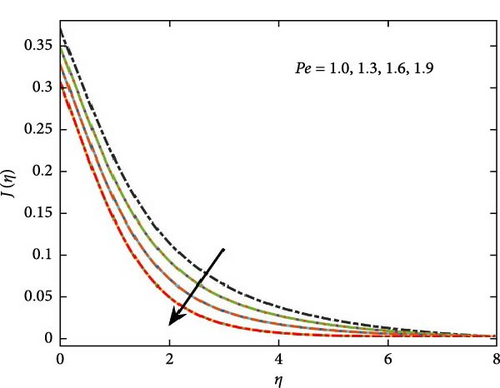
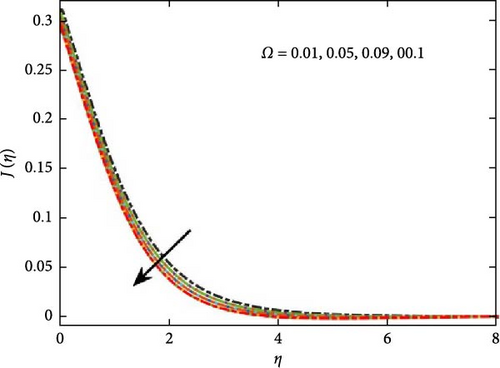
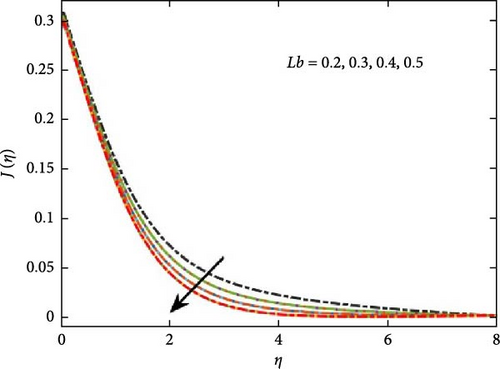
Figure 9 illustrates the influence of the Schmidt number on concentration distribution, indicating that as its value increases, concentration levels diminish. Additionally, Figure 10 explores the role of the Peclet number in microbial growth, highlighting its effect on the proliferation of microorganisms. It shows that the greater values of Peclet number reduce the diffusivity of the microorganism, which result to reduce the motile density profile. Further, Figure 10b interprets the behavior of the concentration difference parameter Ω on microorganism profile, which shows decrease in the growth of the microorganism for positive values. The impact of the Lewis number against microorganism profile is shown in Figure 11. The increase for the range of bioconvection Lewis number 0.2–0.5 shows decline in the growth of micro-organism profile due to decrease in the diffusion rate of microorganism particles. The figure shows that the mass concentration goes down due to the higher momentum diffusion.
3.2. Tabular Discussion
In this section, we present the numerical results of various parameters, organized in Tables 1–4. Table 1 highlights the effects of the Prandtl number, Casson parameter, and variable thermal conductivity on the Nusselt number. The findings reveal that an increase in the Prandtl number and Casson parameter results in a decrease in the Nusselt number, while an increase in variable thermal conductivity enhances the Nusselt number.
| Pr | β | γ | Nu |
|---|---|---|---|
| 0.070 | — | — | 0.898822 |
| 0.200 | — | — | 0.861185 |
| 0.700 | — | — | 0.686157 |
| 1.0 | — | 0.575093 | |
| 3.0 | — | 0.552110 | |
| 5.0 | — | 0.546300 | |
| — | 0.1 | 0.435272 | |
| — | 0.3 | 0.475974 | |
| — | 0.5 | 0.529543 |
| M | β | s | B0 | Cfx |
|---|---|---|---|---|
| 2.0 | — | — | — | 1.31933 |
| 3.0 | — | — | — | 2.20983 |
| 5.0 | — | — | — | 3.27494 |
| 1.0 | — | — | 2.3883 | |
| 3.0 | — | — | 2.01358 | |
| 5.0 | — | — | 1.92868 | |
| — | 2.5 | — | −3.55405 | |
| — | 3.0 | — | −3.95511 | |
| — | 5.0 | — | −5.67904 | |
| — | — | 0.1 | −2.30939 | |
| — | — | 0.2 | −2.41453 | |
| — | — | 0.3 | −2.51468 |
| Sc | δ | M | E | Sh |
|---|---|---|---|---|
| 1.0 | — | — | — | 0.26150 |
| 1.5 | — | — | — | 0.29680 |
| 2.0 | — | — | — | 0.31780 |
| 0.1 | — | — | 0.23690 | |
| 0.3 | — | — | 0.27180 | |
| 0.5 | — | — | 0.31430 | |
| — | 1.0 | — | 1.79500 | |
| — | 2.0 | — | 0.34450 | |
| — | 3.0 | — | 0.31430 | |
| — | — | 0.1 | 0.44880 | |
| — | — | 0.3 | 0.39900 | |
| — | — | 0.5 | 0.36650 |
| Pe | Ω | M | E | Qnx |
|---|---|---|---|---|
| 1.0 | — | — | — | 0.170838 |
| 1.5 | — | — | — | 0.184782 |
| 2.0 | — | — | — | 0.195040 |
| 0.1 | — | — | 0.155251 | |
| 0.3 | — | — | 0.171092 | |
| 0.5 | — | — | 0.193350 | |
| — | 1.0 | — | 0.365562 | |
| — | 2.0 | — | 0.203591 | |
| — | 3.0 | — | 0.193350 | |
| — | — | 0.1 | 0.157089 | |
| — | — | 0.3 | 0.205713 | |
| — | — | 0.5 | 0.193350 |
The effects of the magnetic parameter, Casson parameter, suction parameter, and porosity on skin friction are presented in Table 2. The data reveals that elevated magnitudes of the magnetic parameter, suction parameter, and porosity contribute to an enhancement of skin friction, whereas a rise in the Casson parameter leads to a decline in skin friction. Table 3 examines the effects of changes in the Schmidt number, temperature difference parameter, magnetic number, and activation energy parameter on the Sherwood number. The results demonstrate that the Sherwood number increases with higher values of the Schmidt number and temperature difference parameter. Table 4 provides the variations in the Peclet number, microorganism difference parameter, magnetic parameter, and activation energy parameter on the microorganism number. The results show that the number of motile microorganisms increases with higher values of the Peclet number, microorganism difference parameter, and activation energy parameter, while it decreases with an increase in the magnetic parameter. Table 5 represents the comparison of the different values of M for the skin friction, which shows great harmony with previously published data.
| M | Akbar et al. [27] | Present results |
|---|---|---|
| 1.00 | 1.41421 | 1.41423 |
| 5.00 | 2.44948 | 2.44947 |
| 10.0 | 3.31662 | 3.31666 |
| 50 | 7.141442 | 7.141444 |
| 500 | 22.3830 | 22.3835 |
| 1000 | 31.6386 | 31.6387 |
4. Concluding Remarks
- •
Increment in the porosity and Casson nanofluid parameter shows reduction in the behavior of the velocity profile.
- •
Increase in the value of the λ increases the convergence rate.
- •
Positive increment in the variable thermal conductivity parameter accelerates the fluid temperature.
- •
Thermophoresis and Brownian motion parameter response is contrast to the temperature behavior. It seems that temperature boost for thermophoresis parameter but shows opposite trend for Brownian motion.
- •
Increase in the activation energy parameter accelerates the mass transport rate.
- •
Positive change in Peclet and bioconvection Lewis number decreases the growth of the microorganism.
- •
An enhancement has occurred in the skin friction due to the influence of magnetic and suction effect.
- •
Heat transfer rate reduces due to the increment of the Prandtl number and Casson parameter.
4.1. Future Directions
A potential future direction could involve extending this study to three-dimensional flows, incorporating additional factors such as chemical reactions, non-Newtonian fluid behavior, and advanced boundary conditions over a different geometry, while exploring real-world applications in energy systems, biomedical engineering, and environmental processes.
Nomenclature
-
- u, v:
-
- Velocity components (LT−1)
-
- uw:
-
- Stretching velocity (LT−1)
-
- vw:
-
- Mass flux velocity (LT−1)
-
- cp:
-
- Specific heat (L2T−2θ−1)
-
- α:
-
- Thermal diffusivity (L2T−1)
-
- v:
-
- Kinematic viscosity (L2T−1)
-
- ρ:
-
- Density (ML−3)
-
- μ:
-
- Dynamic viscosity (ML−1T−1)
-
- k:
-
- Thermal conductivity (MLT−3θ−1)
-
- T:
-
- Fluid temperature (θ)
-
- T∞:
-
- Ambient temperature (θ)
-
- σ:
-
- Electrical conductivity (ML−1L−3T3A2)
-
- Bo:
-
- Magnetic field strength (MT−2A−1)
-
- τ:
-
- Spin gradient viscosity (ML−1T−1)
-
- Pe:
-
- Péclet number
-
- Ω:
-
- Micro-organism ratio parameter
-
- λ:
-
- Convergence parameter
-
- Rex:
-
- Local Reynolds number
-
- Cf:
-
- Skin friction coefficient
-
- E0:
-
- Electric field strength
-
- Sc:
-
- Schmidt number
-
- Peb:
-
- Bioconvection Péclet number
-
- M:
-
- Magnetic field parameter
-
- k1:
-
- Mean absorption coefficient (L−1)
-
- σ∗:
-
- Stefan-Boltzmann constant (MT−3θ−4)
-
- DB:
-
- Brownian diffusion coefficient (L2T−1)
-
- DT:
-
- Thermophoresis diffusion coefficient (L2T−1)
-
- qm:
-
- Mass flux (ML−1T−1)
-
- qw:
-
- Heat flux (MT−3)
-
- Nw:
-
- Wall concentration of microorganisms (L−3)
-
- β:
-
- Casson fluid parameter
-
- Nt:
-
- Thermophoresis parameter
-
- Nb:
-
- Brownian motion parameter
-
- Pr:
-
- Prandtl number
-
- δ:
-
- Temperature ratio parameter
-
- Nux:
-
- Local Nusselt number
-
- Shx:
-
- Local Sherwood number
-
- Nnx:
-
- Local bioconvection Nusselt number
-
- α1:
-
- Chemical reaction parameter.
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
Shahzad Khattak: supervising the study, mathematical modeling, analyzing. Muhammad Naveed Khan: writing the draft, collection of data. Mohammad Yar: editing the original draft, visualized the results. Mohamed Hussien: software, methodology, analyze the results. Taoufik Saidani: project administrative, comparing the results. Kaouther Ghachem: construction of coding, figures formulation. Lioua Kolsi: formal analysis, conceptions, investigation.
Funding
The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number (NBU-CRP-2025-2225). Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R41), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number (NBU-CRP-2025-2225). Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R41), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Open Research
Data Availability Statement
All data regarding to the paper is included in the manuscript.




