This paper proposes a robust DC-link voltage controller designed for a multilevel-based static synchronous compensator (STATCOM), addressing both DC-link capacitance degradation and load variations. The uncertainty in DC-link capacitance is modeled as an external perturbation, leading to the development of a second-order sliding mode controller (SOSMC) based on a twisting algorithm. This controller effectively manages these uncertainties, providing high stability and robustness against parameter variations and external disturbances. Furthermore, it reduces unwanted chattering and enhances overall system performance. The impact of DC-link capacitance uncertainty on the reliability of multilevel converters is analyzed, comparing the proposed SOSMC with traditional proportional–integral (PI) controllers in the Simulink MATLAB environment. The results demonstrate that the SOSMC method outperforms the PI controller under 33% uncertainty in DC-link capacitance over 5 years. The proposed control scheme not only meets reactive power demands but also effectively manages uncertainties in DC-link capacitors. Additionally, the twisting algorithm maintains an acceptable total harmonic distortion (THD) index on the AC side, thereby improving overall reliability while reducing maintenance costs.

1. Introduction

The reliable and optimal operation of high-power static synchronous compensators (STATCOMs) is crucial for addressing the challenges faced by modern power grids. These challenges include reactive power demands, nonlinear loads, and unbalanced conditions [1]. STATCOMs provide responsive reactive power control and thus help to stabilize grid voltage, improve power factor, and enhance overall power quality [1]. Maintaining the reliability of these critical compensators is paramount to ensuring the secure and efficient operation of modern power systems.

Since a common two-level converter cannot correct the desired output voltage in high-power applications, it is necessary to use a multilevel converter. Among different multilevel topologies, the cascade H-bridge (CHB) converter is an appropriate choice in STATCOM applications because of its modularity and scalability, especially for high-voltage, high-power applications [2, 3].

In CHB converters, the high number of submodules can negatively impact the overall reliability of the STATCOM system. In this regard, DC-link capacitors contribute to nearly 30% of component failures [4]. Both aging and cell/fuse failures (e.g., thermal and electrical stresses) can degrade DC-link capacitance, leading to an increase in DC-link voltage ripple, fluctuations in grid currents, and an increase in the AC-side current total harmonic distortion (THD) index [5]. This condition not only impacts the optimal performance of the system but can also lead to unexpected outages. The greater the degradation of DC-link capacitance is, the more the result is pronounced. THD can further exceed the permissible range provided by the IEEE 519 standard. Although it does not directly cause a problem, it prompts unstable modes and activates the protection devices to disconnect the entire STATCOM system if the degradation continues [6]. To address this issue, several effective methods must be employed to enhance the system’s reliability while considering the required level of maintenance [7]. These methods cannot only reduce the required repairs and maintenance but also significantly decrease the probability of STATCOM shutdown [8].

Reliability can be improved in the design phase (before operation) using different modification techniques such as reliability-oriented design [9, 10] and analytical analysis [11, 12]. Adding redundant cells [7] can be also helpful in ensuring the reliable operation of the converter after a predefined number of failures. Sousa et al. [11] proposed a reliability-oriented design with redundancy factor selection in a 13.8 kV/17 MVA multilevel STATCOM. Additionally, a redundancy-based fault tolerant strategy has been proposed in [13] to enhance reliability and extend the useful lifetime in postfault conditions.

Instead of the design phase, the reliability can be also examined in the operational phase (during operation) via condition monitoring [14] and fault tolerant control methods [15]. Proposing a new effective control scheme (DC-link control while limiting THD on the load side) is vital to guarantee the STATCOM’s reliable performance without interruption under faulty conditions [16]. This finally leads to a relatively lower need (cost) for repairs and maintenance over a long-term period.

The control schemes in STATCOM are typically implemented in three different stages: DC-link average voltage control, output current control, and capacitor voltage balancing. First, the DC-link voltage control loop is primarily used to eliminate DC-link voltage ripple, followed by a current control loop to inject or absorb reactive power [17]. In the field of modular multilevel STATCOMs, different linear and nonlinear current control schemes are reviewed in [18]. Due to the nonuniform instantaneous active power distribution among cells, an individual DC-link voltage balancing scheme is finally applied by either exploiting switching redundancy [19] or adding a compensating term to the modulation voltage [20].

These controllers are mainly classified into linear and nonlinear methods. Linear controllers, such as proportional-resonance (PR) [17] and proportional–integral (PI) [21] have obtained significant attention in both academic and industrial due to their simplicity. However, they are not model-based and cannot consider uncertainty in the system’s model. Therefore, various nonlinear methods have devoted considerable attention to STATCOM applications, addressing uncertainty, perturbations, and load fluctuations. They include hysteresis control [22], fuzzy control [23], backstopping control [24], model predictive control [25], and neural network passivity-based control [16]. In all aforementioned works, the reliability concern with a specific focus on the capacitor bank (CB) faults has not been addressed yet.

Focusing on reliability, an adaptive nonlinear control algorithm is proposed in [26] to regulate the DC-link voltage of grid-connected converters. An adaptive controller is also introduced in [4] to improve converter reliability by controlling the cell reference voltages based on the minimum required voltage in each operational condition. Sajadi et al. [19] presented a modification mechanism based on modulation index magnitude to regulate the DC-link voltage set-point. In all mentioned studies, the robust DC-link controller is effectively utilized at a lower complexity while achieving the control objectives (improving reliability) efficiently.

In power electronics applications, sliding mode control (SMC) has recently been recognized as a promising method [27] due to its inherent robustness against parameter variations and external disturbances. In this regard, several research studies and practical applications have especially focused on the challenges of implementing SMC in power electronics systems, such as [28] highlighting its industrial applications. However, the implementation of SMC in practical settings also faces certain limitations in real-word such as chattering phenomena, which can result in high-frequency switching and increased system complexity. Furthermore, the appropriate design of sliding surfaces and reaching conditions requires careful consideration to ensure stable and optimal system performance. Ongoing research continues to explore advanced SMC techniques aimed at overcoming these limitations and further enhancing the applicability of SMC in power electronics and other real-world systems [28]. To achieve this goal, the second-order SMC (SOSMC), for example, twisting SMC, not only addresses these aforementioned key concerns but also provides higher accuracy and superior tracking performance in dynamic environments [27]. A SOSMC is also developed in [29] for a three-level four-leg D-STATCOM based on symmetrical components. A fractional-order SMC has been proposed in [30] for the D-STATCOM application, considering its parametric variations in the outer current loop. A SMC has been studied for D-STATCOM application considering DC-link voltage variations [8]. The presented controller is robust against DC-link uncertainties and load variations, offers low current THD in steady-state conditions, and enhances the system’s reliability and stability margins.

Despite the various advantages of SMCs, their implementation remains limited in high-power converters. Although considerable research addresses the use of SMC in the STATCOM’s current control loop, a noticeable gap exists in its performance in other control areas, such as DC-link voltage control. This issue is the focus of the present paper. Based on the literature reviewed, several significant research gaps remain, as follows:

•
PI controllers are often ineffective in handling uncertain conditions over extended periods. Since the reduction in DC-link capacitance can be modeled as an external perturbation in the DC-link equations, there is a need for a robust controller to handle this uncertainty. This paper presents a SOSMC to address the uncertainty in DC-link capacitance.
•
Existing literature largely focuses on developing robust SMCs, but reliability concerns in STATCOM control remain underexplored. In a three-phase multilevel converter, the high number of cells increases the probability of failure, which can lead to lower reliability. Typically, reliability improvements are made during the design phase rather than during actual operation causing higher initial costs. This study investigates the positive impacts of a DC-link voltage controller on reliability, operational lifespan, and required maintenance intervals of a multilevel CHB-based STATCOM system. Consequently, we have developed a new SOSMC approach aimed at enhancing reliability while decreasing the THD index on the AC side during real-time STATCOM operations without incurring additional costs.
•
Primarily, reliability improvements are achieved during the design and operational phase through redundancy assessment and maintenance intervals, which impose additional initial and operational costs on the system. It is important to consider whether to incur higher initial costs for redundancy or to enhance the expected lifetime through a control system, thereby decreasing the maintenance intervals. Implementing the proposed SOSMC method results in an increased lifespan of the STATCOM and a reduced need for redundancy and maintenance intervals, ultimately contributing to the system’s cost-effectiveness.

Considering the existing research gaps, this paper proposes a SOSMC for CHB-based STATCOMs to balance the DC-link voltage under capacitance uncertainties and load variations. The accuracy, effectiveness, and performance of the proposed SOSMC scheme are compared with that of a PI controller. Specifically, the main contributions of this paper are as follows:

•
A novel SOSMC scheme is proposed for controlling the DC-link voltage in a multilevel STATCOM.
•
Compared to the PI controller, the SOSMC demonstrates superior capability in maintaining the THD index within acceptable limits for extended periods, showcasing improved reliability due to its robustness and handling of structural uncertainties.
•
The proposed SOSMC method leads to higher reliability, reduced maintenance intervals, and consequently lower operational and initial costs.

The rest of the paper is organized as follows: Section 2 discusses the modeling of the CHB-based STATCOM system. Section 3 provides details of the controllers and their formulation. In Section 4, we present our proposed twisting-based SOSMC. Section 5 presents the simulation results. Finally, we conclude the paper in Section 6.

2. STATCOM and Uncertainty Modeling

An appropriate model of the AC side of the STATCOM is necessary for the design of the controller. In this section, we develop a mathematical model for multilevel STATCOM applications. Figure 1 shows a CHB-based STATCOM. As illustrated in Figure 1a, it consists of a multilevel cascade-voltage-source converter with separate DC-link capacitors. The coupling inductors in each phase (L_a, L_b, L_c) act as current harmonic filters mainly created by modulation. Since the stray inductance of connections and cables (L_1a, L_1b, L_1c) is much smaller than the filter inductance, they can be ignored in the converter modeling. Each cell contains four switches with antiparallel diodes and one DC-link capacitor (C_SM) as depicted in Figure 1b. The sum of nominal value (C₀) and uncertainties (ΔC) in the equivalent capacity can be considered as C_SM = C₀ + ΔC to account for capacitor uncertainness. Furthermore, the switching and conduction losses in each cell are modeled with a parallel resistor (R_P).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Multilevel CHB-based STATCOM: (a) STATCOM schematic, (b) uncertainty modeling for each H-bridge, (c) phasor representation in capacitive mode, (d) phasor representation in inductive mode, and (e) proposed control system. CHB, cascade H-bridge.

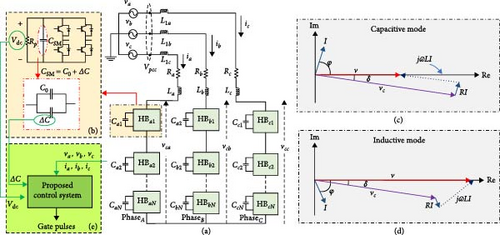
The control system in STATCOM regulates the output reactive current by controlling the fundamental voltage on the AC side of the converter. Additionally, the active power flowing from the grid to the STATCOM is controlled by introducing a small phase shift (δ) between the grid voltage and the AC voltage at the terminals of the H-Bridge. This helps compensate for the losses in the H-bridge cells which are estimated at ~5% of the nominal power of the voltage source converter (VSC) [8]. Figure 1c,d shows the CHB-STATCOM phasor diagram in the inductive and capacitive modes. As it is shown, the reactive power is injected into or absorbed from the grid by STATCOM (capacitive/inductive mode), when v_c = (v_ca, v_cb,v_cc) is greater or smaller than v = (v_a, v_b, v_c).

2.1. AC Side Modeling

Assuming symmetric conditions (L = L_a = L_b = L_c, R = R_a = R_b = R_c), and balanced three-phase voltage sources, the phase currents equations can be written as Equation (1) [31]:

(1)

Then, the ABC stationary frame can be transformed into the d–q synchronous frame, and the state equations can be derived as follows:

(2)

When the three-phase grid voltage(v_a, v_b, v_c) is sinusoidal and balanced, v_q is always zero because v_a is aligned with the d-axis. This alignment allows for independent control of active and reactive power. The instantaneous active power (P) and the instantaneous reactive power (Q) are expressed as follows:

(3)

(4)

According to Equations (3) and (4), the active power reference is derived from the output of average DC-link voltages, while the reactive power reference (Q_ref) can be set by the external control system. Consequently, the q-axis current reference is determined by .

2.2. DC Side Modeling

To model the internal losses of each cell, the dynamic equation of each DC-link capacitor is derived considering a parallel resistor (R_P) associated with the corresponding DC-link. To represent the DC-link voltages (V_dc) in the d–q coordinate framework, Kirchhoff’s Current Law (KCL) must be applied as written in Equation (5) [8, 31]:

(5)

Substituting the equivalent capacity (C_SM = C₀ + Δc) of each cell and drawing certain and uncertain parts, Equation (5) becomes Equation (6) [8]:

(6)

For each phase, the cluster DC-link average voltage V_dcj (j = a, b, c) is calculated as the sum of all DC-link capacitor voltage (V_dc) divided by N. It is then expressed as the total DC-link average capacitor voltage

according to Equation (7):

(7)

Substituting

from Equations (7) in (6) yields the following equation:

(8)

The output voltage error

and its time derivative

are defined as new state variables. As shown in Appendix A, the final state equations for the STATCOM considering DC-link uncertainty are written as Equation (9):

(9)

Since capacitance uncertainty manifests as external perturbations (ΔU) in the model, the conventional PI controller cannot effectively handle these perturbations and does not demonstrate satisfactory dynamic performance. This term must be included in the DC-link voltage control system, as illustrated in Figure 1e. Thus, a SOSMC controller based on a twisting algorithm is introduced and investigated in the following section.

3. Control Scheme

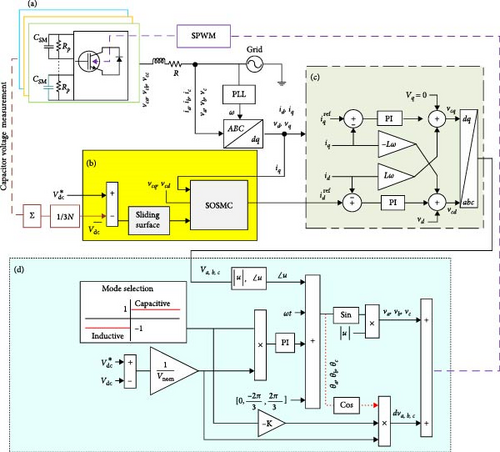
Figure 2 illustrates the proposed overall control scheme for multilevel-based STATCOM. Figure 2a shows the H-bridge converter connected to the grid, while the subsequent sections (Figure 2b–d) depict the various components of the control system. This control scheme aims to achieve the following objectives:

a.
Control the average DC-link voltage to determine the d-axis current reference (Figure 2b).
b.
Manage the exchange of reactive power transmitted between the converter and the PCC point through current control (Figure 2c).
c.
Control the DC-link capacitor voltage to ensure voltage balancing across all cells (Figure 2d).

The DC-link voltage controller operates within the primary control loop to regulate DC-link capacitor voltages in each phase and generates the required d-axis current reference for the secondary loop. The current controller then subsequently produces the reference signals for the PWM modulator to inject or absorb the required reactive power (Figure 2d) [24].

As indicated in Figure 2d, the outer loop facilitates the control of all individual DC-link voltages by effectively exchanging active power with the grid. A balanced voltage across each cell is achieved by incorporating a compensation term into PS-PWM modulation. Consequently, the modulator plays a crucial role in determining the switching performance of the converter. As shown in Figure 2d, a DC term (v_A, v_B, v_C) and a complementary term (dv_A, dv_B, dv_C) are combined to form the reference voltage of each H-bridge. The DC term is derived from the mean DC capacitor voltage and easily provides the jth phase-clustered balancing control signal (v_A, v_B, v_C).

The DC term is a vector that is in phase with the input current and is added to the complementary term. This DC term compensates for the unequal power losses in the H-bridge cells. For the j-phase of the ith converter, the PI controller tracks each H-bridge DC voltage (v_dc,i,j) as well as the actual average capacitor voltage (). To adjust, they are multiplied by the cosine of the reference current angle, and reference phase voltages (v_A, v_B, v_C) are added. By now, the active and reactive powers are equally shared among the cells.

As mentioned above, uncertainty in the DC-link capacitance significantly impacts the control performance of the CHB converter. Capacitor failure can lead to a degradation of the DC-link voltage, resulting in voltage divergence among the capacitors. This may cause unacceptable voltage drop or overvoltage due to non-uniform power distribution across the cells. Therefore, implementing an effective DC-link control scheme is crucial.

The following sections outline the developed SOSMC-based DC-link control scheme designed to address these challenges.

4. Proposed DC-Link Controller

In this section, a second-order sliding-mode controller is designed based on predefined state variables to tackle the challenges mentioned earlier. SMC involves defining a sliding surface (S) that guarantees Lyapunov stability, guiding the system states toward an equilibrium point. Additionally, an appropriate control law (u) is implemented to ensure that the system trajectory not only approaches the equilibrium point (u_eq) but also remains on the sliding surface (u_sw). While a first-order SMC controller can reduce the sliding variables to zero, it cannot deal with zeroing the derivatives of these variables effectively. As a result, even minor fluctuations in the sliding variables can lead to the chattering in the control signal.

This can be mitigated by designing a control signal that aims to set the first derivative of the sliding variable to zero. This approach facilitates the convergence of system trajectories in the plane toward the equilibrium point, thereby enhancing the overall stability and performance of the control system [27].

The sliding surface is defined based on the tracking error (

), where

represents the desired DC-link voltage and

is the actual average DC-link voltage. To minimize the chattering, the sliding surface is constructed as a combination of the tracking error and its integral. This integration allows for smoothing the control signal and enhances the system’s ability to reject disturbances while stabilizing the trajectory toward the desired state:

(10)

In general, the final control law (u) is composed of two components. The first component, the equivalent control law (u_eq) is determined from Equation (10) to ensure that the sliding surface

. This part of the control law is designed to maintain the system on the sliding surface and counteract any perturbations, contributing to the overall stability and performance of the sliding mode controller:

(11)

Based on the power balance equation between the AC and DC sides, Equation (6) yields the following equation:

(12)

By solving Equation (11) and substituting the results from Equation (12), we can express the derivative of the sliding surface

(13)

From this derivative, we can derive an expression for the equivalent control (u_eq):

(14)

This expression for u_eq is critical for ensuring that the system remains on the sliding surface, thereby achieving the desired performance criteria. Besides, the subsequent component of the control law addresses dynamic behavior and facilitates the system’s response to parametric uncertainty.

The discontinuous component (u_sw) is also incorporated into the final control law to ensure convergence to

in finite time. This part of the control law is especially designed to provide the necessary corrective action when the system deviates from the sliding surface. It can be expressed as follows:

(15)

where

By combining the equivalent control (u_eq) with the discontinuous control (u_sw), the overall control law u can be formulated to achieve robust performance and stability in the presence of disturbances and uncertainties. The complete control law is obtained as follows:

(16)

This formulation integrates both the equivalent control and the discontinuous control components, ensuring the system’s stability and convergence to the sliding surface. Figure 3 shows the structural schematic of the proposed SOSMC controller. The relevant SOSMC parameters (k₁, k₂) are essential for deriving the final control law. Consequently, the second derivative and the first derivative be utilized to establish the defined boundary limits for u_sw as follows.

By calculating the first- and second-time derivatives of the sliding surface (S and

, respectively) based on the converter equation given in Equation (11), the corresponding equations can be expressed as follows:

(17)

where ∅(x, t) and γ(x, t) are smooth functions. These equations will facilitate the determination of appropriate boundaries for the discontinuous control component (u_sw).

To ensure finite-time stability and to design a robust controller, the following conditions must be satisfied:

(18)

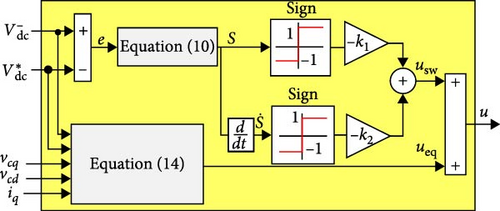
These conditions are crucial for guaranteeing the performance and stability of the sliding-mode control system as outlined in [32].

Therefore, the parameter ∅ and the parameter γ, which is constrained by 0 < Γ_m ≤ γ ≤ Γ_M, can be derived as Equation (19). This derivation is essential for ensuring that the control laws adhere to the specified bounds, contributing to the stability and performance of the system:

(19)

Now, considering the range of allowable parametric uncertainty in the converter, including the permissible perturbation, uncertainties in the inductor (L ± ΔL) and fluctuations in the capacitor (C ± ΔC), the constraint parameters (φ, Γ_m, Γ_M), along with k₁ and k₂, are calculated by establishing the following relationships for and γ:

(20)

The constraint parameters (Γ_m, Γ_M) can be obtained as Equations (21) and (22). These parameters play a significant role in defining the operational boundaries of the control system:

(21)

(22)

The Lyapunov function V(S) is defined as Equation (23) to evaluate the stability of the SOSMC once the states reach the sliding surface:

(23)

Regarding Equations (7), (10), and (15), the time derivative of V(S) is calculated as follows:

(24)

Finally, the stability is guaranteed if the following condition is satisfied:

The controller parameters (k₁, k₂) are determined by the finite-time sliding surface convergence conditions outlined in Equations (22), (23) [26, 27]. Additionally,

represents the upper bound of the uncertainty part of the nonlinear function f:

(25)

Subsequently, the stability of the proposed controller is maintained throughout the sliding phase.

5. Results and Discussion

This section focuses on validating the performance of the developed SOSMC design presented in Section 3. To evaluate the effectiveness of the SOSMC, a three-phase CHB-based STATCOM has been utilized, consisting of 13 power cells per phase. The converter is configured as shown in Figure 1, with a compensation capacity of 10 Mvar, and is connected to a 20 kV voltage network. Additionally, the PWM phase-shift modulation method has been implemented. Relevant technical parameters associated with the STATCOM and control schemes are summarized in Tables 1 and 2, respectively.

Table 1. System parameters.

Converter
Symbol	Value	Symbol	Value
S (MVA)	10		20
L (mH)	4.2	C (mF)	9.2
f (Hz)	50	f_sw (Hz)	500
V_nom,dc (V)	1500	R (Ω)	0.1

Table 2. Control parameters.

Controller
Type		Symbol	Value
DC-link	SOSMC	(k₁, k₂)	(20, 1)
DC-link	PI	(K_P, K_I)	(10, 800)
Current		(K_P, K_I)	(0.8, 8)
Individual balancing		(K_P, K_I)	(0.5, 5)

Abbreviations: PI, proportional–integral; SOSMC, second-order sliding mode control.

The parameters for the PI controller are determined based on [33]. The overall system model changes continuously due to the reduction in DC-link capacitance, making it unfeasible to identify optimal control coefficients for the PI controller. In contrast, the proposed SOSMC consistently demonstrates superior performance.

In the SOSMC method, the controller parameters (k₁, k₂) are calculated as Equation (25), based on the constraint parameters (φ, Γ_m, Γ_M) defined by Equations (20)–(22). These parameters are approximately φ ≈ 11.3 × 10⁶, Γ_m = 12 × 10⁶, and Γ_M = 19.87 × 10⁶. Furthermore, the performance of the presented controller is evaluated and compared under two different operating scenarios.

In Case 1, the reactive power change is analyzed, where it decreases from 10 MVAr to −10MAr at t = 0.4 s. In Case 2, the DC-link capacitance is reduced to 33% of its nominal value at t = 0.4 s, while the reactive power demand also decreases from 10 MVAr to −10 MVAr at t = 1 s. The DC-link side consists of film-type CBs, with a total capacitance of 9.2 millifarads. The failure rates for these capacitors can range from 0.1% to 1% per 1,000 h under nominal operating conditions. Considering these factors, a reasonable assumption of a 30% failure rate has been made over 5 years [8, 34].

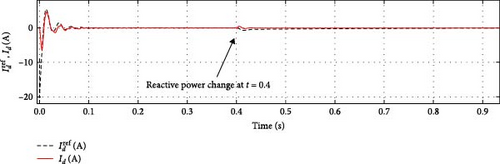
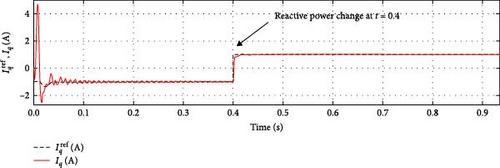
In Case 1, the dynamic performance of the STATCOM is validated in both capacitive and inductive operating modes, where the nominal reactive power transitions from capacitive mode to inductive mode at t = 0.4 s. Figures 4 and 5 illustrate the grid/converter voltage, grid current, average DC-link voltage, and active/reactive power for both the proposed SOSMC and the conventional PI controller. The results indicate that the SOSMC scheme effectively drives the DC-link voltage to track the reference value with minimal overshoot. Assuming that reactive power variation is the only variable, Figures 6 and 7 illustrate the performance of the SOSMC and PI controllers, respectively, regarding the d–q components of grid currents (i_d, i_q).

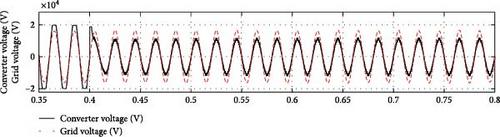
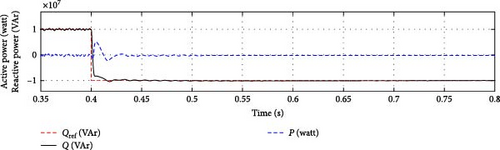
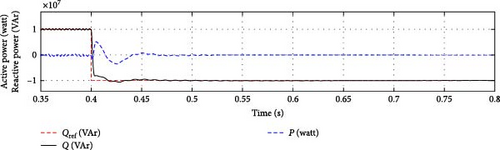
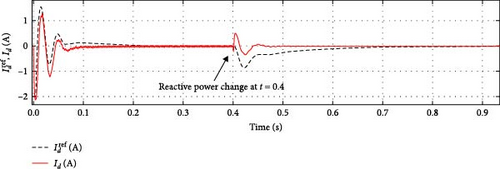
As shown in Figures 4 and 5, both the SOSMC and PI controllers exhibit negligible overshoot in the DC-link voltage during the transition with an approximate peak of 5 V. However, Figure 4 demonstrates that the SOSMC effectively prevents additional overshoots, unlike the results from the PI controller depicted in Figure 5. Both controllers take about 30 ms to track the DC-link reference voltage. Additionally, the proposed SOSMC scheme significantly reduces the chattering problem, resulting in minimal ripple.

The validation of the proposed SOSMC scheme demonstrates the controller’s efficiency, highlighting its robustness, good dynamic response, and rapid tracking of the DC-link reference.

Case 2: Comparing the performance of control systems under DC-link uncertainty.

To investigate and confirm the robustness of the SOSMC controller, the dynamic performance of both the SOSMC and PI controllers under two different scenarios is presented in Figures 8 and 9, respectively. These scenarios are as follows.

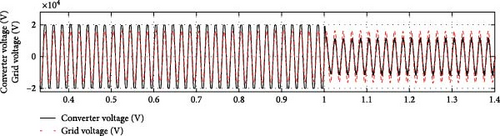
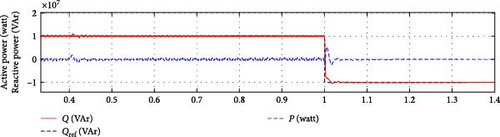
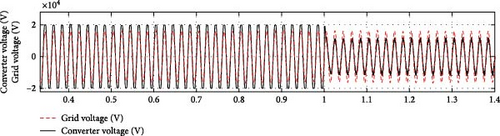
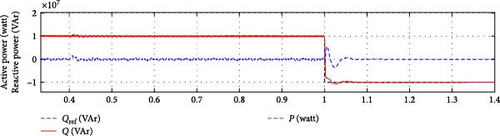
In the first scenario, the converter capacitor was changed from 9.2 mF to 66% × 9.2 mF at t = 0.4 s. In the second scenario, the converter mode transitions from full capacitive operation (10 Mar) to full inductive operation (−10 Mar) at t = 1 s.

Figures 10 and 11 present the performances of the SOSMC and PI controllers, respectively, concerning the d–q components of grid currents (i_d, i_q).

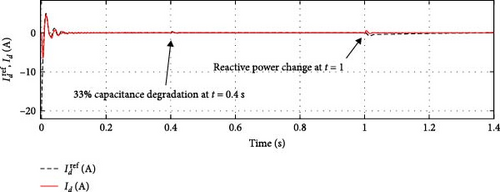
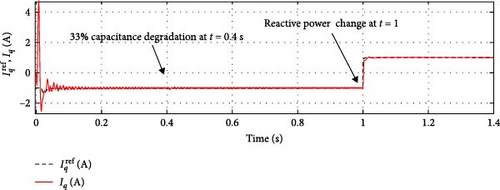
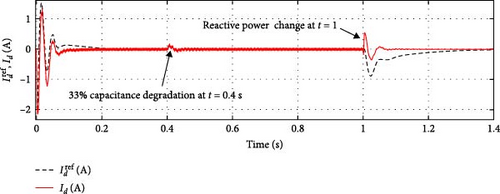
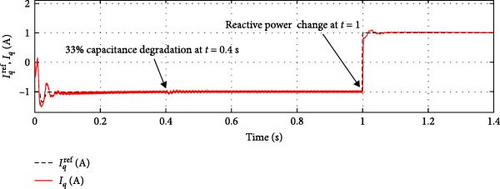
The validation of the proposed SOSMC scheme confirmed that the DC-link tracking process is faster with limited overshoot (approximately 12 V). Additionally, this result illustrates how the proposed SOSMC controller impacts reactive power demand tracking.

Figure 12 compares the DC-link voltages for the PI and SOSMC designs. As shown in this figure, DC-link voltage regulation is maintained throughout the entire duration, with a voltage ripple of less than 5% for each DC link. Although the average voltage ripples for both controllers were approximately the same, the PI controller had a settling time of 13 ms, while the proposed SOSMC controller achieved a significantly faster settling time of ~2 ms. Table 3 displays the THD index for the STATCOM output current, highlighting the superiority of the proposed SOSMC. The THD index of the SOSMC is recorded at 3.27% and 0.87% during capacitance reduction in capacitive mode in inductive modes, respectively. While these results are comparable and acceptable when contrasted with the conventional PI controller, even minor differences can lead to significant discrepancies over time.

Table 3. THD of STATCOM output current index under 33% capacitance variation.

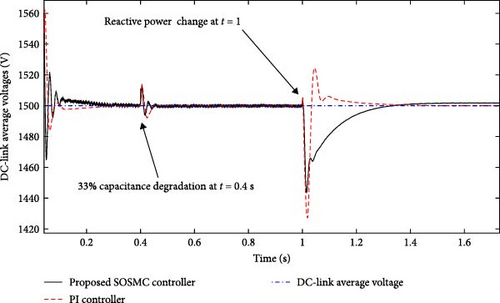
Controller	PI		SOSMC
Mode	Capacitive (%)	Inductive (%)	capacitive (%)	inductive (%)
Steady state response	3.07	0.26	3.12	0.20
Capacitance change	3.27	0.87	3.43	1.20

Abbreviations: PI, proportional–integral; SOSMC, second-order sliding mode control.

Additionally, comparative results of employing a first-order sliding mode controller in a distribution STATCOM indicate that the THD index for the first and SOSMCs, corresponding to inductive and capacitive modes, are similar. According to Hashemzadeh et al. [8], the THD values are 4.37% in capacitive mode and 3.21% in inductive mode, respectively.

5.1. AC Side THD

This section examines the effect of capacitance degradation on the AC side THD. Since the required reactive power (Q) is a constant value, the DC-link voltage ripple of the STATCOM will increase as some of the capacitors in the CB fail. Additionally, when the DC-link capacitance decreases, keeping output voltage constant, the amplitude of will increase, leading to a rise in the AC-side current THD.

Considering that the uncertainty in DC-link capacitance is modeled as an external perturbation in Equation (8), the proposed controller is capable of sustaining enhanced performance during DC-link capacitor failures. As a result, the fluctuations in DC-link voltage are more favorable to the proposed SOSMC controller. The output voltage waveforms under normal and aged conditions are illustrated in Figures 13a,b, respectively.

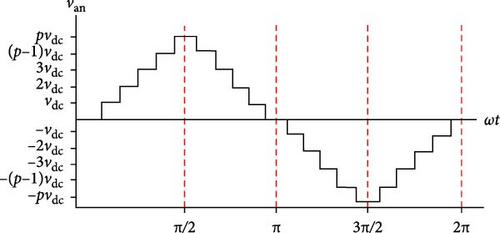
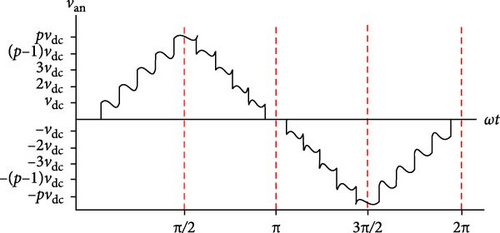
Therefore, when the DC-link capacitors fail, both voltage and current harmonics tend to increase. In this study, the performance of the system is fundamentally linked to the AC-side current THD, in accordance with IEEE−519 standards. The findings indicate that the proposed control system has a more substantial impact on AC-side current THD compared to conventional PI controllers.

5.2. Reliability

This section presents the impact of SOSMC design on the reliability index and the reliability model of the DC-link capacitors. We then estimate the lifetime of the STATCOM by considering the operating lifetime of the capacitors and the permissible THD for the system.

To this end, the expected lifetime of capacitors, as indicated in [34], is considered 155,194 h. The reliability function can also be expressed as follows [16]:

(26)

where f(x) represents the failure probability with a constant failure rate (λ). The probability density function is calculated as described in [16, 34]:

(27)

Figure 14 summarizes the harmonic characteristics of the control schemes and compares them with the operational lifespan.

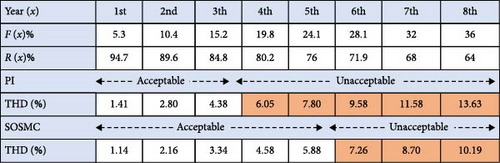
It can be concluded that the probability of capacitor failure increases over time, leading to a decrease in the reliability index. Since capacitor failure contributes to higher THD, a reduction in capacitance over time further elevates THD levels. According to the IEEE-519 standard, the permissible THD zone for high voltage–power levels is set at 6%. Consequently, the proposed SOSMC controller can ensure system performance remains within the acceptable THD range for 5 years, while this duration is shorter for the conventional PI controller, which is only 3 years.

Considering the impact of the proposed SOSMC controller on the expected lifespan of the system, it can be inferred that this controller enhances reliability on the DC-link side. It not only maintains efficient performance while accommodating uncertainties in DC-link capacity within the allowed THD range but also demonstrates improved reliability. As a significant outcome, the proposed SOSMC controller exhibits notable advantages over the conventional PI controller, particularly in terms of achieving a lower THD value and providing a very fast transient response. Overall, the performance of the proposed SOSMC scheme from the point of view of reliability is better than the PI controller. Furthermore, due to the variations in DC-link capacitance, the PI controller cannot be optimized with suitable coefficients, thus failing to achieve high reliability.

5.3. Cost Evaluation

The reliability of multilevel converters is influenced by both redundancy and maintenance levels. While increased redundancy enhances reliability during the design phase, it significantly raises initial costs. Additionally, proper maintenance routines during system operation can improve reliability, although they may also increase operational costs. Therefore, shorter maintenance intervals combined with high redundancy may enhance reliability but also incur high costs.

According to Figure 14, the maintenance interval for the SOSMC scheme is longer than that of the PI controller, allowing for reduced maintenance costs with the SOSMC control system. Consequently, the required redundancy level for the proposed SOSMC is lower than that of the PI controller, leading to decreased redundancy costs.

This paper suggests that implementing the proposed SOSMC method will extend the system’s maintenance interval while reducing shutdown and overall operational costs. Since maintenance costs are inversely related to redundancy costs, a tradeoff between them is necessary. To evaluate this tradeoff, the total cost for a multilevel STATCOM, considering redundancy and maintenance intervals, is calculated in this subsection, considering two different cases. In all scenarios discussed, it is assumed that the STATCOM operates for 8760 h per year and has a lifespan of 20 years. The two case studies are as follows:

Case I: Increasing reliability through maintenance without redundancy.

Case II: Increasing reliability through maintenance with redundancy.

5.4. Case I: Increasing Reliability Through Maintenance

The total cost for Case I is determined by considering maintenance intervals for both PI and SOSMC controllers. The required maintenance intervals are based on the pre-calculated lifetime provided in Figure 14. According to this table, at least 6 maintenance sessions (i.e., 3-year intervals) are recommended for the PI controller to achieve 89.6% reliability. In contrast, ~4 maintenance sessions (i.e., 5-year intervals) are required for the SOSMC controller to attain 99% reliability. The total maintenance cost is calculated based on the average cost associated with each maintenance interval [9]. Further details on the proposed maintenance cost modeling scheme can be found in Appendix B.

The SOSMC controller results in fewer maintenance sessions, leading to a lower overall cost. In this case, the cost of the STATCOM system is 1,518,800 €;. As shown in Table 4, not only is the maintenance interval for the proposed SOSMC longer than that of the conventional PI controller, but the reliability of the proposed SOSMC is also greater at the same cost.

Table 4. Comparison results of Cases I and II.

Case study	Assumption	Cost (€)
Case study	Assumption	Initial cost	Operational cost	Total cost
Case I: maintenance	PI without redundancy (reach 89.6% reliability)	1.779 × 10⁵	1.352 × 10⁶	1.530 × 10⁶
Case I: maintenance	SOSMC without redundancy (reach 99.0% reliability)	1.779 × 10⁵	1.340 × 10⁶	1.518 × 10⁶

Case II: redundancy and maintenance	PI with 10% redundancy (reach 98.6% reliability)	2.053 × 10⁵	1.354 × 10⁶	1.559 × 10⁶
Case II: redundancy and maintenance	SOSMC with 10% redundancy (reach 99.9% reliability)	2.053 × 10⁵	1.342 × 10⁶	1.547 × 10⁶

Abbreviations: PI, proportional–integral; SOSMC, second-order sliding mode control.

A system with more redundancies typically requires longer maintenance intervals; however, the reliability improvement becomes more significant as the redundancy level increases. Therefore, a comprehensive approach addressing reliability assessment in terms of both redundancy and maintenance is still necessary.

5.5. Case II: Increasing Reliability Through Redundancy and Maintenance

The proposed SOSMC does not require redundancy to achieve 99% reliability, whereas the PI controller necessitates at least 10% redundancy. As indicated in Table 4, implementing 10% redundancy along with appropriate maintenance intervals can increase the reliability of the PI controller from 89.6% to 98.6%, although this also raises the total cost of the STATCOM.

6. Conclusion

The reduction in DC-link capacitance increases the output current THD in multilevel-based STATCOM, adversely affecting the reliability. To address this issue, this paper proposes a SOSMC based on a twisting algorithm ensuring that the current THD remains within permissible limits. Simulation results from a 20 KV−10 MVAr multilevel-based STATCOM verify the superior performance of the proposed SOSMC controller in terms of robustness, reliability, operational lifespan, and cost-effectiveness. The proposed strategy achieves the following goals:

•
Employing a robust DC-link controller enhances the operational lifespan of the CHB STATCOM during DC-link faults. The proposed SOSMC controller maintains system performance within the THD range for 5 years, as the current THD remains below 6%, satisfying the IEEE-519 standard. In contrast, the conventional PI controller may require service after just 3 years.
•
The proposed control method improves system performance and leads to reduced maintenance intervals and repair costs, as well as an extended operational lifespan of the STATCOM system, making it economically justifiable.
•
According to the comparative results, a robust controller can achieve desirable dynamic performance over an extended time horizon. This is a significant achievement in terms of reliability and cost considerations, as well as dynamic response.

Nomenclature

Abbreviations

CHB:: Cascade H-bridge
FACTS:: Flexible AC transmission system
PCC:: Point of common coupling
PS-PWM:: Phase-shifted pulse width modulation
SOSMC:: Second-order sliding mode control
THD:: Total harmonic distortion

Indexes

t:: Index of time

Variables

v_c(v_cav_cb, v_cc):: Converter voltages at the three-phase AC terminals (a, b, c)
v(v_a, v_b, v_c):: Grid voltages at the PCC
θ:: Phase angle between the grid voltage and the output current
φ:: Phase angle between the fundamental component of STATCOM output voltage (v_c) and the grid voltage (v)
P/Q:: Instantaneous STATCOM active/reactive power
L(L_a, L_b, L_c):: Inductance of output filter
L_1a, L_1b, L_1c:: Stray inductance of connections and cables
R(R_a, R_b, R_c):: Series resistance of output filter in each phase
i_d/i_q:: Current terms in d-axis/q-axis
v_d/v_q:: Grid voltage components in d-axis/q-axis
v_cd/v_cq:: Converter output voltage components in d-axis/q-axis
V_dc:: DC-link voltage of each cell
:: Total average of DC-link voltages
V_dci,j:: DC-link voltage of the ith: H-bridge cell in jth phase (j = a, b, c)
S:: Sliding surface
:: Derivate of sliding surface
∅(x, t), γ(x, t):: Corresponding smooth functions
Φ:: Upper Limit of ∅(x, t),
Γ_m, Γ_M:: Boundaries of γ(x, t)
k₁, k₂:: Related SOSMC parameters

Parameters

ω:: Angular frequency
C_SM:: Equivalent capacitance of the DC-link
R_P:: Resistive loss model of CHB
S:: Rated apparent power
:: Nominal voltage at PCC
F:: Angular frequency
C₀:: Nominal value of DC-link capacitance
ΔC:: Uncertainties in equivalent capacity
C:: Equivalent capacitance of DC-link for each cell
N:: Number of CHB converters in each phase.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The authors received no specific funding for this work.

Appendix A: State Space Equation

The following relationship can be derived by applying KCL to each cell:

(A.1)

Here, u represents the DC passing through the capacitor, as illustrated in Equation (A.1). The sliding variables are defined as the error of the DC-link voltage and its derivative:

(A.2)

(A.3)

(A.4)

(A.5)

Therefore, the derivative of the second sliding variable can be expressed by the following equation:

(A.6)

Appendix B: Maintenance Cost Modeling

In this appendix, different costs (i.e., average fixed cost (cost_fixed), average cost of power outage time (cost_out) and average cost of SM replacement (cost_replace)) are calculated to contribute the average annual maintenance cost (cost_maintencace). The average fixed cost can be calculated according to Equation (B.1):

(B.1)

where T_m is the predefined maintenance interval. Since system shutdowns and power outage impose additional power loss costs, it is also can be considered in the maintenance cost. The formulation of the power outage cost is obtained based on the following equation:

(B.2)

Then, the average cost of each SM replacement can be calculated as follows:

(B.3)

Where p_i is the probability of ith failure. Also, n and k represent the number of main and redundant cells, respectively. By combining Equations (B.1), (B.2), and (B.3), the total maintenance cost can be determined as shown in Equation (B.4):

(B.4)

The related parameters of maintenance cost are given in Table A1 based on [35].

Table A1. Data of maintenance cost (normalized based on 10 MVA).

Data of maintenance cost
Parameter	Abbreviations	Value
Fixed cost per maintenance (k€)	L_f	1.5
Cost of power outage	L_o	0.15
Maintenance duration (h)	T_o	8
Cost of each SM module replacement (k€)	L_r	1.7

Open Research

Data Availability Statement

The data that support the findings of this study are available upon request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

References

1 Gandoman F. H., Ahmadi A., and Sharaf A. M., et al.Review of FACTS Technologies and Applications for Power Quality in Smart Grids With Renewable Energy Systems, Renewable and Sustainable Energy Reviews. (2018) 82, 502–514.
10.1016/j.rser.2017.09.062
Web of Science® Google Scholar
2 Neyshabouri Y., Chaudhary S. K., Teodorescu R., Sajadi R., and Iman-Eini H., Improving the Reactive Current Compensation Capability of Cascaded H-Bridge Based STATCOM Under Unbalanced Grid Voltage, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2020) 8, no. 2, 1466–1476, https://doi.org/10.1109/JESTPE.2019.2916571.
10.1109/JESTPE.2019.2916571
Web of Science® Google Scholar
3 Dekka A., Wu B., Fuentes R. L., Perez M., and Zargari N. R., Evolution of Topologies Modeling Control Schemes and Applications of Modular Multilevel Converters, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2017) 5, no. 4, 1631–1656, https://doi.org/10.1109/JESTPE.2017.2742938, 2-s2.0-85028514815.
10.1109/JESTPE.2017.2742938
Web of Science® Google Scholar
4 Callegari J. M. S., Cupertino A. F., Ferreira V. D. N., and Pereira H. A., Minimum DC-Link Voltage Control for Efficiency and Reliability Improvement in PV Inverters, IEEE Transactions on Power Electronics. (2021) 36, no. 5, 5512–5520.
10.1109/TPEL.2020.3032040
Web of Science® Google Scholar
5 Hashemzadeh E., Aghamohammadi M., and Asadi M., et al.Secondary Control for a D-ST AT COM DC-Link Voltage Under Capacitance Degradation”, IEEE Trans, Microelectronics Power Electron. (2021) 36, no. 11, 13215–13224.
10.1109/TPEL.2021.3078182
Web of Science® Google Scholar
6 de Sousa R. O., Cupertino A. F., Morais L. M. F., and Pereira H. A., Wear-Out Failure Analysis of Modular Multilevel Converter-Based STATCOM: The Role of the Modulation Strategy and IGBT Blocking Voltage, Microelectronics Reliability. (2022) 128, https://doi.org/10.1016/j.microrel.2021.114426, 114426.
10.1016/j.microrel.2021.114426
CAS Google Scholar
7 Farias J. V. M., Cupertino A. F., and de Nazareth Ferreira V., et al.Redundancy Design for Modular Multilevel Converter Based STATCOMs, Microelectronics Reliability. (2019) 100, 113471.
10.1016/j.microrel.2019.113471
Web of Science® Google Scholar
8 Hashemzadeh E., Khederzadeh M., Aghamohammadi M. R., and Asadi M., A Robust Control for D-STATCOM Under Variations of DC-Link Capacitance, IEEE Transactions on Power Electronics. (2021) 36, no. 7, 8325–8333, https://doi.org/10.1109/TPEL.2020.3026092.
10.1109/TPEL.2020.3026092
Google Scholar
9 Azimi M. and Asadi M., Optimum Number of Cascade Cells for Multilevel Inverter considering Redundancy Strategies Based on Cost and Reliability Optimization, IET Generation, Transmission & Distribution. (2023) 17, no. 19, 4423–4436, https://doi.org/10.1049/gtd2.12985.
10.1049/gtd2.12985
Google Scholar
10 Farias J. V. M., Cupertino A. F., d. N. Ferreira V., Pereira H. A., Seleme S. I., and Teodorescu R., Reliability-Oriented Design of Modular Multilevel Converters for Medium-Voltage STATCOM, IEEE Transactions on Industrial Electronics. (2020) 67, no. 8, 6206–6214, https://doi.org/10.1109/TIE.2019.2937050.
10.1109/TIE.2019.2937050
Web of Science® Google Scholar
11 Sousa R. O., Farias J. V. M., and Cupertino A. F., et al.“Life Consumption of an MMC-STATCOM Supporting Wind Power Plants: Impact of the Modulation Strategies, Microelectronics Reliability, 2018, 88-90, 1063–1070.
Google Scholar
12 Zhang Y., Wang H., Wang Z., Yang Y., and Blaabjerg F., Impact of Lifetime Model Selections on the Reliability Prediction of IGBT Modules in Modular Multilevel Converters, 2017 IEEE Energy Conversion Congress and Exposition (ECCE), 2017, 4202–4207.
10.1109/ECCE.2017.8096728
Google Scholar
13 Farzamkia S., Rizi H. S., Huang A. Q., and Iman-Eini H., Shared Redundancy Strategy to Improve the Reliability and Fault-Tolerant Capability of Modular Multilevel Converter, Industrial Electronics. (2023) 70, no. 4, 3326–3336.
10.1109/TIE.2022.3181416
Web of Science® Google Scholar
14 Sun P., Gong C., Du X., Luo Q., Wang H., and Zhou L., Online Condition Monitoring for Both IGBT Module and DC-Link Capacitor of Power Converter Based on Short-Circuit Current Simultaneously, IEEE Transactions on Industrial Electronics. (2017) 64, no. 5, 3662–3671, https://doi.org/10.1109/TIE.2017.2652372, 2-s2.0-85018972002.
10.1109/TIE.2017.2652372
Web of Science® Google Scholar
15 Rahimpour S., Husev O., Vinnikov D., Kurdkandi N. V., and Tarzamni H., Fault Management Techniques to Enhance the Reliability of Power Electronic Converters: An Overview, IEEE Access. (2023) 11, 13432–13446, https://doi.org/10.1109/ACCESS.2023.3242918.
10.1109/ACCESS.2023.3242918
Web of Science® Google Scholar
16 Wang H., Chung H., Blaabjerg F., and Pecht M., Reliability Engineering in Power Electronic Converter Systems in Reliability of Power Electronic Converter Systems, IET. (2015) .
Google Scholar
17 Ramos E. R., Leyva R., Farivar G. G., Tafti H. D., Townsend C. D., and Pou J., Incremental Passivity Control in Multilevel Cascaded H-Bridge Converters, IEEE Transactions on Power Electronics. (2020) 35, no. 8, 8766–8778.
10.1109/TPEL.2020.2965164
Web of Science® Google Scholar
18 Munoz J., Rohten J., Espinoza J., Melin P., Baier C., and Rivera M., Review of Current Control Techniques for a Cascaded h-Bridge STATCOM, IEEE International Conference on Industrial Technology (ICIT). (2015) 3085–3090, https://doi.org/10.1109/ICIT.2015.7125554, 2-s2.0-84937723704.
10.1109/ICIT.2015.7125554
Google Scholar
19 Sajadi R., Iman-Eini H., Bakhshizadeh M. K., Neyshabouri Y., and Farhangi S., Selective Harmonic Elimination Technique With Control of Capacitive DC-Link Voltages in an Asymmetric Cascaded H-Bridge Inverter for STATCOM Application, IEEE Transactions on Industrial Electronics. (2018) 65, no. 11, 8788–8796, https://doi.org/10.1109/TIE.2018.2811365, 2-s2.0-85043484094.
10.1109/TIE.2018.2811365
Web of Science® Google Scholar
20 Yu J., Wang J., and Liu Y., et al.Analysis of Unbalanced Clustered Voltage and Control Strategy of Clustered Voltage Balancing for Cascaded H-Bridge STATCOM, Journal of Modern Power Systems and Clean Energy. (2019) 7, no. 6, 1697–1708, https://doi.org/10.1007/s40565-019-0520-y, 2-s2.0-85064596219.
10.1007/s40565-019-0520-y
Google Scholar
21 Monfared K. K., Neyshabouri Y., Miremad A., Ahmadi S., and Iman-Eini H., Optimal Switching-Sequence-Based Model Predictive Control for a Hybrid Multilevel STATCOM, IEEE Transactions on Industrial Electronics. (2022) 69, no. 10, 9952–9960, https://doi.org/10.1109/TIE.2022.3146592.
10.1109/TIE.2022.3146592
Google Scholar
22 Chavali R. V., Dey A., and Das B., A Performance Comparison of Hysteresis Current Control Techniques for D-STATCOM Application, Electric Power Systems Research. (2024) 234, https://doi.org/10.1016/j.epsr.2024.110519, 110519.
10.1016/j.epsr.2024.110519
Google Scholar
23 Gadupudi L., Rao G. S., and Divakar R. V. L. N., et al.Fuzzy-Based Fifteen-Level VSC for STATCOM Operations with Single DC-Link Voltage, Sustainability. (2023) 15, no. 7, https://doi.org/10.3390/su15076188, 6188.
10.3390/su15076188
Google Scholar
24 Srief M. L., Soltane B., Lokmane N. A., and Malak G., A Complete Control Structure Based Backstepping Controller Design for Stacked Multi-Cell Multi-Level SPWM VSC STATCOM, Energy Reports. (2024) 12, 687–698, https://doi.org/10.1016/j.egyr.2024.06.051.
10.1016/j.egyr.2024.06.051
Google Scholar
25 Zhang Y., Yuan X., Wu X., Yuan Y., and Zhou J., Parallel Implementation of Model Predictive Control for Multilevel Cascaded H-Bridge STATCOM With Linear Complexity, IEEE Transactions on Industrial Electronics. (2020) 67, no. 2, 832–841, https://doi.org/10.1109/TIE.2019.2901647.
10.1109/TIE.2019.2901647
Google Scholar
26 Merai M., Naouar M. W., Slama-Belkhodja I., and Monmasson E., An Adaptive PI Controller Design for DC-Link Voltage Control of SinglePhase Grid-Connected Converters, IEEE Transactions on Industrial Electronics. (2019) 66, no. 8, 6241–6249, https://doi.org/10.1109/TIE.2018.2871796, 2-s2.0-85054399736.
10.1109/TIE.2018.2871796
Web of Science® Google Scholar
27 Ahmed S., Adil H. M. M., Ahmad I., Azeem M. K., Huma Z., and Khan S. A., Super Twisting Sliding Mode Algorithm Based Nonlinear MPPT Control for a Solar PV System with Artificial Neural Networks Based Reference Generation, Energies. (2020) 13, no. 14, https://doi.org/10.3390/en13143695, 3695.
10.3390/en13143695
Web of Science® Google Scholar
28 Liu J., Gao Y., Yin Y., Wang J., Luo W., and Sun G., Sliding Mode Control Methodology in the Applications of Industrial Power Systems, 2020, Springer International Publishing, New York, NY, USA.
10.1007/978-3-030-30655-7
Google Scholar
29 Bouafia S., Benaissa A., Barkat S., and Bouzidi M., Second Order Sliding Mode Control of Three-Level Four-Leg DSTATCOM Based on Instantaneous Symmetrical Components Theory, Energy Systems. (2018) 9, no. 1, 79–111, https://doi.org/10.1007/s12667-016-0217-5, 2-s2.0-85043240180.
10.1007/s12667-016-0217-5
Google Scholar
30 Ahmed T., Waqar A., Elavarasan R. M., Imtiaz J., Premkumar M., and Subramaniam U., Analysis of Fractional Order Sliding Mode Control in a D-STATCOM Integrated Power Distribution System, IEEE Access. (2021) 9, 70337–70352, https://doi.org/10.1109/ACCESS.2021.3078608.
10.1109/ACCESS.2021.3078608
Web of Science® Google Scholar
31 Neyshabouri Y., Iman-Eini H., and Miranbeigi M., State Feedback Control Strategy and Voltage Balancing Scheme for a Transformer-less STATIC Synchronous Compensator Based on Cascaded H-Bridge Converter, IET Power Electronics. (2015) 8, no. 6, 906–917, https://doi.org/10.1049/iet-pel.2013.0941, 2-s2.0-84930371397.
10.1049/iet-pel.2013.0941
Web of Science® Google Scholar
32 Nachidi M., Hajjaji A. El, and Bosche J., An Enhanced Control Approach for DC-DC Converters, International Journal of Electrical Power & Energy Systems. (2013) 45, no. 1, 404–412, https://doi.org/10.1016/j.ijepes.2012.09.003, 2-s2.0-84868321745.
10.1016/j.ijepes.2012.09.003
Web of Science® Google Scholar
33 Akagi H., Inoue S., and Yoshii T., Control and Performance of a Transformerless Cascade PWM STATCOM With Star Configuration, IEEE Transactions on Industry Applications. (2007) 43, no. 4, 1041–1049, https://doi.org/10.1109/TIA.2007.900487, 2-s2.0-34547885037.
10.1109/TIA.2007.900487
Web of Science® Google Scholar
34 K. Group, Capaitor Useful Life, Kendeil Group, http://www.kendeil.com/Portals/0/pdf/Useful_life.pdf.
Google Scholar
35 Yu P., Fu W., and Wang L., et al.Reliability-Centered Maintenance for Modular Multilevel Converter in HVDC Transmission Application, IEEE Journal of Emerging and Selected Topics in Power Electronics. (2021) 9, no. 3, 3166–3176, https://doi.org/10.1109/JESTPE.2020.3009389.
10.1109/JESTPE.2020.3009389
Google Scholar

All articles

A Robust Control Method for Reliability Improvement of Cascade H-Bridge STATCOM Under DC-Link Capacitance Uncertainty

Abstract

1. Introduction

2. STATCOM and Uncertainty Modeling

2.1. AC Side Modeling

2.2. DC Side Modeling

3. Control Scheme

4. Proposed DC-Link Controller

5. Results and Discussion

5.1. AC Side THD

5.2. Reliability

5.3. Cost Evaluation

5.4. Case I: Increasing Reliability Through Maintenance

5.5. Case II: Increasing Reliability Through Redundancy and Maintenance

6. Conclusion

Nomenclature

Abbreviations

Indexes

Variables

Parameters

Conflicts of Interest

Funding

Appendix A: State Space Equation

Appendix B: Maintenance Cost Modeling

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Robust Control Method for Reliability Improvement of Cascade H-Bridge STATCOM Under DC-Link Capacitance Uncertainty

Abstract

1. Introduction

2. STATCOM and Uncertainty Modeling

2.1. AC Side Modeling

2.2. DC Side Modeling

3. Control Scheme

4. Proposed DC-Link Controller

5. Results and Discussion

5.1. AC Side THD

5.2. Reliability

5.3. Cost Evaluation

5.4. Case I: Increasing Reliability Through Maintenance

5.5. Case II: Increasing Reliability Through Redundancy and Maintenance

6. Conclusion

Nomenclature

Abbreviations

Indexes

Variables

Parameters

Conflicts of Interest

Funding

Appendix A: State Space Equation

Appendix B: Maintenance Cost Modeling

Open Research

Data Availability Statement

References

Figures

References

Related

Information