Battery energy storage systems (BESSs) have recently been utilized in power systems for various purposes. Integrating these devices into power systems can enhance the damping capability of subsynchronous oscillations. The interaction between the control modes of the BESS and synchronous machines, as well as the control parameters of the BESS, reduces subsynchronous oscillations. To damp oscillations and improve dynamic stability, this work develops a linear model of a power system integrated with a BESS to investigate small-signal stability. The gain tuning of the BESS controller is formulated as an optimization problem and is solved using a fuzzy-based algorithm. The efficacy of the proposed method is evaluated under various operating conditions. Furthermore, the proposed method is compared with a power system stabilizer (PSS) damping controller, and the results demonstrate the superiority of the BESS damping method in mitigating subsynchronous oscillations and enhancing the dynamic stability of power systems. Lastly, eigenvalue analysis is employed to determine the permissible ranges of BESS parameters for stable power system operation.

1. Introduction

The increasing demand for electric power forces power systems to operate close to their stability limits. However, extending these limits is challenging due to environmental constraints and resource shortages. Consequently, the power transmission system in interconnected power systems is constrained by transient stability, voltage stability, and small-signal stability [1]. Moreover, power system resources are often geographically distant, which increases subsynchronous or low-frequency oscillations in the range of 0.2–3 Hz. Traditionally, generator local controllers such as governors and automatic voltage regulators (AVRs) have been used to mitigate this issue. However, due to their inherent time delays and limitations, power system stabilizers (PSSs) were developed to address low-frequency oscillations [2]. PSSs provide supplementary signals to excitation systems to generate electrical torque and reduce power oscillations. Nevertheless, PSSs may fail to perform effectively under certain conditions, such as heavy loading, poorly tuned parameters, and interarea oscillation modes [3, 4]. The integration of PSSs into power systems to damp low-frequency oscillations has been extensively studied in [5–7].

In recent years, advancements in the technical specifications of power electronic devices have made flexible alternating current transmission system (FACTS) devices one of the most effective methods for enhancing power system performance. FACTS devices can improve transient stability and reduce power system oscillations [8, 9]. For instance, Mushtaq and Mairaj-ud-din [10] presented a comprehensive approach that employs a thyristor-controlled series compensator (TCSC) combined with a fuzzy logic controller to enhance the damping of critical inter-area modes. However, integrating FACTS devices into power systems requires the coordination of their controllers with other generator local controllers to effectively mitigate power system oscillations. Numerous studies in the literature discuss various types of FACTS devices and their applications as power oscillation damping systems [11–15].

In addition to FACTS devices, HVDC systems can also serve as damping controllers. Furthermore, HVDC power controllers are faster and more adaptable compared to generator controllers. Research on HVDC damping controllers to mitigate interarea oscillations has been extensively conducted [16–19]. While HVDC systems can directly reduce interarea oscillations by regulating active power delivered through tie lines, they are primarily used to connect power grids across different regions. However, implementing HVDC systems often requires costly infrastructure upgrades compared to other damping methods. The increasing penetration of inverter-based renewable energy resources, such as photovoltaic systems and wind turbines, reduces the overall inertia of the power system. Nevertheless, these new resources and their associated technologies can provide virtual inertia and enhance oscillation damping in the power system by adjusting their controllers [20]. Despite challenges such as the intermittent nature of renewable energy resources, numerous studies, and approaches have explored their applications for damping low-frequency oscillations in power systems [21–24].

In modern power systems, energy storage systems (ESSs) are widely used for various purposes, including stability improvement [25, 26], enhancing system self-sufficiency [27, 28], frequency control [29, 30], power quality enhancement [31], and reliability improvement [32]. Although FACTS devices typically control reactive power, ESSs are versatile devices capable of injecting or absorbing active power into or from the power system instantaneously. Since low-frequency oscillations in power systems are influenced by active power oscillations, frequency oscillations can be more effectively suppressed by directly exchanging active power via ESSs rather than using PSS or FACTS devices [33]. Additionally, unlike renewable energy resources, ESS outputs are not intermittent. Consequently, ESSs have garnered significant attention for enhancing power system behavior and are considered as power oscillation damping devices in this study.

The motivation for the current study is to address low-frequency oscillations by proposing a battery energy storage system (BESS) controller. The BESS is connected to the power system through a DC/AC voltage source converter, which is a common configuration for grid-connected BESS systems. The equations governing the power system integrated with the BESS have been derived, and an optimal controller has been designed to damp low-frequency oscillations. For this purpose, the Heffron–Phillips small-signal linear model is utilized for analysis. A proportional–integral–derivative (PID) controller, known for its simplicity and predictability in industrial applications, has been employed as a supplementary controller for the BESS to damp power system oscillations. To design an optimal PID controller and fine-tune its parameters, a fuzzy-based algorithm is applied, minimizing generator speed deviation as the objective function. The robustness of the BESS-based stabilizer against variations in system operating conditions is also considered. Additionally, a PSS, a conventional damping controller widely used in power systems, is analyzed for comparison. The results demonstrate the superior effectiveness of the proposed BESS approach in mitigating low-frequency oscillations and enhancing power system stability. Key aspects of novelty include:

•
Developing a linear model of a power system integrated with a BESS to investigate small-signal stability.
•
Integrating a novel controller design for damping low-frequency oscillations using an adaptive fuzzy particle swarm optimization (PSO) algorithm.
•
Conducting extensive analysis across varying load conditions to demonstrate the controller’s robustness and adaptability.
•
Performing eigenvalue analysis to identify permissible parameter ranges for stable operation.
•
Validating results in real time using Speedgoat, a rarely explored tool in similar studies, adding practical relevance to the findings.

The rest of this paper is organized as follows: Section 2 presents the nonlinear and Heffron–Phillips models of the BESS. Section 3 explains the optimal controller design and optimization algorithm. Section 4 discusses the simulation results and analysis of scenarios. Finally, the conclusions are presented in Section 5.

2. System Modeling and Formulations

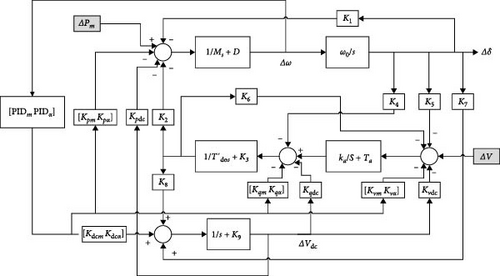
Power systems, as complex dynamic systems, are described by nonlinear differential equations. To analyze power systems for aspects such as small-signal stability and low-frequency studies, state-space equations are employed [34, 35]. For this purpose, it is necessary to linearize the power system equations around an operating point [36]. Consequently, the initial nonlinear equations of the system under study are presented, followed by the formulation of the state-space equations.

The nonlinear equations of the single-machine infinite bus (SMIB) system with a BESS, as shown in Figure 1 [37], are described as follows:

(1)

where

(2)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Single machine infinite bus system with BESS. BESS, battery energy storage system.

The voltage of DC link in BESS is also considered as state variable, therefore according to Figure 1, it can be obtained as follows:

(3)

Here, k represents the DC/AC converter constant, while m and α denote the modulation ratio and phase angle of the DC/AC converter, respectively, which connects the BESS to the power system. It should be noted that m and α are considered as control input variables in this study. The DC-side equations of the converter are expressed as follows:

(4)

According to active power exchange:

(5)

The linear model of the five state variables is given as follows:

(6)

The linear state variables are ∆δ, ∆ω, ∆E′_q, ∆E_fd, and ∆V_dc and input control variables are ∆m and ∆α, therefore the other variable must be substituted:

(7)

(8)

(9)

Using the general form of Tylor series expansion, the linearization is given by the following equation:

(10)

Therefore

(11)

According to KVL in power system to obtain ∆I_td, ∆I_tq, ∆I_ed, and ∆I_eq:

(12)

In d–q reference frame, the equations give:

(13)

By equating the real and imaginary parts:

(14)

To obtain I_td, I_tq, I_ed, and I_eq, Equations (8) and (9) are written in the following matrix form:

(15)

Hence

(16)

The linear values of the four variables are given as follows:

(17)

By substituting ∆I_td, ∆I_tq, ∆I_ed, and ∆I_eq to ∆V_t, ∆E_q, ∆I_ed, and ∆P_e and according to supporting equations which are proven in appendix, the matrix form of final linear model can be obtained as follows:

(18)

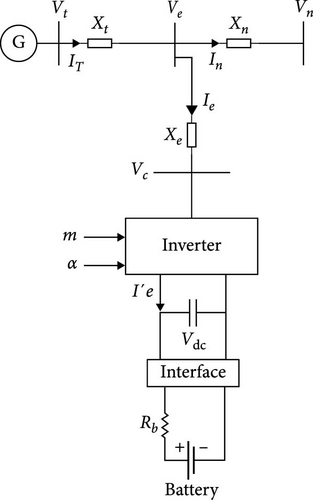
The block diagram of linearized model (Heffron–Phillips model) is shown in Figure 2.

Since the PSS [38] has been widely used to provide damping in power systems and is the most cost-effective approach to improving power system stability, its effect, along with the BESS, is analyzed in this study. A PSS is a control system applied to a generation unit, where its input is the angular frequency. The output of this controller is a control signal sent to the voltage regulator, which compensates for the phase lag between the exciter input and the machine’s electrical torque to damp oscillations in the output frequency. The block diagram of the PSS is shown in Figure 3.

In Figure 3, ∆ω shows the speed deviation, and U_PSS is the output signal sent to the regulator of the excitation system. T_w is the washout filter time constant, while K_PSS and T₁–T₄ represent the additional gain and the time constants of the lead–lag controller, respectively. The tuning of these parameters is performed to achieve acceptable damping capability in power systems.

3. Optimal Controller Design

The main goal of this study is to investigate the damping of low-frequency oscillations in power systems; hence, the speed deviation (∆ω) is used as an indicator of these oscillations. Consequently, a performance index based on the speed deviation is utilized to define the objective function for the controller design problem. In this study, minimizing the generator’s speed deviation is formulated as the objective function, expressed as follows:

(19)

where ts is the simulation time.

Minimizing this objective function improves the system response in terms of settling time and overshoots, as the surface under the speed deviation graph is reduced. Various algorithms can solve this problem; however, this paper employs a modified version of PSO known as adaptive particularly tunable fuzzy PSO (APTFPSO) [39]. This method leverages a knowledge-based fuzzy logic approach to modify the individual and global learning coefficients of each particle during its development at every iteration. The fuzzy operator adjusts the learning coefficients for each particle based on the objective function values and the number of iterations. This procedure results in an algorithm that offers superior performance compared to conventional PSO. The Mamdani fuzzy inference system, consisting of two inputs and two outputs, is utilized to fine-tune the parameters of the method. The first input is the normalized iteration (NIt), which starts at zero and ends at unity. The definition of NIt is as follows.

(20)

The second input is the normalized objective function (NOF), which is calculated based on the minimum and maximum values of the objective function at each iteration, as follows:

(21)

where OF_t,i represents the value of the objective function of the ith particle in the tth iteration, also max (OF_t) and min (OF_t) represent the minimum and maximum values of the objective function in the tth iteration. These two inputs are fuzzified by three Gaussian membership functions, the related membership functions are illustrated in Figure 4.

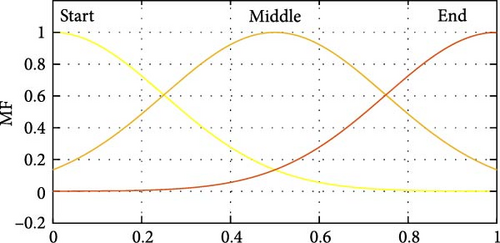
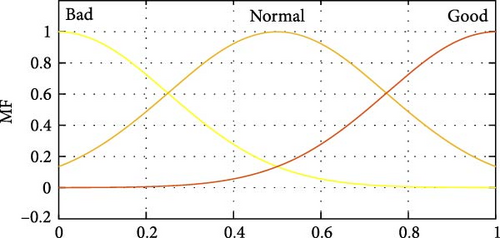
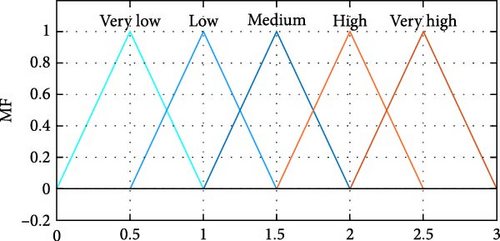
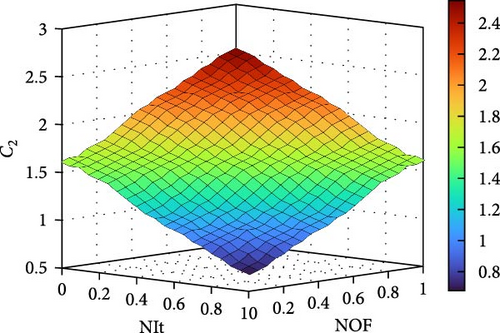
The outputs of the developed fuzzy system are local (C₁i, t) and global (C₂i, t) learning coefficients for the ith particle in tth iteration which are described by five triangular membership functions and are shown in Figure 5. In this work, to develop of the rule base, 2 × 9 IF-THEN rules have been considered and presented in Table 1. Moreover, the three-dimensional plot of embedded rules has been illustrated in Figure 6.

Table 1. Rule table for the outputs C₁ and C₂.

C₁				C₂
NIt	NOF			NIt	NOF
NIt	Bad	Normal	Good	NIt	Bad	Normal	Good
Start	Medium	Low	Very low	Start	Medium	High	Very high
Middle	High	Medium	Low	Middle	Low	Medium	High
End	Very High	High	Medium	End	Very Low	Low	Medium

Abbreviations: NIt, normalized iteration; NOF, normalized objective function.

4. Simulation Results and Discussion

In order to find the optimal parameters of the BESS controller an optimization problem has been solved by APTFPSO. The algorithm has been run several times and the best result BESS controller in normal operation point is as follows. For m as control input k_p = 323, k_i = 20,000, k_d = 25, and for α as control input k_p = 30, k_i = 1, k_d = 37. In order to analyze and validate the proposed method, five scenarios for three different operating conditions: (i) nominal load of the system (P_e = 1, Q_e = 0.25), (ii) heavy loading of the system (P_e = 1.5, Q_e = 0.45), and (iii) light loading of the system (P_e = 0.6, Q_e = 0.15) are defined as follows:

Scenario 1: Stability analysis for fault disturbance in power under different operating conditions.
Scenario 2: Stability analysis for fault disturbance in voltage under different operating conditions.
Scenario 3: Comparison of the proposed approach with conventional controllers (PSS) for damping low-frequency oscillations.
Scenario 4: Investigation of the impact of BESS parameters on system stability.
Scenario 5: Real-time simulation and testing.

4.1. Scenario 1: Fault Disturbance in Power

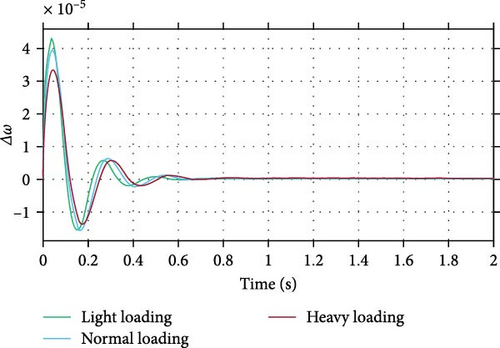
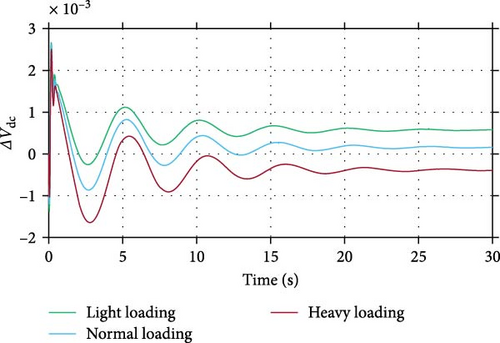
Figure 7 shows the dynamic responses of Δω after a fault disturbance in power in the presence of the optimal BESS controller under different loading conditions. It is evident that the designed controller provides effective damping for low-frequency oscillations and demonstrates robust performance across varying loading conditions. Figure 8 depicts the DC-side voltage of the BESS converter. As shown, the voltage varies at different operating points, with the BESS contributing significantly to mitigating oscillations.

4.2. Scenario 2: Fault Disturbance in Voltage

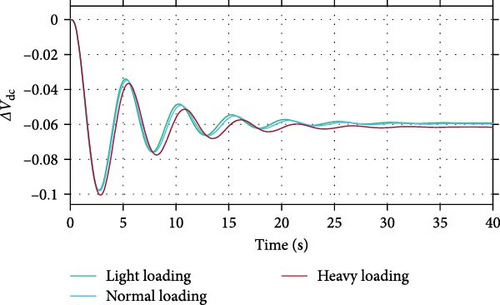
To verify the proposed optimal controller, a fault disturbance in voltage was also applied to the system. As shown in Figure 9, the system oscillations were effectively damped under various loading conditions. Figure 10 illustrates the DC-side voltage of the BESS for different operating points after the fault. In this figure, the voltage reaches a steady state following the fault, with the final value dependent on the loading conditions.

4.3. Scenario 3: Comparing BESS With PSS

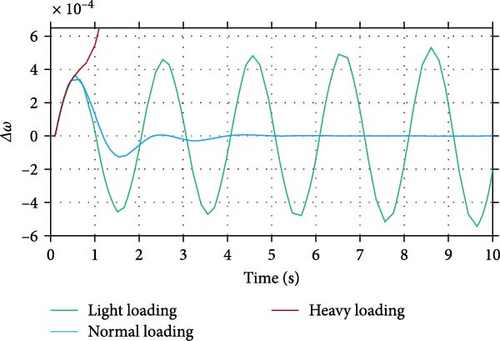
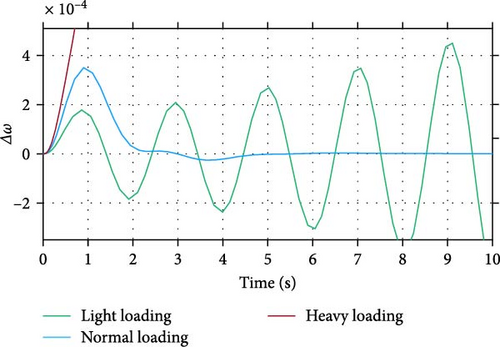
The PSS, an economical and effective controller, has been used for many years to enhance the damping of low-frequency oscillations. In this study, the proposed BESS is compared with the classical PSS. The optimal parameters for the PSS in the power system under study are K_PSS = 200, T_w = 0.33, T₁ = 0.01, T₂ = 23.2, T₃ = 261, and T₄ = 25.7. As shown in Figure 11, the PSS can stabilize the power system only under normal loading conditions; the system becomes unstable at other operating points. In contrast, the proposed BESS demonstrates consistent performance across all operating points, from light loading to heavy loading. Similar results are observed after a fault disturbance in voltage, as illustrated in Figure 12.

4.4. Scenario 4: Investigating the BESS Parameters on Stability

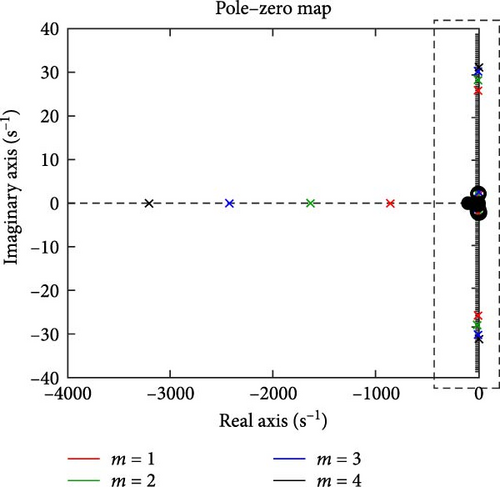
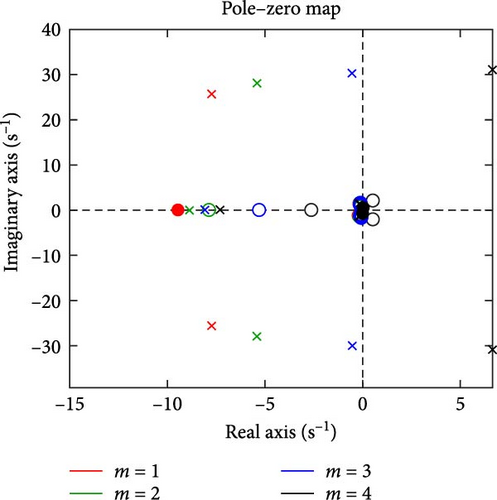
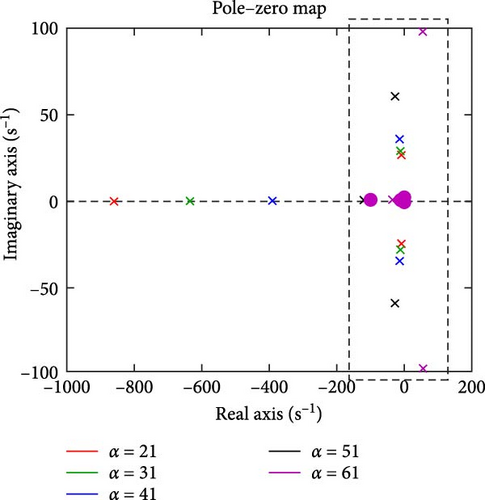
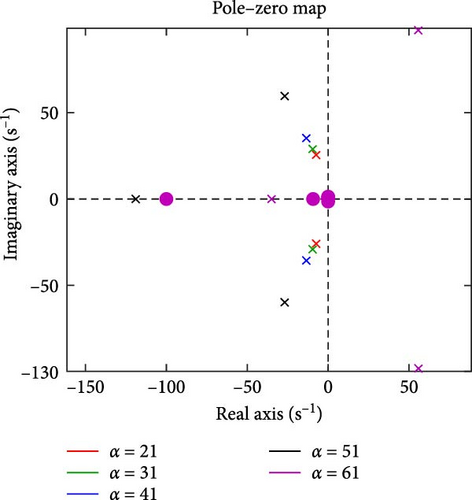
To investigate the impact of the proposed BESS on power system stability, the pole loci were plotted by varying the BESS parameters (m and α). First, m was increased from 1 to 4 while the other parameters remained unchanged. As shown in Figure 13, increasing m causes the poles to move toward the imaginary axis, indicating a slower response and a larger settling time due to a reduced damping coefficient. The black pole corresponding to m = 4 moves to the positive side of the zero–pole map, indicating that for values greater than 3, the system becomes unstable. Additionally, for m = 4, the zeros also shift to the positive side, meaning that a larger controller gain cannot stabilize the system. Next, α was increased from 21° to 51° while keeping the other parameters unchanged. Figure 14 shows that increasing α causes the poles to move away from the imaginary axis, resulting in a larger damping coefficient. However, further increases in α cause the pole direction to change. The magenta pole corresponding to α = 61° shifts to the positive side of the zero–pole map, indicating instability in the system 51°< α < 61°. Since all zeros remain on the negative side, a larger controller gain can stabilize the system in this case.

4.5. Scenario 5: Speedgoat—Real-Time Simulation and Testing

In this section, Speedgoat—real-time simulation and testing (Figure 15) has been performed to investigate the behavior of a physical system by running its simulation model. In this regard, the most severe operating condition means heavy loading has been considered and two fault disturbances in power and voltage are evaluated by using real-time simulation. Figures 16 and 17 show real-time simulation for ∆ω after a fault disturbance in power and voltage, respectively. The SpeedGoat real-time target machine, in conjunction with Simulink RealTime, offers an integrated solution suitable for exploring and instructing design principles across diverse fields such as mechatronics, motion control, power electronics, and signal processing. Serving as a robust platform for real-time simulation and testing, the real-time target machine comes equipped with essential cables, terminal boards, and adapters to facilitate seamless connectivity between the input/output (I/O) of the target machine and the hardware under examination [40]. Comprising two primary components, the SpeedGoat real-time system features a high-performance real-time target machine with an Intel 4.2 GHz i7 multi-core CPU (1), and an IO306-Performance Simulink-programmable FPGA I/O module (2). The IO306 incorporates a Xilinx Kintex-7 FPGA with 64 × 3.3V TTL I/O lines and a Xilinx Spartan 6 FPGA with 24 k logic cells. Simulink models can be automatically converted into code for either the CPU or FPGA using Simulink Real-Time or HDL Coder, respectively. Additionally, the Simscape Electrical model can be transformed into VHDL code using HDL Coder from MathWorks [41, 42].

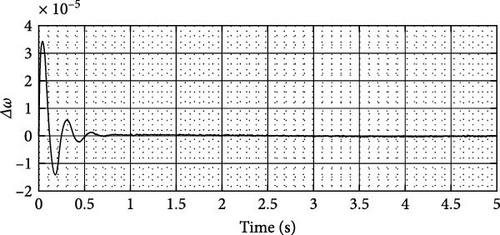
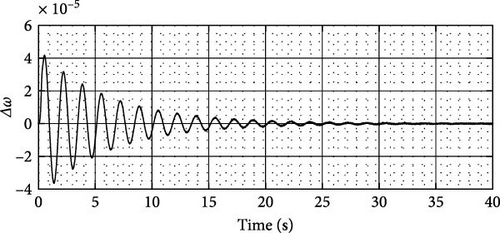
5. Conclusion

This paper developed a linear model of a power system integrated with a BESS to address low-frequency oscillations and improve small-signal stability. The proposed approach incorporates a controller for the BESS to enhance damping capabilities, with optimal parameters obtained through an optimization process. Several scenarios were analyzed to evaluate the performance of the proposed damping approach under various operating conditions. Furthermore, the conventional PSS damping controller, widely used to improve power system stability, was compared to the proposed BESS-based approach. The results demonstrate that the proposed method outperforms the PSS in terms of damping low-frequency oscillations and enhancing the dynamic stability of power systems across different conditions and operating points. Additionally, the effect of BESS parameters on power system stability was analyzed using eigenvalue analysis, identifying the allowable parameter ranges for stable operation. There are several areas for future work:

•
Investigating the nonlinear model of the power system.
•
Developing a linear quadratic regulator (LQR) controller design.
•
Exploring the application of machine learning methods to enhance precision and adaptability.
•
Examining the interaction and coordination between the BESS and other renewable energy sources, such as wind and solar, to improve power system stability.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Appendix 1

This appendix consists of supporting information for the proposed model. Table A1 shows K-constants of the Heffron–Phillips integrated with BESS for different operation points. The system steady state parameters are tabulated in Table A2.

Table A1. K-constants of the modified Heffron–Phillips linearized model with BESS.

Parameter	Light loading	Nominal load	Heavy loading
Pe (pu)	0.6	1.0	1.5
Qe (pu)	0.15	0.25	0.45

K₁	0.290	0.251	0.279
K₂	1.093	1.444	1.760
K₃	2.958	1.458	3.808
K₄	0.3214	0.246	0.269
K₅	−0.052	−0.045	0.059
K₆	0.444	0.533	0.384
K₇	0.284	0.243	0.169
K₈	0.0426	0.0436	0.0476
K₉	−0.0038	−0.0039	−0.003
K_pdc	0.097	0.120	0.110
K_pm	0.443	0.501	0.556
K_pα	0.522	0.584	0.590
K_qdc	0.235	0.243	0.258
K_qm	0.290	0.251	0.279
K_qα	1.093	1.444	1.760
K_vdc	−0.052	−0.045	0.059
K_vm	0.444	0.533	0.384
K_vα	0.284	0.243	0.169
K_dcm	0.097	0.120	0.110
K_dcα	0.443	0.501	0.556

Table A2. System steady state parameters.

	Parameter	Value		Parameter	Value
Generator	M	8 MJ/MVA	BESS	V_dc	1 pu
	D	0		R_b	0.1 pu
	X_q	0.6 pu		C	1 pu
	X_d	1 pu		m	1
	X’_d	0.3 pu		k	1
	T’_do	5.044 s		α	21°
	K_a	10		I_ed	0.1
	T_a	0.05 s		I_eq	0.1
	δ	42°	Operation point	P_e	0.912
	ω	120π		Q_e	0.277
Transmission line	X_T	0.1 pu		E_d	0.4041
	X_n	1 pu		E_q	0.9493
	X_e	0.3 pu		I_td	0.6735
	V_t	1.032 pu		I_tq	0.6736
	V_e	1.02 pu
	V_n	1 pu

Abbreviation: BESS, battery energy storage system.

Appendix 2

The constants of the modified Heffron–Phillips model integrated with BESS for state variables ∆δ, ∆ω, ∆E’_q, ∆E_fd, and ∆V_dc are computed from the following expressions:

1.
The first state variable:

2.
The second state variable:

3.
The third state variable:

4.
The fourth state variable:

5.
The fifth state variable:

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Tambey N. and Kothari M. L., Damping of Power System Oscillations With Unified Power Flow Controller (UPFC), Generation, Transmission and Distribution, IEE Proceedings. (2003) 150, no. 2, 129–140.
Google Scholar
2 Zacharia L., Asprou M., and Kyriakides E., Wide Area Control of Governors and Power System Stabilizers With an Adaptive Tuning of Coordination Signals, IEEE Open Access Journal of Power and Energy. (2020) 7, 70–81, https://doi.org/10.1109/OAJPE.2019.2960376.
10.1109/OAJPE.2019.2960376
Web of Science® Google Scholar
3 Sarkar D. U. and Prakash T., A Recent Review on Approaches to Design Power System Stabilizers: Status, Challenges and Future Scope, IEEE Access. (2023) 11, 34044–34061, https://doi.org/10.1109/ACCESS.2023.3244687.
10.1109/ACCESS.2023.3244687
Web of Science® Google Scholar
4 Anarmarzi E. R., Feyzi M. R., and Hagh M. T., Hierarchical Fuzzy Controller Applied to Multi-Input Power System Stabilizer, Turkish Journal of Electrical Engineering and Computer Sciences. (2010) 18, 541–551, https://doi.org/10.3906/elk-0908-148, 2-s2.0-77955459322.
10.3906/elk-0908-148
Web of Science® Google Scholar
5 Hattabi I., Kheldoun A., and Bradai R., et al.Enhanced Power System Stabilizer Tuning Using Marine Predator Algorithm With Comparative Analysis and Real Time Validation, Scientific Reports. (2024) 14, no. 1, https://doi.org/10.1038/s41598-024-80154-2, 28971.
10.1038/s41598-024-80154-2
CAS PubMed Web of Science® Google Scholar
6 Zhang G., Hu W., Zhao J., Cao D., Chen Z., and Blaabjerg F., A Novel Deep Reinforcement Learning Enabled Multi-Band Pss for Multi-Mode Oscillation Control, IEEE Transactions on Power Systems. (2021) 36, no. 4, 3794–3797, https://doi.org/10.1109/TPWRS.2021.3067208.
10.1109/TPWRS.2021.3067208
Web of Science® Google Scholar
7 Bernal-Sancho M., Comech M. P., and Galán-Hernández N., Damping Control in Renewable-Integrated Power Systems: A Comparative Analysis of PSS, POD-P, and POD-Q Strategies, International Journal of Electrical Power & Energy Systems. (2024) 162, https://doi.org/10.1016/j.ijepes.2024.110308, 110308.
10.1016/j.ijepes.2024.110308
Web of Science® Google Scholar
8 Alajrash B. H., Salem M., Swadi M., Senjyu T., Kamarol M., and Motahhir S., A Comprehensive Review of FACTS Devices in Modern Power Systems: Addressing Power Quality, Optimal Placement, and Stability With Renewable Energy Penetration, Energy Reports. (2024) 11, 5350–5371, https://doi.org/10.1016/j.egyr.2024.05.011.
10.1016/j.egyr.2024.05.011
Web of Science® Google Scholar
9 Zamani M., Shahgholian G., Fathollahi A., Mosavi A., and Felde I., Improving Interarea Mode Oscillation Damping in Multi-Machine Energy Systems Through a Coordinated PSS and FACTS Controller Framework, Sustainability. (2023) 15, no. 22, https://doi.org/10.3390/su152216070, 16070.
10.3390/su152216070
Web of Science® Google Scholar
10 Mushtaq B. and Mairaj-ud-din M., Coordinated Operation of Fuzzy-Based TCSC and SMES for Low-Frequency Oscillation Damping in Interconnected Power Systems, International Journal of Circuit Theory and Applications. (2023) 51, no. 6, 2912–2941, https://doi.org/10.1002/cta.3543.
10.1002/cta.3543
Web of Science® Google Scholar
11 Kamarposhti M. A., Shokouhandeh H., Omali Y. G., Colak I., Thounthong P., and Holderbaum W., Optimal Coordination of TCSC and PSS2B Controllers in Electric Power Systems Using MOPSO Multi-Objective Algorithm, International Transactions on Electrical Energy Systems. (2022) 2022, 18, 5233620.
Google Scholar
12 Sobhani H., Jannesar M. R., Hasanvand S., and Khaledian A., TCSC Application for Transient Stabilization of Wind Turbine With Fixed Speed Induction Generator, International Journal of Energy Research. (2023) 2023, 15, 8193592.
10.1155/2023/8193592
Web of Science® Google Scholar
13 Jokarzadeh M., Abedini M., and Seifi A., Improving Power System Damping Using a Combination of Optimal Control Theory and Differential Evolution Algorithm, ISA Trans. (2019) 90, 169–177.
10.1016/j.isatra.2018.12.039
PubMed Web of Science® Google Scholar
14 Dahat S. A. and Dhabale A., Coordinated Robust Damping Control for Hybrid SVC/SSSC to Enhance Power System Stability in Large-Scale Systems, IEEE Transactions on Industry Applications. (2024) 60, no. 1, 1589–1598, https://doi.org/10.1109/TIA.2023.3325296.
10.1109/TIA.2023.3325296
Web of Science® Google Scholar
15 Fortes E. V., Macedo L. H., deAraujo P. B., and Romero R., A VNS Algorithm for the Design of Supplementary Damping Controllers for Small-Signal Stability Analysis, International Journal of Electrical Power & Energy Systems. (2018) 94, 41–56, https://doi.org/10.1016/j.ijepes.2017.06.017, 2-s2.0-85021454775.
10.1016/j.ijepes.2017.06.017
Web of Science® Google Scholar
16 Renedo J., Rouco L., Garcia-Cerrada A., and Sigrist L., Transient Stability versus Damping of Electromechanical Oscillations in Power Systems With Embedded Multi-Terminal VSC-HVDC Systems, IET Generation, Transmission & Distribution. (2023) 17, no. 15, 3477–3487, https://doi.org/10.1049/gtd2.12874.
10.1049/gtd2.12874
Web of Science® Google Scholar
17 Gupta P., Pal A., and Vittal V., Coordinated Wide-Area Control of Multiple Controllers in a Power System Embedded With HVDC Lines, IEEE Transactions on Power Systems. (2021) 36, no. 1, 648–658, https://doi.org/10.1109/TPWRS.2020.3016354.
10.1109/TPWRS.2020.3016354
Web of Science® Google Scholar
18 Preece R., Milanovic J. V., Almutairi A., and Marjanovic O., Damping of Inter-Area Oscillations in Mixed AC/DC Networks Using WAMS Based Supplementary Controller, IEEE Transactions on Power Systems. (2013) 28, no. 2, 160–169.
10.1109/TPWRS.2012.2207745
Web of Science® Google Scholar
19 Sun K., Qiu W., and Dong Y., et al.WAMS-Based HVDC Damping Control for Cyber Attack Defense, IEEE Transactions on Power Systems. (2023) 38, no. 1, 702–713, https://doi.org/10.1109/TPWRS.2022.3168078.
10.1109/TPWRS.2022.3168078
Web of Science® Google Scholar
20 Basu M., Mahindara V. R., Kim J., Nelms R. M., and Muljadi E., Comparison of Active and Reactive Power Oscillation Damping With PV Plants, IEEE Transactions on Industry Applications. (2021) 57, no. 3, 2178–2186, https://doi.org/10.1109/TIA.2021.3059810.
10.1109/TIA.2021.3059810
Web of Science® Google Scholar
21 Basu M., Kim J., Nelms R. M., and Muljadi E., Coordination of Utility-Scale PV Plant and Wind Power Plant in Interarea-Oscillation Damping, IEEE Transactions on Industry Applications. (2023) 59, no. 4, 4744–4751, https://doi.org/10.1109/TIA.2023.3257829.
10.1109/TIA.2023.3257829
Web of Science® Google Scholar
22 Varma R. K. and Akbari M., Simultaneous Fast Frequency Control and Power Oscillation Damping by Utilizing PV Solar System as PV-STATCOM, IEEE Transactions on Sustainable Energy. (2020) 11, no. 1, 415–425, https://doi.org/10.1109/TSTE.2019.2892943.
10.1109/TSTE.2019.2892943
Web of Science® Google Scholar
23 Li M., Xiong L., Chai H., Xiu L., and Hao J., Mechanism of PV Generation System Damping Electromechanical Oscillations, IEEE Access. (2020) 8, 135853–135865, https://doi.org/10.1109/ACCESS.2020.3011456.
10.1109/ACCESS.2020.3011456
Web of Science® Google Scholar
24 Kumar K., Prakash A., Singh P., and Parida S. K., Large-Scale Solar PV Converter Based Robust Wide-Area Damping Controller for Critical Low Frequency Oscillations in Power Systems, IEEE Transactions on Industry Applications. (2023) 59, no. 4, 4868–4879, https://doi.org/10.1109/TIA.2023.3268632.
10.1109/TIA.2023.3268632
Web of Science® Google Scholar
25 Elalfy D. A., Gouda E., Kotb M. F., Bureš V., and Sedhom B. E., Comprehensive Review of Energy Storage Systems Technologies, Objectives, Challenges, and Future Trends, Energy Strategy Reviews. (2024) 54, https://doi.org/10.1016/j.esr.2024.101482, 101482.
10.1016/j.esr.2024.101482
Web of Science® Google Scholar
26 Datta U., Kalam A., and Shi J., Battery Energy Storage System to Stabilize Transient Voltage and Frequency and Enhance Power Export Capability, IEEE Transactions on Power Systems. (2019) 34, no. 3, 1845–1857, https://doi.org/10.1109/TPWRS.2018.2879608, 2-s2.0-85056199411.
10.1109/TPWRS.2018.2879608
Web of Science® Google Scholar
27 de Oliveira e Silva G. and Hendrick P., Photovoltaic Self-Sufficiency of Belgian Households Using Lithium-Ion Batteries, and Its Impact on the Grid, Applied Energy. (2017) 195, 786–799, https://doi.org/10.1016/j.apenergy.2017.03.112, 2-s2.0-85016441730.
10.1016/j.apenergy.2017.03.112
Web of Science® Google Scholar
28 Krismanto A. U., Mithulananthan N., and Krause O., Stability of Renewable Energy Based Microgrid in Autonomous Operation, Sustainable Energy, Grids and Networks. (2018) 13, 134–147.
10.1016/j.segan.2017.12.009
Web of Science® Google Scholar
29 Hassanzadeh M., Nayeripour M., Hasanvand S., and Waffenschmidt E., Decentralized Control Strategy to Improve Dynamic Performance of Microgrid and Reduce Regional Interactions Using BESS in the Presence of Renewable Energy Resources, Journal of Energy Storage. (2020) 31, 1–16.
10.1016/j.est.2020.101520
Google Scholar
30 Hassanzadeh M. E., Nayeripour M., Hasanvand S., and Waffenschmidt E., Intelligent Fuzzy Control Strategy for Battery Energy Storage System Considering Frequency Support, SoC Management, and C-Rate Protection, Journal of Energy Storage. (2022) 52, https://doi.org/10.1016/j.est.2022.104851, 104851.
10.1016/j.est.2022.104851
Web of Science® Google Scholar
31 Li K., Xu H., Ma Q., and Zhao J., Hierarchy Control of Power Quality for Wind—Battery Energy Storage System, IET Power Electronics. (2014) 7, no. 8, 2123–2132, https://doi.org/10.1049/iet-pel.2013.0654, 2-s2.0-84924970313.
10.1049/iet-pel.2013.0654
Web of Science® Google Scholar
32 Xu Y. and Singh C., Power System Reliability Impact of Energy Storage Integration With Intelligent Operation Strategy, IEEE Transactions on Smart Grid. (2014) 5, no. 2, 1129–1137, https://doi.org/10.1109/TSG.2013.2278482, 2-s2.0-84897632343.
10.1109/TSG.2013.2278482
Web of Science® Google Scholar
33 Sui X., Tang Y., He H., and Wen J., Energy-Storage-Based Low-Frequency Oscillation Damping Control Using Particle Swarm Optimization and Heuristic Dynamic Programming, IEEE Transactions on Power Systems. (2014) 29, no. 5, 2539–2548, https://doi.org/10.1109/TPWRS.2014.2305977, 2-s2.0-84906787371.
10.1109/TPWRS.2014.2305977
Web of Science® Google Scholar
34 Machowski J., Lubosny Z., Bialek J. W., and Bumby J. R., Power System Dynamics: Stability and Control, 2020, Wiley, Hoboken, NJ, USA.
Google Scholar
35 Kundur P., Power System Stability and Control, 1994, McGraw-Hill, New York, NY, USA.
Google Scholar
36 Saadatmand M., Gharehpetian G. B., Moghassemi A., Guerrero J. M., Siano P., and Alhelou H. H., Damping of Low-Frequency Oscillations in Power Systems by Large-Scale PV Farms: A Comprehensive Review of Control Methods, IEEE Access. (2021) 9, 72183–72206, https://doi.org/10.1109/ACCESS.2021.3078570.
10.1109/ACCESS.2021.3078570
Web of Science® Google Scholar
37 Du W., Wang H., Xiao L., and Dunn R., Modeling Energy Storage Systems into Electric Power Transmission Systems, 2010, IEEE International Universities Power Engineering Conference (UPEC), Glasgow.
Google Scholar
38 Shayeghi H., Shayanfar A., Safari R., and Aghmasheh H. A., A Robust PSSs Design Using PSO in a Multi-Machine, Environment Energy Convers Manage. (2010) 51, no. 4, 696–702.
10.1016/j.enconman.2009.10.025
Web of Science® Google Scholar
39 Hassanzadeh M. E., Nayeripour M., Hasanvand S., and Sepehrzad R., Hierarchical Optimal Allocation of BESS Using APT-FPSO Based on Stochastic Programming Model Considering Voltage Sensitivity and Eigenvalues Analyses, International Journal of Electrical Power & Energy Systems. (2023) 153, https://doi.org/10.1016/j.ijepes.2023.109291, 109291.
10.1016/j.ijepes.2023.109291
Web of Science® Google Scholar
40 Delavari A., Brunelle P., and Kamwa I., Real-Time Closed-Loop PQ Control of NPC Multi-Level Converter Using OPAL-RT and Speedgoat Simulators, 2018 IEEE Electrical Power and Energy Conference (EPEC), 2018, Toronto, ON, Canada, IEEE, 2381–2842.
Google Scholar
41 Carpiuc S., Schiesser Ms, and Villegas C., Current Control and FPGA-Based Real-Time Simulation of Grid-Tied Inverters, 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), 2020, Lyon, France, IEEE.
Google Scholar
42 Liu B., Wang Y., Mofid O., Mobayen S., and Khooban M. H., Barrier Function-Based Backstepping Fractional-Order Sliding Mode Control for Quad-Rotor Unmanned Aerial Vehicle Under External Disturbances, IEEE Transactions on Aerospace and Electronic Systems. (2024) 60, no. 1, 716–728, https://doi.org/10.1109/TAES.2023.3328801.
10.1109/TAES.2023.3328801
Web of Science® Google Scholar

All articles

Optimal Design of Battery Energy Storage System Controllers for Damping Low-Frequency Oscillations

Abstract

1. Introduction

2. System Modeling and Formulations

3. Optimal Controller Design

4. Simulation Results and Discussion

4.1. Scenario 1: Fault Disturbance in Power

4.2. Scenario 2: Fault Disturbance in Voltage

4.3. Scenario 3: Comparing BESS With PSS

4.4. Scenario 4: Investigating the BESS Parameters on Stability

4.5. Scenario 5: Speedgoat—Real-Time Simulation and Testing

5. Conclusion

Conflicts of Interest

Funding

Appendix 1

Appendix 2

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Optimal Design of Battery Energy Storage System Controllers for Damping Low-Frequency Oscillations

Abstract

1. Introduction

2. System Modeling and Formulations

3. Optimal Controller Design

4. Simulation Results and Discussion

4.1. Scenario 1: Fault Disturbance in Power

4.2. Scenario 2: Fault Disturbance in Voltage

4.3. Scenario 3: Comparing BESS With PSS

4.4. Scenario 4: Investigating the BESS Parameters on Stability

4.5. Scenario 5: Speedgoat—Real-Time Simulation and Testing

5. Conclusion

Conflicts of Interest

Funding

Appendix 1

Appendix 2

Open Research

Data Availability Statement

References

Figures

References

Related

Information