Design of a SUMO-Based Simulator for Optimal Location of Emergency Vehicles in the Emergency Medical Systems
Abstract
The response time between an accident happening and an ambulance reaching the incident place is a very delicate and crucial time. The time elapsed between those two events could be the determining factor of whether the injured person gets to live or die. Therefore, the response time of the ambulance assisting in the accident should be as small as possible. Response time can directly affect a person’s recovery time and can make the difference between the patient suffering temporary or prolonged disability, or even death. Locating the best position for ambulance bases is a challenge for emergency medical systems (EMSs). This will improve the EMS service in assigning the ambulance that arrives sooner to a given incident, thus reducing the risks associated with long response times. In this paper, we design a SUMO-based simulation framework named SEMSIM (Sistema d’Emergències Mèdiques SIMulator) that mimics the management of ambulances done by the EMS. The goal is to develop a tool to easily explore alternatives of stationing the available ambulances at the available bases, following different configuration settings (i.e., distributing the ambulances in different ways in the current bases or including new base locations), and analyze the average response time for each of those alternative configurations in comparison to the current configuration. The designed tool will help the EMS to explore dynamic configurations that are optimal throughout time, e.g. for different seasons, type of day, or time of the day. The SEMSIM simulation tool accurately replicates the ambulance assignments and response times of the EMS, validating its effectiveness. This allows SEMSIM to test new ambulance distribution configurations, including the addition of new bases, which would be costly or impractical to explore in real life. SEMSIM provides a valuable resource for EMS to optimize their operations using real incident data and maps from OpenStreetMap. The aim in this paper is to design a methodology based on dynamic SUMO simulations to analyze the optimal dynamic configuration of the fleet of ambulances that offers the smallest average response time and thus helps to improve the EMS service. As a case study, we explored various alternative configurations reducing response time by more than 2 min.
1. Introduction
Getting immediate medical assistance is critical when an incident occurs, as it can be the determining factor between life and death. Receiving medical care, even if primitive, when injured, can help reduce a person’s recovery time and make the difference between the patient having a temporary or long-term disability, or even death. As a result, it is critical for emergency vehicles to get to an incident place as fast as possible once an incident takes place and an emergency call (or e-call) arrives to the emergency service [1, 2]. For this reason, it is crucial to effectively plan and allocate emergency response resources for efficient and timely response to incidents, including the most serious ones requiring urgent service. This research work addresses the problem of optimal placement of ambulances in emergency medical systems (EMSs). Although our work is valid for any EMS, we will refer in particular to the EMS in Catalonia, called Sistema d’Emergències Mèdiques (SEM).
Note that in this text ambulance base location refers to determining the geographical area to build a base that will receive ambulances, whereas ambulance location, also known as ambulance deployment, refers to assigning ambulances to ambulance bases, i.e., determining the number of ambulances per base.
Ambulance technicians and EMS medics may sometimes notice that some ambulance locations are not optimal, e.g., there could be two base locations too close and other locations with a lack of ambulance service. Sometimes, ambulance base location is not based on an analytical criterion, but on many other factors, such as the existence of a primary care center, the availability of an appropriate facility, contractual, or even political reasons [3–7]. In addition, ambulance location is usually fixed throughout the service day and throughout the year. Both ambulance base location and ambulance location are usually done in a static way. The SEM, and surely other EMSs, would like to have a tool to help them to improve these two aspects: (i) optimal planning of base locations; and (ii) dynamically plan the allocation of ambulances in these bases. In summary, the SEM has raised the need to study the location of the bases in order to improve their planning and management.
This study aims to optimize the distribution of available ambulances among the different bases in the Catalan area, in order to reduce ambulance response time (RT) as much as possible. This paper explores the modification of the current configuration of ambulances available at current bases to find the optimal configuration that leads to the shortest average ambulance RT to incidents. To do that, we have used the actual incident data base of the SEM [8] that happened during 2018 and 2019. We have done our study in one of the areas of Catalonia. To achieve our goal, we have designed a simulation framework named SEMSIM (Sistema d’Emergències Mèdiques SIMulator), which is based on the Simulation of Urban MObility (SUMO) simulator [9]. SUMO helps us to simulate different scenarios following what happens in real life over a real map taken from OpenStreetMap (OSM) [10]. We are able to simulate an ambulance going from point A (i.e., the base of the ambulance or any location on the map in case the ambulance is returning to its base) to point B (i.e., the incident location) on the real map of Catalonia using OSM [10]. Next, we obtain the time it took the ambulance to reach its destination (i.e., the RT) on the real map.
The simulations are performed for the currently implemented configuration (i.e., one ambulance assigned at each base), as well as for all other possible configurations we would like to explore, i.e., changing the distribution of available ambulances among the bases deployed now. For each configuration, the simulation starts with the ambulances stationed at their corresponding bases; once an incident occurs, the simulation checks the RT of all free ambulances and chooses the available ambulance with the shortest RT to reach the incident location. In this way, our SEMSIM simulation framework mimics what happens in the management of a real EMS service. To begin with, in this work we have only considered advanced life support (ALS) ambulances, which attend the most serious incidents. Note that EMSs have several types of ambulances available and that ambulances are assigned to incidents based on the type of incident and the severity of the incident, see Section 3.1.1.
After completing all simulations for every possible configuration setting, the average RT for each tested configuration is calculated. The configuration with the lowest average RT is identified as the optimal distribution of ambulances across the available bases and would therefore be considered for real-life implementation.
In this work, we have taken the Sanitary Region (SR) of Terres de l’Ebre (TE) in Southern Catalonia, see Figure 1, as a starting point to develop our methodology and as an example to perform our simulations. We fed the SEMSIM simulator with the same incidents occurred during 2018 and 2019, provided by SEM, to obtain significative results.
The objective of our collaboration with the SEM has been to develop a simulation tool that allows them to freely modify base locations and ambulance distribution within a realistic simulation framework that replicates the SEM operation regarding ambulance assignment to incoming incidents. The aim was to identify alternative configurations that could reduce ambulance RTs in a given territory. This open problem is a significant challenge for EMS, as their priority is to reach every incident as quickly as possible. They believed that optimizing ambulance and base configurations could significantly improve RTs, which this work has demonstrated.
- •
We have developed a realistic SUMO-based simulation tool named SEMSIM that includes real maps over which vehicles actually travel to mimic the EMS operation. SEMSIM can assist EMS managers in easily exploring alternative ambulance and base locations, and it also provides researchers with a realistic platform to compare and validate their mathematical models for location optimization.
-
We have designed and implemented SEMSIM as a Python-based simulator that includes SUMO [9] and OSM [10]. SEMSIM mimics the basic operation of the SEM to assign the ambulance that arrives first to each of the incidents that occur over time. We have validated the accuracy of our SEMSIM simulator by comparing the results obtained with the corresponding values from the SEM real incident dataset for the years 2018 and 2019. By using the same incident locations in SEMSIM that occurred in real life, we have compared real values and simulation results to validate the SEMSIM operation.
- •
We have explored other possible ambulance location configurations using SEMSIM, to see if there is an alternative ambulance configuration that would improve the results. That is, we have analyzed what would have happened, using the same SEM real incident dataset for 2018 and 2019, if the available ambulances had been distributed differently among the available bases. We have shown how the SEMSIM tool can help the EMS easily explore other configuration alternatives, for example, adding a new ambulance or adding a new ambulance base. Thus, if the EMS, for example, acquires a new ambulance, the SEMSIM tool can help them decide which is the best base to assign that ambulance to, or even if the ambulance could help by reinforcing the service of the bases where it is most needed depending on the time of year or day of the week. In the case of adding a new ambulance base, the SEMSIM tool can help the EMS decide the best location to ensure that ambulances are strategically distributed to provide the best possible service.
Note that SEMSIM enables us to go back in time and replay the entire sequence of incidents that occurred in a specific time interval, testing alternative ambulance and base configurations that we wish to explore, to analyze what the impact on RT would have been in those cases. This differs from tools such as Google Maps, which accurately estimates current travel times, but only for the existing configuration (which cannot be changed in real life).
The rest of the paper is organized as follows. Section 2 summarizes related work close to our work. Section 3 presents details of the SEM needed to develop our SEMSIM simulator to model the basic SEM operation. In Section 4, we detail the main characteristics of the dataset provided by SEM, composed of incidents occurring during 2018 and 2029, which will be used by the SEMSIM simulator code. Section 5 introduces our SEMSIM simulator highlighting the main features, requirements, and algorithms included, whereas in Section 6, we validate the SEMSIM operation by comparing to real values provided by the SEM. Section 7 explores alternative ambulance configurations to further improve the RT. Appendix 1 discusses simulation results obtained with SEMSIM for alternative configuration settings, including a geographic and temporal study of the distribution of incidents. In Appendix 2, we use the SEMSIM tool to explore other ambulance configurations and more alternative bases. Also, we introduce a free access tool named Visual Power BI-based SEMSIM Tool to analyze results. Finally, Section 8 concludes the manuscript and points out some future work.
2. Related Work
- •
Works based on improving coverage, i.e., the percentage of requests served within a certain threshold RT, as measure of performance of location models. For example, the work [3] reviews covering models and optimization techniques for emergency response facility location and planning. The goal is to obtain the best location for EMS facilities among potential sites to provide efficient and effective service over a wide area with spatially distributed demands. The work [7] integrates interdependencies among ambulances into the well-known maximum expected covering location problem by introducing an upper bound for the busyness of each ambulance. Those mathematical interdependencies among ambulances gather the fact that when the closest ambulance site of an incident is not free, the service is transferred to another ambulance, normally the next closest one. That is, in most cases, the priority of a site decreases with an increasing distance to the incident location. The work [11] proposes a maximal coverage location problem based on joint coverage to locate optimal EMS stations and emergency centers simultaneously with a consideration of the two related trips (to the incident and to the hospital) for Wuhan, China. Similarly, the work [12] designs a numerical simulation model, from the Taipei EMS statistics, to evaluate the existing EMS system and suggest improvements. In [13], an optimization model to minimize the RT was proposed and some experiments were performed to determine better ambulance base locations keeping good coverage.
- •
Works based on survival as measure of performance of location models. For example, the authors of [4] proposed an optimization of EMS vehicle fleet allocation and ambulance base location through the use of a genetic algorithm (GA) with an integrated EMS simulation model. The objective was maximization of the overall expected survival probability across patient classes. The work [14] presents a mathematical modeling and simulation-based optimization approaches to identify the best location of emergency medical centers and assign the ambulance location to the selected centers to maximize survival rate. Other works such as [15] estimate the optimal RT threshold for survival to hospital discharge (which was 6.2 min) in Taiwan. In their study, they state that EMS vehicle bases should be precisely located to ensure RT targeting.
- •
Works based on ambulance relocation and redeployment, i.e., the possibility of changing ambulance locations based on demand. For example, the work [6] develops a Poisson emergency call arrival model to help size the ambulance fleet for increasing demand, assessing the RT when call arrival rates increase. The authors of [5] present a mathematical approach to ambulance fleet allocation and dynamic redeployment based on statistical modeling of request arrivals and service times. Another work [16] presents a discrete event simulation (DES) framework for dynamic ambulance redeployment to improve the ambulance location by capitalizing on the definite geospatial–temporal variations in ambulance demand patterns over the time of the day and day of the week. They model the emergency call arrival pattern in Singapore. Similarly, the authors of [17] and [18] claim that a well-designed EMS to provide the best possible quality of care to patients in emergencies should be flexible in the allocation of resources by dynamically adjusting the location of rescue teams during a day in response to temporal or geographical fluctuations such as demand patterns, traffic conditions, or the number of teams on duty. The goal is to save resources and at the same time maintain a good service.
As far as we are concerned, there is no similar proposal implemented in the Spanish EMS on the analysis of the best ambulance location based on simulation, so that our approach would be pioneer in our country and could also be extended to other regions. Additionally, we would like to highlight the fact that instead of developing a mathematical model that usually requires many assumptions, we have developed a realistic simulation framework over a real map that actually sends the ambulances to the incident locations and the hospitals over the map, and that mimics the real EMS operation. Our simulator SEMSIM will allow the EMS to have a tool to test any configuration of the ambulances and their bases over the real map and assess the results to see how they can improve their service seeking to minimize the RTs in the whole geographical area.
3. SEM
The SEM is an organization of the health public sector which is linked to the health department of the Catalonian government in Spain. The SEM is the only public health system in Catalonia that centralizes and coordinates the out-of-hospital sanitary emergencies in the whole territory.
The SEM service is provided by a team of professionals, including doctors, nurses, on-demand teleoperators, resource managers, and health emergency technicians. Their primary objective is to respond promptly and efficiently to emergencies and out-of-hospital health crises, maintaining the highest level of quality 24 h a day, 365 days a year. The care process is overseen by the Health Coordination Center, commonly referred to as CECOS. This center receives and manages all requests for assistance via telephone, providing tailored responses such as telephone advice or mobilizing the most suitable resources for each situation and pathology. CECOS manages all mobile resources, including ground and air units, distributed throughout the Catalan territory.
The mission of SEM is to deliver healthcare services to address urgent and prehospital emergency situations, while also providing health information and advice in both routine and extraordinary circumstances. Among its various functions, two primary goals stand out: (i) provide assistance to injured and critically ill persons at the scene of the incident or the onset of the illness; (ii) facilitate patient transfers with medical support, whether from the scene of the incident to a care facility, or between health centers when medical needs dictate and bed availability, services offered by each facility, and access time permit.
The SEM has a department of medical researchers dedicated to seeking innovative technologies that can enhance SEM’s objectives [8]. Collaborating with the SISCOM (Smart Services for Information Systems and Communication Networks, https://siscom.upc.edu) research group from the Universitat Politècnica de Catalunya (UPC), these groups form an interdisciplinary research team with the goal of enhancing the public health emergency system.
3.1. Facilities and SRs
In this section, we briefly describe the type of emergency vehicles (for roads and air) currently available in the SEM. Also, we summarize the main features and purpose of each kind of vehicle.
3.1.1. Facilities
- 1.
Basic life support (BLS) unit: Two emergency medical technicians ride in this type of ambulance. This emergency vehicle is typically used in severe and critical cases, where the injured person might require transportation to a hospital.
- 2.
ALS unit: Physicians, nurses, and medical transport technicians usually ride in this type of ambulance. The team lead by the physician is previously trained to assess the patient’s condition, administer necessary medications depending on the case, and provide defibrillation, airway management, and stabilization prior to and during the transportation to the hospital.
- 3.
Rapid intervention vehicle (RIV): Auxiliary vehicle capable of assisting the injured person, in the same way that ALS does, but not performing any transportation duties.
- 4.
Medicalized helicopter: A helicopter with the same staff/paramedics and equipment as the ALS. This includes a physician, a nurse, and a pilot.
To begin with, we have only considered ALS ambulances, as they are a scarce resource in the different regions and are vital for the most serious incidents [20, 21]. Hence, we anticipate that the selection of optimal base locations for ALS ambulances could significantly influence RTs (i.e., the time it takes for the ambulance to reach the scene of the incident). Additionally, in Appendix 2, we will also include BLS ambulances that are intended to assist the nonurgent incidents. Notice that BLS in a serious incident is also activated and usually helps ALS ambulances. Notice also that severe incidents might require more than one EMS vehicle.
3.1.2. SRs
The number of resources (i.e., ambulances, helicopters, and other emergency vehicles) is limited and, moreover, they are distributed asymmetrically along the geography. This underscores the critical need for a robust coordination structure to efficiently manage available resources and deliver the highest level of service in response to incidents occurring at any time and location across the entire territory. Furthermore, EMSs need to dynamically take a lot of decisions, instantaneously, according to the current circumstances for every new incoming incident (e.g., a new emergency call).
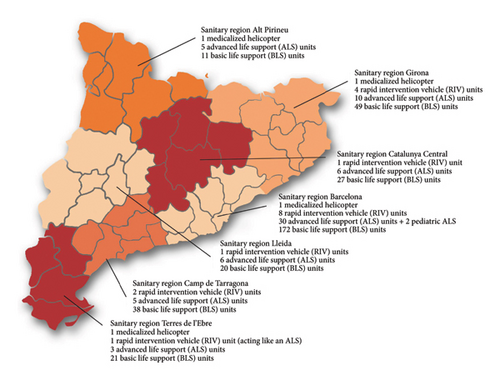
Catalonia has an area of 32,108 km2 and 8,016,606 inhabitants distributed asymmetrically along the territory. To cover the whole area, the SEM divided the region into seven SRs [22] for a more efficient emergency assistance, as it is shown in Figure 1.
The figure shows the SRs and the resources available in each of them. In Catalonia, the SEM currently has 4 helicopters, 67 ALS units, 338 BLS units, and 17 RIVs.
The allocation of ambulances to each health region varies based on factors such as size, population, and historical incident data. Larger and more densely populated areas are assigned a greater number of ambulances, reflecting the higher likelihood of incidents occurring in these regions. Notice in Figure 1 how the Regió Sanitària de Barcelona (SR of Barcelona) has the highest number of vehicles assigned (1 helicopter, 8 RIVs, 30 ALS units, 2 pediatric ALS units, and 172 BLS units), due to the higher density of population and, consequently, the higher number of incidents.
The project aims to be implemented across the EMS of Catalonia. In this work, we have begun with the southeast SR of Catalonia for the initial study. Subsequently, we plan to expand our study to another SR until we encompass the entire Catalonia area.
3.1.3. The SR Studied in This Work
The chosen region to start with is the Regió Sanitària of TE in Catalonia (the red colored region located at the bottom part of the map, see Figure 1). In TE, there are four bases and four ambulances. Currently, each ambulance is stationed in a base (i.e., they follow the configuration: 1111). There are 35 ways to set the 4 ambulances in the 4 bases, e.g., configurations 4000 (4 ambulances in Base A), 3100 (3 ambulances in Base A and 1 ambulance in Base B), 0220 (2 ambulances in Base B and 2 ambulances in Base C), among others.
The goal of this project is to optimize the configuration of these ambulances and to find the configuration that results in the smallest average RT () (smallest time required for the ambulance to reach the incident location from its current position). In this work, we have considered all the incidents attended by the EMS vehicles assigned to TE, that occurred either in the same SR or in other SRs, mostly in the adjacent SRs of Lleida and Tarragona (see Figure 1). Notice that in TE, incidents might also occur that are attended by EMS vehicles assigned to other SRs (mostly from the adjacent SRs). These incidents will be included in the analysis of the SR to which those EMS vehicles are assigned.
In the following sections, we will first validate the operation of SEMSIM and then use it to determine the optimal configuration based on the current number of resources.
4. SEM Dataset of Incidents as Input for SEMSIM
Our SEMSIM simulator mimics the same logical operation as the SEM, i.e., SEMSIM basically follows the same criteria as the SEM to assign ambulances to the sequence of incidents that happen throughout time. To feed the SEMSIM simulator, we have used the basic data included in the SEM dataset of incidents that took place in TE during 2018 and 2019. As said before, in this work, we will focus on the analysis of the SR of TE as a starting point of our study.
In this section, we describe the main features of the dataset provided by the SEM that includes statistics regarding the incidents happened during two years, for the current ambulance base location.
4.1. SEM Dataset Overview
The SEM provided us with records of 12,977 incidents that occurred in TE from January 1st 2018 to December 31st 2019. For each one of those incidents, at least one ALS was assigned (notice that severe incidents might have more than one ALS assigned). In our work, we have considered incidents with origin in TE and also incidents with destination in TE (we have also considered the border regions that belong to Lleida and Camp de Tarragona). Additionally, we have also considered cases with destinations in the SEM hospitals assigned to TE, see Table 1. After selecting those cases from the SEM dataset, we have 6780 incidents.
| Hospitals in/near TE | Probability (%) |
|---|---|
| Hospital de Tortosa Verge de la Cinta | 13.65 |
| Hospital Comarcal de Mora d’Ebre | 5.33 |
| Hospital Universitari Sant Joan de Reus | 1.16 |
| Hospital Comarcal d’Amposta | 0.48 |
| Hospital Universitari de Tarragona Joan XXIII | 0.24 |
| Clínica Terres de l’Ebre | 0.096 |
| Unitat Polivalent Terres de l’Ebre | 0.096 |
| Hospital de Sant Pau i Santa Tecla | 0.072 |
| CAP L’Ametlla de Mar | 0.024 |
| CL La Galera | 0.024 |
| CAP Mora la Nova | 0.024 |
| CAP L’Aldea | 0.024 |
| Comarcal de Vinaròs | 0.024 |
| CSMIJ-Tortosa | 0.024 |
| Hospital Universitari de Bellvitge | 0.024 |
| Unitat Polivalent Salut Mental Amposta-Hospital de Dia | 0.024 |
| N/D | 77.72 |
- Note: Both types of incidents (EmIn and IHT) are considered. CAP stands for primary attention center; N/D means no transport to hospital. The bold value highlights the hospital that received the most incidents during 2018 and 2019.
- •
Incident date and time.
- •
Incident location (longitude and latitude).
- •
Incident type. We consider two type of incidents: (i) we use the code “EmIn” to refer to the emergency incident (EmIn) derived from an emergency call; and (ii) the code “IHT” to refer to an interhospital transfer (IHT).
- •
Location of the destination hospital (longitude and latitude). Note: It is only applicable when the incident type is IHT and for those EmIn incidents that require hospital transfer using an ALS.
- •
RT of the ambulance, i.e., time elapsed from the moment receiving the emergency call till the ambulance arrival time at the incident site. This time includes the activation time (AcT) to decide which ALS/BLS ambulance/s to send, from which base to send it/them, and the rescue team preparation time. Besides, it includes the trip time from the current location of the assigned ambulance to the incident location. This time should be as short as possible, so that the ambulance arrives as quickly as possible to assist potential victims.
- •
Assistance time (AT) of the ambulance at the incident place, i.e., time during which doctors and technicians are taking care of the potential victims in the incident location. This time is inherent to the type of incident and its level of severity.
- •
Occupation time (OT) of the ambulance, i.e., total time during which the ambulance is busy attending the incident, according to equation (1).
- •
Transportation time (TT) of the ambulance from the incident location to the hospital (only when applicable).
- •
Vehicle code name assigned by the SEM to the ambulance dispatched to the incident, as indicated in Table 2.
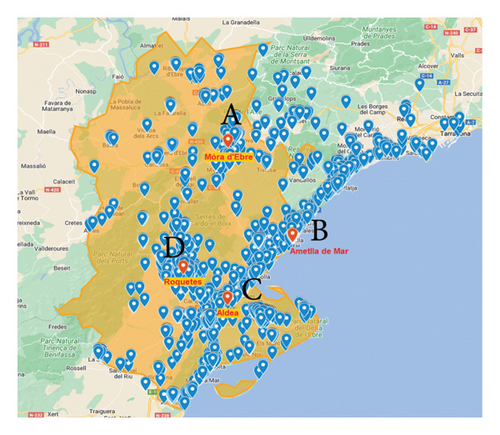
| Ambulance code | Base | Area | LON | LAT | |
|---|---|---|---|---|---|
| A | E405, E605 | Móra d’Ebre 2 | Ribera d’Ebre | 0.6285 | 41.08719 |
| B | E500 | L’Ametlla de Mar | Baix Ebre | 0.8013 | 40.8876 |
| C | E401, E600 | L’Aldea | Baix Ebre | 0.6280 | 40.7511 |
| D | E601 | Roquetes 2 | Baix Ebre | 0.5081 | 40.8179 |
It is important to note that the AT is not influenced by ambulance distribution nor base location (which are the focus of this study), but rather by the severity of the incident. Besides, TT depends on the incident location and, consequently, on the distance to the assigned hospital. Therefore, among the three values, only the RT is affected by the ambulance distribution or the base location, which are the focus of our work. We included the AT and TT description in the paper to provide a complete overview of the total time an ambulance is occupied, which includes RT, AT, and TT, as shown in equation (1).
Nonetheless, both AT and TT values in the SEM dataset have been useful in helping us clean the dataset of incidents. The raw EMS incident dataset contains several errors, primarily due to the stress faced by operators handling emergency calls. In some cases, incidents are logged but ultimately do not require a response, and the operator may forget to close them, leaving these entries in the dataset. As a result, the first step was to clean the dataset. This process is summarized in the next subsection.
4.2. Data Cleaning and Filtering
- •
Duplicates were removed. Notice that for a same incident, several witnesses could have called the emergency services, so that it might happen that several ambulances were assigned to the same incident, although the SEM finally only moved one to assist the incident.
- •
Odd cases (having irregular/odd locations) were deleted. Some incorrect entries present weird incident locations, e.g., in the middle of the sea, which usually are due to GPS errors.
- •
We removed cases whose ATs (time of the doctors/technicians attending the victims at the scene of the incident) are lower than 5 min or more than 2 h, since they are very unlikely, and if they appear in the dataset, it is more likely that they are wrong entries in the dataset. In the same way, we removed from the dataset those cases with TTs (time to transport the victim to a hospital) lower than 5 min or more than 45 min, since they are highly unlikely and probably are due to mistakes wrongly introduced in the dataset. Therefore, we removed from the dataset those cases that fulfilled any of these equations:
(2) -
For example, unusual entries in the dataset, which do not correspond to actual incidents, may occur when an emergency call initially assigns an ALS ambulance to an incident but the decision is quickly changed due to medical reasons. However, if the operator forgets to cancel the assignment in the dataset, the registered RT increases, resulting in an error.
- •
Cases where a helicopter was deployed to assist with an incident were excluded from the analysis, since this paper focuses exclusively on ALS ambulances.
- •
Additionally, any other classified incidents were properly reclassified after correcting any kind of mistake in the fields of the dataset.
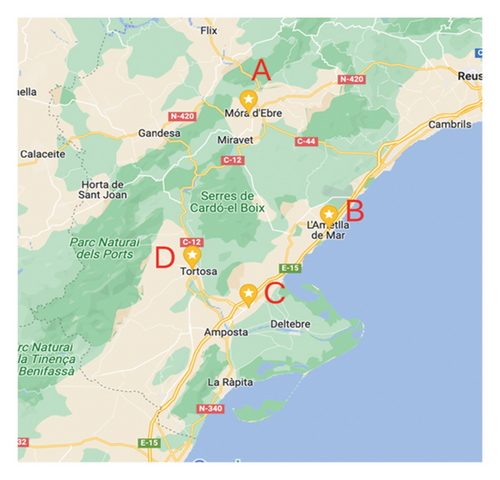
4.3. Coordinates of the Ambulance Bases
Currently, there are four bases in the TE SR, see Figure 2. Ambulances return to their designated base after completing the incident they have responded to. Each vehicle’s code name and its respective location coordinates are shown in Table 2.
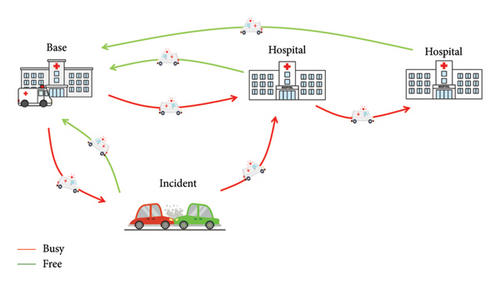
For each new incident/event that occurs (either an incident or a hospital-to-hospital transportation), SEMSIM needs to keep track of all the available ambulances mentioned in Table 2 to assign the best possible ambulance to each incident, i.e., the one that arrives sooner.
In the case of A and C rows, notice that we have two different ambulance code names for the same vehicle. This variation occurs because the ambulance code name changes depending on the personnel it transports.
For instance, when the ambulance stationed at Base A is staffed with a doctor, its code is E605 (and it will be an ALS); however, when it only transports a nursing technician, the code changes to E405 (and it will be a BLS).
4.4. Dataset Features
In the code of our SUMO-based simulator SEMSIM, we input the dataset containing incidents that occurred in 2018 and 2019, provided by the SEM. Subsequently, we simulate the performance of ambulances responding to the temporal sequence of accidents, testing various combinations of ambulance locations at available bases.
In this section, we will provide an overview of the types of incidents and their main statistical features. This will enhance our understanding of the SEM dataset regarding the specific characteristics of the incidents.
4.4.1. Summary of Incident Types
- •
prob (IHT incident): Probability of the ambulance doing an interhospital transportation (i.e., probability of having an IHT type of incident).
- •
prob (EmIn incident): Probability of having an EmIn type of incident. Notice that prob (EmIn incident) = prob (EmIn with ALS hospital transfer) + prob (EmIn without ALS hospital transfer).
- •
prob (EmIn with ALS hospital transfer): Probability of having an EmIn type of incident requiring ALS hospital transfer.
- •
prob (EmIn without ALS hospital transfer): Probability of having an EmIn type of incident not requiring ALS hospital transfer.
- •
prob (transport victim to hospital): Probability of the ambulance going to a hospital (regardless of the incident type, EmIn, or IHT). Notice that prob (transport victim to hospital) = prob (IHT incident) + prob (EmIn with ALS hospital transfer).
| Probabilities | Values (%) |
|---|---|
| Prob (transport victim to hospital) | 22.28 |
| Prob (IHT incident) | 5.84 |
| Prob (EmIn incident) | 94.16 |
| Prob (EmIn with ALS hospital transport) | 16.44 |
| Prob (EmIn without ALS hospital transport) | 77.72 |
- Note: Measured from the real SEM dataset of incidents occurred during 2018 and 2019.
Notice from Table 3 that most of the incidents (94.16%) are of EmIn type, i.e., EmIns derived from an emergency call. Among them, only 16.44% of the cases result in victims being taken to a hospital.
4.4.2. Dataset Statistics for AT and TT
Secondly, we computed the averages, standard deviations (SDs), and minimum and maximum values for AT and TT for all the incidents (either EmIn or IHT types of incidents) measured from the SEM dataset, see Table 4.
| AT (min) | TT (min) | |
|---|---|---|
| Average | μΑΤ = 30.58 | μΤΤ = 6.97 |
| Standard deviation | σΑΤ = 15.62 | σΤΤ = 13.89 |
| Minimum value | ATmin = 5.02 | TTmin = 0 |
| Maximum value | ATmax = 119.55 | ATmax = 45 |
- Note: Both types of incidents are included: EmIn and IHT. Measured from the real SEM dataset of 4001 incidents happened during 2018 and 2019.
Note that in this work we just use the AT and TT to help us to clean the dataset of incidents provided by the SEM, as it was explained at the end of Section 4.1. Notice that the AT is mostly intrinsic to the severity of the incident. In average, medical and technicians were attending the victims during half an hour in the incident location, with a wide range of values from 5 min to 2 h, and a SD of 15 min.
Regarding TT, this value basically depends on the distance from the incident location till the location of the assigned hospital. The hospital is usually the closest one, although it could be another specific hospital that is further away if the type of incident requires it. On average, the TT was 7 min and the maximum TT was 45 min.
4.4.3. Transport to Hospital Statistics
Thirdly, we computed the probability of victims being transferred to the diverse hospitals located in or near TE, including both types of incidents EmIn and IHT. Results are shown in Table 1.
Notice that in Table 1, N/D corresponds to those EmIn type incidents that either (i) did not require urgent ALS hospital transfer in that moment (thus, no hospital was needed as destination for the ambulance upon the incident); or (ii) the patient was transferred to a BLS ambulance to be transported to a hospital. This happens most of the time, that is, in 77.72% of the time the ALS ambulance becomes available after attending to the incident and then returns to its base. However, it is important to consider that in these scenarios, these ambulances may be reassigned to new incidents while returning to their bases.
From Table 1, we can see that most of the incidents (13.65%) that required a transport to hospital were addressed to Hospital Tortosa Verge de la Cinta, which is located in the TE SR. The second most frequent is Hospital Comarcal de Mora d’Ebre (5.33%), also located in TE. Next is Hospital Universitari Sant Joan de Reus (1.16%), which is located in the neighboring region of Tarragona, to the north. Note that some incidents required a more specialized hospital located in Barcelona, e.g., Bellvitge or Sant Pau i Santa Tecla.
5. SEMSIM Simulator to Model the SEM Operation
In this section, we briefly introduce our simulation tool named SEMSIM. SEMSIM mimics the operation of the EMS of Catalonia, named as SEM. As we mentioned previously, in this work, we consider the SR of TE, located at the South of Catalonia, see Figure 1.
5.1. Use of SUMO to Generate the Ambulances’ Trips
First of all, SEMSIM needs to simulate the entire journey of ALS ambulances whenever they are assigned to any incident that occurs over time. This will allow us to optimize the assignment of ambulances to incidents by selecting the most suitable ambulance available, ensuring it arrives first at the scene by traversing the real map on actual roads. Notice that severe incidents might require more than one ALS.
To know which available ambulance is the fastest for a given incident, we need to develop a model that fulfills our objectives. We want simulation results to be as close as possible to the real-life scenario. This is why we decided to include a mobility simulator to carry out the ALS trips in our SEMSIM simulator. SEMSIM includes real maps taken from OSM [10] so that SEMSIM makes ambulances travel over realistic roads.
Notice that roads in OSM have different speed limits assigned. Nonetheless, notice also that, of course in real life, activated EMS vehicles (e.g., with the siren on) will travel at the highest possible speed that the EMS driver can achieve, even crossing red traffic lights if required, although always avoiding dangerous situations for others. In our SEMSIM simulator, we have currently not included normal vehicles, and there are only EMS vehicles. The reason is that in this work, we are interested only in comparing which is the best ambulance configuration (i.e., where to deploy the available ambulance fleet to improve the EMS service). Therefore, to simplify the analysis and decrease simulation time, it was sufficient to compare the available alternatives under the same circumstances (i.e., only ambulances are traveling on the map). In future work, we will also include normal vehicles in the simulations, which will, of course, have to give way to passing EMS ambulances attending a service.
The mobility simulator we used to develop SEMSIM is the widely known SUMO [23] simulator. SUMO allows for intermodal simulation including pedestrians and it comes with a great set of tools to create scenarios. Even though the SUMO framework facilitates the traffic generation with its build-in tools (e.g., OD2Trips, RandomTrips, DUArouter, DUAIterate, and MARouter), the overall traffic demand generation may result in a complex and time-consuming process. To build route traces, SUMO tools require several input files to be configured. Moreover, in order to enable rerouting functionality, additional configurations are required. Rerouting is needed when an ALS ambulance that finishes its service assisting an incident and is now on its way back to the base is assigned to a new incoming incident. In such a case, we need to change during the SUMO simulation the ambulance’s destination to the new incident location.
In this regard, we have used the SUMO Traffic Generation (STG) tool to generate the traffic demand. STG was developed by Barbecho, and it is available in [24]. STG facilitates the traffic demand generation based on SUMO tools. It allows researchers to quickly execute the different SUMO tools to select the appropriate traffic generation tool for a given scenario (e.g., urban and highway). For this, the STG tool automatically generates the required files to execute the different SUMO tools. Additionally, STG uses real traffic statistics to create route traces as realistic as possible.
- •
Find the available ambulance that will arrive first to a given incident and assign it to that incident. This is repeated for the entire sequence of incidents handled by the SEMSIM.
- •
Detect when an ambulance is free after completing its current service, i.e., once it has finished its current job at the incident location or at the hospital if a transport was required. That ambulance can again be considered as available, so it could be assigned to any incoming incident while it returns to its assigned base.
- •
Generate the SEMSIM output dataset for all the incidents, including the various metrics of interest (assigned ambulance, activation moment, RT, AT, TT, and OT) for analysis and discussion of results.
The main features of the SUMO simulation logic are detailed in the following subsection.
5.1.1. SUMO Simulation Logic
SUMO is a microscopic, open-source traffic simulation tool designed to model the movement of vehicles, pedestrians, and other road users in urban environments. SUMO is a specialized traffic simulation tool focusing on the microscopic behavior of individual vehicles and real-time interactions within urban environments, using real-world data like road networks from OSM. It differs from DES and agent-based simulation (ABS) in its specific application to traffic, while DES general-purpose models based on discrete events changing state at specific times often are used in manufacturing and logistics. ABS, on the other hand, simulates complex adaptive systems through interactions of autonomous agents, ideal for studying emergent behaviors in social and economic systems. SUMO’s detailed vehicle-level simulation and real-time capabilities make it uniquely suited for urban traffic analysis, unlike the broader applications of DES and ABS.
- •
Microscopic traffic simulation: SUMO simulates individual vehicles and their interactions in real time. Each vehicle is modeled with unique characteristics such as speed, acceleration, and lane-changing behavior.
- •
Road network representation: The simulation is based on a detailed road network, which includes lanes, intersections, traffic lights, and other road infrastructure. SUMO reads network files that describe these elements.
- •
Vehicle dynamics: The motion of each vehicle is computed based on car-following models, lane-changing models, and traffic light control algorithms. The car-following model ensures that vehicles adjust their speed to maintain a safe distance from the vehicle ahead.
- •
Traffic control: Traffic signals and priority rules are modeled to control vehicle movement at intersections. SUMO allows for dynamic traffic light adjustments to simulate various traffic management strategies.
- •
Routing and assignment: Vehicles follow predefined routes or dynamically generated ones based on real-time conditions, such as traffic congestion. SUMO computes alternative paths when necessary to avoid traffic jams and optimize the flow of vehicles.
- •
Real-time updates: SUMO continuously updates vehicle positions and speeds in small time steps, typically on the order of fractions of a second. This allows for highly detailed and accurate traffic simulations.
- •
Data input and output: SUMO uses XML-based configuration files to define simulation parameters and outputs data on vehicle trajectories, traffic flow, and emissions, which can be analyzed post-simulation.
- •
Discrete time steps: SUMO operates in discrete time steps where vehicle positions, speeds, and interactions are updated at each step.
- •
Car-following model: SUMO’s default is the Krauss model, which calculates vehicle speed based on safe distances and reaction times.
- •
Lane-changing algorithms: SUMO implements models like the MOBIL algorithm to simulate how and when vehicles switch lanes based on traffic density and speed advantages.
- •
Network loading and routing: SUMO uses algorithms to assign vehicles to routes and update their paths dynamically in response to changing traffic conditions.
5.2. Requirements to Develop the SEMSIM Simulator
In this section, we highlight the essential requirements of our research, establishing the foundation for the development of our SEMSIM simulator. Additionally, we offer deeper insights into the implemented code.
5.2.1. SEMSIM Objectives
To start with, in this work, we have considered the SR of TE, although we plan to extend our work to the rest of SRs in Catalonia, see Figure 1. In TE, there are four bases for the ALS ambulances and four ALS ambulances, see Figure 2. The first base will be referenced as Base A, the second base as Base B, the third as Base C, and the fourth as Base D. Currently, each ambulance is stationed in a different base, i.e., they follow configuration 1111 meaning that there is one ambulance per base. The goal of our research is to optimize the ambulance location (i.e., how to optimally distribute ambulances at bases) and to find the configuration that results in the smallest average ambulance RT, i.e., the smallest trip time required from the ambulance coordinates to the location of the assigned incident. Notice that the ambulance location has an impact on the time elapsed from the moment when the ambulance is assigned to an incident to the moment that the ambulance arrives to the incident location (i.e., RT). The other times of equation (1) (AT and TT) are independent of that configuration, and rather depend on the severity of the incident and on the distance to the assigned hospital, respectively. That is, the only parameter from equation (1) that we measure in our simulations is the RT, and we do not measure AT nor TT.
- •
1111: One ambulance at each of the bases. This is the current configuration.
- •
0112: One ambulance at Base B, one ambulance at Base C, and two ambulances at Base D.
- •
1030: One ambulance at Base A and three ambulances at Base C.

After simulating the 35 different configurations, we will find which is the configuration that produces the smallest average RT (). That configuration would be the optimal ambulance configuration. The simulation run time was 2 h per each configuration (server DELL R752, GPU, 12 RAM 64 GB), so that the whole simulation time was 70 h. Note that the simulation is performed only once, and all the results of the 35 configurations can then be visually analyzed using our public Power BI-based SEMSIM tool [25]. Notice that while 2 h of simulation time may seem long to test various ambulance distributions and base locations, doing so in real life would be nearly impossible. SEMSIM enables EMS decision makers to simulate 2 years of real incidents in just 2 h, allowing them to evaluate the impact of different configurations, such as adding new bases or adjusting ambulance assignments.
To fulfill our objectives, we have designed three algorithms in the SEMSIM simulator using Python code to mimic the SEM operation: (i) Algorithm 1 to assign ALS ambulances to incidents; (ii) Algorithm 2 to find out if the ambulances are busy or free; and (iii) Algorithm 3 to find out the location of the free ambulances. In the following, we explain those algorithms.
5.2.2. Proposed Algorithm in SEMSIM to Assign ALS Ambulances to the New Incoming Incidents
- •
Every time a new incident occurs, the ambulances’ states are checked. Then, locations of free ambulances are obtained.
- •
If the ambulance is free (not busy attending a previous incident), a SUMO function is called to measure the RT it would take for that ambulance to reach the incident’s location over the real map [10]. This is repeated for all the free ambulances in that moment.
- •
The algorithm compares the RTs of the available ambulances, selecting the one with the shortest RT to be assigned to assist the incident.
- •
The assigned ambulance will be busy during OT seconds, which is the addition of RT, AT, and TT, see equation (1). Recall that depending on the incident type, TT is either equal to zero (Type = “EmIn without hospitalization”) or it is different from zero (Type = “IHT” or Type = “EmIn with hospitalization”). The record of each incident in the SEM dataset includes the AT value for that incident, and which hospital was assigned to that incident in case a hospital transport was needed. In such a case, SEMSIM changes the ambulance destination to the hospital location and the ambulance will travel to that hospital. We measure TT from the SEMSIM simulation. Once the ambulance arrives to the assigned hospital, the ambulance finishes its service for that incident.
- •
After completing its current service (after OT sec), the ambulance becomes available again and is eligible for the next incoming incident. SEMSIM then updates the ambulance destination to its base location, and the ambulance travels there.
5.2.3. Proposed Algorithm in SEMSIM to Find Out the State of the ALS Ambulances
Upon the event of a new incoming incident, the SEM assigns the best free ALS ambulance, i.e., the ALS ambulance that will arrive first to the incident location. This is precisely what our SEMSIM simulator must do. Recall that in this work, for the sake of simplicity, we are only considering incidents that require an ALS due to their higher level of severity. To fulfill this goal, we have designed an algorithm to be used by SEMSIM to find out the state (i.e., free or busy) of all the ALS ambulances available in the SR, see Figure 4.
-
Algorithm 1: Assign ALS ambulances to incoming incidents following the SEM policy.
-
Input:
-
• SEM dataset of incidents from 2018 to 2019 in Terres de l’Ebre.
-
• Incident details:
-
1. Location: Longitude, latitude.
-
2. Time (t): Moment when the incident occurs.
-
3. Number of ALS ambulances (NALS) in the Sanitary Region: Four in Terres de l’Ebre.
-
4. State of each ALS (ALS_statei,t): Free or busy, determined using Algorithm 2. Find out the state of each ALS ambulance i at moment t, i € (1 … NALS).
-
5. Type of incident (Type): One of:
-
⁃ IHT (interhospital transfer).
-
⁃ EmIn with hospital transport.
-
⁃ EmIn without hospital transport.
-
Output:
- •
Assigned ambulance to the new incoming incident.
-
while not at the end of the list of incidents do:
-
Step 1. New incident detected:
-
o Check the states of all ALS ambulances.
-
o Determine locations of all free ALS ambulances using Algorithm 3.
-
Step 2. Response time calculation:
-
o Compute the response times (RTs) for each free ALS ambulance to the incident location using SUMO functions.
-
Step 3. Assign the ALS that will arrive first:
-
o The ALS ambulance with the smallest RT is assigned to respond to the incident.
-
Step 4. Update ambulance state:
-
o The assigned ALS will remain busy for the duration: OT = RT + AT + TT, see equation (1), where:
-
⁃ RT = Response time to the incident location (simulated with SEMSIM).
-
⁃ AT = Assistance time (retrieved from the SEM dataset).
-
⁃ TT = Trip time to the hospital (if transport is needed, simulated with SEMSIM).
-
o If transport to the hospital is required, the ambulance will travel to the designated hospital and change to “free” state upon arrival.
-
Step 5. Return to base:
-
o After the busy period (OT seconds), the ambulance’s state changes back to “free,” and it returns to its base location.
-
end
-
Description: This algorithm assigns ALS ambulances in real time based on SEM operational policies, minimizing response times and efficiently managing the availability of resources.
To know the state of an ambulance (i.e., if it is busy assisting another incident or available to be chosen to assist the new incident), we compute the time elapsed from the activation moment of the last incident to which that ambulance was assigned to the current moment (Telapsed), see Algorithm 2. If the time elapsed is higher than the last OT, using equation (1), obtained for that ambulance (Telapsed > OT), it means that the ambulance has already finished assisting its last incident assigned, so that now the ambulance is free (ALSst = free). Thus, the ambulance will be included in the set of available ambulances to be chosen for the new incoming incident, according to Algorithm 1. Otherwise, the ambulance is still busy (ALSst = busy) and therefore cannot be considered to attend the new incoming incident.
Notice that SEMSIM (and the EMS in real life) could also know the state of the ambulances (free, busy) once they change their state and communicate it to the EMS. However, for the sake of accurate and up-to-date knowledge of the state of the ambulance fleet, Algorithm 2 tracks the current locations of the ambulances and updates their OTs as soon as they arrive to destination (e.g., incident location, hospital, and base). To achieve this, we assume that the ambulances use a geolocation device and that the EMS tracks the location of the ambulance fleet. This is a reasonable assumption and we certainly know that the SEM applies it. In this way, once the ALS arrives at destination (e.g., the hospital), it updates its OT and becomes available.
-
Algorithm 2: Find out the state of the ALS ambulances.
-
Input:
-
• SEM dataset of incidents from 2018 to 2019 in Terres de l’Ebre.
-
• Ambulance details:
-
1. Number of ALS ambulances (NALS) in the Sanitary Region: Four in Terres de l’Ebre.
-
2. Activation time (ti) of the last incident to which ambulance ALSi was assigned, i € (1 … NALS).
-
3. Occupation time OTi regarding the last incident to which ambulance ALSi was assigned, i € (1 … NALS). Calculated in Algorithm 1.
-
Output:
-
• ALS-statei,t: Free or busy. State of each ALS ambulance i at moment t, i € (1 … NALS).
-
i = 1;
-
whilei ≤ NALSdo
-
Compute Telapsed, i = Time elapsed from the activation moment ti of the last incident to which ambulance i was assigned, to the current moment:
-
ifTelapsed,i > OTithen
-
ALSst, i, t = free; ambulance ALSi already finished its last assigned service and it is free.
-
else
-
ALSst,i,t = busy; ambulance ALSi is still busy with its last assigned service.
-
end
-
i = i + 1;
-
end
-
Description: This algorithm finds out the state (free or busy) of each one of the ALS ambulances of the Sanitary Region.
5.2.4. Proposed Algorithm in SEMSIM to Find Out the Location of the Free Ambulances
- 1.
If, at the time of a new incoming incident t, Telapsed,i is higher than the summation of ambulance i OT (OTi) and the time needed for that ambulance to get back to its base (Telapsed,i > OTi + return trip time to its base), it means that the ambulance already arrived at its base, see Algorithm 3.
- 2.
Conversely, given that ambulance ALSi is free (Telapsed,i ≥ OTi), the time elapsed should be in the range [OTi, OTi + return time). It means the free ambulance is traveling on its trip back to its base, but not yet arrived there. In such a case, the algorithm locates where the ambulance is to be able to compute the trip time from the ambulance’s current location to the new incident location, see Algorithm 3.
6. Validation of the SEMSIM Simulator and Analysis of the Current Configuration
To validate SEMSIM and double check that it works properly, we will first reproduce the current 1111 ambulance configuration (i.e., one ambulance per base) in our simulator and compare it to the actual SEM results to validate the SEMSIM operation.
-
Algorithm 3: Find out the location of the available ambulance ALSi at time t.
-
Input:
-
• SEM dataset of incidents from 2018 to 2019 in Terres de l’Ebre.
-
• Ambulance ALSi, which is available at time t. Its state is ALSst,i,t = free.
-
• Activation time ti of the last incident to which ambulance ALSi was assigned.
-
• Occupation time OTi regarding the last incident to which ambulance ALSi was assigned. Computed in Algorithm 1.
-
Output:
-
• Location of the available ambulance ALSi at moment t.
-
Compute Telapsed,i = Time elapsed from the activation moment ti of the last incident to which ambulance ALSi was assigned, to the current moment t.
-
ifTelapsed,i > OTi + (trip time to get back to the ALSi base) then
-
The location of ambulance ALSi at moment t is its own base.
-
else
-
The ambulance ALSi is traveling on its trip back to the base, but not yet arrived to the base. Its location is obtained from SUMO functions.
-
end
-
Description: This algorithm finds out the location of the free ambulance ALSi at time t (ALSst,i,t = free).
Notice that we only have the real SEM results for one possible configuration of the ambulance distribution, i.e., the 1111 configuration, which is the current distribution of ambulances deployed by the SEM in the SR of TE. We will compare the SEMSIM output results with the values of the real SEM dataset, for the current ambulance configuration. We wanted to see which ambulances were picked in SEMSIM and compare it to the real-life selection for the same incidents that took place during 2018 and 2019. We will calculate the same incident statistics (i.e., ALS assigned, RT, AT, TT, and OT) using our SEMSIM simulator for the current location of the ambulance bases, to validate our simulator.
Once validation shows success, we will use SEMSIM to simulate the same incidents that really happened, but for each one of the possible 35 ambulance configurations to see if there is a better alternative configuration that would have offered a smaller RT. That would be the optimal ambulance configuration using the current resources (i.e., same number of ambulances and location of bases).
Thus, we need to compare real-life ambulance assignation done by SEM with those chosen by SEMSIM for the same incidents recorded in the SEM dataset covering the years 2018 and 2019. Out of the 4001 simulated incidents, we got 540 mismatches. This indicates that SEMSIM selected the same ambulance as in real life 540 times (out of 4001 incidents). This makes a match rate of 540/4001 = 13.49% and a nonmatch rate of (4001-540)/4001 = 86.51%. The two main reasons for this slight difference are detailed in a list below.
In Table 5, we show the average RT and OT about the incidents that occurred during the years 2018 and 2019, for real values taken from the SEM dataset and for values obtained by our SEMSIM simulator. RT measures the trip time of the assigned ambulance to the incident location, while OT measures the total OT of the ambulance till it becomes available again, see equation (1). Notice that among the three components included in equation (1) to compute OT, only RT is influenced by ambulance distribution or base location, which are the main focus of our work. This is because AT depends solely on the severity of the incident, and TT depends on the incident location. Therefore, AT and TT are unaffected by changes in ambulance distribution or base locations considered in this study. Consequently, our simulations focus on identifying ambulance distributions or base locations that minimize RT (see Figures 5, 6, 7, 8, 9, 10, and A1). Nevertheless, we have also presented simulation results for OT as complementary information, solely to visualize the total ambulance OT (see Tables 5, 6, 7, 8, and 9).
| (min) | (min) | |
|---|---|---|
| Real life—SEM | 12.41 | 50.08 |
| Simulated—SEMSIM | 8.28 | 43.25 |
| Simulated—SEMSIM (including activation time) | 11.01 | 45.98 |
- Note: Average response time (RT) and average occupation time (OT). The bold values represent the average response times measured in real life and by the SEMSIM simulator, which differ by only 1.4 minutes.

| Real life SEM | SEMSIM | % real life | % SEMSIM | |
|---|---|---|---|---|
| A | 549 | 552 | 13.7 | 13.8 |
| B | 866 | 834 | 21.6 | 20.8 |
| C | 1342 | 1410 | 33.5 | 35.2 |
| D | 1244 | 1205 | 31.1 | 30.1 |
- Note: Number of times an ambulance was selected from each base, in real life and in the SEMSIM simulator.
| Incidents 2018-2019 | 4001 | 100 (%) | Incidents/day |
|---|---|---|---|
| Summer incidents | 2042 | 51.04 | 5.59 |
| Winter incidents | 1959 | 48.96 | 5.36 |
| Weekday incidents | 2743 | 68.56 | 5.26 |
| Weekend incidents | 1258 | 31.44 | 6.03 |
| Morning incidents | 1535 | 38.36 | 6.31 |
| Afternoon incidents | 1596 | 39.90 | 6.56 |
| Night incidents | 870 | 21.74 | 3.57 |
| Temporal subinterval | Base |
|---|---|
| Winter weekday morning (W/D/M) | A |
| Winter weekday afternoon (W/D/A) | D |
| Winter weekday night (W/D/N) | B |
| Winter weekend morning (W/E/M) | B |
| Winter weekend afternoon (W/E/A) | B |
| Winter weekend night (W/E/N) | D |
| Summer weekday morning (S/D/M) | C |
| Summer weekday afternoon (S/D/A) | C |
| Summer weekday night (S/D/N) | D |
| Summer weekend morning (S/E/M) | B |
| Summer weekend afternoon (S/E/A) | C |
| Summer weekend night (S/E/N) | B |
| No. | Configuration | (min) | (min) |
|---|---|---|---|
| 1 | Amposta | 7.10 | 42.08 |
| 2 | La Ràpita | 7.40 | 42.37 |
| 3 | Alcanar | 7.61 | 42.59 |
| 4 | Deltebre | 7.67 | 42.65 |
| 5 | Ulldecona | 7.69 | 42.66 |
| 6 | Santa Bàrbara | 7.73 | 42.70 |
| 7 | La Sènia | 7.80 | 42.77 |
| 8 | El Temple | 7.84 | 42.80 |
| 9 | Móra la Nova | 7.89 | 42.84 |
| 10 | Flix | 7.92 | 42.87 |
| 11 | L’Ampolla | 7.92 | 42.87 |
| 12 | Baix Ebre | 7.92 | 42.87 |
| 13 | El Perelló | 7.93 | 42.88 |
| 14 | Camarles | 7.94 | 42.88 |
| 15 | Xerta | 7.94 | 42.88 |
| 16 | Gandesa | 7.97 | 42.95 |
| 17 | Batea | 8.03 | 43.00 |
| 18 | Horta Sant Joan | 8.18 | 43.15 |
- Note: The map location of the 18 candidate primary health centers (PHCs) in TE as potential new ambulance bases is shown in Figure 12. The bold values indicate the three PHCs that resulted in the lowest average response times..
Note that RT is defined as the time between receiving the emergency call and the ambulance arrival time at the incident site. Thus, the real-life RT also includes the AcT to decide which ALS/BLS ambulances to send, from which base to send it, and the rescue team preparation time. We have computed the average AcT in TE during 2018 and 2019 and it was AcT = 2.73 min. Then, we have added it to the simulated RT, shown in the third row of Table 5.
- •
The main factor that influences the difference in between SEMSIM and reality is the absence of real unpredictable situations that might appear in real life that affect the traffic in the roads such as road works, construction zones, or protests (although when they are on duty they travel at the maximum possible speed even breaking traffic rules). This fact directly affects the trip times RT and TT, see equation (1). Notice that AT only depends on the severity of the incident and the time required by doctors and technicians to care for the victims.
- •
In the case of our SEMSIM simulator, we have assigned ambulances only based on the lowest RT, i.e., the trip time of each available ambulance to the incident location. However, in reality, ambulance assignments are made by a human who makes choices based on the closeness of the incident and the ambulances and their judgment and experience, among other possible factors.
Those facts explain the discrepancies in the trip times between our SEMSIM program and the reality. Knowing this, the small time difference (barely 1.4 min) between real trip times and computed trip times is not a serious issue since all simulations will have the same average time differences comparing to real life (also around 1.4 min in average). The 1.4-minute discrepancy between simulated and real values is not an issue for the EMS’s objectives, as the optimal configuration identified in the simulator would also be the best configuration in real life.
Considering these two factors that influence ambulance assignments, we consider a 13.49% discrepancy to be very low. This means that in 86.51% of incidents, SEMSIM chose the same ambulance as SEM did in real life as the resource assigned for those incidents. This analysis confirms the effectiveness of our SEMSIM simulator, as it yields results closely aligned with reality. This validates the potential of SEMSIM for simulating alternative ambulance configurations to explore whether there are better distribution options that could minimize RTs and further enhance overall statistics.
To complement the SEMSIM validation, we have also compared the number of times an ambulance was selected from each base, in real life and in the SEMSIM simulator, see Table 6. We can see that results are very similar. For example, the ambulance assigned to Base B attended 21.6% of incidents in real life (866 out of 4001), compared to 20.8% according to SEMSIM (834 out of 4001).
This section is dedicated to validating the SEMSIM tool. To achieve this, we compare the simulation output results (specifically, the ambulance assigned to each incident and the average RT) for the current configuration 1111 (one ambulance per base at the four current locations). The only real data available for correspond to the current SEM configuration (1111). In other words, configuration 1111 is the only scenario for which we have both real-world and simulated results. If these results align with sufficient accuracy, we can conclude that SEMSIM is validated and can confidently be used to explore other alternative configurations.
This underscores the valuable utility of SEMSIM: the ability to explore alternative configurations beyond the current 1111 setup. Conducting such analyses in real life would be impractical or even impossible, which is where the SEMSIM simulation framework becomes an effective tool for assisting EMS decision makers. In Section 7, we conduct several simulations for various base locations and ambulance distributions to demonstrate the potential of the SEMSIM tool in designing better configurations.
6.1. Results of 4 Ambulances in 4 Bases
Our dataset consists of all 4001 incidents that occurred in TE during 2018 and 2019. Table 6 shows the results of the simulations for all the scenarios with n = 4 ambulances combined with r = 4 bases. There is a total of 35 possible configurations, i.e., combination with repetition C4,4 = 35. The goal is to explore if there is a better alternative configuration than the current 1111 (i.e., 1 ambulance per base), after carrying out all the 35 simulation scenarios with SEMSIM. We have arranged the configurations in the table in descending order of the average RT () obtained with SEMSIM. This enables us to promptly identify the top configurations that yielded the lowest , providing the most efficient service as ambulances arrived faster compared to other configurations.
As observed in Table 10, configuration 1111, representing one ambulance at each base, yields the lowest average RT . This configuration is the current ambulance deployment in TE. To sum up, the SEMSIM results reveal that the current configuration of ambulances is the best possible among all the possible configurations that arrange 4 ambulances in the 4 bases following a fixed policy. Nonetheless, maybe there are other better dynamic configurations that could further reduce the RT, as we will see in the next sections.
| No. | Configuration | (min) | (min) |
|---|---|---|---|
| 1 | 1 1 1 1 | 8.28 | 43.25 |
| 2 | 1 0 2 1 | 9.79 | 44.76 |
| 3 | 1 1 2 0 | 9.91 | 44.88 |
| 4 | 1 0 1 2 | 10.13 | 45.11 |
| 5 | 1 1 0 2 | 10.16 | 45.13 |
| 6 | 2 0 1 1 | 10.28 | 45.26 |
| 7 | 0 2 1 1 | 10.61 | 45.58 |
| 8 | 0 1 2 1 | 10.61 | 45.59 |
| 9 | 1 2 0 1 | 10.63 | 45.61 |
| 10 | 0 1 1 2 | 10.71 | 45.69 |
| 11 | 2 1 1 0 | 10.75 | 45.72 |
| 12 | 1 2 1 0 | 10.76 | 45.73 |
| 13 | 2 1 0 1 | 11.01 | 45.98 |
| 14 | 1 0 3 0 | 11.83 | 46.81 |
| 15 | 2 0 2 0 | 12.03 | 47.01 |
| 16 | 0 0 2 2 | 12.61 | 47.59 |
| 17 | 0 2 2 0 | 12.64 | 47.62 |
| 18 | 0 2 0 2 | 12.69 | 47.67 |
| 19 | 0 0 3 1 | 12.79 | 47.76 |
| 20 | 0 1 3 0 | 12.92 | 47.90 |
| 21 | 0 0 1 3 | 13.12 | 48.09 |
| 22 | 0 1 0 3 | 13.16 | 48.13 |
| 23 | 0 3 0 1 | 13.42 | 48.40 |
| 24 | 1 0 0 3 | 13.43 | 48.40 |
| 25 | 0 3 1 0 | 13.46 | 48.43 |
| 26 | 2 0 0 2 | 13.46 | 48.44 |
| 27 | 3 0 1 0 | 14.52 | 49.50 |
| 28 | 3 0 0 1 | 15.33 | 50.30 |
| 29 | 0 0 4 0 | 15.44 | 50.42 |
| 30 | 1 3 0 0 | 16.49 | 51.46 |
| 31 | 2 2 0 0 | 16.80 | 51.77 |
| 32 | 0 0 0 4 | 16.89 | 51.86 |
| 33 | 3 1 0 0 | 19.11 | 54.08 |
| 34 | 0 4 0 0 | 19.44 | 54.41 |
| 35 | 4 0 0 0 | 30.66 | 65.61 |
- Note: Average response time () and average occupation time () in minutes. The bold values represent the ambulance configuration with the lowest average RT.
Results also show us that the second-best configuration is configuration 1021, which means moving one ambulance from Base B to Base C. That configuration has a RT which is 1 min 30 s higher than the best configuration 1111. Similarly, the third best option is configuration 1120, which means moving one ambulance from Base D to Base C. That configuration has an RT 1 min 38 s higher than the best configuration 1111. These results could be useful for instance in case Bases B or D should be annulled temporary (e.g., due to some kind of works in the street), and then their ambulances could be reassigned to Base C as the best option.
7. Exploring Other Alternatives Using SEMSIM to Further Improve the RT of Ambulances
In this section, we will analyze different alternative cases of interest for the ambulance configuration, to explore alternative settings that might further minimize the RT. The goal is to show how the SEMSIM tool can help an EMS make forward-looking decisions using a realistic simulator, given that testing changes in the real world would be difficult or even impossible. The cases we will study include variations of the current configuration based on factors such as the location of the ambulance bases, the number of ambulances, and even a dynamic scheme to arrange ambulances on bases depending on the time of day and on the season of the year.
In all the cases analyzed in this section, the values RT and TT (see equation (1)) have been obtained from simulations, i.e., ambulances actually travel to incidents, hospitals, and bases through the map roads deployed in SEMSIM. On the other hand, notice that the single component in equation (1) that depends on the ambulance configuration is RT, since AT depends on the incident severity and TT depends on the distance from the incident location to the assigned hospital (in case a transport to hospital was needed). Therefore, we will only focus on analyzing the RT.
7.1. Geographical Distribution of Incidents and Ambulance Base Location in TE
- •
The area colored in light orange highlights the SR of TE. This area measures around 3000 km2 and has a population of around 180,000 people.
- •
The red icons show the location of the current 4 ambulance bases deployed in the region. Currently, each base has assigned one ALS ambulance in a fixed scheme.
- •
The blue icons show the locations of the 4001 accidents that were attended by one of the 4 ALS ambulances of TE during 2018-2019. Notice that the 4 ambulances assigned to TE also attended incidents located in the border region to the north, in Tarragona. This is because ambulances do not have a strictly defined border and often travel to neighboring SRs to attend incidents if necessary, e.g., when ambulances in that border region were busy at the time. Additionally, there will be incidents in TE that were attended to by ambulances from neighboring SR.
Looking at the geographical distribution of incidents shown in Figure 11, we can see that as expected, incidents are quite concentrated near the coast and near the largest villages (Tortosa, Amposta, Sant Carles de la Ràpita, Deltebre, Alcanar, and Ametlla de Mar). However, we anticipate that this geographical distribution could change throughout the year, as we will see in the next section.
7.2. Temporal Distribution of Incidents in TE
In this section, we will analyze which times of the day and which seasons of the year have a greater concentration of incidents throughout the territory. Also, we will analyze which temporary intervals suffer the longest ambulance RTs. In Table 10, we see that configuration 1111 shows the best performance with minimum that equals 8.28 min. Note that this RT is averaged for the whole 2018-2019 period.
However, during the summer, there is an increase in tourism and recreational activities, leading to a higher number of incidents, particularly in tourist zones. This influx can result in elevated . Another case of interest is weekend nights, when there is more nightlife (especially in summer) which causes more incidents that affect the RT. These factors contribute to an overall increase in the RT, and the EMS could implement some measures to reduce it. However, it would be advisable to identify those specific moments of the day and of the year that have a significant increase in RT throughout the different areas and then reinforce the system during those specific intervals in the SR. By doing so, we could minimize the and manage the available resources much more efficiently, which also saves money, compared to blindly trying to improve it overall. That is, we want to examine in depth the temporal and geographical distribution of incidents that affect RT in order to act accordingly.
- •
Winter/summer: Division of 6 months each
- –
From October to March: Winter
- –
From April to September: Summer
- –
- •
Weekday/weekend: Division of 5 and 2 days of the week
- –
From Monday to Friday: Weekday
- –
From Saturday to Sunday: Weekend
- –
- •
Morning/afternoon/night: Time division of 8 h each
- –
From 6 h to 14 h: Morning
- –
From 14 h to 22 h: Afternoon
- –
From 22 h to 6 h: Night
- –
Table 7 shows the percentage of incidents in each temporal division. We can see that in general in TE: (i) there are more incidents during the day (6.31 incidents/day) than during the night (3.57 incidents/night); (ii) there are more incidents during weekend (6.03 incidents/day) days than during working days (5.26 incidents/day); and (iii) there are slightly more incidents in summer (5.59 incidents/day) than in winter (5.36 incidents/day).
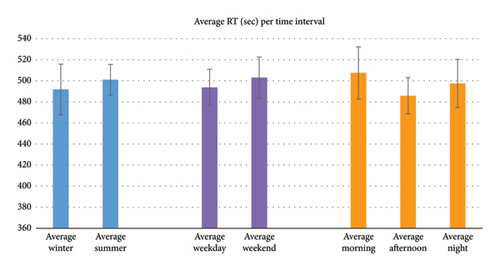
To complement Table 7, Figure 5 depicts the average RT for each of the 7 time intervals presented in the list above. There is a slight 10 s increase in the during summer compared to winter (see blue columns). This is due to the summer holidays and the increase in activity in beach and other touristic areas, which increases the number of incidents (5.59 incidents/day). Additionally, there is a slight increase in (9 s) on weekends (6.03 incidents/day) compared to weekdays (5.26 incidents/day), see purple columns, for similar reasons. Figures show confidence intervals (CIs) of 90%.
In terms of time divisions throughout the day (see orange columns in Figure 5), we can see that there is a slightly higher (of 10 s) during the morning compared to night hours. The reason is that there are more trips during the morning (6.31 incidents/day) than at night (3.57 incidents/night). Although the number of incidents was similar in the morning and the afternoon, the RT is 21 s lower in the afternoon, which may be due to higher traffic conditions in the morning. Additionally, note that although the number of incidents at night (3.57 incidents/night) is around half of those in the afternoon (6.56 incidents/night), the is approximately 10 s higher, likely due to the slightly slower RT of the EMS personnel to activate the vehicle at night and also reduced staffing at night.
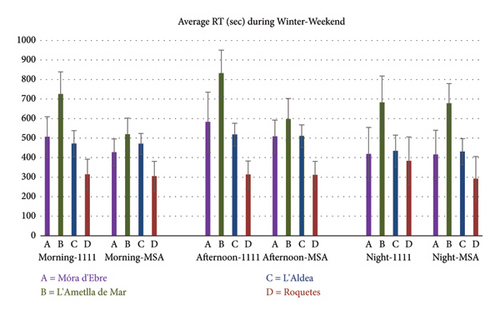
- •
Winter, Weekday, Morning incidents
- •
Winter, Weekday, Afternoon incidents
- •
Winter, Weekday, Night incidents
- •
Winter, Weekend, Morning incidents
- •
Winter, Weekend, Afternoon incidents
- •
Winter, Weekend, Night incidents
- •
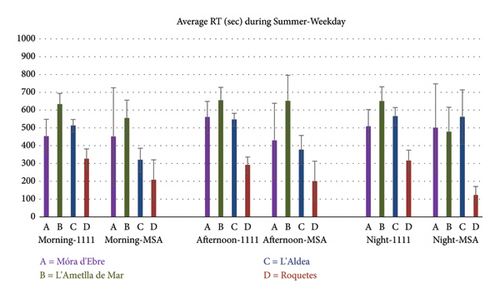
Summer, Weekday, Morning incidents
- •
Summer, Weekday, Afternoon incidents
- •
Summer, Weekday, Night incidents
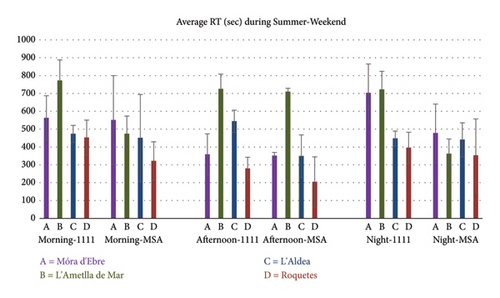
- •
Summer, Weekend, Morning incidents
- •
Summer, Weekend, Afternoon incidents
- •
Summer, Weekend, Night incidents
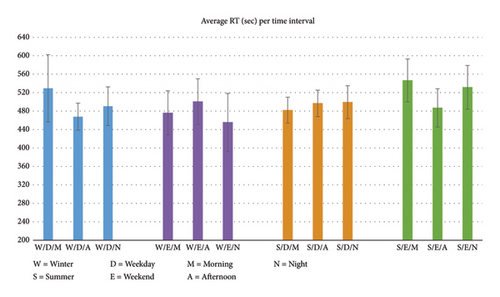
Figure 6 displays the of the 12 temporal subintervals defined in the list above. The figure is divided into four types of temporal intervals represented by four different colors: (i) Winter-Weekday in blue color; (ii) Winter-Weekend in purple color; (iii) Summer-Weekday in yellow color; and (iv) Summer-Weekend in green color. Each of these four intervals has three bars representing morning, afternoon, and night. The maximum RT was 9 min during summer weekend mornings (green column S/E/M).
- •
Weekday mornings in winter (blue column W/D/M) have higher (48 s higher) than in summer (orange column S/D/M). The reason is that more people travel to work during winter, whereas they do not during summer due to vacations.
- •
Weekend mornings in summer (green column S/E/M) have higher (more than 1 min higher) than in winter (purple column W/E/M). The reason is that people tend to go out more for the weekend during summer periods, thanks to better weather and longer days compared to winter.
- •
During nights of the weekends in summer (green column S/E/N), the RT is 1 min higher compared to nights of winter weekends (purple column W/E/N). The reason is attributed to the favorable summer weather and longer days, which encourage people to travel more and spend additional time outdoors during the weekend. In contrast, during winter, people tend to stay home earlier. In essence, there is a significant decrease in outdoor activities during winter weekend nights compared to summer.
- •
We can observe a decrease around 1 min from winter weekday mornings (blue column W/D/M) to winter weekend mornings (purple column W/E/M). This is the contrary during summer, when there is an increase around 1 min from summer weekday mornings (yellow column S/D/M) to summer weekend mornings (green column S/E/M). That is, in winter mornings, people tend to travel more during the week (they go to work) than during the weekends. Conversely, during summer mornings, there is an increase in weekend travel (they go out) than during the weekdays. The same effect takes place for nights (W/D/N with W/E/N, and S/D/N with S/E/N), although the differences are only about 30 s in that case.
Observing the data, we can see a clear correlation between people’s outdoor activities and an increase in ambulance RTs. This correlation is expected, as higher levels of activity lead to more incidents during those time intervals. Consequently, ambulances face increased demand during these periods, inevitably resulting in longer RTs.
Having examined Figure 6 and pinpointed time intervals with elevated ambulance RTs, our attention can now be directed toward optimizing support during these periods to mitigate RTs. This optimization may involve the strategic relocation of specific ambulances or the incorporation of additional support units during intervals with extended RTs. Subsequent sections will delve into addressing and implementing these enhancements.
7.3. Results for 5 Ambulances in 4 Bases
In this section, we consider a scenario where the EMS receives government funding to improve RTs in the TE SR and acquires a new ALS resource.
The question now rises: In which of the four bases in this SR should the new ambulance be assigned to achieve best reduction in the RT? Our tool SEMSIM can help the EMS to conduct some easy simulations to quickly obtain statistical results and analyze which would be the best option.
This way, we have successfully conducted simulations of the incidents using 5 ambulances distributed among the 4 bases in TE, resulting in a total of 56 different possible configurations, i.e., combination with repetition n = 5 ALS, m = 4 bases, CR5,4 = 56. These configurations are presented in Table 11, arranged in descending order of RT, so we can see the best options at the top highlighted in bold.
| No. | Configuration | (min) | (min) |
|---|---|---|---|
| 1 | 2111 | 7.66 | 42.64 |
| 2 | 1112 | 7.80 | 42.77 |
| 3 | 1211 | 7.83 | 42.81 |
| 4 | 1121 | 7.97 | 42.94 |
| 5 | 1022 | 9.40 | 44.38 |
| 6 | 2021 | 9.44 | 44.42 |
| 7 | 1031 | 9.44 | 44.42 |
| 8 | 2120 | 9.58 | 44.56 |
| 9 | 1202 | 9.62 | 44.60 |
| 10 | 1130 | 9.63 | 44.61 |
| 11 | 1103 | 9.69 | 44.67 |
| 12 | 2102 | 9.71 | 44.69 |
| 13 | 2012 | 9.82 | 44.80 |
| 14 | 1013 | 9.86 | 44.84 |
| 15 | 1220 | 9.95 | 44.93 |
| 16 | 2201 | 10.12 | 45.10 |
| 17 | 3011 | 10.14 | 45.12 |
| 18 | 2210 | 10.34 | 45.32 |
| 19 | 1301 | 10.37 | 45.35 |
| 20 | 3101 | 10.47 | 45.45 |
| 21 | 3110 | 10.52 | 45.50 |
| 22 | 0212 | 10.60 | 45.58 |
| 23 | 0221 | 10.61 | 45.59 |
| 24 | 0311 | 10.62 | 45.60 |
| 25 | 0131 | 10.64 | 45.61 |
| 26 | 0113 | 10.64 | 45.61 |
| 27 | 0122 | 10.65 | 45.62 |
| 28 | 1310 | 10.69 | 45.66 |
| 29 | 2030 | 11.53 | 46.50 |
| 30 | 1040 | 11.57 | 46.54 |
| 31 | 3020 | 11.90 | 46.87 |
| 32 | 0203 | 12.53 | 47.50 |
| 33 | 0230 | 12.57 | 47.54 |
| 34 | 0023 | 12.59 | 47.57 |
| 35 | 0302 | 12.63 | 47.61 |
| 36 | 0032 | 12.67 | 47.66 |
| 37 | 0320 | 12.82 | 47.81 |
| 38 | 2003 | 12.85 | 47.84 |
| 39 | 0140 | 12.86 | 47.85 |
| 40 | 0104 | 12.87 | 47.86 |
| 41 | 1004 | 13.01 | 48.01 |
| 42 | 0014 | 13.12 | 48.12 |
| 43 | 3002 | 13.20 | 48.20 |
| 44 | 0041 | 13.23 | 48.23 |
| 45 | 0410 | 13.54 | 48.54 |
| 46 | 0401 | 13.67 | 48.67 |
| 47 | 4010 | 14.45 | 49.45 |
| 48 | 4001 | 15.07 | 50.03 |
| 49 | 0050 | 15.47 | 50.45 |
| 50 | 2300 | 15.84 | 50.82 |
| 51 | 1400 | 15.85 | 50.83 |
| 52 | 3200 | 16.14 | 51.14 |
| 53 | 0005 | 16.72 | 51.72 |
| 54 | 4100 | 18.30 | 53.30 |
| 55 | 0500 | 19.14 | 54.14 |
| 56 | 5000 | 30.01 | 64.95 |
- Note: Average response time () and average occupation time (). The bold values represent the ambulance configurations with the lowest average RT.
Analyzing the 56 configurations in Table 11, we first observe that the top 4 configurations only differ in around 18 s. This indicates that the EMS would have flexibility and could select the base that aligns most effectively with their requirements, considering factors beyond just the , given the marginal difference between them. Those 4 configurations maintain one ambulance at each base and add the additional ambulance at one of the four bases.
These 4 configurations achieve a reduction in of more than 1 min compared to all the other 52 cases, where we can see that at least one base has no ambulance.
Furthermore, we can see that with 5 ambulances and 4 bases, the has decreased by just 37 s compared to the current configuration 1111, see Table 10. Thus, this option does not seem very beneficial.
7.4. Results for 5 Ambulances in 4 Bases, With a Mobile Support Ambulance (MSA) Shared Among the Bases
Based on the results from the previous section, we pose the following question: Why must the new additional ambulance be permanently assigned to a specific base throughout the entire year? This question is particularly relevant after analyzing Figure 6. Alternatively, we suggest deploying the additional ambulance as a reinforcement to support all bases.
This way, the ambulance can be dynamically allocated among the four bases according to where it is most needed during each time interval. This approach may effectively minimize . Of course, there might be other interesting schemes for dynamic ambulance location, e.g., the possibility of placing 4 ambulances (without adding a 5th ambulance) dynamically on the 4 bases. If an EMS deems this alternative appropriate, it could easily be explored. However, after discussion with the SEM team, they suggested exploring the benefit of a single dynamic ambulance, considering EMS staff contracts and schedules.
This objective is in line with the fact that incidents do not occur with the same geographical or temporal distribution throughout the year, but rather, for example, they are more concentrated at certain times of the day, on weekends, and in tourist areas during the summer.
To explore this idea, we have used the 12 temporal subintervals as we did in Section 7.2. To display the results obtained after simulating these 12 temporal subintervals, we have divided them into 4 figures representing the following time intervals: (i) Winter-Weekday; (ii) Winter-Weekend; (iii) Summer-Weekday; and (iv) Summer-Weekend.
Next, we show four figures that represent the per base comparing the current 1111 configuration to a new configuration that includes a MSA in one of the bases for each one of the 12 temporal subintervals of the year, see Section 7.2. Each of the four graphs comprises three divisions corresponding to temporal intervals categorized into the following hourly day segments: Morning, Afternoon, and Night. Inside of each one of these temporal intervals there are 4 colored bars representing the that we obtained per base by adding an extra ambulance to each one of the bases. Colored bars represent the RT of the ambulances assigned to each base: (i) for the current configuration 1111; (ii) for the MSA cases where the extra ambulance was added to each base.
- A.
Móra d’Ebre (purple bars)
- B.
L’Ametlla de Mar (green bars)
- C.
L’Aldea (blue bars)
- D.
Roquetes (red bars)
In Figure 7, we can note two cases that notably improve compared to the current configuration (1111) thanks to the MSA scheme: (i) during the mornings, Base A would reduce its RT in 6 min thanks to the MSA, which represents a 49% of improvement (see purple bars during mornings); and (ii) during the nights, Base B would reduce its RT in more than 1 min, which represents a 10% of improvement (see green bars during nights). In the rest of periods, there is no significant improvement due to the MSA support.
Figure 8 shows the same results for winter weekends. During this temporal period, the MSA is useful for the 3-day segments: (i) during mornings and afternoons, Base B would reduce its RT in more than 3 min thanks to the MSA, equivalent to 28% reduction (see green bars during mornings and afternoons); and (ii) during nights, Base D would reduce its RT in more than 1 min, equivalent to 24% reduction (see red bars during nights).
The benefits of adding a new MSA during summer weekdays are shown in Figure 9: (i) during mornings and afternoons, Bases C and D would experience a reduction around 30% in the RT thanks to the MSA, which equals to around 3 min for Base C and more than 1 min for Base D (see blue and red bars during mornings and afternoons); (ii) during nights, Base D would notably improve in 3 min, which represents a 61% reduction (see red bars during nights).
Finally, in Figure 11, we can analyze the RT reduction for the summer weekend cases thanks to the MSA support: (i) during mornings, Base B would reduce its RT in 5 min (38,6%) while Base D would reduce it in 2 min (29%); (ii) during afternoons, Base C would reduce its RT in 3 min (36%) while Base D would reduce it in 1 min (27%); and (iii) during nights, Base B would reduce its RT in 6 min (50%) while Base A would reduce it in 4 min (32%).
In Figures 7, 8, 9, and 10, we observe that Bases A and B typically show higher CI values, while Bases C and D usually present smaller ones. This is because Bases C and D, covering the southern area, are closer to each other and can provide mutual support if needed. In contrast, Bases A and B, covering the northern area, are farther apart, cover a larger area (see Figure 11), and handle fewer incidents (see Table 6). This variability in incident distribution and response distances (both close and far) contributes to the larger CI values for Bases A and B.
- •
During winter weekdays, the MSA would be allocated at Base A during mornings, at Base D during afternoons, and at Base B during nights.
- •
During winter weekends, the MSA would be allocated at Base B during mornings and afternoons and at Base D during nights.
- •
During summer weekdays, the MSA would be allocated at Base C during mornings and afternoons and at Base D during nights.
- •
During summer weekends, the MSA would be allocated at Base B during mornings and nights and at Base C during afternoons.
Of course, incidents during the transition between weekdays and weekends will be handled appropriately to ensure optimal service, assigning the best available ambulance at that time. Configuration changes for the fifth MSA will only be made when the other ambulance at the same base is not attending any service, to avoid impacting potential new incident victims.
Concluding, the SEMSIM tool helped us to see that the EMS could further reduce the with the help of an MSA doing a dynamic assignment of the supporting ambulance to the four bases, throughout time along the day and the seasons of the year. The optimal assignment throughout the 12 temporal subintervals is shown in Table 8. The using the dynamic MSA would be 6.49 min, which is 1.78 min lower than the with the current 1111 configuration (see Table 10), and 1.16 min lower than the with the best configuration with 5 fixed ambulances, see Table 11.
7.5. Results of 5 Ambulances in 5 Bases
After analyzing the previous two sections, we see that the reduction in the thanks to the addition of an extra ambulance, either fixed assignation in Section 7.3 or dynamic assignation in Section 7.4, is of around 1 min. It is true that every second counts when it comes to saving lives and improving by 1 min is significant, but maybe we could further optimize the use of this additional ambulance. This is another example demonstrating how our SEMSIM tool can effectively assist EMS in exploring alternative solutions within realistic scenarios, enabling informed decision making aimed at optimizing the utilization of available resources.
The approach outlined in this section to optimize the utilization of the additional ambulance is as follows: Instead of assigning the new ambulance to assist one of the existing four bases, potentially leading to instances with two ambulances stationed at the same base, we propose assigning this extra ambulance to a new base.
This configuration ensures that the five ambulances are distributed across five distinct bases, thereby enhancing territorial coverage. As anticipated and validated by our simulation results, a more dispersed distribution of ambulances correlates with a more significant reduction in the average RT.
To implement this, we first studied where it would be optimal to build a new ambulance base. The SEM provided us with a list of possible locations for a new base in TE. The list was made up of the 22 primary health centers (PHCs) of this RS, whose locations are shown in the location icons of Figure 12: (i) four of the PHCs are the current ambulance bases (Móra d’Ebre, L’Ametlla de Mar, L’Aldea, and Roquetes) located in the red icons; and (ii) the remaining 18 PHCs, located in the green icons, are candidate locations for the new ambulance base.
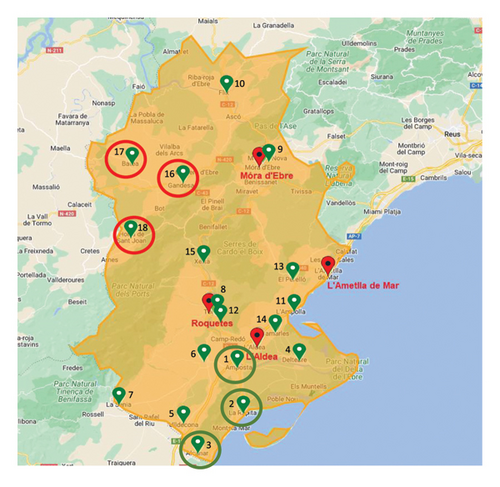
In the next study, we simulated in SEMSIM the same 4001 incidents that happened in TE during 2017-2018, but now with five ambulances located each one in one of the five different bases: the four current ambulances in their respective current bases and the new extra ambulance located at one of the 18 possible new locations. That is, in each of the 18 simulations’ configurations, we assigned the additional ambulance to each of the 18 new candidate locations, while keeping the other 4 ambulances at their current bases.
Table 9 shows the results of the 18 simulated configurations. The configuration name corresponds to the location of the 5th new base. As in previous sections, the table shows the average RT and average OT of the ambulances in descending order of RT to visualize the best configurations at the top of the table. The best options are marked in Figure 12 with green circles, while the worst options are marked with red circles.
Table 9 indicates that the best new base to add our extra ambulance is Amposta (1st in the list). By including an ambulance at that location, we achieve an average RT of 7.10 min, which represents an improvement of 71 s compared to the current 1111 configuration (see Table 10) and of 52 s compared to assigning the 5th ambulance at Base A (configuration 2111), see Table 11.
Surprisingly, the RT obtained with 5 ambulances and 5 bases ( = 7.10 min) is barely the same (1 s worst) than the RT with 4 bases and the extra dynamic MSA ( = 7.08 min), see Section 7.4. In Appendix 1 we add a discussion of the costs associated to each alternative, which would help the EMS to decide between both similar solutions.
Figure 13 highlights (red circle) the Amposta base where the new 5th ambulance would be assigned, constituting the 11111 configuration. We can observe a higher density of incidents (blue icons) occurring around larger populations and coastal areas, logically indicating the need for optimal base locations in these regions as well. The results obtained from these simulations offer valuable insights by quantifying the need for reinforcement in the southern region of TE. Clearly, the SEMSIM tool proves instrumental in enabling the EMS to assess the impact of alternative options, providing them with objective data and results essential for making informed decisions.
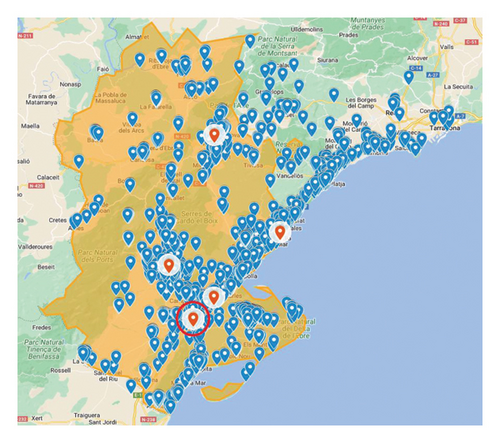
All these examples are case studies that can be easily explored with SEMSIM. Other interesting cases, which we do not include due to space constraints, could be analyzed, such as the scenario with 5 bases and 5 ambulances, considering demand variations (winter/summer; weekdays/weekends; morning/afternoon/evening) in the ambulance location.
7.6. Results of 3 Ambulances in 4 Bases
The final study conducted in this work involves analyzing the potential consequences hypothetically reducing the number of ALS ambulances from four to three. Would such a reduction have a significant impact on the ? If such a measure were to be considered, perhaps due to budget cuts in the health service, determining which base should be removed to minimize the impact on the population and achieve the lowest with the remaining ambulances poses a complex challenge for the EMS. Addressing these questions is intricate, and we will explore how the SEMSIM tool can aid in decision making by providing objective results.
We have modified the SEMSIM code to simulate the 4001 incidents occurred in TE during 2018-2019 with only three ALS ambulances, considering all possible configurations. In this case, having three ambulances distributed across four bases gives us a total of 20 different configurations, i.e., combination with repetition m = 4 bases, n = 3 ALS. We simulated all CR3,4 = 20 different configurations and we show the and in Table 12.
| No. | Configuration | (min) | (min) |
|---|---|---|---|
| 1 | 1011 | 11.39 | 46.36 |
| 2 | 1110 | 11.77 | 46.74 |
| 3 | 0111 | 11.83 | 46.80 |
| 4 | 1101 | 12.05 | 47.01 |
| 5 | 1020 | 13.03 | 48.00 |
| 6 | 0021 | 13.96 | 49.26 |
| 7 | 0120 | 14.07 | 49.37 |
| 8 | 0102 | 14.25 | 49.55 |
| 9 | 0012 | 14.26 | 49.56 |
| 10 | 0201 | 14.47 | 49.94 |
| 11 | 0210 | 14.49 | 49.96 |
| 12 | 1002 | 14.80 | 50.67 |
| 13 | 2010 | 15.89 | 50.85 |
| 14 | 0030 | 16.67 | 51.64 |
| 15 | 2001 | 17.06 | 52.03 |
| 16 | 0003 | 18.19 | 53.16 |
| 17 | 1200 | 18.44 | 53.41 |
| 18 | 0300 | 21.14 | 56.11 |
| 19 | 2100 | 21.29 | 56.26 |
| 20 | 3000 | 33.95 | 68.90 |
- Note: RT and OT. The bold values represent the ambulance configuration with the lowest average RT.
We can notice that the four most favorable configurations (in the top of the table) involve distributing the three ambulances among the four bases, with a difference of more than 1 min to the rest of configurations that have two or more ambulances at the same base. The best configuration in Table 12 is 1011, with an RT of 11.39 min. This configuration involves removing the ambulance assigned at the base L’Ametlla de Mar. The remaining three ambulance bases would be located on the map as shown in Figure 14. The RT with configuration 1011 (11.39 min) would be 3 min higher than the current configuration 1111 (8.28 min), see Table 10, and more than 4 min higher compared to configuration 11111 (7.10 min), see Table 9.
7.7. Discussion of the Previous Simulation Results
To close Section 7, we add Appendix 1 at the end of the manuscript where we summarize the main results of the RT achieved by each alternative ambulance configuration. Additionally, we also add Appendix 2 to include a basic cost analysis associated with each configuration to further aid decision making with the available budget. Also, we discuss the trade-off between RT reduction and cost incurred for each option.
To evaluate the SEMSIM performance with more recent data, we requested the latest dataset from SEM, which includes 2322 incidents from 2023 (after cleaning and filtering, as outlined in Section 4.2). We then calculated the same statistics presented in Section 4.4 for the 2018/2019 dataset to compare them with the new 2023 dataset. We have observed that they align closely, as it is shown in Appendix 3. We have plotted the 2023 incident locations on the map (see Figure A4 in Appendix 3), to compare them with the 2018/2019 incident locations shown in Figure 5. We can see that the incidents occur in similar areas.
Furthermore, by splitting the dataset into Winter/Summer, Weekday/Weekend, and Morning/Afternoon/Night, we observed comparable temporal distributions of incidents throughout the year, yielding results similar to those presented in Section 7.2.
Finally, we have fed the SEMSIM simulator with the new 2023 incident dataset for most of the alternative configurations analyzed in this study, and the results and conclusions closely align with those presented in the paper. Specifically, for the 1111 configuration (one ambulance per base) used to validate SEMSIM (see Section 6), we compared the simulation results to actual outcomes from the SEM dataset.
The percentage of mismatch in selecting the same ambulance is now 12.83%, which corresponds to 298 different selections out of 2322 incidents in the 2023 dataset. This mismatch rate is quite comparable to that of the 2018/2019 dataset, which stands at 13.49%. The reasons behind the discrepancy in the ambulance chosen in real life and in the simulator SEMSIM for the 2018/2019 dataset (13.49%) were analyzed in Section 6. Similar discussion applies for the 2023 dataset, since the mismatch rate is very similar (12.83%).
Based on this analysis, we can conclude that the SEMSIM simulator provides accurate results for evaluating the RTs of any ambulance and base location configurations, offering valuable insights for EMS decision makers.
7.8. Discussion of the Utility of SEMSIM for the EMS Decision Makers
- •
Interactive decision making: EMS managers can experiment with the simulator by adding new ambulance bases at different locations, or adjusting the number of ambulances assigned to each base. They can then analyze the impact of these changes on RTs, using historical incident data provided by SEM as input to carry out the simulations for each different ambulance configuration or base location under exploration.
- •
Dynamic configuration exploration: The tool also allows EMS to easily explore different dynamic configurations based on factors like day type (weekday vs. weekend) or season, helping to identify the optimal setup for each time of year.
- •
Realistic scenario testing: SEMSIM might help EMS make proactive, data-driven decisions with a realistic simulator, offering a safe way to test strategies that would be challenging or impossible to implement in real-life situations. According to our meetings, the SEM recognizes the potential of this tool, which will enable the exploration of alternative ambulance configurations and the easy evaluation of their impact on RT before implementing any decisions in the real service.
Concluding, with SEMSIM the EMS can evaluate the potential outcomes of alternative base and ambulance configurations. Achieving this level of analysis in real life would be nearly impossible due to the logistical and operational challenges involved.
8. Conclusions and Future Work
Our collaboration with SEM aimed to develop a simulation tool that allows flexible modification of base locations and ambulance distribution within a realistic framework that mimics SEM’s operations. The goal was to identify alternative configurations to reduce ambulance RTs in a given territory. Since reaching incidents as quickly as possible is a core challenge for EMS, optimizing these configurations was believed to enhance RTs, a result demonstrated in this work.
The previous results show that the SEMSIM simulation tool achieves accurate results in terms of which was the ambulance chosen to assist the incident compared to the ambulance actually assigned by the EMSs. Also, SEMSIM obtains similar RT values in the scenario with the same ambulance configuration (i.e., 1111) deployed currently in TE by the SEM. This means that the SEMSIM simulator has been validated and therefore it could be used to test out any other possible new configuration of ambulance distribution, either using the available ambulance bases or even adding other possible new bases deployed in the territory. Notice that exploring such alternative configurations in real life would be very difficult and expensive or even impossible for a public administration to afford. Luckily, SEMSIM can be a very useful tool for the EMS that could easily change, add, or delete ambulance bases on the actual map taken from OSM [10] and compute the average RT from realistic simulations fed with the real incidents gathered in their datasets.
SEMSIM is a valuable tool for EMS to efficiently explore alternative ambulance configurations. It enables a rapid analysis, allowing EMS to choose the optimal configuration that minimizes the average RT. Consequently, the SEMSIM tool contributes to enhancing emergency services by facilitating the exploration of alternative solutions with precision before final decisions are made.
Moreover, we would like to underscore the potential of our SEMSIM simulation tool in recommending the optimal ambulance configuration when there are changes in scenario settings. For instance, EMS authorities could use SEMSIM to assess the impact if the number of available ALS ambulances were to decrease in a specific SR. In such a scenario, SEMSIM could aid in determining the best suited base to lose its assigned ALS ambulance, helping to identify an efficient new configuration without compromising coverage. Another application arises when a SR acquires a new ALS ambulance, prompting the EMS to decide on the most effective configuration with the addition of the new ambulance within the existing bases. SEMSIM proves invaluable in assisting EMS decision making in such dynamic situations.
Besides, rather than adhering to a static ambulance configuration distributed across bases, the SEMSIM tool facilitates the creation of a flexible and dynamic setup influenced by diverse factors. For instance, computing average RTs separately for weekdays and weekends allows an assessment of optimal ambulance configurations for each scenario. Similarly, analyzing RTs for summer and winter days becomes relevant, considering that tourist activity increases in summer. Consequently, adjusting ambulance placement near these tourist hubs during the summer months might enhance overall effectiveness.
In this research work, the SEMSIM simulation tool has been validated and we have shown how to use its full potential by exploring new smart and dynamic alternatives to the current fixed ambulance configuration (i.e., one ambulance per base). This way, the EMS will have an efficient tool to help them to analyze different possible configurations seeking to decrease the RT of their service and thus arrive sooner to the incidents while managing efficiently their resources.
We wish to highlight that SEM is aware of the potential for significant improvements in both the location of ambulance bases and the distribution of ambulances, and that finding suitable configuration changes would allow them to reduce RTs. However, conducting real-world tests to validate these changes was previously unfeasible without a comprehensive preliminary study to demonstrate their value. Now, with the support of our SEMSIM tool, SEM has clear evidence of potential configuration changes that could be implemented to enhance their service, see discussion about Figure A1 in Appendix 1. This has provided them with robust, data-driven arguments to engage in serious discussions regarding the reorganization of their resources. In Appendix 1, we add examples of alternative ambulance configurations that have shown a notable impact in reducing average RT.
To conclude, we have illustrated how our simulation tool SEMSIM can aid EMS in decision making related to resource allocation, optimal base placement, and ambulance configurations. The ultimate objective is to minimize RTs while adhering to budgetary limitations. SEMSIM facilitates easy modifications to ambulance numbers and base locations, offering a pragmatic approach to evaluating simulation results for real-life incidents, and performs tasks that would be virtually impossible to accomplish during real emergency situations.
Nomenclature
-
- ALS
-
- Advanced life support
-
- AcT
-
- Activation time
-
- AT
-
- Assistance time
-
- BLS
-
- Basic life support
-
- CAP
-
- Primary attention center
-
- CECOS
-
- Health Coordination Center
-
- CI
-
- Confidence interval
-
- EmIn
-
- Emergency incident
-
- EMS
-
- Emergency medical system
-
- EST
-
- Emergency sanitary technician
-
- IHT
-
- Interhospital transfer
-
- MSA
-
- Mobile support ambulance
-
- OSM
-
- OpenStreetMap
-
- OT
-
- Occupation time
-
- PHC
-
- Primary health center
-
- RIV
-
- Rapid intervention vehicle
-
- RT
-
- Response time
-
- SEM
-
- Sistema d’Emergències Mèdiques
-
- SEMSIM
-
- SEM Simulator
-
- SISCOM
-
- Smart Services for Information Systems and Communication Networks
-
- SD
-
- Standard deviation
-
- SR
-
- Sanitary region
-
- STG
-
- SUMO Traffic Generation
-
- SUMO
-
- Simulation of Urban MObility
-
- TE
-
- Terres de l’Ebre
-
- TT
-
- Transportation time
-
- UDN
-
- University degree in nursing
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This work was partially supported by the Spanish Government under research projects: (i) “DIstributed Smart Communications with Verifiable EneRgy-optimal Yields (DISCOVERY)” PID2023-148716OB-C32, funded by MCIN/AEI/10.13039/501100011033; (ii) “Anonymization technology for AI-based analytics of mobility data (MOBILYTICS)” TED2021-129782B-I00, funded by MCIN/AEI/10.13039/501100011033 and by the European Union NextGenerationEU/ PRTR; (iii) “Enhancing Communication Protocols with Machine Learning while Protecting Sensitive Data (COMPROMISE)” PID2020-113795RB-C31, funded by MCIN/AEI/10.13039/501100011033; and (iv) the Generalitat de Catalunya under AGAUR grant “2021 SGR 01413”.
Appendix 1: Discussion of the RT for Different Configuration Alternatives
To summarize the results of the RT obtained with each one of the options analyzed in the previous sections, Figure A1 presents the best average RT for each one of the cases proposed to minimize the in the SR of TE. CIs of 905 are shown in the figure.
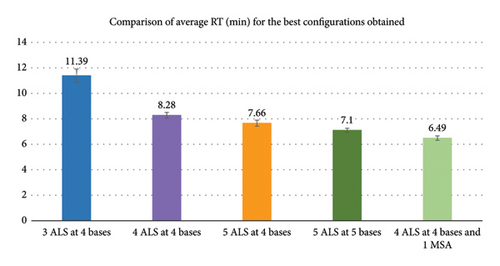
Please note that the scenario involving only 3 ambulances at the 4 bases (refer to Section 7.6) is presented solely for comparative purposes. This allows us to assess the potential impact under a hypothetical worst-case scenario where the EMS is compelled to eliminate one of the four ambulances. In this worst-case situation, the configuration least affecting the RT would be the 1011 configuration, indicating the removal of the ambulance assigned to Base B. The subsequent sections will exclusively focus on analyzing potential enhancements achievable over the current configuration to reduce the average RT. Consequently, the scenario involving 3 ambulances and 4 bases will not be considered in the subsequent discussions.
- •
The purple column (8.28 min) is the current configuration 1111 (4 ambulances at 4 bases), see Table 10.
- •
The orange column (7.66 min) represents configuration 2111 (5 ambulances at 4 bases), see Table 11. This option consists of adding a fifth ambulance to Base A, which reduces the RT by 37 s.
- •
The dark green column (7.1 min) corresponds to configuration 11111 (5 ambulances at 5 bases), see Table 9. This option reduces the average RT by roughly 1 min.
- •
The light green column (6.49 min) represents the alternative with 4 ambulances per base and 1 MSA that gives support to the bases when it is more needed according to a temporal interval scheme, see Section 7.4. This option gives the highest improvement of approximately 1.8 min with respect to the current configuration 1111 (4 ALS at 4 bases, see purple column). Note that this is a notable improvement that represents a 21.6% reduction in the RT.
- •
The blue column (11.39 min) serves as a reference to see the impact on RT if there were only 3 ambulances at the 4 bases, see Table 12.
By introducing a fifth ambulance (orange and both green bars), either assigned to its dedicated base (configuration 11111, dark green colored bar) or providing support to the existing four bases (light green colored bar), we can observe a substantial enhancement in the overall average RT, reducing it to approximately 7 min, which represents an improvement of around 70 s compared to the current configuration 1111 (purple colored bar). This signifies a noteworthy reduction in time, which is crucial in the context of saving human lives.
Nonetheless, it is imperative to conduct a thorough analysis of the cost associated with each proposed option to determine their cost-effectiveness ratio. The EMS also needs to carefully consider the economic impact of alternative solutions, particularly when the two most favorable options (depicted by dark and light green columns in Figure A1) offer a very similar improvement in the average RT. Consequently, next we will delve into evaluating the costs associated with the three options that improve the average RT and involve the incorporation of a new ambulance.
Discussion of the Cost of the Best Configuration Alternatives. Now we will compute the cost incurred to deploy the three alternatives that reduce the average RT compared to the current 1111 configuration (purple column), see Figure A1 [8]: 5 ALS at 4 bases (orange column), 4 ALS at 4 bases and 1 MSA (dark green column), or 5 ALS at 5 bases (light green column). In Table A1, we can observe the cost per year of enabling the medicalized ALS (ALSm).
| Concept | ALSm 24 h |
|---|---|
| Staff cost (uniforms and training included) | 1 EST + 1 M + 1 UDN = 1,218,562.84 € |
| Vehicle, ICT equipment, and electromedicine | 90,653.35 € |
| Consumables and gases | 18,158.45 € |
| Total cost per year | 1,327,374.64 € |
- Note: M = doctor. UDN = person with a university degree in nursing.
- Abbreviation: EST = emergency sanitary technician.
In this work, we have only considered ALSm ambulances; therefore, the cost per year of each ambulance is 1,327,374.64 €/year. Table A2 shows the cost per year of a new ALS ambulance (computed in Table A1) together with the cost per year of a base in which one or more ALS ambulances are assigned.
| Concept | Cost per year |
|---|---|
| New ALSm 24 h | 1,327,374.64 €/year |
| New base for the ALSm | 20,000 €/year |
| Shared base for the ALSm | 10,000 €/year |
- 1.
In the case of having 5 ambulances at 4 bases, we have to consider the cost of adding a new ambulance and the cost of adding a base where there is more than one ALS; in this scenario, the extra ambulance would be accommodated in an existing base along with another ambulance. Cost per year of alternative “5 ambulances at 4 bases” is: 1 × “New ALSm 24 h” + 1 × “Base for more than one ALS” = 1,337,374.64 €/year.
- 2.
In the case of having 4 ambulances at 4 bases along with 1 MSA giving dynamic support to the bases, we would need to consider the cost of the new ALS, the cost of a shared base where there is more than one ALS, and the cost of the additional mobilizations that this MSA ambulance would make. In the other cases without the MSA, the number of mobilizations is the same as the number of incidents. However, as we have seen in Section 7.4, having an MSA adds more mobilizations between bases. From Table 8, we have calculated a number of 792 additional trips of the MSA between bases in a year. We have estimated a gasoline cost of 2582.4 €/year due to those additional trips between bases, using the distance between bases (see Figure 2) and an approximate cost of 10 €/100 km. The cost per year of alternative “4 ALS + 1 MSA at 4 bases” is: 1 × “New ALSm 24 h” + 1 × “Shared base for the ALSm” + gasoline cost = 1,349,957.04 €/year. This amount is 115,200 € higher than the previous option.
Finally, we can analyze the trade-off between RT reduction and cost associated to each option, compared to the current configuration of 1 ambulance per base (configuration 1111), see Table A3. The table also shows the average standard deviation () of the RT.
| Ambulance configuration | (min) | (min) | Additional cost (€/year) |
|---|---|---|---|
| Current: 4 ALS at 4 bases (configuration 1111) | 8.28 | 8.60 | — |
| Opt. 1: 5 ALS at 4 bases (configuration 2111) | 7.66 | 6.28 | 1,337,374.64 €/year |
| Opt. 2: 4 ALS + 1 MSA giving support to the 4 bases | 6.49 | 5.59 | 1,349,957.04 €/year |
| Opt. 3: 5 ALS at 5 bases (configuration 11111) | 7.1 | 6.56 | 1,347,374.64 €/year |
- Abbreviations: ALS = advanced life support; MSA = mobile support ambulance.
To see it clearer, since all three proposed alternative options involve adding a new ambulance, in Table A4, we do not include the cost of the new ALSm ambulance (1,327,374.64 €/year, see Table A1) in the comparative calculation. Therefore, from Table A4, we can deduce that adding an ambulance either to an existing base (Option 1) or to an additional base (Option 3) is a viable alternative, offering a low ratio between RT reduction and cost (≈ 0.0036 s/euro). That is, we achieve a reduction of 0.6 minutes (36 seconds) with an investment of 10,000 euros per year. This results in a ratio of 0.0036 seconds per euro each year. Furthermore, although Option 3 (5 ambulances at 5 bases) incurs twice the cost of Option 1 (5 ambulances at 4 bases), the improvement in reducing average RT is doubled. Nonetheless, Option 2 stands out as the most favorable choice, given that it yields the lowest ratio between RT reduction and cost (0.0047 s/euro), with the lowest and , that are almost 2 and 3 min lower, respectively, compared to the current configuration 1111.
| Ambulance configuration | (min) | (min) | Additional cost (€/year) |
|---|---|---|---|
| Opt. 1: 5 ALS at 4 bases (configuration 2111) | −0.6 | −2.32 | +10,000 €/year |
| Opt. 2: 4 ALS + 1 MSA giving support to the 4 bases | −1.8 | −3.01 | +22,582 €/year |
| Opt. 3: 5 ALS at 5 bases (configuration 11,111) | −1.2 | 6.56 | +20,000 €/year |
- Note: Additional cost without including the common cost of a new ALSm present in the three options.
Regarding the SD, we can observe a substantial improvement around 2 min with options 1 and 3, whereas the reduction of is 3 min with alternative 2.
It is very positive to reduce the SD of the RT, which makes all cases closer to the mean (). When applied to ambulances, it implies a reduction in incidents whose ambulance RTs are significantly longer than average. Although these cases may be few, it is always better to minimize them since those who have to wait much longer than average could be seriously affected.
In summary, we have demonstrated how our simulation tool, SEMSIM, can assist EMS in decision making regarding resource allocation, optimal base locations, and ambulance configurations, all aimed at minimizing RTs within budget constraints. SEMSIM facilitates convenient adjustments to ambulance numbers and base locations, providing a practical means to assess simulation outcomes for real-life incidents. This is an endeavor that would be nearly impossible in actual emergency scenarios.
Appendix 2: Exploring Configurations Using SEMSIM Including ALS, BLS, and More Alternative Bases
In this section, we will explore more alternatives to analyze other possible ambulance location configurations using the SEMSIM simulation tool. We have now included the 21 BLS vehicles, collaborating with the 4 ALS vehicles available in TE. Also, we have considered 17 additional alternative possible bases to allocate ambulances, which are located in the current CAPs of TE, so we have in total 21 bases.
Notice that an incident might activate a BLS or both an ALS and a BLS, or even several ALS/BLS ambulances depending on the incident severity. In incidents where both ALS and BLS may be dispatched, the BLS is typically the first responder to provide initial medical assistance, followed by the ALS, which includes a doctor. Besides, it is important to note that in the Barcelona Metropolitan SR, there are incidents for which only an ALS is dispatched without a BLS. Notice that now the simulation time increased to 4 h per configuration (server DELL R752, GPU, 12 RAM 64 GB), since the scenarios are more complex (21 bases and ALS and BLS ambulances). We have analyzed 21 different configurations where we have added a new BLS in one base in each configuration test, so the total simulation time was 4 h.
Notice that while 4 h of simulation might seem lengthy for testing various ambulance distributions and base locations, doing this in reality would be nearly unfeasible. SEMSIM allows EMS decision makers to simulate 2 years of incidents within that time, making it easier to assess different configurations, such as adding new bases or adjusting ambulance assignments.
Note that once we replicate the global methodology for the other six SRs of Catalonia (see Figure 1), it will not be necessary to conduct further simulations (unless a new not evaluated yet configuration needs to be explored). All the simulation results gathered regarding the various ambulance location configurations with all possible ambulance distributions, including possible new bases that could currently be deployed in the territory (at the current CAPs), will be available in an easy-to-use visual tool designed in Power BI, see Figures A2 and A3. Users (SEM doctors and technicians, researchers, etc.) can easily analyze the impact on RT if they add or remove an ambulance, change a base location, and more.
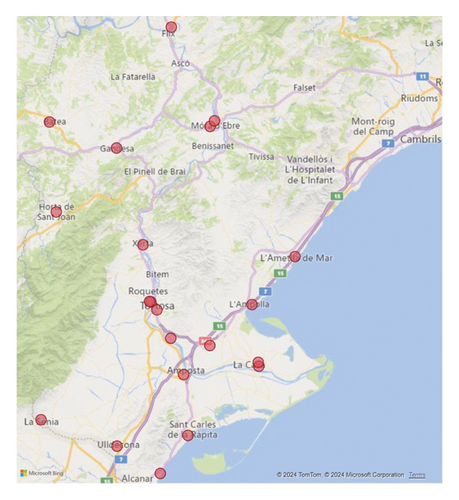

Additionally, researchers designing mathematical approaches to address the challenge of optimal ambulance deployment can use this realistic simulation framework, along with the visual tool, to validate their strategies. The most important results of our study are compiled in our public Visual Power BI-based SEMSIM Tool to analyze results [25].
The run time and computational resources needed to simulate, in a single simulation, all possible configurations across the entire territory of Catalonia to test all scenarios and find an optimal solution would have been prohibitive. Nonetheless, since the territory is administratively organized by the SEM into seven SRs (see Figure 1), the objective can be easily fulfilled, as we have done with TE.
Appendix 3: Analysis of the Latest 2023 Incident Dataset
- •
The distribution of type of incidents for 2023 dataset shown in Table A5 is similar to the one for 2018/1019, see Table 2.
- •
Both datasets show similar statistics for the average and SD of AT and TT, see Table A6 and Table 4.
- •
Both datasets show similar statistics for the transport of victims to the different hospitals, see Table A7 and Table 1.
Regarding the geographical distribution of incidents, in Figure A4, we have plotted the 2023 incident locations on the map to compare them with the 2018/2019 incident locations shown in Figure 11. We can see that the incidents occur in similar areas along the roads, along the touristic zones on the coast and around the main cities like Tortosa, L’Ametlla de Mar, Amposta, La Ràpita, or Móra d’Ebre.
| Probabilities | Values (%) |
|---|---|
| Prob (transport victim to hospital) | 26.35 |
| Prob (IHT incident) | 7.84 |
| Prob (EmIn incident) | 92.16 |
| Prob (EmIn with ALS hospital transport) | 18.51 |
| Prob (EmIn without ALS hospital transport) | 73.65 |
- Note: Measured from the real SEM dataset of incidents occurred during 2023.
| AT (min) | TT (min) | |
|---|---|---|
| Average | mAT = 26.81 | mTT = 11.72 |
| Standard deviation | sAT = 13.38 | sTT = 9.2 |
| Minimum value | ATmin = 5.43 | TTmin = 0 |
| Maximum value | ATmax = 86.52 | TTmax = 45.15 |
- Note: Both types of incidents are included: EmIn and IHT. Measured from the real SEM dataset of 2322 incidents happened during 2023.
| Hospitals in/near TE | Probability (%) |
|---|---|
| Hospital de Tortosa Verge de la Cinta | 17.78 |
| Hospital Comarcal de Mora d’Ebre | 2.49 |
| Hospital Universitari de Tarragona Joan XXIII | 1.94 |
| Hospital Universitari Sant Joan de Reus | 1.29 |
| Hospital Universitari de Bellvitge | 0.17 |
| Unitat Polivalent Terres de l’Ebre | 0.13 |
| Unitat Polivalent Salut Mental Amposta-Hospital de Dia | 0.086 |
| CAP Gandesa | 0.086 |
| Hospital de la Santa Creu de Tortosa | 0.086 |
| CAP L’Ametlla de Mar | 0.043 |
| Hospital de Sant Pau i Santa Tecla | 0.043 |
| Hospital del Vendrell | 0.043 |
| CAP Dr. Ramon Vinyes | 0.043 |
| Institut Pere Mata | 0.043 |
| N/D | 75 |
- Note: Both types of incidents (EmIn and IHT) are considered. CAP stands for primary attention center; N/D means no transport to hospital.

We also analyzed the temporal distribution of incidents (Figures 5, 6, 7, 8, 9, and 10) showing similar behavior, although we do not include the new 2023 figures to avoid overloading the manuscript with repetitive results.
Additionally, we have computed the average RT and OT for the 2023 dataset: min and min, while the values for the 2018/2019 dataset were (see Table 5): min and min.
We conclude that both datasets show very similar behavior. Therefore, we determine that the 2-year 2018/2019 dataset of incidents is sufficiently representative for conducting multiple simulations to explore alternative ambulance and base configurations. Adding more incidents would only increase simulation time without affecting conclusions, so including additional data is unnecessary at this time.
However, if environmental conditions change significantly (e.g., a new highway, new roundabouts, zebra crossings, and traffic lights), it would be advisable to perform new simulations using the most recent 2-3 years of incident data.
Open Research
Data Availability Statement
The raw incident data used in this study were collected from the incidents handled by the Emergency Medical System of Catalunya (SEM).




