Distributed Event-Triggered Adaptive Control for Consensus of Actuator Fault Multiagent Systems With Parameter Uncertainty and External Disturbances
Abstract
The leader–follower consensus problem in the presence of parameter uncertainty and external disturbances is investigated for multiagent systems (MASs) with actuator faults, which are based on event-triggered control. First, a new distributed event triggering strategy is proposed which avoids continuous communication between agents and is based on the state estimation of neighbouring agents. Instead, the growing estimation error is reset by communication updates. An adaptive update mechanism is also proposed which does not need any knowledge of the global aspects of the communication topology graph and does not need an upper threshold for parameter uncertainty and external disturbances in the protocol. The results show that the tracking error under the event-triggered protocol asymptotically converges to zero, while avoiding Zeno behaviour. Finally, a numerical simulation confirms the feasibility of the theoretical results.
1. Introduction
Multiagent systems (MASs) are a class of dynamic systems that are relatively common in real life. It is usually composed of many interacting agents. Each of these agents operates independently, and all of them possess certain perception, computation, and execution capabilities and are capable of handling large-scale and difficult tasks which a single individual is unable to deal with. MASs [1–3] have the advantages of high fault tolerance, fast operation speed, wide coverage, scalability and strong functionality.
The consensus problem is the basic problem of multiagent coordinated control. MASs consensus means that individuals in the system can exchange information and adjust their states based on the control laws, and finally, each agent reaches state or output consensus [4–6]. Many researchers have studied the system consensus cooperative control problem in depth. In [7], consensus controllers with different control gains were developed. Using Lyapunov function technique, it was shown that the secure consensus problem for linear MASs can be reached. In [8], the consensus problem for MASs with disturbances is considered. By proposing three fixed-time prescribed performance approaches, the consensus tracking error can be gradually driven to zero.
The development of MASs in recent years has led to higher demands on the control methods of the control system under the constraints of wide spatial distribution of agents and limited sensor communication. Distributed cooperative control [9–11] is often used to replace the traditional centralised control method. In distributed control, the agents mainly rely on local information interaction with each other to accomplish the cooperative control task. The design of individual individuals in distributed control is simple, and the failure of the function of a single agent will not affect the function of the whole, these features well reduce the difficulty of individual design and increase the anti-interference ability of the whole system [12]. In [13], a completely distributed consensus protocol is proposed, in which the protocol relies only on the instant partial messages of each node and not the global messages. Robust and secure consensus is studied against DoS attacks and external disturbances. In [14], the authors developed an enhanced extended state observer specifically designed to accurately estimate unknown disturbances within the system. Furthermore, they established an output estimator that integrates both the triggered output and the estimated output, thereby improving the overall estimation accuracy and system robustness. In [15], a fully distributed design scheme and an adaptive neural control approach are used to engineer an adaptive neural consensus control protocol that enables MASs to achieve the consensus goal. It is important to note that information regarding the amount of agents and the interaction topology is not considered as part of the protocol description procedure.
Despite the numerous advantages of distributed control in MASs, these systems inherently present complex global characteristics, including multivariability, strong coupling, and nonlinearity. Such complexity, coupled with prolonged high-load operation of individual agents or sudden adverse changes in the external environment, makes the occurrence of failures in MASs [16–19] an inevitable problem. Once the failure occurs, it may lead to information mismatch, signal loss or even the loss of execution capability of an agent in the MASs, resulting in system instability and loss of the expected target task, which will cause huge losses. Therefore, in view to enhance the security and dependability of MASs, distributed controllers with fault tolerance are worthy of in-depth study. In [20], actuator faults are compensated by designing a novel fault-tolerant controller. The developed controller resolves the issue of error-tolerant output regulation in heterogeneous linear MASs and does not to cause chattering behaviour. In [21], a new bipartite adaptive control algorithm is put forward by bringing in an observer. From it, the output regulation issue of linear MASs in the presence of actuator faults is addressed.
Unnecessary communication within the network can potentially result in information congestion, thereby imposing additional burdens on the network and ultimately degrading the system’s overall performance. To address this issue, the mechanism of event triggering mainly relies on preset triggering conditions to update the control information, and only when the system meets these conditions, the transmission information will be updated. Therefore, the introduction of event triggering mechanism [11, 22–24] is of great practical significance. In [25], the consensus of MASs with general linear dynamics is investigated. It is achieved by an adaptive event triggering strategy that reduces the communication frequency as well as avoids the dependence on global information. In [26], in order to decrease the communication affordance, we propose an adaptive event-triggered control strategy which relates only to limited local information and derive a model-based stability criterion which ensures that MASs arrive at an asymptotic consensus. In [27], the consensus issue of discrete-time MASs with directed switching topology is explored, where an event-triggered strategy is employed to drive the state variables of each agent to eventually converge to the same value.
In practical applications, the agents will mostly be in complex and changing scenarios, so they cannot only consider the research in the ideal situation. It is difficult to avoid external interference in the process of information exchange between agents [28, 29], which will lead to poor system stability and even the loss of the expected target task, which will cause great losses. In [30], a protocol using relative state information is proposed to study the output consensus of discrete-time MASs affected by input saturation and external interference. In [31], the two-end output consensus tracking issue for MASs under external disturbances is studied using neural networks to evaluate and eliminate uncertain disturbances, in which the agents have diverse state dimensions. It is worth noting that the above study did not consider the existence of uncertainties. In practical engineering, parameter uncertainty in MASs is prevalent and unavoidable due to natural losses of components in multiagent devices and external influences. In [32], a parameter estimator is introduced to study the consensus issue for nonlinear MASs with uncertain leaders using an event-triggered communication mechanism. In [33], the fixed-time time-varying formation control issue for heterogeneous MASs in the presence of parameter uncertainty is addressed.
- i.
In this paper, a new event-triggered controller is devised that uses the state estimates of neighbouring agents, rather than the true state values of the agents. Compared to the authors in [25, 34], the consensus protocol introduced in this paper incorporates a piecewise continuous input signal. This design significantly reduces the communication burden among neighbouring agents, enhancing the overall efficiency of the system.
- ii.
Compared with most existing policies [35, 36], the event-triggered control strategy proposed above implements consensus control in a distributed manner, avoiding the use of the graph of the network with any global knowledge, which can greatly decrease the transmission of communication. At the same time, because each agent has its own unique moment of event triggering, the information is transmitted asynchronously. It can usefully help the network system to cut down the communication load.
- iii.
The existence of parameter uncertainty and exogenous interference [11] is considered to make it more practical compared to the existing literature on consensus. Furthermore, the incorporation of adaptive gain into the protocol eliminates the need for predefined bounds on actuator faults, uncertainties and disturbances.
The rest of the research in this paper is described below. Section 2 presents some preparatory knowledge for the subsequent research and a description of the research problem. Section 3 develops a new event-triggered controller. And it is shown that Zeno behaviour can be ruled out. Section 4 illustrates the feasibility of the theory using numerical simulations. In Section 5, the research is summarised and examples of future research directions are provided.
2. Preliminaries
2.1. Graph Theory
In MASs, each agent can be represented as a node, and the communication relationship between agents can be represented as an edge, so the communication topology between agents can be represented by the graph , where denotes the set of vertices, vertex vi represents the ith agent. denotes the set of boundaries, and (vj, vi) denotes that the agent vi can receive the information from vj. This defines vj as a neighbour of vi. All neighbours of vi are defined as the set . We call an edge undirected if both agent vi and agent vj can obtain information from each other. In a graph G, we call it an undirected graph if all edges are undirected, otherwise we call it a directed graph. Define an adjacency matrix , if and only if exists aij > 0, otherwise aij = 0. The Laplacian matrix be defined as with gii = ∑j≠iaij and gij = −aij if i ≠ j. Based on the leader–follower topology, can be expressed as . For MASs, an agent is said to be a follower if it has at least one neighbour and leader when it has no neighbours.
Rs means real vector space of s dimensions, and Rs×t means real matrix space of s × t dimensions. IN represents a unit matrix of order N, and 1 represents an arbitrary matrix with all one elements. ‖E‖ denotes the 2-parameter of the matrix E. λmin(E) and λmax(E) represent the minimum and maximum eigenroots of matrix E. diag{E1, E2, …, EN} denotes the diagonal matrix with diagonal elements E1, E2, …, EN of the diagonal matrix. ⊗ represents the Kronecker product. As for the function means supt≥0‖p(t)‖ < ∞ and means .
2.2. Definitions and Lemmas
Definition 1 (see [37].)For any given bounded initial state, if the state trajectory of all follower agents is synchronised to that of the leader agent, i.e.,
Then, the MASs (1) are said to be able to reach consensus based on the designed control protocol.
Assumption 1 (see [37].)The edges connecting the followers are assumed to be undirected, meaning that all followers have access to each other’s information. Moreover, for a follower, at least one leader has a directed path with it.
Assumption 2 (see [38].)The matrix pair (A, B) is stable.
Assumption 3 (see [39].)The vector and the matrix Si(t) exist that allow and ΔAi(t) = BSi(t) to hold.
Assumption 4 (see [39].)The presence of uncertain positive constants ρi and ϖi leads to and ‖Si(t)‖ ≤ ϖi.
Assumption 5 (see [40].)It exist the uncertain positive constants and that can make hold for i = 1, 2, …, N. Furthermore, θi(t) is not available.
Lemma 1 (see [41].)For any vectors m, n ∈ Rs, for which the following inequality holds
Lemma 2 (see [42].)For the case of some q ∈ [1, ∞), if and , so it can be assumed that limt⟶∞ p(t) = 0.
2.3. Formulation of the Problem
Remark 1. In [30, 31], the control protocols often rely on continuous communication between agents, which can lead to significant communication overhead, especially in large-scale MASs. In contrast, the piecewise continuous input signal in this paper is based on a distributed event-triggered strategy, which significantly reduces the frequency of communication. Communication only occurs when specific triggering conditions are met, thereby reducing the overall communication load among neighbouring agents. And the piecewise continuous input signal in this paper incorporates an adaptive mechanism that does not require prior knowledge of the global communication topology or upper bounds on parameter uncertainties and external disturbances.
Depending on (5) and (14), it is easy to know ξ(t) = (L1 ⊗ Is)ε(t).
The main conclusions of this subsection will be presented in the following theorems.
3. Main Result
Theorem 1. Considering that the MASs in (1) satisfies Assumptions 1–5. Choosing the matrices Hu = −BTP and Ha = PBBTP, where P is the positive definite solution in the Riccati inequality below:
Then, in the presence of parameter uncertainty, external disturbances and actuator faults, MASs (1) can complete time-varying consensus tracking via a distributed event-triggered protocol (6).
Proof 1. Build a Lyapunov function that is engineered to take the following form:
The Zeno behaviour is known to occur in many practical cases. The behaviour describes a process that generates countless event triggers in succession within a finite period of time. Usually this behaviour requires removal since Zeno behaviour interferes with the normal operation of event trigger and may lead to system instability. In the following theorem, we will prove that Zeno behaviour can be avoided.
Theorem 2. Assuming that Theorem 1 holds, the Zeno behaviour of the MASs (1) can be ruled out under the designed control protocol (6) and trigger function (17).
Proof 2. Assuming that agent i undergoes Zeno behaviour, the time interval between successive trigger moments is defined as . There exists a finite constant satisfying . By the nature of the limit, it follows that holds.
It can be seen that this is paradoxical. Thus, we obtain , which indicates there will be no Zeno behaviour occurring with the control protocol (6). Thus, the proof is completed.
4. Simulations
In this section, MASs consisting of a leader and four followers are considered to verify the reliability of the proposed control algorithm and disturbance observer. In this case, the subscript of the leader is labelled as 0 and the subscripts of the followers are labelled as 1, 2, 3 and 4, respectively.
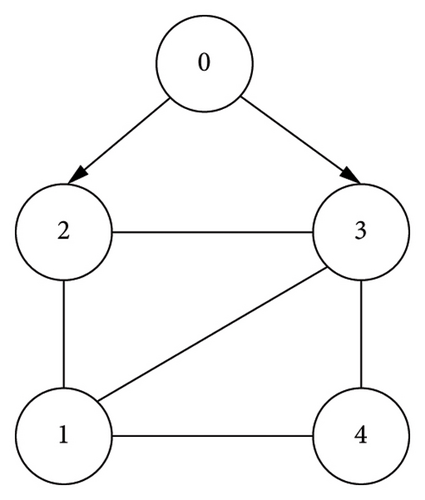
Assuming that the four followers are subject to parameter uncertainty and external disturbances and that ΔAi(t) and di(t) satisfied Assumptions 3 and 4. For follower (i = 1, 2, …, 4), let κi1 = 1, κi2 = 1, κi3 = 1, κi4 = 1, πi1 = 0.1, πi2 = 0.05, ηi = 2 and ϕi = 0.45. The initial state of each agent is set to , , and . The simulation is executed under the controller (6) and the trigger function (17).
The adaptive gains for and are displayed in Figures 2, 3, 4, and 5, from which it can be concluded that all gains are bounded. and converge to stable values over time, indicating that the adaptive mechanism effectively adjusts the control gains to compensate for uncertainties and disturbances. The three plots in Figure 6 depict the error of the estimator converging asymptotically to 0, from which it is shown that the states are observable. The three plots in Figure 7 show the leader–follower tracking error converging asymptotically to 0. The convergence of the tracking error indicates that the system can achieve consensus despite the presence of actuator faults, parameter uncertainty and external disturbances. That is, consensus tracking behaviour is achievable. The moments of the event trigger time are shown in Figure 8 for each agent. The agents only communicate when necessary, which helps in reducing the network burden and avoiding information congestion.
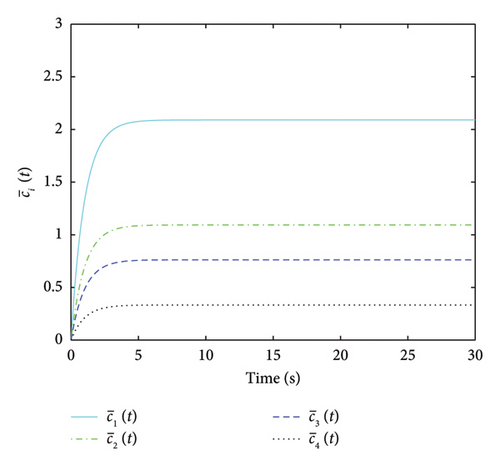
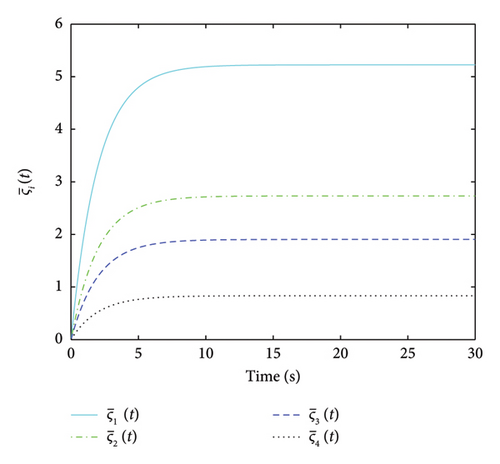
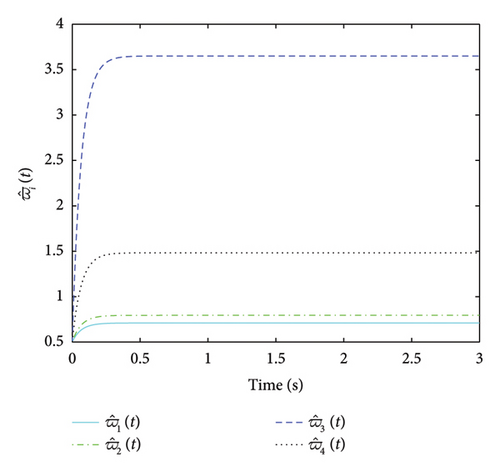
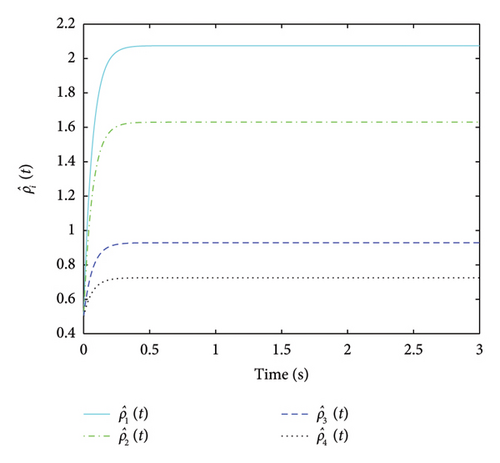
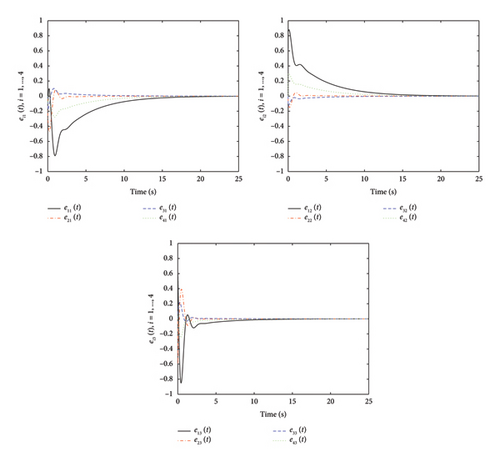
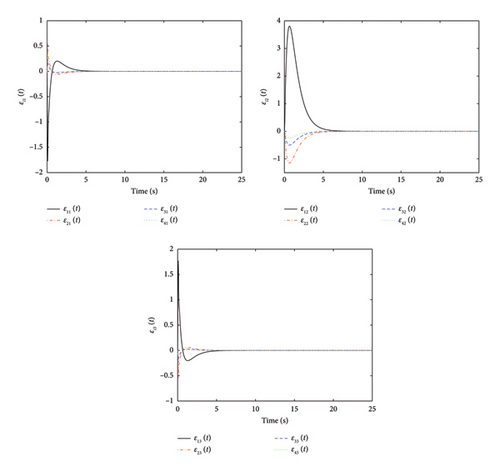
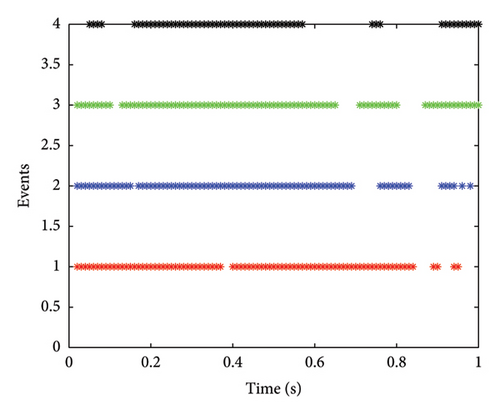
Remark 2. The MASs comprises one leader and four followers. We selected a total of five agents to simulate representative dynamic behaviours. The initial states of the agents were randomly distributed within the range of [−10, 10]. The simulation was conducted over a 30-s period, with a time step of 0.01 s. This time step ensures the precision of the numerical simulations while maintaining a reasonable simulation duration within the constraints of available computational resources. The parameters in the proposed design are chosen based on the system dynamics, desired performance and stability requirements. The adaptive laws and event-triggering conditions are designed to ensure that the system can handle uncertainties and disturbances without requiring exact knowledge of their bounds. The specific values of the parameters can be tuned through simulation to achieve the desired balance between performance and communication efficiency.
5. Conclusion
On the basis of a dynamic event-triggered strategy, this article takes into account the leader–follower consensus tracking of MASs in the form of parameter uncertainty and external disturbances with actuator faults. Building on the neighbouring agents’ estimation states, a novel event-triggered consensus protocol is proposed, in which we bring in an estimator in each agent’s estimation state. Also employing an adaptive mechanism, for which the protocol requires no global information about the communication topology and no upper limits in terms of parameter uncertainty and external disturbances. Then, the stability analysis using Lyapunov technique can show the suggested protocol is able to implement the leader-following consensus and can eliminate the Zeno behaviour. It is notable that in this article, the distributed fault-tolerant control issue is considered only on the undirected topology graph. Therefore, the next extension of this result to directed topologies will be a very interesting work.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This work is supported by the National Natural Science Foundation of China under Grants (62271195 and 62303169) and in part by the Natural Science Foundation of Hubei Province of China under Grants (2025AFA040, 2023AFD006 and 2024AFD008).
Acknowledgements
This work is supported by the National Natural Science Foundation of China under Grants (62271195 and 62303169) and in part by the Natural Science Foundation of Hubei Province of China under Grants (2025AFA040, 2023AFD006 and 2024AFD008).
Open Research
Data Availability Statement
This article does not contain applied data.




