Volume 2025, Issue 1 9968119

Research Article

Open Access

Dynamics and Robust Synchronization of an Oscillator With Cubic and Signum Terms

Fernando E. Serrano,

Fernando E. Serrano

orcid.org/0000-0002-8800-7578

Institute of Robotics , Technical University of Catalonia , Barcelona , Spain , upc.edu

Institute of Energy Research , Honduras National Autonomous University , Tegucigalpa , Honduras

Search for more papers by this author

Viet-Thanh Pham,

Corresponding Author

Viet-Thanh Pham

[email protected]

orcid.org/0000-0001-5151-9812

Faculty of Electronics Technology , Industrial University of Ho Chi Minh City , Ho Chi Minh City , Vietnam , hui.edu.vn

Search for more papers by this author

Giuseppe Grassi,

Corresponding Author

Giuseppe Grassi

[email protected]

orcid.org/0000-0002-8876-3760

Department of Engineering for Innovation , University of Salento , Lecce , Italy , unisalento.it

Search for more papers by this author

Fernando E. Serrano,

Fernando E. Serrano

orcid.org/0000-0002-8800-7578

Institute of Robotics , Technical University of Catalonia , Barcelona , Spain , upc.edu

Institute of Energy Research , Honduras National Autonomous University , Tegucigalpa , Honduras

Search for more papers by this author

Viet-Thanh Pham,

Corresponding Author

Viet-Thanh Pham

[email protected]

orcid.org/0000-0001-5151-9812

Faculty of Electronics Technology , Industrial University of Ho Chi Minh City , Ho Chi Minh City , Vietnam , hui.edu.vn

Search for more papers by this author

Giuseppe Grassi,

Corresponding Author

Giuseppe Grassi

[email protected]

orcid.org/0000-0002-8876-3760

Department of Engineering for Innovation , University of Salento , Lecce , Italy , unisalento.it

Search for more papers by this author

First published: 02 May 2025

https://doi.org/10.1155/cplx/9968119

Academic Editor: Chittaranjan Hens

Share a link

Email
Wechat
Bluesky

Abstract

In recent years, there has been a marked surge in research focused on nonlinear oscillators. Among these, a particular emphasis has been placed on a class of oscillators distinguished by their concealed attractors, drawing considerable attention due to their unique characteristics. This paper delves into the exploration of an elegant oscillator belonging to this distinctive class. Despite comprising five terms and lacking equilibrium points, this oscillator displays remarkably intricate dynamics. The study covers various aspects such as chaos, hidden attractors, offset boosting, and notably, different strange attractors exhibited by this oscillator. Additionally, approaches involving synchronization for such oscillators are introduced. Apart from the presentation of the novel chaotic oscillator, the synchronization of a nominal and uncertain chaotic system is evinced by the sliding mode technique (super-twisting algorithm) in the first case, and a robust controller is synthesized, respectively. The appropriate Lyapunov functions are implemented in the two synchronization strategies leading to obtain suitable control strategies to achieve fast and accurate control laws. The respective simulations are performed along with the conclusions of this work.

1. Introduction

Oscillators constitute crucial components within electronic circuits, serving as sources for fundamental reference signals such as sine or squared waveforms. These oscillators find extensive application in signal generators employed for measurement and testing purposes [1]. Acquiring knowledge about diverse types of oscillators not only aids in selecting the most suitable variant for particular projects but also facilitates the creation and realization of innovative designs [2]. Notably, oscillators imbued with chaotic behavior have garnered significant attention due to their intricately complex dynamics [3]. The presence of chaos in oscillators has broad applications across a spectrum of fields, spanning from security and signal processing to the realm of mobile robotics [4–7].

A self-excited attractor commonly emerges in conventional oscillators through computational procedures. Upon detecting an unstable equilibrium, it becomes possible to derive a basin of attraction. In recent years, there has been a surge in the development of oscillators housing hidden attractors, where the basins of attraction are independent of equilibria [8, 9]. Investigating these hidden attractors necessitates specialized computational approaches, posing a considerable challenge in their determination [10]. Nevertheless, in practical applications, it becomes imperative to discern the presence of these hidden attractors to ensure that the system operates in accordance with the anticipated attractor [11, 12]. This identification serves to mitigate undesired system behaviors, thereby enhancing system safety and reliability.

In their study of nonlinear oscillators, researchers observed the presence of multiscrolls within attractors. These multiscrolls not only signified intricate dynamics but also showcased the practical applications of these oscillators [13]. As a result, a range of oscillators featuring multiscroll attractors has been developed. Furthermore, the existing literature has documented diverse methods for constructing multiscroll structures [14, 15]. For instance, Matouk et al. [16] employed the Caputo operator in their investigation of fractional multiscroll systems. Hu et al. proposed a 5D system that exhibited hidden attractors [17]. Memristor was a versatile component for creating multiscrolls [18]. Hyperchaos was observed by Vaidyanathan et al. [19]. Multiscroll oscillators were implemented in [20]. Li and Zeng reported multiple scrolls in a jerk system [21].

Synchronization of two dynamic systems possesses importance in many physical systems such as optical and mechanical oscillators; therefore, it is important to mention some research studies, considering that in this paper the synchronization of the elegant chaotic system presented in this research study is performed by a super-twisting sliding algorithm. It is worthy to mention that the super-twisting algorithm provides a higher order sliding mode synchronization proving that it is an efficient control/synchronization algorithm as validated by numerical experiments. In the following reference [22], the design of a synchronizer for a financial chaotic system is realized by means of an integral sliding mode controller, proving the validity of the synchronization strategy. Besides in papers such as [23], a microcontroller implementation of a fractional order chaotic dynamic system by the sliding mode is provided. Meanwhile, in [24], a fractional order sliding mode controller is used to stabilize a secure system communication system.

Another control synchronization technique used in this research study is performed by means of a robust controller/synchronizer for the uncertain elegant chaotic system. The type of uncertainty analyzed in this research study is based on parametric uncertainties, which is one of the most common uncertainties found taking into consideration unmodelled dynamics. For example, in [25], the synchronization is realized by means of a Chlodowsky approximator for the uncertainties found in this system. Then, in [26], the robust synchronization of financial chaotic systems is performed by considering unknown parametric uncertainties. Finally, in [27], a robust controller based on neural networks is proposed for the synchronization of chaotic systems by a generalized projective strategy.

It is noted that the theory on simple chaotic circuits has been extensively developed in recent years, with applications in telecommunications. The dynamic analysis, stabilization, and synchronization of the found chaotic system are applied in the following implementations in addition to the use of the research study’s findings in secure communications:

•
Chaotic optic systems.
•
Chaotic electromagnetic systems.
•
Chaotic kinetic chemical reactions.
•
Chaotic mechanical systems and oscillators.

The following reference survey is illustrated in order to clarify and validate the implementations of the identified chaotic system that is presented in this research study, as well as to observe the several applications in which it can be applied. In addition to secure communications, the following literature publications support the applicability of these results in chaotic optic systems. For example, Ref. [28] describes the subharmonic path to chaos in a laser beam system. Reference [29] then shows hyperchaotic behavior in a three-ring mutually connected laser. Reference [30] shows how to create chaos in a laser with optical feedback.

References related to electromagnetic chaos include papers such as [31] that provide a bifurcation analysis and nonlinear dynamic analysis of active magnetic bearings under complex resonance. Then, in [32], it is shown that a single photon in a cavity electromechanical device causes instability.

Meanwhile, instances of chaotic chemical reactions may be found in articles such as [33] oscillations and chaos in a chemical process incorporating heterogeneous catalysis. Then, in [34], kinetic chaotic responses are thoroughly examined. Last but not least, papers on the dynamic analysis of chaotic mechanical systems and oscillators, such as [35–38], provide fascinating findings that might be used in the ongoing study.

Finally, the next three sources are noteworthy due to the applications of chaotic dynamics. For example, Ref. [39] describes the nonlinear dynamics of three-layer microplates, while Ref. [40] offers a special adaptive filtering for cooperative localization. Lastly, Ref. [41] introduces the adaptive pseudoinverse control for constrained hysteretic nonlinear systems.

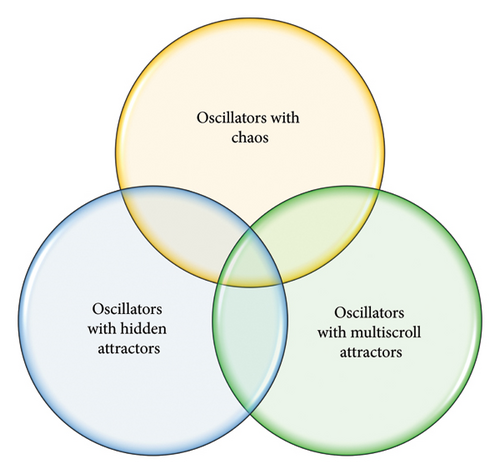
Our studied oscillator is not only simple but also has distinct features. The oscillator exhibits chaos, hidden attractors, offset boosting, and different strange attractors. In addition, the synchronization approaches have been developed for robust synchronization. They are useful for application scenarios such as mobile robot coverage path planning or chaotic path synchronization. The accuracy and stability during the path planning process are maintained despite the presence of uncertain disturbances. Figure 1 illustrates three discussed types of special oscillators. Our proposed oscillator, distinguished by its unique features, is prominently positioned at the center of Figure 1, where it intersects with three different types of oscillators. Notably, our oscillator exhibits elegance in comparison to previously published works, as illustrated in Table 1. The oscillator and its dynamics are explicated in Sections 2 and 3. Sections 4 and 5 delve into a comprehensive exploration of synchronization for this distinctive oscillator. The concluding section synthesizes the findings and implications, offering a comprehensive closure to our work.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Three types of special oscillators and their overlap.

Table 1. Oscillators with dimensions and terms.

Oscillator	Dimension	Term	Hidden attractor
[17]	5	11	Yes
[18]	4	12	Yes
[19]	4	9	No
[15]	3	10	No
[14]	3	8	No
[20]	3	7	No
[21]	3	5	No
This work	3	6	Yes

2. An Elegant Oscillator

We study the oscillator

()

with a, b, c > 0. The oscillator equation (1) is the generalized model of the reported one [42]. We can change the parameter b to obtain multiple-scroll attractors.

Equilibrium points satisfy

()

The oscillator has no equilibrium point for

()

The oscillator generates chaos (see Figure 2) for

()

and initial condition (0.3, 0.2, 0.3).

When applying the transformation

()

the oscillator is invariant. Figure 3 displays chaos and symmetry for c = ±1.

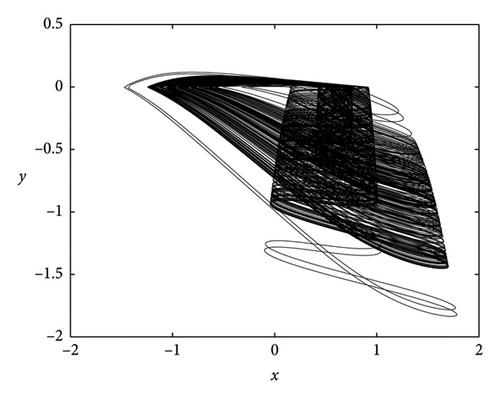
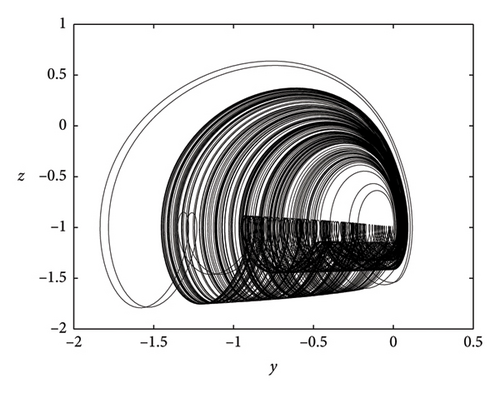
3. Dynamics of the Oscillator

3.1. Chaotic Attractors

Dynamics of the oscillator is shown in Figure 4 via the bifurcation diagram and Lyapunov exponents for b. We applied Wolf’s method to calculate the Lyapunov exponents [43]. The nonsmooth term sgn(y) was replaced with the smooth approximation tan h(Ky), where K = 500 [44]. Chaotic and nonchaotic behaviors are observed for b ∈ [1, 4].

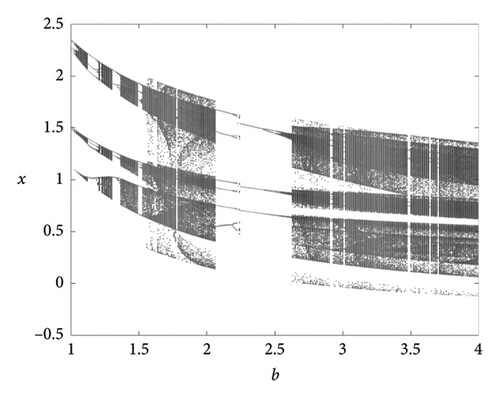
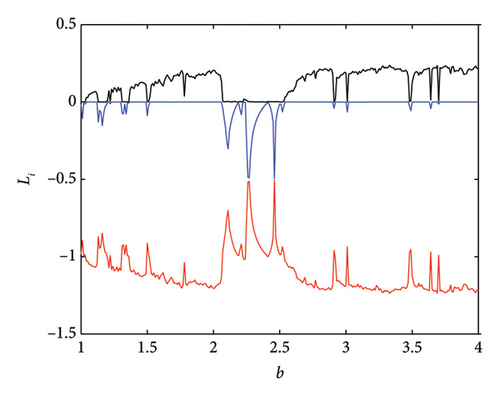
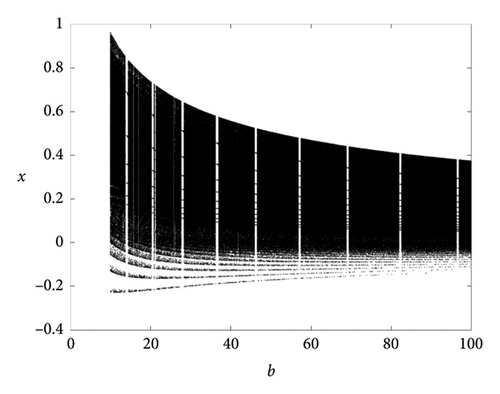
Interestingly, the value of b can be varied in a large range as illustrated in Figure 5.

3.2. Strange Attractors

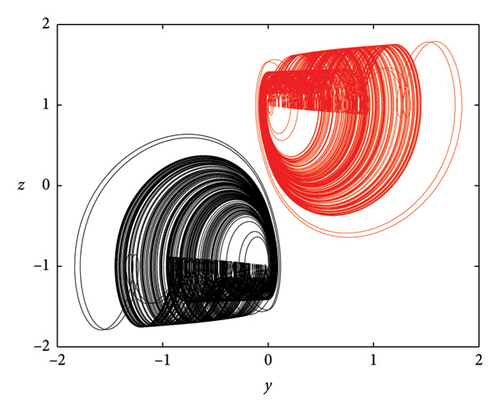
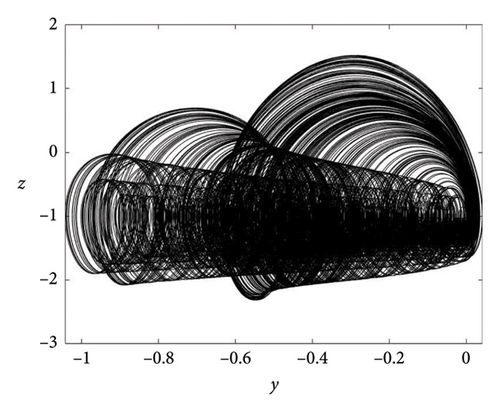
The literature has confirmed the association between strange attractors and equilibria. However, an intriguing aspect is the presence of strange attractors within oscillators featuring hidden attractors. Our proposed oscillator lacks equilibrium but demonstrates the capability to generate different strange attractors, as depicted in Figure 6. Notably, the number of shapes can be effortlessly manipulated by adjusting a single parameter, b, offering considerable flexibility. It is important to highlight that, typically, achieving different strange attractors necessitates the introduction of additional elements.

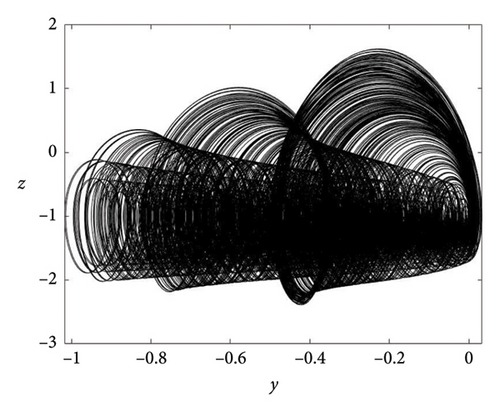
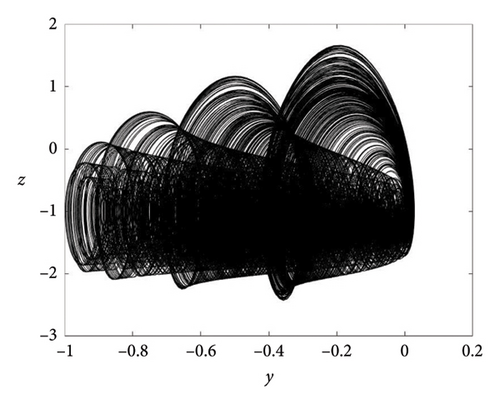
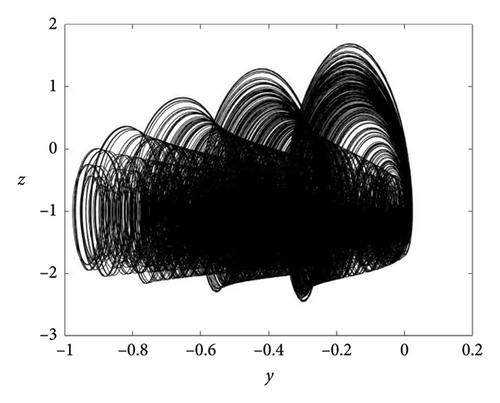
3.3. Offset Boosting

In real situation, a boostable variable of the chaotic oscillator is useful, where the variable is varied conveniently through only one control parameter [45]. As shown in equation (6), the additional parameter k is applied to shift the variable x (see Figure 7).

()

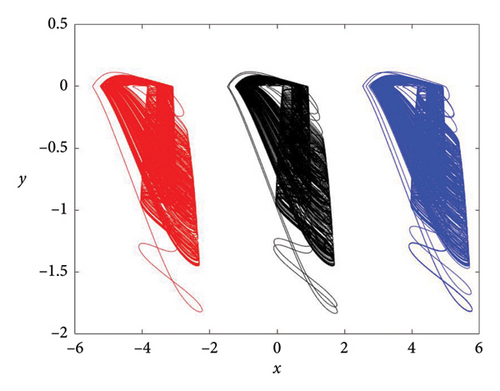
4. Synchronizer Design for the Elegant Oscillator

This section provides the design methodology of a control synchronization strategy for the elegant oscillator provided in this research study. This section is divided into the following subsections:

•
Problem statement and formulation.
•
Super-twisting sliding mode control synchronization strategy for the elegant oscillator.
•
Numerical simulation.

The main objective in this section is to design the appropriate robust control synchronization strategy in order to synchronize the response system with the drive system. The chaotic dynamic systems in this case are considered in the nonuncertain form, so in this way, the synchronization is achieved by considering only the nominal systems. As explained before, the main purpose is to synchronize the two identical chaotic systems in order to obtain the maximum advantages for applications such as secure communications, electromagnetic chaos, and chaos found in artificial electrical and mechanical systems. Considering that this is a novel discovered elegant oscillator is necessary to design the appropriate control strategies for synchronization purposes for future implementations.

4.1. Theoretical Framework

The main objective of this section is to elucidate the fundamentals of the elegant oscillator discovered in order to design the appropriate synchronization strategy in the following section. There are the drive uncontrolled system and the controlled dynamic system in which control inputs are included for synchronization purposes. Consider the following drive and response system to be synchronized by the super-twisting sliding mode control technique:

()

Now, consider the vectors

and

as the drive and response variables with the input

. Meanwhile, the constants a, b, and c are selected as explained before in this paper. So the following drive and systems can be represented in vector form as follows:

()

in which the vector fields f(X) and g(Y) are given by

and

with the initial conditions as given in the numerical experiment section.

4.2. Super-Twisting Sliding Mode Control Synchronizer

This strategy has been proven to be effective for synchronization control. The super-twisting sliding mode algorithm, as it is known, is an appropriate control strategy, as it is fast and minimizes the chattering effect caused by the oscillatory dynamics of the chaotic systems, so there is no problem for a physical synchronization implementation in mechanical, electrical, or chemical systems, for example. The following theorem establishes the control law for synchronization purposes based on the work of [46]:

Theorem 1. Consider the following super-twisting algorithm [46]:

()

with the sliding variables

and

and the gain positive definite diagonal matrices

and

. The error variable and its first derivative is given by

()

so the error e is asymptotically stable approaching zero in finite time iff the control law U is given by

()

with the following matrix

which is positive definite.

Proof 1. Consider the Lyapunov functional:

()

So by obtaining the derivative in time of the previous Lyapunov function yields

()

Now, substituting equation (11) into equation (13) yields the following negative semidefinite function:

()

and the proof is finalized.

4.3. Experimental Results

This numerical experiment consists of testing and validating the theoretical results explained in this section. The main objective is to verify if the proposed control strategy yields an effective synchronization with a fast and accurate response. The other reason is to evince that the super-twisting sliding mode controller does not produce chattering, proving the effectiveness of the proposed control synchronization strategy. For this example, take into consideration the gain matrices:

()

The initial conditions are X = [0.3, 0.2, 0.3]^T. For the response system, the conditions are Y = [3, 8, −2]^T with the following constants for both systems a = 2, b = 2, and c = 1.

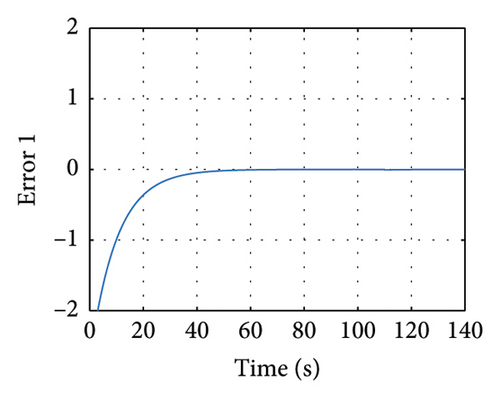
In Figures 8 and 9, the variables X and Y are presented, in which it is noticed how the three state variables are stabilized accurately. It is noticeable that as long as the gain matrices must be positive definite diagonal, the synchronicity is ensured. It is important to mention that the super-twisting sliding mode controller ensures that the error variables are driven to the origin in finite time.

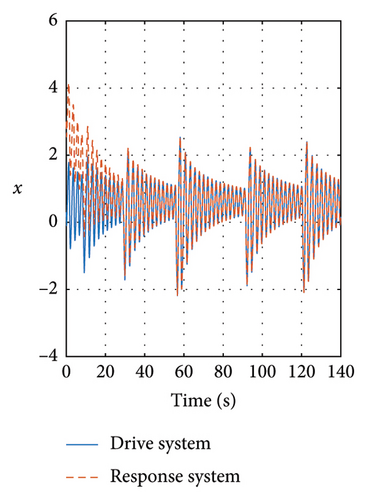
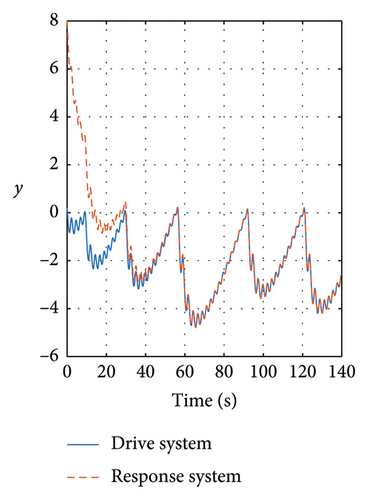
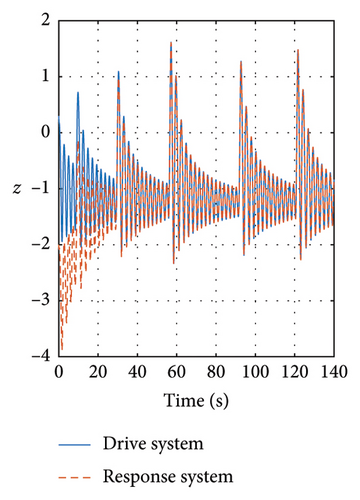
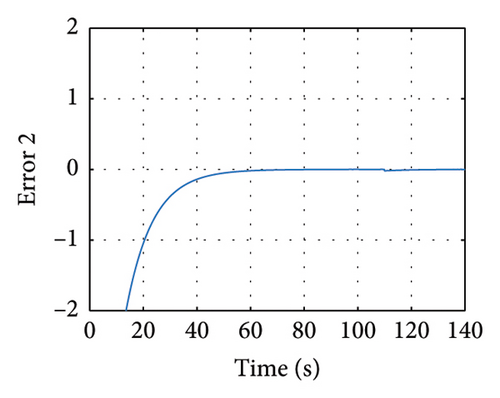
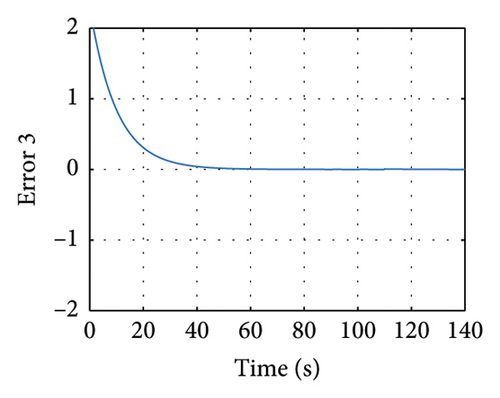
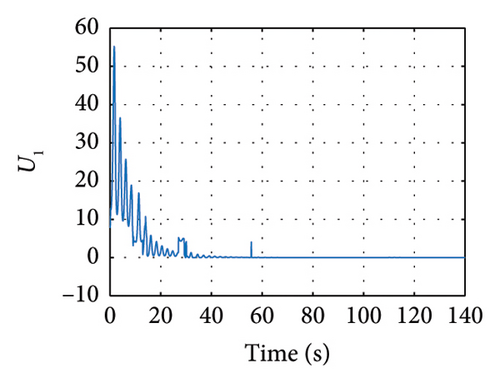
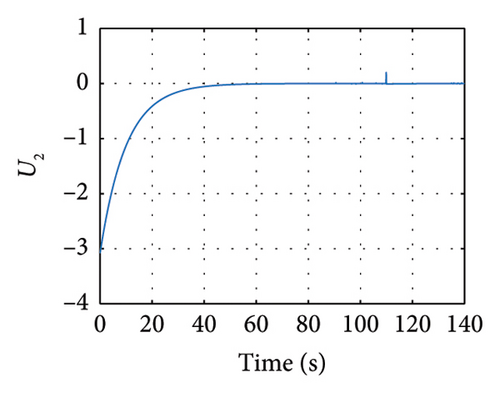
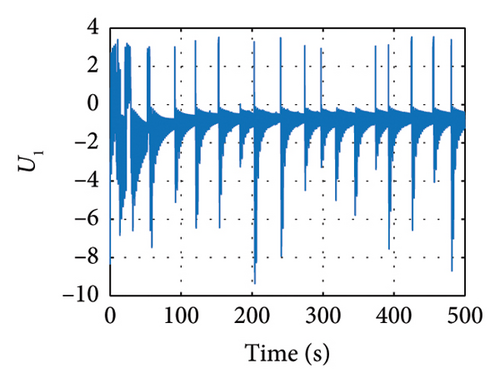
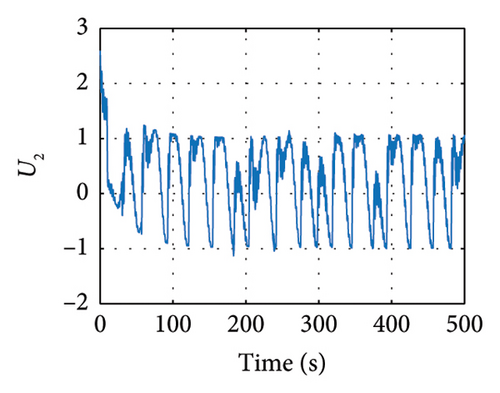
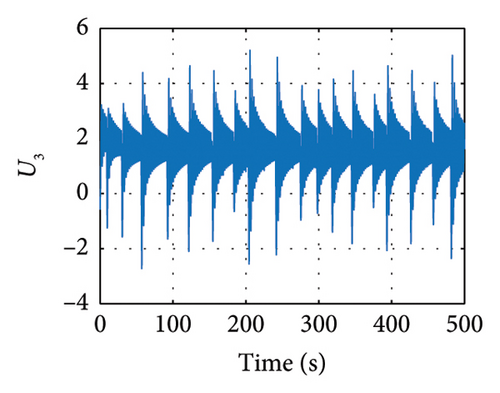
Meanwhile in Figure 10, the control synchronizing input is presented, evincing the control effort of the synchronization approach.

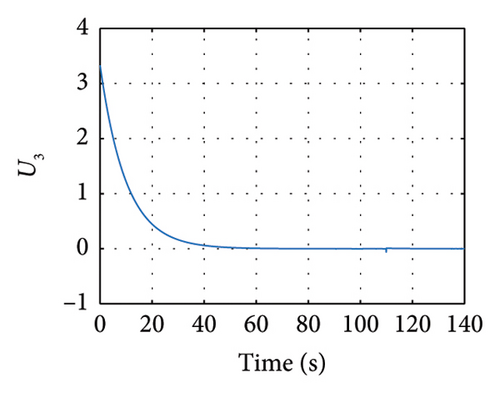
Meanwhile, in Figures 11 and 12, the sliding variables σ and z showing the response of these variables are evinced.

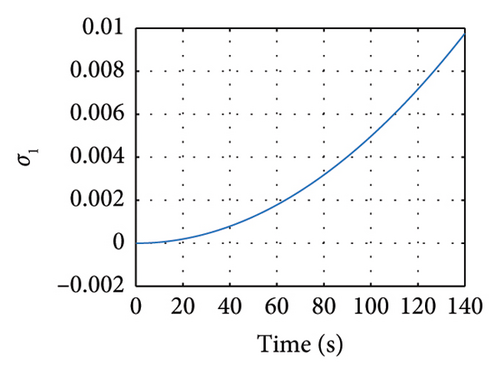
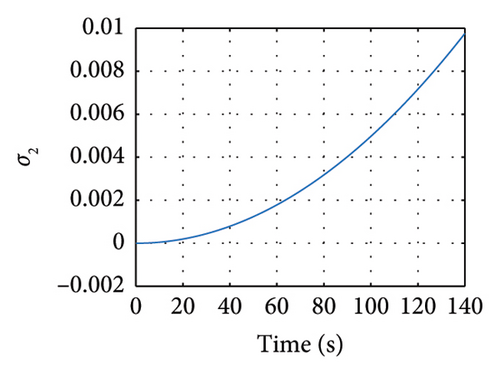
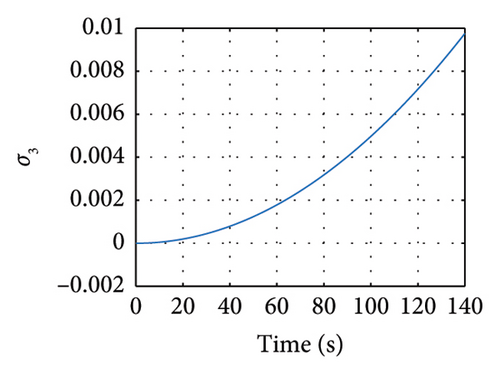
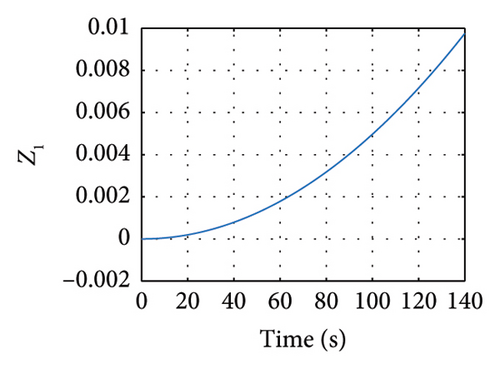
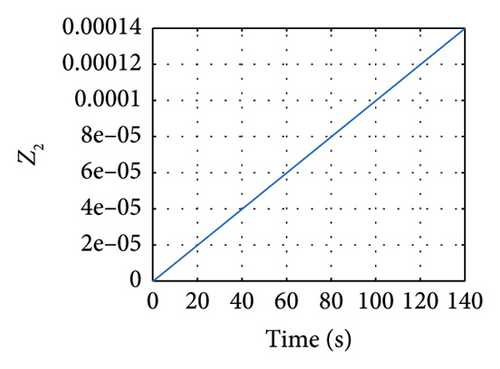
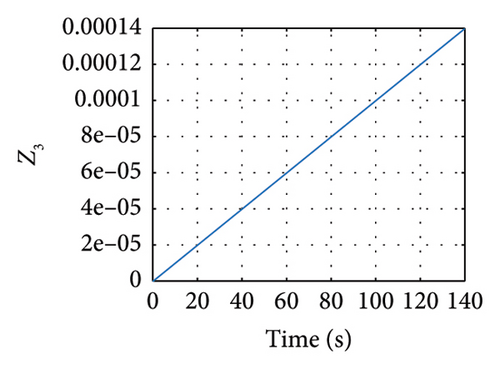
5. Robust Synchronization of the Uncertain Elegant Oscillator

In this section, the synchronization of the uncertain elegant oscillator is achieved. It is important to mention that the kind of uncertainty considered in this research study and in this section are parametric uncertainties. As a future direction, other kinds of uncertainties according to their topology are included in this research study. First, the response chaotic system is considered as an uncertain nonlinear dynamic system, and then by selecting the appropriate robust control Lyapunov function (RCLF), the robust control synchronization law is obtained. For this objective, consider the following corollary without proof [47]:

Corollary 1. Consider the following RCLF and the three class functions α₁(.), α₂(.), and α₃(.). So the control law is obtained if the following are valid:

()

in which e = X − Y is the synchronization error variable and u is the response system input.

5.1. Theoretical Framework

Take into consideration the uncertain chaotic response system:

()

in which Δg(Y) is the uncertainty found in the system and g₀(Y) is the nominal system. The uncertainty has the following property [47]:

Property 1. The parametric uncertainty Δg(Y) is bounded as shown in the following:

()

in which ϵ > 0 is a positive constant.

Considering the different types of physical systems in which uncertainties are found, such as mechanical, electrical, chemical, and optical, as it is known, the most commonly found uncertainties found in these kinds of systems are basically parametric uncertainties. Despite that this kind of uncertainty is the most simple, they are found in many kinds of physical systems, so the robustness of the open loop nonlinear dynamic system depends on the parameter ϵ. If this parameter is smaller, the effect in the open loop stability is smaller, but if this parameter is high, the open loop stability of the nonlinear chaotic system is significantly affected. Because this elegant oscillator is a newly discovered chaotic system and parametric uncertainties are most commonly found in physical systems, it is not necessary to evince a complete open loop robustness analysis. In the following section is evinced how to obtain the robust control law. The nominal system is given by .

5.2. Robust Synchronizer Design

In this section, the robust synchronization of the elegant oscillator is presented. Firstly, the response system, which is the uncertain system, is divided into each vector field component, in specific the nominal system g₀(Y) as appears below [47]:

()

and the vector field f is divided into the following components:

()

To obtain a robust control strategy, consider the following theorem.

Theorem 2. Consider the error variables and their first derivative:

()

So the error variable is asymptotically stable if the robust control laws are implemented to drive the error variables to zero:

()

in which

, and

are positive gain constants.

Proof 2. Consider the following RCLF:

()

Obtaining the first derivative of the previous RLCF yields

()

With the suitable substitution, the previous RCLF first derivative yields

()

By substituting the control laws, equations (22)–(24) yield

()

So asymptotical stability is achieved, and the proof is completed.

5.3. Numerical Experiment

In this section, a numerical experiment is performed. For this numerical experiment, the following parametric uncertainty is implemented:

()

Considering the following gain constants k₁ = 30, k₂ = 30, and k₃ = 30, the simulation was realized by t_f = 500 s.

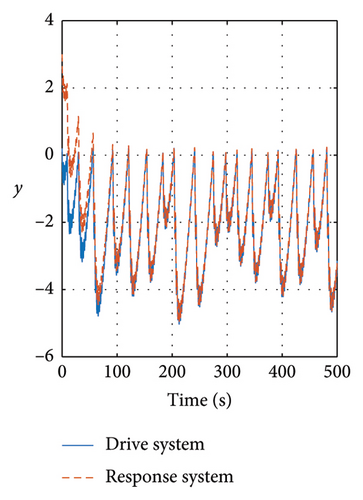
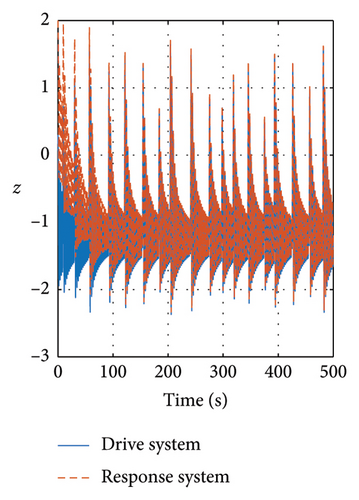
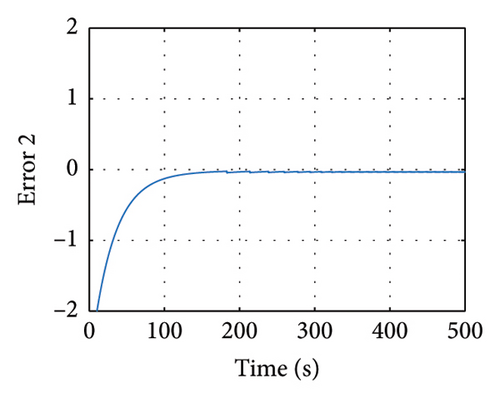
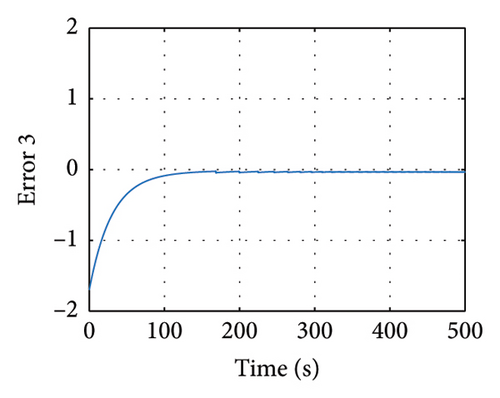
In Figures 13 and 14, the evolution of the state variables of the drive and response systems is shown. It is evinced how these variables are synchronized. In this way, it is achieved efficiently the synchronization by making the trajectory tracking of the response system in comparison with the drive system. Finally in Figure 15, the evolution in time of the input variables is depicted, showing how these variables evolve in time in order to keep an accurate synchronicity between the drive and response system variables until the error reaches the zero value in finite time.

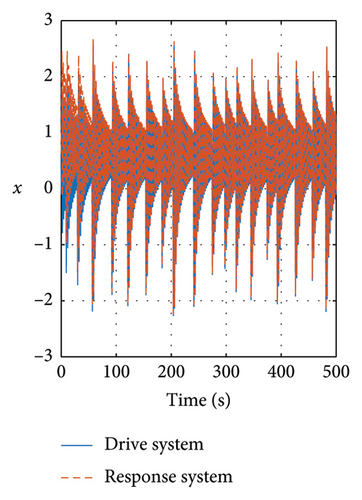
6. Conclusions

Through the introduction of this oscillator, we observe that an elegant oscillator displays distinct and appealing dynamics. Positioned at the intersection of three special classes of oscillators, its location is defined by unique characteristics. Our exploration not only unveils the dynamics but also elucidates the synchronization mechanisms for this oscillator. The results underscore the efficacy of our developed super-twisting sliding mode controller. The forthcoming focus of our research will revolve around the application of this elegant oscillator, opening avenues for further investigation.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this research.

Open Research

Data Availability Statement

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

1 Ndjountche T., Amplifiers, Comparators, Multipliers, Filters, and Oscillators, 2017, CRC Press.
Google Scholar
2 Senani R., Bhaskar D. R., Singh V. K., and Sharma R. K., Sinusoidal Oscillators and Waveform Generators Using Modern Electronic Circuit Building Blocks, 2016, Springer.
10.1007/978-3-319-23712-1
Google Scholar
3 Lin H., Wang C., Yu F. et al., A Review of Chaotic Systems Based on Memristive Hopfield Neural Networks, Mathematics. (2023) 11, no. 6, https://doi.org/10.3390/math11061369.
10.3390/math11061369
Web of Science® Google Scholar
4 Wang X., Akgul A., Cavusoglu U., Pham V.-T., Vo Hoang D., and Nguyen X. Q., A Chaotic System With Infinite Equilibria and Its S-Box Constructing Application, Applied Sciences. (2018) 8, no. 11, https://doi.org/10.3390/app8112132, 2-s2.0-85055999155.
10.3390/app8112132
Google Scholar
5 Gao S., Wu R., Wang X. et al., A 3d Model Encryption Scheme Based on a Cascaded Chaotic System, Signal Processing. (2023) 202, https://doi.org/10.1016/j.sigpro.2022.108745.
10.1016/j.sigpro.2022.108745
Web of Science® Google Scholar
6 Charalampidis N., Iatropoulos A., and Volos C., Chaos Based Speech Encryption Using Microcontroller, Integration. (2024) 95, https://doi.org/10.1016/j.vlsi.2023.102128.
10.1016/j.vlsi.2023.102128
Web of Science® Google Scholar
7 Moysis L., Lawnik M., Volos C., Baptista M. S., and Goudos S. K., Chaotic Maps With Tunable Mean Value—Application to a Uav Surveillance Mission, Symmetry. (2023) 15, no. 12, https://doi.org/10.3390/sym15122138.
10.3390/sym15122138
PubMed Web of Science® Google Scholar
8 Dudkowski D., Jafari S., Kapitaniak T., Kuznetsov N., Leonov G., and Prasad A., Hidden Attractors in Dynamical Systems, Physics Reports. (2016) 637, 1–50, https://doi.org/10.1016/j.physrep.2016.05.002, 2-s2.0-84973525493.
10.1016/j.physrep.2016.05.002
Web of Science® Google Scholar
9 Pham V.-T., Volos C., and Kapitaniak T., Systems With Hidden Attractors: From Theory to Realization in Circuits, 2018, Springer.
Google Scholar
10 Brezetskyi S., Dudkowski D., and Kapitaniak T., Rare and Hidden Attractors in Van der Pol–Duffing Oscillators, The European Physical Journal—Special Topics. (2015) 224, no. 8, 1459–1467, https://doi.org/10.1140/epjst/e2015-02471-2, 2-s2.0-84937945783.
10.1140/epjst/e2015-02471-2
Web of Science® Google Scholar
11 Jafari S., Pham V.-T., Moghtadaei M., and Kingni S. T., The Relationship Between Chaotic Maps and Some Chaotic Systems With Hidden Attractors, International Journal of Bifurcation and Chaos. (2016) 26.
10.1142/S0218127416502114
Web of Science® Google Scholar
12 Khennaoui A. A., Ouannas A., Bekiros S. et al., Hidden Homogeneous Extreme Multistability of a Fractional-Order Hyperchaotic Discrete-Time System: Chaos, Initial Offset Boosting, Amplitude Control, Control, and Synchronization, Symmetry. (2023) 15, no. 1, https://doi.org/10.3390/sym15010139.
10.3390/sym15010139
PubMed Web of Science® Google Scholar
13 Lü J. and Chen G. R., Generating Multiscroll Chaotic Attractors: Theories, Methods and Applications, International Journal of Bifurcation and Chaos. (2006) 16, no. 04, 775–858, https://doi.org/10.1142/s0218127406015179, 2-s2.0-33745314032.
10.1142/S0218127406015179
Web of Science® Google Scholar
14 Liu X., Shen X., and Zhang H., Multi-Scroll Chaotic and Hyperchaotic Attractors Generated From Chen System, International Journal of Bifurcation and Chaos. (2012) 22, no. 2, https://doi.org/10.1142/s0218127412500332, 2-s2.0-84862776773.
10.1142/S0218127412500332
Web of Science® Google Scholar
15 Ye Y. and He J., Constructing a New Multi-Scroll Chaotic System and its Circuit Design, Mathematics. (2024) 12, no. 13, https://doi.org/10.3390/math12131931.
10.3390/math12131931
Web of Science® Google Scholar
16 Matouk A. E., Almutairi D. K., Herzallah M. A. E., Abdelkawy M. A., and Abdelhameed T. N., Symmetry in a Fractional-Order Multi-Scroll Chaotic System Using the Extended Caputo Operator, Symmetry. (2023) 15, https://doi.org/10.3390/sym15081582.
10.3390/sym15081582
PubMed Web of Science® Google Scholar
17 Hu X., Liu C., Liu L., Yao Y., and Zheng G., Multi-Scroll Hidden Attractors and Multi-Wing Hidden Attractors in a 5-Dimensional Memristive System, Chinese Physics B. (2017) 26, no. 11, https://doi.org/10.1088/1674-1056/26/11/110502, 2-s2.0-85033792577.
10.1088/1674-1056/26/11/110502
Web of Science® Google Scholar
18 Li Y., Xia X., Zeng Y., and Hong Q., Composite One-to Six-Scroll Hidden Attractors in a Memristor-Based Chaotic System and Their Circuit Implementation, Complexity. (2020) 2020, 1–13, https://doi.org/10.1155/2020/3259468.
10.1155/2020/8882813
Web of Science® Google Scholar
19 Vaidyanathan S., Moroz I. M., and Sambas A., A New Two-Scroll 4-d Hyperchaotic System With a Unique Saddle Point Equilibrium, Its Bifurcation Analysis, Circuit Design and a Control Application to Complete Synchronization, Archives of Control Sciences. (2023) 33, 277–298.
Web of Science® Google Scholar
20 Lin Y., Gong J., Yu F., and Huang Y., Current Mode Multi Scroll Chaotic Oscillator Based on Cdta, Frontiers in Physiology. (2023) 11, https://doi.org/10.3389/fphy.2023.1202398.
10.3389/fphy.2023.1202398
Google Scholar
21 Li F. and Zeng J., Multi-Scroll Attractors and Multi-Stable Dynamics of a Three-Dimensional Jerk System, Energies. (2023) 16.
PubMed Google Scholar
22 Johansyah M. D., Sambas A., Zheng S. et al., A Novel Financial System With One Stable and Two Unstable Equilibrium Points: Dynamics, Coexisting Attractors, Complexity Analysis and Synchronization Using Integral Sliding Mode Control, Chaos, Solitons & Fractals. (2023) 177, https://doi.org/10.1016/j.chaos.2023.114283.
10.1016/j.chaos.2023.114283
Web of Science® Google Scholar
23 Zhou Z., Yu W., Wang J., Zhao Y., and Liu M., Design of a Fractional-Order Chaotic Secure Communication Circuit Based on Sliding Mode Theory and Microcontroller, Circuit World. (2023) 49, no. 4, 480–492, https://doi.org/10.1108/cw-03-2021-0078.
10.1108/CW-03-2021-0078
Web of Science® Google Scholar
24 Nguyen Q. D., Huang S.-C., and Giap V. N., Lyapunov-Based Fractional Order of Disturbance Observer and Sliding Mode Control for a Secure Communication of Chaos-Based System, International Journal of Control, Automation and Systems. (2023) 21, no. 11, 3595–3606, https://doi.org/10.1007/s12555-022-1088-2.
10.1007/s12555-022-1088-2
Web of Science® Google Scholar
25 Izadbakhsh A., Khalesi H., and Khorashadizadeh S., Chaos Synchronization Using Q-Chlodowsky Operators as Uncertainty Approximator, Journal of Vibration and Control. (2023) 29, no. 17-18, 4107–4117, https://doi.org/10.1177/10775463221111839.
10.1177/10775463221111839
Web of Science® Google Scholar
26 Shafiq M. and Ahmad I., Robust Synchronization of Four-Dimensional Chaotic Finance Systems With Unknown Parametric Uncertainties, Automatika. (2024) 65, no. 1, 217–234, https://doi.org/10.1080/00051144.2023.2295204.
10.1080/00051144.2023.2295204
Web of Science® Google Scholar
27 Xiao L., Li L., Cao P., and He Y., A Fixed-Time Robust Controller Based on Zeroing Neural Network for Generalized Projective Synchronization of Chaotic Systems, Chaos, Solitons & Fractals. (2023) 169, https://doi.org/10.1016/j.chaos.2023.113279.
10.1016/j.chaos.2023.113279
Web of Science® Google Scholar
28 Kang H., Zhou A., Zhang Y. et al., Observation of Optical Chaotic Solitons and Modulated Subharmonic Route to Chaos in Mode-Locked Laser, Physical Review Letters. (2024) 133, no. 26, https://doi.org/10.1103/physrevlett.133.263801.
10.1103/PhysRevLett.133.263801
Web of Science® Google Scholar
29 Sen-Lin Y., Displays of High-Grade Hyperchaos and Bi-Stability in an Erbium-Doped Fiber Three-Ring Mutual-Coupled Laser, Optics Communications. (2025) 577, https://doi.org/10.1016/j.optcom.2024.131338.
10.1016/j.optcom.2024.131338
Google Scholar
30 Li Q., Jia Z., Wang A., and Wang Y., Parallel Generation of Multi-Channel Broadband Chaos by a Long-Cavity Fp Laser With Optical Feedback, Optics Letters. (2024) 49, no. 24, 7126–7129, https://doi.org/10.1364/ol.546270.
10.1364/OL.546270
CAS PubMed Web of Science® Google Scholar
31 Ma W., Liu F., Lu S. et al., Nonlinear Dynamics and Motion Bifurcations of 12-Pole Variable Stiffness Rotor Active Magnetic Bearings System Under Complex Resonance, International Journal of Non-linear Mechanics. (2025) 169, https://doi.org/10.1016/j.ijnonlinmec.2024.104958.
10.1016/j.ijnonlinmec.2024.104958
Web of Science® Google Scholar
32 Bera T., Kandpal M., Agarwal G. S., and Singh V., Single-Photon Induced Instabilities in a Cavity Electromechanical Device, Nature Communications. (2024) 15, no. 1, https://doi.org/10.1038/s41467-024-51499-z.
10.1038/s41467-024-51499-z
Web of Science® Google Scholar
33 Li H.-Y., Chien Y.-S., and Chiou M.-S., Mixed-Mode Oscillations and Chaos in a Complex Chemical Reaction Network Involving Heterogeneous Catalysis, Chaos. (2024) 34, no. 11, https://doi.org/10.1063/5.0231992.
10.1063/5.0231992
PubMed Web of Science® Google Scholar
34 Susits M. and Tóth J., Rigorously Proven Chaos in Chemical Kinetics, Chaos. (2024) 34, no. 10, https://doi.org/10.1063/5.0206749.
10.1063/5.0206749
PubMed Web of Science® Google Scholar
35 Ngamsa Tegnitsap J. V., Tabekoueng Njitacke Z., Barà C. et al., A van der Pol-Like Complementary Chaotic Oscillator: Design, Physical Realizations, Dynamics, and Physiological Data Augmentation Prospect, Chaos, Solitons & Fractals. (2025) 191, https://doi.org/10.1016/j.chaos.2024.115886.
10.1016/j.chaos.2024.115886
Google Scholar
36 Wang L., Guo C., Xu F., and Xiao H., Hybrid Uncertainty Propagation for Mechanical Dynamics Problems via Polynomial Chaos Expansion and Legendre Interval Inclusion Function, Mechanical Systems and Signal Processing. (2025) 223, https://doi.org/10.1016/j.ymssp.2024.111826.
10.1016/j.ymssp.2024.111826
Web of Science® Google Scholar
37 Amer A., Zhang W., and Amer T., Parametric Excitation and Chaos in a Nonlinear Forced Mathieu System: A Comprehensive Analysis, Alexandria Engineering Journal. (2025) 116, 35–54, https://doi.org/10.1016/j.aej.2024.12.050.
10.1016/j.aej.2024.12.050
Web of Science® Google Scholar
38 Song Y., Zhou H., Tuo Y., and Zhao Z., Finite-Time Prescribed Performance Adaptive Control of Mems Micromirror Stochastic System With Event-Triggered Mechanism, Nonlinear Dynamics. (2025) 113, no. 3, 2315–2331, https://doi.org/10.1007/s11071-024-10336-0.
10.1007/s11071-024-10336-0
Web of Science® Google Scholar
39 Wu Q., Wang S., Yao M., Niu Y., and Wang C., Nonlinear Dynamics of Three-Layer Microplates: Simultaneous Presence of the Micro-Scale and Imperfect Effects, The European Physical Journal Plus. (2024) 139, no. 5, https://doi.org/10.1140/epjp/s13360-024-05255-3.
10.1140/epjp/s13360-024-05255-3
Web of Science® Google Scholar
40 Xu B., Wang X., Zhang J., Guo Y., and Razzaqi A. A., A Novel Adaptive Filtering for Cooperative Localization Under Compass Failure and Non-Gaussian Noise, IEEE Transactions on Vehicular Technology. (2022) 71, no. 4, 3737–3749, https://doi.org/10.1109/tvt.2022.3145095.
10.1109/TVT.2022.3145095
Web of Science® Google Scholar
41 Zhang X., Liu Y., Chen X., Li Z., and Su C.-Y., Adaptive Pseudoinverse Control for Constrained Hysteretic Nonlinear Systems and Its Application on Dielectric Elastomer Actuator, IEEE. (2023) 28, no. 4, 2142–2154, https://doi.org/10.1109/tmech.2022.3231263.
10.1109/tmech.2022.3231263
Google Scholar
42 Serrano F. E., Munoz-Pacheco J. M., and Flores M. A., Fractional-Order Projection of a Chaotic System With Hidden Attractors and Its Passivity-Based Synchronization, Frontiers in Applied Mathematics and Statistics. (2023) 9, https://doi.org/10.3389/fams.2023.1267664.
10.3389/fams.2023.1267664
PubMed Web of Science® Google Scholar
43 Wolf A., Swift J. B., Swinney H. L., and Vastano J. A., Determining Lyapunov Exponents From a Time Series, Physica D: Nonlinear Phenomena. (1985) 16, no. 3, 285–317, https://doi.org/10.1016/0167-2789(85)90011-9, 2-s2.0-0008494528.
10.1016/0167-2789(85)90011-9
CAS Web of Science® Google Scholar
44 Li C., Sprott J. C., Thio W., and Zhu H., A New Piecewise Linear Hyperchaotic Circuit, IEEE Transactions on Circuits and Systems II: Express Briefs. (2014) 61, no. 12, 977–981, https://doi.org/10.1109/tcsii.2014.2356912, 2-s2.0-84914682972.
10.1109/tcsii.2014.2356912
Web of Science® Google Scholar
45 Li C. and Sprott J. C., Variable–Boostable Chaotic Flows, Optik. (2016) 127, no. 22, 10389–10398, https://doi.org/10.1016/j.ijleo.2016.08.046, 2-s2.0-84983738931.
10.1016/j.ijleo.2016.08.046
Web of Science® Google Scholar
46 Mujumdar A., Kurode S., and Tamhane B., Control of Two Link Flexible Manipulator Using Higher Order Sliding Modes and Disturbance Estimation, IFAC Proceedings Volumes. (2014) 47, no. 1, 95–102, https://doi.org/10.3182/20140313-3-in-3024.00055, 2-s2.0-84899563980.
10.3182/20140313-3-IN-3024.00055
Google Scholar
47 Pati T. and Yong S. Z., Robust Control Barrier Functions for Control Affine Systems With Time-Varying Parametric Uncertainties, IFAC-PapersOnLine. (2023) 56, no. 2, 10588–10594, https://doi.org/10.1016/j.ifacol.2023.10.679.
10.1016/j.ifacol.2023.10.679
Google Scholar

All articles

Dynamics and Robust Synchronization of an Oscillator With Cubic and Signum Terms

Abstract

1. Introduction

2. An Elegant Oscillator