An Advanced DNA-Inspired Gray Wolf Algorithm for Kinetic Parameter Estimation in Supercritical Water Oxidation
Abstract
Inspired by the genetic evolution mechanism of DNA, a hybrid DNA Gray Wolf Optimizer (hDNA-GWO) is proposed to develop an accurate kinetic model. This algorithm incorporates innovative DNA encoding, selection, crossover, and mutation operators inspired by genetic processes. We adopt the roulette-wheel method to select individuals with greater environmental adaptability from the current population to form the next population. The crossover operation involves swapping gene segments between paired chromosomes to create new individuals and maintain the population diversity. The mutation operator can maintain the diversity of the population, avoid the phenomenon of “premature” convergence, and effectively improve the local search capability. The performance of hDNA-GWO is investigated on typical benchmark functions compared to GWO, PSO, GWO-PSO, and GWO-GA. In addition, the superior search capabilities of our model are validated by kinetic parameter estimation using experimental data from supercritical water oxidation processes. The results indicate that the hDNA-GWO can overcome premature convergence and obtain higher-quality global optimal solutions.
1. Introduction
As industrial activity and agricultural production have increased, so has environmental pollution, particularly in the treatment of wastewater, gases, and residues. This is particularly challenging for organic wastewater, where traditional biological methods struggle to remove heavy metals and physical and chemical techniques often fall short of expected results. In this context, supercritical water oxidation (SCWO) technology has emerged as a promising solution for sewage treatment because of its high conversions and broad applicability. SCWO is an advanced technology that uses Super Critical Water to oxidize and break down hazardous organic materials. It is particularly effective in treating a wide range of waste streams, including industrial wastewater, hazardous chemicals, and even certain types of municipal solid waste. SCWO offers an efficient, environmentally friendly alternative to traditional waste treatment methods by utilizing the unique properties of water at supercritical conditions. Water becomes supercritical when heated above its critical temperature of 374°C and pressure of 22.06 MPa. At this point, water exhibits unique properties that differ from its liquid and gas phases. In particular, supercritical water behaves like a dense gas with high diffusivity and low viscosity, while retaining the solvating power of a liquid. These properties make SCW a powerful medium for chemical reactions, especially oxidation processes. The SCWO technology uses supercritical water as a medium for oxidation reactions, where oxygen (usually in the form of pure oxygen or air) is introduced to react with organic waste in the supercritical water environment. The process takes place at high temperatures and pressures, typically around 400°C–650°C and 22–30 MPa. The oxidation reactions occur due to the combined effects of (1) high temperature: accelerates the oxidation reactions and promotes the breakdown of complex organic molecules, (2) High pressure: ensures that water remains in its supercritical state, which is critical for maintaining high reaction rates and achieving a near-complete oxidation. The primary reaction in SCWO is the oxidation of organic materials to form carbon dioxide (CO2), water (H2O), and other nontoxic byproducts (e.g., mineral salts, if present). These reactions effectively broke down the organic compounds into simple molecules, leaving little or no waste. Under the action of supercritical water, SCWO has very powerful oxidation abilities, excellent diffusion, and effective solubility for organic materials. This results in over 99% COD removal from organic wastewater and sludge within a comparatively short reaction time, making SCWO a perspective technique for the dealing with organic pollutants in the forestry sector. The study of organic oxidation kinetics in supercritical water is a meaningful work, and the accurate estimation of kinetic parameters is essential to elucidate the mechanism of SCWO so as for the convenience of industrial application. Parameter estimation is fundamentally a kind of complex optimization problem, aiming to fit the dynamic model closely to the experimental data. However, the optimization process in SCWO kinetics is complex, involving high-dimensional, nonlinear features with multiple potential local optima. Traditional gradient-based optimization methods, such as Newton [1], quasi-Newton, and conjugation direction methods [2], are prone to local extreme point and rely heavily on initial conditions.
Inspired from natural phenomenon such as biological mechanisms, evolutionary behavior, and foraging behavior, metaheuristic algorithms have gained popularity among researchers and scientists as an effective alternative due to their simplicity, efficiency, and broader applicability in tackling such complex problems. The more common algorithms among them are genetic algorithm (GA) [3], differential evolution (DE) [4], particle swarm optimization (PSO) [5], cuckoo search (CS) [6], gray wolf optimizer (GWO) [7], ant lion optimizer (ALO) [8], and sparrow search algorithm (SSA) [9]. Researchers have applied these metaheuristic algorithms to tackle various optimization problems such as production scheduling, dynamic transportation, and slope monitoring problems [10–12]. The GWO, introduced by Mirjalili et al. in 2014, is particularly notable for its popularity. It adapts the hierarchical structure and hunting strategy of gray wolves into an optimization framework and is famous for its simplicity, minimal parameter requirements, and ease of implementation. Lots of achievements had demonstrated the superior performance of GWO compared to that of DE, PSO, and GA.
The basic GA uses binary chromosome strings to represent variables in optimization problems, which evolve toward optimal solutions through selection, crossover, and mutation over successive generations. This process mirrors the genetic manipulation of biological DNA, where nucleotide bases are modified in the double-helix DNA. Consequently, DNA computing models that simulate genetic mechanisms are closely related to GA concepts, leading to advances in swarm intelligence optimization algorithms based on genetic operations. Introducing molecular concepts into metaheuristic algorithms had been proven to be feasible and effective methods, as demonstrated by Tao and Wang’s development of RNA-GA for chemical engineering parameter estimation [13]. This paved the way for various RNA-GA and DNA-GA models [14–18]. However, based on the theory of “no free lunch,” there is no such single optimal algorithm that is universally applicable. Improving the balance between the exploitation and exploration, meanwhile increasing search efficiency in GWO remains a major challenge. Up to date, the integration of DNA molecular operations with GWO has been relatively unexplored, with notable exceptions such as Liu’s work [19]. This thesis introduces a novel hybrid DNA-GWO algorithm that incorporates DNA crossover and mutation operators. Compared with the literature [14–18], the innovation of this paper is that new crossover and mutation operators are presented in the modified basic GWO. These innovations are designed to increase population diversity and escape local optima, especially in later search stages. The algorithm is applied to optimize kinetic parameter estimation in SCWO, with comparative studies against standard GWO PSO, GWO-PSO, and GWO-GA to establish its effectiveness.
The structure of the paper is arranged to firstly collate the related work in Section 2, and secondly, the basic principles of the gray wolf algorithm are discussed in Section 3. The newly developed DNA crossover and mutation operators are then described in Section 4, along with the introduction of the hybrid DNA-GWO algorithm. Section 5 presents the numerical simulations and comparative analyses between GWO and other optimization algorithms by considering different benchmark functions. Section 6 demonstrates the application of the hybrid DNA-GWO algorithm for parameter estimation in SCWO. Finally, Section 7 concludes with a summary of the results and contributions of the work.
2. Related Work
2.1. GWO Algorithm and Its Application
Among the many metaheuristic algorithms, the GWO algorithm has been successfully applied to solve various types of optimization problems due to its many advantages. Firstly, it does not require gradient information of the problem, making it applicable to nonlinear, high-dimensional, unconstrained or constrained complex optimization problems. Secondly, the computational process of GWO is simple and easy to implement and has a fast convergence speed. Furthermore, the global search capability of the GWO is strong. However, like other optimization algorithms, GWO faces challenges such as balancing exploitation and exploration, maintaining population diversity, and avoiding premature convergence [20]. To address these issues, researchers have explored various extensions. For example, Luo et al. [21] introduced an advanced version of GWO that incorporates complex-valued encoding to improve its search efficiency. Madhiarasan [22] simplified the wolf hierarchy to three levels, resulting in a reduced computational complexity and faster convergence. Gao and Zhao’s VM-GWO [23], based on the notion that wolf social hierarchies influence their search behavior, provided a unique perspective. Saxena [24] introduced a novel position update strategy incorporating a sinusoidal mechanism, tournament selection, crossover, and mutation, which enhanced E-GWO and improved the search performance, particularly in the multipeak function although challenges remained in unimodal problems and in balancing search strategies. Further developments included Mohammad et al.’s dimension learning-based hunting (DLH) strategy [25], which promotes information sharing among search agents, ensuring diverse populations and balanced global-local searches. The trend of hybridizing GWO with other metaheuristic algorithms has gained traction. For instance, GWO-PSO [26] combines the strengths of GWO and PSO, and GWOSCW [27] combines GWO with the sine cosine algorithm (SCA). Gaidhane et al. [28] developed a GWO-ABC, which combines GWO with the artificial bee colony (ABC) algorithm, while Bouchair [29] developed a HS-GWO to tackle virtual network embedding problems. In addition, the synergy of GWO with GA has also shown promise in improving optimization performance by exploiting their respective strengths to mitigate their weaknesses. The application of these GWO-GA hybrids has been successful in areas such as improving intrusion security in IoT wireless networks [30], assessing the likelihood of soil liquefaction [31], and improving the efficiency of combined solar and wind energy systems [32].
In addition, the researchers have successfully applied GWO to solve other types of optimization problems, such as hyperparameter tuning of machine learning models, data prediction, combinatorial optimization problems, multiobjective problems, and scheduling problems. Kapoor [33] transformed GWO into a clustering algorithm and applied it to calculate the davies bouldin (DB) index and the average intercluster distance, and the average intracluster distance between two satellite images calculated has higher precision. In the field of data prediction, the GWO-SVM prediction model [34] was proposed and the GWO was used to adjust the parameters of support vector machines (SVMs), the overall average absolute error of the model achieved only 3.2%. Mahmoodzadeh et al. [35] utilized GWO to optimize the hyperparameters of long short-term memory (LSTM) networks and applied it to estimate the performance reliability of tunnel boring machines. Sulaiman [36] solved the reactive power scheduling problem in power systems with the help of GWO. The iteration strategy and GWO were used to train neural networks and achieved good results in solving the position tracking control of servo system in [37].
According to the above achievements, the GWO had proved to achieve better results in various engineering practices, especially in the parameter tuning problem of nonlinear systems. Therefore, further research on the application of GWO has great significance for expanding the application area of GWO.
2.2. DNA Genetic Algorithm
In 1994, Professor Aldeman from the University of Southern California published a pioneering paper on DNA computing in Science. By using biochemical experimental methods, he solved a 7-node Hamiltonian path (HP) problem, and for the first time, a completely new computing model called DNA computing was proposed. Researchers have discovered that DNA computing can simulate the genetic information expression mechanisms of biological organisms, and further proposed the DNA GA because various biochemical reactions of biological molecules are used to perform the computational processes in DNA computing. Due to the numerous advantages of DNA GAs, many scholars conducted extensive research and discussion on DNA GA. In [38], the author put forward a DNA GA based on DNA computing and GAs for the identification problem of fuzzy neural networks (FNNs), which accelerated the training of FNN. An innovative GA based on DNA encoding methods was proposed and applied to the optimization design process of TS fuzzy control systems in [39]. In a different study presented in [40], the authors proposed a hybrid DNA GA based on the (μ, λ) evolutionary strategy by combining the population update operation of the evolutionary and self-adaptive strategies of the parameter interval with the DNA-GA operators, and the efficiency of the proposed method was validated by solving the benchmark function and the actual parameter estimation problem. Benefiting from the genetic mechanism of biological DNA molecules and chaotic optimization algorithms, the authors in [17] proposed a chaotic DNA GA to optimize the parameters of TS fuzzy recursive neural network for modeling the pH neutralization process.
DNA GA is more suitable for simulating biological genetic and evolutionary processes because of the advantages of GA and the incorporation of DNA’s genetic information expression mechanism, which is of great significance for solving the modeling and optimization problems of complex chemical processes. Inspired by the above, this paper designs an advanced GWO by improving the structure of the algorithm and the operator manipulation of the DNA molecule, to assist the GWO to achieve a more efficient search.
3. Basic GWO (BGWO)
The BGWO algorithm, introduced by Mirjalili in 2014, is a newly discovered heuristic optimization method inspired by the hunting practices and social structures observed in gray wolves. Central to BGWO is its simulation of the wolves’ social hierarchy. At the top of this hierarchy are the alphas, who guide all wolves in various activities including hunting and settling. Next in line are the betas, who help the alphas make decisions and often succeed them as leaders in the event of old age, illness, or death. Below the betas are the deltas, who follow the directives of both alphas and betas. At the bottom of the hierarchy are the omegas, who are guided and influenced by the decisions and actions of the higher-ranking wolves.
Each individual’s performance is assessed, and then the results are classified into four levels. The optimum solution is designated as the alpha (α), following by the beta (β) and delta (δ) for the second and third best solutions, respectively. All other solutions are categorized as omega (ω).
3.1. Encircling
In this equation, and are the random vectors ranging from 0 to 1, and T represents the maximum number of iterations. The value of a gradually diminishes from 2 to 0 throughout the course of the iterative process.
3.2. Hunting
In this formulation, , , and represent the positions of the alpha, beta, and delta wolves, respectively. denotes the operation for the final location update. The terms and are analogous to those defined in equations (2) and (3).
3.3. Attacking
When the hunting sequence concludes, the wolves initiate their attack on the prey. This phase is simulated by the parameter a, which governs both the exploitation and the exploration phases by gradually decreasing from 2 to 0. As indicated in equation (2), is a random vector within the range [−a, a], constrained by the absolute magnitude of a. A scenario where signifies that the wolves diverge from the prey to explore new search areas. On the other hand, a situation where depicts the wolves converging toward the prey, symbolizing a more targeted approach.
The pseudocode of the BGWO algorithm is shown as follows (see Algorithm 1).
-
Algorithm 1: The pseudocode of the BGWO algorithm.
-
Initialize the population with size N and dimension D;
-
Set up the a variable and both the A and C vectors;
-
Calculate the fitness of each individual, where Xα, Xβ, and Xδ represent the current best, second best, and third best individuals;
-
While (t < T)
-
For each search agent
-
Update the position of the current search agent by equation (5)
-
End for
-
Update a and vectors A and C;
-
Compute the suitability of all revised entities;
-
Update Xα, Xβ, and Xδ
-
t = t + 1
-
End while
-
Return Xα.
4. hDNA-GWO Algorithm
The genetic information of living organisms is encoded in the form of codes on DNA molecules, which are transmitted from parents to offspring through DNA replication prior to cell division. In the process of expressing genetic information, DNA molecules perform a variety of gene-level operations in the presence of biological enzymes; these operations can more effectively simulate the genetic evolution process of organisms. Inspired by the biological background of DNA computing, we believe that the rich genetic information manipulation of DNA can promote the GWO to further simulate the expression mechanism of individual genetic information, thereby improving the performance of the algorithm. For the sake of improving search efficiency of the BGWO, innovative stem-loop crossover and mutation operator have been developed and integrated. This section introduces the updated version of the algorithm, called hDNA-GWO, and outlines its specific features and mechanisms.
4.1. Encoding and Decoding of DNA
In this expression, f(x) represents the objective function, x = [x1, x2, …, xn] and xj denote j th variables subject to optimization, and [xjmin, xjmax] are the defined bounds for the variable xj.
In implementing the hDNA-GWO algorithm for universal optimization, we initially establish the representations of candidate solutions. Each solution is visualized as a chromosome, akin to a DNA strand in biology. It is well-known that a typical DNA sequence is composed of four nucleotides. For computational efficiency, we use integers E = {0, 1, 2, 3}L to denote E = {C, T, A, G}L, where L signifies a DNA sequence length. We propose that each variable xj is encoded as a substring with a specific encoding length L. Consequently, a solution with n is encoded as a chromosome comprising a total length of n × L.
Accordingly, the decoding process can be described by the following formulation.
4.2. Crossover Operators
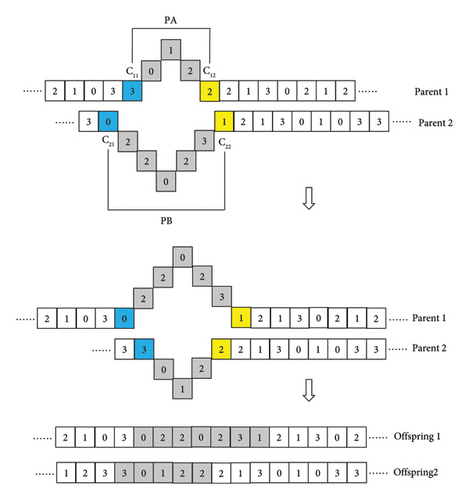
In evolutionary algorithms, the crossover operator is crucial for generating new individuals and is key to the algorithm’s global search capability. A pair of children is produced by swapping segments of the chromosomes, a process determined by the random selection of two parent individuals. The common crossover methods, for instance, single-point, multipoint, and uniform crossover, are often inadequate for complex challenges. To address this, we have developed an innovative crossover operator using operation-based DNA molecular to strengthen the global searching efficiency in the hDNA-GWO algorithm.
-
Step 1: Initially, a quaternary encoding is conducted on two randomly selected positions of the parent gray wolfs, each corresponding to a DNA nucleotide E = {C, T, A, G}. To keep simple, each string of digital code comprises 16 bits.
-
Step 2: A crossover site C11 is stochastically chosen within the range [1, L − 1] in parent one, where L represents the individual coding length. A corresponding search is then carried out in parent two, starting from the first position until a complementary base C21 is located.
-
Step 3: If an acceptable C21 remains undiscovered, the process in step 2 is repeated until success, followed by progressing to step 4.
-
Step 4: Another crossover point, C12, is randomly determined within the interval [C11 + 1, L] in parent 1. The search then continues from position C21 + 1 in parent 2 until a matching complementary base C22 is discovered.
-
Step 5: If the satisfactory C22 remains elusive, the search from step 4 is repeated until a match is found, leading to step 6.
-
Step 6: The section between C11 and C12 is labeled as PA, whereas the section between C21 and C22 is labeled as PB.
-
Step 7: The segments between PA and PB are then swapped between the two parent individuals, resulting in offspring one and offspring two.
-
Step 8: Should the offspring differ in length, the excess portion of the longer offspring is trimmed and appended to the beginning of the shorter one.
An illustrative case about this crossover operation is depicted in Figure 1.
4.3. Mutation Operators
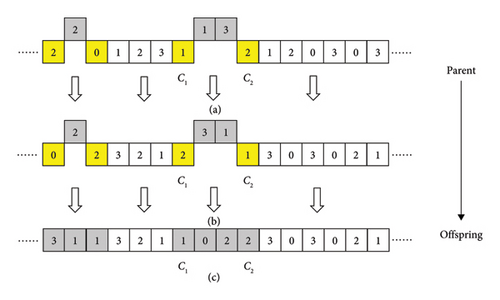
In the BGWO algorithm, the hunting (or optimization) process is primarily driven by the three best leading agents—the alpha, beta, and delta wolves—with the remaining agents (the omega wolves) following their lead. However, this approach can converge toward a local optimum as the iterations advance, causing other individuals to increasingly follow this local peak, potentially leading to suboptimal global solutions. Merely relying on the crossover operation may not be sufficient to address this issue. To counteract this, a mutation operator, inspired by DNA molecule mutations, is integrated into the hDNA-GWO algorithm. This operator aims to preserve population diversity and boost local search capabilities.
-
Step 1: As an initial step in the mutation operator, a quaternary encoding is carried out. This involves randomly selecting a position in the gray wolf’s genetic makeup to correspond with a DNA nucleotide E = {C, T, A, G}. Each digital code string in this process comprises 16 bits for simplification.
-
Step 2: Label the initial bit of the digital code string as C1 = 1.
-
Step 3: Initiate a search in the parent for the first complementary base C2 from C1 + 1.
-
Step 4: If the satisfactory C2 is not located, adjust C1 = C1 + 1 and repeat the search in step 3 until it is found, then move to step 5.
-
Step 5: Invert the sequence of DNA bases located between C2 and C2.
-
Step 6: Substitute the DNA bases in the range between C2 and C2 with their respective complementary bases.
-
Step 7: Set C1 = C2 + 1.
-
Step 8: Apply steps 3 to 7 for each individual in the population until the iteration completes for the maximum designated position.
4.4. The hDNA-GWO Algorithm
- •
dk,ij = 0 represents chromosome i that shares all of its genes with chromosome j at site k.
- •
dk,ij = 0.25 represents chromosome i that shares a quarter of its genes with chromosome j at site k.
- •
dk,ij = 0.5 represents chromosome i that shares a half of its genes with chromosome j at site k.
- •
dk,ij = 0.75 represents chromosome i that shares three-fourths of its genes with chromosome j at site k.
- •
dk,ij = 1 represents chromosome i that shares none of its genes with chromosome j at site k.
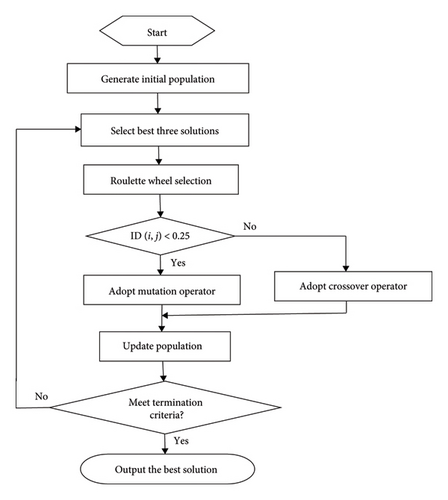
-
Step 1: Define the algorithm’s parameters, including the population size N, the maximum evolutionary generations T, the scale of the optimization issue D, and the coding length L of each individual.
-
Step 2: Create an initial population of N individuals using quaternary DNA encoding.
-
Step 3: Evaluate the suitability score of each individual utilizing the designated fitness function and rank them based on their fitness scores. Label the top three parameters as Xα, Xβ, and Xδ.
-
Step 4: Implement tournament selection to produce N new individuals and then sort the individuals according to their fitness. Conduct mutation operations on those individuals while the difference degree between them is less than 0.25, instead, conducted by crossover operations on the individuals in pairs.
-
Step 5: Modify the location of each individual as per equations (5) and (6) and adjust the coefficients C and A;
-
Step 6: Iterate through steps 3–5 until the termination criteria are fulfilled, at which point the optimal solution is identified.
4.5. Complexity Analysis
According to the execution steps of GWO, the time complexity depends on the population size Ng, the maximum evolutionary generations Tg, and the scale of the optimization issue Dg. Considering fitness evaluation, position update, and sorting the fitness, the total time complexity of GWO is O(Ng × Tg × Dg). Similarly, the time complexity of PSO depends on the number of particles in the swarm Np, the maximum evolutionary generations Tp, and the scale of the optimization issue Dp. The total time complexity of PSO is O(Np × Tp × Dp). The main difference of time complexity between GWO and hDNA-GWO is that the hDNA-GWO contains mutation operator or crossover operator. Assume the coding length of each individual is L, we can obtain the total time complexity of hDNA-GWO as O(L × Ng × Tg × Dg); hence, the time complexity of hDNA-GWO is L times as great as GWO and PSO.
The space complexity of the algorithm depends on the population size and problem’s dimension; however, none of those parameters change when solving the optimization problem regardless of the GWO, PSO, or hDNA-GWO algorithm. Therefore, the GWO and hDNA-GWO have the same space complexity of O(Ng × Dg). The space complexity of the PSO is O(Np × Dp).
5. Quantitative Trials and Outcomes
To determine the validity of the hDNA-GWO algorithm, nine selected benchmark functions are used for numerical simulation testing. Table 1 lists all functions with their search spaces and minimum values. These functions are categorized into three groups: unimodal, multimodal and fixed-dimension multimodal functions.
| Attributes | Formulas | Range | Dim | Optima |
|---|---|---|---|---|
| Unimodal | [−100, 100] | 30 | 0 | |
| [−100, 100] | 30 | 0 | ||
| [−10, 10] | 30 | 0 | ||
| Multimodal | [−5.12, 5.12] | 30 | 0 | |
| [−500, 500] | 30 | −418.9829∗n | ||
| [−32, 32] | 30 | 0 | ||
| Fix-dimension multimodal | [−65, 65] | 2 | 1 | |
| [−5, 5] | 4 | 0.00030 | ||
| [0, 10] | 4 | −10.1532 | ||
- ∗means multiplication.
For a fair comparison of the hDNA-GWO, the standard GWO, PSO, GWO-PSO, and GWO-GA have been carried out to work with identical test functions and parameter configurations: the population size is N = 30, and a predefined maximum iteration is T = 500. Each algorithm was run independently on each benchmark function 20 times. Table 2 presents the results, showcasing the optimal, average, and standard values, with the top optimization results highlighted in bold for clarity.
| F | GWO | PSO | GWO-PSO | GWO-GA | hDNA-GWO | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| f1 | 9.13E − 28 | 1.48E − 27 | 1.44E − 04 | 1.49E − 04 | 3.34E + 03 | 8.92E + 03 | 4.45E − 27 | 5.48E − 27 | 4.34E − 54 | 1.52E − 53 |
| f2 | 9.96E − 06 | 1.87E − 05 | 8.14E + 01 | 3.26E + 01 | 5.16E + 03 | 1.19E + 04 | 6.53E − 05 | 2.48E − 04 | 5.90E − 06 | 9.75E − 06 |
| f3 | 1.04E − 16 | 7.91E − 17 | 1.15E − 01 | 8.10E + 00 | 3.38E + 01 | 1.04E + 02 | 1.36E − 16 | 7.89E − 17 | 1.25E − 29 | 1.63E − 29 |
| f4 | 4.19E + 00 | 2.92E + 00 | 1.07E + 02 | 2.49E + 01 | 1.15E + 02 | 1.14E + 02 | 2.46E + 00 | 3.65E + 00 | 4.02E − 01 | 1.20E + 00 |
| f5 | −6.66E + 03 | −6.09E + 03 | −4.64E + 03 | 1.21E + 03 | −7.27E + 03 | 8.07E + 02 | −6.00E + 03 | 8.74E + 02 | −8.09E + 03 | 1.08E + 03 |
| f6 | 1.08E − 13 | 1.60E − 14 | 9.05E − 02 | 3.33E − 01 | 4.32E + 00 | 5.40E + 00 | 1.12E − 13 | 1.41E − 14 | 1.33E − 14 | 2.70E − 15 |
| f7 | 3.94E + 00 | 3.86E + 00 | 2.77E + 00 | 2.95E + 00 | 4.13E + 00 | 4.22E + 00 | 4.52E + 00 | 4.28E + 00 | 1.10E + 00 | 4.44E − 01 |
| f8 | 4.43E − 03 | 8.15E − 03 | 3.64E − 03 | 6.40E − 03 | 3.47E − 03 | 7.30E − 03 | 4.48E − 03 | 8.15E − 03 | 1.41E − 03 | 4.47E − 03 |
| f9 | −9.27E + 00 | 2.20E + 00 | −6.27E + 00 | 3.39E + 00 | −6.12E + 00 | 3.49E + 00 | −9.14E + 00 | 2.07E + 00 | −9.39E + 00 | 1.86E + 00 |
- Note: The bold values indicate the optimal results compared with other algorithms.
Observations from Table 2 show that the best solutions of the hDNA-GWO algorithm are comparable to those of the standard GWO, GWO-PSO, and GWO-GA algorithms and much better than PSO in solving all the benchmark functions. It is worth noting that unimodal functions and simple multimodal functions are well suited for benchmarking exploitation. The hDNA-GWO is also capable of providing highly competitive results on fix-dimension multimodal functions f6-f9 in terms of the average value and standard deviation.
Figure 4 shows the convergence characteristics of GWO, PSO, GWO-PSO, GWO-GA, and hDNA-GWO algorithms. It can be observed that the hDNA-GWO algorithm exhibits higher convergence accuracy when compared to the GWO, PSO, GWO-PSO, and GWO-GA and faster convergence speed, especially for the multimodal and fix-dimension multimodal benchmark functions. This is primarily because with the assistance of the newly developed crossover and mutation operation strategy, the hDNA-GWO is able to skip the local optimum solution even during the intermediate and final stages.
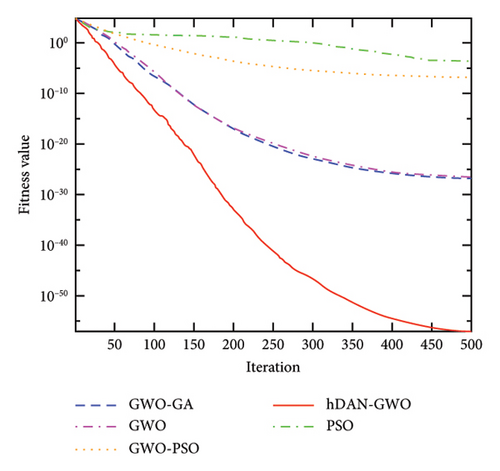
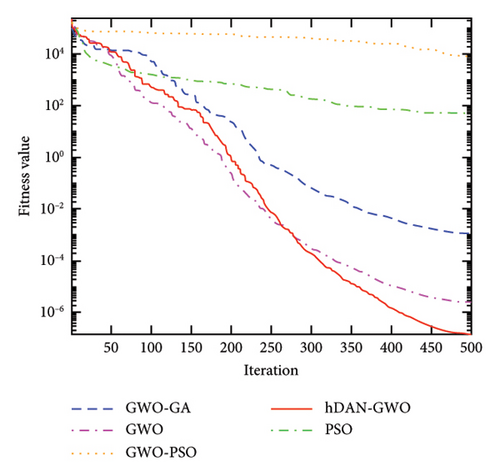
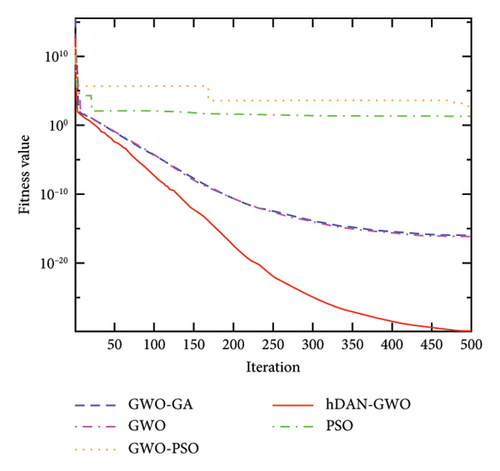
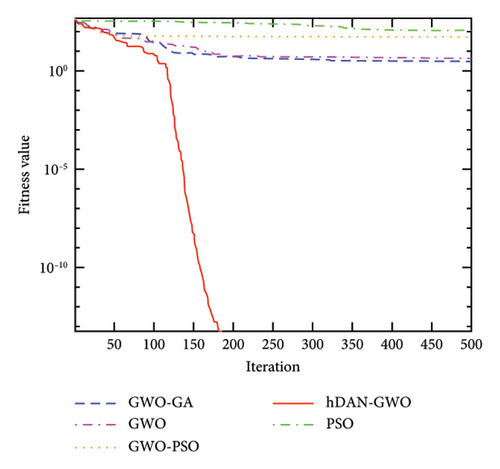
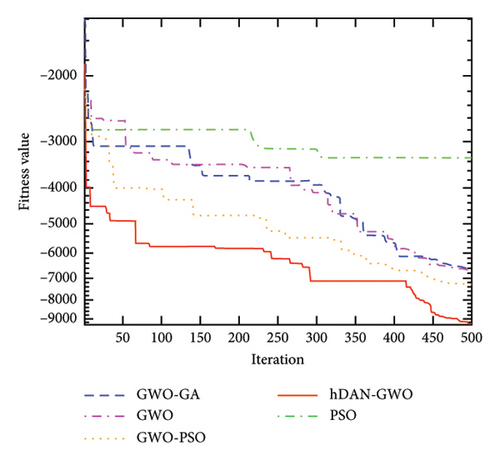
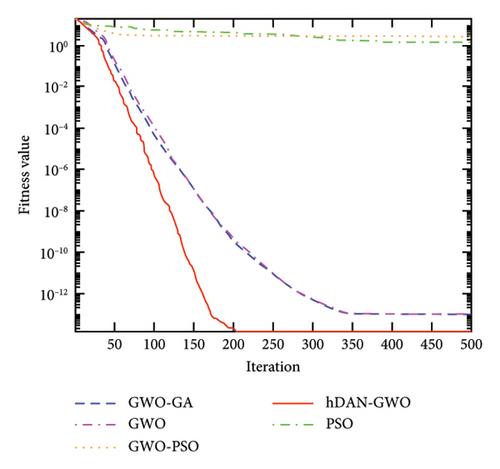

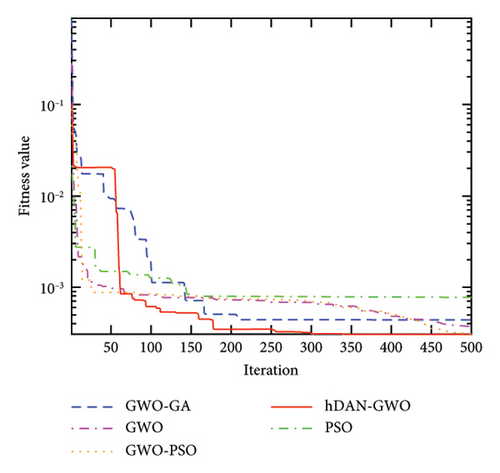
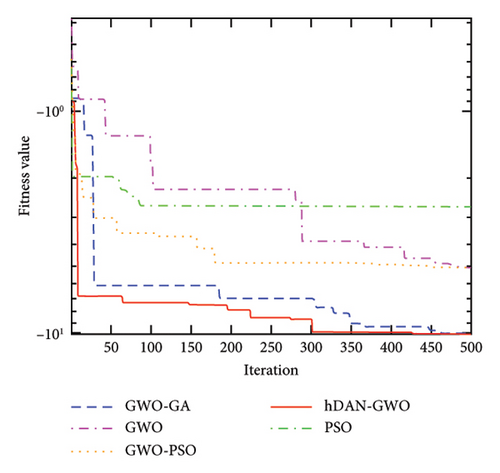
All the above analysis results demonstrate that the hDNA-GWO algorithm is more accurate in identifying global optima. This underscores the effectiveness of the hDNA-GWO algorithm, making it a powerful tool for tackling complex functional optimization challenges.
6. Utilizing hDNA-GWO to Estimate Parameters of 2-CP in SCWO
6.1. Overview of 2-CP in SCWO
In this formula, Rate symbolizes the rate of reaction, while [2CP], [O2] and [H2O] denote the concentrations of 2-CP, O2, and H2O, respectively. The corresponding reaction orders are represented by a, b, and c. A refers to the preexponential factor. Ea refers to the activation energy. T represents the temperature at which the reaction occurs. τ represents the duration of the reaction within the system, and R denotes the universal gas constant (8.314J·(mol·k)−1).
6.2. Result Analysis
The reaction of SCWO involves multiple chemical reaction stages and reactants. The estimation of kinetic parameters for SCWO reactions is essentially an optimization problem that is high-dimensional and contains multiple local extrema. Therefore, in this part of the study, we used the proposed hDNA-GWO method for estimating the kinetic parameters in SCWO. We used a dataset containing experimental data from 62 samples provided in [41] as shown in Table 3, which includes variables such as pressure P, temperature T, reaction time τ, and concentrations of [2CP], [O2], [H2O], and X. This dataset served as the training ground to assess the validity of the hDNA-GWO algorithm. Additionally, for a comparative perspective, we also optimized the parameters by applying the standard GWO, PSO, GWO-PSO, and GWO-GA algorithms and using the identical dataset. According to the results presented in Table 4, the hDNA-GWO achieved an optimal objective function value of 0.122, surpassing the results of the basic GWO, PSO, GWO-PSO, and GWO-GA algorithms.
| T (°C) | P (atm.) | τ (s) | 2CP (Conc.M) | O2 (Conc.M) | H2O (Conc.M) | X |
|---|---|---|---|---|---|---|
| 300 | 278 | 14.6 | 5.99 × 10−4 | 4.12 × 10−2 | 41.51 | 24.3 |
| 330 | 278 | 13.6 | 5.51 × 10−4 | 3.79 × 10−2 | 38.20 | 29.5 |
| 360 | 278 | 11.8 | 4.85 × 10−4 | 3.33 × 10−2 | 33.61 | 31.0 |
| 380 | 185 | 13.2 | 8.03 × 10−5 | 5.49 × 10−3 | 5.71 | 8.6 |
| 380 | 205 | 17.7 | 1.04 × 10−4 | 7.12 × 10−3 | 7.40 | 16.7 |
| 380 | 219 | 19.0 | 1.32 × 10−4 | 8.99 × 10−3 | 9.28 | 23.6 |
| 380 | 225 | 22.9 | 1.56 × 10−4 | 1.06 × 10−2 | 10.97 | 41.1 |
| 380 | 225 | 26.8 | 1.54 × 10−4 | 1.05 × 10−2 | 10.97 | 60.6 |
| 380 | 232 | 34.5 | 2.28 × 10−4 | 1.55 × 10−2 | 15.97 | 72.1 |
| 380 | 246 | 24.1 | 3.42 × 10−4 | 2.57 × 10−2 | 24.22 | 65.2 |
| 380 | 260 | 27.1 | 3.77 × 10−4 | 2.89 × 10−2 | 26.96 | 67.5 |
| 380 | 278 | 20.4 | 3.19 × 10−4 | 1.07 × 10−2 | 28.42 | 45.7 |
| 380 | 278 | 35.1 | 3.28 × 10−4 | 9.63 × 10−3 | 28.42 | 62.0 |
| 380 | 278 | 49.2 | 3.70 × 10−4 | 1.01 × 10−2 | 28.42 | 76.0 |
| 380 | 278 | 69.8 | 3.26 × 10−4 | 9.76 × 10−3 | 28.42 | 85.2 |
| 380 | 278 | 5.9 | 3.86 × 10−4 | 2.97 × 10−2 | 28.42 | 17.2 |
| 380 | 278 | 10.2 | 4.00 × 10−4 | 2.87 × 10−2 | 28.42 | 23.4 |
| 380 | 278 | 21.1 | 4.02 × 10−4 | 3.02 × 10−2 | 28.42 | 59.0 |
| 380 | 278 | 32.8 | 3.76 × 10−4 | 3.22 × 10−2 | 28.42 | 76.4 |
| 380 | 278 | 44.4 | 3.84 × 10−4 | 3.02 × 10−2 | 28.42 | 88.9 |
| 380 | 278 | 59.1 | 3.95 × 10−4 | 3.08 × 10−2 | 28.42 | 98.6 |
| 380 | 278 | 19.9 | 9.90 × 10−4 | 3.76 × 10−2 | 28.42 | 57.5 |
| 380 | 278 | 34.0 | 1.03 × 10−3 | 3.50 × 10−2 | 28.42 | 74.1 |
| 380 | 278 | 47.3 | 1.04 × 10−3 | 3.47 × 10−2 | 28.42 | 93.2 |
| 380 | 278 | 59.6 | 1.04 × 10−3 | 3.65 × 10−2 | 28.42 | 98.5 |
| 380 | 278 | 7.2 | 1.41 × 10−3 | 3.60 × 10−2 | 28.42 | 19.1 |
| 380 | 278 | 29.6 | 1.55 × 10−3 | 3.64 × 10−2 | 28.42 | 68.9 |
| 380 | 278 | 40.2 | 1.60 × 10−3 | 3.58 × 10−2 | 28.42 | 82.4 |
| 380 | 278 | 50.1 | 1.48 × 10−3 | 3.74 × 10−2 | 28.42 | 93.6 |
| 380 | 278 | 58.6 | 1.57 × 10−3 | 3.61 × 10−2 | 28.42 | 99.0 |
| 380 | 278 | 69.5 | 1.64 × 10−3 | 3.53 × 10−2 | 28.42 | 98.6 |
| 380 | 278 | 3.6 | 1.95 × 10−3 | 4.09 × 10−2 | 28.42 | 9.2 |
| 380 | 278 | 5.2 | 1.98 × 10−3 | 4.29 × 10−2 | 28.42 | 11.4 |
| 380 | 278 | 7.3 | 2.05 × 10−3 | 4.19 × 10−2 | 28.42 | 13.2 |
| 380 | 278 | 10.1 | 2.03 × 10−3 | 3.97 × 10−2 | 28.42 | 18.9 |
| 380 | 278 | 13.9 | 2.04 × 10−3 | 4.20 × 10−2 | 28.42 | 34.7 |
| 380 | 278 | 18.6 | 2.13 × 10−3 | 3.80 × 10−2 | 28.42 | 46.7 |
| 380 | 278 | 24.7 | 2.07 × 10−3 | 3.88 × 10−2 | 28.42 | 54.7 |
| 380 | 278 | 29.5 | 2.04 × 10−3 | 4.07 × 10−2 | 28.42 | 67.2 |
| 380 | 278 | 33.9 | 2.15 × 10−3 | 3.77 × 10−2 | 28.42 | 69.1 |
| 380 | 278 | 40.0 | 2.09 × 10−3 | 3.99 × 10−2 | 28.42 | 78.7 |
| 380 | 278 | 49.5 | 1.97 × 10−3 | 4.14 × 10−2 | 28.42 | 82.1 |
| 380 | 278 | 57.4 | 2.12 × 10−3 | 3.95 × 10−2 | 28.42 | 97.1 |
| 380 | 278 | 67.5 | 2.05 × 10−3 | 4.03 × 10−2 | 28.42 | 99.7 |
| 380 | 278 | 29.4 | 1.82 × 10−3 | 1.94 × 10−2 | 28.42 | 75.4 |
| 380 | 278 | 39.7 | 1.98 × 10−4 | 1.47 × 10−2 | 28.42 | 79.5 |
| 380 | 278 | 41.0 | 2.32 × 10−4 | 1.21 × 10−2 | 28.42 | 70.9 |
| 380 | 278 | 27.9 | 2.52 × 10−4 | 1.42 × 10−2 | 28.42 | 61.0 |
| 380 | 278 | 40.5 | 3.02 × 10−4 | 7.01 × 10−2 | 28.42 | 58.3 |
| 380 | 278 | 38.4 | 4.41 × 10−4 | 4.44 × 10−2 | 28.42 | 92.2 |
| 380 | 278 | 40.9 | 5.79 × 10−4 | 3.63 × 10−2 | 28.42 | 83.5 |
| 380 | 278 | 11.4 | 6.27 × 10−4 | 3.47 × 10−2 | 28.42 | 28.4 |
| 380 | 278 | 5.8 | 6.46 × 10−4 | 3.41 × 10−2 | 28.42 | 20.7 |
| 380 | 278 | 40.5 | 8.17 × 10−4 | 2.21 × 10−2 | 28.42 | 66.4 |
| 380 | 278 | 14.7 | 1.13 × 10−3 | 3.73 × 10−2 | 28.42 | 30.4 |
| 380 | 294 | 29.9 | 4.06 × 10−4 | 3.19 × 10−2 | 29.37 | 76.0 |
| 390 | 278 | 45.2 | 3.15 × 10−4 | 2.58 × 10−2 | 23.09 | 89.1 |
| 400 | 278 | 28.1 | 1.98 × 10−4 | 1.62 × 10−2 | 14.50 | 69.7 |
| 410 | 278 | 21.6 | 1.50 × 10−4 | 1.22 × 10−2 | 10.96 | 54.4 |
| 420 | 278 | 10.0 | 5.04 × 10−4 | 1.27 × 10−2 | 9.40 | 25.4 |
| 420 | 278 | 16.9 | 5.08 × 10−4 | 1.26 × 10−2 | 9.40 | 40.7 |
| 420 | 278 | 24.0 | 5.43 × 10−4 | 1.22 × 10−2 | 9.40 | 58.1 |
| Method | A | Ea | a | b | c | fmin |
|---|---|---|---|---|---|---|
| GWO | 296.056 | 41,433.423 | 0.760 | 0.304 | 0.994 | 0.141 |
| PSO | 183.753 | 39,578.732 | 0.915 | 0.072 | 1.071 | 0.162 |
| GWO-PSO | 51.579 | 30,198.911 | 0.745 | 0.502 | 0.633 | 0.131 |
| GWO-GA | 239.158 | 37,895.244 | 0.794 | 0.358 | 0.862 | 0.134 |
| hDNA-GWO | 168.213 | 34,851.375 | 0.737 | 0.504 | 0.700 | 0.122 |
- Note: The bold value indicates the minimum value.
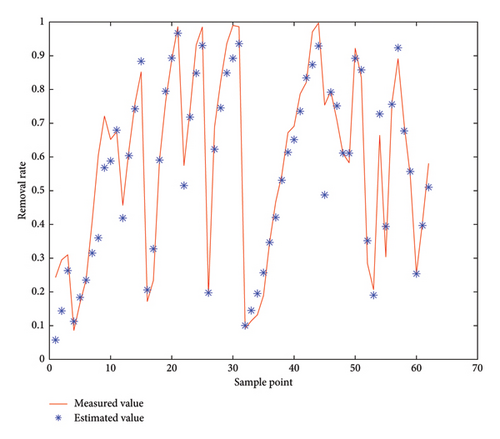
Incorporating the estimated parameters into the 2-chlorophenol kinetic model, we compared the actual measurements with the predicted results, as illustrated in Figure 5. The observations from Figure 5 clearly indicate that the output from the hDNA-GWO optimized kinetic model is in close agreement with the actual measured data.
7. Conclusions
This paper has introduced an innovative hybrid GWO algorithm that integrates DNA crossover and mutation operations. These operators are used to increase diversity within the population and to effectively navigate away from local optima. The effectiveness of this method is demonstrated by its superior performance in searching for and avoiding local optima, as demonstrated by the numerical optimization of nine classic benchmark functions. This novel algorithm is then applied to the challenge of parameter estimation in the kinetic model of SCWO reactions. The five unknown model parameters are successfully estimated. Furthermore, the measured and calculated data on the 2-CP removal rate are in good agreement, indicating that the model obtained by hDNA-GWO can accurately reflect the actual characteristics of the reaction system. Furthermore, this approach shows promise for application in several other nonlinear modeling scenarios.
As we have seen that high-performance computing (HPC) systems are essential for handling the massive amounts of data, our future focus will be on integrating HPC and hDNA-GWO to efficiently analyze large data sets and extract meaningful insights. HPC systems will enable the hDNA-GWO to run multiple instances of the algorithm simultaneously, significantly speeding up the search for optimal solutions while supporting the scalability of the hDNA-GWO, allowing it to handle larger datasets and more complex problems without significant performance degradation. Similarly, by using distributed computing systems and grid technology, the hDNA-GWO can efficiently handle large amounts of data from sensors. The parallel processing capabilities, scalability, and resource optimization provided by these technologies will enhance the performance of the algorithm, enabling faster and more accurate optimization of kinetic parameter estimation in SCWO.
Although the proposed hDNA-GWO algorithm has achieved good results, there are also some limitations that need further exploration in the future, including the following work: the paper aims at single objective optimization problem, and how to extend it to solve multiobjective optimization problem needs to be taken for further consideration. The hDNA-GWO algorithm could achieve higher accuracy, but it also results in increased running time; this is not friendly for scenarios that require shorter computation times. Seeking the balance between search accuracy and efficiency (computational complexity) is another meaningful issue.
Disclosure
This manuscript was submitted as a pre-print in the link https://www.researchgate.net/publication/367382367.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This work was supported by the Open Research Project of the State Key Laboratory of Industrial Control Technology, Zhejiang University, China (No. ICT2023B39), and the Science and Education Integration Incubation Project (No. A-0271-21-207).
Open Research
Data Availability Statement
The data and the source code of the algorithm in this paper are available upon request.




