Volume 2024, Issue 1 2910833

Research Article

Open Access

Chaotic Image Encryption Scheme Based on Improved Z-Order Curve, Modified Josephus Problem, and RNA Operations: An Experimental Li-Fi Approach

S. B. Nono Fotso

orcid.org/0000-0002-1538-8234

Department of Physics , Research Unit of Condensed Matter, Electronics and Signal Processing , University of Dschang , P.O. Box 67, Dschang , Cameroon , univ-dschang.org

Search for more papers by this author

J. H. Talla Mbé,

Corresponding Author

J. H. Talla Mbé

[email protected]

orcid.org/0000-0002-4928-6578

Department of Physics , Research Unit of Condensed Matter, Electronics and Signal Processing , University of Dschang , P.O. Box 67, Dschang , Cameroon , univ-dschang.org

Search for more papers by this author

W. N. Atchoffo,

W. N. Atchoffo

Department of Physics , Research Unit of Condensed Matter, Electronics and Signal Processing , University of Dschang , P.O. Box 67, Dschang , Cameroon , univ-dschang.org

Search for more papers by this author

A. C. Nzeukou,

A. C. Nzeukou

Department of Physics , Research Unit of Condensed Matter, Electronics and Signal Processing , University of Dschang , P.O. Box 67, Dschang , Cameroon , univ-dschang.org

Department of General and Scientific Education , Laboratory of Industrial Systems and Environmental Engineering , Fotso Victor University Institute of Technology , University of Dschang , P.O. Box 134, Bandjoun , Cameroon , univ-dschang.org

Search for more papers by this author

A. R. Ndjiongue,

A. R. Ndjiongue

orcid.org/0000-0002-7774-6164

School of Electrical and Information Engineering , Faculty of Engineering and the Built Environment , University of the Witwatersrand , Johannesburg , South Africa , wits.ac.za

Search for more papers by this author

S. B. Nono Fotso,

S. B. Nono Fotso

orcid.org/0000-0002-1538-8234

Department of Physics , Research Unit of Condensed Matter, Electronics and Signal Processing , University of Dschang , P.O. Box 67, Dschang , Cameroon , univ-dschang.org

Search for more papers by this author

J. H. Talla Mbé,

Corresponding Author

J. H. Talla Mbé

[email protected]

orcid.org/0000-0002-4928-6578

Department of Physics , Research Unit of Condensed Matter, Electronics and Signal Processing , University of Dschang , P.O. Box 67, Dschang , Cameroon , univ-dschang.org

Search for more papers by this author

W. N. Atchoffo,

W. N. Atchoffo

Department of Physics , Research Unit of Condensed Matter, Electronics and Signal Processing , University of Dschang , P.O. Box 67, Dschang , Cameroon , univ-dschang.org

Search for more papers by this author

A. C. Nzeukou,

A. C. Nzeukou

Department of Physics , Research Unit of Condensed Matter, Electronics and Signal Processing , University of Dschang , P.O. Box 67, Dschang , Cameroon , univ-dschang.org

Search for more papers by this author

A. R. Ndjiongue,

A. R. Ndjiongue

orcid.org/0000-0002-7774-6164

School of Electrical and Information Engineering , Faculty of Engineering and the Built Environment , University of the Witwatersrand , Johannesburg , South Africa , wits.ac.za

Search for more papers by this author

First published: 18 November 2024

https://doi.org/10.1155/cplx/2910833

Citations: 2

Academic Editor: Jesus Manuel Munoz-Pacheco

Share a link

Email
Wechat
Bluesky

Abstract

Image encryption schemes are predominantly software-based. Only a select few have been implemented in real-life communication systems. This paper introduces a novel chaotic image encryption scheme based on a modified Z-order curve, a modified Josephus problem, and an improved Vigenère cipher–based ribonucleic acid (RNA) operation. It is implemented and assessed within a light-fidelity (Li-Fi) infrastructure, comprising two core components: software and hardware. The software component manages data encryption and decryption, while the hardware ensures efficient data transmission. The proposed encryption scheme starts with a pixel-level permutation based on an improved Z-order curve, applicable to rectangular images, optimizing efficiency and increasing permutation ability. This is followed by a bit-level permutation using a modified Josephus problem, which enhances the diversity of generated sequences and introduces additional dislocation effects. Subsequently, a Vigenère cipher–based RNA operation serves for diffusion alongside basic RNA operations and the cipher block chaining (CBC) mode. Theoretical analyses and experimental findings demonstrate that the proposed encryption scheme is highly robust, outperforming several existing cryptosystems. Moreover, owing to its successful implementation, the proposed encryption scheme signifies a compelling stride toward bolstering secure visible light communication systems.

1. Introduction

The rapid advancement of information and communication technologies has markedly enhanced daily conveniences. The Internet facilitates the exchange of a wide array of information, yet the security of exchanged data, particularly when it is confidential, remains paramount [1, 2]. Over recent decades, encryption algorithms such as the data encryption standard (DES) and advanced encryption standard (AES) have emerged to safeguard sensitive data [3, 4]. However, these conventional schemes often prove inadequate in effectively securing images due to their inherent high correlation and data redundancy [5]. Consequently, chaos-based image encryption schemes have been introduced to address these challenges. They can be classified into several categories.

In the first category, schemes leveraging the inherent advantages of low-dimensional chaotic systems and chaotic maps, such as their high sensitivity to system parameters, their simple structure that facilitates implementation, and their high encryption rates, were proposed. For instance, in Reference [6], a medical image encryption scheme based on a one-dimensional chaotic logistic map and the generalized Arnold map was introduced. An encryption scheme based on a chaotic sequence and wavelet transform was proposed in Reference [7]. In Reference [8], an image encryption scheme based on delay-induced hyperchaos, the Arnold map, and a multishift cipher function was proposed. In Reference [9], the authors designed a visualized image encryption scheme based on a two-dimensional logistic-adjusted Chebyshev map. The authors of Reference [10] introduced a color image encryption scheme that considered the properties of color images and Latin squares. In Reference [11], the authors constructed a novel 2D cosine–sine interleaved chaotic map using two separate trigonometric functions, without composite operations. In Reference [12], the authors introduced a 1D chaotic model termed the cosine-coupled chaotic model, based on the absolute value function and the cosine function. The authors of Reference [13] presented an image encryption scheme utilizing a two-dimensional enhanced logistic modular map based on vector-level operations. In Reference [14], the authors presented a multispace confusion image encryption methodology utilizing a 2D Vincent map. This technique significantly bolstered security through the implementation of a two-stage permutation process encompassing both column and row permutations. However, image encryption schemes based on low-dimensional chaotic systems and maps [6, 7] generally exhibit lower security due to their uneven distribution, small chaotic intervals, limited key space, and inadequate randomness. This has led to the cryptanalysis of some encryption schemes [15–17]. For instance, Reference [17] proposed a chosen ciphertext attack method to break a bit-level image encryption algorithm based on chaotic maps.

To address the limitations inherent in low-dimensional systems, the second category of encryption schemes leverages high-dimensional and hyperchaotic systems, as well as their combinations. In Reference [18], a medical image encryption scheme utilizing a memristive ring neural network was presented. Reference [19] proposed a chaos-based image cryptosystem integrating Gray codes with a hyperchaotic system and an S-box. Reference [20] introduced an image encryption scheme leveraging a four-wing hyperchaotic system. In Reference [21], a multi-image encryption algorithm was introduced, utilizing a novel fractional-order 3D Lorenz chaotic system in conjunction with a 2D sinusoidally constrained polynomial hyperchaotic map. Reference [22] proposed a cross-channel color image encryption scheme to address challenges such as low disordering capability, inadequate dynamic performance, and insufficient sensitivity observed in certain schemes. Despite their advancements, these schemes remain susceptible to attacks due to inherent computational limitations [23, 24]. For instance, Reference [23] identified vulnerabilities in an encryption scheme based on the combination of multiple chaotic systems, while Reference [24] performed a cryptanalysis of a novel encryption scheme grounded in a hyperchaotic system. Consequently, the third category emphasizes enhanced confusion and diffusion mechanisms. Proposed strategies include the use of DNA coding for diffusion and confusion [20, 25], ribonucleic acid (RNA) coding for diffusion [26], zigzag transformations during the confusion phase [27], Josephus problem applications [28], space-filling curves for scrambling [29], bit-level permutation for simultaneous confusion and diffusion [30], pixel-level permutation for confusion [24], and plane-level image filtering [31]. Some of these approaches incorporate permutation and diffusion processes independent of the plaintext image, rendering them vulnerable to chosen plaintext and ciphertext attacks [32–34]. Additionally, existing encryption methods often operate at the pixel level, lacking the necessary granularity for robust security. Furthermore, while certain references, such as References [35–37], include encryption schemes implemented in real-world communication systems, many other studies lack such practical implementations, which are essential for thorough validation. Building on the preceding analysis, we introduce a novel image encryption scheme, implemented and evaluated within a straightforward two-way Li-Fi infrastructure. This novel chaotic image encryption technique is based on an improved Z-order curve, a modified Josephus problem, and a novel RNA operation. The chaotic system used in this study is the delayed Hopfield neural network (HNN), known for its capability to generate highly intricate dynamics, including hyperchaos. It boasts a substantial chaotic interval while also being cost-effective and time-efficient. The encryption procedure includes both confusion and diffusion mechanisms. First, a pixel-level permutation and a bit-level permutation are performed using the improved Z-order curve and the modified Josephus problem, respectively. Second, diffusion is achieved through a novel RNA operation based on the Vigenère cipher, combined with basic RNA operations and cipher block chaining (CBC) mode. Besides, the chaotic system is synchronized with the plain image and the computer’s timestamp via the SHA3-512 hash function, thereby increasing plain image sensitivity and unpredictability. Moreover, the key parameters of the proposed scheme are safeguarded through the RSA public key cryptosystem to achieve asymmetric encryption. The Li-Fi infrastructure comprises two components: software, designated as the Li-Fi application; and hardware, denoted as the Li-Fi modem. Li-Fi, or visible light communication (VLC), represents a wireless technology leveraging on light for data transmission from an emitter to a receiver. This technology provides many advantages including exemption from licensing fees, extensive spectrum utility, intrinsic security, health safety, energy efficiency, and cost-effectiveness. Consequently, it finds diverse applications across domains such as intelligent transportation systems, military communications, underwater communication, wireless sensor networks, and internet connectivity [38]. The contributions and innovations of this work include the following:

•
Proposing an improved Z-order curve-based permutation to address limitations observed with the standard Z-order curve-based approach. The proposed improved Z-order curve is versatile, suitable for square and rectangular images, thereby enhancing efficiency and improving permutation complexity, essential for robust image encryption.
•
Introducing a modified Josephus problem–based permutation that enhances the granularity required for robust encryption schemes.
•
Developing a novel RNA operation based on the Vigenère cipher, aiming at reducing computational time, since there is no need to code the key sequence and perform item-to-item operations as usual.
•
Enhancing unpredictability of the system by synchronizing the chaotic system with the computer’s timestamp using the SHA3-512 hash function.
•
Designing a robust encryption scheme applicable to all types of images.
•
Validating the proposed encryption scheme in a real-life communication system.
•
Achieving superior performance metrics compared to several existing schemes in the literature.
•
Using a delayed HNN characterized by its infinite-dimensional properties and hyperchaotic dynamics to significantly enhance the robustness of the encryption mechanism.

The remainder of this paper is structured as follows: Section 2 outlines the proposed system and model, while Section 3 covers experimental results, safety analysis, and comparative analysis. Finally, conclusions are presented in Section 4.

2. System and Model

In this section, we introduce and elaborate on the proposed system and model, detailing its architecture, components, and the underlying theoretical framework that distinguishes it from existing methodologies.

2.1. Proposed Li-Fi Infrastructure

Figure 1 presents two nodes (laptops) in which our Li-Fi application is installed. This Li-Fi application encrypts and decrypts the images using the proposed encryption scheme and further encrypts the key parameters of the proposed encryption scheme using the RSA algorithm to achieve an asymmetric encryption architecture. Each node interfaces with a microcontroller unit (MCU) through a universal serial bus (USB) cable. The MCU drives (i) a light-emitting diode (LED) serving as the emitting antenna for the light signals (ii) and a photodetector (PD) functioning as the receiving antenna for the reverse light signals. Consequently, a Li-Fi modem comprises an LED and a PD integrated within a single MCU. Encrypted data can be bidirectionally transmitted between node 1 and node 2, as indicated by the double arrow.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) Experimental setup of the proposed two-way Li-Fi infrastructure. LED, light-emitting diode; MCU, microcontroller unit; PD, photodetector; VLC, visible light communication. (b) Device in the laboratory.

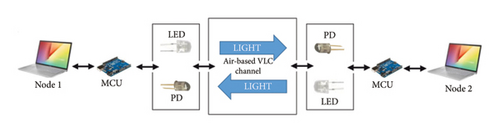
2.1.1. Transmission Process

Our system is designed to handle image files with pixel values ranging from 0 to 255. Each encrypted pixel is encoded using 8 bits (1 byte). Following encoding, the data are structured into universal asynchronous receiver transmitter (UART) data frames. In the Li-Fi modem, the incoming bit stream undergoes modulation into unipolar on–off keying non-return-to-zero (OOK-NRZ) electrical pulses. OOK-NRZ modulation involves toggling the carrier’s amplitude between two states (0 and 1), aligning with binary data transmission principles [39]. These pulses drive the emitting antenna (LED), where the optical power output correlates directly with the intensity of the forward current [40].

2.1.2. Reception Process

Let P_t(t) denote the instantaneous optical power transmitted by the LED. This modulated light propagates through the air-based VLC channel and is detected by the receiving antenna (PD) of the other node. Assuming Lambertian radiation pattern for the emitting antenna (LED), the instantaneous optical power received by the PD at the other node is expressed as [41]

(1)

where A_phy denotes the physical area of the receiver, ψ represents the angle of incidence of the received radiation relative to the axis of the PD, m indicates Lambert’s mode number of the emitting LED, d is the separation distance between the two transceivers, ϕ signifies the angle between the emitter’s axis and the emitted light beam, and FOV refers to the field of view of the receiving antenna (PD). Moreover, the receiving antenna is a square-law optoelectronic transducer that generates an electrical current (I_P(t)) proportional to the square of the instantaneous optical beam impinging on its detection area [41]. Thus, I_P(t) is proportional to P_r(t), as follows [42]:

(2)

where hf represents the photon energy, l denotes the junction width, q is the elementary charge of an electron, α signifies the absorption coefficient, and

refers to the quantum efficiency. At the Li-Fi modem, all the UART data frames are transferred to the Li-Fi application using the USB cable. Afterward, the Li-Fi application processes to decrypt and then reconstruct the initial image file.

2.2. Encryption Algorithm Foundation

2.2.1. Delayed HNN

Compared with traditional chaotic systems, neural networks exhibit several advantages, such as high security and high processing speeds. The chaotic system of interest in this paper is the delayed HNN due to its complex chaotic characteristics [43]. Its dynamic variable y is governed by the following equation [44]:

(3)

where i = 1, …, n and n denotes the number of units in the neural network. Here, c_ij is a diagonal matrix, a_ij and b_ij are the weight matrix used for each connection and the delayed connection weight matrix, respectively, f_j(y_j(t)) = tanh(y_j(t)) serves as the activation function, y_j(t) is the state variable associated with the neurons, I_i represents the external input vector, and τ_ij(t) is the time delay. The initial conditions for implementing the neural network are y_j(t) = ϕ_j(t) ∈ ς([−r, 0], R), where ς([−r, 0], R) denotes the set of all continuous functions from [−r, 0] to R, and r = max_{i≥1,j≤n,t∈R} τ_ij(t) [44]. For simplicity, we choose n = 2, resulting in

(4)

where the parameters a_ij, b_ij, c_ij, τ_ij(t), and I_i are chosen to induce chaotic dynamics in the neural network [45]:

(5)

(6)

(7)

(8)

(9)

2.2.2. SHA3-512

SHA3-512 is a cryptographic hash function designed to irreversibly transform inputs of arbitrary size into a fixed-length output of 512 bits, known as a hash value or digest [46]. Among its notable attributes, SHA3-512 offers enhanced security and longer hash outputs compared to other hash functions. Its irreversibility ensures resilience against plaintext and ciphertext attacks.

2.2.3. Improved Z-Order Curve-Based Permutation

The Z-order curve, also known as the Lebesgue curve, is a function used to map multidimensional data into a single dimension [27, 47]. In the literature, alongside the Lebesgue curve, there exist two quasi-Lebesgue curves, each offering eight distinct transformation modes [29]. In the standard Z-order transformation of a matrix, approximately 50% of elements remain unchanged in position, which poses limitations for effective pixel scrambling [27]. To address this issue, we propose an improved Z-order curve-based permutation method, outlined as follows (Figure 2):

•
Step 1: Divide the plain 2D array X of size M × N into small blocks Xb_i of size M_r × N_c as follows:
(10)
where i = 1, 2, …, (M × N/M_r × N_c), r = 1, 2, …, M_r, and c = 1, 2, …, N_c. M_r and N_c are determined following Algorithm 1. Then, each block undergoes the following steps.
•
Step 2: Generate two equal-sized square matrices per block. If the block is square, duplicate it; otherwise, scan bidirectionally along its shorter side to derive two square matrices.
•
Step 3: Randomly select two complementary transformation modes from one of the three types of Z-order filling curves. Apply them individually to each of the two squared matrices to generate two vectors.
•
Step 4: Cross-combine the two vectors to form a new vector matching the original block’s size.
•
Step 5: Reshape the vector to obtain the scrambled block.

Algorithm 1: Algorithm used to determine the optimal size of an image block.

Input:M, N
Output:M_r, N_c
1.
fori = 1 to M − 1do
2.
Compute a = (M/M − i)
3.
Ifis integer(a)then
4.
A(i) = a
5.
End if
6.
End for
7.
forj = 1 to N − 1do
8.
Compute b = (N/N − j)
9.
Ifis integer(b)then
10.
B(j) = b
11.
End if
12.
End for
13.
Randomly select two integers M_r from set A and N_c from set B, ensuring that the smaller of the two integers is a power of 2.

Figure 2 illustrates steps 2–5 applied to a block of size 4 × 6.

The results demonstrate that our framework offers enhanced robustness compared to the standard model, as the positions of nearly all elements in the scrambled block have been altered. Additionally, the improved Z-order curve can be applied to nonsquare images, enhancing efficiency and increasing permutation complexity, which is critical for robust image encryption.

2.2.4. Modified Josephus Problem–Based Permutation

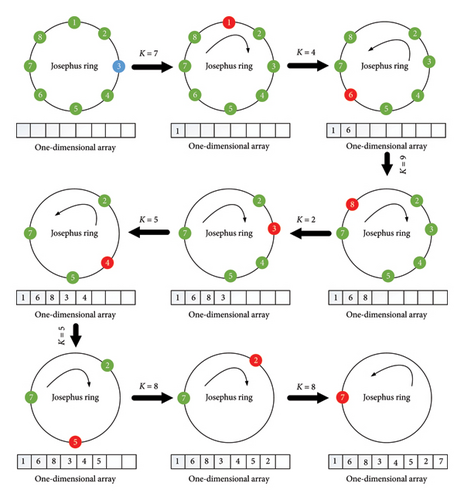
The Josephus problem describes a scenario where N individuals stand in a circle awaiting execution. They are counted in a fixed direction, and K people are skipped while the next is killed until only one person is left [28]. Recently, this problem has found application in pixel-level permutation for image encryption [48]. In the traditional Josephus problem, the step size K is constant, and the scan proceeds either clockwise or counterclockwise. In contrast, the modified Josephus problem proposed in this study introduces variability by randomly altering the starting position, step size, and direction. This approach increases the diversity of generated sequences and introduces an additional dislocation effect, enhancing the effectiveness of the permutation. Figure 3 illustrates this process for N = 8.

2.2.5. Proposed RNA Operation

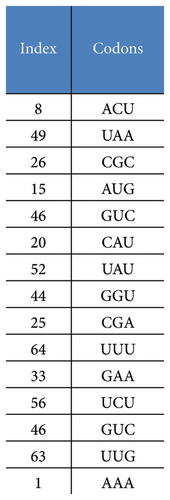
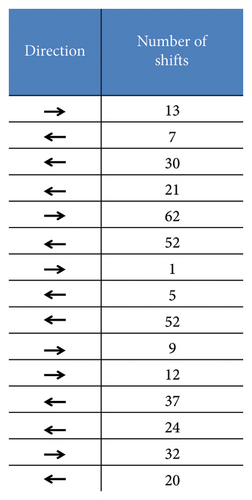
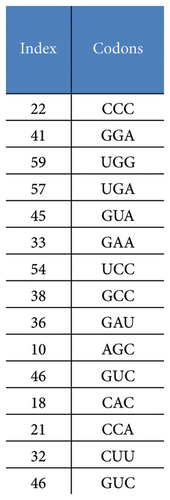
The RNA sequence plays a pivotal role across diverse scientific disciplines, including basic biological research, diagnostics, biotechnology, forensics, biological systematics, and cryptography [20, 49, 50]. An RNA molecule consists of four distinct nucleic acids: adenine (A), cytosine (C), guanine (G), and uracil (U). In the context of protein synthesis, sets of three consecutive bases within the messenger RNA (mRNA) chain encode specific amino acids and are known as genetic codons. Typically, there are 64 unique codons that facilitate the translation of mRNA into proteins [51]. In this paper, leveraging the principle from Vigenère cipher [52], we propose an RNA operation aimed at transforming an input RNA array. Each codon within the array is substituted with another codon selected from a comprehensive set of 64 possibilities to produce an output RNA array (Figure 4). The substitution process involves determining the index of the replacement codon using a transition table generated dynamically by chaotic sequences. This table includes parameters that dictate the number and direction of shifts applied during the substitution process. Notably, this operation is time-efficient since there is no need to code the key sequence and perform item-to-item operations as usual.

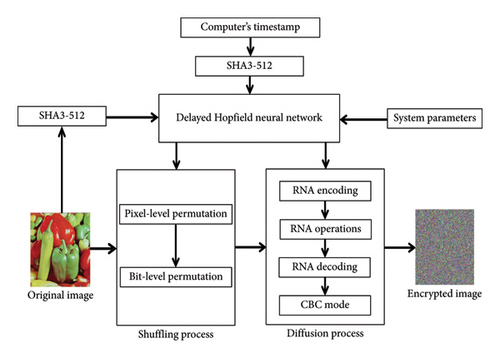
2.3. Encryption Scheme

The proposed encryption scheme supports digital images of any size and type (binary, grayscale, color) with pixel values ranging from 0 to 255, encoded across 256 levels. In this subsection, we consider X as a matrix representing a plain image and Y as the matrix of an encrypted image, all of the same size [M, N, O]. The encryption process flowchart is illustrated in Figure 5, and its detailed description follows in the subsequent sub-subsections.

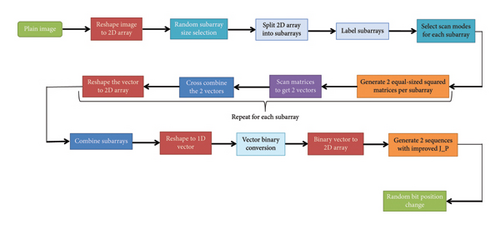
2.3.1. Key’s Parameters and System Initial Values Generation

The key parameters of the proposed encryption scheme include (1) the initial values of the delayed HNN derived from two 512-bit parameters (γ₁, γ₂) generated by applying the SHA3-512 hash function to both the plain image (X) and the computer timestamp (TS), i.e., γ₁ = SHA3 − 512(X) and γ₂ = SHA3 − 512(TS); and (2) the parameters of the delayed HNN (a_ij, b_ij, c_ij, I_i, τ_ij(t)). Note that TS is under the format “yyyy/MM/dd HH:mm:ss.SSS.” Thus, the initial values of the delayed HNN (y₁(1) and y₂(1)) are calculated as follows:

(11)

(12)

with “mod” representing the modulo function, and “HEX2DEC” is a function that converts a hexadecimal number to its decimal representation.

2.3.2. Shuffling Process

The proposed encryption scheme achieves pixel-level permutation and bit-level permutation following several steps as illustrated in Figure 6.

•
Step 1: Obtain the two 512-bit parameters (γ₁ and γ₂) and the system parameters (a_ij, b_ij, c_ij, I_i, τ_ij(t)).
•
Step 2: Using γ₁ and γ₂, calculate the initial values of the delayed HNN following equations (11) and (12).
•
Step 3: Iterate the delayed HNN for 8 × M × N × O + 1000 times, discarding the initial 1000 values. The resulting elements are then converted into a sequence of integers ranging from 0 to 255. These integers are assigned to a vector S_q as follows:
(13)
where i = 1, 2, 3, …, 8 × N × M × O.
•
Step 4: Transform image X into a single 2D array X₁ of dimension [M, N × O] as
(14)
The function “reshape(Q, [H, U])” reshapes Q into a H-by-U matrix.
•
Step 5: Use the method outlined in 2.2.3 to perform a pixel-level permutation on X₁, resulting in the 2D array X_en2; the corresponding transformation modes (Z_mode) are selected as follows:
(15)
Z_mode values range from 1 to 8 for the Lebesgue curve, from 9 to 16 for the first quasi-Lebesgue curve, and from 17 to 24 for the second quasi-Lebesgue curve.
•
Step 6: Transform X_en2 into a one-dimensional row vector and convert each of its elements into bits using
(16)
The function “dec2base” converts a decimal number to a character vector representing a base 2 number.
•
Step 7: Reshape X_en2b into a 2D array C_q as
(17)
with N_P1 = 8 × M and N_P2 = N × O.
•
Step 8: Use the modified Josephus problem (denoted as J_P) proposed in 2.2.4 to generate two sequences as follows:
(18)
where the start positions (start_pos1, 2), steps size (step_size1, 2(i)), and directions (dir1, 2(i)) are given as
(19)

(20)

(21)
•
Step 9: Finally, each bit’s position in C_q undergoes random modification to yield X_en3 as follows:

(22)

with i = 1, 2, 3, …, 8 × M, j = 1, 2, 3, …, N × O, and k = 1, 2, 3, …, 8 × M × N × O.

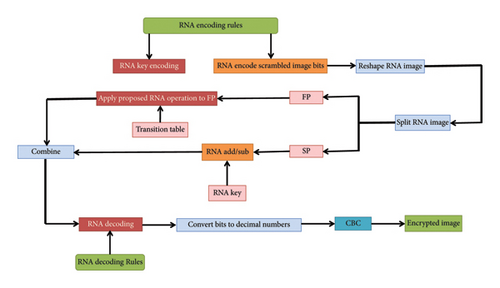
2.3.3. Diffusion Process

Based on the RNA operations and the CBC mode, the diffusion process, as illustrated in Figure 7, is outlined as follows:

•
Step 1: The chaotic sequence S_q is first converted into a sequence of bits, which are then concatenated to form a one-dimensional binary vector.
•
Step 2: The encryption and decryption rules (Enc_rule(i)), (Dec_rule(i)) are, respectively,
(23)
Then, following the specified encoding rules Enc_rule(i) as described in equation (23), dynamic RNA encoding operations are applied to the vector X_en3 and S_q, resulting in the vectors X_en3RNA and S_qRNA:
(24)
where i = 1, 2, 3, …, M × N × O and k = 1, 3, 5, …, M × N × O.
•
Step 3: Reshape the vector X_en3RNA into an L × 4 matrix as follows:
(25)
with L = M × N × O/4.
•
Step 4: Split X_en4RNA into two parts FP and SP as
(26)
•
Step 5: Depending on whether y₁(i) ≤ y₂(i), perform RNA addition or subtraction operation between the samples of SP(i) and S_qRNA(i) to generate SP_RNA(i);
•
Step 6: The proposed Vigenère cipher–based RNA operation described in 2.2.5 is employed on the vector FP to derive FP_RNA. The parameters governing this operation, including the number of shifts (C_V) and their direction (Dr), are dynamically generated using chaotic sequences as specified in the following equation.
(27)
•
Step 7: Concatenate SP_RNA with FP_RNA horizontally and transform the result into a one-dimensional vector X_en5RNA.
•
Step 8: Decode X_en5RNA according to the rule specified in sequence Dec_rule(i) to obtain X_en5,
(28)
and concatenate it into a one-dimensional binary vector before converting it into decimal representation as
(29)
with k = 1, 9, 17, …, M × N × O/8, i = 1, 2, 3, …, M × N × O, and base2dec, a function which converts text representing a number in base 2, into its decimal equivalent.
•
Step 9: The CBC mode is applied to X_en6 to obtain X_en7 as follows:
(30)
where X_en7(1) = index(max(S_q(1 : 255))) is the initialization vector of the CBC mode.
•
Step 10: The final encrypted image is given as follows:

(31)

3. Experimental Results and Comparative Analysis

This section presents and analyzes the results obtained by our innovative encryption method. These results are compared with existing techniques in the literature to demonstrate their advantages in terms of security, robustness, and efficiency.

3.1. Experimental Results

This subsection presents the experimental results and performance analysis of the proposed encryption scheme. A robust image encryption scheme must withstand various attacks to ensure the security of images during transmission. We evaluate the performance of our encryption scheme using 15 metrics on binary images (binary, QR code), grayscale images (boat, cameraman, male), and color images (airplane, couple, peppers, female, house). The performance analysis of the proposed encryption scheme is conducted within the context of a Li-Fi infrastructure, where the plain images are the transmitted images and the decrypted images are those received at the destination node (Figure 1).

3.1.1. Key Space Analysis

The key space of an encryption scheme is a fundamental metric that determines its resilience to brute-force attacks, calculated based on the total possible combinations of all key parameters [20, 26]. In our proposed encryption scheme, the key space is shaped by the initial values and system parameters of the delayed HNN. Additionally, our computational environment operates with a numerical precision of 10⁻¹⁶. Specifically, we use two initial values for the HNN, each with an accuracy of 10⁻¹⁶, leading to 10¹⁶ possible values per parameter and a total of 10³² combinations. Additionally, the HNN comprises of 20 system parameters, each with the same accuracy of 10⁻¹⁶, contributing 10³²⁰ possible combinations. As a result, the overall key space is 10³² × 10³²⁰ = 10³⁵² ≈ 2¹¹⁶⁶, which is vastly larger than the recommended threshold for secure encryption schemes. For comparison, modern cryptographic standards suggest a key space of at least 2¹²⁸ (approximately 10^38.5) to guard against brute-force attacks [53]. With a total key space of 10³⁵², our scheme provides a high level of security, offering robust resistance to exhaustive search attacks. Given that the key space may fluctuate depending on the computational environment, it is crucial to carefully select the implementation platforms to optimize the key space. This ensures maximization of cryptographic robustness and significantly enhances the security of the algorithms against brute-force attacks.

3.1.2. Encryption Effect

Figure 8 presents the plain, encrypted, and decrypted images for various image types (binary, boat, cameraman, airplane, couple, peppers). The encrypted images (Figure 8(b, e, h, k, n, q)) are completely unrecognizable, demonstrating the effectiveness of the encryption process. Furthermore, the decrypted images (Figure 8(c, f, i, l, o, r)) closely match their corresponding plain images (Figure 8(a, d, g, j, m, p)), indicating the high accuracy and reliability of the decryption process. These results highlight the robustness of the proposed scheme in effectively encrypting and decrypting various types of images.

3.1.3. Statistical Analysis

Statistical analysis is a critical test to assess the robustness of an encryption scheme. This analysis encompasses several parameters, including (1) the entropy of images, (2) the correlation coefficients of adjacent pixels, (3) the histogram of images, (4) the chi-square test, and (5) the deviation of the histogram of the encrypted images from the ideal uniform histogram.

3.1.3.1. Entropy Analysis

The degree of randomness of an information source can be assessed by computing its entropy E using the formula [54]:

(32)

where P(x) denotes the occurrence probability of the value x. An image encryption scheme is considered well-secured when the entropies of the encrypted images are approximately 8 [54]. The proposed encryption scheme has been evaluated using entropy analysis, and the results are presented in Table 1. The table indicates that the entropy values are closely clustered around 8 for all encrypted images. Therefore, it is evident that our scheme effectively mitigates entropy-based attacks.

Table 1. Entropy values of plain and encrypted images.

Images	Original images	Encrypted images
Binary	0.3926	7.9993
QR code	1.9437	7.9992
Boat	7.1914	7.9993
Cameraman	7.0097	7.9968
Male	7.5237	7.9998
Airplane	6.6639	7.9998
Couple	6.2945	7.9992
Peppers	7.6698	7.9998
Female	6.8981	7.9990
House	7.0686	7.9990

3.1.3.2. Pixels Correlation Coefficients Analysis

Calculating correlation coefficients between adjacent pixels in three directions (horizontal, vertical, and diagonal) before and after image encryption is essential for assessing the strength of an encryption scheme. Typically, adjacent pixels in plain images exhibit high correlation, so a robust encryption scheme should minimize this correlation. The formula for computing correlation coefficients is given by [54]

(33)

with

(34)

where x and y represent the two adjacent pixels in the same direction and N represents the number of selected pixels. We have chosen N = 3000; that is, 3000 pairs of adjacent pixels are randomly selected. Table 2 reports the results.

Table 2. Correlation coefficients of adjacent pixels in plain and encrypted images; comparison across horizontal (H), vertical (V), and diagonal (D) directions.

Images		Plain images			Encrypted images
Images		H	V	D	H	V	D
Binary		0.9798	0.9830	0.9424	−0.0029	0.0132	−0.0071

QR code		0.9710	0.9693	0.9349	−0.0179	−0.0023	−0.0107

Boat		0.9478	0.9706	0.9272	−0.0178	−0.0051	0.0015

Cameraman		0.9299	0.9595	0.9055	−0.0066	−0.0069	−0.0116

Male		0.9777	0.9813	0.9739	−0.032	−0.016	−0.0091

Airplane	R	0.9739	0.9488	0.9337	0.0219	−0.0032	0.0243
	G	0.9614	0.9689	0.9419	0.0163	0.0007	−0.0111
	B	0.9096	0.9418	0.8717	−0.0083	0.0312	0.0095

Couple	R	0.9492	0.9638	0.9193	0.0033	0.0063	0.0056
	G	0.9193	0.9496	0.9007	−0.0196	−0.0149	0.0080
	B	0.9096	0.9418	0.8717	−0.0083	−0.0142	0.0191

Peppers	R	0.9592	0.9690	0.9551	0.0311	−0.0119	0.0159
	G	0.9820	0.9801	0.9666	0.0041	−0.0140	−0.0096
	B	0.9701	0.9693	0.9364	−0.0151	−0.0069	−0.0314

Female	R	0.9751	0.9642	0.9667	−0.0350	0.0049	−0.0037
	G	0.9692	0.9618	0.9528	0.0056	−0.0122	−0.0067
	B	0.9618	0.9516	0.9392	0.0472	−0.0178	−0.0017

House	R	0.9695	0.9397	0.9020	0.0061	0.0099	−0.0281
	G	0.9814	0.9482	0.9370	−0.0175	−0.0313	0.0142
	B	0.9819	0.9774	0.9653	0.0006	−0.0219	0.0162

From Table 2, it is evident that the correlation coefficients of adjacent pixels in the encrypted images are significantly reduced, indicating the high security level of the proposed encryption scheme. Figures 9 and 10 depict the correlation distribution diagrams of adjacent pixels in the horizontal (H), vertical (V), and diagonal (D) directions for two example images: “cameraman” and “airplane.”

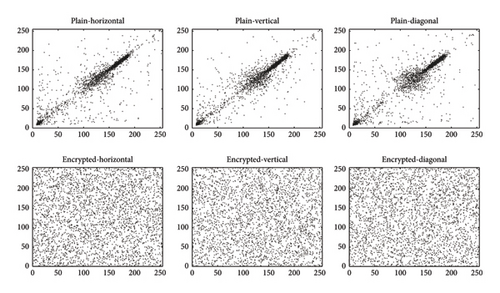
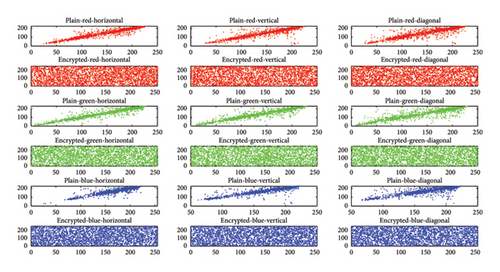
One can observe that the correlation distribution diagrams of adjacent pixels in plain images show high correlation, whereas those of encrypted images exhibit uniform and irrelevant correlation. This observation highlights our scheme’s effectiveness in minimizing correlations between adjacent pixels, thereby achieving robust encryption.

3.1.3.3. Histogram Analysis

One can evaluate an image encryption scheme by plotting the distribution of pixel values in images before and after encryption; this is referred to as an image histogram [54]. Figures 11 and 12 show the histograms of some plain and encrypted grayscale (cameraman) and color (airplane) images.

In both histograms, the pixel distributions of encrypted images are notably flatter and more uniform compared to those of the plain images. This flatness can be quantitatively assessed using the chi-square test, whose mathematical formulation is given by [55]

(35)

where expected = (M × N/256), with L representing the gray level values and M × N denoting the image size.

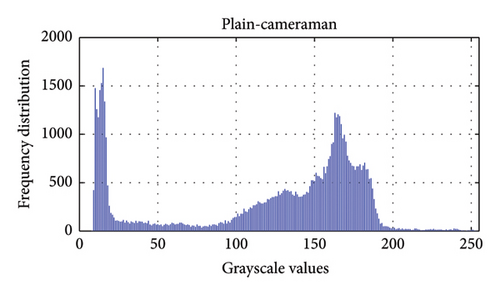
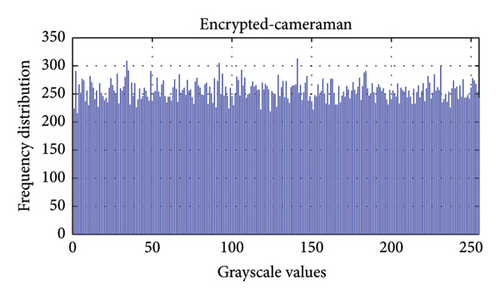
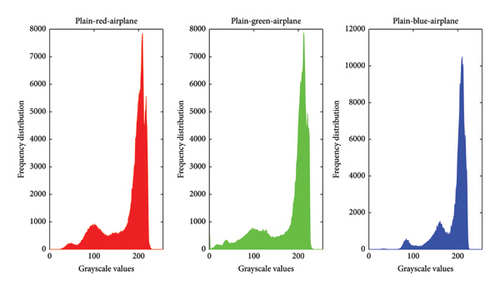
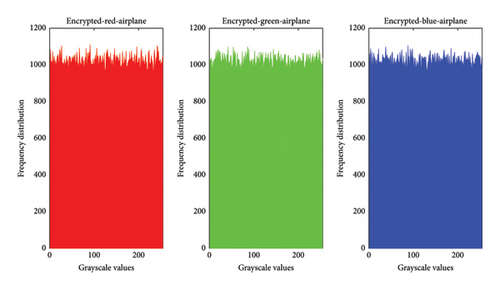
Table 3 presents the chi-square values of encrypted images. A histogram’s flatness is typically confirmed if its chi-square value is less than 293.2478 [25]. Furthermore, the deviation of the encrypted histogram from the ideal histogram serves to evaluate resistance against statistical attacks. From Table 3, it is evident that all deviations are minimal, affirming that the proposed encryption scheme closely approximates the ideal standard.

Table 3. Chi-square test values and deviation of histogram from ideality for encrypted images.

Images		Chi-square values	Deviations
Binary		248.15	0.025

QR code		272.77	0.025

Boat		252.39	0.024

Cameraman		291.5078	0.053

Male		252.62	0.012

Airplane	R	243	0.048
	G	272.32	0.050
	B	253.26	0.051

Couple	R	200.20	0.044
	G	283.66	0.052
	B	247.89	0.049

Peppers	R	251.19	0.024
	G	267.21	0.025
	B	258.93	0.024

Female	R	281.17	0.051
	G	279.03	0.054
	B	274.80	0.051

House	R	286.78	0.051
	G	272.88	0.052
	B	285.15	0.053

3.1.4. Differential Attack

The differential attack aims to observe the impact of minor differences between pairs of inputs on their corresponding outputs. This cryptanalytic approach helps adversaries deduce confidential key information. Therefore, an effective image encryption scheme must exhibit high sensitivity to small changes in the plaintext. To evaluate an encryption system’s resilience against differential attacks, two metrics are employed: the number of pixel change rate (NPCR) and the unified average changing intensity (UACI). NPCR and UACI are calculated as follows [54]:

(36)

and

(37)

where

(38)

In equations (37) and (38), Y1_i and Y2_i denote the pixel values of the two encrypted images and N represents the total number of pixels. According to the literature, the minimum expected values for NPCR and UACI are 99.6094%, and 33.4635%, respectively [56]. In our evaluation, we conducted tests by randomly altering a single pixel in the plain image. The results are summarized in Table 4.

Table 4. NPCR and UACI values.

Images	NPCR (%)	UACI (%)
Binary	99.6284	33.5432
QR code	99.6240	33.5055
Boat	99.6298	33.4380
Cameraman	99.6231	33.5393
Airplane	99.6226	33.4650
Couple	99.6592	33.4613
Peppers	99.6109	33.4527
Female	99.6134	33.5324
House	99.6129	33.5483

Table 4 demonstrates that the proposed encryption scheme successfully meets the NPCR and UACI criteria across various images, indicating its robustness against differential attacks.

3.1.5. Peak Signal-to-Noise Ratio

The peak signal-to-noise ratio (PSNR) is a means for assessing the capacity of an encryption scheme to noise a signal. The lower the PSNR, the more robust the encryption scheme. It is calculated as follows [54]:

(39)

where MAX is the maximum possible value of pixels (255) and MSE is the mean square error computed as follows:

. As seen in Table 5, PSNR values obtained are small, which means that all encrypted images have a very high noise level. Therefore, it is clear that our scheme effectively noises the plain images.

Table 5. PSNR values.

Images	PSNR (dB)
Binary	4.7582
QR code	4.9803
Boat	9.2952
Cameraman	8.3579
Male	8.003
Airplane	7.9710
Couple	6.2761
Peppers	8.0679
Female	7.2854
House	8.9204

3.1.6. Occlusion Attacks Analysis

Occlusion attacks analysis is crucial for assessing the robustness of an encryption scheme. Occlusion attacks occur when parts of the encrypted image are lost during transmission [57]. A reliable encryption scheme must effectively mitigate such vulnerabilities. Figure 13 presents the experimental results of the proposed scheme under occlusion attacks. Despite losses of approximately 16.66% (Figures 13(a) and 13(c)) and 33.33% (Figures 13(b) and 13(d)) of encrypted images, the corresponding decrypted images (Figures 13(e), 13(f), 13(g), and 13(h)) remain identifiable. This demonstrates the scheme’s resilience against occlusion attacks.

3.1.7. Noise Attacks Analysis

Another crucial metric for evaluating an encryption scheme is its resistance against noise attacks [58]. To assess this, an amount of salt-and-pepper noise was added to some encrypted images. Figure 14 demonstrates that our scheme successfully reconstructs readable images from the corrupted encrypted ones.

3.1.8. Key Sensitivity Analysis

Sensitive key parameters are crucial for the effectiveness of an encryption scheme during both encryption and decryption processes [56, 59, 60]. Key sensitivity serves as a fundamental metric for assessing the reliability of a cryptographic system. To evaluate the sensitivity of the keys employed in our proposed scheme, we defined three secret keys (K₁, K₂, K₃), where K₂ and K₃ were derived from K₁ with a minute variation affecting one key parameter by a magnitude of 10⁻¹⁶, outlined as follows: K₁(a₁₁ = 2, a₁₂ = −0.1, a₂₁ = −5, a₂₂ = 3), K₂(a₁₁ = 2, a₁₂ = −0.1, a₂₁ = −5, a₂₂ = 3 + 10⁻¹⁶), and K₃(a₁₁ = 2, a₁₂ = −0.1, a₂₁ = −5, a₂₂ = 3 + 2 × 10⁻¹⁶).

Figure 15 illustrates the outcomes of key sensitivity experiments conducted during the encryption and decryption processes. It is evident that when using secret keys K₂ and K₃ for decryption, which differ slightly from the encryption key K₁, the resulting decrypted images are rendered unintelligible (Figures 15(f) and 15(g)). However, when employing the correct key K₁, the decrypted image closely resembles the original plain image (Figure 15(h)). Table 6 reveals a significant mean square error (MSE) between the encrypted images, despite the similarity of the keys used. This observation holds true for the decrypted images as well. Therefore, these findings underscore the sensitivity of the secret keys in our proposed scheme during both the encryption and decryption processes.

Table 6. Mean square error values.

Data 1	Data 2	MSE between data 1 and data 2
E₁ = (P, K₁)	E₂ = (P, K₂)	1.0918 × 10⁴
E₁ = (P, K₁)	E₃ = (P, K₃)	1.0918 × 10⁴
E₂ = (P, K₂)	E₃ = (P, K₃)	1.0903 × 10⁴
D₁ = (E₁, K₃)	D₂ = (E₁, K₂)	2.0637 × 10⁴
D₂ = (E₁, K₂)	D₃ = (E₁, K₁)	2.0681 × 10⁴
D₁ = (E₁, K₃)	D₃ = (E₁, K₁)	1.0893 × 10⁴
P	D₃ = (E₁, K₁)	0

3.1.9. Time Complexity

The time complexity of an encryption scheme is critical, especially in real-time communication applications [61, 62]. The proposed image encryption scheme exhibits linear complexity, specifically O(m × n × o), where [m, n, o] denote the dimensions of the input image file. That confirms the suitability of our algorithm for real-time communication applications executed on computer systems.

3.1.10. Speed for the Encryption Process

To measure the speed of our encryption scheme, we used images of different sizes with hardware configuration 3.4 GHz, Intel^(R)Core^(TM) i76600U, 16 GB RAM, Windows 10, and MATLAB 2018. Table 7 reports the findings. The encryption time is notably substantial, resulting in diminished throughput, likely attributable to the implementation of the encryption algorithm in MATLAB. To mitigate this issue, it would be advantageous to employ compiled languages such as C++, which could significantly enhance computational efficiency and improve throughput.

Table 7. Speed for the encryption process.

Images	Size	Time (s)	Throughput (Mbps)
Binary	500 × 500	5.021	0.398
QR code	500 × 500	5.250	0.381
Boat	512 × 512	5.523	0.379
Cameraman	256 × 256	1.580	0.332
Male	1024 × 1024	22.825	0.367
Airplane	512 × 512 × 3	17.122	0.367
Couple	256 × 256 × 3	4.334	0.362
Peppers	512 × 512 × 3	17.036	0.369
Female	256 × 256 × 3	4.10091	0.383
House	256 × 256 × 3	4.523	0.347

3.1.11. Checksum Using SHA-256

Ensuring data integrity is crucial across various applications, necessitating robust and fully reversible encryption schemes. Checksums, typically computed using cryptographic hash functions, verify the integrity of received data. In our evaluation, we employ the SHA-256 hash function to compare hash values of received images with their transmitted counterparts [59]. Table 8 shows identical hash values for transmitted and received images, confirming lossless transmission and decryption processes. These results underscore the complete reversibility and high reliability of both the proposed encryption scheme and the Li-Fi infrastructure.

Table 8. Hash values of transmitted and received images.

Images	Hash values of transmitted images	Hash values of received images
Binary	8cc371c3d3118a192f26a24a8bd21db8eb831814f91820c5b25e169056988006	8cc371c3d3118a192f26a24a8bd21db8eb831814f91820c5b25e169056988006
Airplane	ae9eba12b80df955e47585bf4a16332ea0dadc753668d3457c509564934dbd40	ae9eba12b80df955e47585bf4a16332ea0dadc753668d3457c509564934dbd40

3.1.12. Known Plaintext and Chosen Plaintext Attacks

The principal aim of cryptanalysis is to recover the secret key or its components in order to decrypt ciphertexts produced by a cryptographic system. The literature delineates four primary attack scenarios: ciphertext-only attack, known plaintext attack, chosen plaintext attack, and chosen ciphertext attack. Among these, known plaintext and chosen plaintext attacks are particularly powerful and require careful consideration. To crack a cryptographic scheme, two scenarios may be considered: (1) cracking the secret key parameters of the system which is often impossible and (2) cracking the encryption sequence which is more feasible depending on the type of cryptographic scheme used. Often two different types of cryptographic schemes may be considered: the first is the open-loop scheme, in which the secret key parameters are independent from the plaintext, and the second is close-loop scheme, in which the parameters are linked to the plaintext. In the open-loop schemes, the encryption sequence is the same for different encryption schemes therefore making it easy to recover it through chosen plaintext attack; while, the close-loop system is a one-tap system in which each plaintext is encrypted with a different sequence. Our encryption algorithm is robust to known plaintext and chosen plaintext attacks for the following reasons: (1) It is a close-loop scheme in which the secret keys are intricately linked to both the input image and the computer’s timestamp via the SHA3-512 hash function. Therefore, any given plain image (even one chosen by the attacker) is encrypted by a different encryption sequence making it difficult to obtain the encryption sequence. Moreover, repeated encryption of the same plain image is done with different encryption keys due to the use of the computer’s timestamp which further improves the difficulty to obtain the encryption sequence. (2) It uses the CBC mode which makes it difficult to predict the encryption sequence. Indeed, a random IV is used in the diffusion of the first block in the CBC mode. This therefore makes it harder for the attackers to establish a meaningful relationship between the plaintexts and ciphertexts. Besides, the random IV serves as salt in the confused image and contributes to destroy predictable patterns in it. The destruction of predictable patterns increases as the chaining evolves in such a way that the obtained ciphertext cannot easily be linked to the plaintext.

3.2. Comparative Analysis

Numerous image encryption schemes have been proposed in the literature. To showcase the contribution of our scheme, we compare its experimental results with those of existing schemes. Table 9 presents the outcomes of this comparative analysis, focusing on metrics such as information entropy, correlation coefficients of encrypted images, NPCR, UACI, key space, and experimental realization.

Table 9. Outcome of comparative analysis.

References	Entropy	Correlation coefficients			NPCR	UACI	Key space	Throughput (Mbps)	Experimental realization
References	Entropy	H	V	D	NPCR	UACI	Key space	Throughput (Mbps)	Experimental realization
[6]	—	0.0361	−0.0408	−0.0088	99.64	33.54	k	5.66	No
[8]	7.9998	0.00075	0.0078	−0.0063	99.6102	33.4695	2²⁵⁶	2.27	No
[9]	7.9965	0.0023	−0.0020	−0.0073	99.6141	33.4977	10⁹⁸	31.45	No
[10]	7.9994	0.0020	−0.0009	−0.0031	99.6644	33.4670	10¹²⁸	—	No
[13]	7.9994	−0.0024	0.0007	0.0018	99.6095	33.4633	2²⁰⁵	22.90	No
[19]	7.9998	0.00007	0.00007	−0.00014	99.6127	33.4862	2²¹³	—	No
[21]	7.9998	−0.0025	0.0013	0.0009	99.6084	33.4659	2⁵⁴¹	168.56	No
[25]	7.9998	0.0206	0.0003	−0.0141	99.6150	33.5106	10¹²⁸	248.08	No
[30]	7.9994	−0.0026	−0.0012	−0.0011	99.62	33.50	0.09 × 2¹⁰⁸⁰	—	No
[31]	7.9993	−0.0014	−0.0008	−0.0038	99.6095	33.4640	2²⁶⁰	2.30	No
[35]	7.9997	−0.0013	0.0080	−0.00113	99.59161	33.3834	2³²⁰	—	Yes
[36]	7.9993	0.0007	0.0011	0.0012	99.6112	33.3747	—	—	Yes
[37]	7.9993	—	—	—	99.6120	—	—	—	Yes
[63]	7.9981	0.0005	−0.0032	−0.0032	99.59138	33.3861	10¹⁶⁰	—	No
This work	7.9998	−0.03	−0.016	−0.0091	99.6592	33.5483	10³⁵² ≈ 2¹¹⁶⁶	0.3685	Yes

Note: The bold fonts mean the best results.

In terms of information entropy, our proposed scheme achieves results comparable to those reported in [8, 19, 21, 25], while notably surpassing other references, indicating a high degree of randomness. Moreover, our system exhibits the lowest correlation coefficients among recent advancements in encrypted image correlations. Regarding NPCR and UACI, our scheme outperforms several recent achievements, although the NPCR value reported in Reference [10] slightly exceed ours. Notably, our scheme boasts a larger key space and higher key sensitivity compared to findings in the literature. While our algorithm exhibits linear time complexity, its throughput is currently lower than that reported in the literature. We attribute this discrepancy to the use of MATLAB, an interpreted language. We anticipate that transitioning to a compiled language, such as C++, would substantially enhance execution speed and improve overall throughput. Furthermore, our scheme demonstrates greater resilience against occlusion attacks compared to References [25, 59], where encrypted image segments lost during transmission were not recoverable after decryption, and compared to References [8, 20], where even slight losses resulted in significant degradation of recovered images. Apart from Reference [35], which explores chaos generators on Raspberry Pis for MQTT-based IoT, Reference [36], which details an optimized bit insertion method on a Nios II system, and Reference [37], which employs chaotic binary sequences with artificial neurons for IoT, numerous prior studies are confined to theoretical analyses and simulations. In contrast, our encryption scheme has been empirically validated through its implementation in a Li-Fi infrastructure, thereby demonstrating its efficacy in securing image transmissions over VLC channels.

4. Conclusion

This paper introduced a novel chaotic image encryption scheme based on an improved Z-order curve, a modified Josephus problem, and a Vigenère cipher–based RNA operation. This proposed scheme enhances the efficiency and robustness of traditional encryption schemes and solves the lack of empirical validation. The proposed encryption scheme achieves pixel-level and bit-level permutations of plain images using the improved Z-order curve and the modified Josephus problem, respectively. The diffusion process incorporates a Vigenère cipher–based RNA operation alongside basic RNA operations. The findings demonstrate that the improved Z-order curve-based permutation is suitable for both square and nonsquare images, thereby enhancing efficiency and increasing permutation complexity, which are essential for robust image encryption. Additionally, the modified Josephus problem–based permutation improves the granularity required for secure encryption schemes. Furthermore, the streamlined Vigenère cipher–based RNA operation optimizes the diffusion process for greater computational efficiency. The synchronization of the chaotic system with the plain image and the computer’s timestamp, utilizing the SHA3-512 hash function, significantly enhances unpredictability. Performance analysis conducted in a Li-Fi infrastructure demonstrated the scheme’s effectiveness, security, robustness, and practicality. Future research could focus on (1) optimizing the scheme with higher complex dynamical systems [64–66] or its implementation using compiled languages like C++ for real-time applications and (2) exploring its adaptability across various scenarios and environments.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Open Research

Data Availability Statement

The data supporting the findings of this study are available from the corresponding author upon reasonable request.

References

1 Suman R. R., Mondal B., and Mandal T., A Secure Encryption Scheme Using a Composite Logistic Sine Map (CLSM) and SHA-256, Multimedia Tools and Applications. (2022) 81, no. 19, 27089–27110, https://doi.org/10.1007/s11042-021-11460-4.
10.1007/s11042-021-11460-4
Google Scholar
2 Zhou M. and Wang C., A Novel Image Encryption Scheme Based on Conservative Hyperchaotic System and Closed-Loop Diffusion between Blocks, Signal Processing. (2020) 171, https://doi.org/10.1016/j.sigpro.2020.107484.
10.1016/j.sigpro.2020.107484
Web of Science® Google Scholar
3 Lin X. J., Sun L., and Qu H., An Efficient RSA-Based Certificateless Public Key Encryption Scheme, Discrete Applied Mathematics. (2018) 241, 39–47, https://doi.org/10.1016/j.dam.2017.02.019, 2-s2.0-85015274859.
10.1016/j.dam.2017.02.019
Google Scholar
4 Toughi S., Fathi M. H., and Sekhavat Y. A., An Image Encryption Scheme Based on Elliptic Curve Pseudo Random and Advanced Encryption System, Signal Processing. (2017) 141, 217–227, https://doi.org/10.1016/j.sigpro.2017.06.010, 2-s2.0-85020844411.
10.1016/j.sigpro.2017.06.010
Web of Science® Google Scholar
5 Li C., Luo G., Qin K., and Li C., An Image Encryption Scheme Based on Chaotic Tent Map, Nonlinear Dynamics. (2017) 87, no. 1, 127–133, https://doi.org/10.1007/s11071-016-3030-8, 2-s2.0-84984653532.
10.1007/s11071-016-3030-8
Web of Science® Google Scholar
6 Abdulbaqi A. S., Obaid A. J., and Mohammed A. H., ECG Signals Recruitment to Implement a New Technique for Medical Image Encryption, Journal of Discrete Mathematical Sciences and Cryptography. (2021) 24, no. 6, 1663–1673, https://doi.org/10.1080/09720529.2021.1884378.
10.1080/09720529.2021.1884378
Google Scholar
7 Pourasad Y., Ranjbarzadeh R., and Mardani A., A New Algorithm for Digital Image Encryption Based on Chaos Theory, Entropy. (2021) 23, no. 3, https://doi.org/10.3390/e23030341.
10.3390/e23030341
PubMed Web of Science® Google Scholar
8 Zhao C., Wang T., Wang H., Du Q., and Yin C., Novel Image Encryption Algorithm by Delay Induced Hyper-Chaotic Chen System, Journal of Imaging Science and Technology. (2023) 1–15.
10.2352/J.ImagingSci.Technol.2023.67.4.040409
Google Scholar
9 Liu L., Jiang D., Wang X., Rong X., and Zhang R., 2D Logistic-Adjusted-Chebyshev Map for Visual Color Image Encryption, Journal of Information Security and Applications. (2021) 60, https://doi.org/10.1016/j.jisa.2021.102854.
10.1016/j.jisa.2021.102854
Google Scholar
10 Hua Z., Zhu Z., Chen Y., and Li Y., Color Image Encryption Using Orthogonal Latin Squares and a New 2D Chaotic System, Nonlinear Dynamics. (2021) 104, no. 4, 4505–4522, https://doi.org/10.1007/s11071-021-06472-6.
10.1007/s11071-021-06472-6
Web of Science® Google Scholar
11 Tang J., Zhang Z., and Huang T., Two-Dimensional Cosine-Sine Interleaved Chaotic System for Secure Communication, IEEE Transactions on Circuits and Systems II: Express Briefs. (2024) 71, no. 4, 2479–2483, https://doi.org/10.1109/tcsii.2023.3337145.
10.1109/tcsii.2023.3337145
Google Scholar
12 Tang J., Zhang Z., Chen P., Huang Z., and Huang T., A Simple Chaotic Model with Complex Chaotic Behaviors and Its Hardware Implementation, IEEE Transactions on Circuits and Systems I: Regular Papers. (2023) 70, no. 9, 3676–3688, https://doi.org/10.1109/tcsi.2023.3283877.
10.1109/TCSI.2023.3283877
Google Scholar
13 Li H., Yu S., Feng W. et al., Exploiting Dynamic Vector-Level Operations and a 2D-Enhanced Logistic Modular Map for Efficient Chaotic Image Encryption, Entropy. (2023) 25, no. 8, https://doi.org/10.3390/e25081147.
10.3390/e25081147
Google Scholar
14 Erkan U., Toktas A., Memiş S., Lai Q., and Hu G., An Image Encryption Method Based on Multi-Space Confusion Using Hyperchaotic 2D Vincent Map Derived from Optimization Benchmark Function, Nonlinear Dynamics. (2023) 111, no. 21, 20377–20405, https://doi.org/10.1007/s11071-023-08859-z.
10.1007/s11071-023-08859-z
Google Scholar
15 Feng W., He Y., Li H., and Li C., Cryptanalysis and Improvement of the Image Encryption Scheme Based on 2D Logistic-Adjusted-Sine Map, IEEE Access. (2019) 7, 12584–12597, https://doi.org/10.1109/access.2019.2893760, 2-s2.0-85061311644.
10.1109/ACCESS.2019.2893760
Web of Science® Google Scholar
16 Zhang Y. and Xiao D., Cryptanalysis of S-Box-Only Chaotic Image Ciphers against Chosen Plaintext Attack, Nonlinear Dynamics. (2013) 72, no. 4, 751–756, https://doi.org/10.1007/s11071-013-0750-x, 2-s2.0-84878622548.
10.1007/s11071-013-0750-x
Web of Science® Google Scholar
17 Wen H., Lin Y., and Feng Z., Cryptanalyzing a Bit-Level Image Encryption Algorithm Based on Chaotic Maps, Engineering Science and Technology, an International Journal. (2024) 51, https://doi.org/10.1016/j.jestch.2024.101634.
10.1016/j.jestch.2024.101634
Google Scholar
18 Lin H., Wang C., Cui L., Sun Y., Zhang X., and Yao W., Hyperchaotic Memristive Ring Neural Network and Application in Medical Image Encryption, Nonlinear Dynamics. (2022) 110, no. 1, 841–855, https://doi.org/10.1007/s11071-022-07630-0.
10.1007/s11071-022-07630-0
Google Scholar
19 El-Latif A. A. A., Abd-El-Atty B., Belazi A., and Iliyasu A. M., Efficient Chaos-Based Substitution-Box and its Application to Image Encryption, Electronics. (2021) 10, no. 12, https://doi.org/10.3390/electronics10121392.
10.3390/electronics10121392
Web of Science® Google Scholar
20 Wang X. and Su Y., Image Encryption Based on Compressed Sensing and DNA Encoding, Signal Processing: Image Communication. (2021) 95, https://doi.org/10.1016/j.image.2021.116246.
10.1016/j.image.2021.116246
Google Scholar
21 Feng W., Wang Q., Liu H. et al., Exploiting Newly Designed Fractional-Order 3D Lorenz Chaotic System and 2D Discrete Polynomial Hyper-Chaotic Map for High-Performance Multi-Image Encryption, Fractal and Fractional. (2023) 7, no. 12, https://doi.org/10.3390/fractalfract7120887.
10.3390/fractalfract7120887
Google Scholar
22 Toktas F., Erkan U., and Yetgin Z., Cross-channel Color Image Encryption through 2D Hyperchaotic Hybrid Map of Optimization Test Functions, Expert Systems with Applications. (2024) 249, https://doi.org/10.1016/j.eswa.2024.123583.
10.1016/j.eswa.2024.123583
Google Scholar
23 Wen H. and Lin Y., Cryptanalyzing an Image Cipher Using Multiple Chaos and DNA Operations, Journal of King Saud University-Computer and Information Sciences. (2023) 35, no. 7, https://doi.org/10.1016/j.jksuci.2023.101612.
10.1016/j.jksuci.2023.101612
Google Scholar
24 Feng W. and Zhang J., Cryptanalzing a Novel Hyper-Chaotic Image Encryption Scheme Based on Pixel-Level Filtering and DNA-Level Diffusion, IEEE Access. (2020) 8, 209471–209482, https://doi.org/10.1109/access.2020.3038006.
10.1109/ACCESS.2020.3038006
Google Scholar
25 Tamang J., Dieu Nkapkop J. D., Ijaz M. F. et al., Dynamical Properties of Ion-Acoustic Waves in Space Plasma and its Application to Image Encryption, IEEE Access. (2021) 9, 18762–18782, https://doi.org/10.1109/access.2021.3054250.
10.1109/ACCESS.2021.3054250
Web of Science® Google Scholar
26 Wang X. and Guan N., A Novel Chaotic Image Encryption Algorithm Based on Extended Zigzag Confusion and RNA Operation, Optics & Laser Technology. (2020) 131, https://doi.org/10.1016/j.optlastec.2020.106366.
10.1016/j.optlastec.2020.106366
Google Scholar
27 Wang X. and Chen X., An Image Encryption Algorithm Based on Dynamic Row Scrambling and Zigzag Transformation, Chaos, Solitons & Fractals. (2021) 147, https://doi.org/10.1016/j.chaos.2021.110962.
10.1016/j.chaos.2021.110962
Google Scholar
28 Wang L., Cao Y., Jahanshahi H., Wang Z., and Mou J., Color Image Encryption Algorithm Based on Double Layer Josephus Scramble and Laser Chaotic System, Optik. (2023) 275, https://doi.org/10.1016/j.ijleo.2023.170590.
10.1016/j.ijleo.2023.170590
Google Scholar
29 Sagan H., Space-filling Curves, 2012, Springer Science & Business Media.
Google Scholar
30 Zhou W., Wang X., Wang M., and Li D., A New Combination Chaotic System and its Application in a New Bit-Level Image Encryption Scheme, Optics and Lasers in Engineering. (2022) 149, https://doi.org/10.1016/j.optlaseng.2021.106782.
10.1016/j.optlaseng.2021.106782
Google Scholar
31 Feng W., Zhao X., Zhang J., Qin Z., Zhang J., and He Y., Image Encryption Algorithm Based on Plane-Level Image Filtering and Discrete Logarithmic Transform, Mathematics. (2022) 10, no. 15, https://doi.org/10.3390/math10152751.
10.3390/math10152751
Google Scholar
32 Wen H., Lin Y., Yang L., and Chen R., Cryptanalysis of an Image Encryption Scheme Using Variant Hill Cipher and Chaos, Expert Systems with Applications. (2024) 250, https://doi.org/10.1016/j.eswa.2024.123748.
10.1016/j.eswa.2024.123748
Google Scholar
33 Wen H. and Lin Y., Cryptanalysis of an Image Encryption Algorithm Using Quantum Chaotic Map and DNA Coding, Expert Systems with Applications. (2024) 237, https://doi.org/10.1016/j.eswa.2023.121514.
10.1016/j.eswa.2023.121514
Google Scholar
34 Feng W., Qin Z., Zhang J., and Ahmad M., Cryptanalysis and Improvement of the Image Encryption Scheme Based on Feistel Network and Dynamic DNA Encoding, IEEE Access. (2021) 9, 145459–145470, https://doi.org/10.1109/access.2021.3123571.
10.1109/ACCESS.2021.3123571
Google Scholar
35 Guillén-Fernández O., Tlelo-Cuautle E., de la Fraga L. G., Sandoval-Ibarra Y., and Nuñez-Perez J. C., An Image Encryption Scheme Synchronizing Optimized Chaotic Systems Implemented on Raspberry Pis, Mathematics. (2022) 10, no. 11, https://doi.org/10.3390/math10111907.
10.3390/math10111907
Google Scholar
36 Yang C. H., Wu H. C., and Su S. F., Implementation of Encryption Algorithm and Wireless Image Transmission System on FPGA, IEEE Access. (2019) 7, 50513–50523, https://doi.org/10.1109/access.2019.2910859, 2-s2.0-85065143721.
10.1109/ACCESS.2019.2910859
Web of Science® Google Scholar
37 González-Zapata A. M., Tlelo-Cuautle E., Cruz-Vega I., and León-Salas W. D., Synchronization of Chaotic Artificial Neurons and Its Application to Secure Image Transmission Under MQTT for IoT Protocol, Nonlinear Dynamics. (2021) 104, no. 4, 4581–4600, https://doi.org/10.1007/s11071-021-06532-x.
10.1007/s11071-021-06532-x
Web of Science® Google Scholar
38 Aboagye S., Ndjiongue A. R., Ngatched T. M., Dobre O. A., and Poor H. V., RIS-Assisted Visible Light Communication Systems: A Tutorial, IIEEE Communications Surveys & Tutorials. (2022) .
Google Scholar
39 Dahri F. A., Ali S., and Jawaid M. M., A Review of Modulation Schemes for Visible Light Communication, International Journal of Computer Science and Network Security. (2018) 18, no. 2.
Google Scholar
40 Talla Mbé J. H. and Woafo P., Modulation of Distributed Feedback (DFB) Laser Diode with the Autonomous Chua’s Circuit: Theory and Experiment, Optics & Laser Technology. (2018) 100, 145–152, https://doi.org/10.1016/j.optlastec.2017.09.042, 2-s2.0-85031712879.
10.1016/j.optlastec.2017.09.042
Google Scholar
41 Ndjiongue A. R., Ferreira H. C., and Ngatched T. M., Visible Light Communications (VLC) Technology, Wiley Encyclopedia of Electrical and Electronics Engineering. (2015) 1–15, https://doi.org/10.1002/047134608x.w8267.
10.1002/047134608x.w8267
Google Scholar
42 Talla Mbé J. H., Woafo P., and Fotsin H. B., Experimental Direct Modulation of a Laser Diode With a Van Der Pol Circuit and Applications, Optical Engineering. (2019) 58, no. 06, https://doi.org/10.1117/1.oe.58.6.066114, 2-s2.0-85069494737.
10.1117/1.OE.58.6.066114
Google Scholar
43 Lin H., Wang C., Yu F. et al., A Review of Chaotic Systems Based on Memristive Hopfield Neural Networks, Mathematics. (2023) 11, no. 6, https://doi.org/10.3390/math11061369.
10.3390/math11061369
Web of Science® Google Scholar
44 Nong J., Global Exponential Stability of Delayed Hopfield Neural Networks, International Conference on Computer Science and Network Technology, 2012, 193–196.
Google Scholar
45 Yu W. and Cao J., Cryptography Based on Delayed Chaotic Neural Networks, Physics Letters A. (2006) 356, no. 4-5, 333–338, https://doi.org/10.1016/j.physleta.2006.03.069, 2-s2.0-33745387345.
10.1016/j.physleta.2006.03.069
CAS Web of Science® Google Scholar
46 Choi H. and Seo S. C., Fast Implementation of SHA-3 in GPU Environment, IEEE Access. (2021) 9, 144574–144586, https://doi.org/10.1109/access.2021.3122466.
10.1109/ACCESS.2021.3122466
Google Scholar
47 Pascucci V. and Frank R. J., Global Static Indexing for Real-Time Exploration of Very Large Regular Grids, Proceedings of the 2001 ACM/IEEE Conference on Supercomputing, November 2001, Denver, CO.
Google Scholar
48 Guan Z., Li J., Huang L., Xiong X., Liu Y., and Cai S., A Novel and Fast Encryption System Based on Improved Josephus Scrambling and Chaotic Mapping, Entropy. (2022) 24, no. 3, https://doi.org/10.3390/e24030384.
10.3390/e24030384
Google Scholar
49 Zhang Q., Han J., and Ye Y., Image Encryption Algorithm Based on Image Hashing, Improved Chaotic Mapping and DNA Coding, IET Image Processing. (2019) 13, no. 14, 2905–2915, https://doi.org/10.1049/iet-ipr.2019.0667.
10.1049/iet-ipr.2019.0667
Web of Science® Google Scholar
50 Yu J., Xie W., Zhong Z., and Wang H., Image Encryption Algorithm Based on Hyperchaotic System and a New DNA Sequence Operation, Chaos, Solitons & Fractals. (2022) 162, https://doi.org/10.1016/j.chaos.2022.112456.
10.1016/j.chaos.2022.112456
Google Scholar
51 Cun Q., Tong X., Wang Z., and Zhang M., A New Chaotic Image Encryption Algorithm Based on Dynamic DNA Coding and RNA Computing, The Visual Computer. (2023) 39, no. 12, 6589–6608, https://doi.org/10.1007/s00371-022-02750-5.
10.1007/s00371-022-02750-5
Google Scholar
52 Mandal S. K. and Deepti A. R., A Cryptosystem Based on Vigenere Cipher by Using Mulitlevel Encryption Scheme, International Journal of Computer Science and Information Technologies. (2016) 7, no. 4, 2096–2099.
Google Scholar
53 Huang Z. W. and Zhou N. R., Image Encryption Scheme Based on Discrete Cosine Stockwell Transform and DNA-Level Modulus Diffusion, Optics & Laser Technology. (2022) 149, https://doi.org/10.1016/j.optlastec.2022.107879.
10.1016/j.optlastec.2022.107879
Google Scholar
54 Zhu C., A Novel Image Encryption Scheme Based on Improved Hyperchaotic Sequences, Optics Communications. (2012) 285, no. 1, 29–37, https://doi.org/10.1016/j.optcom.2011.08.079, 2-s2.0-80255123805.
10.1016/j.optcom.2011.08.079
CAS Web of Science® Google Scholar
55 Khanzadi H., Eshghi M., and Borujeni S. E., Image Encryption Using Random Bit Sequence Based on Chaotic Maps, Arabian Journal for Science and Engineering. (2014) 39, no. 2, 1039–1047, https://doi.org/10.1007/s13369-013-0713-z, 2-s2.0-84893095068.
10.1007/s13369-013-0713-z
Web of Science® Google Scholar
56 Li Z., Peng C., Li L., and Zhu X., A Novel Plaintext-Related Image Encryption Scheme Using Hyper-Chaotic System, Nonlinear Dynamics. (2018) 94, no. 2, 1319–1333, https://doi.org/10.1007/s11071-018-4426-4, 2-s2.0-85049141882.
10.1007/s11071-018-4426-4
Web of Science® Google Scholar
57 Singh P., Yadav A. K., and Singh K., Phase Image Encryption in the Fractional Hartley Domain Using Arnold Transform and Singular Value Decomposition, Optics and Lasers in Engineering. (2017) 91, 187–195, https://doi.org/10.1016/j.optlaseng.2016.11.022, 2-s2.0-84999749719.
10.1016/j.optlaseng.2016.11.022
Web of Science® Google Scholar
58 Shafique A., Ahmed J., Rehman M. U., and Hazzazi M. M., Noise-resistant Image Encryption Scheme for Medical Images in the Chaos and Wavelet Domain, IEEE Access. (2021) 9, 59108–59130, https://doi.org/10.1109/access.2021.3071535.
10.1109/ACCESS.2021.3071535
Web of Science® Google Scholar
59 Anwar M. R., Apriani D., and Adianita I. R., Hash Algorithm in Verification of Certificate Data Integrity and Security, Aptisi Transactions on Technopreneurship (ATT). (2021) 3, no. 2, 65–72, https://doi.org/10.34306/att.v3i2.212.
10.34306/att.v3i2.212
Google Scholar
60 Masood F., Driss M., Boulila W. et al., A Lightweight Chaos-Based Medical Image Encryption Scheme Using Random Shuffling and XOR Operations, Wireless Personal Communications. (2022) 127, no. 2, 1405–1432, https://doi.org/10.1007/s11277-021-08584-z.
10.1007/s11277-021-08584-z
Google Scholar
61 Kamal S. T., Hosny K. M., Elgindy T. M., Darwish M. M., and Fouda M. M., A New Image Encryption Algorithm for Grey and Color Medical Images, IEEE Access. (2021) 9, 37855–37865, https://doi.org/10.1109/access.2021.3063237.
10.1109/ACCESS.2021.3063237
Web of Science® Google Scholar
62 Fotso S. B. N., Atchoffo W. N., Nzeukou A. C., and Talla Mbé J. H., Enhanced Security in Lossless Audio Encryption Using Zigzag Scrambling, DNA Coding, SHA-256, and Hopfield Networks: a Practical VLC System Implementation, Multimedia Tools and Applications. (2024) https://doi.org/10.1007/s11042-024-20196-w.
10.1007/s11042-024-20196-w
Google Scholar
63 Djimasra F., Nkapkop J. D. D., Tsafack N. et al., Robust Cryptosystem Using a New Hyperchaotic Oscillator with Stricking Dynamic Properties, Multimedia Tools and Applications. (2021) 80, no. 16, 25121–25137, https://doi.org/10.1007/s11042-021-10734-1.
10.1007/s11042-021-10734-1
Google Scholar
64 Talla Mbé J. H., Atchoffo W. N., Tchitnga R., and Woafo P., Dynamics of Time-Delayed Optoelectronic Oscillators with Nonlinear Amplifiers and its Potential Application to Random Numbers Generation, IEEE Journal of Quantum Electronics. (2021) 57, no. 5, 1–7, https://doi.org/10.1109/jqe.2021.3093902.
10.1109/JQE.2021.3093902
Google Scholar
65 Atchoffo W. N., Talla Mbé J. H., Woafo P., and Tchitnga R., Time-delay Signature Suppression in Single Loop Optoelectronic Oscillators Based on Sine Hyperbolic Nonlinear Amplifier, Optical and Quantum Electronics. (2023) 55, no. 4, 355–367, https://doi.org/10.1007/s11082-023-04625-y.
10.1007/s11082-023-04625-y
Google Scholar
66 Talla Mbé J. H., Chiajeu Njidjou M., Talla A. F., Woafo P., and Chembo Y. K., Multistability, Relaxation Oscillations, and Chaos in Time-Delayed Optoelectronic Oscillators with Direct Laser Modulation, Optics Letters. (2024) 49, no. 5, 1277–1280, https://doi.org/10.1364/ol.516965.
10.1364/OL.516965
PubMed Google Scholar

Citing Literature

All articles

Chaotic Image Encryption Scheme Based on Improved Z-Order Curve, Modified Josephus Problem, and RNA Operations: An Experimental Li-Fi Approach

Abstract

1. Introduction

2. System and Model

2.1. Proposed Li-Fi Infrastructure

2.1.1. Transmission Process

2.1.2. Reception Process

2.2. Encryption Algorithm Foundation

2.2.1. Delayed HNN

2.2.2. SHA3-512

2.2.3. Improved Z-Order Curve-Based Permutation

2.2.4. Modified Josephus Problem–Based Permutation

2.2.5. Proposed RNA Operation

2.3. Encryption Scheme

2.3.1. Key’s Parameters and System Initial Values Generation

2.3.2. Shuffling Process

2.3.3. Diffusion Process

3. Experimental Results and Comparative Analysis

3.1. Experimental Results

3.1.1. Key Space Analysis

3.1.2. Encryption Effect

3.1.3. Statistical Analysis

3.1.3.1. Entropy Analysis

3.1.3.2. Pixels Correlation Coefficients Analysis

3.1.3.3. Histogram Analysis

3.1.4. Differential Attack

3.1.5. Peak Signal-to-Noise Ratio

3.1.6. Occlusion Attacks Analysis

3.1.7. Noise Attacks Analysis

3.1.8. Key Sensitivity Analysis

3.1.9. Time Complexity

3.1.10. Speed for the Encryption Process

3.1.11. Checksum Using SHA-256

3.1.12. Known Plaintext and Chosen Plaintext Attacks

3.2. Comparative Analysis

4. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Related

Information