Novel Soliton and Wave Solutions for the Dual-Perturbed Integrable Boussinesq Equation
Abstract
Nonlinear science represents a foundational frontier in scientific inquiry that explores the shared characteristics inherent in nonlinear phenomena. This study focused on the perturbed Boussinesq (PB) equation incorporating dual perturbation terms. Soliton solutions were deduced by leveraging the traveling wave hypothesis. Furthermore, by employing the generalized Jacobi elliptic expansion function (JEEF) method and the improved tan (Λ/2) method, diverse nonlinear wave solutions, including kink, dark, periodic, bright, singular, periodic waves, bell-shaped solitons, solitary waves, shock waves, and kink-shaped soliton solutions, were acquired. The establishment of constraint relations is detailed to delineate the criteria for the existence of these wave solutions. Notably, these solutions are innovative and present novel contributions that have not yet been documented in the literature. In addition, 2D and 3D graphics were constructed to visually elucidate the physical behavior inherent to these newly acquired exact solutions.
1. Introduction
The exploration of exact solutions to nonlinear evolution equations (NEEs) is of fundamental importance in understanding nonlinear phenomena [1–3]. NEEs are extensively applied across various scientific disciplines such as chemical diffusion dynamics [4, 5], fluid mechanics [6–8], ion acoustics [9, 10], solid-state mechanics [11, 12], nonlinear vibrations [13, 14], and atmospheric physics [15–17]. Among these equations, the Boussinesq equation serves as a prominent model for shallow water waves [18–20], and it can be reduced to the Korteweg-de Vries (abbreviated as KdV) equation [21]. Several other NEEs, including the Kawahara equation, Peregrine equation, modified KdV equation, and Benjamin–Bona–Mahoney (BBM) equation, also describe such wave phenomena. This study focuses on investigating the perturbed Boussinesq (PB) equation with power law nonlinearity.
The study of the PB equation is the central focus of this paper. Several methodologies exist for integrating NEEs, including the improved tan (Λ/2) method [22, 23], the generalized Jacobi elliptic expansion function (JEEF) method [24–26], the modified simple equation method [27], the F-expansion methods [28, 29], the auxiliary differential equation method [30, 31], and the Ansatz function method [32]. In this study, the initial approach involves employing the generalized JEEF method, specifically the traveling wave approach, to derive the solitary wave solution for the PB equation. Moreover, the improved tan (Λ/2) method will be employed to extract additional analytical solutions.
The generalized JEEF method [24–26] and the improved tan(Λ/2) method [22, 23] offer significant advantages in terms of effectiveness and versatility when compared with many traditional solution techniques used for NEEs. Unlike classical methods such as the inverse scattering transform, Hirota’s bilinear method, or the sine-cosine method, which may be restricted to specific integrable models or yield only limited types of solutions (e.g., solitary or periodic), the methods employed in this study are capable of generating a broader spectrum of exact solutions, including singular, kink-shaped, and hybrid elliptic waveforms. The generalized JEEF method systematically constructs solutions by leveraging the properties of Jacobi elliptic functions and allows for flexible balancing of nonlinear and dispersive effects. Similarly, the improved tan(Λ/2) method enhances traditional expansion techniques by incorporating a richer functional form, enabling the derivation of new classes of solutions under more general conditions. Together, these methods provide a more robust analytical framework that can handle higher-order perturbations and power-law nonlinearities effectively, which are often challenging for standard approaches. This makes them particularly suitable for exploring complex wave dynamics in perturbed nonlinear systems.
This article focuses on the integration of the PB equation, which arises in various physical phenomena such as long water waves, acoustic waves, quantum mechanics, nonlinear optics, and plasma waves using two contemporary techniques: the generalized JEEF method and the improved tan (Λ/2) method. These methods offer distinct advantages, enabling the construction of a wide range of solutions including dark, kink, periodic, singular, bright, periodic waves, solitary waves, bell-shaped solitons, shock waves, and kink-shaped solitons.
The organization of the manuscript is as follows: Section 2 establishes the theoretical framework for traveling wave solutions. In Section 3, the generalized JEEF method is formulated, and its implementation is demonstrated on the PB equation characterized by power-law nonlinearity. Section 4 presents a concise exposition of the improved tan(Λ/2) method and applies it to the same class of equations. Section 5 offers a physical interpretation of the derived wave solutions. Lastly, Section 6 provides concluding remarks and outlines potential directions for future research.
2. Proposed Framework of Traveling Waves
3. Generalized JEEF Method
-
Step 1: we consider a nonlinear PDE-expressed explicitly in terms of the dependent variable
() -
Step 2: we find a transformation that includes both scaling and translation, represented by
() -
Here, the parameter μ denotes the wave speed, and for stationary solutions, μ = 0. Equation (19) preserves its invariance under the transformation equation (20), which serves as a necessary condition for the existence of waveform solutions. The application of transformation equation (20) results in
() -
This ordinary differential equation (ODE) (21) facilitates the classification of solitary and soliton waves for the PDE (19).
-
Step 3: now, we propose the ansatz solution of ODE (21) in the following form:
() -
where the parameters βq (where q = 1, 2, …, M) can be determined, and the function Q(θ) must satisfy the relation
() -
where a1, a2, and a3 are the parameters for elliptic equation (23). The specific values for these parameters are detailed in Table 1.
-
Step 4: following this, the balance principle is employed to ascertain the value of M.
-
Step 5: we solve (the system) Qq = 0 for all values of q generating a set of parameters. The balance principle is a fundamental step in many analytical methods for solving nonlinear PDEs, including the generalized JEEF method and the improved tan(Λ/2) method. It is used to determine the appropriate form or degree of the solution Ansatz by balancing the highest-order linear derivative terms with the highest-order nonlinear terms in the governing equation. This ensures that all significant terms are properly accounted for in the solution structure and helps avoid underfitting or overfitting the solution space. By equating the degrees (or orders) of the dominant terms, the balance principle guides the construction of a consistent and solvable Ansatz, serving as a crucial preparatory step before applying the full solution technique.
Elliptic functions exhibit trigonometric characteristics for ϑ⟼0, while Table 2 illustrates hyperbolic functions as ϑ⟼1.
| No. | a1 | a2 | a3 | Q(θ) |
|---|---|---|---|---|
| 1 | 1 | −(1 + ϑ2) | 2ϑ2 | sn(θ) |
| 2 | −ϑ2(1 − ϑ2) | 2ϑ2 − 1 | 2 | ds(θ) |
| 3 | 1 − ϑ2 | 2 − ϑ2 | 2 | cs(θ) |
| 4 | 1 − ϑ2 | 2ϑ2 − 1 | −2ϑ2 | cn(θ) |
| 5 | ϑ2 − 1 | 2 − ϑ2 | −2 | dn(θ) |
| 6 | 1/4 | (ϑ2 − 2)/2 | ϑ2/2 | (sn(θ))/(1 ± dn(θ)) |
| 7 | ϑ2/4 | (ϑ2 − 2)/2 | ϑ2/2 | (sn(θ))/(1 ± dn(θ)) |
| 8 | (ϑ2 + 1)/2 | (−1)/2 | ϑcn(θ) ± dn(θ) | |
| 9 | (ϑ2 − 1)/4 | (ϑ2 + 1)/2 | (ϑ2 − 1)/2 | (dn(θ))/(1 ± sn(θ)) |
| 10 | (1 − ϑ2)/4 | (1 − ϑ2)/2 | (1 − ϑ2)/2 | (cn(θ))/(1 ± sn(θ)) |
| 11 | 1/4 | (sn(θ))/(dn(θ) ± cn(θ)) | ||
| 12 | 0 | 0 | 2 | |
| 13 | 0 | 1 | 0 |
| No. | a1 | a2 | a3 | Q(θ) |
|---|---|---|---|---|
| 1 | 1 | −2 | 2 | tanh(θ) |
| 2 | 0 | 1 | 2 | csch(θ) |
| 3 | 0 | 1 | 2 | csch(θ) |
| 4 | 0 | 1 | −2 | sech(θ) |
| 5 | 0 | 1 | −2 | sech(θ) |
| 6 | 1/4 | (−1)/2 | 1/2 | (tanh(θ))/(1 ± sech(θ)) |
| 7 | 1/4 | (−1)/2 | 1/2 | (tanh(θ))/(1 ± sech(θ)) |
| 8 | 0 | 1 | (−1)/2 | sech(θ) ± sech(θ) |
| 9 | 0 | 1 | 0 | (sech(θ))/(1 ± tanh(θ)) |
| 10 | 0 | 0 | 0 | (sech(θ))/(1 ± tanh(θ)) |
| 11 | 1/4 | 0 | 0 | (tanh(θ))/(sech(θ) ± sech(θ)) |
| 12 | 0 | 0 | 2 | |
| 13 | 0 | 1 | 0 |
3.1. Solutions to the PB Equation
Equation (26) yields a varied set of solutions for the PB equation (1), accomplished by adjusting the parameters as specified in Table 1.
Group 1: for the parameter values a1 = 1, a2 = −(1 + ϑ2), and a3 = 2ϑ2.
Group 2: for the parameter values a1 = −ϑ2(1 − ϑ2), a2 = 2ϑ2 − 1, and a3 = 2.
Group 3: for the parameter values a1 = 1 − ϑ2, a2 = 2 − ϑ2, and a3 = 2.
Group 4: for the parameter values a1 = 1 − ϑ2, a2 = 2ϑ2 − 1, and a3 = −2ϑ2.
Group 5: for the parameter values a1 = ϑ2 − 1, a2 = 2 − ϑ2, a3 = −2.
Group 6: for the parameter values a1 = (1/4), a2 = ((ϑ2 − 2)/2), a3 = (ϑ2/2).
Group 7: for the parameter values a1 = (ϑ2/4), a2 = ((ϑ2 − 2)/2), and a3 = (ϑ2/2).
Group 8: for the parameter values
Group 9: for the parameter values a1 = ((ϑ2 − 1)/4), a2 = ((ϑ2 + 1)/2), a3 = ((ϑ2 − 1)/2).
Group 10: for the parameter values a1 = ((1 − ϑ2)/4), a2 = ((1 − ϑ2)/2), and a3 = ((1 − ϑ2)/2).
Group 11: for the parameter values
Group 12: for the parameter values a1 = 0, a2 = 0, and a3 = 2.
Group 13: for the parameter values a1 = 0, a2 = 1, a3 = 0.
4. Improved tan(Λ(θ)/2) Method
-
Step 1: consider a nonlinear PDE-expressed explicitly in terms of the dependent variable
() -
Step 2: seek a transformation
() -
Here, the parameter μ denotes the wave speed, and for stationary solutions, μ = 0. Using transformation equation (66), one can get
() -
This ODE (67) facilitates the classification of solitary and solitons for the PDE (65).
-
Step 3: now, we propose the ansatz solution of the ODE (67) in the following form:
() -
where ci(0 ≤ i ≤ M) and di(1 ≤ i ≤ M) are the constants to be evaluated later. The function Λ = Λ(θ) satisfies the ODE
() -
Following are some special solutions of equation (69).
-
Case 1: for and δ2 − δ3 ≠ 0,
() -
Case 2: for and δ2 − δ3 ≠ 0,
() -
Case 3: for , δ2 ≠ 0 and δ3 = 0,
() -
Case 4: for , δ3 ≠ 0 and δ2 = 0,
() -
Case 5: for , δ2 − δ3 ≠ 0 and δ1 = 0,
() -
Case 6: for δ1 = 0 and δ3 = 0,
() -
Case 7: for δ2 = 0 and δ3 = 0,
() -
Case 8: for ,
() -
Case 9: for δ1 = δ2 = δ3 = ic0,
() -
Case 10: for δ1 = δ3 = ic0 and δ2 = −ic0,
() -
Case 11: for δ3 = δ1,
() -
Case 12: for δ1 = δ3,
() -
Case 13: for δ3 = −δ1,
() -
Case 14: for δ2 = −δ3,
() -
Case 15: for δ2 = 0, δ1 = δ3,
() -
Case 16: for δ1 = 0 and δ2 = δ3,
() -
Case 17: for δ1 = 0 and δ2 = −δ3,
() -
Case 18: for δ1 = 0 and δ2 = 0,
() -
where δ1, δ2, δ3, and ci, di(i = 1, 2, …, M) are to be valued.
-
-
Step 4: then, the balancing principle is used to identify M.
-
Step 5: we solve the system Qq = 0 for all q values and yields a set of parameters.
4.1. Implementation of the Method for the PB Equation (1)
-
Set 1: δ1 = (1/2)d1(δ2 + δ3)/d2, δ2 = δ2, δ3 = δ3, , c1 = 0, c2 = 0, d1 = d1, d2 = d2, k = k, r = r, ρ = ρ, , .
() -
where δ1, δ2, and δ3 represent arbitrary constants, and θ = x − νt. Employing (91) in conjunction with Families 1 − 18 yields
()()()()()()()()()()()()()()()()()() -
Set 2: δ1 = 0, δ2 = δ2, δ3 = δ3, k = k, r = r, ρ = ρ, c0 = (2/3)(c2(δ2 + δ3))/(δ2 − δ3), c1 = 0, c2 = c2, d1 = 0, , , .
() -
where δ1, δ2, and δ3 represent arbitrary constants, and θ = x − νt. Employing equation (110) in conjunction with Families 1 − 18 yields
()()()()()()()()()()()()()()()()()()
5. Physical Interpretations of the Solutions
This section presents graphical illustrations of selected solutions derived through the improved tan (Λ/2) method, encompassing traveling wave solutions characterized by rational, trigonometric, exponential, and hyperbolic functions. These visualizations offer valuable insights into the dynamic behavior described by the original equation (1), thereby contributing to the understanding of soliton propagation in relevant physical contexts. A rich assortment of soliton solutions, shock waves 1, periodic wave solutions 2-5, kink, periodic, dark, bright, and singular solitons, has been observed by appropriately adjusting the free parameters. Moreover, employing the generalized JEEF method yielded a diverse range of solutions, including periodic wave solutions and soliton solutions. The graphical representations show various traveling waveforms, such as periodic waves, solitary waves, bell-shaped solitons, and shock waves, with specific emphasis on kink-shaped solitons. The shallow water-wave characteristics inherent in these solutions are demonstrated in Figures 1, 2, 3, 4, and 5.
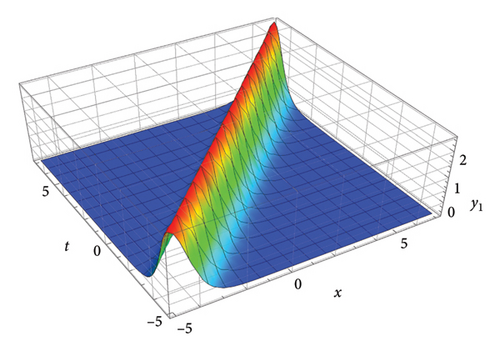
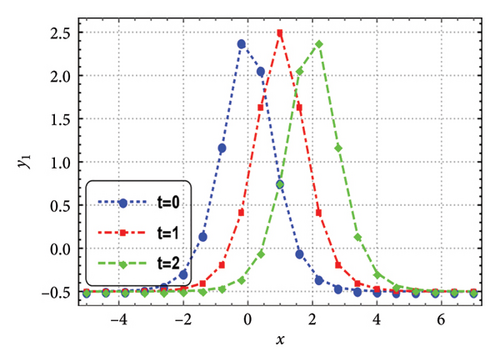
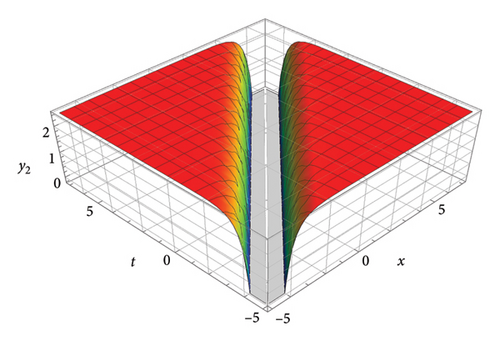
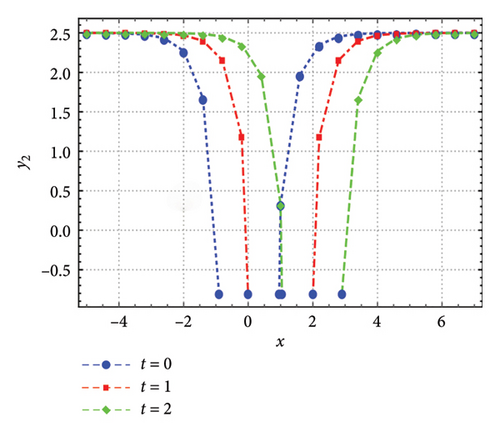
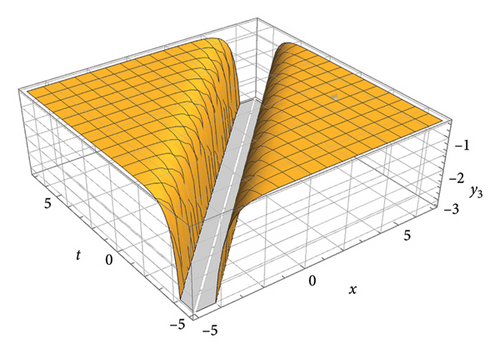

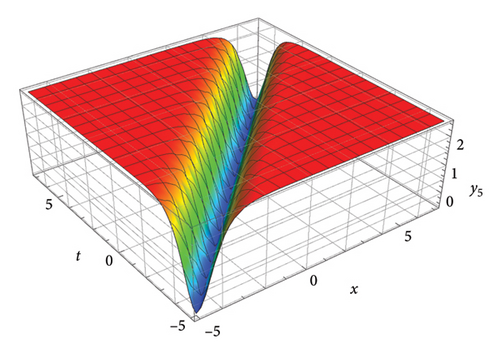
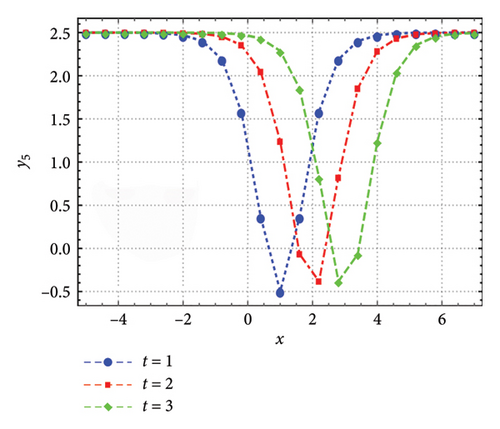
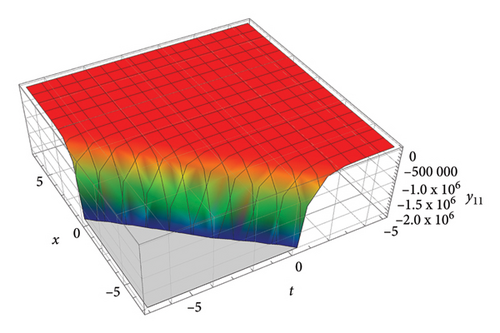
6. Discussion and the Conclusions
The systematic resolution of the nonlinear equation (23) remains elusive. Nevertheless, the adoption of an ansatz featuring three arbitrary parameters—a1, a2, and a3—proves judicious owing to the ensuing solution expressible in terms of specialized functions. In particular, the functions of the generalized JEEF method are more general to nonlinear, such as domains, and converge to well-known expressions such as sech θ and tanh θ under specific limiting conditions, characterizing phenomena such as solitary and shock wave propagation. The determination of the constant βq in equation (22) is dependent on the intrinsic characteristics of the differential equations. Different solution classes, delineated by the values of a1, a2, and a3, are expounded upon in Cases 1–13.
In this investigation, the incorporation of Jacobi elliptic functions has proven instrumental in deducing solutions for the PB equation, yielding both periodic wave and multiple soliton solutions. The obtained results encompass a diverse array of novel traveling waveforms, including periodic waves, solitary waves, bell-shaped solitons, and shock waves, which are denoted as kink-shaped solitons.
The improved tan (Λ/2) method has emerged as a notably fruitful and significant as it possesses a diverse array of soliton solutions. Noteworthy among these are dark, bright, singular, demonstrated visually soliton solutions for the PB equation (1), as visually demonstrated. Thus, this method was facilitated through the utilization of Maple software. Importantly, our application of the improved tan (Λ/2) method to this model represents a novel contribution to the field. The soliton solutions elucidated for this work’s PB equation (1) are unprecedented in the existing literature. Consequently, these findings underscore the efficacy of both the generalized JEEF and the improved tan (Λ/2) method as valuable tools for analytically investigating a wide spectrum of nonlinear PDEs, spanning mathematical physics, optical fibers, and engineering disciplines. Moreover, these methodologies hold promise for applications across diverse fields such as mathematical biology and physics, offering novel solutions that deepen our understanding of dynamic frameworks associated with optical phenomena and other physical phenomena. In future, the authors are interested to use machine learning techniques [35–37] to deal with the same model.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through a large research project under grant number RGP2/55/46. The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number “NBU-FFR-2025-1102-08.”
Open Research
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.




