Computational and Mathematical Methods
Volume 2025, Issue 1 1087525
Research Article
Open Access

Estimating the Trends of Volatility in the Risk Equity Market Over the Short and Long Terms

Valeriana Lukitosari, 

Corresponding Author

Valeriana Lukitosari

Industrial and Financial Mathematics Laboratory , Department of Mathematics , Sepuluh Nopember Institute of Technology , Surabaya , Indonesia , its.ac.id

Search for more papers by this author
Eva O. Pristia, 

Eva O. Pristia

Industrial and Financial Mathematics Laboratory , Department of Mathematics , Sepuluh Nopember Institute of Technology , Surabaya , Indonesia , its.ac.id

Search for more papers by this author
Sentot D. Surjanto, 

Sentot D. Surjanto

Industrial and Financial Mathematics Laboratory , Department of Mathematics , Sepuluh Nopember Institute of Technology , Surabaya , Indonesia , its.ac.id

Search for more papers by this author
Amirul Hakam, 

Amirul Hakam

Industrial and Financial Mathematics Laboratory , Department of Mathematics , Sepuluh Nopember Institute of Technology , Surabaya , Indonesia , its.ac.id

Search for more papers by this author
Suhud Wahyudi, 

Suhud Wahyudi

Industrial and Financial Mathematics Laboratory , Department of Mathematics , Sepuluh Nopember Institute of Technology , Surabaya , Indonesia , its.ac.id

Search for more papers by this author
First published: 17 March 2025
https://doi.org/10.1155/cmm4/1087525
Academic Editor: Rajesh Kumar

Abstract

Market fluctuations in the stock sector are common. The possible loss that investors may incur because of their investment activity is referred to as investment risk. Returns on investments may fall short of expectations due to a variety of circumstances. Fit of the model to the data; performance in representing volatility, prediction, stability, and analysis; and interpretation goals are all factors to consider. This study investigates the volatility of the Indonesian composite index (ICI) using the GARCH-MIDAS model, integrating daily ICI returns with monthly macroeconomic indicators: Indonesian bank interest rates (BIIR), consumer price index (CPI), effective federal fund rate (EFFR), and inflation rate (IR). We begin by graphically analysing the trends in ICI returns and macroeconomic variables to identify potential patterns and shifts. Descriptive statistics offer a detailed numerical summary, setting the stage for in-depth empirical analysis. The long-run component of stock market volatility is estimated using the GARCH-MIDAS model, with macroeconomic variables included to capture their impact on market fluctuations. Maximum likelihood estimation (MLE) is employed to estimate the model parameters, ensuring a robust fit to the observed data. Our findings indicate that the EFFR has the most significant impact on ICI volatility, contrary to previous studies. Forecasting performance is evaluated using mean squared error (MSE) and mean absolute error (MAE), confirming the superior predictive capability of the EFFR variable. The study assesses risk using value at risk (VaR) for the ICI, incorporating the EFFR to account for macroeconomic influences on market volatility. VaR values at 99% and 95% confidence levels provide insights into potential maximum losses, aiding in informed investment decision-making. This research enhances knowledge of the relationship between macroeconomic variables and stock market volatility, providing investors and policymakers with important information for risk management and investment strategy optimization in the Indonesian equity market.

1. Introduction

Currently, there are many investment instruments that can be selected according to needs. Investment keeps money moving and rotating so that it can bring benefits both in the long term and in the short term. Stock investment is a small capital investment and can be done at any time. Stock investment is certainly able to provide benefits for investors. But so far, most people talk about the benefits too often, even though behind that there are also risks that need to be considered. Paying attention to the risks of investing in stocks is not something that should make investors afraid. However, by understanding the risks, investors can avoid large investment losses and can even maintain the investment profits that have been obtained so that they are not reduced due to risk [1].

In general, risk and investment go along with one another regarding stock investments. This is because demand and supply for shares are what determine share prices, and these two components are affected by both internal and external (macroeconomic) forces. Every investor should therefore analyse stock volatility and the relationship between profit potential and risk. The concept of value at risk (VaR) is discussed in depth, covering its theoretical foundations, practical applications, and role in financial risk management [1]. This is founded on the idea that in risk management, risk is more significant than earning risk [2–4]. VaR is a measure of the loss because of market movements.

A stock index is a benchmark used to assess the performance of share price changes. A stock index is a metric used in statistics to represent the total price movement of a collection of stocks that are chosen using specific criteria and methods and examined on a regular basis. The “Indonesian composite index” (ICI) is one of the 34 categories of stock indexes that are officially recognized on the Indonesia Stock Exchange. The key benchmark for the performance of stock investments in Indonesia is the ICI, an index that tracks and combines the price movements of all shares on the Indonesia Stock Exchange [5]. The stock index’s data consists of time series or time-oriented data. Since time series regression models typically analyse data using samples with the same frequency, they are unable to directly employ high-frequency data when some of the available variables have lower frequencies.

The evolution of volatility models highlights the potential of the generalized autoregressive conditional heteroskedasticity (GARCH) model to capture volatility clustering in financial time series, as it extends Engle’s ARCH model [6]. To determine volatility in the present or the future, this model incorporates the impact of past volatility. Nelson [7] developed the EGARCH (exponential generalized autoregressive conditional heteroskedasticity) model, which improves upon GARCH by capturing asymmetries in volatility, allowing for different responses to positive and negative shocks. Despite its advantages, EGARCH has limitations, including its inability to incorporate macroeconomic variables over varying time horizons directly. The mixed data sampling regression, also known as the MIDAS regression, was created by Ghysels et al. [8] and directly accommodates sample variables with varying frequencies. The same model is fed data from various frequencies via MIDAS. With the use of MIDAS, it is possible to merge macroeconomic data that is only recorded on a monthly or quarterly basis with high-frequency return data. The GARCH-MIDAS model was further developed by Engle et al. [9]. The GARCH-MIDAS model links daily observations to less frequent variables.

The study on the application of GARCH-MIDAS to time series data was carried out by several researchers such as Girardin and Joyeux [10], Naumann et al. [11], Fang et al. [12], Zhou et al. [13], Liu et al. [14], and Yang et al. [15]. Based on previous research, GARCH-MIDAS performs well in predicting volatility. In many facets of finance, such as risk and asset management, financial market volatility is essential [16]. Therefore, it is crucial to perform research on stock market volatility utilizing the GARCH-MIDAS model and adding other variables in line with Indonesian conditions. The variables considered in this study set it apart from earlier studies.

The analysis utilizes ICI return variables as stock market data alongside interest rate, consumer price index (CPI), effective federal fund rate (EFFR), and inflation rate (IR) variables as macroeconomic indicators. To quantify risk, the VaR of the ICI is calculated, providing an estimate of the maximum potential investment loss.

For volatility estimation, the GARCH-MIDAS model is employed due to its distinctive ability to integrate information across multiple time scales. This approach is particularly suited to the ICI, as it combines high-frequency stock return data with lower frequency macroeconomic indicators. Unlike traditional models, GARCH-MIDAS captures both short-term market fluctuations and long-term economic influences, offering a comprehensive evaluation of volatility dynamics. This dual-frequency framework is especially valuable for analysing financial markets, such as Indonesia’s, where macroeconomic factors significantly shape market volatility. These shortcomings necessitate models like GARCH-MIDAS, which integrate both short-term market dynamics and long-term macroeconomic influences, offering a more comprehensive approach for analysing volatility driven by multifrequency data. The GARCH-MIDAS model bridges these gaps by linking economic conditions to market volatility, offering enhanced interpretability and relevance for macrofinancial analysis.

In addition to conventional techniques, the current trend of artificial intelligence (AI) models in forecasting offers insightful information. An AI-based model identifies and models key factors influencing sales volume by combining macroeconomic variables and price data on iron and steel industry sales [17]. The purpose of this paper is to illustrate the value of applying sophisticated adaptive forecasting models, like our GARCH-MIDAS technique, in the context of complex and variable data. Sophisticated AI models have shown significant promise in recent years for predicting complex nonlinear systems in a variety of domains. An innovative approach to handling nonlinear dynamics in wind speed data can significantly improve the efficiency of wind energy usage AI methods [18, 19]. By considering both short-term and long-term variations, these models successfully capture complex relationships and provide in-depth information on data with high volatility and sophisticated dynamics. This strategy is like the focus of our study, which uses GARCH-MIDAS models to address a comparable problem in financial volatility forecasting for the Indonesia Composite Stock Price Index. For the nonlinear and complex nature of financial markets, the GARCH-MIDAS model works effectively by combining low-frequency macroeconomic variables with high-frequency stock data. Drawing on the methodology used in chaotic system forecasting, our study contributes to the literature by showing how a robust and adaptive model can improve volatility prediction in emerging markets.

The main contributions of this research are as follows:
  • •

    Introduction of the GARCH-MIDAS model for ICI: applies the GARCH-MIDAS model to analyse the volatility of the ICI, integrating daily returns with monthly macroeconomic indicators.

  • •

    Comprehensive integration of macroeconomic variables: incorporated Indonesian bank interest rates (BIIR), CPI, EFFR, and IR to evaluate their impact on stock market volatility.

  • •

    Identification of significant macroeconomic influences: finds that the EFFR has the most substantial impact on ICI volatility, contrasting with previous research findings.

  • •

    Enhanced risk assessment and forecasting: utilizes VaR to quantify potential maximum losses and employment mean squared error (MSE) and mean absolute error (MAE) to demonstrate superior forecasting performance with the EFFR variable, offering valuable insights for investment strategies and risk management. Provides insightful information to help investors and policymakers manage risks and maximize investment plans in the Indonesian equity market.

The research delves into an explication of the remaining sections outlined. In the second section, Materials and Methods, the study navigates through the methodological terrain, elucidating key frameworks such as GARCH-MIDAS, maximum likelihood estimation (MLE), forecasting methodologies, and the theoretical underpinnings of VaR. Subsequently, the focus shifts to the Data Description section, offering a comprehensive overview of the dataset under examination. Moving forward, the Results and Discussion section engages in rigorous analysis, encompassing empirical investigations, parameter estimation, detailed discussions on MLE, and thorough examinations of forecasting calculations, supplemented by insights into the application of VaR within the equity market domain. Finally, the Conclusions section ties together the research journey, encapsulating the study’s findings, implications, and avenues for future exploration. Figure 1 presents the study’s framework.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Flowchart of this study.

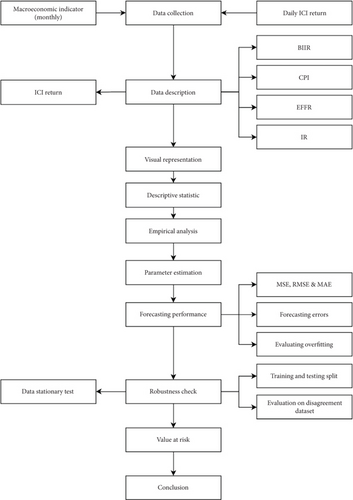
2. Materials and Methods

2.1. GARCH-MIDAS

We present simple examples/scenarios to demonstrate the differences between conventional GARCH and GARCH-MIDAS models. This example might help to grasp each model’s distinct traits and advantages in capturing volatility patterns across varied data frequencies. These pictures illustrate the distinguishing elements of each model and contribute to a clearer understanding of their relevance in capturing and forecasting volatility across various time frames.

Scenario: forecasting monthly volatility using daily high-frequency data in financial markets.

Model implementation:
  • a.

    Traditional GARCH Model: A standard GARCH (1,1) model might use only lagged daily squared returns to forecast future daily volatility. .

  • b.

    GARCH-MIDAS model: The GARCH-MIDAS model can extend this by incorporating daily returns (high-frequency data) as MIDAS regressors to predict monthly volatility. .

Here, represents the lagged squared returns (used in traditional GARCH), and zt−j are daily returns (high-frequency data) weighted by MIDAS coefficients γj.

To illustrate the difference between a traditional GARCH model and a GARCH-MIDAS model using a numerical example, let us consider a simplified scenario of forecasting daily stock volatility using GARCH only versus GARCH-MIDAS with daily and monthly data.

Scenario: We want to forecast the volatility of daily returns (rt) for a stock using historical data. We will compare two approaches:
  • a.

    GARCH only: using a traditional GARCH (1,1) model.

  • b.

    GARCH-MIDAS: incorporating both daily returns and monthly data into the volatility forecast.

Data:
  • -

    Daily returns (rt): assume we have daily returns data for a stock over a period.

  • -

    Monthly volatility (σt−M): we also have monthly volatility data for the same stock.

  • a.

    GARCH only model: a standard GARCH (1,1) model is defined by

  • b.

    GARCH-MIDAS model: incorporate monthly volatility (σt−M) as an additional regressor into the GARCH model: .

Numerical example: we use hypothetical data to demonstrate the forecasting process.

Assume:
  • -

    Daily returns (rt): r1 = 0.02, r2 = −0.01, r3 = 0.03, r4 = −0.005, r5 = 0.015.

  • -

    Monthly volatility (σt−M): σ1−M = 0.08, σ2−M = 0.07, σ3−M = 0.09.

  • a.

    GARCH only model: using the GARCH (1,1) model:

Initialize parameters: ω = 0.0001, α = 0.1, β = 0.8.

Compute volatility forecast for t = 6:
  • -

    .

  • -

    .

  • b.

    GARCH-MIDAS model: using the GARCH-MIDAS model with monthly volatility:

    • -

      Initialize parameters: ω = 0.0001, α = 0.1, γ = 0.5 (hypothetical weight for monthly volatility).

    • -

      Compute volatility forecast for t = 6:

Comparison:
  • a.

    GARCH only: uses only lagged squared returns to forecast volatility, ignoring the impact of monthly data.

  • b.

    GARCH-MIDAS: incorporates monthly volatility data into the forecast, providing a more comprehensive and potentially accurate estimate of volatility.

This numerical example demonstrates how the GARCH-MIDAS model can leverage additional data (monthly volatility) to improve volatility forecasts compared to the traditional GARCH model, which relies solely on high-frequency data. The choice of parameters (α, γ) would depend on the specific data characteristics and the relationship between daily and monthly volatility. In practice, these parameters would be estimated using historical data to optimize forecasting performance.

In this example, the GARCH-MIDAS model demonstrates its superiority over traditional GARCH models by effectively utilizing high-frequency data to enhance the forecasting of volatility at a lower frequency (monthly level). By leveraging the MIDAS regression framework, the GARCH-MIDAS model captures the nuanced relationship between daily and monthly data dynamics, ultimately leading to more accurate and responsive volatility forecasts in financial markets.

Engle et al. [9] developed the GARCH-MIDAS model using the MIDAS framework to investigate markets with changing times. Daily observations with a high frequency can be linked to macroeconomic variables with a lower frequency using the GARCH-MIDAS model. By assuming the return forecast on the i-th day of the t-month , the general form of the GARCH-MIDAS model is given by the following [11]:
()
()

Equation (1) incorporates this mean return, allowing investors to make informed decisions based on expected returns, where μ is the average of time-invariant returns. The mean return represents the expected average return on an investment. In financial markets, investors are often interested in estimating the average return of an asset or portfolio. is the return volatility of the i-th day of the t-th month. A trade price series’ degree of fluctuation over time is measured by its volatility. Volatility is a tool used by risk managers and investors to evaluate the degree of risk involved in an investment. The square root of the volatility provides a forecast of the uncertainty or risk associated with the return. This information is crucial for risk management and portfolio optimization. is the random error of the i-th day of the t-th month; the random error term captures unobservable factors affecting the return. In real cases, financial markets are influenced by various unpredictable events, news, or market shocks. The inclusion of the random error term allows the model to account for these unforeseen factors, making the return forecast more robust and reflective of market dynamics. εi,t|ϕi−1,t ~ N(0, 1), Nt is the number of days in 1 month.

Equation (2) in the GARCH-MIDAS model represents the calculation of the volatility (), incorporating both short-run and long-run components. gi,t is a short-run component with high frequency data that represents daily ICI data that uses the GARCH model (1,1). The long-run component represents (τt) the influence of lower frequency macroeconomic variables on volatility. This equation has practical benefits in real cases, especially in the context of financial markets.

Equation (3) represents the calculation of the short-run component gi,t as follows:
()
with α > 0, β ≥ 0, and α + β + γ/2 < 1. is an indicator function the same as 1 if Condition A is satisfied and 0 if otherwise. This term (1 − α − β − γ/2) represents the baseline volatility level. It is the sum of all the parameters subtracted from 1. It establishes a base level of volatility before considering other factors. This part () adjusts the baseline volatility based on whether the return (ri−1,t) from the previous day is less than the average return (μ); α controls the weight of the past volatility in the short run and γ adjusts the impact of the past volatility based on whether the return was negative or not.
Furthermore, to help capture long-term volatility trends or patterns by including macroeconomic variables over time, as seen in Equation (4), it is important to understand the underlying factors that drive changes in volatility. τt is a long-run component with the low frequency that Xt−k is representing macroeconomics as monthly, quarterly, or even annually. This is estimated using MIDAS regression.
()
in which φk(ω1, ω2) is the weighting scheme that is described as follows:
()
Equation (5) determines how much weight each past variable should contribute to the long-run component. The parameters ω1 and ω2 control the shape of the weighting scheme. Conrad and Loch’s [20] earlier research established weights with ω1 = 1 as a limitation. The following is a limited weighting scheme that has been obtained:
()

Equation (6) plays a crucial role in determining how past observations contribute to the estimation of volatility in the GARCH-MIDAS model, providing flexibility and control over the weighting of historical data.

2.2. MLE

Parameter estimation is carried out using MLE. By maximizing the likelihood function, MLE can determine the parameter value. Likelihood function of a random sample of x1, x2, ⋯, xT from f(x; θ) is defined as follows:
()
Equation (7) is calculated by multiplying the probabilities of each data point (xi) occurring according to the assumed probability distribution with parameters (θ). It simply represents how well the chosen parameters explain the observed data. The value from at Ω, whereas is the MLE of θ. is in θ if it satisfies the following condition [21]:
()

Equation (8) finds the values of parameters (θ) that make the observed data most likely. The goal is to maximize the likelihood function, which means finding the parameters that make the observed data the most probable.

MLE is widely utilized in many disciplines, including data science, statistics, economics, and social sciences. If the observed data comes from a known or planned probabilistic distribution, this method enables the acquisition of optimal parameter estimation based on the seen data.

2.3. Likelihood Function for Normal Distribution

When a function is unimodal, symmetric, and cantered on μ and the data distribution can be observed from σ2, the function is said to be normally distributed. The density function of is as follows [2]:
()
Equation (9) delineates the probability of encountering a value x inside a normally distributed dataset characterized by mean μ and standard deviation σ. Then, the likelihood function of normal distribution is as follows:
()
where σ is the standard deviation and μ is the mean. Equation (10) is useful for estimating parameters using likelihood maximization, making it an important tool in statistical modelling, hypothesis testing, risk management, and data analysis in a variety of domains.

2.4. Forecasting Performance

Observing how forecasting outcomes function is crucial in the forecasting idea. Calculating the error from the results of the prediction is a typical practice. This is done to assess performance, evaluate different forecasting approaches, and make forecasting decisions.

2.5. Mean Squared Forecast Error

A forecasting context uses the evaluation metric known as MSE to calculate the MSE between anticipated values and actual values. MSE is frequently used to assess the effectiveness of forecasting models and to contrast various forecasting models. The definition of MSE is as follows:
()
where RVi represents the actual daily volatility, which can be calculated with the interday return square i-th day; represents the result of return forecast volatility (τtgi,t); and n is the number of observation data [15]. The forecasting model performs better at guessing the true value when the MSE value is lower. The most accurate forecasting model can be selected by comparing and evaluating the quality of predictions made by several forecasting models using MSE. The MSE is a widely used statistic for evaluating the accuracy and predictive analytic representation of financial models in Equation (11). Its advantages include a straightforward measure of prediction accuracy, sensitivity to deviations, and applicability in a wide range of industries, including finance, forecasting, and model optimization.

MSE offers several advantages that make it a widely adopted metric in regression analysis and predictive modelling. First, MSE calculations are simple and straightforward, making them easy to implement across different modelling frameworks. Second, MSE has a quadratic dimension and is always positive since it squares the differences between actual and predicted values, ensuring a non-negative result. This characteristic allows for clearer interpretation and easier application of mathematical statistics compared to metrics that may yield negative values. Third, MSE is one of the most used performance metrics, with numerous algorithms and modelling frameworks optimizing models based on this criterion. Its widespread adoption contributes to its ease of understanding and application in various research contexts, supported by numerous studies [22].

In addition to MSE, root mean squared error (RMSE) is another essential evaluation metric derived from MSE by taking its square root. Unlike MSE, expressed in squared units of the dependent variable, RMSE provides a measure of error in the same units as the original data, making it more interpretable for practical applications. RMSE penalizes larger errors more heavily due to its quadratic nature, making it particularly useful when significant deviations are critical to understanding model performance. MSE and RMSE are pivotal in model evaluation, with their complementary properties providing robust insights into predictive accuracy and model fit.

2.6. MAE

In a forecasting setting, the MAE is a measurement statistic that is used to assess the absolute mean error between anticipated values and actual values. Due to its very straightforward and straightforward formula, MAE is simple to calculate and interpret. MAE is defined as follows:
()
where RVi denotes the realized daily volatility, which is determined by squaring the intraday returns for the i-th day. Meanwhile, represents forecasted volatility of returns, expressed as (τtgi,t), with n referring to the total number of observations [15]. The performance of the forecasting model in predicting the true value improves with the decreasing of MAE values. To select the most accurate forecasting model, MAE can be used to assess and compare the accuracy of predictions made by several forecasting models. The adjusted MAE (Equation (12)) is a valuable statistic to evaluate the precision of forecasting models, with advantages such as robustness to outliers and easy interpretability. Its applications are diverse, ranging from time series analysis to finance and predictive modelling.

2.7. VaR

Risk can be defined as the erratic nature of outcomes that may reflect the value of assets, equity, or income. Although risks can cause losses if not anticipated. Even so, risks might present opportunities for profit when appropriately managed. Credit risk, operational risk, and market risk are the three primary categories of risk in the financial sector. Market risk and VaR are closely related, although other types of risk can also benefit from its use [6]. J. P. Morgan came up with VaR in the 1980s. VaR is a metric for losses brought on by changes in the market. VaR is frequently used in risk management to assess and manage the risk of impairment in a financial asset, portfolio, or trading position. VaR with a loss probability of p can be written as follows:
()
where σ is the standard deviation of return, γ(p) is the level of significance of the probability function, and μ is the mean return [2]. Equation (13) expresses the possible loss at a given confidence level using the mean return, standard deviation, and z-score. It is an important instrument in financial risk management because it allows institutions to assess and control their exposure to market risk.

2.8. Data Description

In this research, we utilize a comprehensive dataset that includes daily returns of the ICI and key macroeconomic indicators. The macroeconomic variables comprise BIIR, CPI, EFFR, and IR. Daily ICI return data span from January 2, 2018, to December 30, 2022, while macroeconomic data are captured monthly from January 2018 to December 2022.

Figure 2 graphically represents the trends and fluctuations in the daily returns of the ICI over the specified time. This visual depiction allows for an intuitive understanding of the dynamics in ICI returns, aiding in the identification of potential patterns or shifts in market behaviour. The figure serves as a valuable tool for uncovering insights into the volatility and performance of the Indonesian stock market. The y-axis displays data based on the title, while the x-axis displays the period (months).

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Indonesian composite index (ICI).

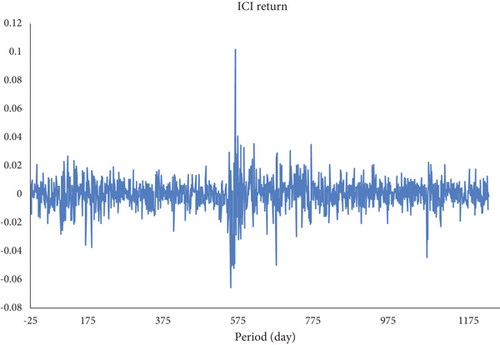
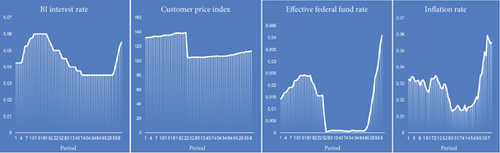
Figure 3 illustrates the monthly trends of four key macroeconomic indicators from January 2018 to December 2022: BIIR, CPI, EFFR, and IR. This graphical representation enables the visualization of potential patterns and shifts in these variables over time, offering insights into their behaviour and interconnections. Table 1 provides a comprehensive set of descriptive statistics for both Figures 2 and 3. The table includes key statistical measures such as mean, standard deviation, minimum, maximum, and quartiles for each variable—return ICI, BIIR, CPI, EFFR, and IR. This tabular representation provides a nuanced numerical summary of the central tendencies and distributional characteristics of the dataset. It serves as a quick reference for understanding the variability and characteristics of the ICI returns and macroeconomic variables, laying the groundwork for more in-depth analysis and interpretation. The inclusion of these statistics enhances our quantitative understanding of the dataset, supporting robust research findings and conclusions.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Trends in macroeconomic indicators (BIIR, CPI, EFFR, and IR) from January 2018 to December 2022.
Table 1. Descriptive statistic.
Variable Mean Max Min SD Skew Kurt Obs
Return ICI 0.0001 0.0970 −0.0681 0.0108 −0.1296 9.3851 1219
BIIR 0.0450 0.0600 0.0350 0.0092 0.3816 −1.3356 60
CPI 118.7287 139.07 104.33 14.0044 0.3727 −1.7829 60
EFFR 0.0123 0.0410 0.0005 0.0109 0.4032 −0.7527 60
IR 0.0281 0.0595 0.0132 0.0115 0.8373 0.5893 60

3. Results and Discussion

3.1. Empirical Analysis

Analysing real-world data allows empirical analysis to validate theories, test hypotheses, and provide practical insights. A theoretical framework for examining how systemic risk management affects the ideal wealth policies and equilibrium asset prices of financial institutions is presented by Bernard and Cui [17]. We looked at how macroeconomic variables affect the stock market’s long-run volatility. The long-run component is estimated in accordance with Equation (4), which can be written as follows:
()
()
()
()

The empirical analysis for Equations (14)–(17) involves estimating the long-run component of volatility using macroeconomic variables and assessing the model’s performance in capturing the dynamics of stock market volatility over time. By predicting the long-run component of volatility using BIIR, CPI, EFFR, and IR, this equation captures the impact of variable changes on stock market volatility over time. It helps to understand how monetary policy influences market volatility.

3.2. Parameter Estimation

The normal distribution MLE is employed in line with Equation (10) to estimate the parameters of the GARCH-MIDAS model, and the number of lags is set to K = 12, since it is assumed that the ICI return data between January 3, 2018, and December 30, 2022, is normally distributed. As a result, the following is the log-likelihood equation:
()
()

Equation (18) plays a crucial role in the estimation, and the log-likelihood function provides a measure of how well the GARCH-MIDAS model fits the observed data. Higher values of the log-likelihood indicate a better fit, suggesting that the model parameters effectively capture the underlying distribution of the ICI returns. On the other hand, Equation (19) represents the negative log-likelihood function. It is used for parameter estimation in the GARCH-MIDAS model. The negative log-likelihood function is typically minimized to find the maximum likelihood estimates of the model parameters as expressed in Algorithm 1. So, while both equations are related to likelihood functions, Equation (18) calculates the joint likelihood for the entire dataset, while Equation (19) calculates the negative log-likelihood for parameter estimation. Table 2 displays the estimation outcomes for each parameter in the training data.

    Algorithm 1: Likelihood function

  • import numpy as np

  • import pandas as pd

  • def betaWeight ( w1 : float , w2 : float , K : int ) -> float:

  •   array = []

  •   for k in range (1 , K +1) :

  •     array . append ((( k / K )  ∗∗ ( w1 - 1) )  ∗ ((1 - ( k / K

  •       ) )  ∗∗ ( w2 - 1) ) )

  •   array = np . array ( array ) / np . sum ( array )

  •   return array [: , np . newaxis]

  • def lagMatrix ( df : pd . DataFrame , K : int ) -> pd . DataFrame :

  •   array = np . zeros (( df . shape [0] , K ) )

  •   for i in range (K , df . shape [0]) :

  •     choice = np . flip ( df . iloc [ i - K : i ]. values , axis =0)

  •     array [i , :] = choice [:]. T

  •   return pd . DataFrame ( array , index = df . index )

  • def simpleGM_asym ( p : np . ndarray , data : list ) -> float :

  •   mu , a1 , b1 , gamma , m , theta , w1 , w2 = p [0] , p [1] , p

  •      [2] , p [3] , p [4] , p [5] , p [6] , p [7]

  •   K , ret , macro = data [0] , data [1] , data [2]

  •   first_tau = ret . index . get_loc ( macro . index [ K ])

  •   midas = lagMatrix ( macro , K ) . values @ betaWeight ( w1 ,

  •     w2 , K )

  •   tau = pd . DataFrame ( np . exp ( m + ( theta  ∗ midas ) ) , index

  •     = macro . index )

  •   resample = ret . index . to_period ( ’M ’) . to_timestamp ()

  •   d_tau = tau . loc [ resample ]. values [ first_tau : , :]

  •   r2 = ( ret . iloc [ first_tau : , :]. values - mu )  ∗∗ 2

  •   shocks = r2 / d_tau

  •   ind = 1  ∗ (( ret . iloc [ first_tau : , :]. values - mu ) < 0)

  •   g = np . zeros ( d_tau . shape )

  •   g [0] = 1

  •   for i in range (1 , g . shape [0]) :

  •     g [ i ] = (1 - a1 - b1 - ( gamma / 2) ) + ( a1 + gamma

  •        ∗ ind [ i - 1])  ∗ shocks [ i - 1] + b1  ∗ g [ i - 1]

  •   vol = d_tau  ∗ g

  •   lpi = np . log (2  ∗ np . pi  ∗ np . ones ( vol . shape ) )

  •   lvol = np . log ( vol )

  •   nllf = 0.5  ∗ np . sum ( lpi + lvol + ( r2 / vol ) )

  •   if np . isnan ( nllf ) or np . isinf ( nllf ) : nllf = 9 e15

  •   return nllf

Table 2. Parameter estimation of GARCH-MIDAS.
Variable μ α β γ m θ ω1 ω2
BIIR 0.1313 0.0101 0.9273 0.1199 −0.6074 0.0730 1 5.6191
CPI −0.0071 0.0365 0.9019 0.1228 −0.1480 0.3129 1 5.0388
EFFR −0.0011 0.0091 0.6792 0.6233 −0.4968 0.1099 1 3.3953
IR 0.0989 0.0061 0.9327 0.1208 −0.5279 0.0543 1 5.0499

3.3. Forecasting Performance Calculation

Table 3 displays the MSE, MAE, and RMSE calculations made using Equations (11) and (12). Table 3 shows that the EFFR variable’s MSE, MAE, and RMSE values are lower than those of the other variables. In contrast to previous research, this study demonstrates that the EFFR variable has the greatest impact on the volatility of ICI returns compared to other variables. To evaluate the volatility of ICI returns, the GARCH-MIDAS model’s long-run component most effectively uses the EFFR macroeconomic variable. This finding indeed suggests that the EFFR variable has a significant impact on the volatility of ICI returns, contrary to previous research. To determine whether there is overfitting, we would need additional information such as the methodology used, the dataset, and the complexity of the model. However, we can analyse the forecasting performance using MSE, MAE, and RMSE values from Table 3. Overfitting happens when a model becomes overly tailored to the training data, capturing random noise or fluctuations instead of the true underlying patterns. It is crucial to assess the model’s performance on a separate validation dataset to ensure it generalizes well to new, unseen data.

Table 3. MSE, MAE, and RMSE.
Variable MSE MAE RMSE
BIIR 0.014300 0.083511 0.066809
CPI 0.030739 0.056266 0.059502
EFFR 0.003320 0.009280 0.011484
IR 0.014520 0.065848 0.083923

In the absence of information about a validation dataset or the model’s complexity, it is challenging to definitively conclude whether there is overfitting. Further analysis, such as cross-validation or testing on an independent dataset, would be necessary to make a more accurate assessment of the model’s generalization performance.

The study has taken several steps to ensure the robustness of the model and its generalization ability. The process involves checking and addressing data stationarity, dividing the dataset into training and testing sets, and using a disagreement dataset for further evaluation as follows:
  • a.

    Data stationarity test: The study conducted a data stationarity test using both the augmented Dickey–Fuller (ADF) test and the Phillips–Perron (PP) test to ensure the reliability of the model. Stationarity is a crucial assumption for many time series models, and the tests used assess whether the mean and variance of the data remain constant over time. If the data fails the stationarity test for the mean, we apply differentiation, and if it fails for variance, a transformation is performed. This rigorous preprocessing step is fundamental for accurate modelling, preventing issues arising from nonstationary data.

  • b.

    The division into training and testing data: Following the stationarity tests, the dataset was meticulously divided into training and testing sets. The training data encompassed ICI return data from January 3, 2018, to February 26, 2021, and macroeconomic data spanning from January 2018 to February 2021. This separation ensures that the model is trained on a substantial historical period, allowing it to learn patterns and relationships within the data. The testing data, on the other hand, comprises ICI return data from March 1, 2021, to December 30, 2022, and macroeconomic data from March 2021 to December 2022. This temporal split is crucial for assessing how well the model generalizes to unseen data, providing insights into its predictive performance.

  • c.

    Evaluation of disagreement dataset: The study introduced a disagreement dataset to gain a more comprehensive understanding of the model’s performance and generalization ability. This dataset is separate from both the training and testing data and serves as an additional layer of evaluation. Evaluating the model on this independent dataset, which includes ICI return data and macroeconomic variables not seen during training, allows us to test the model’s ability to make predictions on truly novel and unforeseen data. This step is essential for confirming the model’s reliability in real-world scenarios beyond the training and testing periods.

We were approached with thorough data preprocessing, careful division into training and testing sets, and a final evaluation on a separate disagreement dataset. These steps collectively contribute to a robust model, demonstrating a commitment to addressing potential biases and ensuring the model’s applicability to new and unforeseen scenarios.

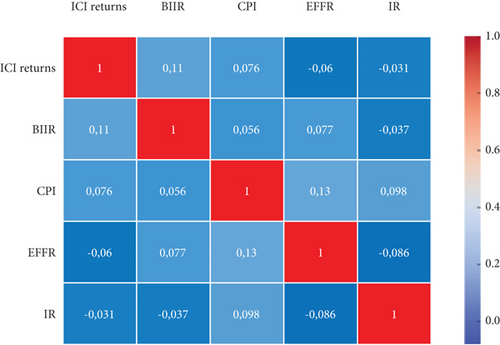
To enhance the interpretability of our results, we have incorporated detailed data visualizations that illustrate the trends in ICI returns and macroeconomic variables over time. These visualizations include time-series line plots for each macroeconomic indicator and ICI returns, enabling the observation of fluctuations and patterns within the data, as shown in Figure 4. By plotting these variables together, potential correlations and shifts in volatility corresponding to macroeconomic changes are highlighted, offering a clearer view of the dynamic interplay between these factors. Additionally, a correlation heatmap illustrates the strength and direction of relationships between ICI returns and the macroeconomic variables, visually emphasizing significant correlations or unique patterns within the dataset. This heatmap serves as a valuable tool for identifying predictors of ICI volatility and elucidating connections between various economic indicators and market fluctuations. These visual aids clarify complex data relationships while enhancing the overall impact and accessibility of the findings for investors, policymakers, and academics.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Correlation heatmap between ICI returns and the macroeconomic variables.

3.4. VaR in Equity Market Domain

VaR is a quantitative metric that estimates the potential loss in a portfolio or investment value over a defined time and at a given confidence level. This measure enables investors and financial institutions to assess the maximum expected loss under typical market conditions. Based on the estimated return value and the macroeconomic variable EFFR, the VaR calculation is performed. VaR is calculated using Equation (13). Based on the estimated return value and the macroeconomic variable EFFR, the VaR calculation is performed. VaR was obtained using Table 3 with varying degrees of confidence. Two VaRs are obtained from Table 4, corresponding to different levels of confidence: 99% and 95%.

Table 4. VaR.
p VaR
0.01 0.2255
0.05 0.1598

VaR is calculated based on the estimated return value and the macroeconomic variable EFFR. This means that VaR considers both the expected returns from investments and the impact of EFFR, which likely represents a key macroeconomic factor influencing market volatility.

These values represent the maximum expected loss in the portfolio’s value with a given probability of occurrence.
  • 1.

    The VaR value at a 99% confidence level, with a probability of loss of 0.01, indicates that there is only a 1% chance of the portfolio experiencing losses greater than 22.55%.

  • 2.

    Similarly, the VaR value at a 95% confidence level, with a probability of loss of 0.05, suggests that there is a 5% chance of the portfolio’s losses exceeding 15.98%.

Investors can make better judgments on risk management and portfolio diversification by using VaR, which gives them information about the possible downside risk connected to their investments.

VaR is a critical tool in risk management, offering investors and policymakers a quantifiable estimate of potential losses over a specified time horizon. In this study, we calculate VaR at both 99% and 95% confidence levels, providing a robust range for assessing market exposure within the ICI. At the 99% level, VaR indicates the threshold below which only the worst 1% of potential returns fall, giving a stringent measure of potential extreme losses. The 95% confidence level, meanwhile, offers a broader perspective, capturing the range where only the worst 5% of outcomes would occur. Together, these VaR estimates allow market participants to prepare capital buffers proportionate to the level of risk they are willing to tolerate, making them practical tools for both institutional and individual investors.

From a policymaking standpoint, VaR is equally valuable, as it can reveal potential systemic risks within the financial market. By monitoring the frequency and magnitude of potential losses as indicated by VaR, regulators can better assess the stability of the market and preemptively implement measures to mitigate financial distress. For example, during periods of elevated volatility, policymakers may introduce policies to limit excessive leverage or strengthen capital requirements, ensuring that financial institutions remain resilient against sharp market downturns. In emerging markets like Indonesia, where volatility can be more pronounced due to economic fluctuations and external influences, VaR offers essential insights for maintaining market stability and investor confidence.

However, the calculation of VaR is not without limitations. VaR estimates assume a stable distribution of returns, which may not fully capture extreme market conditions, particularly during rare or unexpected economic events. VaR’s dependence on historical data and model-specific assumptions can result in limitations under highly volatile or atypical market conditions. These limitations highlight the importance of using VaR in conjunction with other risk management tools and adjusting risk measures dynamically to better capture market conditions as they evolve. This nuanced approach enables investors and policymakers to use VaR more effectively within the Indonesian market context, balancing its practical benefits with an understanding of its assumptions and limitations.

4. Discussion

The study highlights the significant influence of macroeconomic indicators, particularly the EFFR, on the volatility of the ICI. EFFR emerges as a critical variable due to its role in shaping global liquidity conditions, influencing investor risk appetite, capital flows, and portfolio adjustments, which collectively drive market volatility. This underscores the importance of integrating macroeconomic indicators, like EFFR, into volatility models to capture the dynamic interplay between monetary policy and market behaviour in emerging economies such as Indonesia.

The GARCH-MIDAS model demonstrates superior forecasting accuracy compared to traditional models by effectively incorporating both short-term and long-term volatility components, alongside macroeconomic data. This approach enables the model to capture nuanced volatility patterns and macroeconomic shocks that simpler models may overlook, making it particularly suitable for markets sensitive to economic fluctuations and policy shifts. By emphasizing the relevance of macroeconomic variables, such as EFFR, in volatility modelling, the study provides valuable insights for investors and policymakers focused on enhancing market stability and managing risk.

Time-series visualizations for macroeconomic indicators (e.g., BIIR, CPI, EFFR, and IR) and ICI returns are used to reveal trends, cyclical patterns, and potential turning points, offering a comprehensive perspective on their behaviour over the study period. Additionally, a correlation heatmap highlights the strength and direction of relationships between ICI returns and macroeconomic variables, providing a concise overview of their interconnectedness.

The study acknowledges certain limitations, including the reliance on specific model assumptions and the potential sensitivity to dataset constraints, which may affect the generalizability of results under atypical conditions. Future research directions include exploring additional macroeconomic indicators and enhancing model structures to improve predictive accuracy. This approach is aimed at deepening the understanding of the complex interactions between economic factors and market volatility, further strengthening the robustness and applicability of volatility forecasting models.

5. Conclusions

This study uses the GARCH-MIDAS model to examine the volatility of the ICI by combining daily stock returns with monthly macroeconomic indicators such as the BIIR, CPI, EFFR, and IR. The empirical analysis shows that the EFFR has a considerable impact on ICI volatility, surpassing other macroeconomic indicators in prediction accuracy, as seen by reduced MSE, MAE, and RMSE values. This discovery emphasizes the EFFR’s critical role in driving stock market volatility, contrasting earlier research findings. Robust parameter estimation with MLE validates the model’s effectiveness. Detailed descriptive statistics provide a thorough knowledge of the dataset’s central tendencies and distribution. Rigorous preparation, such as data stationarity tests, separation into training and testing sets, and evaluation with a disagreement dataset, ensures that the model is reliable and generalizable to new data. The VaR analysis provides useful information for risk management, with VaR values estimated at 99% and 95% confidence levels, indicating potential maximum losses. This allows investors to make more informed decisions and better manage portfolio risks. Future studies ought to tackle the drawbacks of the GARCH-MIDAS model, including its dependence on the quality and availability of high-frequency and low-frequency data, which might negatively impact performance in the event that the data is sparse or of low quality. Additionally, the granularity of the mixed-frequency data used, such as the inclusion of monthly macroeconomic variables that might not fully capture rapid changes in the market, can affect the performance of the model. To improve the model’s robustness and application, future research should investigate the effects of adding more macroeconomic variables, look at the policy implications of macroeconomic volatility on market stability and investor behaviour, and suggest regulatory frameworks.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This study was entirely self-funded by the authors, with no financial support from any external organization. Therefore, there are no associated grant numbers or supporting bodies to be named.

Acknowledgments

The authors are grateful to the referees for providing valuable comments and suggestions.

    Data Availability Statement

    The data used to support this study have been previously reported and are appropriately cited at relevant points within the text as references [5].

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.