Analysis of Cascading Failure in Urban Metro Networks: A Dynamic Perspective Incorporating Changes in Travel Decisions
Abstract
Accidents in urban subway networks often exert substantial and enduring impacts on urban transportation, drawing widespread attention from researchers. However, prevailing studies predominantly employ static methodologies to scrutinize incidents in urban subway systems, frequently assuming constancy in network topology and individual travel plans. Nonetheless, alterations in subway passenger flow also wield influence over network resilience. The manifold fluctuations in post-accident traffic flow and their repercussions on elastic transportation demand have hitherto been inadequately explored in the extant literature. Moreover, existing cascading failure models often lack precise definitions of scenarios, as in actual scenarios, passenger overflow following station closures can lead to cascading failures in subway networks. To bridge this gap, this study meticulously defines the research scenario, demarcates potential post-accident travel decisions, and analyzes the multifaceted factors influencing cascading failures in urban subway networks. Specifically, the proposed cascading failure model takes into consideration both the static characteristics of network topology and the fluctuations in passenger volume, along with their interplay. Additionally, when assessing station importance and quantifying network resilience, multiple travel decisions under different fault durations are duly considered. The study’s validation is conducted within the urban subway network of Nanjing, China. The findings suggest that accidents and fault stations of varied durations exert disparate impacts on passenger travel decisions, thereby influencing subway resilience. Notably, stations with integrated functionalities may hold more significant roles than those with singular functions. Furthermore, our results indicate a V-shaped effect concerning event duration—as the duration increases, the proportion of passengers canceling subway travel rises, thereby enhancing the likelihood of stabilizing the subway network. Consequently, this study, by incorporating realistic variations in travel decisions, furnishes a comprehensive understanding of the impact of events on urban subway networks. This dynamic perspective yields valuable insights for optimizing strategies in responding to events.
1. Introduction
Urban rail transit, with its extensive coverage and high transportation capacity, has become an indispensable part of urban transportation systems. However, with the continuous increase in passenger demand, operational challenges in rail systems are becoming more pronounced. In 2021 alone, there were 1540 incidents of train delays exceeding five minutes and 6777 incidents of trains deviating from their tracks due to technical failures in urban centers across mainland China. These statistics reveal long-standing safety challenges within urban rail systems, including train malfunctions, electrical anomalies, and communication system failures [1]. The frequent occurrence of such failures not only inconveniences passengers but also imposes significant economic and opportunity costs on cities, which continue to accumulate until transportation services are restored [2, 3]. Therefore, accurately assessing metro network performance, identifying key lines most affected under different incident scenarios, and developing effective recovery strategies are of utmost importance [4].
Key concepts in metro network performance evaluation include resilience, vulnerability, robustness, and reliability, with “resilience” being the most closely linked to overall network performance [5]. Previous studies have primarily analyzed the resilience of metro networks from the perspective of network topology, using indicators such as connectivity distribution [6], betweenness centrality [7, 8], the average number of connections per vertex [9], and degree centrality [10]. For instance, Domenico et al. [11] proposed a network topology and geographical evaluation method based on indicators such as the number of nodes, loops, and lines, using metro network data from 13 major metropolitan areas. Derribe et al. [12] constructed the physical metro networks of 33 countries applying graph theory and introduced a methodology for analyzing transportation system resilience based on three network features: state, form, and structure. The study further found that most metro systems are scale-free and small-world networks [13]. However, Auckland’s public transportation system was found to be a hybrid of both scale-free and exponential networks, characterized by high clustering and longer average shortest path lengths, which exhibited strong resilience when subjected to disruptions [14].
Furthermore, passenger flow in metro networks may shift due to station failures, leading to overloading at other stations, triggering a cascading series of node failures, and ultimately causing a large-scale network collapse. This phenomenon, known as “cascading failure”, has been extensively studied [15, 16]. Existing models to describe this process include the load-capacity model [17], the coupled lattice model [18], the binary model [19], Potts model [20], and Cascade model [21]. Most studies focus on the spatial network changes during the cascading failure process. A hybrid cascading failure model considering multiple node dependencies was proposed, showing that cluster size and average node degree significantly affect resilience to cascading failures [22]. The introduction of weighted public transportation network models that incorporate factors such as bus line density and departure frequency has demonstrated the importance of station failure intensity and station load in determining the resilience of cascading failures under different types of single-station intentional attacks [23]. Additionally, research has shown that the relationship between initial disturbance intensity and cascading failure intensity has a significant effect on network resilience [24]. In complex networks, where nodes are more concentrated, even minor initial shocks can lead to large-scale cascading failures [25]. Zhang et al. [26] introduced the important evaluation metric of “relative edge capacity” based on cascading failure node distribution, providing a new perspective on network resilience. Moreover, using the concept model of the fiber bundle model, Moreno et al. [27] calculated the critical point of cascading failures in scale-free networks. Subsequently, a cascading failure threshold model was proposed to improve the precision of large-scale network modeling and resilience analysis [28].
Some scholars have also explored passenger flow redistribution during cascading failures from an operational perspective, combining network flow theory. López et al. [29] considering node demand changes, demonstrated that network vulnerability should be assessed from both node-level indicators and link flow perspectives, confirming the significant role of traffic distribution in network resilience. A dynamic weighted network model that integrates passenger flow indicators was further developed to assess metro network resilience. The model revealed that the scale of cascading failures and time step intervals follow a normal distribution [30]. A load-capacity model incorporating average passenger flow intensity and average shortest path as resilience evaluation metrics was used to analyze key factors in the cascading failure process [31]. Yin et al. [32] validated the cascading failure model through scale-free and random networks based on the daily traffic flow, obtaining joint parameters for load thresholds and load redistribution factors, thus providing solutions for routine network management. These scholars examined cascading failures from various perspectives and offered valuable insights, which are crucial for the safety design and protection of urban transportation networks.
In summary, existing studies on cascading failures in transportation networks have primarily focused on network topology and passenger flow redistribution perspectives, while neglecting the impact of incident duration on passenger behavior. In recent years, some studies have begun to focus on passenger behavior changes during cascading failures [33]. Lu [34] investigated the resilience of rail transit networks under varying accident durations, proposing a resilience evaluation method based on importance impedance, which was validated through a Shanghai case study. Zhu et al., [35] by incorporating passenger perception and generalized cost, distributed passenger flow during incidents, identifying passengers’ travel paths and flow intervals. This approach enabled a more accurate assessment of metro network performance, simulating various failure scenarios and recovery strategies, and providing useful insights for emergency management. Moreover, a dynamic resilience evaluation framework that considers passenger decision changes between different transportation modes and routes was developed. This framework captures variations in passengers’ choices of paths and departure times, offering a more comprehensive evaluation of metro network resilience. A case study of Beijing further validated the superiority of this framework [36].
However, most existing research has focused primarily on analyzing passengers’ choice changes between stations, neglecting the diversity of passenger choices in real-world scenarios. The example from two incidents of different durations on Beijing Metro Line 10 in March 2022 demonstrated the necessity. Passengers during short-term disruptions mostly chose to wait. In contrast, during long-term disruptions, coupled with real-time station closure notifications, some passengers opted to change their routes or abandon metro travel altogether. In such cases, metro network resilience is significantly impacted, yet existing studies often overlook the possibility that passengers may choose to abandon metro travel in the event of an incident. Furthermore, the impact of incidents at different stations on passenger behavior varies. For instance, when a transfer station fails, passengers can switch to other lines at the same station. However, when a nontransfer station fails, passengers are forced to either abandon their journey or wait. Previous studies have not fully accounted for these differences, leading to a research gap on the impact of various incidents on metro network resilience.
To address these issues, this study considers the changes in passenger flow and travel decisions over time as incidents unfold. It further refines the analysis of passenger decisions during different cascading failure processes. Based on the load-capacity model, this research proposes a metro network performance evaluation method that incorporates passenger travel changes under varying incident durations. This method integrates topology structure indicators with dynamic passenger flow indicators to examine the changes in network performance following incidents. It identifies critical stations and failure durations that most significantly impact network resilience. Additionally, it proposes several recovery strategies aimed at enhancing network recovery. Our findings contribute to a deeper understanding of how incidents affect metro network resilience and provide practical insights for improving recovery strategies.
The remainder of this study is structured as follows. Section 2 elaborates on travelers’ travel decisions in response to subway emergencies and the modeling approach. Section 3 outlines Nanjing’s subway system, the preprocessing steps used in this research, and the questionnaire survey methodology along with its primary results. Sections 4 and 5 focus on result analysis and discussion, respectively. Finally, the last section summarizes the research findings and offers insights for future research directions.
2. Methodology
2.1. Cascade Failure Process and Passenger Behavior
To define the cascade failure scenarios under investigation, this study designates an affected station as failed following a subway accident, which consequently results in its closure. Subsequently, passenger flows shift to adjacent stations, while the subway line associated with the affected station remains operational. Due to the significant transfer of passenger flows, surrounding stations experience an upsurge in passenger volume. At a critical juncture, if the passenger volume at any given station exceeds its capacity, a secondary flow redirection process ensues, classifying the station as a secondary failure point. This cycle persists until the passenger volume at all subway network stations aligns with their capacity limits, as depicted in Figure 1.
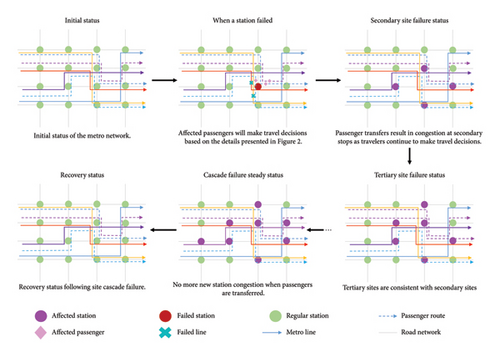
- •
The arrival rate of passengers at the station during peak hours is assumed to be constant.
- •
Passengers traveling on the subway network follow the shortest path.
The description of potential passenger decisions in response to a station failure provides a framework for exploring the impact of such disruptions on the resilience of subway networks.
- •
Scenario 1 (S1): Passengers whose travel routes bypass the affected station remain unaffected, choosing to maintain their current status: MT.
- •
Scenario 2 (S2): Passengers currently inside the affected station or about to arrive can make three travel decisions: TF, W, and CT.
- •
Scenario 3 (S3): Passengers at a normal station, yet to board but with their route passing through the affected station, have three travel options: TF, CT, and MT.
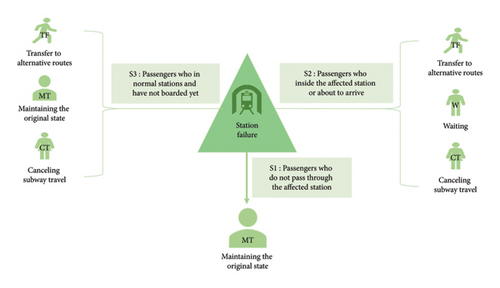
Notably, transfer options encompass both in-station and inter-station transfers.
2.2. Cascading Failure Model
2.2.1. Initial Load and Node Capacity
In the analysis of existing research, it was found that experts often use node betweenness or degree as the initial load of nodes when studying the cascading propagation phenomenon of network failures. While this approach can, to some extent, measure the burden of nodes and study the cascading failure phenomenon, it differs from the real-world situation. In this paper, we adopt the average passenger flow of each station (boarding and alighting numbers) during the entire operating period as the initial load Fi of nodes, which better reflects the actual conditions.
However, the number of transfer passengers, who move between different lines at transfer stations without exiting through the gates, also contributes significantly to the load. These transfer passengers cannot be directly counted by gate systems. To estimate the number of transfer passengers, we rely on smart card data, which records entry and exit points of passengers in the network. By analyzing the sequence of entry and exit records, we can infer transfer passengers based on those who enter one station and exit from another without leaving the network. Specifically, for a given transfer station, passengers who enter on one line and do not exit but later continue their journey on a different line are considered transfer passengers. This method allows us to approximate the transfer load at each station. Additionally, transfer passenger data can be supplemented through passenger flow surveys conducted at the stations, where manual or automated counting methods track movements within the transfer areas.
2.2.2. Load-Capacity Model
The widely accepted linear load-capacity model was proposed by Motter [17], where each node or edge in the network carries a load under normal circumstances. In general, the removal of a node changes the distribution of shortest paths, which results in a change in the node’s capacity. When a portion of nodes or edges in the network fails or when the load of a node exceeds its maximum capacity, the load of the failed node or edge will be redistributed to other nodes connected to the failed node. This failure process may stop after a few steps, but it may also spread or even shut down a part of the network, and this spreading process is known as cascading failure. Prior research indicates that a larger traffic load amplifies the impact of cascading failures resulting from node failure.
As the load redistribution process changes the load of adjacent stations to the failed station, it is necessary to reevaluate the relationship between Lj(t) and Cj. If Lj(t) > Cj, the station will fail, and a new round of load redistribution will be initiated until the allocation complies with the node capacity constraint. If Lj(t) ≤ Cj, no new round of load redistribution process is required.
2.2.3. Model Implementation Steps
- •
Step 1: Calculate the current subway performance Q(t0).
- •
Step 2: Assume the failure of the node ni, which represents a node that cannot function properly (i.e., passengers cannot board the subway at this node, and the subway cannot pass through this node).
- •
Step 3: Remove the node ni and the edges connected to ni.
- •
Step 4: Redistribute the load of the failed node according to the load redistribution model. Allocate the load from the failed node to its adjacent nodes and update the network state.
- •
Step 5: Check the node status and determine if the load of each adjacent node to the failed node exceeds its node capacity. If not, the cascading failure process ends, proceed to Step 6. If it exceeds the capacity, initiate a new round of the cascading failure process, remove the failed node from the network, and return to Step 4.
- •
Step 6: The cascading failure process ends. Calculate the subway performance Q(t1) after the cascading failure process ends and compare it with the initial state Q(t0).
2.3. Subway Performance Function
3. Case Study
3.1. Case Raw Data and Network Basic Characterization
To facilitate an accurate evaluation based on the patterns contained in each indicator during the cycle, the selected time range in this study is the card-swiping records from 1 to 6 November 2015. The data are collected at a minute granularity. The data was provided by Nanjing Metro and includes transaction timestamps, entry timestamps, exit timestamps, entry stations, and transaction stations, among other information.
Additionally, the geographical coordinates of each subway station in the Nanjing subway network and the station connectivity information were obtained using the Amap API and performing data transformation. As the card-swiping data was generated in 2015, the data was filtered accordingly. The final dataset comprises the geographical coordinates of each subway station and the station connectivity information for the Nanjing subway network in 2015. The spatial distances between stations were derived from the geographical coordinates to construct the topological structure of the studied network. The node attributes of this network include the geographical coordinates of each station, while the edge attributes consist of the station connectivity and distance between stations.
The obtained subway network in Nanjing in 2015 consisted of 113 nodes and 115 edges. The average degree of the network is 2.04, indicating that each station in the network is connected to an average of 2.04 other stations. The average shortest path length is 15.29, meaning that, on average, it takes 15.29 stations to travel between any two stations in the network. The average betweenness centrality, average clustering coefficient, network global efficiency, and connectivity are all relatively low. The specific values are shown in Table 1.
| Attribute | Value |
|---|---|
| Sites | 113 |
| Edges | 115 |
| Network density | 0.0181 |
| Average betweenness centrality | 0.1287 |
| Network global efficiency | 0.1153 |
| Average degree | 2.04 |
| Network diameter | 44 |
| Average shortest path length | 15.29 |
| Average clustering coefficient | 0.0054 |
3.2. Data Processing
- •
Matching station names to station codes for entry and transaction stations.
- •
Extracting subway OD (Origin-Destination) travel within the duration of train operation and service intervals in Nanjing Metro.
- •
Utilizing the original attributes of entry timestamps, transaction timestamps, transaction stations, and entry stations to remove duplicate records (same station entry and exit) and trips with excessively short durations, resulting in data suitable for further analysis.
- •
Processing the cleaned data to obtain passenger OD paths on the subway network, entry and exit volumes at each station, station capacity, average travel speeds, and average arrival rates per unit time, which are utilized in subsequent modeling.
- •
Using the Floyd algorithm for shortest path search on the original road network to obtain the shortest paths between each pair of stations in the Nanjing subway network, which serves as the basis for passenger travel paths.
- •
Assigning station entry and exit volumes and station capacity as node attributes in the network. The passenger flow for each segment and station connectivity in the shortest path are considered edge attributes, and these attribute values are integrated into the original network, resulting in the finalized dataset for analysis of the 2015 Nanjing subway network.
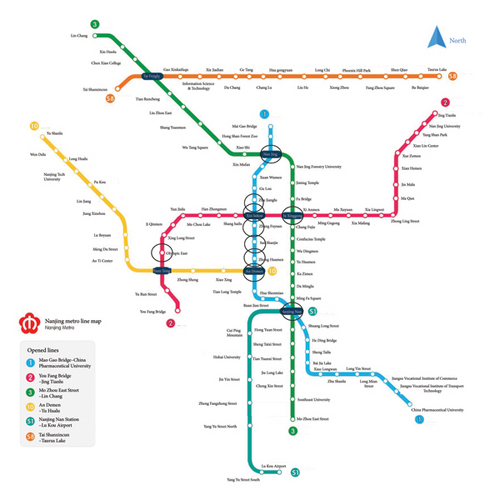
Each station’s unit-time average arrival volume was calculated and sorted, with the specifics of the top 10 sites shown in Table 2 and Figure 3.
| Station ranking | Station name | Abbreviations |
|---|---|---|
| 1 | Xinjiekou | XJK |
| 2 | Daxinggong | DXG |
| 3 | Andemen | ADM |
| 4 | Nanjing Railway Station | NJR |
| 5 | Zhangfuyuan | ZFY |
| 6 | Sanshanjie | SSJ |
| 7 | Zhujianglu | ZJL |
| 8 | Zhonghuamen | ZHM |
| 9 | Nanjing Nan Station | NJNS |
| 10 | Olympic East | OE |
3.3. Behavioral Questionnaire Analysis
In order to obtain the distribution of behavioral choices of Nanjing residents in metro trips under different failure scenarios, questionnaires were distributed in major metro entrances and streets of Nanjing from April 3–9, 2023 to conduct a survey, which mainly investigated the choices of passengers’ behaviors of waiting, transferring, and canceling metro trips under different failure durations and different failure station scenarios.
In order to discern the subway travel behavior preferences among residents of Nanjing in response to various fault scenarios, a meticulously designed questionnaire was distributed online from April 3 to 9, 2023. Simultaneously, printed surveys were strategically disseminated at crucial entrances/exits of Nanjing subway stations and in public thoroughfares. The survey rigorously examined passengers’ decision-making processes concerning waiting, transferring, and canceling subway travel, particularly within the framework of diverse fault durations and the closure of fault stations. The contents of the questionnaire are shown in Appendix Table A1.
While the questionnaire survey period does not coincide with the timeframe of the card data utilized in this study, its temporal misalignment is deemed unlikely to exert a significant impact on the analytical outcomes. This assertion is predicated on the fact that the proportions reflecting passengers’ travel decisions in the survey stem from hypothetical choices derived from questionnaire descriptions of distinct scenarios. These choices remain unaffected by the temporal occurrences of events, thereby bolstering the robustness and independence of the survey-based insights from the specific temporal constraints of the card data.
Following rigorous processes encompassing questionnaire design, reliability and validity testing, questionnaire distribution, data processing, and analysis, the proportions of passenger behavior choices under different scenarios were derived, as elucidated in Table 3.
| Duration of failure | Failed station function | Waiting ratio | Transferring ratio | Canceling ratio |
|---|---|---|---|---|
| 15 min | Nontransfer station | 0.63 | 0.21 | 0.16 |
| 15 min | Transfer station | 0.78 | 0.13 | 0.09 |
| 2h | Nontransfer station | 0.35 | 0.44 | 0.21 |
| 2h | Transfer station | 0.51 | 0.27 | 0.22 |
4. Result Analysis and Comparison
4.1. Performance Analysis With and Without Variations in Travelers’ Decisions
This section addresses a critical lacuna in existing literature, which frequently overlooks the influence of variable incident durations on passenger travel choices. The present study investigates these dynamics through an analysis of cascading failures within a metro network. Initially, stations are ranked according to their relative importance, without consideration of alterations in passenger behavior, such as trip cancellations or inter-station transfers. Subsequently, the analysis examines the propagation of cascading failures under diverse incident duration scenarios, with a particular focus on adaptive passenger decision-making.
Using the 2015 Nanjing metro network as a case study, the research contrasts scenarios incorporating and excluding adaptive passenger behavior. The failure duration for each station is set to 40 min, a choice based on its ability to capture meaningful behavioral changes while avoiding extreme cases where disruptions have minimal or overwhelming impact. Shorter durations often lead to negligible adjustments, as passengers tend to wait, whereas longer disruptions result in widespread trip cancellations or shifts to alternative transport modes, limiting the ability to analyze intermediate behavioral adaptations. Moreover, the 40-min interval is representative of typical metro incident lengths, thereby facilitating a realistic analysis of cascading failure phenomena. This methodological approach enables a detailed assessment of passenger rerouting strategies, inter-station transfers, and trip adjustments, all of which are salient factors in evaluating metro network resilience. The parameters governing the metro network performance function are specified as follows: α = 0.8, β = 0.1, γ = 0.05, μ = 0.05.
According to Figure 4, disregarding changes in passenger travel decisions, the top 10 stations based on passenger flow are ranked as follows: Nanjing Railway station > Nanjing Nan station > Andemen station > Daxingong station > Xinjiekou station > Zhujiang Road station > Zhonghuamen station > Sanshanjie station > Zhangfuyuan station > Olympic East station. However, when factoring in variations in passenger travel decisions, these rankings shift to: Nanjing Nan station > Daxingong station > Xinjiekou station > Andemen station > Zhonghuamen station > Sanshanjie station > Zhangfuyuan station > Zhujiang Road station > Nanjing Railway station > Olympic East station.
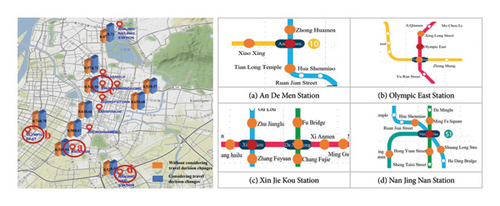
This shift underscores that passenger adaptation fundamentally alters the relative criticality of stations to network resilience, influencing the patterns of cascading failure. When passenger adaptation is not considered, stations with the highest aggregate passenger volume are deemed most critical. This is because a disruption at such a station (e.g., Nanjing Railway station) precipitates a substantial, localized surge in passenger flow, potentially exceeding the capacity of adjacent stations and initiating a concentrated cascading failure. However, when passenger adaptation is considered, major transfer hubs like Nanjing Nan station become most critical. While the initial impact of a failure at a transfer hub might be less pronounced, these hubs are crucial for managing the redistribution of passengers across the network during disruptions. Their capacity to facilitate transfers and reroute passengers effectively dictates the network’s ability to absorb and mitigate the effects of the disruption.
Figure 4 visually represents the impact range of station failures, with red circles indicating failed stations and orange circles representing affected stations, illustrating the spatial propagation of cascading failures under different scenarios. This aligns with the broader understanding of metro network resilience, as highlighted by Sun et al. [4], who identified passenger flow as a crucial determinant. Our findings extend this understanding by demonstrating that the manner in which passenger flow is managed and adapts during disruptions significantly influences overall network stability, thereby substantiating and refining previous research.
Recognizing that passengers realistically modify their travel decisions in response to sudden events is crucial for accurately assessing station importance. Incorporating this adaptive behavior yields a more precise and nuanced evaluation, enabling operators to more effectively identify critical stations under various disruption scenarios and implement proactive, targeted responses to mitigate the impact of sudden incidents. Operators can utilize this enhanced understanding to: (1) prioritize the dissemination of real-time, personalized information to passengers regarding alternative routes, multi-modal transportation options, and estimated travel durations; (2) implement flexible routing strategies, potentially incorporating dynamic pricing mechanisms or incentives to encourage passengers to utilize less congested pathways and modalities; (3) strategically augment capacity at critical transfer hubs through infrastructure enhancements, optimized platform architecture, and refined passenger flow management protocols; and (4) develop and maintain comprehensive operational protocols for responding to disruptions, encompassing pre-planned rerouting algorithms and coordinated communication strategies across disparate transportation agencies. This refined comprehension of network vulnerability, incorporating adaptive passenger behavior, ultimately facilitates more robust and resilient urban transportation systems.
4.2. Comparison Between Station With Variations in Travelers’ Decisions
Based on the proposed model in this study, we investigated the factors influencing cascading failures and overall network performance. To this end, the model was applied to simulate the Nanjing subway network under a 40-min station failure scenario. Utilizing cascading failure modeling and flow redistribution principles, passenger flow within the subway network was redistributed. A stable state is defined as the point at which the network accommodates the impact of the initial station failure without inducing further failures or network collapse, representing the subway network’s final resilient state.
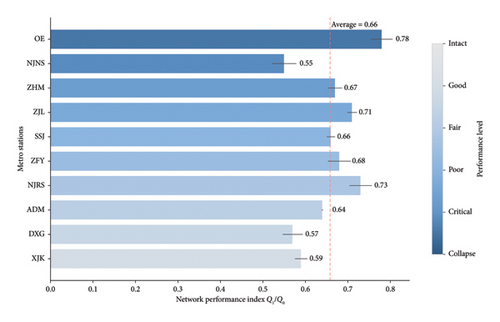
By employing the constructed performance function for the Nanjing subway network, the performance Q1 in the stable state was calculated and compared with the original performance Q0 of the network under normal operating conditions (i.e., without any station failures). These calculations were performed for 10 different failure stations, each subjected to the same 40-min failure duration, and the results are presented in Figure 5. The data indicate a range of impacts on network performance depending on the initially failed station. As seen in Figure 5, failure of Olympic East Station resulted in the least impact on network performance, yielding a Q1/Q0 ratio of approximately 0.85, categorized as “Intact,” which denotes minimal disruption to overall network functionality. Conversely, failure of Xinjiekou station led to the most significant performance degradation, with a Q1/Q0 ratio of roughly 0.48, falling into the “Collapse” category, representing a severe compromise of network operations. Stations such as Zhonghuamen and Zhujianglu, with Q1/Q0 ratios approximating 0.7, exhibit “Fair” performance, closely aligned with the average network performance across all 10 failure scenarios, represented by the red dashed line at approximately 0.66. This average suggests a typical level of vulnerability for stations within the network. The observed vulnerability of Xinjiekou station likely arises from its serving a high volume of passengers. Disruptions at such high-throughput nodes can engender substantial bottlenecks and cascading effects throughout the network. Conversely, Olympic East station’s relative resilience may be attributed to lower passenger demand, facilitating more readily facilitated flow redistribution. These findings emphasize the necessity for targeted resilience strategies, focusing on reinforcing vulnerable stations such as Xinjiekou station and implementing mitigation measures to prevent cascading failures, thereby ensuring the sustained operational integrity of the Nanjing subway system.
However, as shown in Table 4, the changes in the individual indicators are inconsistent across different failure scenarios. For example, the failure of Xinjiekou station results in a 44% decline in network global efficiency but only a 32% decline in mileage service passenger flow rate. In contrast, the failure of Nanjing Nan station leads to a 48% decline in network global efficiency but a 19% decline in mileage service passenger flow rate. This variability stems from the distinct roles each station plays within the network topology and the differences in passenger flow, as highlighted in the studies by Zhu et al. [34] and Zhang et al. [36]. This discrepancy underscores the limitation of relying solely on individual indicators to assess station importance.
| Failed station | E1/E0 | O1/O0 | D1/D0 | P1/P0 |
|---|---|---|---|---|
| XJK | 0.56 | 0.72 | 0.75 | 0.68 |
| DXG | 0.54 | 0.68 | 0.71 | 0.72 |
| ADM | 0.63 | 0.74 | 0.64 | 0.64 |
| NJRS | 0.72 | 0.76 | 0.77 | 0.74 |
| ZFY | 0.65 | 0.84 | 0.81 | 0.78 |
| SSJ | 0.63 | 0.81 | 0.79 | 0.75 |
| ZJL | 0.68 | 0.86 | 0.84 | 0.82 |
| ZHM | 0.64 | 0.79 | 0.76 | 0.72 |
| NJNS | 0.52 | 0.58 | 0.62 | 0.81 |
| OE | 0.76 | 0.88 | 0.82 | 0.87 |
Given these complexities, the performance function developed in this study—integrating both static and dynamic indicators—becomes indispensable for a robust and holistic assessment. Static indicators, such as network global efficiency and the maximum connected subgraph ratio, offer insights into the ramifications of station failures on the network’s topological structure. Complementarily, dynamic indicators, including network’s service flow rate and mileage service passenger flow rate, elucidate the extent to which these failures disrupt passenger movement. This integrated approach enhances the robustness of the analysis and ensures the evaluation captures both the structural impacts and operational realities precipitated by station failures, thereby providing a more comprehensive understanding of network vulnerability. When the combined performance function is applied to assess critical stations such as Nanjing Nan, Daxinggong, and Xinjiekou, the most pronounced declines in performance are observed. This observation reinforces their pivotal roles as key nodes within the network and substantiates the function’s capacity to accurately reflect the combined influence of passenger flow and topological structure on assessments of station importance.
Consequently, the developed performance function provides an invaluable instrument for informing targeted resilience-enhancement strategies. The research underscores the necessity of a nuanced approach, moving away from uniform solutions to address the unique vulnerabilities of critical stations such as Nanjing Nan, Xinjiekou, and Daxinggong. For Nanjing Nan station, this translates to enhanced passenger flow management systems and optimized interchange layouts to mitigate disruption-related bottlenecks. In contrast, for Xinjiekou station, improving resilience requires structural retrofitting and the implementation of advanced monitoring systems designed to prevent cascading failures. Finally, for Daxinggong station, effective contingency planning necessitates dynamic rescheduling of train services and the strategic deployment of mobile support teams. These station-specific strategies, informed by the comprehensive assessment facilitated by the performance function, promise to significantly augment the overall resilience of the subway network by directly addressing the distinct vulnerabilities present at each critical node.
4.2.1. Comparison Between Stations With Different Capacity
Cascading failures in subway networks are critically influenced by the capacity asymmetry between a disrupted station and its adjacent stations. The probability of cascading failures increases when a failed station is adjacent to stations with significantly lower capacity. This phenomenon is clearly illustrated by the contrasting instances of Nanjing Nan station and Nanjing Railway station. While both stations exhibit high passenger throughput, Nanjing Nan station’s extensive connectivity, coupled with the lower capacity of its directly connected stations, exacerbates the impact of any failure at that node. Conversely, Nanjing Railway station exhibits connectivity to a smaller number of lines, and its neighboring stations generally possess a relatively higher capacity. Consequently, while disruptions at Nanjing Railway station invariably affect network performance, the greater capacity of the surrounding stations facilitates a more effective absorption of the resultant impact. This observation underscores that, beyond topological centrality metrics, the capacity of adjacent stations, and its resultant impact on passenger route choice behavior, exerts a significant influence on the overall degree of network vulnerability. This finding is consistent with the conclusions reached by Lu et al. [37], who emphasize the critical role of adjacent station characteristics in shaping the propagation pathways of cascading failures.
To mitigate the risks associated with capacity asymmetry and enhance overall network resilience, a two-pronged strategy is warranted. First, future subway system development should prioritize the reduction of capacity imbalances through strategic infrastructure investment, specifically targeting capacity upgrades at stations adjacent to critical nodes. Second, incident response protocols should incorporate strategies that explicitly account for capacity differentials, including proactive passenger diversion to higher-capacity stations through real-time information systems, targeted resource allocation to facilitate passenger flow at these stations, and adaptive service reconfiguration to leverage available capacity on less congested lines. By proactively addressing existing capacity asymmetries and implementing capacity-sensitive remedial measures, network operators can substantially reduce the risk of cascading failures and enhance the overall resilience of the subway system.
4.2.2. Comparison Between Stations With Different Roles
In the subway network, the importance of each station is also influenced by its role. Stations contributing to significant network degradation may fall into two categories: transfer stations or nontransfer stations along network legs. However, as demonstrated in Figure 5, when a transfer station fails, and it bears a heavier passenger flow and plays a role in supporting multiple lines, its impact on the network will be higher than that of nontransfer stations. For instance, consider the Xinjiekou and Zhonghuamen stations, located on Line 1. Xinjiekou station serves as a transfer station, while Zhonghuamen station is not. Additionally, Xinjiekou station has a slightly higher passenger flow than Zhonghuamen station. As a result, when these two stations fail, Xinjiekou, a station connecting multiple lines, has a more significant impact on the network and is more susceptible to cascading failures, leading to lower performance indicators. This outcome corroborates the research developed by Zhang et al., which determined that Xinjiekou station holds a more significant role in the Nanjing subway network compared to Zhonghuamen station [36].
This phenomenon can be explained from several angles. On the one hand, as a downtown interchange station, it has a higher degree of line redundancy, possibly due to its higher redundancy and the availability of alternative transportation options for commuters when stations are affected. Additionally, in large Chinese cities like Nanjing, numerous urban sub-centers lead to residents living and working near metro stations, due to diverse land uses and the convenience of commuting to the city center, which further complicates the resilience during disruptions, as suggested by Lu [34].
Identifying interchange stations as critical nodes in the subway network is essential for maintaining system stability during disruptions. Unlike traditional methods that primarily evaluate overall network degradation, this approach underscores the significant impact that transfer stations have on passenger flow and overall system resilience. Transfer stations not only serve as major hubs for passenger transfers but also play a crucial role in mitigating cascading failures when disruptions occur.
Given their significance, subway operators should implement targeted strategies to enhance network resilience. First, proactive measures should be taken to minimize disruptions at transfer stations, such as conducting regular infrastructure inspections, improving maintenance protocols, and deploying real-time monitoring systems to detect anomalies early. Second, contingency plans should be developed with a focus on dynamic passenger flow management, including temporary route adjustments, emergency bus bridging services, and real-time passenger guidance through digital information systems. Third, response mechanisms should prioritize rapid restoration of transfer stations, as their recovery has the most significant impact on overall network stability. In the event of simultaneous disruptions at multiple stations, resource allocation should prioritize restoring the functionality of key interchange stations to prevent network-wide congestion. Additionally, increasing redundancy in the network—such as optimizing alternative transfer routes and expanding multimodal connectivity—can further enhance the system’s ability to absorb shocks and maintain efficient operations under stress.
5. Discussion
5.1. Analysis of Subway Network Performance Under Different Failure Durations
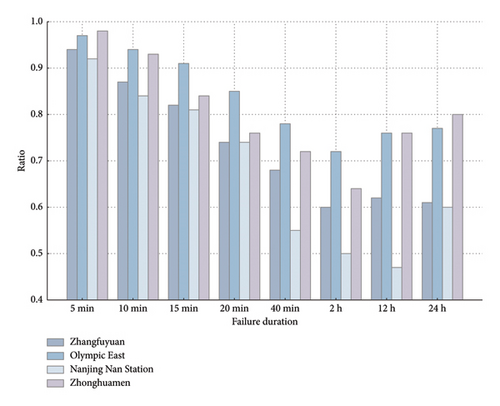
Recognizing that varying failure durations influence passenger travel choices and the propagation of cascading failures, we investigated the impact of these durations on subway network performance. Specifically, short durations (5, 10, and 15 min) simulate the immediate post-failure period, capturing the reactions of passengers both directly impacted at the incident station and those who are en route. A 40-min duration permits observation of initial adaptive behaviors, such as passengers seeking alternative routes or delaying their journeys. The 2-h duration represents a more stabilized state wherein a substantial proportion of passengers have adjusted travel plans, and the network exhibits emergent congestion or alternative flow patterns. Protracted durations (12 and 24 h) reflect a marked shift in passenger behavior, with a significant number of individuals opting for alternative transportation modalities (e.g., buses, taxis, and private vehicles) or electing to forego travel. To achieve this, we simulated a range of failure durations across the selected stations to analyze the resulting changes in station flow patterns and their implications for overall network resilience. The results of this comparative analysis, focusing on Zhangfuyuan station, Olympic East station, Nanjing Nan station, and Zhonghuamen station, are shown in Figure 6.
5.1.1. Analysis of Station Flow Comparison
Given the sensitivity of passenger travel behavior to station failures, and recognizing that the duration of these disruptions also influences passenger choices, we aimed to isolate the effect of failure duration on network performance. We selected two nontransfer stations with significantly different passenger flows—Zhangfuyuan station and Olympic East station—to determine if a consistent trend emerged despite variations in station traffic. Notably, the results shown in Figure 6 displayed a generally similar ‘V-shaped’ pattern: network performance showed an initial decline, reaching a minimum, before exhibiting a recovery at longer failure durations. This observation supports findings by Lu [33], which indicate that railway network resilience varies depending on incident duration, thereby reinforcing our conclusions.
Within relatively short failure durations, the proportion of affected passenger travel choices continuously changes with the increase in failure duration, leading to a continuous decline in subway network performance. However, as the failure duration increases to more extended periods, most passengers can plan their travel decision, thereby improving subway network performance, and the reconstructed network reaches a stable state. Station flow also affects subway performance, where stations with higher passenger flows have a more significant impact on the network when they fail than stations with lower passenger flows.
Given the close relationship between station failures and failure duration, transit authorities should prioritize minimizing initial disruptions through swift incident response and real-time passenger communication. For short-duration failures, rapid service restoration is essential to mitigate further declines in network performance. For longer disruptions, attention should shift to optimizing passenger decision-making by offering alternative transport options and accurate travel information. Moreover, developing flexible recovery strategies, such as re-routing services and improving station coordination, will help stabilize network performance as failure duration increases. To these ends, transit authorities should proactively maintain infrastructure via predictive maintenance programs to reduce failure likelihood. They should also develop dynamic passenger information systems that provide real-time updates on disruptions and alternatives, empowering informed passenger choices. Enhancing inter-modal coordination with bus, taxi, and ride-sharing services offers seamless transfer options. Prioritizing service restoration on critical lines and at key stations minimizes network-wide impacts, and investing in redundant infrastructure ensures continued operation during failures.
5.1.2. Comparative Analysis of Station Location and Function
This study compares Nanjing Nan station, a transfer hub and intercity transportation node, with Zhonghuamen station, a nontransfer station, both located on Line 1, to examine how their distinct roles and locations influence their responses to failures. Although both stations experience similar trends as failure duration increases, the underlying mechanisms differ significantly due to their distinct operational roles and passenger dynamics.
Nanjing Nan station’s ability to mitigate disruptions is largely attributable to its designation as a transfer hub, where multiple redundant metro lines facilitate the redirection of passenger flows. In contrast, Zhonghuamen station, which relies on a single metro line, experiences significant capacity limitations during service disruptions. Furthermore, as an intercity travel hub, Nanjing Nan station exhibits higher passenger throughput and a lower trip cancellation rate compared to Zhonghuamen station. This dynamic leads to more pronounced performance fluctuations at Nanjing Nan station, highlighting its vulnerability to cascading failures owing to its interconnectedness with adjacent lines and its broader operational impact.
These findings underscore the necessity for tailored contingency planning that accounts for the specific functional roles of different stations. For transfer stations such as Nanjing Nan, which are critical to the broader transit network, contingency strategies should prioritize enhancing redundancy and operational flexibility. Practical measures could include increasing the frequency of shuttle services between adjacent stations during disruptions, optimizing signal systems to minimize delays, and deploying additional staff to manage passenger flow.
For nontransfer stations like Zhonghuamen, where capacity constraints are a primary concern, targeted interventions are essential to minimize disruption. Such interventions may involve expanding station infrastructure to accommodate higher passenger volumes during peak disruptions, implementing crowd control measures to ensure orderly flow, and enhancing communication systems to provide timely updates to passengers. Moreover, the development of alternative transportation options, such as bus bridging services, can serve as a supplementary means of transport during metro service interruptions, thereby alleviating pressure on the affected station.
5.2. Joint Analysis of Changes in Failure Durations and Variations in Travelers’ Decisions
As demonstrated in this study, subway network performance and cascading failures are significantly influenced by both fault duration and passenger behavior. Prior analyses compared network performance across various stations, examining the impact of different station functionalities and disruption scenarios. Building upon those broader comparisons, the study used Xinjiekou station to conduct a sensitivity analysis, in order to provide a more granular understanding of these dynamics by focusing on the interplay of fault duration and passenger cancellation rates at a single location. The contrasting subway network performance under different fault durations and corresponding passenger cancellation percentages is illustrated in Figure 7. The lower x-axis represents different fault durations, ranging from 5 min to 24 h. The upper x-axis displays the corresponding passenger cancellation percentages, which increase with fault duration. The y-axis represents the value of Q1/Q0, where a higher value indicates stronger performance.
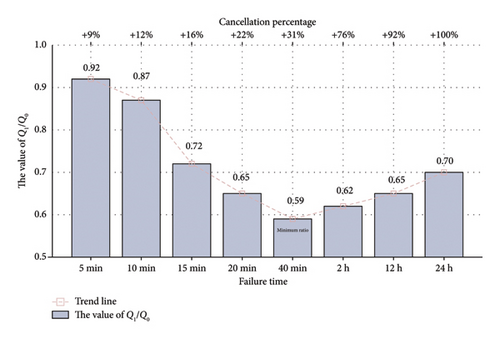
The changes of network performance with different duration time and different decisions of the travelers for the candidate stations are illustrated in Figure 7. Under station incidents, the network is increasingly degraded with the proposed 5, 10, 15, 20, 40 min’ and 2, 12, 24 h’ incidents, but the degrees of degradation are reduced differently among proportion of the travelers eliminating the subway trips. Variations of network degradation rates depend on the topological and functional importance of a station under incidents. Besides, the volume of passengers and the different travel decisions also have an impact on the performance of the network.
Figure 7 shows that with an increase in failure duration and the proportion of travelers choosing to cancel their subway travel, subway network performance exhibits a trend of initial decline followed by improvement to stability. Under short failure durations, the proportion of travelers canceling subway travel is relatively small. Since the impact period is short, the minimal cascading effect results in a minor impact on the subway network. As the failure duration increases, the proportion of travelers choosing to cancel subway travel gradually rises, and the cascading effect becomes more significant, leading to a more substantial impact on subway network performance. However, when the failure duration reaches a certain extent, travelers have enough time to react to the unexpected event. Most of them will alter their travel decisions to minimize the impact of the incident, such as revising their subway routes, thereby gradually restoring subway network performance to stability. Zhu et al. [34] demonstrate that the resilience of subway networks experiences a swift decline with the prolongation of incident durations. However, beyond a certain threshold, this rate of decline diminishes, and there may be a subsequent recovery. These findings corroborate the credibility of the results within this paper.
To effectively mitigate the impacts of subway service disruptions, a structured response strategy encompassing immediate interventions, mid-term operational adjustments, and long-term resilience planning is essential. In the immediate response phase, rapid incident detection and containment measures should be prioritized to minimize cascading failures. Real-time monitoring and predictive modeling can facilitate the identification of disruption patterns, enabling dynamic passenger flow management to alleviate congestion. Strategies such as adaptive crowd control, enhanced station staff coordination, and real-time rerouting guidance can effectively redistribute passenger demand and prevent secondary network failures. For prolonged disruptions, timely and accurate information dissemination is critical. Transit authorities should leverage multiple communication channels, including official mobile applications, digital displays, and social media platforms, to provide real-time updates on service conditions and recommended travel alternatives. Additionally, pre-established contingency measures, such as emergency bus bridging services and enhanced coordination with other public transportation modes, can help mitigate the adverse effects of extended service interruptions. In the long term, enhancing the structural resilience of the subway network is imperative. This requires the reinforcement of critical transfer hubs, capacity expansion at high-risk nodes, and the development of flexible scheduling strategies to accommodate network disruptions. Furthermore, station-specific emergency response protocols should be refined based on empirical passenger behavior data to ensure targeted and efficient mitigation strategies. By integrating these measures, subway systems can improve service recovery efficiency, minimize economic and operational losses, and enhance overall network robustness in the face of unforeseen disruptions.
6. Conclusions
This study, grounded in real-world scenarios, systematically constructs a cascading failure model triggered by passenger overflow resulting from subway faults leading to station closures. By incorporating diverse passenger travel decisions, the research presents a comprehensive method for evaluating the resilience of urban rail transit networks. Unlike conventional models, this approach dynamically identifies critical stations while capturing the interaction between passenger flow dynamics and static network characteristics, which critically influencing its robustness. In particular, the analysis meticulously explores the nuanced variations in passenger travel decisions induced by varying fault durations and the temporal evolution of network performance. This methodological approach significantly advances our comprehension of the mechanisms governing network resilience, effectively addressing fault duration and travel demand. Distinguishing itself from conventional cascading failure models, this approach not only acknowledges the cascading effects but also circumvents potential overestimation of the propagation scale resulting from overlooking changes in travelers’ travel decisions.
The analysis yields several key insights. First, the impact of operational incidents on network degradation is influenced by a station’s topological significance, geographical location, passenger volume, and the capacity of adjacent stations. Stations with high ridership, multiple intersecting lines, prolonged disruptions, and limited capacity at neighboring stations are more susceptible to cascading failures, amplifying their effect on overall network performance. Second, multifunctional stations, particularly transfer hubs serving intercity travel, exhibit a disproportionately large influence during disruptions due to their high passenger sensitivity to time constraints. Consequently, transit operators must prioritize both preventive measures and tailored post-incident recovery strategies for these critical nodes. Third, the degree of variation in passenger travel decisions significantly affects the severity and spatial extent of cascading failures. When a substantial proportion of passengers opt for alternative routes or modes of transportation, the network can better absorb disruptions, reducing the severity of performance degradation. Finally, diversified travel choices enhance network resilience by improving load distribution, mitigating the risk of extensive cascading failures, and facilitating a more efficient recovery process.
The aforementioned findings and conclusions offer salient implications for the management and decision-making processes governing railway transportation network incidents. The incorporation of dynamic passenger decisions into the analytical framework serves to fortify resilience and facilitate the implementation of appropriate emergency response measures aimed at optimizing network functionality amidst crises. To enhance the efficacy of management strategies, the development of differentiated response protocols, predicated on the functional characteristics of individual stations, is paramount. For critical intermodal transfer hubs, exemplified by Nanjing Nan station, priority should be given to augmenting redundancy and flexibility. This may be achieved through the implementation of supplementary shuttle services, optimization of signaling systems to minimize delays, and the strategic deployment of personnel to facilitate effective crowd management, thereby ensuring the continued operability of transfer functionalities during exigencies. For typical commuter stations, such as Zhonghuamen station, addressing capacity constraints through targeted infrastructure enhancements and the implementation of precise crowd control measures, coupled with the provision of timely and pertinent information, can mitigate congestion stemming from information asymmetries. Furthermore, the establishment of a dynamic emergency management framework, predicated on the analysis of real-time passenger flow data, is essential. Such a framework would necessitate the rapid identification of affected stations during incident events, the accurate prediction of passenger overflow trajectories, and the deployment of dynamic scheduling interventions, including temporary train rerouting and the adaptive modulation of train frequencies, to effectively manage system loads and attenuate the potential for cascading failure scenarios. Moreover, investment in intelligent monitoring systems, facilitating both predictive maintenance and rapid recovery capabilities, is warranted. Through the application of big data analytics to forecast potential failure points, and the concurrent implementation of automated response mechanisms, operators can efficiently coordinate resources to alleviate localized congestion during periods of disruption. The integration of machine learning algorithms to optimize post-incident train scheduling has the potential to maximize system throughput and enhance overall operational resilience. In the long term, strategic adaptation of infrastructure investment, prioritizing redundancy and flexibility, coupled with the implementation of adaptive scheduling mechanisms, will significantly enhance the system’s inherent capacity to respond to unforeseen events. The formulation and promulgation of standardized emergency response protocols at the policy level will further ensure coordinated interagency collaboration, thereby augmenting the network’s holistic responsiveness and resilience.
The primary contribution of this study is the introduction of a robust method for assessing the resilience of urban rail transit networks, thoughtfully considering the impact of variations in traveler decision-making. Furthermore, following the meticulous definition of subway accident failure scenarios, critical stations are discerned employing the cascading failure model. Despite the comprehensive nature of this research, several notable limitations warrant acknowledgment. The study is exclusively grounded in the Nanjing subway system, which inherently constrains the generalizability of our findings. The unique topological, geographical, and demographic characteristics of Nanjing’s urban rail transit network may not seamlessly translate to other urban contexts, necessitating cautious interpretation and further validation through comparative studies. Moreover, the research relies substantially on self-reported questionnaire data, which introduces potential methodological biases. Participants’ retrospective accounts of travel decisions may not fully capture the complex, real-time cognitive processes underlying passenger behavior during actual transit disruptions. These methodological constraints suggest the need for more sophisticated data collection approaches and multifaceted behavioral analysis in future research. Future research will extend the methodological framework to urban transit networks across different cities by integrating advanced data collection techniques and machine learning algorithms, enhancing its generalizability and enabling the development of more precise passenger behavior models to assist urban planners in predicting and mitigating network disruptions.
Consent
Informed consent was obtained from all subjects involved in the study.
Disclosure
A preprint has previously been published [38].
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This study was supported by the National Natural Science Foundation of China (52432010), and the National Key Research and Development Program of China (2022XAGG0126).
Acknowledgments
The authors confirm that no AI tools were used in the preparation of this manuscript.
Appendix
| Items | Answers |
|---|---|
| Upon learning that the nearest subway station (a nontransfer station) on your route is closed, and entry is impossible within 5 min, what would you opt for? | A. Waiting at the station. B. Transferring to another station. C. Choosing an alternative mode of transportation |
| Upon learning that the nearest subway station (a nontransfer station) on your route is closed, and entry is impossible within 10 min, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a nontransfer station) on your route is closed, and entry is impossible within 15 min, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a nontransfer station) on your route is closed, and entry is impossible within 20 min, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a nontransfer station) on your route is closed, and entry is impossible within 40 min, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a nontransfer station) on your route is closed, and entry is impossible within 2 h, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a nontransfer station) on your route is closed, and entry is impossible within 12 h, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a nontransfer station) on your route is closed, and entry is impossible within 24 h, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a transfer station) on your route is closed, and entry is impossible within 5 min, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a transfer station) on your route is closed, and entry is impossible within 10 min, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a transfer station) on your route is closed, and entry is impossible within 15 min, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a transfer station) on your route is closed, and entry is impossible within 20 min, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a transfer station) on your route is closed, and entry is impossible within 40 min, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a transfer station) on your route is closed, and entry is impossible within 2 h, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a transfer station) on your route is closed, and entry is impossible within 12 h, what would you opt for? | Ditto |
| Upon learning that the nearest subway station (a transfer station) on your route is closed, and entry is impossible within 24 h, what would you opt for? | Ditto |
| Have you even used the subway? | 1-yes, 2-no |
| How often do you use the subway? | 1-never, 2-seldom, 3-sometimes, 4-often, 5-always |
| If the subway fails, the likelihood that you will change your travel behavior is | 1-do not change, 2-unlikely to change, 3-likely to change, 4-likely to change, 5-certain to change |
| Whether subway failures of different duration have different effects on you | 1-yes, 2-no |
Open Research
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.




