Journal of Advanced Transportation
Volume 2025, Issue 1 2239983
Research Article
Open Access

Real-Time Traffic Conflict Prediction at Intersections: A Novel Approach Integrating Statistical Models and Machine Learning

Chuanyun Fu, 

Chuanyun Fu

School of Transportation Science and Engineering , Harbin Institute of Technology , Harbin , 150090 , Heilongjiang, China , hit.edu.cn

Search for more papers by this author
Jiaming Liu, 

Jiaming Liu

School of Transportation Science and Engineering , Harbin Institute of Technology , Harbin , 150090 , Heilongjiang, China , hit.edu.cn

Search for more papers by this author
Huahua Liu, 

Huahua Liu

School of Transportation Science and Engineering , Harbin Institute of Technology , Harbin , 150090 , Heilongjiang, China , hit.edu.cn

Search for more papers by this author
Xiaoli Wang, 

Xiaoli Wang

Jiaozhou Transportation Bureau , Jiaozhou , 266300 , Shandong, China

Search for more papers by this author
Zhaoyou Lu, 

Zhaoyou Lu

School of Transportation Science and Engineering , Harbin Institute of Technology , Harbin , 150090 , Heilongjiang, China , hit.edu.cn

Search for more papers by this author
Jushang Ou, 

Jushang Ou

Department of Road Traffic Management , Sichuan Police College , Luzhou , 646000 , Sichuan, China , scpolicec.com

Intelligent Policing Key Laboratory of Sichuan Province , Luzhou , 646000 , Sichuan, China

Search for more papers by this author
Wei Bai, 

Corresponding Author

Wei Bai

Department of Road Traffic Management , Sichuan Police College , Luzhou , 646000 , Sichuan, China , scpolicec.com

Intelligent Policing Key Laboratory of Sichuan Province , Luzhou , 646000 , Sichuan, China

Search for more papers by this author
First published: 04 June 2025
https://doi.org/10.1155/atr/2239983
Academic Editor: Kun Wang

Abstract

Real-time traffic conflict prediction is crucial for developing proactive safety management strategies and improving overall traffic safety. However, existing studies have failed to fully consider the entire process of traffic conflict generation at both signalized and unsignalized intersections. Given this, this study proposes a real-time three-stage approach integrating statistical and machine learning models developed from three perspectives to reveal the influencing factors, occurrence identification, and quantity prediction of traffic conflicts. The results show that the proposed approach can effectively predict traffic conflicts at signalized and nonsignalized intersections. The findings of this study provide new ideas for proactive safety management in urban road networks.

1. Introduction

Real-time crash risk prediction is a crucial prerequisite for proactive safety in the field of traffic management. Traditional traffic safety analysis has predominantly relied on historical crash data. However, this approach presents several inherent limitations. First, to ensure the reliability of statistical evaluations based on crash data, it is essential to collect data over extended periods. However, it can be resource-intensive and time-consuming [1–3]. Moreover, crash data often suffer from various issues related to both availability and quality, including underreporting, small sample sizes, relative scarcity, randomness, excessive dispersion, overdispersion, an overabundance of zero observations, unobserved heterogeneity, and temporal and spatial correlations. These factors contribute to the potential inaccuracy and bias of the data [4–6]. Furthermore, the issue of data imbalance remains unresolved and directly affects the reliability of traffic safety assessments derived from crash data [7]. Given these limitations, there has been a growing shift toward the use of traffic conflict data in safety evaluation. Unlike crashes, traffic conflicts are more frequent and can be directly observed. While they share the same underlying failure mechanisms as crashes, traffic conflicts do not result in tangible crash outcomes. Traffic conflict data, compared with crash data, offer distinct advantages such as shorter time periods and easier accessibility, making it a more viable alternative. In recent years, the use of traffic conflict data has garnered increasing attention from scholars in the field of traffic safety due to its potential for more accurate and timely safety assessments [8, 9].

Typically, prediction models based on traffic conflicts primarily include statistical regression models and extreme value theory (EVT) [10–14]. Commonly used statistical regression models include linear discriminant analysis (LDA), generalized linear regression models, Bayesian Tobit models, and binary logistic regression models. For instance, Xu et al. [15] developed a Bayesian random parameter logistic regression model to assess the impact of traffic variables on conflicts under different service levels on highways. Caleffi et al. [16] applied the LDA method to establish a model between real-time traffic states and the probability of traffic conflicts, with the established model showing a satisfactory classification rate. Essa and Sayed [17] used traffic video data from six signalized intersections and employed a fully Bayesian approach to develop a conflict-based safety performance function (SPF) for signalized intersections, demonstrating that the developed SPF exhibited good fit, with all explanatory variables showing statistical significance. In recent years, EVT has been widely applied in real-time crash risk prediction based on conflicts. For example, Wang et al. [18] proposed a safety evaluation method for signalized intersections that integrates microtraffic simulation with EVT, introducing three calibration strategies—basic, semicalibration, and full calibration—to develop the simulation model. The results indicated that the EVT based on the full calibration strategy was a better choice for simulation-based safety assessment. Wang et al. [19] proposed a bivariate EVT framework-based conflict prediction method, finding that the bivariate EVT model more accurately predicts rear-end and side-swipe conflicts. Fu and Sayed [20] introduced a dynamic Bayesian hierarchical peak threshold modeling approach to estimate real-time crash risk based on traffic conflict. Zheng and Sayed [21] applied the EVT method for real-time safety analysis at signalized intersections, establishing a Bayesian hierarchical extreme value model based on traffic conflicts and dynamic traffic parameters as covariates. The performance of the developed EVT model was validated by comparing the cumulative crash estimates with the observed crashes. Fu and Sayed [22] introduced a random-parameter Bayesian hierarchical extreme value model with heterogeneity in means and variances (RPBHEV-HMVs), with results indicating that the RPBHEV-HMV model outperforms existing RPBHEV models in terms of goodness of fit, explanatory power, and crash estimation accuracy and precision. Fu and Sayed [23] constructed a Bayesian dynamic conflict extreme value model based on conflicts, allowing the model parameters to change over time, thus improving the real-time prediction accuracy and portability of crash risk based on conflict extreme value models.

Regarding real-time traffic conflict prediction, Katrakazas et al. [24] used traffic data from highway sections in the UK and traffic simulations to study four different time intervals of traffic data. Their results confirmed the feasibility of using microscopic traffic simulation and the SSAM model for real-time conflict prediction. Fu et al. [25] proposed a dynamic safety warning distance (SWD) and explored its application under adverse weather conditions. The results demonstrate that SWD, as a novel safety warning distance, can more effectively identify both longitudinal and lateral conflicts in mixed traffic flow, particularly under harsh weather conditions. Formosa et al. [26] proposed a real-time traffic conflict prediction model based on deep learning. They developed a deep neural network (DNN) model to predict conflicts in real-time, and their results showed that the best DNN model achieved an accuracy rate of 94%. Meanwhile, Hu et al. [27] proposed a real-time traffic safety assessment method using high-resolution trajectory data, which combined traffic states and conflicts. They used the HighD trajectory dataset from Germany, with data collection intervals of 1 min and 30 s, and employed time-to-collision (TTC) as the conflict indicator. By applying machine learning algorithms for predictive modeling, their results showed that the random forest (RF) model, using resampling techniques, achieved the best performance. Yuan et al. [28], considering data heterogeneity, used the HighD trajectory data to explore the relationship between traffic flow characteristics and conflicts. Analyzing trajectory data at 30-s intervals, they found that the Extreme Gradient Boosting (XGBoost) model, trained on an undersampled dataset, performed the best. In addition, Fu and Sayed [23] introduced a real-time safety analysis method for traffic conflicts based on a Bayesian dynamic extreme value model. This method combined machine learning techniques with the EVT framework and was applied to real-time safety analysis at the cycle level for signalized intersections. Islam and Abdel-Aty [29] developed a long short-term memory (LSTM) model, which used the trajectory, speed, acceleration, and heading of individual connected vehicles as inputs to predict whether a conflict would occur in the short term. Their results showed that this model achieved a conflict prediction accuracy of 72%.

In summary, scholars have made considerable progress in the areas of traffic conflict prediction models and real-time traffic conflict prediction, with a relatively mature research framework. However, there remains room for further development in the fields of traffic conflict influencing factors and the construction of traffic conflict prediction models. Existing studies on traffic conflicts tend to focus on one aspect, rarely considering both the factors influencing the occurrence of conflicts and the frequency of conflicts. In particular, in the field of traffic conflict prediction models, due to issues such as high computational costs, difficulty in data acquisition, and data imbalance, limited attention has been given to short-term conflict prediction, especially the prediction of short-term conflict frequencies.

To address these issues, this paper explores the relationship between traffic states and traffic conflicts (including the occurrence and frequency of conflicts) based on the high-resolution trajectory dataset pNEUMA from Greece. It proposes a real-time intersection traffic conflict prediction method that integrates statistical models with machine learning techniques. This research aims to broaden the scope of real-time traffic safety assessment and provide more accurate prediction tools for traffic safety management.

2. Relevant Data Extraction

2.1. Data Acquisition

This study utilizes the pNEUMA high-resolution trajectory dataset from Greece [30]. The pNEUMA dataset was collected in October 2018 by researchers using 10 drones in the city center of Athens. The dataset records data during the morning peak hours (8:00–10:30 AM) over four working days within 1 week. The study area spans 1.3 square kilometers, with over 100 km of roadways and approximately 100 busy intersections. The data cover a 10-h period and include over 500,000 detailed trajectories of nearly all vehicles within the study area.

Given that the focus of this study is on conflicts between motor vehicles at intersections and recognizing that motorcycle trajectory data often deviate from the road network, it was necessary to remove motorcycle-related data from the dataset. After excluding motorcycle data, intersection-related data were extracted. Based on the study area, 102 intersections were identified, of which 60 were signalized intersections and 42 were unsignalized intersections. The study area and the intersection distribution are shown in Figure 1.

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Study area and intersection distribution. (a) Study area. (b) Intersection distribution.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Study area and intersection distribution. (a) Study area. (b) Intersection distribution.

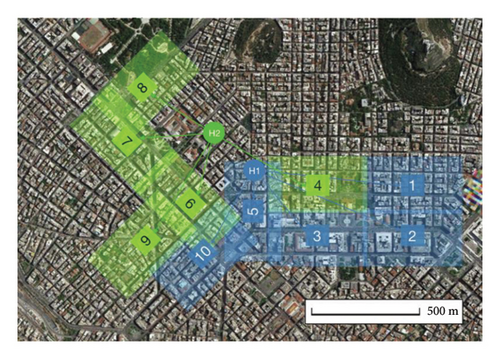
2.2. Extraction of Conflict Indicators

This paper uses TTC and postencroachment time (PET) as the discrimination indicators for conflicts between motor vehicles at intersections. The specific calculation methods are as follows:
()
where Δl is the distance between the preceding and following vehicles; L represents the length of the preceding vehicle; vsub is the speed of the following vehicles; and vpre is the speed of the preceding vehicle.
()
where tsub represents the time when the following vehicle reaches the conflict point; tpre represents the time when the preceding vehicle reaches the conflict point; Δl is the distance between the preceding and following vehicles; and vsub represents the speed of the following vehicle.

For the conflict indicators TTC and PET, thresholds must be established to determine whether a conflict occurs and the severity of the conflict. Based on the relevant literature and the content of this study, a threshold of 1–5 s is comprehensively considered to reflect the severity of the conflict. Within a specific time interval of 1 min, conflicts can be categorized into two types: binary safety conditions (denoted as Bi_conflict, abbreviated as z) and conflict frequency (Num_conflict, abbreviated as n). Herein, Bi_conflict is derived from Num_conflict such that if the conflict frequency n is greater than 0, then z = 1; if the conflict frequency n equals 0, then z = 0.

From the dataset processed in the previous section, conflict data were extracted, totaling 54,244 instances of conflict data, of which 31,816 instances were from signalized intersections and 20,428 instances were from unsignalized intersections. The traffic conflict data are presented in Tables 1 and 2, where “Mean” denotes the average value and “SD” represents the standard deviation.

Table 1. Descriptive statistics of conflict data at signalized intersections.
Conflict indicators Definition∗ Num_conflict Bi_conflict
Mean SD z = 0
TTC1 TTC ≤ 1s 0.1674 0.7354 29,980 (94.23%)
TTC2 TTC ≤ 2s 0.3617 0.8623 27,852 (87.54%)
TTC3 TTC ≤ 3s 0.9870 1.2316 22,093 (69.44%)
TTC4 TTC ≤ 4s 1.7059 1.6002 15,278 (48.02%)
TTC5 TTC ≤ 5s 2.3614 2.1284 11,282 (35.46%)
PET1 PET ≤ 1s 0.1805 0.7203 29,837 (93.78%)
PET2 PET ≤ 2s 0.7709 0.9611 23,366 (73.44%)
PET3 PET ≤ 3s 1.2642 1.3521 18,501 (58.15%)
PET4 PET ≤ 4s 1.6212 1.5223 15,758 (49.53%)
PET5 PET ≤ 5s 2.0754 1.7758 14,874 (46.75%)
  • ∗Represents the number of conflicts within 1-min intervals under a certain threshold of conflict indicators.
Table 2. Descriptive statistics of conflict data at unsignalized intersections.
Conflict indicators Definition∗ Num_conflict Bi_conflict
Mean SD z = 0
TTC1 TTC ≤ 1 s 0.1846 0.8324 19,002 (93.02%)
TTC2 TTC ≤ 2 s 0.3679 0.7357 17,774 (87.01%)
TTC3 TTC ≤ 3 s 1.0655 1.1087 13,388 (65.54%)
TTC4 TTC ≤ 4 s 2.0059 1.6942 9170 (44.89%)
TTC5 TTC ≤ 5 s 2.2068 1.9387 7730 (37.84%)
PET1 PET ≤ 1 s 0.1974 0.8342 19,031 (93.16%)
PET2 PET ≤ 2 s 0.9634 0.8977 14,269 (69.85%)
PET3 PET ≤ 3 s 1.1231 1.2143 11,123 (54.45%)
PET4 PET ≤ 4 s 1.9798 1.5753 10,267 (50.26%)
PET5 PET ≤ 5 s 2.2769 1.5532 9693 (47.45%)
  • ∗Represents the number of conflicts within 1-min intervals under a certain threshold of conflict indicators.

2.3. Extraction of Traffic State Variables

In alignment with the research objectives of this paper and the characteristics of the selected dataset, three types of traffic state variables were chosen: indicators based on spatiotemporal trajectories (Type 1), first-order indicators (Type 2), and second-order indicators (Type 3). Drawing from the generalized definition of traffic variables by scholar Edie, for any spatiotemporal region S, the Type 1 indicators can be derived as follows:
()
where K is the density, veh/km; Q is the flow of traffic, veh/h; V is the speed of traffic, km/h; Δx represents the size of the intersection, m; Δt is the time interval, s; n is the number of vehicles, veh; ti is the travel time of the vehicle, s; and di is the travel distance of vehicle, m.
Furthermore, assuming a very small time interval, the spatiotemporal region can be divided into an infinite number of small subregions such that
()
where m represents the number of subregions.
Consequently, the indicators for the other two categories can be obtained, which are the first-order indicators (Type 2) and the second-order indicators (Type 3):
()
where xi represents a specific index value within the i − th subregion; Me stands for the mean value of xi; Sd is the standard deviation of xi; xi,j represents the index value of the j − th vehicle within the i − th subregion; ni refers to the number of vehicles in the i − th subregion; Mei represents the average value of a particular index within the i − th subregion; and represents the mean value of Mei

The descriptions of the three types of traffic state variables are presented in Table 3.

Table 3. Definitions and explanations of traffic state variables.
Type Variable symbol Variable explanation Unit
Type 1 Q Volume veh/h
K Density veh/km
V Speed km/h
  
Type 2 Hm Headway mean s
Hs Headway standard deviation s
Nm Vehicle count mean —
Ns Vehicle count standard deviation —
  
Type 3 Vmm Mean of average vehicle speed km/h
Vsm Mean of vehicle speed standard deviation km/h
Vms Standard deviation of average vehicle speed km/h
Amm Mean of average vehicle acceleration m/s2

3. Models and Methods

3.1. Binary Logistic Model

Due to the inherent lack of interpretability in machine learning classifiers, it is essential to prefilter the factors influencing the occurrence of traffic conflicts. Therefore, this study employs a binary logistic regression model to conduct a preliminary screening and identify statistically significant factors associated with conflict occurrence. By incorporating logistic regression, the analysis can effectively quantify the influence of each factor while enhancing the transparency and interpretability of the overall modeling framework. The specific expression of the model is presented as follows:
()
where p represents the probability of conflicts occurring in the sample data; xi stands for the selected traffic state variable; σi represents the regression coefficient of the variable xi; and σ0 refers to the constant.
In addition, to quantify the correlation between conflicts and the selected traffic state variables, the odds ratio (OR) is introduced for quantitative analysis. The OR represents the OR, which is the increase in f(x) for each unit increase in x.
()

In the binary logistic regression model, OR serves as a metric to measure the degree of influence of a particular independent variable. The range of OR values is from 0 to infinity, with specific interpretations as follows: when OR = 1, it indicates that the independent variable has no effect on the occurrence of the dependent variable, implying that the two are unrelated; when OR > 1, it suggests that the independent variable is a risk factor, indicating a positive correlation between the two; and when OR < 1, it indicates that the independent variable is a protective factor, implying a negative correlation between the two.

3.2. Machine Learning Algorithms

3.2.1. Algorithm Selection

In the field of machine learning, training samples can be categorized into two types: supervised learning and unsupervised learning. Supervised learning relies on labeled data, where each sample has a known label, and the model is trained using these labeled samples before being employed to generate predictions. When the model’s output variable is continuous, the task is considered a regression problem; conversely, if the output variable is discrete, it is regarded as a classification problem. In contrast, unsupervised learning deals with unlabeled samples, which precludes the use of labels in model training. Instead, unsupervised learning analyzes the hidden structure within the data to uncover its underlying patterns and characteristics. Based on these definitions, the real-time prediction of intersection conflicts studied in this paper falls under the binary classification category within supervised learning. To address this binary classification problem, the study employs four different machine learning algorithms—support vector machine (SVM), K-nearest neighbors (KNNs), RF, and XGBoost.

SVMs are a robust classification algorithm. For real-time prediction of traffic conflicts, SVMs can effectively handle high-dimensional data. Currently, SVMs have been applied to the real-time prediction of crashes and traffic flow. For instance, Li et al. [31] compared SVMs with the negative binomial model in predicting highway crashes, and the results indicated that the SVM model exhibited a better fit.

The KNN algorithm is a simple, easily understood, and implementable method that performs exceptionally well in classification problems and is suitable for real-time prediction. Recently, KNN has been applied in the field of traffic prediction. For example, Lin et al. [32] conducted conflict prediction with time intervals of 5 and 10 min, and the results demonstrated that KNN is effective in predicting conflicts.

RF is an ensemble learning method based on Bagging. Data for real-time prediction of traffic conflicts often contain complex nonlinear relationships, which RF algorithms can effectively handle. For instance, Hu et al. [27] proposed a real-time traffic safety assessment method that combines traffic state and conflict based on high-resolution trajectory data. The RF prediction model achieved optimal performance using resampling techniques.

The XGBoost algorithm is an ensemble learning method based on Boosting, characterized by its high accuracy and robust performance on large-scale datasets. For real-time prediction of traffic conflicts, the XGBoost algorithm is capable of processing large-scale and diverse feature data, providing predictions with high precision. For example, Yuan et al. [28] explored the relationship between conflicts and traffic flow characteristics under the premise of considering heterogeneity, and the results indicated that XGBoost trained on the undersampled dataset was the optimal model.

The advantages and disadvantages of the four algorithms are presented in Table 4.

Table 4. Advantages and disadvantages of four machine learning algorithms.
Algorithm Advantage Disadvantage
SVM Possessing strong nonlinear processing capabilities and being able to effectively handle high-dimensional data Not suitable for solving multiclassification problems and training large-scale datasets and sensitive to missing data
KNN The algorithm is simple and easy to implement, making it suitable for large-scale data Computationally intensive, the presence of noise data affects prediction accuracy, and the prediction speed is slow
RF The training speed is fast, overfitting is minimal, it can handle both categorical and continuous prediction variables, and the model variance is low Not suitable for multiclass classification problems and sensitive to noise
XGBoost Simple to use, fast in execution, effective in performance, and capable of avoiding overfitting High memory and time consumption and are not suitable for processing data with extremely high-dimensional features

3.2.2. Data Preprocessing

Within the dataset, conflict data are imbalanced, meaning that the number of samples without conflicts significantly exceeds the number of samples with conflicts, particularly when the threshold is low. When conflict data are imbalanced, the classifier’s predictions may be biased toward the class with a larger number of samples, leading to erroneous prediction outcomes. Before conflict prediction, the Borderline SMOTE algorithm is employed to resample the data. Table 5 delineates the sample counts in the dataset both before and following the implementation of oversampling.

Table 5. The sample size after the dataset is oversampled.
Intersection type Conflict indicators Before After
z = 0 z = 1 z = 0 z = 1
Signalized intersections TTC1 29,980 1836 29,980 29,980
TTC2 27,852 3964 27,852 27,852
TTC3 22,093 9723 22,093 22,093
TTC4 15,278 16,538 16,538 16,538
TTC5 11,282 20,534 20,534 20,534
PET1 29,837 1979 29,837 29,837
PET2 23,366 8450 23,366 23,366
PET3 18,501 13,315 18,501 18,501
PET4 15,758 16,058 16,058 16,058
PET5 14,874 16,942 16,942 16,942
  
Unsignalized intersections TTC1 19,002 1426 19,002 19,002
TTC2 17,774 2654 17,774 17,774
TTC3 13,388 7040 13,388 13,388
TTC4 9170 11,258 11,258 11,258
TTC5 7730 12,698 12,698 12,698
PET1 19,031 1397 19,031 19,031
PET2 14,269 6159 14,269 14,269
PET3 11,123 9305 11,123 11,123
PET4 10,267 10,161 10,267 10,267
PET5 9693 10,735 10,735 10,735

3.2.3. Model Training and Hyperparameter Optimization

To mitigate model overfitting, enhance generalization performance on unseen data, and reduce the impact of random factors on the prediction results, this study employed a grid search combined with 5-fold cross-validation to optimize the hyperparameters of the four machine learning models. With 5-fold, the data are divided into five equal parts. Four of them are in turn for training, while the remaining part is used for testing. The average of the five test results is taken as the final hyperparameters of the model, which are shown in Table 6.

Table 6. The value of hyperparameters.
Model Hyperparameter Value
SVM C 5
Kernel RBF
Gamma 0.005
  
KNN n_neighbors 7
Metric Euclidean distance
  
RF n_estimators 150
max_depth 12
min_samples_split 5
min_samples_leaf 3
  
XGboost learning_rate 0.07
max_depth 6
Subsample 0.8
colsample_bytree 0.7
Gamma 0.2
Lambda 1
Alpha 0.5

3.2.4. Model Evaluation

In evaluating the real-time prediction model of intersection conflict occurrence based on machine learning, it is essential to select appropriate evaluation methods and metrics to obtain effective and reliable results. Before evaluation, the confusion matrix must be computed, with its explanation provided in Table 7.

Table 7. Confusion matrix.
  Actual
Positive example Counter example Total
Prediction Positive example (z = 1) TP FP TP + FP
Counter example (z = 0) FN TN FN + TN
Total TP + FN FP + TN TP + FN + FP + TN

Here, TP denotes the correct prediction of conflict occurrence z = 1, TN represents the correct prediction of safe conditions z = 0, FP indicates samples that did not experience a conflict but were incorrectly predicted as having a conflict, and FN refers to conflicting samples that were incorrectly predicted as being free of conflict.

Through the confusion matrix, three model evaluation metrics required in this paper can be calculated as follows:
  • (1)

    Accuracy: the percentage of correctly predicted samples out of the total test samples, with the specific calculation formula as follows:

    ()

  • (2)

    False alarm rate (FAR): the percentage of incorrect predictions among the positive instances, with the specific calculation formula as follows:

    ()

  • (3)

    Missed alarm rate (MAR): the percentage of incorrect predictions among the negative instances, with the calculation formula as follows:

    ()

  •  

    Here, a higher Accuracy and lower FAR and MAR indicate superior performance of the intersection conflict prediction model.

3.3. Bayesian Spatial Poisson Model

The Poisson model is a commonly used model for analyzing traffic-related data. The Poisson distribution assumes that the number of occurrences of an event within a certain time or spatial range is random, but the average occurrence rate is known, and the occurrences are independent of previous events. The Poisson model is simple, easy to understand, and widely applicable. Models based on the Poisson distribution have been extensively used in accident frequency analysis, as the Poisson model effectively captures the randomness and discreteness of traffic accidents. The Poisson-lognormal model introduces a residual random term to address data dispersion and heteroscedasticity, making it suitable for cases where the Poisson distribution alone is inadequate due to data overdispersion.

Spatial correlation is extensively present among neighboring intersections, thereby affecting the accuracy of conflict frequency prediction at intersections. This paper introduces the conditional autoregressive (CAR) model into the Bayesian spatial-Poisson log model to predict the frequency of conflicts occurring at intersections. Let Yi be the frequency of conflicts at the ith intersection, and the structure of the model is as follows:
()
where λ represents the intensity parameter, which reflects the expected number of conflicts within the intersection; Xi is the vector of explanatory variables; β0 is the coefficient to be estimated; and β represents the coefficient to be estimated.
Compared with the maximum likelihood estimation method, which only uses the collected sample data for parameter estimation without considering other information about the parameters, Bayesian estimation emphasizes the consideration of uncertainty, allowing for a more comprehensive and flexible inference of models and parameters. In essence, the core idea of Bayesian estimation is to use both sample information and prior information to solve for the posterior information of the parameters. The fundamental Bayesian formula is presented as follows:
()
where f(x|θ) is the likelihood function; π(θ) is the prior distribution of the parameter; and π(θ|x) is the posterior distribution of the parameter.
In Bayesian estimation, noninformative prior distributions are assigned to β and θi.
()
The spatial correlation term ϕi is prespecified using a CAR model.
()

When intersections i and j are adjacent, the value of ωij is 1; when intersections i and j are not adjacent, the value of ωij is 0.

To ensure the convergence of the model, this paper employs the prior distribution form established.
()
where τθ represents the overdispersion characteristic caused by the spatial effect and τc represents the overdispersion characteristic caused by the random effect.

4. Results and Discussion

4.1. Analysis of Factors Influencing Traffic Conflicts

Given the diverse nature of the selected variables, there may exist strong correlations among them, leading to multicollinearity. This can adversely affect the accuracy of the constructed model, thereby impacting the analysis of factors influencing traffic conflicts. Consequently, before modeling the factors affecting traffic conflicts, a multicollinearity test is conducted using the Pearson correlation coefficient method. A correlation coefficient heatmap for the 13 variables is depicted in Figure 2.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Correlation coefficient heatmap.

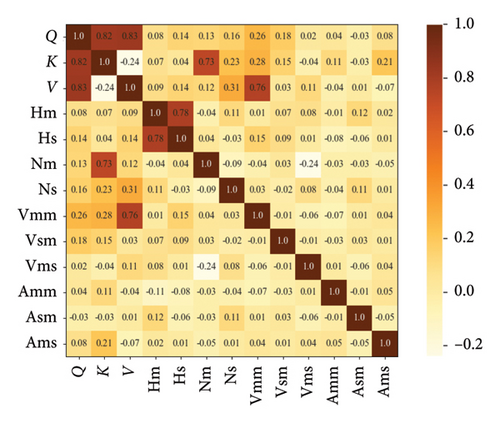
Analysis of the heatmap reveals that the correlation coefficients between flow Q and density K, flow Q and velocity V, the average value of vehicle average speed Vmm and velocity V, the standard deviation of headway Hs and the average headway Hm, as well as density K and the average number of vehicles Nm, are depicted in deep red within the heatmap, indicating correlation coefficients greater than 0.7 and thus exhibiting strong correlations. To enhance the accuracy of the model and to better analyze the factors influencing conflict occurrence, it has been decided to exclude the four traffic state variables of flow Q, the average value of vehicle average speed Vmm, the standard deviation of headway Hs, and the average number of vehicles Nm. Apart from these five sets of variables, the correlation coefficients among the remaining traffic state variables are all less than 0.5, with the majority being below 0.1, suggesting that the other nine traffic state variables do not exhibit multicollinearity issues and can be selected as independent variables in subsequent modeling analyses.

A binary logistic regression model was constructed to analyze the significant factors affecting the occurrence of conflicts, with the results presented in Table 8.

Table 8. Results of the binary logistic regression model.
Model K V Hm Ns Vsm Vms Amm Asm Ams
TTC1 Coefficient 0.3691 −0.3731 0.001 0.038 −0.053 0.105 0.4292 0.265 0.046
p 0.001 0.001 0.876 0.463 0.621 0.265 0.005 0.071 0.604
OR 1.481 0.663 1.001 1.043 0.905 1.114 1.536 1.279 1.054
  
TTC2 Coefficient 0.4191 −0.3511 −0.001 0.059 −0.039 0.1822 0.3143 0.323 0.098
p 0.001 0.001 0.756 0.221 0.544 0.005 0.021 0.025 0.074
OR 1.543 0.711 0.998 1.063 0.924 1.183 1.428 1.424 1.105
  
TTC3 Coefficient 0.5031 −0.3391 −0.002 0.0933 0.1372 0.2991 0.4211 0.158 0.064
p 0.001 0.001 0.325 0.023 0.003 0.001 0.001 0.231 0.118
OR 1.713 0.736 0.996 1.098 1.136 1.324 1.554 1.201 1.097
  
TTC4 Coefficient 0.6351 −0.2541 −0.004 0.1691 0.2541 0.3941 0.4531 0.124 0.073
p 0.001 0.001 0.374 0.001 0.001 0.001 0.001 0.153 0.068
OR 1.916 0.779 0.994 1.222 1.268 1.499 1.679 1.165 1.063
  
TTC5 Coefficient 0.7071 −0.2291 −0.0082 0.3831 0.3311 0.4721 0.5141 0.117 0.059
p 0.001 0.001 0.009 0.001 0.001 0.001 0.001 0.324 0.089
OR 2.132 0.793 0.992 1.492 1.451 1.698 1.733 1.154 1.063
  
PET1 Coefficient 0.4611 0.1833 0.009 0.3231 −0.113 −0.006 0.231 0.124 0.063
p 0.001 0.032 0.425 0.001 0.164 0.868 0.352 0.164 0.565
OR 1.684 1.185 1.008 1.424 0.913 0.993 1.232 1.178 1.072
  
PET2 Coefficient 0.4981 −0.004 −0.002 0.2031 0.063 0.2471 0.3421 0.102 −0.028
p 0.001 0.894 0.265 0.001 0.143 0.001 0.001 0.254 0.533
OR 1.702 0.994 0.996 1.197 1.072 1.259 1.471 1.109 0.968
  
PET3 Coefficient 0.5231 −0.1231 −0.0082 0.1861 0.1781 0.3761 0.4061 0.114 −0.047
p 0.001 0.001 0.009 0.001 0.001 0.001 0.001 0.163 0.137
OR 1.732 0.894 0.992 1.189 1.176 1.493 1.521 1.149 0.949
  
PET4 Coefficient 0.5461 −0.1641 −0.0121 0.2231 0.2161 0.4531 0.4131 0.131 −0.034
p 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.094 0.413
OR 1.721 0.876 0.990 1.211 1.202 1.668 1.539 1.183 0.953
  
PET5 Coefficient 0.5771 −0.1831 −0.0091 0.2411 0.2251 0.4391 0.4431 0.158 −0.026
p 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.132 0.667
OR 1.764 0.857 0.992 1.252 1.213 1.647 1.652 1.203 0.960
  • 1Indicates a significance level of α = 0.001.
  • 2Indicates a significance level of α = 0.01, and.
  • 3Indicates a significance level of α = 0.05.

Based on Table 8, it can be observed that the traffic state variables significantly associated with different conflict indicators and varying levels of conflict severity, that is, different thresholds, are distinct. When the threshold of a conflict indicator is higher, it tends to have more significant explanatory variables. Specifically, for TTC thresholds ranging from TTC1 (TTC threshold of 1 s) to TTC5 (TTC threshold of 5 s), the number of significant factors influencing conflict occurrence are 3, 4, 6, 6, and 7, respectively. Correspondingly, for PET thresholds ranging from PET1 (PET threshold of 1 s) to PET5 (PET threshold of 5 s), the number of significant factors influencing conflict occurrence are 3, 4, 7, 7, and 7, respectively.

From the results of the regression model, it is evident that regardless of whether the conflict indicator is TTC or PET, and irrespective of the threshold values of these two indicators, density K and velocity V are consistently significant factors influencing the occurrence of conflicts. The impact of other traffic state variables on conflict occurrence, however, varies depending on the severity of the conflict. This suggests that the severity of conflicts significantly affects the scale of the data, meaning that the more severe the conflict, the sparser the corresponding dataset. Due to the sparsity of the dataset, there is a certain challenge in identifying significant traffic variables that affect conflict occurrence, which in turn leads to differences in significant influencing factors when the threshold values of conflict indicators vary.

For TTC and PET with thresholds of 3 s, 4 s, and 5 s, their significant variables are largely consistent, showing statistically significant correlations with density K, velocity V, the standard deviation of vehicle count Ns, the average value of vehicle speed standard deviation Vsm, the standard deviation of vehicle average speed Vms, and the average value of vehicle average acceleration Amm. When density K, the standard deviation of vehicle count Ns, the average value of vehicle speed standard deviation Vsm, the standard deviation of vehicle average speed Vms, and the average value of vehicle average acceleration Amm serve as significant influencing factors, their coefficients are all positive whereas the impact of velocity V and the average headway Hm on conflict occurrence is negative, with the exception of velocity V in PET1. These results indicate that when the density of vehicles within an intersection is high, the average acceleration is large, the variability in vehicle count is significant, and the likelihood of conflicts occurring within the intersection will markedly increase. In addition, if the temporal Vms and spatial Vsm variability of vehicle speeds within the intersection increases, the risk of conflicts will also significantly rise. Conversely, it can be inferred that when vehicles travel at higher speeds, have larger headways between them, enjoy better traffic conditions within the intersection, and the traffic flow is stable, the driving environment will be safer with a lower probability of conflicts. However, this state implies that fewer vehicles are waiting at the traffic light during the current cycle, resulting in a sparse traffic flow that can pass freely without the need for queuing. From another perspective, density K, velocity V, and the average value of vehicle average acceleration Amm are the three most significant factors influencing conflicts (except Amm and V in PET1), as they exhibit statistical significance and are significantly correlated with conflict occurrence across the 10 models with different thresholds of TTC and PET compared with other traffic state variables.

4.2. Real-Time Prediction of Conflict Occurrence Based on Machine Learning

Four machine learning algorithms—SVM, KNN, RF, and XGBoost—are selected to construct real-time prediction models for conflict occurrence at signalized and unsignalized intersections, respectively. The model prediction results are presented in Tables 9 and 10.

Table 9. Comparison of conflict prediction results for signalized intersections using machine learning algorithms.
  Accuracy (%) FAR (%) MAR (%)
SVM KNN RF XGB SVM KNN RF XGB SVM KNN RF XGB
TTC1 84.2 77.3 91.8 84.2 38.5 40.3 0.0 8.9 16.8 16.8 5.5 15.6
TTC2 70.5 74.8 90.9 83.8 30.2 31.5 8.4 10.7 29.6 21.9 6.4 17.4
TTC3 69.7 72.1 89.3 82.5 31.3 28.3 7.8 11.3 29.9 23.8 6.8 18.9
TTC4 69.3 72.6 87.6 81.6 30.8 29.4 7.4 10.6 30.4 24.5 5.9 19.3
TTC5 68.9 70.5 86.4 78.7 32.1 24.8 7.7 12.5 30.2 28.4 6.6 20.8
TTC (mean) 72.5 73.5 89.2 82.1 32.6 30.9 6.3 10.8 27.4 23.1 6.3 18.4
PET1 77.3 75.4 89.5 82.4 46.2 42.8 24.1 23.6 22.9 20.1 8.3 18.3
PET2 65.8 68.2 83.7 79.7 44.7 36.5 22.8 25.3 33.4 27.3 13.8 25.1
PET3 66.4 66.9 81.3 75.3 44.9 35.9 24.3 26.8 31.8 30.4 17.2 25.9
PET4 64.9 64.2 79.9 72.7 43.8 34.6 27.1 25.9 33.7 33.8 18.5 28.8
PET5 64.7 63.7 78.6 72.2 42.6 31.2 26.8 28.6 33.1 34.3 20.0 30.4
PET (mean) 67.8 67.7 82.6 76.5 44.4 36.2 25.0 26.0 31.0 29.2 15.6 25.7
Table 10. Comparison of conflict prediction results for unsignalized intersections using machine learning algorithms.
  Accuracy (%) FAR (%) MAR (%)
SVM KNN RF XGB SVM KNN RF XGB SVM KNN RF XGB
TTC1 80.8 75.4 88.1 91.5 38.9 42.5 5.3 3.4 20.3 20.7 7.9 8.9
TTC2 66.4 70.6 86.5 89.4 31.8 33.6 8.8 8.6 30.8 25.2 10.3 9.7
TTC3 68.6 71.1 84.9 87.5 31.1 31.5 13.0 9.9 29.7 27.6 14.3 10.6
TTC4 67.9 68.5 82.7 86.1 32.3 29.8 11.9 10.1 31.2 30.3 16.9 13.5
TTC5 65.4 66.9 80.5 84.7 32.9 26.7 13.8 11.4 31.7 32.1 17.4 15.3
TTC (mean) 69.8 70.5 84.5 87.8 33.4 32.8 10.6 8.7 28.7 27.2 13.4 11.7
PET1 70.8 70.7 86.4 85.5 48.9 45.5 26.9 19.5 25.1 25.2 12.4 13.8
PET2 65.4 68.3 80.9 82.1 45.2 40.8 27.5 21.1 35.4 30.3 16.1 15.2
PET3 63.9 64.8 77.5 78.5 45.5 39.4 28.9 23.4 36.8 33.7 18.8 17.6
PET4 63.0 63.2 75.8 76.4 47.7 37.5 30.6 23.9 34.7 34.9 20.7 18.9
PET5 61.6 60.5 73.3 73.3 44.6 32.3 33.4 25.8 34.3 36.8 23.4 21.4
PET (mean) 64.9 65.5 78.8 79.2 46.4 39.1 29.5 22.7 33.3 32.2 18.3 17.4

From the tables, it can be observed that for the prediction of traffic conflict occurrence at both signalized and unsignalized intersections, the prediction models using the conflict indicator TTC generally outperform those using PET. This is because the average accuracy of TTC (72.5%–89.2% for signalized intersections and 69.8%–87.8% for unsignalized intersections) is higher than that of PET (67.7%–82.6% for signalized intersections and 64.9%–79.2% for unsignalized intersections), the average FAR of TTC (6.3%–32.6% for signalized intersections and 8.7%–33.4% for unsignalized intersections) is lower than that of PET (25.0%–44.4% for signalized intersections and 22.7%–46.4% for unsignalized intersections), and the average MAR of TTC (6.3%–27.4% for signalized intersections and 15.6%–31.0% for unsignalized intersections) is lower than that of PET (15.6%–31.0% for signalized intersections and 16.1%–46.4% for unsignalized intersections). Furthermore, overall, for the same machine learning algorithm and the same conflict indicator, the predictive performance of the model tends to decline as the threshold of the conflict indicator increases.

In terms of algorithm comparison, for the prediction of traffic conflicts at signalized intersections, regardless of the conflict indicator and its corresponding severity, RF demonstrates significantly superior performance compared to the other three algorithms. Its average accuracy for TTC and PET is 89.2% and 82.6%, with average FAR of 6.3% and 25.0%, and average MAR of 6.3% and 15.6%. For the prediction of traffic conflicts at unsignalized intersections, the XGBoost algorithm outperforms the other three algorithms, with average accuracies for TTC and PET of 87.8% and 79.2%, respectively, average FARs of 8.7% and 22.7%, and average MARs of 11.7% and 16.1%, respectively.

In addition, the receiver operating characteristic (ROC) curves and area under the curve (AUC) values corresponding to the prediction models for conflict occurrence at signalized and unsignalized intersections are depicted in Figures 3 and 4, respectively. From these figures, it can be observed that consistent with the model evaluation metrics, RF performs better than other algorithms for signalized intersections, with an AUC value ranging from 0.745 to 0.845, particularly when the threshold of the conflict indicator is higher. For unsignalized intersections, the XGBoost algorithm demonstrates the best performance, with an AUC value ranging from 0.730 to 0.822.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
ROC curves corresponding to four machine learning algorithms for signalized intersections.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
ROC curves corresponding to four machine learning algorithms for unsignalized intersections.

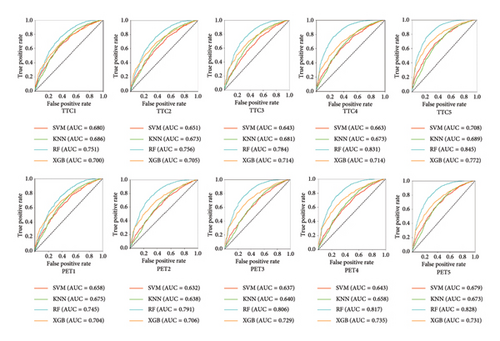
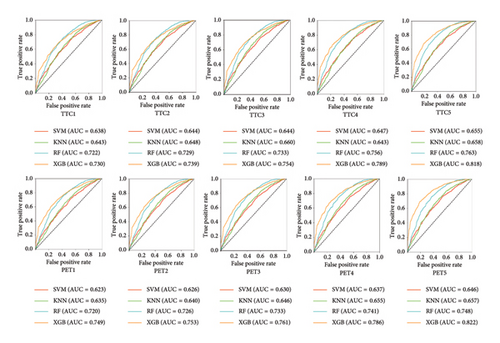
Based on the comprehensive evaluation of model metrics and the ROC curve diagrams, it is evident that the AUC values of the four machine learning algorithms selected in this study are all greater than 0.6, indicating satisfactory predictive performance. Specifically, for the prediction of traffic conflicts at signalized intersections, the RF algorithm is the most optimal whereas for the prediction of traffic conflicts at unsignalized intersections, the XGBoost algorithm is the most optimal. Consequently, these two algorithms are chosen for application in subsequent predictions of traffic conflict frequency.

4.3. Analysis of Factors Influencing Traffic Conflict Frequency

A Bayesian spatial Poisson model is constructed, and Bayesian parameter estimation is performed using the WinBUGS software. To ensure the convergence speed of the model and the accuracy of the results, this paper sets up two Markov Chain Monte Carlo (MCMC) chains for 50,000 iterations, discarding the first 20,000 unstable samples.

Table 11 presents the parameter estimation results of 10 Bayesian spatial Poisson models trained using the conflict dataset. As expected, the results of the spatial model are largely consistent with those of the binary logistic regression model, indicating that the significant factors influencing conflict frequency vary depending on different conflict indicators and different levels of severity for the same indicator. However, for the same indicator and severity level, the significant influencing factors identified by the binary logistic model and the Bayesian spatial Poisson model differ, suggesting that the significant factors affecting conflict occurrence and conflict frequency are not the same. This implies that before predicting the frequency of traffic conflicts at intersections, it is necessary to estimate the significant correlation between the explanatory variables and conflict frequency.

Table 11. Parameter estimation results of the Bayesian spatial Poisson model.
Model TTC1/PET1 TTC2/PET2 TTC3/PET3 TTC4/PET4 TTC5/PET5
Mean Confidence interval Mean Confidence interval Mean Confidence interval Mean Confidence interval Mean Confidence interval
TTC K 0.328∗ (0.052, 0.751) — — 0.328 (0.032, 0.623) 0.355 (0.125, 0.582) 0.463 (0.278 0.667)
V — — — — — — −0.295 (-0.528, −0.063) −0.397 (-0.613, −0.221)
Hm — — — — −0.143 (-0.288, −0.020) −0.169 (-0.698, −0.229) −0.156 (-0.251, −0.067)
Vms — — — — −0.549 (-0.866, −0.213) −0.458 (-0.843, −0.165) −0.481 (-0.678, −0.293)
Amm — — 0.433 (-0.100, 1.221) — — — — — —
Asm −0.143 (-0.837, 0.106) −0.289∗ (-1.163, 0.020) −0.600∗ (-1.073, −0.145) −0.512 (-0.828, −0.177) −0.509 (-0.769, −0.208)
Ams — — — — 0.456 (0.199, 0.726) 0.392 (0.193, 0.599) 0.344 (0.183, 0.522)
α 0.211 (0.058, 0.482) 0.167 (0.045, 0.418) 0.259 (0.085, 0.508) 0.201 (0.073, 0.417) 0.212 (0.069, 0.500)
sd(ϕ) 0.214 (0.019, 1.375) 0.082 (0.009, 0.327) 0.227 (0.013, 1.933) 0.066 (0.019, 0.231) 0.099 (0.012, 0.487)
sd(θ) 0.473 (0.210, 1.906) 0.295 (0.203, 0.564) 0.378 (0.143, 2.123) 0.232 (0.175, 0.397) 0.301 (0.212, 0.725)
  
PET K — — 0.046∗ (-0.837, 0.106) — — 0.131∗ (-0.078, 0.364) 0.246 (0.041, 0.499)
V — — — — — — −0.354 (-0.612, −0.117) −0.422 (-0.653, −0.176)
Hm — — — — −0.075 (-0.210, 0.011) −0.161 (-0.277, −0.040) −0.162 (-0.278, −0.053)
Vms −0.462∗ (-1.138, 0.089) −0.177∗ (-0.544, −0.061) −0.349∗ (-0.593, 0.115) −0.322 (-0.545, −0.044) −0.358 (-0.592, −0.033)
Asm — — — — — — −0.448 (-0.693, −0.157) −0.455 (-0.788, −0.103)
Ams — — — — 0.211 (0.025, 0.448) 0.258 (0.039, 0.455) 0.311 (0.111, 0.523)
α 0.165 (0.045, 0.441) 0.281 (0.083, 0.499) 0.203 (0.080, 0.441) 0.199 (0.056, −0.408) 0.214 (0.065, 0.501)
sd(ϕ) 0.093 (0.011, 0.459) 0.704 (0.022, 2.903) 0.066 (0.021, 0.266) 0.073 (0.014, 0.260) 0.092 (0.021, 0.412)
sd(θ) 0.362 (0.238, 0.736) 1.277 (0.144, 4.719) 0.224 (0.163, 0.449) 0.231 (0.178, 0.411) 0.266 (0.187, 0.611)
  • Note: An asterisk (∗) indicates credibility within a 90% confidence interval, while all others are credible within a 95% confidence interval.

From the table, it can be observed that the models with conflict indicators TTC4, TTC5, PET4, and PET5 share the same significant variables, and these models have the highest number of significant variables among the 10 models. In addition, the impact of all variables on conflict frequency is consistent, with density K, the standard deviation of vehicle average acceleration Ams, and the average value of vehicle average acceleration Amm being positively correlated with conflict frequency. In contrast, velocity V, the average headway Hm, the standard deviation of vehicle average speed Vms, and the mean of vehicle acceleration standard deviation Asm are negatively correlated with conflict frequency. An unexpected result is that, compared with the binary logistic model, the three acceleration-related variables in the spatial model—the average value of vehicle average acceleration Amm, the mean of vehicle acceleration standard deviation Asm, and the standard deviation of vehicle average acceleration Ams—have different effects on conflict frequency. The coefficients of Amm and Ams are positive, while the coefficient of Asm is negative. This suggests that if the temporal variability of vehicle acceleration within the intersection Ams is greater and the spatial variability of vehicle acceleration Asm is smaller, the frequency of conflicts occurring at the intersection will be higher.

Furthermore, regarding the impact of the residual term, α represents the ratio of the sum of spatial residuals to overdispersion residuals. The closer the value of α is to 0, the stronger the spatial correlation, indicating that the influence between conflicts at adjacent intersections is greater. Generally, a smaller value of α suggests a better model fit; otherwise, the spatial correlation within the model should be reconsidered. Based on the values of α from the parameter estimation results (for TTC models, α ranges from 0.167 to 0.259; for PET models, α ranges from 0.165 to 0.281), it can be concluded that the model fit is satisfactory, that is, considering the spatial correlation between adjacent intersections helps to predict the frequency of conflicts at intersections more accurately.

From the perspective of explanatory variables, it can be observed that unlike the factors influencing the occurrence of conflicts, the average value of vehicle speed standard deviation Vsm and the standard deviation of vehicle count Ns are not statistically significant in predicting conflict frequency across the 10 spatial models. This suggests that changes in vehicle speed and vehicle count over a certain time interval are not suitable for predicting the frequency of conflicts at intersections. In contrast, the variables density K and the standard deviation of vehicle average speed Vms are statistically significant in most models, K is significant in seven models and Vms is significant in eight models. Therefore, it can be inferred that during conflicts, the high density of vehicles within an intersection and significant temporal fluctuations in average speed may lead to an increase in conflict frequency. In addition, the results of the Bayesian spatial Poisson model indicate that the most significant variables for models with conflict indicators TTC and PET are different. For models with the TTC conflict indicator, the most significant variable is the mean of vehicle acceleration standard deviation Asm; for models with the PET conflict indicator, the most significant variable is the standard deviation of vehicle average speed Vms, as they consistently exhibit statistical significance under different thresholds of their respective conflict indicators. Consequently, it can be deduced that speed variation indicators are more applicable to models with the PET conflict indicator, while acceleration variation indicators are more suitable for models with the TTC conflict indicator.

4.4. Analysis of Conflict Frequency Prediction Accuracy

The conflicting samples predicted as 1 by the RF and XGBoost algorithms are input into the Bayesian spatial Poisson model for the prediction of traffic conflict frequency at signalized and unsignalized intersections.

After proposing the method for predicting intersection conflict frequency, it is necessary to evaluate the method. Referring to previous studies, this paper selects three evaluation metrics—root mean square error (RMSE), mean absolute percentage error (MAPE), and mean absolute error (MAE)—to assess the superiority or inferiority of the model.
()
where xi represents the actual value of the conflict frequency and represents the predicted value of the conflict frequency.

Tables 12 and 13, respectively, present the final results of traffic conflict prediction at signalized and unsignalized intersections. The smaller the values of RMSE, MAPE, and MAE in the tables, the better the performance of the model.

Table 12. Final results of conflict prediction at signalized intersections.
  TTC1 TTC2 TTC3 TTC4 TTC5 PET1 PET2 PET3 PET4 PET5
RMSE 0.153 0.359 0.568 0.986 1.232 0.134 0.376 0.661 0.883 1.102
MAPE (%) 8.9 13.4 19.7 25.5 30.6 8.5 13.8 20.8 22.9 27.1
MAE 0.010 0.032 0.085 0.297 0.526 0.007 0.065 0.193 0.276 0.352
Table 13. Final results of conflict prediction at unsignalized intersections.
  TTC1 TTC2 TTC3 TTC4 TTC5 PET1 PET2 PET3 PET4 PET5
RMSE 0.168 0.332 0.586 1.059 1.313 0.175 0.413 0.624 1.132 1.400
MAPE (%) 9.9 12.2 19.9 26.3 35.8 12.3 18.3 20.1 27.9 38.2
MAE 0.015 0.027 0.135 0.320 0.575 0.012 0.077 0.231 0.306 0.628

For signalized intersections, from TTC1 to TTC5 and from PET1 to PET5, as the threshold values of conflict indicators increase, the values of the three evaluation metrics, namely, RMSE, MAPE, and MAE, all increase, which mean that the performance of the models gradually deteriorates. Regarding the two conflict indicators, TTC and PET, the performance of the models with TTC1, TTC2, and TTC3 are, respectively, superior to that of the models with PET1, PET2, and PET3, while the performance of the models with PET4 and PET5 is, respectively, better than that of the models with TTC4 and TTC5. Among the 10 models for traffic conflict prediction at signalized intersections, the model with the PET1 conflict indicator performs the best, with an RMSE of 0.134, a MAPE of 8.5%, and an MAE of 0.007, which are the lowest among all; the model with the TTC5 conflict indicator performs the worst, with an RMSE of 1.232, a MAPE of 30.6%, and an MAE of 0.526, which are the highest.

For unsignalized intersections, similarly to signalized intersections, from TTC1 to TTC5 and from PET1 to PET5, as the threshold values increase, the performance of the models deteriorates gradually. However, differing from signalized intersections, for the two conflict indicators, TTC and PET, when the conflict indicator thresholds are the same, the performance of the models corresponding to TTC is superior to that of the models corresponding to PET. Among the 10 prediction models, the prediction model with the TTC1 conflict indicator performs the best, with an RMSE of 0.168, a MAPE of 9.9%, and an MAE of 0.015. The prediction model with the PET5 conflict indicator performs the worst, with an RMSE of 1.400, a MAPE of 38.2%, and an MAE of 0.628.

By comparing the conflict frequency prediction results of signalized and unsignalized intersections, for the same threshold of the same conflict indicator, the performance of the conflict prediction model for signalized intersections is superior to that of the conflict prediction model for unsignalized intersections (except for TTC2 and PET3). Among all 20 models, the model with the PET5 conflict indicator for unsignalized intersections performs the worst. Taking it as an example, when predicting the number of conflicts within a one-minute time interval at the intersection, the accuracy is 66.23%, which means that 66.23% of the predicted values match the actual values. Given the actual data background, this prediction result is relatively satisfactory. In fact, in routine research, conflict thresholds of 3 and 4 s are the most commonly used indicators, and the corresponding models (TTC3, TTC4, PET3, and PET4) perform well, with RMSE ranging from 0.568 to 1.132, MAPE ranging from 19.7% to 27.9%, and MAE ranging from 0.085 to 0.320. Therefore, the proposed method performs well in predicting real-time conflicts.

In addition, Figure 5 further intuitively depicts the actual conflict frequencies, the predicted conflict frequencies, and the prediction accuracy at the intersection.

Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
The prediction results of the proposed model. (a) Actual conflict frequencies. (b) Predicted conflict frequencies. (c) Prediction accuracy.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
The prediction results of the proposed model. (a) Actual conflict frequencies. (b) Predicted conflict frequencies. (c) Prediction accuracy.
Details are in the caption following the image
Figure 5 (c)
Open in figure viewerPowerPoint
The prediction results of the proposed model. (a) Actual conflict frequencies. (b) Predicted conflict frequencies. (c) Prediction accuracy.

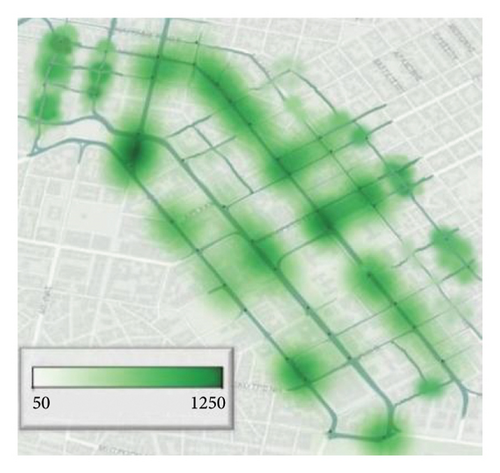
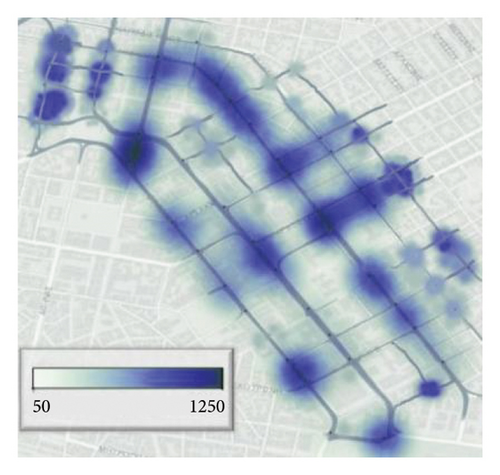
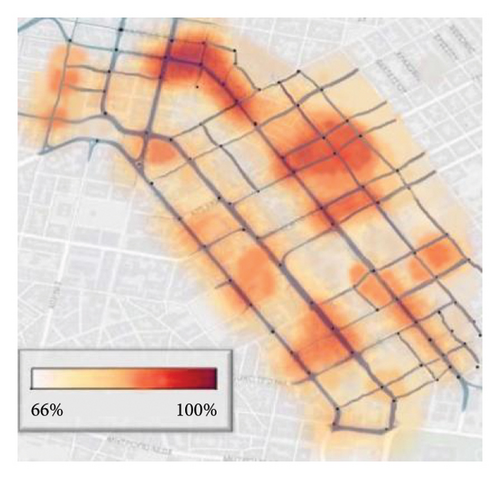
As can be seen from Figure (a) and Figure (b), the conflict occurrences at different intersections vary. However, due to the clustering characteristics of the spatial heat map, there are certain similarities among adjacent intersections, which also indicate that it is necessary to consider spatial correlation when predicting traffic conflicts. Meanwhile, it can be observed from Figure (a) and Figure (b) that the predicted conflict frequencies are nearly consistent with the actual ones, highlighting the excellent performance of this method. Moreover, the prediction accuracy (the average of the prediction accuracies of the 10 models) for each intersection in Figure (c) is above 66%, demonstrating good prediction accuracy. This shows that the prediction method proposed in this paper is reasonable and effective.

5. Conclusion

This study proposes a real-time prediction method for traffic conflicts at intersections that integrates statistical models and machine learning. First, high-resolution unmanned aerial vehicle (UAV) trajectory data are utilized to extract two conflict indicators, namely, TTC and PET. Subsequently, four machine learning algorithms are employed to construct prediction models for the occurrence of traffic conflicts at signalized and unsignalized intersections, respectively, to predict whether conflicts will occur or not. Finally, the samples predicted as “1” are further input into the Bayesian spatial Poisson model to predict the conflict frequencies.
  • (1)

    A real-time prediction model for the occurrence of traffic conflicts at intersections based on machine learning was constructed. The RF algorithm achieved the best results in the real-time prediction of conflict occurrences at signalized intersections. For the TTC model, its average accuracy rate is 89.2%, while for the PET model, its average accuracy rate is 82.6%. The XGBoost algorithm performs best in the real-time prediction of conflict occurrences at unsignalized intersections. For the models with conflict indicators of TTC and PET, their average accuracy rates are 87.8% and 79.2%, respectively.

  • (2)

    A Bayesian spatial Poisson prediction model for conflict frequencies at intersections was constructed. The Bayesian spatial Poisson model explains the correlation between traffic state variables and conflict frequencies, indicating that it is necessary to consider the spatial correlation among adjacent intersections and analyze the influencing factors of conflict frequencies for predicting conflict frequencies. In addition, the Bayesian spatial Poisson model effectively estimates conflict frequencies. The results of model evaluation indicators show that the model has good prediction performance, and the prediction accuracy of the model is above 66%, which demonstrates that it is reasonable and effective to use the Bayesian spatial Poisson model to predict conflict frequencies at intersections.

  • (3)

    A real-time prediction method for traffic conflicts at intersections that integrates statistical models and machine learning is proposed. First, the binary logistic model is used to identify the significant factors influencing the occurrence of conflicts. Then, based on traffic state variables and conflict data, machine learning algorithms are employed to conduct real-time prediction of the occurrence of intersection conflicts. Finally, the Bayesian spatial Poisson model is adopted to predict the frequency of conflicts marked as “1” identified by the machine learning algorithms in the previous step and to identify the significant factors influencing the conflict frequencies.

The limitations of this paper are as follows:
  • (1)

    The research object of this paper is intersections rather than road sections or highways. Therefore, when conducting the research, the signal cycle at intersections should be taken into account. However, due to the limitations of the dataset, only fixed time intervals were considered. In future research, a more comprehensive dataset can be adapted to incorporate the signal cycle and thus improve the integrated method proposed in this paper.

  • (2)

    In the analysis of the influencing factors for conflict occurrence and conflict frequency, this paper only considered dynamic variables related to vehicle speed, the number of vehicles, headway, and acceleration, without taking static variables such as the number of lanes and road channelization into consideration. In future research, a combination of dynamic and static variables can be considered to make the model prediction results more accurate.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Chuanyun Fu: conceptualization, methodology, writing the original draft, reviewing and editing, and funding acquisition. Jiaming Liu: conceptualization, methodology, and writing the original draft. Huahua Liu: methodology and reviewing and editing. Xiaoli Wang: data collection and software. Zhaoyou Lu: visualization. Jushang Ou and Wei Bai: reviewing and editing and interpretation of results.

Funding

The work was jointly supported by the National Natural Science Foundation of China (72371082), the Natural Science Foundation of Sichuan Province of China (2024NSFSC0184), the Opening Project of Intelligent Policing Key Laboratory of Sichuan Province (ZNJW2023KFZD001), and the Fundamental Research Funds for the Central Universities (FRFCUAUGA5710010222).

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.