Advances in Mathematical Physics
Volume 2025, Issue 1 9963822
Research Article
Open Access

Triple Diffusive Convection in a Fluid Layer Under an A.C Electric Field

Sureshkumar S., 

Sureshkumar S.

Department of Mathematics , Siddaganga Institute of Technology , Tumakuru , 572103 , India , sit.ac.in

Search for more papers by this author
Krishna B. Chavaraddi, 

Krishna B. Chavaraddi

Department of Mathematics , Government First Grade College , Ganghipur, Haveri , 581128 , India

Search for more papers by this author
Priya M. Gouder, 

Priya M. Gouder

Department of Mathematics , Belagavi Campus , KLE Technological University , Belagavi , 590008 , India , kletech.ac.in

Search for more papers by this author
G. K. Ramesh, 

G. K. Ramesh

Department of Mathematics , K.L.E. Society’s J.T. College , Gadag , 582101 , India

Search for more papers by this author
J. K. Madhukesh, 

J. K. Madhukesh

Department of Mathematics , GM University , Davangere , 577006 , Karnataka , India

Search for more papers by this author
Umair Khan, 

Corresponding Author

Umair Khan

Department of Mathematics , Saveetha School of Engineering , Saveetha Institute of Medical and Technical Sciences , Saveetha University , Chennai , 602105 , Tamil Nadu , India , saveetha.com

Department of Mathematical Sciences , Faculty of Science and Technology , Universiti Kebangsaan Malaysia, UKM , Bangi , 43600 , Selangor , Malaysia , ukm.my

Department of Mathematics , Faculty of Science , Sakarya University , Serdivan/Sakarya , 54050 , Türkiye , sakarya.edu.tr

Department of Computer Science and Mathematics , Lebanese American University , Byblos , Lebanon , lau.edu.lb

Search for more papers by this author
Anuar Ishak, 

Anuar Ishak

Department of Mathematical Sciences , Faculty of Science and Technology , Universiti Kebangsaan Malaysia, UKM , Bangi , 43600 , Selangor , Malaysia , ukm.my

Search for more papers by this author
Syed Modassir Hussain, 

Syed Modassir Hussain

Department of Mathematics , Faculty of Science , Islamic University of Madinah , Madinah , 42351 , Saudi Arabia , iu.edu.sa

Search for more papers by this author
First published: 28 February 2025
https://doi.org/10.1155/admp/9963822
Academic Editor: S. A. Edalatpanah

Abstract

The effect of an imposed alternating current (A.C) electric field on the onset of convective instability in a horizontal triply diffusive fluid layer is investigated. Analytical solutions are obtained for steady and oscillatory onset when imposed gradients of the stratifying agencies are constant and vertical. It was found that A.C electric Rayleigh number did not affect the necessary conditions for oscillatory convection. The stability boundaries are drawn and it is observed that an increase in the A.C electric field strength is to hasten the onset of convection. The evolution of neutral curves is analyzed in detail by varying the A.C electric Rayleigh number and other physical parameters. For certain choices of physical parameters, it is noted that the oscillatory part will give rise to two oscillatory neutral solutions for each wave number and closed disconnected neutral curves are found to exist, suggesting the requirement for three critical Rayleigh numbers to specify the linear stability criterion.

1. Introduction

Buoyancy-driven convection in a horizontal fluid layer heated uniformly below and the problems including the effect of vertical magnetic field and/or rotation there upon are discussed in detail in the monograph by Chandrasekhar [1] because of their applications in many science and engineering problems. The magnetic field effects become dominant on convective instability, only when the fluid is highly electrically conducting. To the contrary, if the fluid is dielectric with low electrical conductivity, then, the electric forces play a major role in driving the motion. In dielectric fluids, an applied temperature gradient produces nonuniformities in the electrical conductivity σ and the dielectric permittivity ε. If ∇σ is nonzero, then, free charge builds up and which can be acted upon by the electric field to produce a force that eventually cause fluid motion. On the other hand, if ∇ε is nonzero and the electric field is intense, then, polarization forces cause fluid motion. In either case, convection can occur in a dielectric fluid layer even if the temperature gradient is stabilizing and such instability is called electroconvection, which is analogs to Rayleigh–Benard instability. In addition, if the applied temperature gradient is also destabilizing, then, such an instability problem is called electro-thermo-convection [2].

In a dielectric fluid layer, the onset of convection in the existence of an electric fluid has been analyzed both experimentally and theoretically in the recent past. Due to its applications in many practical problems such as liquid heat exchangers, thermal convection laboratory models in the cores of the Earth and planets, enhanced recovery of petroleum reservoirs, understanding of atmospheric electricity, and control of convection to mention a few (for details see [3]). In a dielectric fluid layer, Roberts [4] was the first to study the effects of alternating current (A.C) and D.C electric fields as well on the onset of convection. Natural convection by applying an A.C or D.C electric field has been examined by Turnbull [5, 6], Turnbull and Melcher [7], Takashima and Aldridge [8], and Jones [9] have presented an extensive study on the subject in addition to exhaustive review by Saville [3], Enagi et al. [10], and Sureshkumar et al. [11]. Maekawa, Abe, and Tanasawa [12] have recently explored numerically the beginning of electroconvection, Marangoni convection, and buoyancy convection in D.C and A.C electric fields. Char and Chiang [13] investigated the boundary influences on the development of coupled Benard–Marangoni instability in an A.C electric field. Douiebe et al. [14] considered the impacts of a vertical A.C electric field combined with uniform rotation on coupled thermocapillary and buoyancy instability in an electrically conducting fluid medium. Othman [15] examined the spinning layer stability of viscoelastic dielectric liquid heated from the lower side by an alternating current electric fluid.

All the abovementioned investigations have been concerned with single component systems in which the density variations are only due to temperature. However, many of the practical problems mentioned above involve compositional gradients in addition to temperature gradient affecting the fluid density. In such circumstances, several interesting phenomena not noticed in the single-component system would occur. Therefore, it would be more appropriate and interesting to investigate the problem related to electro-thermo-convection in the presence of additional diffusing components having different diffusivities. Pearlstein, Harris, and Terrones [16], Terrones and Pearlstein [17], and Lopez, Romero, and Pearlstein [18] have all considered the problem of triple diffusive convection in an ordinary viscous fluid layer in detail. The aim of the study is to address a gap in the understanding of the influence of external fields—specifically an A.C electric field—on the stability of a triply diffusive dielectric fluid layer. While the natural occurrence of triple diffusive convection is complex and involves practical challenges, the addition of an A.C electric field introduces a new dimension to the problem, offering insights into the stability and behavior of such systems under controlled conditions. As a result, the aim of this paper is to look into the effect of an A.C electric field applied vertically on the steadiness of a triply diffusive dielectric fluid layer. The aim of the present paper is, therefore, to investigate the effect of vertical A.C electric field on the stability of a triply diffusive dielectric fluid layer. The linear stability theory is applied and the resulting eigenvalue problem is solved using normal mode analysis. In addition, there are comparisons made with previously published data [19]. The main novelty of studying the effects of an induced A.C electric field on the convective instability of a horizontal layer of triple-diffusive fluid lies in the unique interactions and complex dynamics introduced by the combined effects of the electric field and the triple diffusion process. The following are key novel aspects:
  • 1.

    Triple-diffusive convection involves the simultaneous influence of three diffusive components (e.g., temperature, salinity, and solute concentration) on buoyancy-driven flow. The novelty arises from combining this complex system with an induced A.C electric field, which adds an additional layer of complexity. This integration leads to new phenomena that are not observed in conventional double-diffusive or single-component convection under an electric field.

  • 2.

    The study introduces the frequency-dependent behavior of the A.C electric field on the onset of convective instability. Unlike steady electric fields, the alternating nature of the A.C field can dynamically modulate the stability characteristics of the fluid layer, affecting the critical Rayleigh number and altering convective patterns. This introduces novel control mechanisms for tuning the stability and flow behavior of the fluid by varying the frequency of the applied electric field.

  • 3.

    The study provides insights into new methods for controlling mixing and heat transfer in fluids. By adjusting the amplitude, frequency, and orientation of the A.C electric field, it is possible to achieve targeted control over convective processes in the triple-diffusive fluid layer. This approach presents a novel technique for optimizing heat and mass transfer in engineering applications.

  • 4.

    While stability analysis has been well-developed for classical convection problems, extending it to triple-diffusive systems under the influence of A.C electric fields introduce novel mathematical and theoretical challenges. The study contributes by advancing the techniques used for linear and nonlinear stability analysis, incorporating the effects of time-dependent electric fields and multiple diffusive components.

2. Formulation of the Problem

Take a look at a liquid layer with weak electrical conductivity that is stratified with three components, namely, temperature T and solute concentration Ci (i = 1,  2) in the existence of a vertical uniform A.C electric field. The upper surface z = d is retained at an alternating potential having V1 as root-mean square value. The lower boundary is kept at constant temperature T0 with Ci0 (i = 1,  2) as solute concentration, when temperature is present, the upper boundary is kept. T0 − ΔT with solute concentration Ci0 − ΔCi (i = 1,  2) with ΔT > 0 and ΔCi > 0 (i = 1,  2). A Cartesian frame of reference (x, y, z) is applied at the bottom of the fluid layer, with the origin and the z-axis is vertically upward. The boundaries considered here are stress-free boundaries. These conditions imply that the tangential stress at both the upper and lower boundaries is zero, allowing the fluid to slide along the boundaries without resistance. The stress-free conditions are idealized and used for theoretical analysis of the convective instability problem under the influence of an A.C electric field.

The appropriate governing basic equations [2, 19], such a system is:
()
()
()
()
()
()
The quantities appeared in above equations are defined in Nomenclature. The solute concentration Ci = Ci0 and term is the electrical force that is specified in the form:
()
As there are no free charges, the fluid is poorly conducting. Then, appropriate Maxwell equations are:
()
()
Considering Equation (6), the expression for can be given by:
()
The mean square root value is presented by V is used for electric potential. For electric potential, the root-mean square value indicated by V is employed. The Coulomb force dominates the initial component on the right-hand side of Equation (7) in its absence of an A.C electric field. This word includes gratuity. The second component, on the other hand, is affected by the gradient ε of the dielectric constant. In Equation (2), the final electrostriction term is included simultaneously with pressure p, and it does not influence an incompressible fluid. When an alternating current electric field with a frequency of 50 or 60 Hz is applied, the Coulomb force disappears. This is because the electric relaxation period for most fluids ranges between 10 and 100 s. In these circumstances, the force caused by nonuniformity is solely taken into account for the dielectric constant, and hence, it is supposed to be a linear function of temperature expressed as:
()
The fundamental state is quiescent and is defined as:
()
where the basic state is denoted by the subscript b. Let us substitute Equation (12) in Equations (1)–(10), we get:
()
()
()
()
()
()
()
Solving Equation (15) using the boundary conditions:
()
we get:
()
Similarly solving Equation (16) using the boundary conditions:
()
we get:
()
From Equation (19) and observing that Ebx = Eby = 0, it implies that:
()
Thus, we have:
()
and
()
where,
()
is the electric field’s root-mean square value at z = 0.
To examine the stability of the above basic state the variables are perturbed in the form:
()
where , T′, , , ε′, p′, and ρ′ consecutively denotes perturbed velocity, temperature, concentration, electric field, dielectric constant, pressure, and density. Let us substitute Equation (28) in Equations (1)–(6), by ignoring the primed quantities products, linearize the equations, eliminate the pressure term by operating curl twice from momentum equation, and vertical component is retained, we find relevant perturbation equations in the following form (for simplicity, the primes are neglected):
()
()
()
()
where is horizontal Laplacian operator.
The dimensionless quantities are introduced as:
()
Substituting Equation (33) into Equations (29)–(32) and for simplicity let us drop the asterisks, we get:
()
()
()
()
Let us confine ourselves to the problem having stress free surfaces with fixed heat, solute concentrations, and electric potential. Then required boundary conditions are:
()

3. Linear Stability Analysis

To carry out the linear stability analysis, we employ the normal mode analysis procedure in which we look for the solution of the form:
()
where l and m terms denotes horizontal wave numbers, σ term is for growth rate (in general it is a complex quantity) and A1–A5 are constants. Substituting Equation (39) into Equations (34)–(37), the matrix equation is obtained as given by Equation (40).
()
The quantities are defined in the Nomenclature. For the above system of equations, a nontrivial solution exists if:
()
For neutral solutions, we put σ = iω in the characteristic equation Equation (41) and from the denominator, let us clear the complex quantities, we get an expression for Rt as:
()
where,
()

As Rt being a physical quantity, it must be real and from Equation (42) it infers with ω = 0 or M = 0. These two requirements offer the criterion for the development of stationary and oscillatory instabilities, respectively [20].

3.1. Stationary Convection (ω = 0)

The case ω = 0 relates to the onset of stationary convection. Enforcement of ω = 0 in Equation (42) gives the Rayleigh number:
()
With respect to steady onset, the fluid layer is unstable above the value of the Rayleigh number. Let us equate the derivative of Equation (44) with respect to α to zero, in order to establish the critical value of α that provides the minimum value of . Then, we get:
()
Here, it is mainly observed that αc is not depending on additional diffusing components but depends on Re.
In the previous works, for existing results, it is interesting to check Equations (44) and (45) in only certain limiting cases. In the nonexistence of an A.C electric field, Equation (44) reduces as:
()
which agrees with Griffiths [21]. Equation (46) attains its critical value at and is given by:
()
If no further diffusing components are present (i.e., Rs1 = Rs2 = 0), Equation (44) reduces to:
()
and coincides with Roberts [4].
For a single component system, we note that:
()

This is the precise value determined by Chandrasekhar [1].

3.2. Oscillatory Convection (ω ≠ 0)

For oscillatory convection, ω ≠ 0 and from Equation (42) it requires that M = 0. The condition M = 0 produces a dispersion relation expressed as:
()
where,
()
It is interesting to note that an A.C electric Rayleigh number does not affect the frequency of oscillations. We note that Δ1 > 0 always and if Δ2 < 0 and Δ3 > 0 for some appropriate combinations of the parameters, then, it implies from Descartes’ rule of signs that Equation (50) may result in two positive real values of ω2 for the same wave number resulting in two different onset frequencies. In that case, the oscillatory neutral curve to each such frequency then results in the exact value of the Rayleigh number, which has significant impacts as much as the linear stability of the system is considered. From the following expression, we can obtain the oscillatory Rayleigh number:
()
where ω2 has to be calculated from Equation (50) for the parametric values chosen.
From Descartes’ rule of signs, Equation (50) may have two positive roots provided Δ2 < 0 and Δ3 > 0. That is,
()
()
Multiplying Equation (54) by and adding to −1× Equation (53) gives:
()
That is,
()
Similarly, multiplying Equation (54) by and adding to −1× Equation (53) gives:
()
That is,
()
As a result, the required requirements for the presence of two frequencies are present on the oscillatory curve.
()
()

From the above conditions, it is noted that oscillatory convection is possible through the ratio of diffusivities τ22 and τ33 is more than unity. However, this is not the case with double-diffusive systems, wherein the ratio of diffusivities must be less than unity for oscillatory instability occurrence. Besides, the necessary conditions are independent of the A.C electric field.

4. Results and Discussion

The effect of vertical A.C electric field on the onset of convective instability in a triply diffusive horizontal fluid layer is investigated theoretically. Condition for the occurrence of steady and oscillatory instability is obtained analytically. Numerical computations are carried out based on the data for the diffusivity terms experimentally obtained by Noulty and Leaist [22]. Binary diffusion coefficients for potassium chloride, potassium phosphate, and phosphoric acid in water are considered [23].

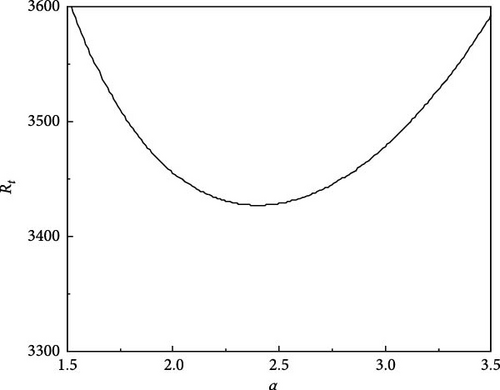
The critical Rayleigh number Rtc is determined numerically as follows: For chosen parametric values, the minimum value of and with wave number determined and the smaller among these two is considered as Rtc. Figure 1 shows the variation of critical Rayleigh number Rtc with the solute Rayleigh number Rs1 for different values of A.C electric Rayleigh number Re for Pr = 464, Rs2 = −13, 528, τ22 = 0.5907, and τ33 = 0.5670. In the figure, the portion of each stability boundary lying to the left of the discontinuity in slope corresponds to a steady onset (ω = 0) while to the right, the onset is of oscillatory type (ω2 > 0). From the figure, it is evident that the effect of an increase in the value of Re is to hasten the onset of convection due to an increase in electrical energy to the system.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Variation of critical Rayleigh number Rt with Rs1 for several values of Re with Pr = 464, Rs2 = −13528, τ22 = 0.5907, and τ33 = 0.5670.

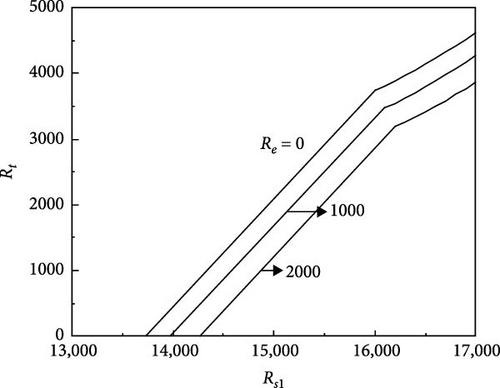
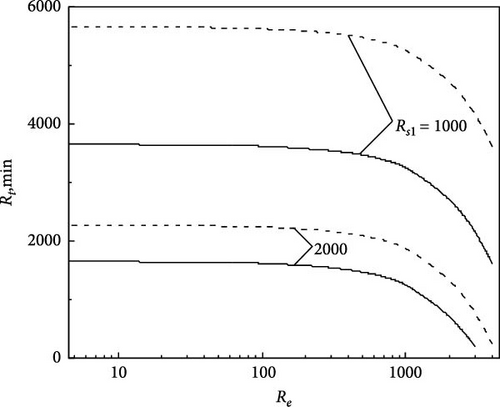
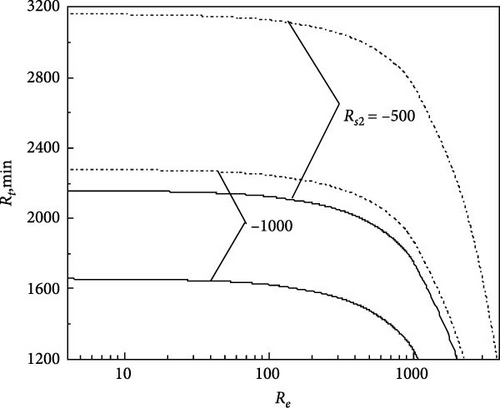
Figure 2a,b depict the variation of the minimum Rayleigh number Rt,min versus electric Rayleigh number for different values of solute Rayleigh numbers Rs1 and Rs2, respectively, for both steady and oscillatory convection. Figure 2a is drawn for τ22 = 0.5907, τ33 = 0.5670, and Pr = 464 [24]. We observe that an increase in the value of the electric Rayleigh number decreases the value Rt,min, indicating that the effect of Re is to destabilize the system. Also, it is observed that the increase in the value of Rs1 stabilizes both steady and oscillatory convection by increasing Rt,min (Figure 2a). We note that increase in |Rs2| decreases the value Rt,min and the same is evident from Figure 2b.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Variation of and with Re for τ22 = 0.5907, τ33 = 0.5670, and Pr = 464. (a) For different values of Rs1 with Rs2 = −1000, (b) for different values of Rs2 with Rs1 = 2000.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Variation of and with Re for τ22 = 0.5907, τ33 = 0.5670, and Pr = 464. (a) For different values of Rs1 with Rs2 = −1000, (b) for different values of Rs2 with Rs1 = 2000.

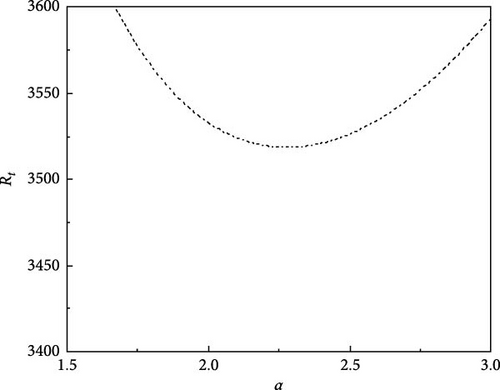
Impact of Rt,min with Rs1 for variation in the values of Re, when Rs2 = 1000, τ22 = 0.5907, τ33 = 0.5670, and Pr = 464 are fixed and are displayed in Figure 3. It has been found that a higher value of Re has the effect of destabilization in steady and oscillatory convection. The value of Rs1 improves as the value of Rt,min rises, showing that a rise in the value of Rs1 has the impact of stabilizing the system. It is commonly known that under certain conditions, some triple diffusive systems behave qualitatively differently from singly and doubly diffusive examples. Disconnected neutral curves, in particular, are recognized as integral features of triple diffusive systems, with significant effects on the problem’s linear stability. A thorough study is performed on the topology of neutral curves to assess the influence of the A.C electric field on the system’s stability to investigate this distinctive behavior in such dynamical systems.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Variation of and with Rs1 for τ22 = 0.5907, τ33 = 0.5670, Pr = 464, and Rs2 = 1000.

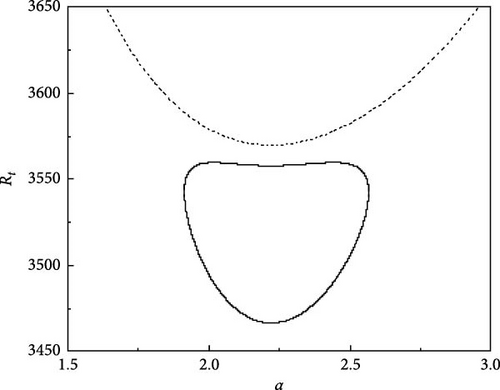
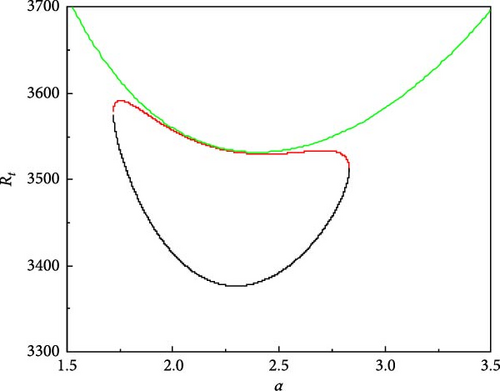
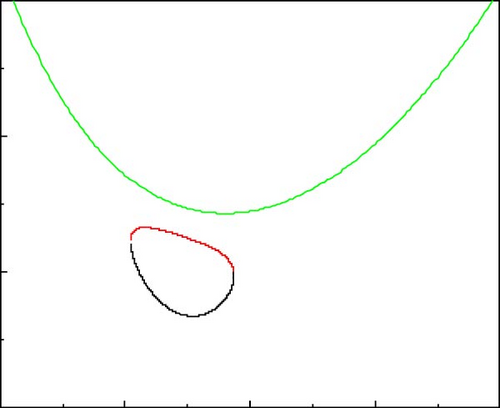
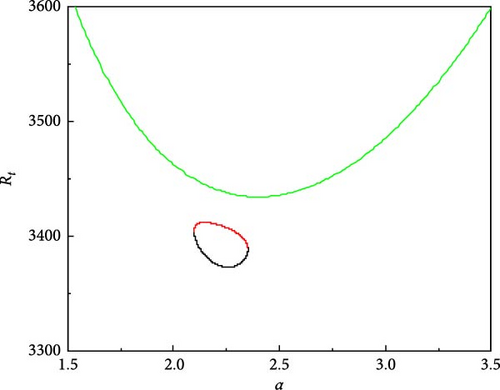
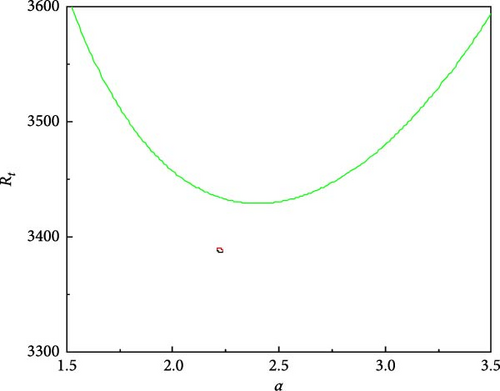
The consequence of A.C electric Rayleigh number Re on the system stability is evident from Figure 4a–h, which exhibits the growth of neutral curves with Re for Rs1 = 13, 730.72, Rs2 = −11, 528.58, τ22 = 0.5907, τ33 = 0.5670, and Pr = 464. Figure 4a shows the results when Re = 0 (i.e., in the absence of A.C electric field) and observes the existence of heart shaped oscillatory neutral curve and lies at the lower side of the stationary neutral curve. The significance of such a heart-shaped disconnected neutral curve is twofold. First, three different critical values of Rt are necessary to state the linear stability criteria. Second, at the same value of Rt onset of oscillatory instability simultaneously happens at two different wave numbers and two different frequencies. However, in the presence of an A.C electric field with Re = 100, we observe that the heart-shaped oscillatory neutral curve is slightly skewed towards the left as shown in Figure 4b. The skewing that has resulted from the presence of an A.C electric field envisages that the oscillatory convection occurs at a given thermal Rayleigh number, but at different wave numbers and the twin maxima on the heart-shaped oscillatory neutral curve is not recovered here. As the value of Re is increased, the skewing effect becomes more noticeable (see Figure 4c,d). Further, in Figure 4e, the increase in Re shows that the minimum on the stationary curve is less than the minimum on the oscillatory curve (at Re = 1500). For Re = 2000, we see that the minimum on the oscillatory curve is less than the minimum on the stationary curve as shown in Figure 4f. At some value of Re the minima should occur at the same Rayleigh number. This value was found to be attained at Re = 1695 with Rt,min, αosc = 2.54, and αstat = 3.27 (Figure 4g,h).

Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Rs2 = −11528, τ22 = 0.5907 and τ33 = 0.5670. (a) Re = 0, (b) Re = 100, (c) Re = 300, (d) Re = 600, (e) Re = 1500, (f) Re = 2000, (g) Re = 3500, and (h) Re = 6500.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Rs2 = −11528, τ22 = 0.5907 and τ33 = 0.5670. (a) Re = 0, (b) Re = 100, (c) Re = 300, (d) Re = 600, (e) Re = 1500, (f) Re = 2000, (g) Re = 3500, and (h) Re = 6500.
Details are in the caption following the image
Figure 4 (c)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Rs2 = −11528, τ22 = 0.5907 and τ33 = 0.5670. (a) Re = 0, (b) Re = 100, (c) Re = 300, (d) Re = 600, (e) Re = 1500, (f) Re = 2000, (g) Re = 3500, and (h) Re = 6500.
Details are in the caption following the image
Figure 4 (d)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Rs2 = −11528, τ22 = 0.5907 and τ33 = 0.5670. (a) Re = 0, (b) Re = 100, (c) Re = 300, (d) Re = 600, (e) Re = 1500, (f) Re = 2000, (g) Re = 3500, and (h) Re = 6500.
Details are in the caption following the image
Figure 4 (e)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Rs2 = −11528, τ22 = 0.5907 and τ33 = 0.5670. (a) Re = 0, (b) Re = 100, (c) Re = 300, (d) Re = 600, (e) Re = 1500, (f) Re = 2000, (g) Re = 3500, and (h) Re = 6500.
Details are in the caption following the image
Figure 4 (f)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Rs2 = −11528, τ22 = 0.5907 and τ33 = 0.5670. (a) Re = 0, (b) Re = 100, (c) Re = 300, (d) Re = 600, (e) Re = 1500, (f) Re = 2000, (g) Re = 3500, and (h) Re = 6500.
Details are in the caption following the image
Figure 4 (g)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Rs2 = −11528, τ22 = 0.5907 and τ33 = 0.5670. (a) Re = 0, (b) Re = 100, (c) Re = 300, (d) Re = 600, (e) Re = 1500, (f) Re = 2000, (g) Re = 3500, and (h) Re = 6500.
Details are in the caption following the image
Figure 4 (h)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Rs2 = −11528, τ22 = 0.5907 and τ33 = 0.5670. (a) Re = 0, (b) Re = 100, (c) Re = 300, (d) Re = 600, (e) Re = 1500, (f) Re = 2000, (g) Re = 3500, and (h) Re = 6500.

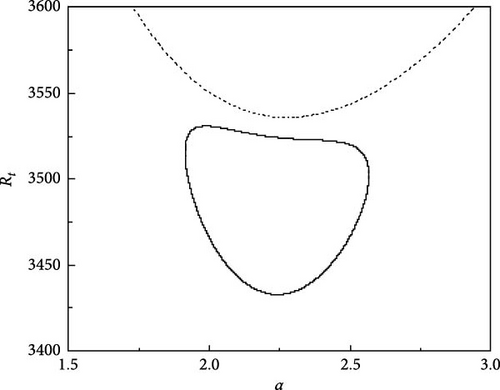
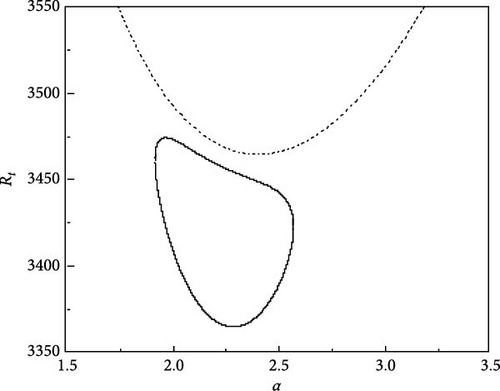
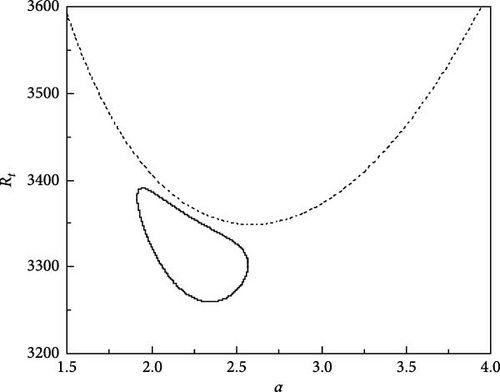
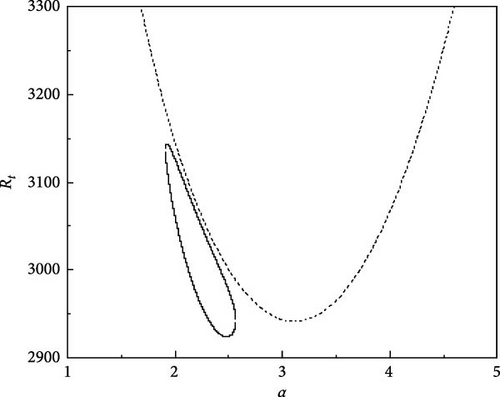
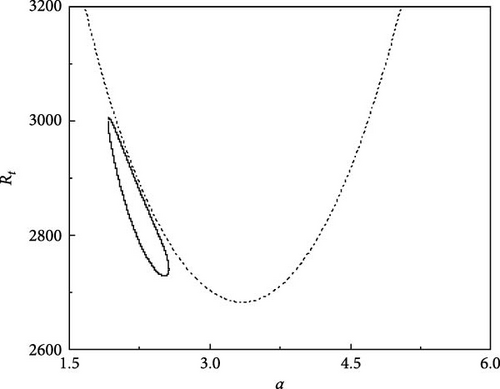
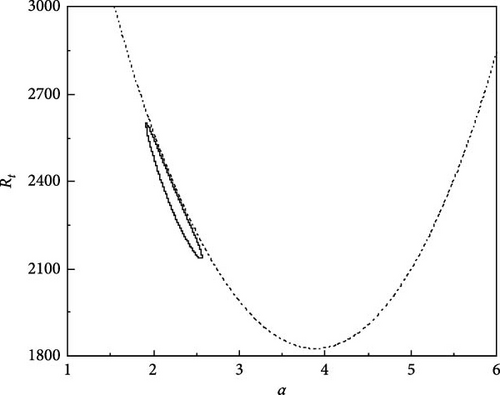
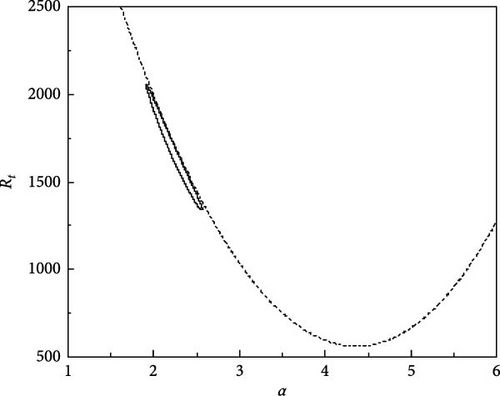
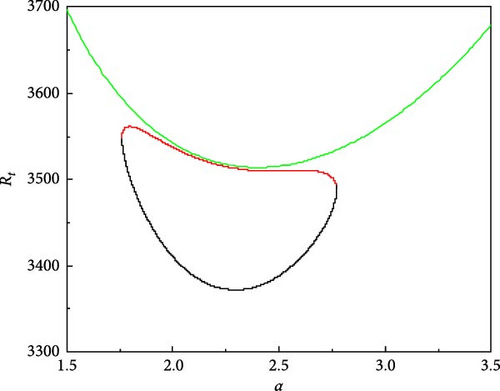
The growth of neutral curves for various values of τ22 and τ33 is displayed in Figure 5a–f. The results presented here are for Rs1 = 13, 730.72, Rs2 = −11, 528.58, Pr = 464, and Re = 100. Figure 5a shows the neutral curves for τ22 = 0.5907 and τ33 = 0.5670, we observe that the oscillatory neutral curve is slightly skewed away from symmetry and disconnected from the stationary neutral curve which needs three Rayleigh numbers to establish the criteria for linear stability. As the value of τ22 and τ33 are further increased, the closed neutral oscillatory curve tends to be more skewed and the same is observed from Figure 5b,c. With the further rise in τ22 and τ33, the closed oscillatory neutral curve converts to a closed convex curve which is evident from Figure 5d,e. Interestingly, at τ22 = 0.5957 and τ33 = 0.5720, the closed oscillatory neutral curve collapses to a point and then vanishes by leaving the stationary neutral curve only (Figure 5f). Therefore, it is obvious that small changes in diffusivity ratios have an intense effect on the nature of instability.

Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
Growth of neutral curves for various values of τ22 and τ33 with Pr = 464, Rs1 = 13730, Rs2 = −11528, and Re = 100. (a) τ22 = 0.5907,  τ33 = 0.5670, (b) τ22 = 0.5917,  τ33 = 0.5680, (c) τ22 = 0.5927,  τ33 = 0.5690, (d) τ22 = 0.5937,  τ33 = 0.5700, (e) τ22 = 0.5950,  τ33 = 0.5713, and (f) τ22 = 0.5957,  τ33 = 0.5720.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
Growth of neutral curves for various values of τ22 and τ33 with Pr = 464, Rs1 = 13730, Rs2 = −11528, and Re = 100. (a) τ22 = 0.5907,  τ33 = 0.5670, (b) τ22 = 0.5917,  τ33 = 0.5680, (c) τ22 = 0.5927,  τ33 = 0.5690, (d) τ22 = 0.5937,  τ33 = 0.5700, (e) τ22 = 0.5950,  τ33 = 0.5713, and (f) τ22 = 0.5957,  τ33 = 0.5720.
Details are in the caption following the image
Figure 5 (c)
Open in figure viewerPowerPoint
Growth of neutral curves for various values of τ22 and τ33 with Pr = 464, Rs1 = 13730, Rs2 = −11528, and Re = 100. (a) τ22 = 0.5907,  τ33 = 0.5670, (b) τ22 = 0.5917,  τ33 = 0.5680, (c) τ22 = 0.5927,  τ33 = 0.5690, (d) τ22 = 0.5937,  τ33 = 0.5700, (e) τ22 = 0.5950,  τ33 = 0.5713, and (f) τ22 = 0.5957,  τ33 = 0.5720.
Details are in the caption following the image
Figure 5 (d)
Open in figure viewerPowerPoint
Growth of neutral curves for various values of τ22 and τ33 with Pr = 464, Rs1 = 13730, Rs2 = −11528, and Re = 100. (a) τ22 = 0.5907,  τ33 = 0.5670, (b) τ22 = 0.5917,  τ33 = 0.5680, (c) τ22 = 0.5927,  τ33 = 0.5690, (d) τ22 = 0.5937,  τ33 = 0.5700, (e) τ22 = 0.5950,  τ33 = 0.5713, and (f) τ22 = 0.5957,  τ33 = 0.5720.
Details are in the caption following the image
Figure 5 (e)
Open in figure viewerPowerPoint
Growth of neutral curves for various values of τ22 and τ33 with Pr = 464, Rs1 = 13730, Rs2 = −11528, and Re = 100. (a) τ22 = 0.5907,  τ33 = 0.5670, (b) τ22 = 0.5917,  τ33 = 0.5680, (c) τ22 = 0.5927,  τ33 = 0.5690, (d) τ22 = 0.5937,  τ33 = 0.5700, (e) τ22 = 0.5950,  τ33 = 0.5713, and (f) τ22 = 0.5957,  τ33 = 0.5720.
Details are in the caption following the image
Figure 5 (f)
Open in figure viewerPowerPoint
Growth of neutral curves for various values of τ22 and τ33 with Pr = 464, Rs1 = 13730, Rs2 = −11528, and Re = 100. (a) τ22 = 0.5907,  τ33 = 0.5670, (b) τ22 = 0.5917,  τ33 = 0.5680, (c) τ22 = 0.5927,  τ33 = 0.5690, (d) τ22 = 0.5937,  τ33 = 0.5700, (e) τ22 = 0.5950,  τ33 = 0.5713, and (f) τ22 = 0.5957,  τ33 = 0.5720.

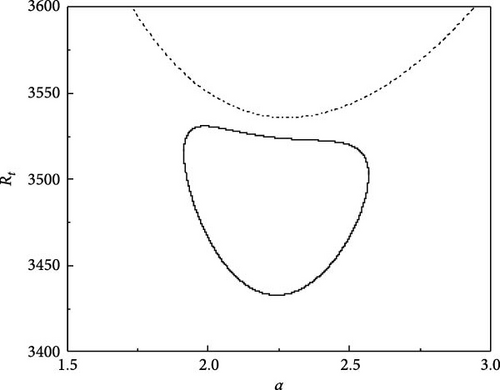
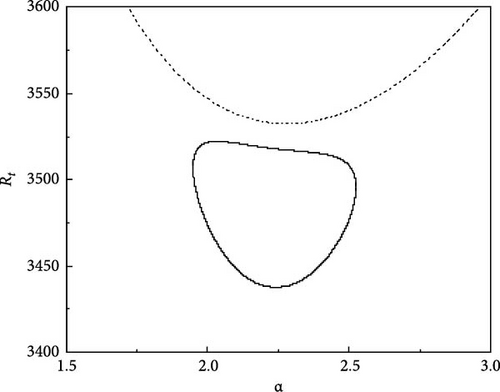
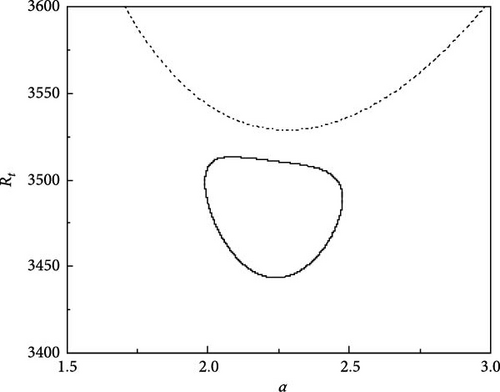
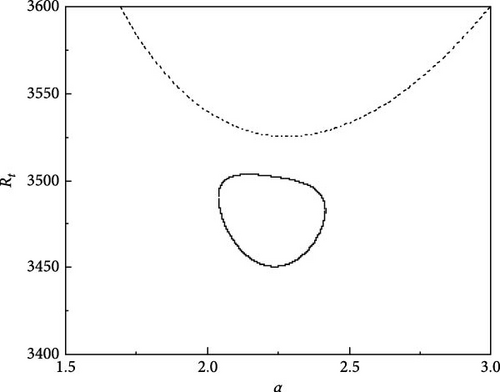
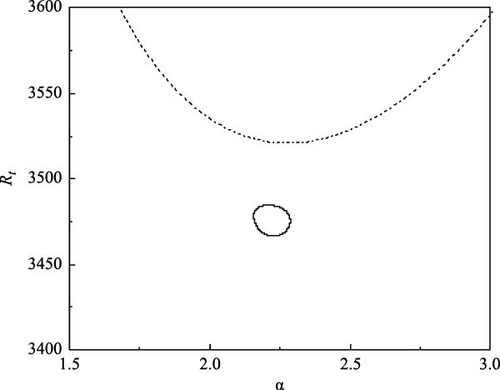
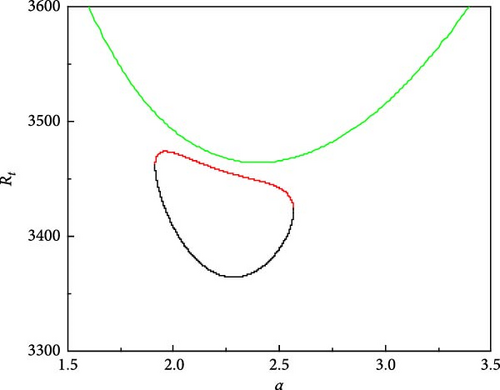
A similar analysis as above is carried out to know the effect of varying one of the solute Rayleigh numbers (say Rs2) on the growth of neutral curves in the existence of an A.C electric field. For different values of Rs2, the steady and oscillatory neutral curves are obtained when Rs1 = 13, 730, τ22 = 0.5907, τ33 = 0.5670, Pr = 464, and Re = 300 as shown in Figure 6a–f. Figure 6a shows the results for Rs2 = −11, 490. We observe that the oscillatory neutral curve is slightly skewed towards the left of the stationary neutral curve and the oscillatory neutral curve is related to the stationary neutral curve, which requires only one Rayleigh number to obtain linear stability criteria. As we further vary Rs2, the heart-shaped oscillatory neutral curve separates from the stationary neutral curve as revealed in Figure 6b. For Rs2 = −11, 528 (Figure 6c), the skewing impact becomes more evident and the closed oscillatory neutral curve lies below the stationary neutral curve, thus, signifying the necessity of three critical values of Rt to specify the linear stability criteria rather than a single usual value. As Rs2 is varied further the skewed oscillatory neutral curve moves further down and the same is evident from Figure 6d,e. Interestingly, at Rs2 = −11, 548, the neutral closed oscillatory curve collapses to a single point (Figure 6f) and at Rs2 = −11, 549 leaves only the stationary neutral curve as a result of disappears (Figure 6g).

Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Re = 300, τ22 = 0.5907, and τ33 = 0.5670. (a) Rs2 = −11490, (b) Rs2 = −11500, (c) Rs2 = −11528, (d) Rs2 = −11540, (e) Rs2 = −11545, (f) Rs2 = −11548, and (g) Rs2 = −11549.
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Re = 300, τ22 = 0.5907, and τ33 = 0.5670. (a) Rs2 = −11490, (b) Rs2 = −11500, (c) Rs2 = −11528, (d) Rs2 = −11540, (e) Rs2 = −11545, (f) Rs2 = −11548, and (g) Rs2 = −11549.
Details are in the caption following the image
Figure 6 (c)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Re = 300, τ22 = 0.5907, and τ33 = 0.5670. (a) Rs2 = −11490, (b) Rs2 = −11500, (c) Rs2 = −11528, (d) Rs2 = −11540, (e) Rs2 = −11545, (f) Rs2 = −11548, and (g) Rs2 = −11549.
Details are in the caption following the image
Figure 6 (d)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Re = 300, τ22 = 0.5907, and τ33 = 0.5670. (a) Rs2 = −11490, (b) Rs2 = −11500, (c) Rs2 = −11528, (d) Rs2 = −11540, (e) Rs2 = −11545, (f) Rs2 = −11548, and (g) Rs2 = −11549.
Details are in the caption following the image
Figure 6 (e)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Re = 300, τ22 = 0.5907, and τ33 = 0.5670. (a) Rs2 = −11490, (b) Rs2 = −11500, (c) Rs2 = −11528, (d) Rs2 = −11540, (e) Rs2 = −11545, (f) Rs2 = −11548, and (g) Rs2 = −11549.
Details are in the caption following the image
Figure 6 (f)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Re = 300, τ22 = 0.5907, and τ33 = 0.5670. (a) Rs2 = −11490, (b) Rs2 = −11500, (c) Rs2 = −11528, (d) Rs2 = −11540, (e) Rs2 = −11545, (f) Rs2 = −11548, and (g) Rs2 = −11549.
Details are in the caption following the image
Figure 6 (g)
Open in figure viewerPowerPoint
Neutral curves for various values of Re with Pr = 464, Rs1 = 13730, Re = 300, τ22 = 0.5907, and τ33 = 0.5670. (a) Rs2 = −11490, (b) Rs2 = −11500, (c) Rs2 = −11528, (d) Rs2 = −11540, (e) Rs2 = −11545, (f) Rs2 = −11548, and (g) Rs2 = −11549.

5. Final Remarks

The consequence of an induced A.C electric field of convective instability on the evolution in a horizontal layer of triple diffusive fluid is analyzed in the present study, when the imposed gradients of the stratifying factors are constant and vertical, analytical solutions are established for both steady and oscillatory onset. From our study, we conclude as follows:
  • 1.

    Increasing the value of Re has the effect of accelerating the start of convection by supplying the system with more electrical energy, and thus, having a destabilizing influence on both oscillatory and steady convection.

  • 2.

    When the electric Rayleigh number increases, the Rt,min value decreases, indicating that Re is destabilizing the system. Also, the dual maxima on the heart-shaped oscillatory neutral curve are not recovered at this point because of the skewing caused by the existence of an A.C electric field at specified thermal Rayleigh number, which occurs at distinct wave numbers. The skewing effect is increasingly pronounced as Re’s value rises.

  • 3.

    The nature of instability is significantly impacted by even slight changes in the diffusivity ratios.

  • 4.

    The stationary neutral curve is connected to the oscillating neutral curve, which is inclined significantly to the left of the stationary neutral curve and needs just one Rayleigh number to fulfill the criteria for linear stability.

Building upon the fundamental understanding of triple diffusive convection influenced by an A.C electric field, further and future studies can explore more advanced and applied aspects of the phenomenon. The following some are potential directions for advancing this research:
  • 1.

    Study how nonuniform or oscillating spatial profiles (e.g., electric field gradients or patterned electrodes) impact convection patterns and stability.

  • 2.

    Develop advanced models that capture nonlinear interactions among the thermal, solutal, and electric field-induced effects more comprehensively.

  • 3.

    Incorporate nanoparticles to study their influence on thermal and solutal diffusion and the coupling with electric fields.

Nomenclature

  • :
  • Velocity vector
  • T:
  • Temperature
  • Ci(i = 1, 2):
  • ith component solute concentration
  • ρ:
  • Liquid density
  • :
  • Acceleration due to gravity
  • ρ0:
  • Density
  • :
  • Electric field
  • ε:
  • Dielectric constant
  • η:
  • Dielectric constant’s thermal expansion
  • R t = β1gd3ΔC1/νD11:
  • Thermal Rayleigh number
  • R s1 = β2gd3ΔC2/νD11, R s2 = β3gd3ΔC3/νD11:
  • Solute Rayleigh numbers
  • τ22 = D22/D11 and τ33 = D33/D11:
  • Ratios of diffusivities
  • σ:
  • Growth rate
  • :
  • Horizontal wave number
  • p:
  • Pressure
  • D11:
  • Thermal diffusivity
  • D22 and D33:
  • Solutes
  • μ:
  • Liquid viscosity
  • β1:
  • Thermal expansion coefficient
  • :
  • Electrical force
  • ρe:
  • Charge density
  • V:
  • Electric potential
  • :
  • Horizontal Laplacian operator
  • Pr = ν/D11:
  • The Prandtl number
  • :
  • A.C electric Rayleigh number
  • l and m:
  • Horizontal wave numbers
  • δ2 = π2 + α2:
  • Total wave number
  • αc:
  • Critical wave number.

    • Conflicts of Interest

    The authors declare no conflicts of interest.

    Author Contributions

    S. Sureshkumar and J. K. Madhukesh: conceptualization, methodology, software, formal analysis, validation, writing–original draft. Priya M. Gouder and Krishna B. Chavaraddi: writing–original draft, data curation, investigation, visualization, validation. G. K. Ramesh: conceptualization, writing–original draft, writing–review and editing, supervision, resources. Umair Khan and Syed Modassir Hussain: validation, software, investigation, writing–review and editing, formal analysis, project administration, funding acquisition. Anuar Ishak: writing–review and editing, writing–original draft, software, data curation, validation, resources.

    Funding

    This work has been funded by the Universiti Kebangsaan Malaysia project number (DIP-2023-005).

    Acknowledgments

    This work has been funded by the Universiti Kebangsaan Malaysia (project number DIP-2023-005). Also, the authors thank the Deanship of Scientific Research, Islamic University of Madinah, Madinah, Saudi Arabia, for supporting this research work. In addition, the authors would like to thank the learned referee for their valuable comments and suggestions for the improvement of the quality of the paper. The author (S. Sureshkumar) is grateful to Management of SIT for their encouragement and support in doing research. The authors (Priya M. Gouder, J. K. Madhukesh, and G. K. Ramesh) thank the Management of KLE Society, University, and Principal for their kind support in taking up the research. The author (Krishna B. Chavaraddi) is also grateful to the UGC and DCE for their everlasting support and encouragement.

      Data Availability Statement

      The data used to support the findings of this study are available within the manuscript.

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.