Energy-Minimization Models for Hybrid Carbon Nanotori Production
Abstract
The merging of carbon nanostructures has been extensively studied due to their outstanding properties. However, prior research neglected the rotational curvature through merging process, consequently restricting their advantages in the production of complex hybrid nanostructures in three-dimensional (3D). This paper addresses a novel energy minimization approach that includes the effects of the axial and rotational curvatures to model the hybrid carbon nanotori (CNTRs), providing a more complete foundation for the formation of stable CNTRs structures with different radii and curvature features. Two methodologies in energy minimization were used, namely elastic energy for 2D merging and the Willmore energy approach for 3D merging. The results confirm that both models in two-dimensional (2D) and 3D scenarios produce efficient and smooth joining curves. First model produces a minimum mean curvature around 0.15 and a total bending energy reduction of 18% which supports the stability of the configuration at the joining. While the second model uses zero mean curvature for the join. Moreover, the rotational curvature implication enhancing stability throughout the 3D connection process. By addressing the limitations of prior studies, this study develops an effective framework in production of stable hybrid nanostructures for future applications.
1. Introduction
Carbon nanostructures have transformed materials science and nanotechnology, providing new opportunity to deal with difficulties across a wide range of scientific and industrial sectors. Since their discovery, carbon nanoparticles (CNPs) have gained massive interest from the scientific community because of their outstanding versatility. Through the numerous carbon-based nanoscale structures, like graphene sheets (CGSs), nanotubes (CNTs), nanocones (CNCs), nanotori (CNTRs), and fullerenes (CNFs), their exceptional properties including high electrical and thermal conductivities, unusual flexibility, and remarkable tensile strength, have allowed for revolutionary developments in energy storage, biotechnology, sensing, actuation systems, and microelectronics [1–4]. Latest studies focus in increasing applicability of nanostructures in numerous areas by energy effectiveness method as in [5] and [6]. The above characteristics may increase applications in preceding technologies as gigahertz oscillators, gas reduction, gene delivery methods, and biosensing devices [7–13]. Furthermore, the improvement of computational modeling proves the consuming of the energy and capacity of these nanostructures [14].
CNTRs, a special class of toroidal-shaped carbon-based nanostructures, have become an interested structure in the scientific community because of their unique electrical and magnetic characteristics. The process of CNTRs fabrication might be achieved by joining sliced nanotube segments, reshaping fullerene structures or joining open-ended CNTs [12, 15, 16]. In the aspect of magnetic, these distinguished materials have special manner, for example as a response to changes in magnetic flux, they provide a fixed current [17–20]. Additionally, they are attractive options for biomolecular design and complex drug delivery systems due to their potential application as charge-free caged structures [21, 22].
The merging of carbon nanostructures states a significant frontier in nanotechnology, authorizing the production of hybrid systems with enhanced properties [23, 24]. Merged nanostructures have confirmed enhanced electrochemical and physicochemical performance in contrast to their individual components, giving rise to breakthroughs in nanosensors, nanooscillators, energy storage devices, and drug delivery systems [25–29]. Energy optimization methods have improvement progress that emphasizes the applications of the hybrid structures in nanotechnology and beyond [30]. As a result of the growth and developments in this topic, researches have studied different techniques in synthesizing carbon nanostructures with conformation on theoretical modeling and experimental aspects.
To identify the ideal curves in connection cases, elastic energy minimization technique is used to determine the connection area between two-dimensional (2D) nanostructures, including CNTs with (CGSs, CNCs, and CNFs), CNFs with (CNFs and CGSs), and two CNCs [29, 31]. Different method applied to merge nanostructures is the Willmore energy method. Enhancing the equilibrium configurations for conjoining nanostructures has been proven by utilizing Willmore energy as a geometric optimization standard [32]. This method assumes that, as a general case of elastic energy, both rotational and axial curvatures are considered to determine the surface conjunction between two nanostructures in three dimensional (3D). Particularly, different structures have been merged based on this approach, such as CNTs with CNFs, CNTs with carbon nanotorus, and two CNFs [33–37]. This study pioneers in the consideration of carbon-based CNTRs connection by employing energy minimization aforementioned models. To model the geometry of the hybrid CNTRs, this approach combines the two curvatures. The axial curvature considers the compression or elongation throughout the produced configuration length. While the bending of torsion is considers by the rotational curvature. Using both curvatures, the proposed model promises fixed configurations with minimized energy that includes difference in segment radii and types of curvatures. The importance of this model can appear in CNTRs smooth and realistic designing which can be applied in drug delivery and molecular design. The purpose of this study is to provide models for improving carbon nanostructures. The potential contribution of the results is enhancing the development of the next-generation biomolecular designs and drug delivery systems. The growing interest in analytical and computational approaches for designing stable geometries is highlighted by recent studies that have investigated curvature-driven energy minimization in carbon nanostructures, including simulations of nanotorus stability and variations of the Willmore energy model for example [25, 32]. By include both axial and rotational curvatures, our study goes one step farther in this direction and provides a single model for hybrid structures.
The remainder of this study is organized as follows: The details of the mathematical model of the merging energies are presented in Section 2. The results of these methods are discussed in Section 3, and the conclusions are presented in Section 4.
2. Modeling Approach
2.1. Structure of Torus
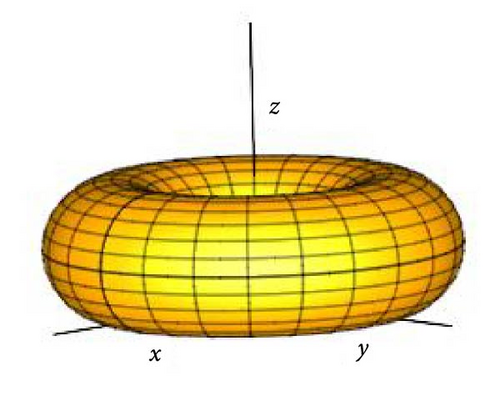
“Torus equation is identified as , which may be transformed as, it yields x(ϕ, θ) = (R + a cosϕ)cosθ, y(ϕ, θ) = (R + a cosϕ)sinθ, and z(ϕ, θ) = a sinϕ, where θ is the polar angle and ϕ is the azimuthal angle in the x-axis and xy-plane. Moreover, R refers to the major radius of the torus and a refers to the minor radius” [25] (P. 4), as shown in Figure 1.
2.2. First Model: Energy Minimisation in Terms of Axial Curvature
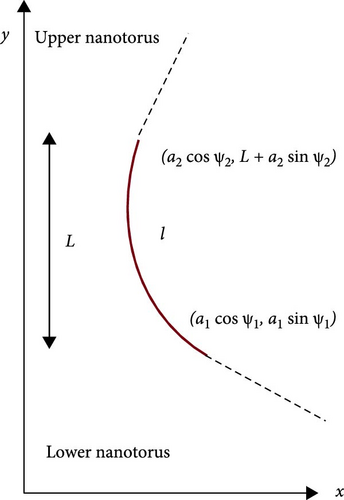
This case formulates the connecting areas among nanostructures by calculus of variations. The lower torus had radii of a1 as a minor and R1 as a major centered at the origin. Furthermore, the upper torus had radii of a2 as a minor and R2 as a major, which collinear with y-axis, and y0 is the starting unspecified distance overhead the xz-plane. In particular, L is the distance determined in the solution between the two structures in the y-direction. Assuming that the CNTRs are positioned symmetrically among axis of y, y0 is positioned on the 2D xyplane. Referring to Figure 2.
2.3. Second Model: Energy Minimisation in Terms of Axial and Rotational Curvatures
The assumptions of this model are linear elasticity, moderate curvature, and fixed boundary conditions. Thus, they make it appropriate for ideal cases while it may be not suitable for powerful boundary, major deformations, and extreme curvature.
3. Results and Discussion
3.1. Results of First Model
First model identifies the connecting curve between the CNTRs. When y′ ranged from (a1 cosψ1) to (a2 cosψ2), such that (−cotψ1) to (−cotψ2), the B.C. was y′(a2 cosψ2) = −cotψ2. Based on this, the joint curvature, in this situation, remains positive along the arc lengthl; therefore, positive sign of Equation (2) is examined only.
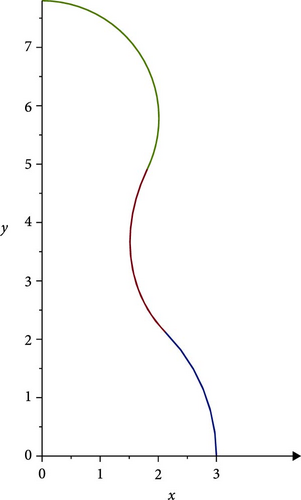
For stability and reliability of the numerical solution, we use Maple fsolve function with different initial estimates with the correct range of k between 0 and 1. As a result, the findings demonstrated uniform convergence. Furthermore, a sensitivity analysis was conducted by changing the input parameters a1, a2, ψ1, ψ2, and L by a maximum of ±5%. The robustness of the numerical solution was confirmed by the ensuing fluctuations in β and L being within acceptable boundaries.
3.2. Results of Second Model
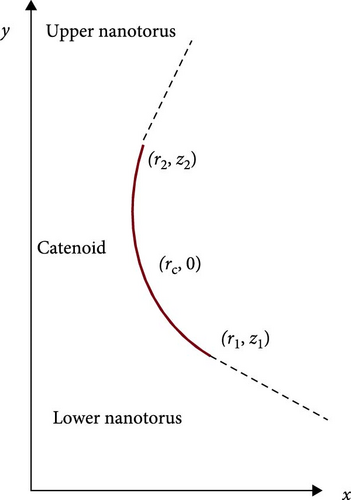
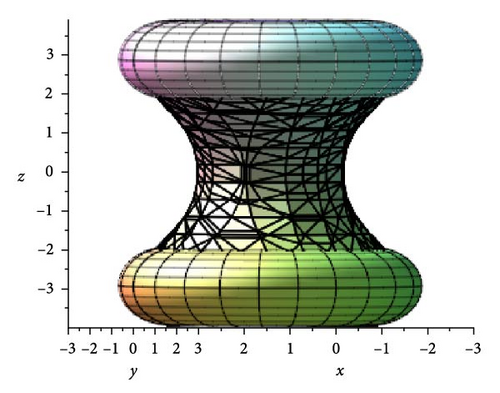
The outcomes of this research confirm that minimizing bending energy produces stable structures for hybrid CNTRs, mostly next to junctions with the variation of curvatures. While the using of the above curvatures shows the influence of the configuration stability by longitudinal and radial bending. This differ from the previous studies which suppose constant curvature or depend only on Willmore energy [25]. This approach considers actual geometries and provides elasticity in constructing nanostructures with mechanical features control. Our dual-curvature formulation captures more realistic geometrical transitions in hybrid CNTRs, especially when curvature discontinuities or varying radii are present, than recent models that only focus on uniform curvature or Willmore energy [25, 32]. The literature used the merging process of nanostructures depending on axial curvature only with symmetric transitions. However, the proposed model here incorporates both axial and rotational curvatures which provides more flexibility and actual of the produced structure.”
4. Conclusion
- 1.
Axial-curvature energy model:
- •
This model focuses on minimizing the axial-curvature energy to outline the merging curve in the xy-plane.
- •
It assumes rotational symmetry for both carbon nanostructures, simplifying the problem to two dimensions.
- •
- 2.
Willmore energy model:
-
This model depends on minimizing the Willmore energy to identify the merging surface, considering the catenoid surface as a minimal energy surface to merge carbon nanostructures.
- •
This model merged perfectly carbon-based nanostructures in 3D scenarios.
-
- 3.
Utilizations to CNTRs:
- •
In this study, the elastic and Willmore energy minimization methods were expanded to obtain the connection framework of other nanomaterials, Namely, two CNTRs.
- •
The results can be provided for two different joining constructions; that is, we can obtain the hybrid structures between two CNTRs in 2D and 3D, obtaining estimation for other complex cases.
- •
- 4.
Future utilizations:
- •
The merged structures can be applied in scanning tunnelling microscopy usage.
- •
Simple models can be developed to offer a foundation for relevant approximations to complicated structures, which may be useful for future work.
- •
- 5.
Limitations and future work: Although there are no experimental or computational validation results for direct comparison, the simplicity of the indicated models offers a useful basis for modeling complex situations. Some computational methods may be include in the future studies to improve the theoretical results. For example, molecular dynamics simulations or density functional theory computations. That is providing the numerical insights into the energy profiles and mechanical stability of produced configuration. Furthermore, because of the mathematical formulation simplification and analytical treatment, this study assumes the rotational symmetry. While real nanostructures may offer local defects or asymmetries, the symmetric situation provides a valuable idealization for determining the fundamental energy-minimizing behavior. This method is consistent with previous studies, such as [25, 36], also can be use as a baseline for asymmetries or structural irregularities. Future investigation would be studied to explore a wider range of applications for the models presented here.
Conflicts of Interest
The author declares no conflicts of interest.
Author Contributions
Nawa A. Alshammari wrote the main manuscript text, prepared all figures, and reviewed the manuscript.
Funding
The author did not receive support from any organization for the submitted work.
Open Research
Data Availability Statement
All data that support the findings of this study are included within the article.




