This study examines the optical soliton structure solutions, sensitivity, and modulation stability analysis of the chiral nonlinear Schrödinger equation (NLSE) with Bohm potential, a basic model in nonlinear optics and quantum mechanics. The equation represents wave group dynamics in numerous physical systems, involving quantum Hall and nonlinear optical structures. To attain exact solutions, we utilize the generalized exponential rational function (GERF) method and the Paul-Painlevé (PP) approach, revealing a various set of optical soliton solutions, containing exponential, hyperbolic, and trigonometric function-based solitons. By utilizing suitable parametric values, we provide 3D, 2D, and contour visualizations to demonstrate the soliton characteristics. Moreover, a comprehensive sensitivity and modulation stability analysis is carried out, presenting the impact of parametric alteration on soliton behavior. The findings exhibit the emergence of dark, bright, and periodic soliton solutions, which play a key role in understanding nonlinear wave propagation in topological and optical systems. The novelty of this work lies in enhancing the study of chiral soliton within the Bohm potential framework, yielding new observations into their stability, modulation, and structural properties.

1. Introduction

Nonlinear partial differential equations (NLPDEs) are fundamental in modeling a wide range of physical phenomena and dynamic processes. The study of NLPDEs is essential due to their widespread applications in distinct fields such as fluid dynamics, optics, control theory, quantum mechanics, and plasma physics [1–12]. One of the most key challenges in nonlinear physics is attaining analytical solutions for NPDEs, particularly solitary wave solutions, which deliver valuable insights into nonlinear wave propagation phenomena. Solitary waves, or solitons, are unique in that they kept their amplitude, shape, and speed while traveling through a medium, unlike most waves, which disperse and lose energy over time. The persistence of soliton waves has led to their application in fields such as optical communication, plasma wave propagation, and water waves. Moreover, fractional-order derivatives, a key feature in nonlinear fractional differential equations (NFDEs), have become increasingly important in scientific research. The incorporation of fractional derivatives introduces complexity to these equations, adding a layer of nonlinearity that makes the analysis of solitary waves in NFDEs particularly challenging yet valuable for understanding complex dynamic systems [13–24].

Recently, distinct efficient methods have been utilized to attain soliton solutions for NLPDEs. The modified expansion rational function method (MERFM) has been utilized to acquire diverse soliton solutions for the unstable nonlinear Schrödinger equation (NLSE), exhibiting its applicability to nonlinear physical models [25]. Additionally, the MRE method delivered bright-dark soliton and kink solutions for the (2 + 1)-dimensional elliptic NLSE, which is suitable for optical pulse propagation [26]. The -expansion method derived soliton solutions for the (3 + 1)-dimensional Zakharov–Kuznetsov model, with applications in plasma physics [27]. The GREM method created novel analytical solutions for the Gardner–Kadomtsev–Petviashvili equation, enabling the study of shallow-water waves [27]. The three-wave, positive-quadratic, and double-exponential techniques were employed to produce soliton solutions for the unstable NLSE, verified through modulational instability analysis [28]. The dynamic wave behaviors of the M-fractional nonlinear Gross–Pitaevskii equation have been analyzed by utilizing advanced analytical methods in [29]. The soliton neuron model is investigated to analyze the propagation of action potentials through soliton solutions, applying multiple integration approaches [30]. The fractional telegraph equation is studied for its solitary wave dynamics and chaotic behavior by utilizing novel analytical methods and graphical sensitivity analysis [31]. The (2 + 1)-dimensional graphene sheet equation is analyzed for its thermal wave transmission behavior, by using the Hirota bilinear method to derive multiple soliton solutions [32]. Additionally, nonlinear wave dynamics in a magneto-electro-elastic circular rod are studied by utilizing fractional soliton solutions and chaotic sensitivity analysis [33]. Finally, the (3 + 1)-dimensional Kadomtsev–Petviashvili equation is examined for its hybrid wave structures, employing the Hirota bilinear method and long-wave technique [34].

Nonlinear PDEs prescribe most physical events and dynamic techniques. The past decade has yet to see a reduction in the search for new ways to solve problems and different types of solitary wave solutions. Many theoretical components for developing alternative procedures can be found in the literature as: authors have implemented the functional variable approach to solve the 2-dimensional Maccari system and the (3 + 1)-dimensional fractional modified KdV-ZK equation [35]. Zafar et al. [36] have investigated and analyzed the optical solitons of the complicated Ginzburg–Landau equation by utilizing the Kudryashov method. Discover new kinds of one-soliton and two-soliton solutions to the Burgers equation by using the Darboux transformation through the Lax pair [37]. Investigating soliton solutions by using the simplest sine-cosine method for an inherent fractional discrete nonlinear electrical communication network in [38]. The NLSE with group velocity dispersion, which describes the motion of optical solitons in nonlinear media, is solved by using the modified extended direct algebraic approach for acquiring optical solitons [39]. The fractional simplified Camassa–Holm equation’s closed-form wave solutions have been investigated using possible methods, namely the sine-Gordon expansion method [40, 41]. Tianle et al. found straightforward, broad, and efficient solutions by using the modified Hirota bilinear technique [42, 43]. The double integral approach is accurate and suitable for use in metal solidification applications [44]. For the model under consideration, four types of nonlinearity are found that produce bright, dark, and singular solitons solutions [45]. Investigation of the complex Ginzburg–Landau problem that arises in nonlinear optics analytically by using -expansion approach [46]. Using the two-variable -expansion method and the modified Riemann–Liouville fractional derivative, this work tries to find exact solutions for fractional dispersive longwave (DLW) equation and approximate long water wave (ALW) equation [47–49]. Dark and rational solitons have been obtained by using the unified technique and the local M-derivative qualities [50].

While this study provides significant contributions to the optical soliton structure of the CNSE with Bohm potential, it has specific limitations. The examination is restricted to distinct parameter choices, as the exact soliton solutions attained by utilizing the generalized exponential rational function (GERF) method and the Paul-Painlevé (PP) approach may not fully generalize to all nonlinear optical and quantum systems. Additionally, the analysis remains purely theoretical, lacking experimental validation, which is crucial for validating the real-world applicability of the findings. The model also considers a two-dimensional framework, whereas higher-dimensional effects, which play a key role in practical systems, are not studied. Furthermore, external perturbations such as loss, dispersion variations, and nonlinear gain are not included. While sensitivity and modulation stability analyses are executed, a more extensive numerical stability analysis, such as linear stability analysis or direct numerical simulations, would deliver deeper observation. However, this work lays a theoretical foundation for understanding chiral solitons in nonlinear optical and quantum systems, representing a basis for future experimental and computational studies.

The novelty of the present study lies in tackling a critical research gap in the analysis of the chiral NLSE with Bohm potential (CNLSE-BP). While Rizvi et al. [51] examined chirped soliton solutions by utilizing the Jacobian elliptic function method, their solutions exhibited singularities, limiting their practical applicability. In contrast, our study utilizes the GERF method and the PP approach, yielding singularity-free soliton solutions and demonstrating a distinct set of optical solitons, including dark, bright, and periodic structures. Moreover, we conduct a comprehensive sensitivity and modulation stability analysis, delivering new insights into soliton behavior under parametric variations. These contributions advance the understanding of chiral solitons within the Bohm potential framework, enhancing their applicability in quantum mechanics and nonlinear optics.

The remaining part of the manuscript is divided into different sections. A successful and effective GERF method for obtaining analytical solitary wave solutions to the CNLSE-BP, along with its steps, are briefly described in Section 2. The types of analytical wave solutions, such as trigonometric, hyperbolic, exponential function, rational form, and so on, are covered in Section 3. In Section 4, we provide a summary of PPA. We use the PPA to obtain an exact soliton shape in Section 5. In Section 6, accurate soliton solutions are physically presented using Mathematica 11 software, sensitivity and modulation stability analysis are analyzed in the purposed model. Section 7 contains the conclusion of this article.

2. The Summary of GERF Method

The particular method for solving NLPDEs is the GERF method [19]. The important steps are specified as:

Step 1

Suppose the NLPDE as,

()

where ψ = ψ(x, t) is the wave variable function, ℑ is a polynomial in ψ(x, t) and its partial derivatives contains highest order derivative with highest order nonlinear parts.

Suppose the traveling wave transformation,

()

where ξ = x − νt, Θ(x, t) = −κx + ςt + m₀, ν is the velocity of traveling wave.

Substituting Equation (2) into Equation (1), then we get

()

Step 2

The solution of Equation (3) assumes as,

()

where l₀, l_q and n_q are undetermined parameters to be found. The function Ξ(ξ) is defined as

()

Step 3

To determine the value of N by utilizing the homogeneous balance method in Equation (4).

Step 4

The system of algebraic equations is obtained by substituting Equation (4) into Equation (3) using Equation (5). We used Mathematica software to get the solution for this system, and then we used Equation (2) to insert the solution we acquired for Equation (5) into Equation (4). At last, the solution for Equation (1) has been acquired.

The reliable soliton solutions of NLPDEs are investigated using the GERF technique, which produced helpful, more general, and exact wave solutions of NLPDEs. In short, the GERF approach may be utilized for organizing the wave velocity and is powerful, prevailing, and more broadly applicable to investigate various exact traveling wave solutions for NLPDEs.

3. Mathematical Analysis

In this article, we investigate the solutions of CNLSE-BP [52–54].

()

where ϖ(x, t) is the profile of optical soliton with space and time coordinates x and t, respectively. The superscript ∗ is a representation of a complex conjugate. In this model, γ and η are coefficients of dispersion and nonlinear coupling constant. The right side of CNLSE-BP is called the perturbation term (Bohm potential). This term has many results in quantum behavior. It has a lot of applications in physics, the quantum Hall effect, and mechanics. We utilized the following transformation [53]:

()

Putting Equation (7) into Equation (6), then we have

()

The equation has distinct real and imaginary parts. The real part of the equation is given by

()

and imaginary component of equations is

()

We can find the velocity by using Equation (10)

()

Applying the homogenous balancing technique on Equation (8), then we get N = 1. Putting N = 1 into Equation (4), we have

()

The formal solution of Equation (6) is

()

Here, we find the value of unknown constants, which are l₀, l₁, and n₁. The solution of Equation (6) is determined under the following cases:

Case 1: If [σ₁, σ₂, σ₃, σ₄] = [1, −1, 1, 1] and [μ₁, μ₂, μ₃, μ₄] = [1, −1, 1, −1] then Equation (5) becomes,

()

A system of algebraic linear equations is obtained by placing Equation (12) and Equation (14) into Equation (9). We can get the following set of solitary wave solutions by solving all of those equations.

Set 1

()

Putting the values of the unknown above parameters into Equation (12), then a solution of Equation (6) have

()

Set 2

()

Putting the values of the unknown above parameters into Equation (12), then a solution of Equation (6) have

()

Set 3

()

Putting the values of the unknown above parameters into Equation (12), then a solution of Equation (6) have

()

Set 4

()

Putting the values of the unknown above parameters into Equation (12), then a solution of Equation (6) have

()

Case 2: If [σ₁, σ₂, σ₃, σ₄] = [i, −i, 1, 1] and [μ₁, μ₂, μ₃, μ₄] = [i, −i, i, −i] then Equation (5) becomes,

()

A system of algebraic linear equations is acquired by putting Equation (12) and Equation (23) into Equation (9). Solving those equations allows us to get the following set of solitary wave solutions.

Set 1

()

Putting the values of the unknown above parameters into Equation (12), then a solution of Equation (6) have

()

Set 2

()

Putting the values of the unknown above parameters into Equation (12), then a solution of Equation (6) have

()

Set 3

()

Putting the values of the unknown above parameters into Equation (12), then a solution of Equation (6) have

()

Set 4

()

Putting the values of the unknown above parameters into Equation (12), then a solution of Equation (6) have

()

Case 3: If [σ₁, σ₂, σ₃, σ₄] = [1 + i, 1 − i, 1, 1] and [μ₁, μ₂, μ₃, μ₄] = [i, −i, i, −i] then Equation (5) becomes,

()

A system of algebraic linear equations is acquired by putting Equation (12) and Equation (32) into Equation (9). Solving those equations can acquire the following set of solitary wave solutions.

Set 1

()

Putting the values of the unknown parameters Equation (57) into Equation (12), then a solution of Equation (6) have

()

Case 4: If [σ₁, σ₂, σ₃, σ₄] = [2 + i, 2 − i, 1, 1] and [μ₁, μ₂, μ₃, μ₄] = [i, −i, i, −i] then Equation (5) becomes,

()

A system of algebraic linear equations is acquired by putting Equation (12) and Equation (35) into Equation (9). Solving these equations allows us to get the following set of solitary wave solutions.

Set 1

()

Putting the values of the unknown parameters Equation (57) into Equation (12), then a solution of Equation (6) have

()

Set 2

()

Putting the values of the unknown parameters Equation (38) into Equation (12), then a solution of Equation (6) have

()

Set 3

()

Putting the values of the unknown parameters Equation (40) into Equation (12), then a solution of Equation (6) have

()

Set 4

()

Putting the values of the unknown parameters Equation (42) into Equation (12), then a solution of Equation (6) have

()

Set 5

()

Putting the values of the unknown parameters Equation (44) into Equation (12), then a solution of Equation (6) have

()

Set 6

()

Putting the values of the unknown parameters Equation (46) into Equation (12), then a solution of Equation (6) have

()

Case 5: If [σ₁, σ₂, σ₃, σ₄] = [2, 1, 1, 1] and [μ₁, μ₂, μ₃, μ₄] = [1, 0, 1, 0] then Equation (5) becomes,

()

A system of algebraic linear equations is acquired by setting Equation (12) and Equation (48) into Equation (9). Solving those equations can acquire the following set of solitary wave solutions.

Set 1

()

Equation (12) can be solved by utilizing diverse values of the known parameters from Set 1, then a solution of Equation (6) is defined as:

()

Set 2

()

Equation (12) can be solved by utilized diverse values of the known parameters from Set 2, and then a solution of Equation (6) is determined as:

()

Case 6: If [σ₁, σ₂, σ₃, σ₄] = [2, 0, 1, 1] and [μ₁, μ₂, μ₃, μ₄] = [−1, 0, 1, −1] then Equation (5) becomes,

()

A system of algebraic linear equations is acquired by setting Equation (12) and Equation (53) into Equation (9). Solving those equations allows us to get the following set of solitary wave solutions.

Set 1

()

Equation (12) can be solved by utilized diverse values of the known parameters from Set 1, then a solution of Equation (6) is identified as:

()

Case 7: If [σ₁, σ₂, σ₃, σ₄] = [−3, −1, −1, 1] and [μ₁, μ₂, μ₃, μ₄] = [−1, 1, −1, 1] then Equation (5) becomes,

()

A system of algebraic linear equations is received by putting Equation (12) and Equation (56) into Equation (9). Solving those equations allows us to get the following set of solitary wave solutions.

Set 1

()

Equation (12) can be solved by utilizing diverse values of the known parameters from Set 1, then a solution of Equation (6) is specified as:

()

4. Summary of PP Approach

The PP technique is mostly used to solve nonintegrable nonlinear PDEs. The following are the key steps:

Step 1

Consider the NLPDE as,

()

where ψ = ψ(x, t) is the wave variable function and ℑ is a polynomial in ψ(x, t), and its partial derivatives contain highest order derivative and highest order nonlinear parts.

Suppose the given traveling wave transformation,

()

where ξ = x − νt, Θ(x, t) = −κx + ςt + m₀, ν is the velocity of traveling wave.

Substituting Equation (59) into Equation (60), then we have

()

where ϝ is a polynomial of U(ξ).

Step 2

By using the PPA technique [55], analytical solutions of Equation (61) will be obtained in this form

()

where the value of n is attained by the homogenous balance method.

and Riccati-equation of the form

is satisfied by H(Y).

Step 3

Riccati-equation gives the solutions in the form of

()

where C₀ and K are constant.

Step 4

In this step, we find the values of K,N, and B_i where i = 1, 2 … n by using Equation (62) in Equation (61) and comparing the coefficient of different exponent of H(y)e^−Nξ.

5. Implementation of PP Approach on CNLSE-BP

For getting analytical solutions, we implement the PPA technique on the CLNSE-BP model. By using the homogenous balance method, we find that n = 1 and expand Equation (62) upto n = 1 as:

()

We have to find the value of constant B₀,B₁,N, and

. Furthermore, H(Y) satisfied the Riccati-equation of the type

whose solution is provided by Equation (63).

U_ξ = B₁KH(Y)²e^−2Nξ − B₁H(Y)Ne^−Nξ.

U_ξξ = 2B₁K²H(Y)³e^−3Nξ − 3B₁KH(Y)²Ne^−2Nξ + B₁H(Y)N²e^−Nξ.

Substituting the values of U, U_ξξ, U³ into Equation (8) and accumulate the coefficient of different powers of H(Y)e^−Nξ equal to zero.

By solving the above system of algebraic equations, then we have

()

By using Equation (65) along with Equation (62) and Equation (63), we get the solution

()

The solution of Equation (6) can be written as

()

6. Results and Discussion

Employing the GERF approach and the PP strategy, we emanated three different soliton solutions for the chiral NLSE: dark solitons 1, 2, periodic solitons 3, 5, 6, and bright solitons 7, 8.

•
Figures 1 and 2 yield a comprehensive visualization of the real and imaginary parts of the attained soliton solution with parametric values c = 1.01, γ = 1.01, η = 1.03, κ = 1.06, m₀ = 0.07, ς = 0.05. The 3D plots show the high degree of localization and stability of the soliton, with both components revealing well-defined peaks that keep their form across the propagation domain. The 2D plots further verify that the amplitude remains stable over time, representing minimal dispersion effects. The contour plots show clear and sharp boundaries, showcasing the soliton’s robust structure. Dynamically, the soliton solutions illustrate typical characteristics of stable dark solitons maintaining their amplitude and shape during propagation. The parametric changes investigated in the 2D plots present that while the soliton’s amplitude is sensitive to certain parameter changes the overall structure remains unchanged. This represents that the soliton solutions possess good stability against small perturbations, which is important for real-world applications in nonlinear optics and chiral media systems.
•
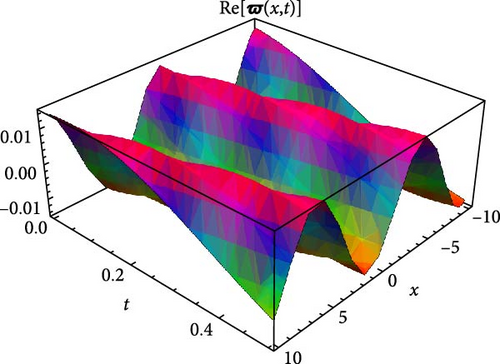
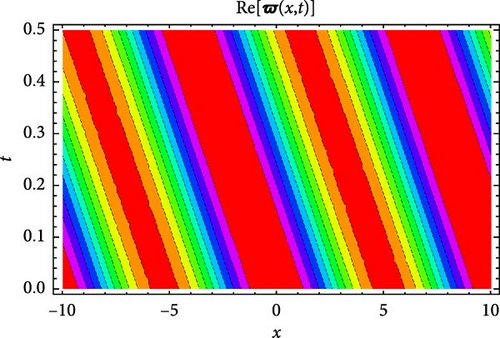
Figures 3 and 4 show periodic soliton solutions exhibiting stable, cyclic behavior across the space-time domain with parametric values c = 1.1, γ = 1.1, η = 1.3, κ = 1.6, m₀ = 0.07, ς = 0.5. Both 3D and contour plots show that the solutions keep their wave patterns without distortion, revealing a robust dynamical balance between nonlinearity and dispersion impact. The 2D plots further clarify the spatial sensitivity of amplitude but confirm that periodicity is kept over time. Dynamically, these periodic solitons show characteristics essential for applications needing stable wave propagation, such as in optical fiber systems, photonic crystals, and chiral materials.
•
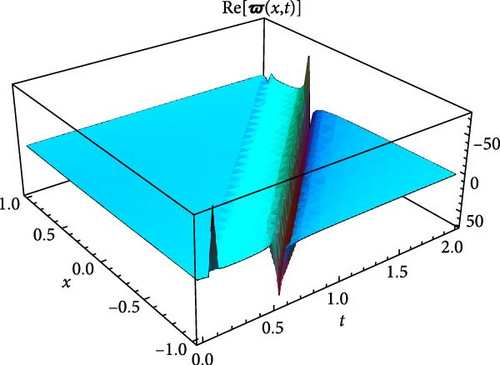
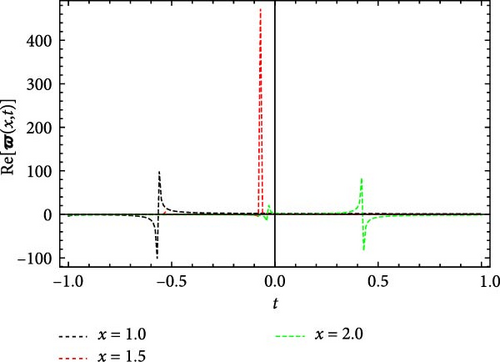
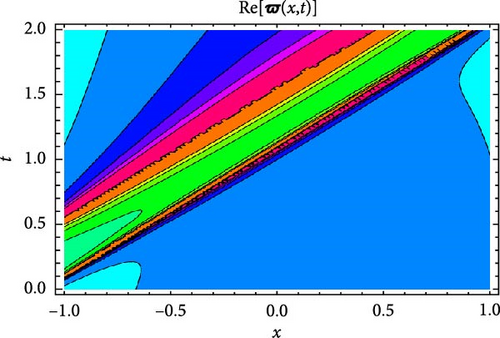
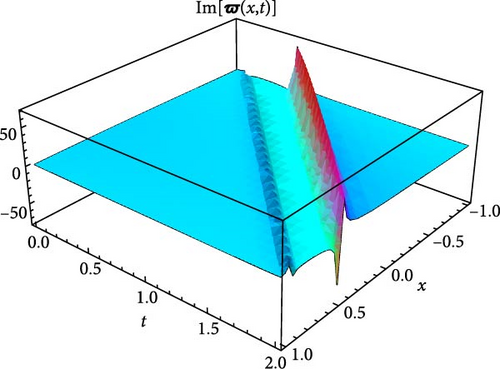
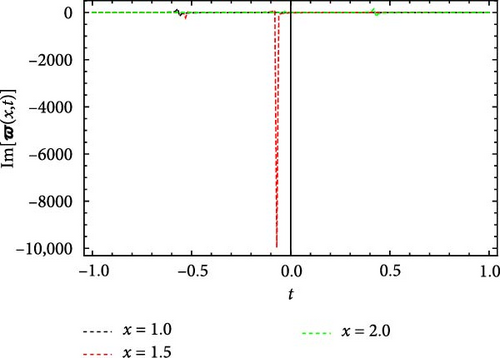
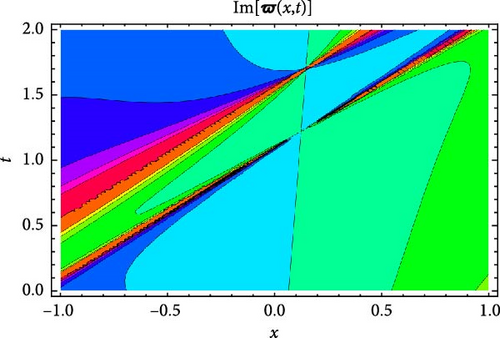
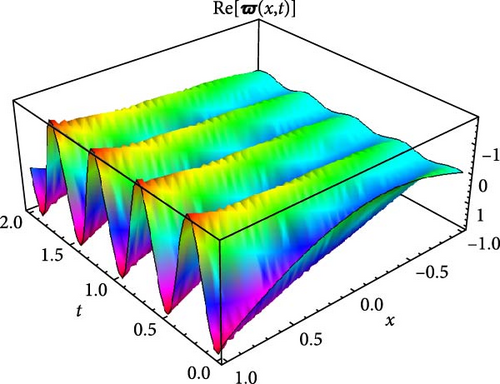
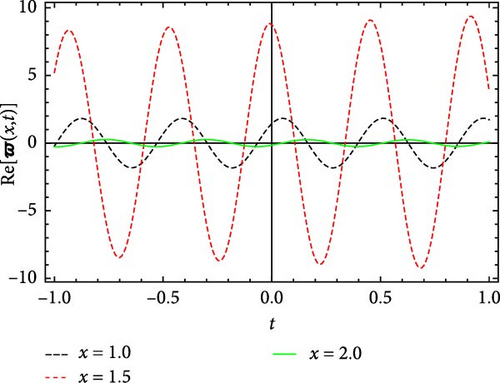
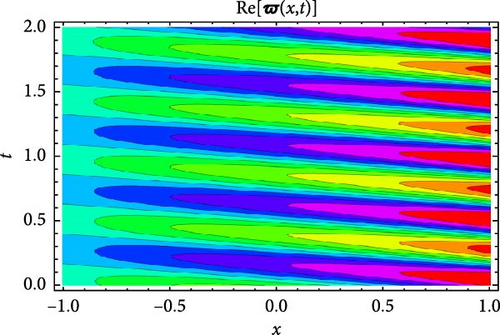
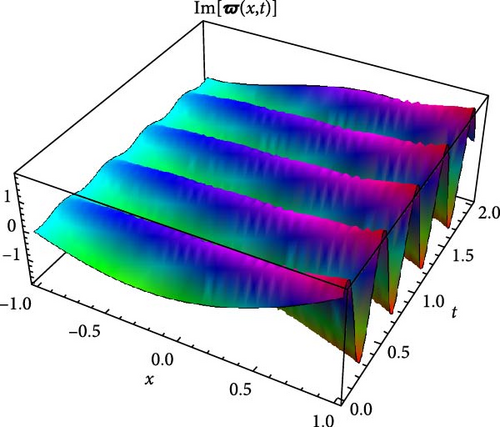
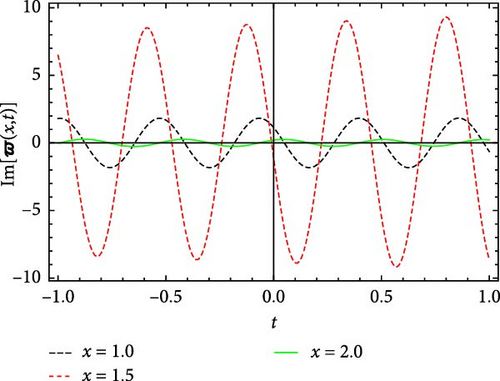
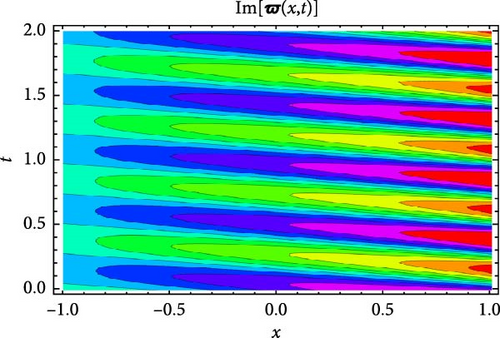
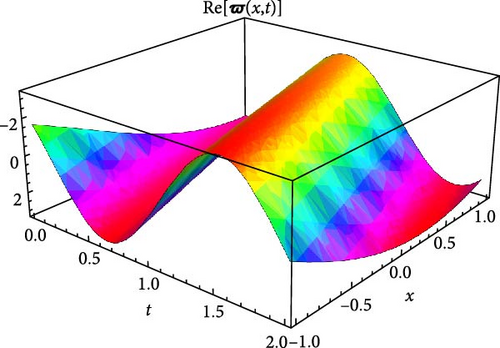
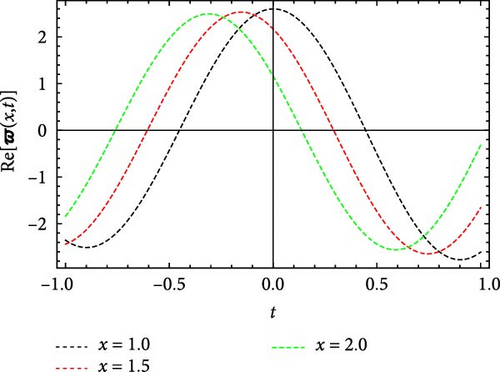
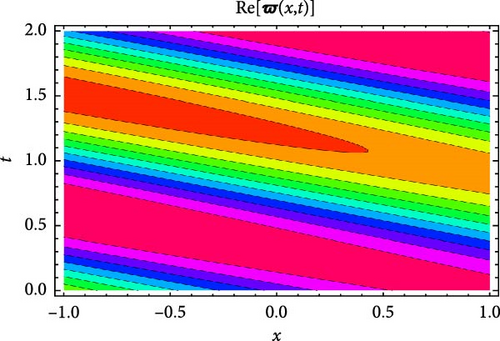
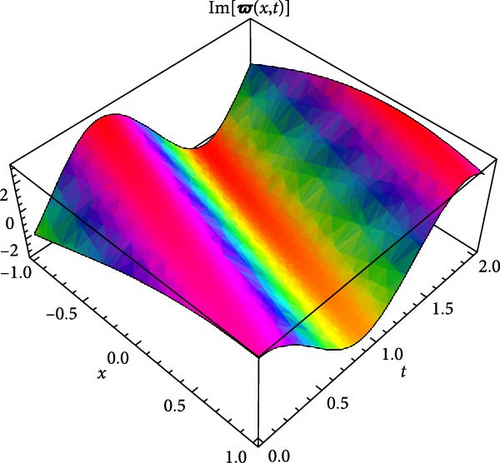
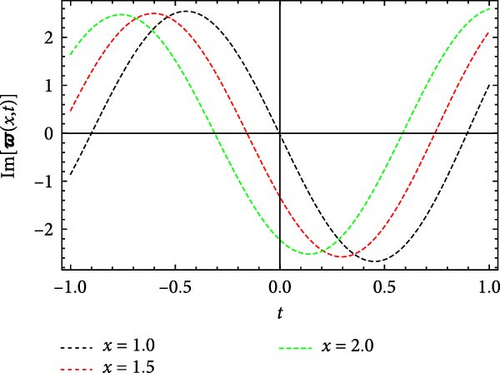
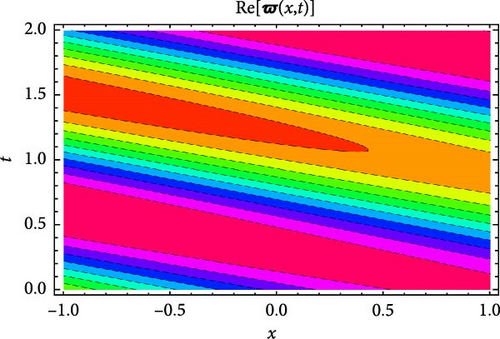
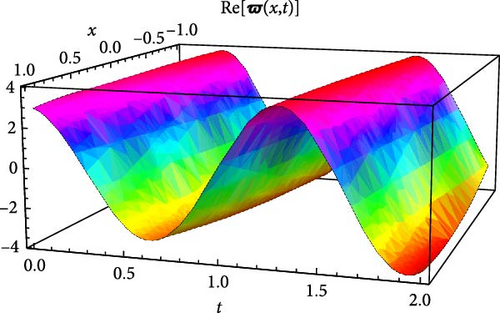
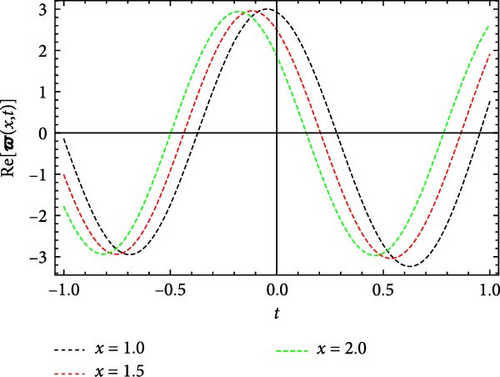
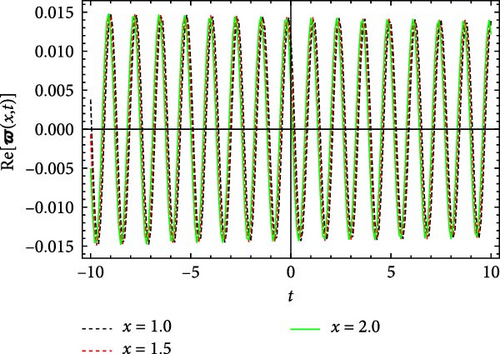
Figures 5 and 6 depict the real and imaginary parts of the attained soliton solution of Equation (50) for distinct parameter values c = 1.1, γ = 2.1, η = 2.03, κ = 1.08, m₀ = 1.07, ς = 0.05. The 3D plots in Figures 5 and 6 show the localized nature of the solution, where the wave peaks are well-defined and keep their structure during propagation in the space-time domain. The real and the imaginary parts of Figures 5 and 6 show smooth, stable waveforms without significant dispersion, which are typical characteristics of bright soliton solutions. The 2D plots further depict this behavior by representing periodic oscillations of the solution’s amplitude for different spatial values (x = 1.0, 1.5, 2.0). The oscillations remain bounded and stable, showing that the soliton maintains its shape over time. Moreover, the contour plots deliver a clear top-down view of the propagation dynamics, where consistent wave structures and sharp gradients are examined, reinforcing the localized and nondispersive nature of the soliton. This behavior is essential for applications in nonlinear optical systems and chiral media, where keeping energy localization and minimizing dispersion are critical for effective signal transmission and wave control.
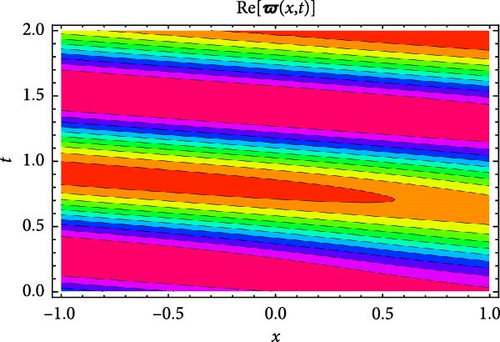
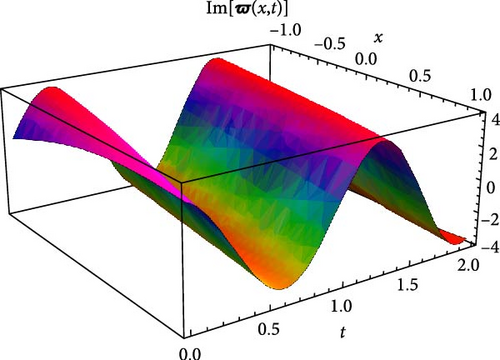
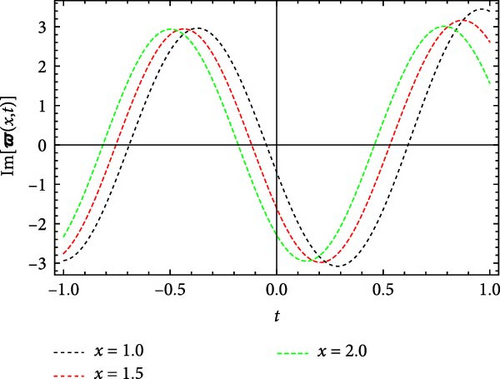
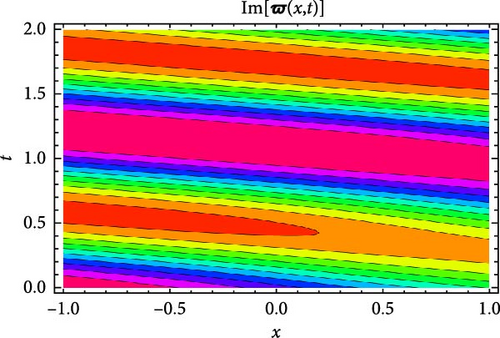
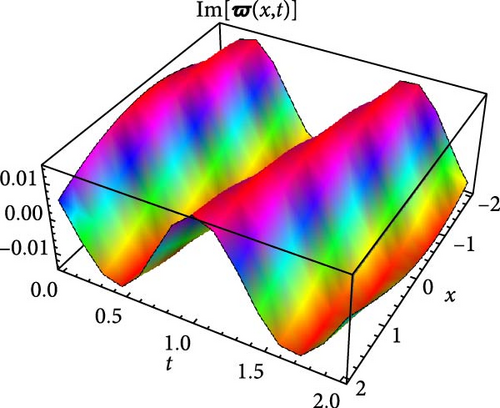
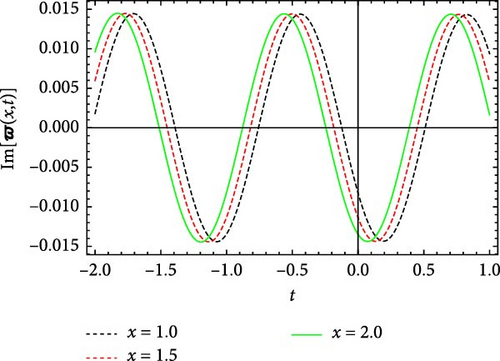
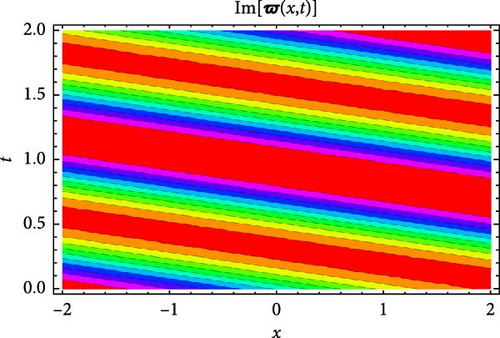
Figures 7 and 8 display the real and imaginary parts of the solution to Equation (58) under specific parameter values: c = 1.3, γ = 2.1, η = 4.3, κ = 0.6, m₀ = 4.7. Figures 7 and 8 show the solution’s features through 3D plots, 2D projections, and contour plots. The 3D plots demonstrate the wave-like behavior of the solution, presenting periodic oscillations over time. The 2D plots, which show the solution as a function of t for distinct values of x, further verify its periodic nature by revealing sinusoidal-like patterns. The contour plots deliver an alternative perspective, clarifying the propagation of wavefronts in the x–t plane, which also shows periodicity.
•
Figures 9 and 10 represent the real and imaginary components of the solution to Equation (67) for the given parameter values: c = 1.3, γ = 2.1, η = 1.3, κ = 0.6, m₀ = 4.7, C₀ = 1, K = 1, A = 2, N = 0.02. Figures 9 and 10 provide diverse visual representations, including 3D plots, 2D projections, and contour plots. The 3D plots in Figures 9 and 10 clarify an oscillatory nature of the solution in both space and time. The 2D plots present periodic waveforms that fluctuate over time for different values of x, further confirming a periodic behavior. The contour plots illustrate wavefront propagation in the x–t plane with a structured, repeating pattern, reinforcing the periodic nature of the solution.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Real plot solution of Equation (37) when c = 1.01, γ = 1.01, η = 1.03, κ = 1.06, m₀ = 0.07, ς = 0.05. (a) 3D-plot; (b) 2D-plot; (c) contour plot.

The application of the GERF method and PP close not only shows their utility in getting exact solutions for complex nonlinear equations but also delivers understanding into the design and optimization of devices that leverage these nonlinear chiral interactions, paving the way for creations in photonics and material science. In the Quantum Hall effect, edge states play a crucial role in the transport properties of the system. These edge states are chiral, meaning they move in a single direction along the boundary of the sample. Stable solitons, localized wave packets that keep their shape during propagation, can be employed to model these edge states. Chiral solitons can explain the unidirectional movement of electrons along the edge of a Quantum Hall system. The GERF Method is more straightforward and concentrates on yielding a wide diversity of soliton solutions, involving exponential, hyperbolic, trigonometric, bright, periodic, and dark soliton solutions. It involves directly creating solutions by utilizing exponential functions and is highly effective for visualizing soliton characteristics, such as in 2D, 3D, and contour plots. On the other hand, by utilizing the PP method, we attained a limited set of soliton solutions, primarily focusing on periodic solitons, in contrast to the GEFM, which provides a broader range of soliton solutions, including exponential, hyperbolic, and trigonometric types. Moreover, we compared our results with the existing paper [51], as shown in Table 1.

Table 1. Results comparison.

Contents	Solutions	Type of soliton
GERF method		Periodic, bright, and dark
		—

Paul-Painlevé approach		Periodic
		—
		—

Extended fan method [51]		Dark, singular periodic
		—
		—

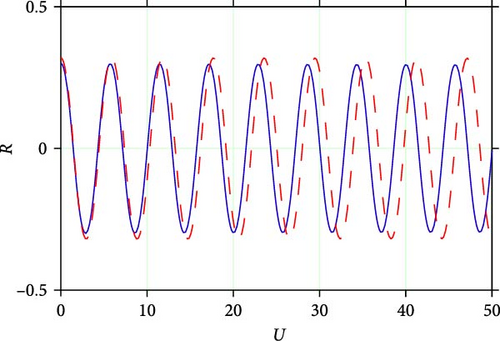
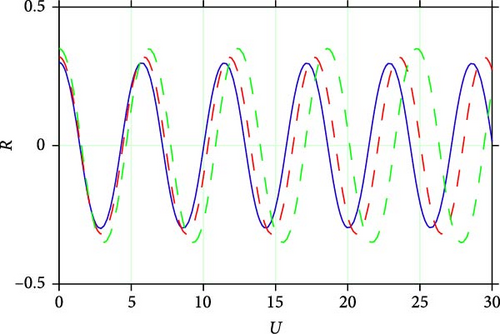
6.1. Sensitivity Analysis

From Equation (9),

()

Now, we can write in the form of a dynamical system as,

()

In this study, we highlight the significance of small input alterations on the results by presenting results with relevant parameter values γ = 0.03, η = 1, κ = 0.1, ς = −0.05. A small effect denotes low sensitivity, while a significant change denotes high sensitivity. We examine two and three different sets of initial conditions in order to assess the sensitivity of the model. Figures 11–13 show how even little changes to the starting circumstances can cause little changes in the system’s behavior (Equation (69)), but when time increases, waves are not followed. As a result, we conclude that the suggested system exhibits sensitivity, just not excessively.

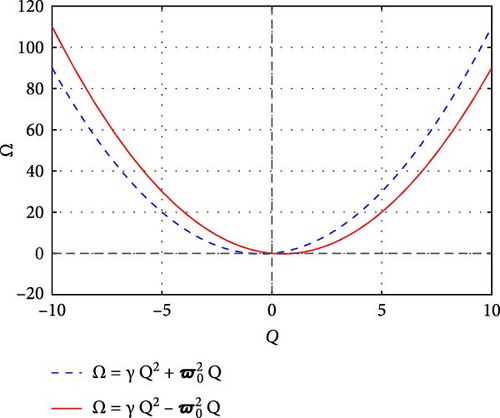
6.2. Modulation Stability

Assume the steady-state solution of Equation (6) is perturbed as:

()

where ϖ₀ > 0 is the constant steady-state solution and (|η| ≪ 1) is the small perturbation (|η| ≪ 1). After substituting Equation (6) into Equation (70) and collecting the first-order terms in η, the linearized equation has

()

For simplification higher-order terms in |r|_xx or |r| are negligible, yielding:

()

To study of instability then, we need solutions that increase exponentially, such as:

()

where, Q is the wave number, Ω is the frequency, and p₁, p₂ are the constants. Putting Equation (73) into Equation (72), then we have

()

Separate terms proportional to e^{i(Qx − Ωt)} and e^{−i(Qx − Ωt)}. This yields the following coupled equations:

Solving the above-coupled equations then, we attained the following dispersion relation

()

•
If Im(Ω) > 0, the system is unstable (modulation instability).
•
If Im(Ω) = 0, the system is stable.

Since Ω is real, there is no modulation instability.

7. Conclusion

This research utilized the GERF method and the PP approach to attain novel and effective optical soliton structure solutions for the CNLSE-BP model. The acquired solutions, including periodic wave solitons, trigonometric and hyperbolic solitons, as well as bright and dark solitons, reveal the impact of these approaches in solving nonlinear wave equations. As, related to previous studies, the results yield new insights into soliton dynamics and contribute to the broader understanding of NLSEs. Furthermore, the study demonstrates the potential applications of the CNLSE-BP model in quantum Hall systems and nonlinear optics, especially in describing the unidirectional propagation of long waves. A detailed sensitivity and modulation stability analysis was executed to explore the behavior of solitons under different parametric conditions, enhancing the comprehension of their stability and modulation characteristics.

Although these significant contributions, there are several promising directions for future research. Expanding the current study to higher-dimensional CNLS models could contribute deeper insights into soliton interactions and wave turbulence in complex physical systems. Exploring the effects of perturbations, nonlocal interactions, and fractional-order derivatives may further refine the stability analysis and reveal new soliton behaviors under more realistic conditions. Additionally, experimental validation of these theoretical results in quantum optics, photonic lattices, and Bose-Einstein condensates would strengthen their practical applicability. Moreover, investigating the role of CNLSE-BP solitons in nonlinear optical applications, such as fiber optics, metamaterials, and optical communication systems, could open new technological possibilities.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

All authors contributed equally to this article.

Funding

This research is funded by researchers supporting project number (RSPD2025R733), King Saud University, Riyadh, Saudi Arabia.

Acknowledgments

The authors have nothing to report.

Open Research

Data Availability Statement

All data that support the findings of this study are included within the article.

References

1 Akram G., Sadaf M., Khan M. A. U., and Hosseinzadeh H., Analytical Solutions of the Fractional Complex Ginzburg-Landau Model Using Generalized Exponential Rational Function Method With Two Different Nonlinearities, Advances in Mathematical Physics. (2023) 2023, no. 1, https://doi.org/10.1155/2023/9720612, 9720612.
10.1155/2023/9720612
Google Scholar
2 Shakeel M., Bibi A., Chou D., and Zafar A., Study of Optical Solitons for Kudryashov’s Quintuple Power-Law With Dual Form of Nonlinearity Using Two Modified Techniques, Optik. (2023) 273, https://doi.org/10.1016/j.ijleo.2022.170364, 170364.
10.1016/j.ijleo.2022.170364
Google Scholar
3 Zhang T., Xu S., and Zhang W., New Approach to Feedback Stabilization of Linear Discrete Time-Varying Stochastic Systems, IEEE Transactions on Automatic Control. (2024) 99, 1–8, https://doi.org/10.1109/TAC.2024.3482119.
10.1109/TAC.2024.3522762
CAS Google Scholar
4 Guo Y., Wang P., Gui W., and Yang C., Set Stability and Set Stabilization of Boolean Control Networks Based On Invariant Subsets, Automatica. (2015) 61, 106–112, https://doi.org/10.1016/j.automatica.2015.08.006, 2-s2.0-84943374270.
10.1016/j.automatica.2015.08.006
Web of Science® Google Scholar
5 AL-Taie M. S. J., Bright and Dark Soliton Pulse in Solid Core Photonic Crystal Fibers, Journal of Optics and Photonics Research. (2024) 1, no. 1, 23–31, https://doi.org/10.47852/bonviewJOPR32021585.
10.47852/bonviewJOPR32021585
Google Scholar
6 Almusawa H. and Jhangeer A., A Study of the Soliton Solutions With an Intrinsic Fractional Discrete Nonlinear Electrical Transmission Line, Fractal and Fractional. (2022) 6, no. 6, https://doi.org/10.3390/fractalfract6060334, 334.
10.3390/fractalfract6060334
Web of Science® Google Scholar
7 Hussain A., Jhangeer A., Abbas N., Khan I., and Sherif E. S. M., Optical Solitons of Fractional Complex Ginzburg-Landau Equation With Conformable, Beta, and M-Truncated Derivatives: A Comparative Study, Advances in Difference Equations. (2020) 2020, no. 1, 1–19, https://doi.org/10.1186/s13662-020-03052-7.
10.1186/s13662-020-03052-7
PubMed Web of Science® Google Scholar
8 Yao S.-W., Zafar A., Urooj A., Tariq B., Shakeel M., and Inc M., Novel Solutions to the Coupled KdV Equations and the Coupled System of Variant Boussinesq Equations, Results in Physics. (2023) 45, https://doi.org/10.1016/j.rinp.2023.106249, 106249.
10.1016/j.rinp.2023.106249
Google Scholar
9 Shakeel M., Bibi A., Zafar A., and Sohail M., Solitary Wave Solutions of Camassa-Holm and Degasperis-Procesi Equations With Atangana’s Conformable Derivative, Computational and Applied Mathematics. (2023) 42, no. 2, https://doi.org/10.1007/s40314-023-02238-5.
10.1007/s40314-023-02238-5
Google Scholar
10 Henari F. Z. and Deen G. R., Green Synthesis of Noble Metal Nanoparticles: Nonlinear Optics and Applications, Journal of Optics and Photonics Research. (2023) https://doi.org/10.47852/bonviewJOPR42023911.
10.47852/bonviewJOPR42023911
Google Scholar
11 Feng L. L. and Zhu Z. N., Darboux Transformation and Soliton Solutions for a Nonlocal Two-Component Complex Modified Korteweg-de Vries Equation, Journal of Nonlinear Mathematical Physics. (2023) 30, no. 3, 1011–1031, https://doi.org/10.1007/s44198-023-00112-w.
10.1007/s44198-023-00112-w
Google Scholar
12 Charles S. and Natarajan J., Identification of Key Gene Modules and Novel Transcription Factors in Tetralogy of Fallot Using Machine Learning and Network Topological Features, Medinformatics. (2024) 1, no. 1, 27–34, https://doi.org/10.47852/bonviewMEDIN32021554.
10.47852/bonviewMEDIN32021554
Google Scholar
13 Rasool T., Hussain R., Rezazadeh H., and Gholami D., The Plethora of Exact and Explicit Soliton Solutions of the Hyperbolic Local (4 + 1)-Dimensional BLMP Model via GERF Method, Results in Physics. (2023) 46, 106298.
10.1016/j.rinp.2023.106298
Google Scholar
14 Li B.-Q. and Ma Y.-L., Optical Soliton Resonances and Soliton Molecules for the Lakshmanan–Porsezian–Daniel System in Nonlinear Optics, Nonlinear Dynamics. (2023) 111, no. 7, 6689–6699, https://doi.org/10.1007/s11071-022-08195-8.
10.1007/s11071-022-08195-8
Google Scholar
15 Li Z. and Huang C., Bifurcation, Phase Portrait, Chaotic Pattern and Optical Soliton Solutions of the Conformable Fokas-Lenells Model in Optical Fibers, Chaos, Solitons & Fractals. (2023) 169, https://doi.org/10.1016/j.chaos.2023.113237, 113237.
10.1016/j.chaos.2023.113237
Google Scholar
16 Zhang R.-F., Li M.-C., Cherraf A., and Vadyala S. R., The Interference Wave and the Bright and Dark Soliton for Two Integro-Differential Equation by Using BNNM, Nonlinear Dynamics. (2023) 111, no. 9, 8637–8646, https://doi.org/10.1007/s11071-023-08257-5.
10.1007/s11071-023-08257-5
Google Scholar
17 Wang K.-J., Diverse Soliton Solutions to the Fokas System via the Cole–-Hopf Transformation, Optik. (2023) 272, https://doi.org/10.1016/j.ijleo.2022.170250, 170250.
10.1016/j.ijleo.2022.170250
Google Scholar
18 Rasool T., Hussain R., Al Sharif M. A., Mahmoud W., and Osman M. S., A Variety of Optical Soliton Solutions for the M-Truncated Paraxial Wave Equation Using Sardar-Subequation Technique, Optical and Quantum Electronics. (2023) 55, no. 5, https://doi.org/10.1007/s11082-023-04655-6.
10.1007/s11082-023-04655-6
Google Scholar
19 Shakeel M., Bibi A., AlQahtani S. A., and Alawwad A. M., Dynamical Study of a Time Fractional Nonlinear Schrödinger Model in Optical Fibers, Optical and Quantum Electronics. (2023) 55, no. 11, https://doi.org/10.1007/s11082-023-05301-x.
10.1007/s11082-023-05301-x
Google Scholar
20 Wang K.-J., Si J., and Liu J.-H., Diverse Optical Soliton Solutions to the Kundu–Mukherjee–Naskar Equation via Two Novel Techniques, Optik. (2023) 273, https://doi.org/10.1016/j.ijleo.2022.170403, 170403.
10.1016/j.ijleo.2022.170403
Google Scholar
21 Hou T., Liu X., Li Z., Wang Y., Chen T., and Huang B., Numerical Investigation of Cavitation Induced Noise and Noise Reduction Mechanism for the Leading-Edge Protuberances, Applied Ocean Research. (2025) 154, https://doi.org/10.1016/j.apor.2024.104361, 104361.
10.1016/j.apor.2024.104361
Web of Science® Google Scholar
22 Gao W., Veeresha P., Prakasha D. G., Baskonus H. M., and Yel G., A Powerful Approach for Fractional Drinfeld–Sokolov–Wilson Equation With Mittag–Leffler Law, Alexandria Engineering Journal. (2019) 58, no. 4, 1301–1311, https://doi.org/10.1016/j.aej.2019.11.002.
10.1016/j.aej.2019.11.002
Web of Science® Google Scholar
23 Saifullah S., Ali A., Shah K., and Promsakon C., Investigation of Fractal Fractional Nonlinear Drinfeld–Sokolov–Wilson System with Non-Singular Operators, Results in Physics. (2022) 33, https://doi.org/10.1016/j.rinp.2021.105145, 105145.
10.1016/j.rinp.2021.105145
Google Scholar
24 Yao S.-W., Behera S., and Inc M., et al.Analytical Solutions of Conformable Drinfel’d–Sokolov–Wilson and Boiti Leon Pempinelli Equations via Sine-Cosine Method, Results in Physics. (2022) 42, https://doi.org/10.1016/j.rinp.2022.105990, 105990.
10.1016/j.rinp.2022.105990
Google Scholar
25 Li Y., Lu D., Arshad M., and Xu X., New Exact Traveling Wave Solutions of the Unstable Nonlinear Schrödinger Equations and Their Applications, Optik. (2021) 226, https://doi.org/10.1016/j.ijleo.2020.165386, 165386.
10.1016/j.ijleo.2020.165386
Google Scholar
26 Seadawy A. R., Arshad M., and Lu D., The Weakly Nonlinear Wave Propagation Theory for the Kelvin–Helmholtz Instability in Magnetohydrodynamics Flows, Chaos, Solitons & Fractals. (2020) 139, https://doi.org/10.1016/j.chaos.2020.110141, 110141.
10.1016/j.chaos.2020.110141
Google Scholar
27 Arshad M., Seadawy A. R., Tanveer M., and Yasin F., Study On Abundant Dust-Ion-Acoustic Solitary Wave Solutions of a (3 + 1)-Dimensional Extended Zakharov–Kuznetsov Dynamical Model in a Magnetized Plasma and Its Linear Stability, Fractal and Fractional. (2023) 7, no. 9, https://doi.org/10.3390/fractalfract7090691, 691.
10.3390/fractalfract7090691
Web of Science® Google Scholar
28 Arshad M., Umer M. A., Xu C., Almehizia A. A., and Yasin F., Exploring Conversation Laws and Nonlinear Dynamics of the Unstable Nonlinear Schrödinger Equation: Stability and Applications, Ain Shams Engineering Journal. (2025) 16, no. 1, https://doi.org/10.1016/j.asej.2024.103210, 103210.
10.1016/j.asej.2024.103210
Google Scholar
29 Ajmal M., Muhammad J., Younas U., Hussian E., El-Meligy M., and Sharaf M., Exploring the Gross-Pitaevskii Model in Bose-Einstein Condensates and Communication Systems: Features of Solitary Waves and Dynamical Analysis, International Journal of Theoretical Physics. (2025) 64, no. 3, 1–26, https://doi.org/10.1007/s10773-025-05937-3.
10.1007/s10773-025-05937-3
Google Scholar
30 Younas U., Muhammad J., Almutairi D. K., Khan A., and Abdeljawad T., Analyzing the Neural Wave Structures in the Field of Neuroscience, Scientific Reports. (2025) 15, no. 1, https://doi.org/10.1038/s41598-025-91397-y.
10.1038/s41598-025-91397-y
Google Scholar
31 Younas U., Muhammad J., Murad M. A. S., Almutairi D. K., Khan A., and Abdeljawad T., Investigating the Truncated Fractional Telegraph Equation in Engineering: Solitary Wave Solutions, Chaotic and Sensitivity Analysis, Results in Engineering. (2025) 25, https://doi.org/10.1016/j.rineng.2025.104489, 104489.
10.1016/j.rineng.2025.104489
Google Scholar
32 Younas U., Sulaiman T. A., Rahimzai A. A., Ismael H. F., Nasreen N., and Jhangeer A., Dynamics of Thermophoretic Waves in Graphene Sheets: On the Study of Interaction Phenomena, Discover Applied Sciences. (2025) 7, no. 3, https://doi.org/10.1007/s42452-024-06452-6.
10.1007/s42452-024-06452-6
Google Scholar
33 Younas U., Hussain E., Muhammad J., Sharaf M., and Meligy M. E., Chaotic Structure, Sensitivity Analysis and Dynamics of Solitons to the Nonlinear Fractional Longitudinal Wave Equation, International Journal of Theoretical Physics. (2025) 64, no. 2, https://doi.org/10.1007/s10773-025-05916-8.
10.1007/s10773-025-05916-8
Google Scholar
34 Ismael H. F., Sulaiman T. A., Nabi H. R., and Younas U., On the Study of Dynamical Wave’s Nature to Generalized (3 + 1)-Dimensional Variable-Coefficient Kadomtsev–Petviashvili Equation: Application in the Plasma and Fluids, Nonlinear Dynamics. (2025) 113, no. 3, 2653–2665.
10.1007/s11071-024-10338-y
Google Scholar
35 Çenesiz Y., Tasbozan O., and Kurt A., Functional Variable Method for Conformable Fractional Modified KdV-ZK Equation and Maccari System, Tbilisi Mathematical Journal, 2017, 10, no. 1, 117–125, https://doi.org/10.1515/tmj-2017-0010.
10.1515/tmj-2017-0010
Google Scholar
36 Zafar A., Shakeel M., Ali A., Akinyemi L., and Rezazadeh H., Optical Solitons of Nonlinear Complex Ginzburg–Landau Equation via Two Modified Expansion Schemes, Optical and Quantum Electronics. (2022) 54, no. 1, 1–15, https://doi.org/10.1007/s11082-021-03393-x.
10.1007/s11082-021-03393-x
Google Scholar
37 Saha D., Chatterjee P., and Raut S., Multi-Shock and Soliton Solutions of the Burgers Equation Employing Darboux Transformation With the Help of the Lax Pair, Pramana. (2023) 97, no. 2, https://doi.org/10.1007/s12043-023-02534-z.
10.1007/s12043-023-02534-z
Google Scholar
38 Fendzi-Donfack E., Temgoua G. W. K., Djoufack Z. I., Kenfack-Jiotsa A., Nguenang J. P., and Nana L., Exotical Solitons for an Intrinsic Fractional Circuit Using the Sine-Cosine Method, Chaos, Solitons & Fractals. (2022) 160, https://doi.org/10.1016/j.chaos.2022.112253, 112253.
10.1016/j.chaos.2022.112253
Google Scholar
39 Ghayad M. S., Badra N. M., Ahmed H. M., and Rabie W. B., Derivation of Optical Solitons and Other Solutions for Nonlinear Schrödinger Equation Using Modified Extended Direct Algebraic Method, Alexandria Engineering Journal. (2023) 64, 801–811, https://doi.org/10.1016/j.aej.2022.10.054.
10.1016/j.aej.2022.10.054
Google Scholar
40 Khatun M. A., Arefin M. A., Akbar M. A., and Uddin M. H., Numerous Explicit Soliton Solutions to the Fractional Simplified Camassa–Holm Equation Through Two Reliable Techniques, Ain Shams Engineering Journal. (2023) 14, no. 12, https://doi.org/10.1016/j.asej.2023.102214, 102214.
10.1016/j.asej.2023.102214
Google Scholar
41 Khatun M. A., Arefin M. A., Islam M. Z., Akbar M. A., and Uddin M. H., New Dynamical Soliton Propagation of Fractional Type Couple Modified Equal-Width and Boussinesq Equations, Alexandria Engineering Journal. (2022) 61, no. 12, 9949–9963, https://doi.org/10.1016/j.aej.2022.03.033.
10.1016/j.aej.2022.03.033
Google Scholar
42 Yin T., Xing Z., and Pang J., Modified Hirota Bilinear Method to (3 + 1)-D Variable Coefficients Generalized Shallow Water Wave Equation, Nonlinear Dynamics, 2023, 111, 1–12, https://doi.org/10.1007/s11071-023-08356-3.
Google Scholar
43 Tang W., Soliton Dynamics to the Higgs Equation and Its Multi-Component Generalization, Wave Motion. (2023) 120, https://doi.org/10.1016/j.wavemoti.2023.103144, 103144.
10.1016/j.wavemoti.2023.103144
Google Scholar
44 Canzian E. P., Santiago F., Lopes A. B., Barbosa M. R., and Barañano A. G., On the Application of the Double Integral Method With Quadratic Temperature Profile for Spherical Solidification of Lead and Tin Metals, Applied Thermal Engineering. (2023) 219, https://doi.org/10.1016/j.applthermaleng.2022.119528, 119528.
10.1016/j.applthermaleng.2022.119528
CAS Google Scholar
45 Biswas A., Mirzazadeh M., Eslami M., Zhou Q., Bhrawy A., and Belic M., Optical Solitons in Nano-Fibers With Spatio-Temporal Dispersion by Trial Solution Method, Optik. (2016) 127, no. 18, 7250–7257, https://doi.org/10.1016/j.ijleo.2016.05.052, 2-s2.0-84990898407.
10.1016/j.ijleo.2016.05.052
Web of Science® Google Scholar
46 Zafar A., Shakeel M., Ali A., Rezazadeh H., and Bekir A., Analytical Study of Complex Ginzburg–Landau Equation Arising in Nonlinear Optics, Journal of Nonlinear Optical Physics & Materials. (2023) 32, no. 1, https://doi.org/10.1142/S0218863523500108, 2350010.
10.1142/S0218863523500108
Google Scholar
47 Arefin M. A., Khatun M. A., Uddin M. H., and Inc M., Investigation of Adequate Closed Form Travelling Wave Solution to the Space-Time Fractional Non-Linear Evolution Equations, Journal of Ocean Engineering and Science. (2022) 7, no. 3, 292–303, https://doi.org/10.1016/j.joes.2021.08.011.
10.1016/j.joes.2021.08.011
Google Scholar
48 Uddin M. H., Khan M. A., Akbar M. A., and Haque M. A., Analytical Wave Solutions of the Space Time Fractional Modified Regularized Long Wave Equation Involving the Conformable Fractional Derivative, Karbala International Journal of Modern Science. (2019) 5, no. 1, https://doi.org/10.33640/2405-609X.1010.
10.33640/2405-609X.1010
Google Scholar
49 Uddin M. H., Akbar M. A., Khan M. A., and Haque M. A., Families of Exact Traveling Wave Solutions to the Space Time Fractional Modified KdV Equation and the Fractional Kolmogorov–Petrovskii–Piskunovequation, Journal of Mechanics of Continua and Mathematical Sciences. (2018) 13, no. 1, 17–33, https://doi.org/10.26782/jmcms.2018.04.00002.
10.26782/jmcms.2018.04.00002
Google Scholar
50 Raza N. and Rafiq M. H., Abundant Fractional Solitons to the Coupled Nonlinear Schrödinger Equations Arising in Shallow Water Waves, International Journal of Modern Physics B. (2020) 34, no. 18, https://doi.org/10.1142/S0217979220501623, 2050162.
10.1142/S0217979220501623
Google Scholar
51 Rizvi S. T. R., Seadawy A. R., and Mustafa B., Discussion On Chirped Periodic and Optical Soliton Solutions for Chiral Nonlinear Schrödinger Dynamical Equation With Bohm Potential, Optical and Quantum Electronics. (2024) 56, no. 5, https://doi.org/10.1007/s11082-024-06658-3.
10.1007/s11082-024-06658-3
Google Scholar
52 Biswas A. and Milovic D., Chiral Solitons With Bohm Potential by Hes Variational Principle, Physics of Atomic Nuclei. (2011) 74, no. 5, 755–757, https://doi.org/10.1134/S1063778811050048, 2-s2.0-79957660983.
10.1134/S1063778811050048
CAS Google Scholar
53 Younis M., Cheemaa N., Mahmood S. A., and Rizvi S. T. R., On Optical Solitons: The Chiral Nonlinear Schrödinger Equation With Perturbation and Bohm Potential, Optical and Quantum Electronics. (2016) 48, no. 12, 1–14, https://doi.org/10.1007/s11082-016-0809-2, 2-s2.0-84996497348.
10.1007/s11082-016-0809-2
Google Scholar
54 Ebadi G., Yildirim A., and Biswas A., Chiral Solitons With Bohm Potential Using G’/G Method and Exp-Function Method, Romanian Reports in Physics. (2012) 64, no. 2, 357–366.
Google Scholar
55 Kudryashov N. A., The Painlevé Approach for Finding Solitary Wave Solutions of Nonlinear Nonintegrable Differential Equations, Optik. (2019) 183, 642–649, https://doi.org/10.1016/j.ijleo.2019.02.087, 2-s2.0-85062330102.
10.1016/j.ijleo.2019.02.087
Google Scholar

All articles

Optical Soliton Structure Solutions, Sensitivity, and Modulation Stability Analysis in the Chiral Nonlinear Schrödinger Equation With Bohm Potential

Abstract

1. Introduction

2. The Summary of GERF Method

3. Mathematical Analysis

4. Summary of PP Approach

5. Implementation of PP Approach on CNLSE-BP

6. Results and Discussion

6.1. Sensitivity Analysis

6.2. Modulation Stability

7. Conclusion

Conflicts of Interest

Author Contributions

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Optical Soliton Structure Solutions, Sensitivity, and Modulation Stability Analysis in the Chiral Nonlinear Schrödinger Equation With Bohm Potential

Abstract

1. Introduction

2. The Summary of GERF Method

3. Mathematical Analysis

4. Summary of PP Approach

5. Implementation of PP Approach on CNLSE-BP

6. Results and Discussion

6.1. Sensitivity Analysis

6.2. Modulation Stability

7. Conclusion

Conflicts of Interest

Author Contributions

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information