In this paper, a numerical scheme for a time-dependent singularly perturbed parabolic convection–diffusion problem with boundary turning points is presented. The problem exhibits a left boundary layer in the spatial domain. We use the Crank–Nicolson method for temporal discretization and a nonstandard finite difference approach for spatial discretization on uniform meshes. Through rigorous error analysis, it has been shown that the scheme is stable and parameter-uniform convergence with a second-order accuracy in time and a first-order accuracy in space. Three model examples are provided to show the applicability of the scheme. It is shown that the numerical results are in agreement with the theoretical findings.

1. Introduction

Time-dependent singularly perturbed parabolic convection–diffusion equations are partial differential equations (PDEs) with the small parameter ε(0 < ε ≪ 1) multiplying the highest derivative term in the PDEs which leads to a stiff behaviour in a certain region of the solution domain. These types of problems arise in the drift–diffusion equation of semiconductor device [1], thermal boundary layers in the laminar flow [2], modelling of transport phenomena [3] and heat flow [4]. It is well-known that the numerical methods using standard finite difference operators on uniform mesh for boundary layer problems give unsatisfactory results of the exact solution unless very fine mesh is used in the approximation process [5]. However, this approach increases the round-off error and the computational cost. These side effects motivated the development of a suitable numerical method whose convergence to the exact solution is independent of the perturbation parameter ε. Some of the parameter uniform convergence numerical methods are fitted operator approach, fitted mesh approach, grid equi-distribution approach and domain decomposition approach. Related to these, one can refer the survey articles on the singularly perturbed parabolic differential equations with boundary turning points [6–14], and the singularly perturbed delay, and the nondelay problem with different boundary conditions [15–33] whose solutions are convergent to the exact solution independent of the perturbation parameter.

Kumari, Kumar and Calle [10] considered singularly perturbed problems including boundary turning points of multiplicity greater than or equal to one. They proposed a numerical scheme comprising the Crank–Nicolson finite difference method in the temporal direction and an upwind finite difference method on Shishkin mesh in the spatial direction. They analysed the scheme for convergent and obtained a second-order accuracy in time and a first-order accuracy in space. Yadav, Rai and Sharma [11] proposed a numerical scheme comprising an implicit finite difference method for time discretization on a uniform mesh and a hybrid scheme for spatial discretization on a generalized Shishkin mesh for solving singularly perturbed parabolic turning point problems. They analysed the method for convergence and obtained second-order accuracy in space except for a logarithm factor and a first-order accuracy in time. These authors used the Richardson extrapolation technique to increase the order of convergence in the time direction. Sahoo and Gupta [12] had developed a first-order ε-uniform convergent scheme for solving singularly perturbed parabolic problems with a boundary turning point. They discretized the time variable using the implicit Euler method on uniform mesh and a simple upwind scheme on piece-wise uniform mesh in space variable. These authors used the Richardson extrapolation technique to increase the order of convergence in both directions. Majumdra and Natesan [13] proposed an ε-uniform hybrid numerical scheme for a singularly perturbed degenerate parabolic convection–diffusion problem consisting of implicit-Euler finite difference method on uniform mesh in temporal direction and the hybrid finite difference method, which is a combination of central difference and midpoint upwind schemes on piece-wise uniform shishkin mesh in spatial direction. They derived the error estimates and obtained ε-uniform convergent of almost a second-order accuracy (up to a logarithmic factor) in space and a first-order accuracy in time.

One can see [34, 35] for more details of existing literature on asymptotic analysis and numerical methods for the turning point problems.

As we observed, the developed schemes enumerated above used the fitted mesh method for solving the problem of type in [10], which requires prior knowledge about the location and width of the boundary layer. Sometimes, this requirement is difficult to be satisfied.

Mbroh and Munyakazi [36] proposed a robust numerical method for solving one- and two-dimensional singularly perturbed parabolic reaction–diffusion problems via method of lines. They discretized first the space variable using fitted operator finite difference method and then integrated in time with the Crank–Nicolson finite difference method. These authors established a second-order accuracy both in time and in space. Ayele, Tiruneh and Derese [37] proposed a numerical scheme to solve singularly perturbed space delay parabolic problem of convection–diffusion type using Crank–Nicolson method in time variable and nonstandard fitted operator method in space variable. Tiruneh, Derese and Tefera [38] proposed a second-order accuracy nonstandard fitted operator numerical scheme to solve singularly perturbed time delay parabolic problem of reaction–diffusion type. Hassen, Duressa and Liu [15] proposed parameter-uniformly convergent numerical method for singularly perturbed delay parabolic convection–diffusion problems using Crank–Nicolson method in time and fitted operator up wind finite difference method in space by applying zeroth-order asymptotic expansion of the exact solution and they have got first order convergence in space and second order convergence in time. Hailu and Duressa [20] proposed parameter-uniformly convergent numerical scheme using Crank–Nicolson finite difference method for the temporal direction and the nonstandard finite difference scheme for the spatial direction on uniform meshes. The Simpson’s integration rule is used to handle the integral boundary condition. They used Richardson extrapolation technique to enhance the order of convergence of the spatial variable. Kumie et al. [22] proposed a first-order numerical scheme to solve time-fractional singularly perturbed delay PDEs using Crank–Nicolson method in time and nonstandard finite difference method in space. Woldaregay and Duressa [39] proposed parameter-uniformly convergent numerical schemes using the nonstandard finite difference method on uniform and Shishkin meshes in space and the Crank–Nicolson method on uniform mesh in time for solving the singularly perturbed convection–diffusion–reaction equation. The schemes on uniform mesh showed better accuracy and order of convergence than Shishkin mesh. Motivated by the work of [20, 22, 39], we aimed to develop and analyse a parameter uniform fitted operator numerical scheme based on the exact finite difference method [40] to solve singularly perturbed parabolic convection–diffusion problem with multiple boundary turning points that does not require the location and width of boundary layer. This approach is also advantageous for easily solving singularly perturbed nonlinear problems and can extend to higher dimensions.

The purpose of this paper is to construct and analyse a numerical scheme that has a better accuracy for solving singularly perturbed parabolic convection–diffusion problems with multiple boundary turning points. We proposed a method of line consisting of Crank–Nicolson method in time and the nonstandard finite difference method in space with uniform meshes to solve the problem of concern. Theoretically, we showed that the proposed scheme has accuracy O(M⁻² + N⁻¹), where N and M are the number of mesh intervals in space and in time, respectively.

Throughout this article, C denotes a generic positive constant independent of ε and the mesh parameters. All the functions defined on the domain W = ⊖×(0, T], ⊖ = (0, 1), T > 0 are measured in maximum norm as

The boundary of the domain is

, where

2. Properties of Continuous Problem

Consider the following time-dependent singularly perturbed parabolic convection–diffusion initial-boundary value problem on W = ⊖×(0, T], ⊖ = (0, 1), T > 0 with smooth boundary

()

where

()

such that a₀(x, t), b(x, t) and f(x, t) are smooth and bounded in

and ψ, ϕ and u₀ are smooth and bounded on ∂W where 0 < ε ≪ 1 is the singularly perturbed parameter. Problems of Equation (1) are called singularly perturbed turning point problem, and the point x = 0 is the turning point since the coefficient of convection term is zero at this point. For p > 1, the problem in Equation (1) is called the multiple boundary turning point problem. Otherwise, it is a simple boundary turning point problem. Setting ε = 0 in Equations (1) and (2) gives the reduced problem:

which is the first-order hyperbolic PDE along with initial and boundary conditions:

Since only one boundary condition is needed to solve this reduced problem, one boundary condition will be underutilized, resulting in boundary layer in that neighbourhood. The convective term is positive over the domain W, as you can see. The boundary layer will therefore be found close to x = 0. According to Kumari, Kumar and Calle [10], the layer’s width is expressed as .

Let u₀(x) ∈ C²[0, 1], ψ, ϕ ∈ C¹[0, T], and we impose the compatibility conditions:

()

and

()

so that the data match at the two corners (0, 0) and (1, 0). These assumptions ensure that there exist a constant C such that

()

Lemma 1. The bound on the solution u(x, t) of the continuous problem in Equation (1) is given by

Proof. From Equation (5), we have

Now,

Which implies that

Since t ∈ [0, T] and u₀(x) is bounded, it gives

Lemma 2 The minimum principle. Let ϝ(x, t) be a sufficiently smooth function defined on W which satisfies ϝ(x, t) ≥ 0, ∀(x, t) ∈ ∂W and Then

Proof. Let the point and Since ϝ(x, t) ≥ 0, ∀(x, t) ∈ ∂W, we have (y, z) ∉ ∂W. The inequality implies that , and Giving that

which contradict the assumption that

≤0, ∀(x, t) ∈ W.

Therefore,

Lemma 3 Stability estimate. Suppose u(x, t) be the solution of Equation (1), then it satisfies

Proof. Consider the barrier functions

On the boundary points,

And in the interior points,

Using Lemma 2,

This implies that

Theorem 1. Under the compatibility conditions of Equations (3) and (4), the problem in Equation (1) satisfies the following bounds for 0 ≤ i + 3j ≤ 4:

Proof. For the proof, refer in [2, 7, 41].

3. Formulation of the Numerical Scheme

To obtain the full discrete scheme, first discretize the time variable using Crank–Nicolson method with uniform mesh and then apply nostandard finite difference technique [40] in space variable.

3.1. Temporal Discretization

We discretize the time domain [0, T] using uniform mesh with step length k by

()

where M is the number of mesh intervals in the temporal discretization. Now, using the Crank–Nicolson method, we have

()

where

The time semidiscretized problem in Equation (8) can be rewritten as

()

where

The operator

satisfies the following semidiscrete minimum principle.

Lemma 4 Minimum principle for temporal discretization. Suppose ϝ^j+1(x) be the smooth function satisfying ϝ^j+1(0) ≥ 0, ϝ^j+1(1) ≥ 0 and Then and j = 0, 1, 2, …M − 1.

Proof. Let ℓ ∈ ⊖ such that ϝ^j+1(ℓ) = minϝ^j+1(x) < 0, ∀x ∈ ⊖, which implies that and .

Then, we have

since

This contradict the assumption that . Therefore, ϝ^j+1(x)≥ 0 on

Lemma 5. If u^j+1(0) ≥ 0 and u^j+1(1) ≥ 0, then

Proof. The proof is similar to the proof in [42].

The local error of the time semidiscretization method in Equation (8) is given by e_j+1 ≡ u(x, t_j+1) − U^j+1(x), where U^j+1(x) is the solution obtained after one step by taking the exact value u(x, t_j) instead of U^j(x) as the starting data. Concretely, we have

()

subject to the initial boundary conditions

where

Theorem 2. Suppose that

The local truncation error at (j + 1)^th time step is given by

Proof. Using Taylor series expansion, we have

()

Subtracting Equation (11) from Equation (12), we have

where

etc.

Further simplification yields

()

From Equations (10) and (13), the local truncation error satisfies

()

Then, Lemma 5 gives the required result.

The local error estimate of each time step contributes to the global error in the temporal semidiscretization which is denoted by E_j.

Theorem 3. The global truncation error for temporal discretization up to j^th time level is given by

Proof. Using the local error estimate up to the j^th time step, we obtain the global error estimate at the j^th time step:

3.2. Spatial Discretization

For the spatial derivative approximations, the procedures of nonstandard finite difference approximations stated in [40] are used. The spatial domain

is discretized using uniform space length h as

()

where N is the number of mesh intervals in the spatial discretization. Now, consider Equation (9) using the lower bounds of the coefficients and the homogeneous part:

()

According to Ayele, Tiruneh and Derese [37], the layer behaviour of Equations (16) and (17) is the same. The finite difference scheme that replaced h² by a non-negative denominator function ξ² is

()

We can find

using the following procedures. First, we rewrite Equation (17) equivalently as a first-order coupled system of differential equations:

()

From Equation (20), we have

By applying the first-order difference scheme for Equation (19), we have the following:

()

then substituting Equations (21) into (18), we obtain the denominator function

. So Equation (18) becomes

Therefore, the denominator function

can replace h².

Adopting this denominator function to the variable coefficient problem written as

()

where

is a function of

Using Equations (22) and (9), the full discrete scheme is

()

where

After rearranging the terms in Equation (23), we arrive the following recurrence relation of the form

()

where the coefficients are given by

Since

the tridiagonal system in Equation (24) is a diagonally dominant system of equations. So it has a unique solution. Thus, we can use any tridiagonal solver, such as Thomas algorithm, to solve this system of equations.

4. Stability and Uniform Convergence Analysis

In this section, we study the discrete minimum principle, stability and ε uniform convergence for the scheme in Equation (23).

Lemma 6 The discrete minimum principle. The operator defined by discrete scheme in Equation (23) satisfies the discrete minimum principle. That is, let be any mesh function satisfying and ∀i = 1, 2, …, N − 1. Then

Proof. Suppose there exist s ∈ {0, 1, 2, …, N} such that which implies k ≠ 0 and k ≠ N. Also we have and Then,

since

It contradict the assumption that

for 0 < i < N, 0 ≤ j < M.

Therefore, the operator satisfies the discrete minimum principle.

Lemma 7. The solution of the discrete problem in Equation (23) satisfies the bound

Proof. Consider the barrier functions

Using the boundary points, we have

For the interior points, we have

Using Lemma 6, we have ð^±(x_i, t_j+1) ≥ 0. This implies that

Lemma 8. For ε → 0 and for fixed mesh, it holds

Proof.

Let and then

Applying L’Hospitals rule repeatedly, we have

And

Let and then using L’Hospital’s rule repeatedly, we have the following:

Therefore, for σ ∈ (0, ∞).

Theorem 4. Let U^j+1(x_i) and are the solutions of Equations (8) and (23), respectively, and then the error bounds at (j + 1)^th time level are given by

Proof. The truncation error in the spatial discretization is

where

Now, using Taylor series expansion and Theorem 1, we have the following:

Using Lemmas 7 and 8, we have

Theorem 5. The solution of the fully discrete scheme in Equation (23) converges uniformly to the solution u(x_i, t_j+1) of Equation (1), and the error estimate is given by

Proof. The uniform convergence of the scheme follows from Theorems 3 and 4.

We justify it as follows:

5. Numerical Results and Discussion

In this section, we present numerical results in the form of tables and graphs to validate the proposed scheme in Equation (23) using MATLAB2015a software package. We considered three numerical examples to verify the applicability of the scheme.

Example 1. Consider the singularly perturbed multiple boundary turning point problem [9]:

The source function f(x, t) and the boundary function g(x, t) can be obtained from the exact solution:

Example 2. Consider singularly perturbed multiple boundary turning point problem in [10]:

Example 3. Consider the singularly perturbed multiple boundary turning points problem in [7]:

For each ε, the maximum absolute errors are used to measure the accuracy of the method. Since the exact solution of Equation (1) is known, we can find the maximum point-wise errors using the following formula:

Since the exact solution of Equations (2) and (3) are not available, the double mesh principle is used to find the maximum point-wise error:

The corresponding rate of convergence is

Furthermore, ε-uniform point-wise error is defined by

and its corresponding ε-uniform rate of convergence is

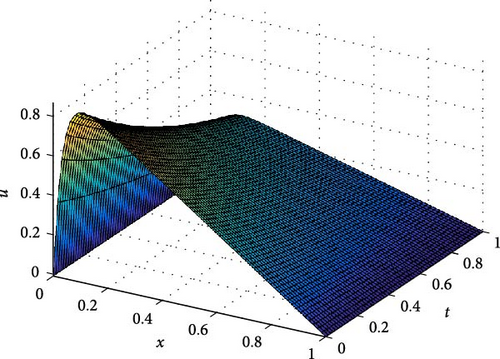
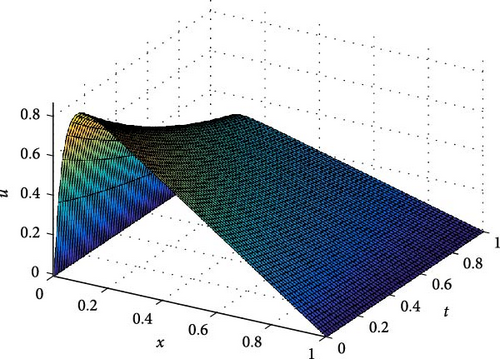
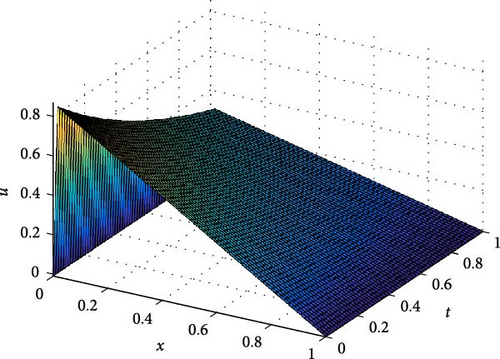
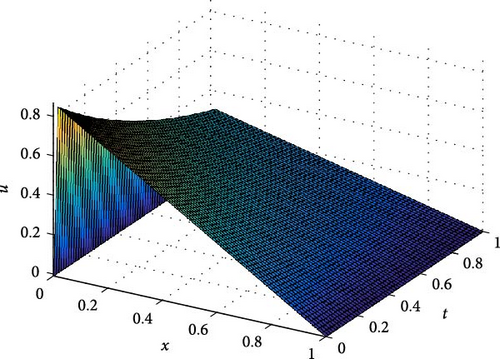
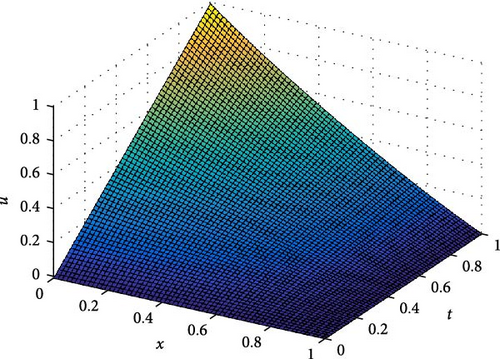
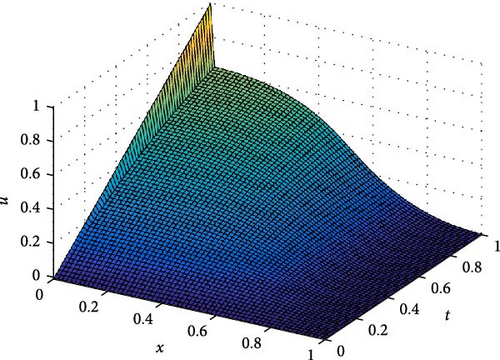
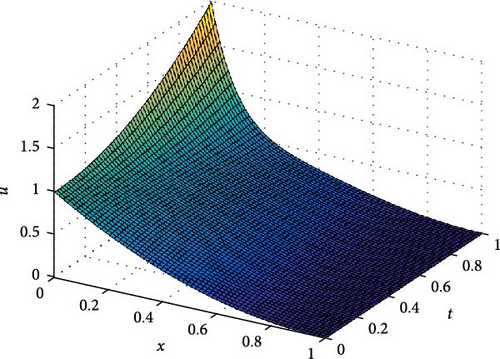
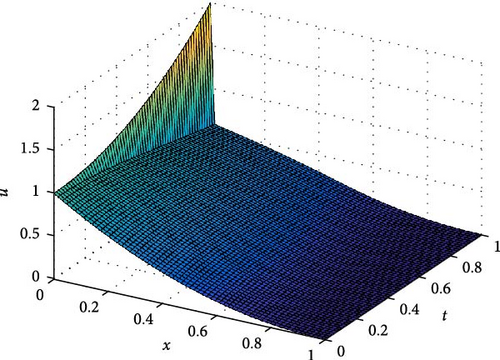
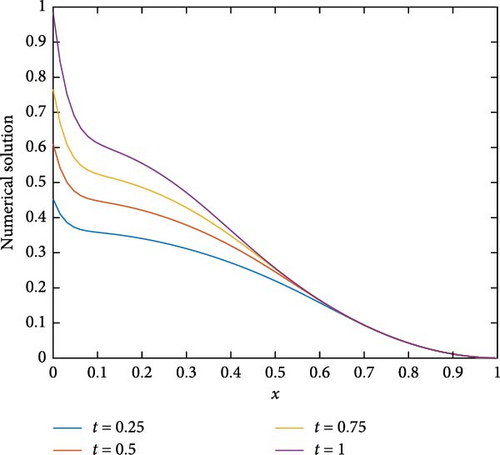
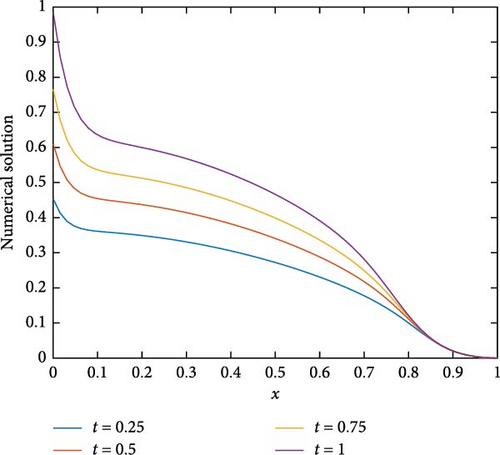
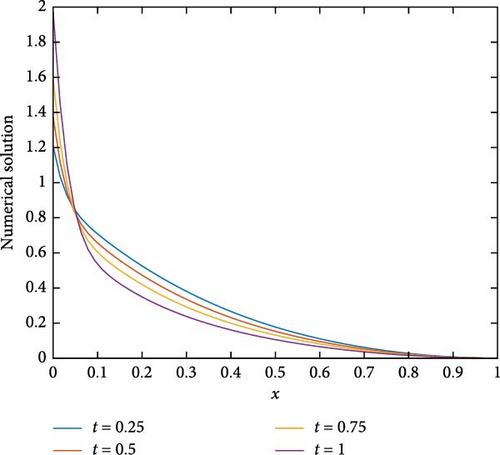
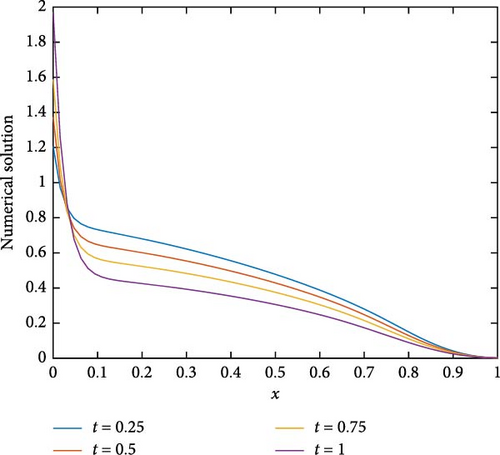
The maximum absolute errors and the rate of convergence of the proposed method for Example 1 at p = 1 are displayed in Table 1. From this table, it is observed that for fixed mesh parameters as the singular perturbation parameter ε decreases to zero, the maximum absolute error is constant, and as the mesh parameter increases, the maximum absolute error decreases. This indicates that the proposed method is ε-uniform convergence. Parameter uniform error and its rate of convergence for Example 1 using different values of p are displayed in Table 2. From the results in this table, it can be observed that the error bound is also independent of p and its order of convergence is first order. Further, Tables 3–5 are displayed to compare the proposed method with the methods in [10] and [7] using model Examples 2 and 3, respectively. From the displayed results, it is shown that the proposed method has better accuracy and order of convergence than the existing different schemes in the literature. Surface plots for each example are displayed using Figures 1–3 for different singular perturbation parameters. The displayed figures show that the solution of the problems exhibits a left boundary layer in the spatial domain. As ε → 0, the thickness of the boundary layer decreases. Also, the numerical solution profiles for different time levels at a fixed ε for Examples 2 and 3 are displayed in Figures 4 and 5, respectively, for different values of p to show the effect of p on the solution.

Table 1. Maximum absolute error and rate of convergence for Example 1 for p = 1.

ε↓M = N→	32	64	128	256	512
2⁻⁰	8.8304e−04	4.5397e−04	2.3010e−04	1.1583e−04	5.8110e−05
2⁻⁰	0.9599	0.9803	0.9903	0.9951	—

2⁻²	1.4197e−03	7.5125e−04	3.8591e−04	1.9552e−04	9.8397e−05
2⁻²	0.9182	0.9610	0.9810	0.9906	—

2⁻⁴	4.0702e−03	2.1042e−03	1.0685e−03	5.3822e−04	2.7009e−04
2⁻⁴	0.9518	0.9777	0.9893	0.9948	—

2⁻⁶	5.2903e−03	2.7155e−03	1.3726e−03	6.8965e−04	3.4562e−04
2⁻⁶	0.9621	0.9843	0.9930	0.9967	—

2⁻⁸	5.3771e−03	2.7809e−03	2.7727e−04	7.0952e−04	3.5565e−04
2⁻⁸	0.9513	0.9791	0.9915	0.9964	—

2⁻¹⁰	5.3773e−03	2.7828e−03	1.4144e−03	7.1277e−04	3.5763e−04
2⁻¹⁰	0.9503	0.9764	0.9887	0.9950	—

2⁻¹²	5.3773e−03	2.7828e−03	1.4144e−03	7.1277e−04	3.5763e−04
2⁻¹²	0.9503	0.9764	0.9887	0.9950	—

e^N,M	5.3773e−03	2.7828e−03	1.4144e−03	7.1277e−04	3.5763e−04

p^N,M	0.9503	0.9764	0.9887	0.9950	—

Table 2. ε–uniform absolute error and rate of convergence for Example 1 for different values of p.

p↓M = N→	32	64	128	256	512
2	5.3653e−03	2.7814e−03	1.4142e−03	7.1286e−04	3.5785e−04
2	0.9479	0.9758	0.9883	0.9943	—

3	5.3530e−03	2.7799e−03	1.4140e−03	7.1283e−04	3.5785e−04
3	0.9453	0.9752	0.9882	0.9942	—

4	5.3402e−03	2.7784e−03	1.4139e−03	7.1281e−04	3.5784e−04
4	0.9426	0.9746	0.9880	0.9942	—

5	5.3271e−03	2.7769e−03	1.4137e−03	7.1279e−04	3.5784e−04
5	0.9399	0.9740	0.9879	0.9942	—

Table 3. Comparison of

for Example 2 when p = 1.

ε↓M = N→		32	64	128	256	512
2⁻⁰	PM	1.0391e−04	2.5380e−05	6.3168e−06	1.5785e−06	3.9456e−07
	PM	2.0336	2.0064	2.0006	2.0002	—
	Method in [10]	5.16e−04	2.69e−04	1.38e−04	6.95e−05	3.49e−05
	Method in [10]	0.94	0.96	0.99	0.99	—

2⁻⁴	PM	3.5367e−04	8.8881e−05	2.2251e−05	5.5648e−06	1.3913e−06
	PM	1.9925	1.9980	1.9994	1.9999	—
	Method in [10]	6.42e−03	2.56e−03	9.98e−04	4.09e−04	1.79e−04
	Method in [10]	1.33	1.36	1.29	1.19	—

2⁻⁸	PM	4.3765e−03	1.5863e−03	4.5374e−04	1.1789e−04	2.9767e−05
	PM	1.4642	1.8057	1.9445	1.9856	—
	Method in [10]	1.22e−02	5.68e−03	2.704e−03	1.31e−03	6.73e−04
	Method in [10]	1.10	1.07	1.04	0.96	0.98

2⁻¹²	PM	4.9556e−03	2.6327e−03	1.3661e−03	6.8706e−04	3.0147e−04
	PM	0.9125	0.9464	0.9916	1.1884	—
	Method in [10]	1.24e−02	5.98e−03	2.92e−03	1.58e−03	8.37e−04
	Method in [10]	1.05	1.03	0.89	0.92	—

2⁻²⁰	PM	4.9556e−03	2.6327e−03	1.3664e−03	6.9824e−04	4.0519e−04
	PM	0.9125	0.9461	0.9686	0.7851	—
	Method in [10]	1.24e−02	5.99e−03	2.94e−03	1.60e−03	8.57e−04
	Method in [10]	1.05	1.03	0.88	0.90	—

2⁻³²	PM	4.9556e−03	2.6327e−03	1.3664e−03	6.9824e−04	4.0519e−04
	PM	0.9125	0.9461	0.9686	0.9820	—
	Method in [10]	1.24e−02	5.99e−03	2.94e−03	1.60e−03	8.57e−04
	Method in [10]	1.05	1.03	0.88	0.90	—

e^N,M	PM	4.9556e−03	2.6327e−03	1.3664e−03	6.9824e−04	4.0519e−04
e^N,M	PM	0.9125	0.9461	0.9686	0.9820	—

e^N,M	Method in [10]	1.24e−02	5.99e−03	2.94e−03	1.60e−03	8.57e−04
e^N,M	Method in [10]	1.05	1.03	0.88	0.90	—

Table 4. Comparison of maximum absolute error and rate of convergence for Example 2 for ε = 2⁻¹⁰ with different values of p.

p↓M = N→	32	64	128	256	512
Proposed method

2	4.8802e−03	2.5150e−03	1.2743e−03	6.4108e−04	3.2150e−04
2	0.9564	0.9809	0.9911	0.9957	—
4	4.5478e−03	2.3839e−03	1.2162e−03	6.1380e−04	3.0827e−04
4	0.9319	0.9709	0.9866	0.9935	—
6	3.9892e−03	2.1621e−03	1.1179e−03	2.9815e−04	9.8769e−05
6	0.8836	0.9517	0.9779	0.9918	—

Method in [10]

2	1.11e−02	5.56e−03	3.07e−03	1.69e−03	8.96e−04
2	1.00	0.86	0.86	0.92	—
4	1.11e−02	5.59e−03	3.26e−03	1.81e−03	9.60e−04
4	0.99	0.78	0.85	0.91	—
6	1.11e−02	5.86e−03	3.30e−03	1.81e−03	9.53e−04
6	0.92	0.83	0.87	0.93	—

Table 5. Comparison of maximum absolute error and rate of convergence for Example 3 for different values of p.

p↓M = N→	32	64	128	256	512
PM for e^N,M and p^N,M (ε—uniform errors)

1	4.2861e−03	2.2276e−03	1.1347e−03	5.7213e−04	2.8721e−04
1	0.9442	0.9732	0.9879	0.9942	—
2	3.5515e−03	1.9370e−03	1.0293e−03	5.3742e−04	2.7716e−04
2	0.8746	0.9121	0.9375	0.9553	—
3	3.9398e−03	2.1777e−03	1.1643e−03	6.0914e−04	3.1418e−04
3	0.8553	0.9034	0.9346	0.9552	—
4	4.1942e−03	2.3380e−03	1.2558e−03	6.5790e−04	3.3948e−04
4	0.8431	0.8968	0.9326	0.9545	—
5	4.3430e−03	2.4465e−03	1.3185e−03	6.9270e−04	3.5760e−04
5	0.8280	0.8919	0.9285	0.9539	—

Method in [7] for ε = 2⁻¹⁵

1	1.6983e−02	1.0060e−02	5.8145e−03	3.3187e−03	1.8729e−03
1	0.7554	0.7901	0.8090	0.8254	—
2	5.2597e−03	3.1615e−03	1.7846e−03	9.5309e−04	4.9762e−04
2	0.7344	0.8250	0.9049	0.9376	—
3	6.0131e−03	3.5487e−03	2.0113e−03	1.0731e−03	5.6104e−04
3	0.7608	0.8192	0.9063	0.9356	—
4	6.7491e−03	3.94871e−03	2.1852e−03	1.1564e−03	6.0515e−04
4	0.7733	0.8536	0.9181	0.9342	—
5	7.3137e−03	4.2306e−03	2.3353e−03	1.2144e−03	6.3693e−04
5	0.8797	0.8572	0.9434	0.9311	—

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Surface plots of the solution with N = M = 64 for Example 1 at p = 1. (a) numerical solution for ε = 2⁻¹⁰; (b) exact solution for ε = 2⁻¹⁰; (c) numerical solution for ε = 2⁻³⁰; and (d) exact solution for ε = 2⁻³⁰.

6. Conclusion

Singularly perturbed convection–diffusion parabolic PDE with multiple boundary turning point problems is considered. The stiffness of this problem is due to the existence of a boundary turning point and the singular perturbation parameter ε. The solution of the considered problem exhibits a left boundary layer on the spatial domain. We developed a numerical scheme to solve this problem using Crank–Nicolson in time and nonstandard finite difference method in space with uniform meshes. The solution behaviour on the perturbation parameter is displayed using figures and tables. These results proved that the proposed scheme is stable and parameter uniform convergence with second-order accuracy in time- and first-order accuracy in space, and the error bound is independent of p. This analysis is also valid for p = 0, but the solution behaviour on the layer region is different from the considered problem. The numerical solution of the considered model examples agreed with the theoretical findings. The proposed method can be extended to solve singularly perturbed parabolic turning point problems with an interior layer and higher dimensions.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research work does not have any financial support.

Open Research

Data Availability Statement

No external data are used in this article.

References

1 Polak S. J., Den Heijer C., Schilders W. H. A., and Markowich P., Semiconductor Device Modelling From the Numerical Point of View, International Journal for Numerical Methods in Engineering. (1987) 24, no. 4, 763–838, https://doi.org/10.1002/nme.1620240408.
10.1002/nme.1620240408
Web of Science® Google Scholar
2 Vulanović R. and Farrell P. A., Continuous and Numerical Analysis of a Multiple Boundary Turning Point Problem, SIAM Journal on Numerical Analysis. (1993) 30, no. 5, 1400–1418, https://doi.org/10.1137/0730073.
10.1137/0730073
Web of Science® Google Scholar
3 Shishkin G. I., Grid Approximations to Singularly Perturbed Parabolic Equations With Turning Points, Differential Equations. (2001) 37, no. 7, 1037–1050, https://doi.org/10.1023/A:1011978225750.
10.1023/A:1011978225750
Google Scholar
4 Hanks T. C., Model Relating Heat-Flow Values Near, and Vertical Velocities of Mass Transport Beneath, Oceanic Rises, Journal of Geophysical Research. (1971) 76, no. 2, 537–544, https://doi.org/10.1029/JB076i002p00537.
10.1029/JB076i002p00537
Web of Science® Google Scholar
5 Farrell P. A., Hegarty A. F., Miller J. J. H., O’Riordan E., and Shishkin G. I., Robust Computational Techniques for Boundary Layers, 2000, Chapman & Hall/CRC, Boca Raton, Florida.
10.1201/9781482285727
Google Scholar
6 Rai P. and Yadav S., Robust Numerical Schemes for Singularly Perturbed Delay Parabolic Convection-Diffusion Problems With Degenerate Coefficient, International Journal of Computer Mathematics. (2021) 98, no. 1, 195–221, https://doi.org/10.1080/00207160.2020.1737030.
10.1080/00207160.2020.1737030
Google Scholar
7 Majumdar A. and Natesan S., Second-Order Uniformly Convergent Richardson Extrapolation Method for Singularly Perturbed Degenerate Parabolic Partial Differential Equations, International Journal of Applied and Computational Mathematics. (2017) 3, no. S1, 31–53, https://doi.org/10.1007/s40819-017-0380-y.
10.1007/s40819-017-0380-y
Google Scholar
8 Dunne R. K., O’Riordan E., and Shishkin G. I., A Fitted Mesh Method for a Class of Singularly Perturbed Parabolic Problems With a Boundary Turning Point, Computational Methods in Applied Mathematics. (2003) 3, no. 3, 361–372, https://doi.org/10.2478/cmam-2003-0023.
10.2478/cmam-2003-0023
Google Scholar
9 Kumar S. and Vigo-Aguiar J., A Parameter-Uniform Grid Equidistribution Method for Singularly Perturbed Degenerate Parabolic Convection-Diffusion Problems, Journal of Computational and Applied Mathematics. (2020) 404.
Google Scholar
10 Kumari P., Kumar D., and Calle H. R., Parameter Independent Scheme for Singularly Perturbed Problems Including a Boundary Turning Point of Multiplicity Greater Than or Equal to One, Journal of Applied Analysis & Computation. (2023) 13, no. 3, 1304–1320, https://doi.org/10.11948/20220123.
10.11948/20220123
Google Scholar
11 Yadav S., Rai P., and Sharma K. K., A Higher Order Uniformly Convergent Method for Singularly Perturbed Parabolic Turning Point Problems, Numerical Methods for Partial Differential Equations. (2020) 36, no. 2, 342–368, https://doi.org/10.1002/num.22431.
10.1002/num.22431
Web of Science® Google Scholar
12 Sahoo S. K. and Gupta V., Second-Order Parameter-Uniform Finite Difference Scheme for Singularly Perturbed Parabolic Problem With a Boundary Turning Point, Journal of Difference Equations and Applications. (2021) 27, no. 2, 223–240, https://doi.org/10.1080/10236198.2021.1887157.
10.1080/10236198.2021.1887157
Web of Science® Google Scholar
13 Majumdar A. and Natesan S., An ε-Uniform Hybrid Numerical Scheme for a Singularly Perturbed Degenerate Parabolic Convection-Diffusion Problem, International Journal of Computer Mathematics. (2019) 96, no. 7, 1313–1334.
10.1080/00207160.2018.1485896
Web of Science® Google Scholar
14 Melesse W. G., Tiruneh A. A., and Derese G. A., Fitted Mesh Method for Singularly Perturbed Delay Differential Turning Point Problems Exhibiting Twin Boundary Layers, Journal of Applied Mathematics & Informatics. (2020) 38, no. 1-2, 113–132.
Google Scholar
15 Hassen Z. I., Duressa G. F., and Liu L., New Approach of Convergent Numerical Method for Singularly Perturbed Delay Parabolic Convection-Diffusion Problems, Research in Mathematics. (2023) 10, no. 1, https://doi.org/10.1080/27684830.2023.2225267, 2225267.
10.1080/27684830.2023.2225267
Google Scholar
16 Yadav S. and Rai P., A Higher Order Scheme for Singularly Perturbed Delay Parabolic Turning Point Problem, Engineering Computations. (2020) 38, no. 2, 819–851, https://doi.org/10.1108/EC-03-2020-0172.
10.1108/EC-03-2020-0172
Google Scholar
17 Hassen Z. I. and Duressa G. F., Parameter Uniform Hybrid Numerical Method for Time-Dependent Singularly Perturbed Parabolic Differential Equations With Large Delay, Applied Mathematics in Science and Engineering. (2024) 32, no. 1, https://doi.org/10.1080/27690911.2024.2328254, 2328254.
10.1080/27690911.2024.2328254
Google Scholar
18 Hassen Z. I. and Duressa G. F., Parameter-Uniformly Convergent Numerical Scheme for Singularly Perturbed Delay Parabolic Differential Equation via Extended b-Spline Collocation, Frontiers in Applied Mathematics and Statistics. (2023) 9, https://doi.org/10.3389/fams.2023.1255672, 1255672.
10.3389/fams.2023.1255672
Google Scholar
19 Hailu W. S., Duressa G. F., and Lishan L., A Robust Collocation Method for Singularly Perturbed Discontinuous Coefficients Parabolic Differential Difference Equations, Research in Mathematics. (2024) 11, no. 1, https://doi.org/10.1080/27684830.2024.2301827, 2301827.
10.1080/27684830.2024.2301827
Google Scholar
20 Hailu W. S. and Duressa G. F., Uniformly Convergent Numerical Scheme for Solving Singularly Perturbed Parabolic Convection-Diffusion Equations With Integral Boundary Condition, Differential Equations and Dynamical Systems. (2023) 1–27, https://doi.org/10.1007/s12591-023-00645-y.
10.1007/s12591-023-00645-y
Google Scholar
21 Hailu W. S. and Duressa G. F., Accelerated Parameter-Uniform Numerical Method for Singularly Perturbed Parabolic Convection-Diffusion Problems With a Large Negative Shift and Integral Boundary Condition, Results in Applied Mathematics. (2023) 18, https://doi.org/10.1016/j.rinam.2023.100364, 100364.
10.1016/j.rinam.2023.100364
Google Scholar
22 Kumie H. G., Tirunehi A. A., Derese G. A., and Shah F. A., Crank–Nicolson Method for Solving Time-Fractional Singularly Perturbed Delay Partial Differential Equations, Research in Mathematics. (2024) 11, no. 1, https://doi.org/10.1080/27684830.2023.2293373, 2293373.
10.1080/27684830.2023.2293373
Google Scholar
23 Rao S. C. S. and Kumar S., Second Order Global Uniformly Convergent Numerical Method for a Coupled System of Singularly Perturbed Initial Value Problems, Applied Mathematics and Computation. (2012) 219, no. 8, 3740–3753, https://doi.org/10.1016/j.amc.2012.09.075.
10.1016/j.amc.2012.09.075
Web of Science® Google Scholar
24 Linß T., Sufficient Conditions for Uniform Convergence on Layer-Adapted Grids, Applied Numerical Mathematics. (2001) 37, no. 1-2, 241–255, https://doi.org/10.1016/S0168-9274(00)00043-X.
10.1016/S0168-9274(00)00043-X
Web of Science® Google Scholar
25 Sumit, Kumar S., Kuldeep, and Kumar M., A Robust Numerical Method for a Two-Parameter Singularly Perturbed Time Delay Parabolic Problem, Computational and Applied Mathematics. (2020) 39, no. 3, https://doi.org/10.1007/s40314-020-01236-1, 209.
10.1007/s40314-020-01236-1
Google Scholar
26 Clavero C. and Gracia J. L., On the Uniform Convergence of a Finite Difference Scheme for Time Dependent Singularly Perturbed Reaction-Diffusion Problems, Applied Mathematics and Computation. (2010) 216, no. 5, 1478–1488, https://doi.org/10.1016/j.amc.2010.02.050.
10.1016/j.amc.2010.02.050
Web of Science® Google Scholar
27 Kumar S. and Kumar M., Analysis of Some Numerical Methods on Layer Adapted Meshes for Singularly Perturbed Quasilinear Systems, Numerical Algorithms. (2016) 71, no. 1, 139–150, https://doi.org/10.1007/s11075-015-9989-2.
10.1007/s11075-015-9989-2
Web of Science® Google Scholar
28 Kumar S. and Vigo-Aguiar J., A High Order Convergent Numerical Method for Singularly Perturbed Time Dependent Problems Using Mesh Equidistribution, Mathematics and Computers in Simulation. (2022) 199, 287–306, https://doi.org/10.1016/j.matcom.2022.03.025.
10.1016/j.matcom.2022.03.025
Web of Science® Google Scholar
29 Singh J., Kumar S., and Kumar M., A Domain Decomposition Method for Solving Singularly Perturbed Parabolic Reaction-Diffusion Problems With Time Delay, Numerical Methods for Partial Differential Equations. (2018) 34, no. 5, 1849–1866, https://doi.org/10.1002/num.22256.
10.1002/num.22256
Web of Science® Google Scholar
30 Kumar S., Singh J., and Kumar M., A Robust Domain Decomposition Method for Singularly Perturbed Parabolic Reaction-Diffusion Systems, Journal of Mathematical Chemistry. (2019) 57, no. 5, 1557–1578, https://doi.org/10.1007/s10910-019-01026-z.
10.1007/s10910-019-01026-z
CAS Web of Science® Google Scholar
31 Tefera D. M., Tirunehi A. A., and Derese G. A., Absolutely Stable Fitted Mesh Scheme for Singularly Perturbed Parabolic Convection Diffusion Equations, Reaction Kinetics, Mechanisms and Catalysis. (2024) 137, no. 2, 755–776, https://doi.org/10.1007/s11144-024-02570-9.
10.1007/s11144-024-02570-9
CAS Google Scholar
32 Ejere A. H., Duressa G. F., Woldaregay M. M., and Dinka T. G., A Parameter-Uniform Numerical Scheme for Solving Singularly Perturbed Parabolic Reaction-Diffusion Problems With Delay in the Spatial Variable, International Journal of Mathematics and Mathematical Sciences. (2023) 2023, no. 1, 17, https://doi.org/10.1155/2023/7215106, 7215106.
10.1155/2023/7215106
Google Scholar
33 Ejere A. H., Duressa G. F., Woldaregay M. M., and Dinka T. G., A Robust Numerical Scheme for Singularly Perturbed Differential Equations With Spatio-Temporal Delays, Frontiers in Applied Mathematics and Statistics. (2023) 9, https://doi.org/10.3389/fams.2023.1125347, 1125347.
10.3389/fams.2023.1125347
Google Scholar
34 Sharma K. K., Rai P., and Patidar K. C., A Review on Singularly Perturbed Differential Equations With Turning Points and Interior Layers, Applied Mathematics and Computation. (2013) 219, no. 22, 10575–10609, https://doi.org/10.1016/j.amc.2013.04.049.
10.1016/j.amc.2013.04.049
Web of Science® Google Scholar
35 Miller J. J. H., O’riordan E., and Shishkin G. I., On Piecewise-Uniform Meshes for Upwind-and Central-Difference Operators for Solving Singularly Perturbed Problems, IMA Journal of Numerical Analysis. (1995) 15, no. 1, 89–99, https://doi.org/10.1093/imanum/15.1.89.
10.1093/imanum/15.1.89
Web of Science® Google Scholar
36 Mbroh N. A. and Munyakazi J. B., A Robust Numerical Scheme for Singularly Perturbed Parabolic Reaction-Diffusion Problems via the Method of Lines, International Journal of Computer Mathematics. (2022) 99, no. 6, 1139–1158, https://doi.org/10.1080/00207160.2021.1954621.
10.1080/00207160.2021.1954621
Google Scholar
37 Ayele M. A., Tiruneh A. A., and Derese G. A., Uniformly Convergent Scheme for Singularly Perturbed Space Delay Parabolic Differential Equation With Discontinuous Convection Coefficient and Source Term, Journal of Mathematics. (2022) 2022, no. 1, 15, https://doi.org/10.1155/2022/1874741, 1874741.
10.1155/2022/1874741
Google Scholar
38 Tiruneh A. A., Derese G. A., and Tefera D. M., A Nonstandard Fitted Operator Method for Singularly Perturbed Parabolic Reaction-Diffusion Problems With a Large Time Delay, International Journal of Mathematics and Mathematical Sciences. (2022) 2022, 11, https://doi.org/10.1155/2022/5625049, 5625049.
10.1155/2022/5625049
Google Scholar
39 Woldaregay M. M. and Duressa G. F., Boundary Layer Resolving Exact Difference Scheme for Solving Singularly Perturbed Convection-Diffusion-Reaction Equation, Mathematical Problems in Engineering. (2022) 2022, 16, https://doi.org/10.1155/2022/2043323, 043323.
10.1155/2022/2043323
Google Scholar
40 Mickens R. E., Advances in the Applications of Nonstandard Finite Difference Schemes, 2005, World Scientific.
10.1142/5884
Google Scholar
41 Kellogg R. B. and Tsan A., Analysis of Some Difference Approximations for a Singular Perturbation Problem Without Turning Points, Mathematics of Computation. (1978) 32, no. 144, 1025–1039, https://doi.org/10.1090/S0025-5718-1978-0483484-9.
10.1090/S0025-5718-1978-0483484-9
Web of Science® Google Scholar
42 Kaushik A. and Sharma N., An Adaptive Difference Scheme for Parabolic Delay Differential Equation With Discontinuous Coefficients and Interior Layers, Journal of Difference Equations and Applications. (2020) 26, no. 11-12, 1450–1470, https://doi.org/10.1080/10236198.2020.1843645.
10.1080/10236198.2020.1843645
Web of Science® Google Scholar

All articles

Crank–Nicolson Method for Singularly Perturbed Unsteady Parabolic Problem With Multiple Boundary Turning Points

Abstract

1. Introduction

2. Properties of Continuous Problem

3. Formulation of the Numerical Scheme

3.1. Temporal Discretization

3.2. Spatial Discretization

4. Stability and Uniform Convergence Analysis

5. Numerical Results and Discussion

6. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley