Volume 2024, Issue 1 1378156

Research Article

Open Access

Wave Dynamics in Design: The Role of Nonlinear Potential Burgers’ Equation With Variable Coefficients

Xiuchuan He,

Xiuchuan He

orcid.org/0000-0002-2427-5047

Design and Art School , Shanghai Dianji University , Shanghai , 201306 , China , sdju.edu.cn

Search for more papers by this author

Hui Xiong,

Hui Xiong

orcid.org/0009-0005-6088-2126

Design and Art School , Shanghai Dianji University , Shanghai , 201306 , China , sdju.edu.cn

Search for more papers by this author

Jianming Qi,

Corresponding Author

Jianming Qi

[email protected]

orcid.org/0000-0002-0458-2525

School of Business , Shanghai Dianji University , Shanghai , 201306 , China , sdju.edu.cn

Search for more papers by this author

Yiqun Sun,

Yiqun Sun

orcid.org/0009-0002-6860-5818

School of Business , Shanghai Dianji University , Shanghai , 201306 , China , sdju.edu.cn

Search for more papers by this author

Xiuchuan He,

Xiuchuan He

orcid.org/0000-0002-2427-5047

Design and Art School , Shanghai Dianji University , Shanghai , 201306 , China , sdju.edu.cn

Search for more papers by this author

Hui Xiong,

Hui Xiong

orcid.org/0009-0005-6088-2126

Design and Art School , Shanghai Dianji University , Shanghai , 201306 , China , sdju.edu.cn

Search for more papers by this author

Jianming Qi,

Corresponding Author

Jianming Qi

[email protected]

orcid.org/0000-0002-0458-2525

School of Business , Shanghai Dianji University , Shanghai , 201306 , China , sdju.edu.cn

Search for more papers by this author

Yiqun Sun,

Yiqun Sun

orcid.org/0009-0002-6860-5818

School of Business , Shanghai Dianji University , Shanghai , 201306 , China , sdju.edu.cn

Search for more papers by this author

First published: 17 December 2024

https://doi.org/10.1155/admp/1378156

Academic Editor: Ivan Giorgio

Share a link

Email
Wechat
Bluesky

Abstract

This paper investigates exact solutions of the potential Burgers equation with variable coefficients (PBEVCs), contributing to communication engineering, nonlinear acoustics, and fluid mechanics. It explores novel solutions using the improved modified extended tanh–function method (IMETFM), revealing diverse characteristics and providing deeper insights into nonlinear wave dynamics. The study also analyzes the long-term behavior of PBEVC under noise influence, highlighting insights into noise-perturbed systems’ robustness. Moreover, it establishes connections to practical applications like 5G optical fiber transmission and ocean wave oscillations, showcasing the wide applicability of the IMETFM approach. This work’s novelty lies in uncovering diverse solution characteristics and bridging theoretical understanding with real-world applications.

1. Introduction

It is well-known that the world is filled with marvelous and complex natural phenomena, many of which entail numerous mathematical applications. These mathematical applications are not only limited to describing natural phenomena but also widely employed in solving real-world problems. For instance, nonlinear differential equations and soliton theory play crucial roles in fields such as physics, engineering, and biology. Nonlinear differential equations can describe the behavior of many complex systems, including climate models, fluid dynamics, and cardiac biomechanics. Soliton theory finds extensive applications in describing one-dimensional (1D) nonlinear waves, such as in water waves and optics. The application of these mathematical tools enables us to better understand natural phenomena and provides important theoretical foundations and computational methods for addressing complex real-world problems [1–10]. One class of equations that is used to simulate the propagation and reflection of shockwaves is called the Burgers equation. The Burgers equation is a fundamental partial differential equation that finds wide-ranging applications in fields such as fiber-optic communications, ocean engineering, fluid mechanics, and nonlinear acoustics [11]. The study of ocean physics, fluid dynamics, and acoustics has long been focused on the research of the potential Burgers equation variable coefficient (PBEVC), which stands for partial differential equations with variable coefficients. The PBEVC is extensively used in various fields of applied mathematics, such as analyzing waves in fluid dynamics, studying nonlinear waves in atmospheric and oceanic dynamic systems, investigating dynamics with exact closed-form solutions, and studying generalized traveling waves in dynamics [12–16]. Understanding the physical phenomena through the analysis of the PBEVC’s representational and quantitative features is of utmost importance. Therefore, the research on variable coefficient equations is significant in providing solutions for diverse dynamics within wave phenomena.

In 1948, Burgers [17] developed a mathematical model for turbulence theory. In 1991, Oliveri and Painlevé [18] analyzed the PBEVC and found a similar solution using the Painlevé analysis method. In 2002, Wang and Wang, Wang, and Zhou [19] investigated the variable coefficient generalized KdV equation by employing the automatic B

cklund transformation. Transformation properties of the PBEVC were studied by Sophocleous [20] in 2004. In 2005, Abdou and Soliman [21] solved the Burger equation and the coupled Burger equation using the variational iteration method. Abdou and Soliman [21] considered the homogeneous form of the 1D Burger equation:

()

where v is the discretional constant. In the interest of solving the second shape of the coupling Burger equation, Abdou and Soliman. [21] also had considered the following equations using the mutation iteration methods:

()

In 2006, Vaganan and Kumaran [22] developed a broad and unsolved broad definition of linear damping and variable viscosity Burger equations. In 2007, Cui and Geng [23] calculated the 1D PBEVC. In 2008, Xieaet al. [24] applied reproducing kernel function to resolve the numerical solution of 1D Burgers equation.

Ivanova, Sophocleous, and Tracina [25] empolyed the Lie group analysis to study two-dimensional (2D) variable coefficient Burgers equation in 2010. Yu and Ma [26] obtained the exact solution of variable coefficient KdV–Burgers composite equation. In 2011, Ma, Deng, and Wang [27] investigated the exact solution about variable coefficients KdV equation. In 2012, Bekir, Aksoy, And Güner [28] studied the dark and bright solitons of variable coefficient diffusion reaction. El-Shiekh [29] studied the new exact solutions of the modified KdV equation and the 2D PBEVC. In 2013, Büyükaşık and Pashaev [30] obtained the exact solution of the forced Burgers equation with time-varying coefficients. Jiwari and Mittal [31] solved the numerical format of the numerical solution of the Burgers’ equation based on the weighted means differential method of quadrature. Aminikhah and Malekzadeh [32] studied the effective method of variable coefficient coupling Burgers’ equations with time fractional derivatives. Zhang [33] studied the conservation laws of (2 + 1)-dimensional KP equation and PBEVC and cross clauses. In 2014, Pocheketa and Popovych et al. [34] obtained the group classification and exact solution of the linear damped variable coefficient generalized Burgers equation. In 2015, Schulze-Halberg [35] studied the Burgers equation with time-dependent coefficients and nonlinear forcing terms: linearization and exact solvability. Younis, Ali, and Mahmood [36] studied the solitons of the composite KdV–Burgers equation with variable coefficients and power-law nonlinearity. In 2016, Gaur and Singh [37] used the variable coefficient space–time fractional potential Burgers equation to study its symmetry classification and exact solution. Pandir, Demiray, and Bulut [38] also studied the exact solution of the fractional PBEVC. In 2017, Mamo, Shiferaw, and Tsegaye [39] solved the value of the Burgers equation based on the Fourier’s expansion in the microscoring accumulation method. In 2018, Seydaoğlu [40] studied the accurate approximate algorithm of Burgers equation at low viscosity. Huda, Akbar, and Shanta [41] studied the new wave solutions of the Burger equation and the Benjamin–Bona–Mahony equation. Christov [42] studied the numerical solution of PBEVC in Granuler segregation. Gupta and Ray [43] studied the KdV–Burgers equation of shallow water long wave propagation time fraction with Petrov–Galerkin method. In 2019, Büyükaşık and Bozaci [44] studied the Dirichlet problem and the exact solvable model of the semiline of the forced Burgers equation with time-varying coefficients. Chen and Zhang [45] studied the weak Galerkin finite element method for Burgers equation. In 2020, in view of on the ideas of symmetrical analytical, Opanasenko, Bihlo, and Popovych [46] considered a kind of PBEVC in general form:

()

where R²K ≠ 0 and both are smoothness functions of (t, x). In 2021, Mohammed et al. [47] rigorously investigated the dynamics of the stochastic Burgers’ equation with multiplicative noise, utilizing the Stratanovich interpretation, and shared their insightful findings in their study:

()

where d and h are constants and W_t = dW/dt is the time derivative of criterion Wiener technics W(t).

In recent years, research on nonlinear differential equations related to the variable coefficient model has always been a hot issue [48–51]. In 2022, Mohanty et al. [15] employed the expanded widespread

-expansion method to investigate the exact solution of the PBEVCs, as detailed in their research. In this work, we still further research the exact solutions and related properties about the PBEVC. To attain our objective, the equations which we introduce remain in the following pattern:

()

where g(t) and a(t) both are slick functions of the variable t and u(x, t) is a function which contains only two free variables x and t.

In this equation, a(t) can be understood as the coefficient function describing the nonlinear term uu_x. In other words, it controls the degree of influence of the nonlinear term on the evolution of the solution u(x, t). By adjusting the form and value of a(t), different types of nonlinear effects on the equation solution can be explored, providing a deeper understanding of the characteristics of nonlinear waves.

Here, g(t) is the coefficient function describing the diffusion term u_xx. Diffusion terms are usually associated with the conduction properties of the medium, and the value of g(t) will affect the way and rate at which the solution propagates in space. By studying the characteristics of g(t), a better understanding of the diffusion behavior of the medium and the interaction of nonlinear waves can be obtained, providing important clues for further investigating the dynamic properties of the system.

As early as 2002, Fan [52] utilized symbolic computation to discover traveling wave solutions for nonlinear equations. In 2003, Fan [53] conducted extensive research on obtaining various forms of exact solutions of nonlinear equations. Later in 2006, Yang and Hon [54] conducted a comprehensive study on the improved modified extended tanh–function method (IMETFM). Recently in 2022, Ananna et al. [55] investigated the exact traveling wave solutions of a class of 3D fractional WBBM equations using the IMETFM. In 2023, Alhojilan and Ahmed [56] conducted further research on the analytical solutions of stochastic Ginzburg–Landau equation driven by Wiener process via the IMETFM. Within our cognitive range, no one has yet studied exact solutions of PBEVC using the IMETFM. In this paper, we apply the IMETFM technique to study the exact solution of PBEVC.

The PBEVCs, as a mathematical physics model, hold significant research importance not only in the field of fluid dynamics but also in nonlinear acoustics and optical fiber communications. In fluid dynamics, it is utilized to characterize the nonsteady behavior of fluids, particularly in examining phenomena such as shock waves, turbulence, and wave propagation. This model provides a profound understanding of complex fluid motion, serving as a basis for designing various engineering applications. In the realm of nonlinear acoustics, the PBEVC aids in comprehending the propagation of sound waves in nonlinear media and phenomena-like wave breaking and dissipation. By modeling and analyzing the process of sound wave propagation, we can better understand the behavior of sound waves in different media, guiding the development of acoustic technologies. Additionally, in optical fiber communications, the PBEVC contributes to modeling and analyzing the transmission and modulation of light signals in fiber-optic systems. Through studying the propagation characteristics of light signals in optical fibers, we can optimize the performance and capacity of optical communication systems, driving the advancement of optical communication technology. Therefore, research on the PBEVC not only deepens our understanding of physical phenomena but also fosters scientific and technological progress in related fields, holding significant theoretical and practical value.

This article is arranged as follows: the precise solution of PBEVC is explored through the utilization of IMETFM in Section 2. We also give some concrete examples of the exact solutions of PBEVC in Section 3. The discussion about the relevance between PBEVC and the stochastic differential equation (SED) is arranged in Section 4. In Section 5, the physical interpretation of the graphs obtained through computer simulations is presented. Section 6 establishes a correlation between mathematical visualizations and real-world phenomena. Section 7 provides a comparative analysis and discussion. Ultimately, the paper provides a comprehensive summary and conclusion in Section 8.

2. Apply the IMETFM to Equation (6)

Investigating the PDE, we have the following:

()

where W is the differential polynomial which contains the partial derivatives. Denoting alternation ξ = p(t)x + q(t) as the nontravelling wave transformation, here, q(t) and p(t) are the suspensive functions. Here, p(t) is a function of time t used to regulate the scaling effect within the wave transformation on the spatial variable x. By adjusting the value of p(t), one can control the degree of expansion or compression of the wave solution in the spatial direction, thereby affecting the spatial distribution changes of the phenomenon. In physical problems, the variation of p(t) can reflect the regularity of the medium’s properties evolving over time or the influence of certain parameters changing over time within the system. q(t) is also a function of time t used to describe the translation effect within the wave transformation. This function can control the translation of the wave solution in the spatial direction, that is, the speed and position of the wave packet moving in space. In physics, the change of q(t) typically reflects the influence of some external driving force or boundary conditions within the system, affecting the spatiotemporal evolution process of the wave phenomenon.

Using the nontravelling wave conversion, u(x, t) = U(ξ) = U(p(t)x + q(t)), we may transform the PDE into an ODE:

()

We change Equation (6) to the following form:

()

Next, we will skip the intricate steps of the IMETFM [53–58] and instead utilize this approach to derive a broader nontraveling wave exact solution for this issue.

After conducting research on the homogeneous counterpoise term between u_xx and uu_x in Equation (6), we can readily derive the following refined expression for Equation (6):

()

where α₀(t), α₁(t), and β₁(t) will be resolved backward. Here, φ satisfies the following:

()

According to Equation (6), the expression of Equation (10) is derived using the method of homogeneous balance, with the highest order dispersion and nonlinear terms leading to the aforementioned Equation (10). Equation (11) corresponds to the detailed steps of the IMETFM method documented in references [53, 58].

Employing Equations (10) and (11), and gathering the same power as φ(ξ), we deduce the following forms:

()

The system of equations (refer to Appendix A) was solved using Maple 2021, resulting in solutions for the unknown constants as follows:

Result 1.c₁ = c₂ = c₃ = c₄ = 0, c₀ > 0.

()

Result 2.

()

Result 3.

()

Result 4.

()

Result 5.

()

Result 6.c₀ = c₁ = c₂ = c₃ = 0, c₄ > 0.

()

Result 7.

()

Result 8.

()

3. The Exact Solution of PBEVC Is Applied in Some Concrete Examples

The analytic solutions in Equations (14)–(21) for the mentioned function equations involve various forms, including polynomial, exponential, trigonometric, hyperbolic, rational, and Jacobi elliptic function solutions. In these equations, g(t), a(t), q(t) can be chosen as some basic elementary functions. p(t) remains as a nonzero constant p, which is consistent with the literature [59]. To enrich the diversity of our solutions, we can introduce a simple elementary function and attempt to include more different elementary functions. Furthermore, it would be meaningful for our future waveform studies if q(t), a(t), g(t) can be selected as trigonometric, hyperbolic, exponential, or linear functions. The inclusion of these additional elementary functions will contribute to the variety and richness of the solution forms, thereby expanding the scope and significance of our future waveform research. In this chapter, we will provide some particular examples.

To obtain a polynomial form solution for Equation (14), we make the following assumptions: p(t) is a constant,

; g(t) is the hyperbolic secant function, sech(t); a(t) is the cosecant function, csc(t); and q(t) is the sine function, sin(t). With these assumptions, the specific functional form of Equation (14) can be derived as follows:

()

To obtain the specific representation of the exponential solution for Equation (15), we take

, g(t) = tanh(t), a(t) = csc(t), and q(t) = t⁴. We then obtain the following form:

()

In order to derive the specific form of the trigonometric solution for Equation (16), we have utilized

, g(t) = sech(t), a(t) = csch(t), q(t) = tanh(t), c₄ = 1, c₂ = 2, and c₀ = 1. With these choices, Equation (16) can be transformed into the following:

()

By choosing

, g(t) = cos(t), a(t) = sin(t), and q(t) = csc(t) and constants

, and

, we can derive the explicit representation of the hyperbolic trigonometric solution for Equation (17), which is given by the following expression:

()

By selecting

, g(t) = sec(t), a(t) = csc(t), and q(t) = tanh(t) and constants c₂ = c₄ = 1, we can derive the explicit representation of the degenerate hyperbolic trigonometric solution for Equation (18), which takes the following form:

()

In order to obtain a meaningful and explicit representation of the rational solution for Equation (19), we adopt the following choices:

, and q(t) = tanh(t). These selections lead us to a refined functional expression:

()

By selecting

, g(t) = sec(t), a(t) = csc(t), q(t) = sech(t), c₂ = 1, c₄ = −1, m = 0.8, and

, we can derive a sophisticated and precise representation of the solution for Equation (20) using Jacobi elliptic functions. The resulting functional expression is as follows:

()

4. Connection to SED

The energy landscape is an important tool to understand the behavior of a system:

()

It allows us to visualize the states of the system and analyze their interactions. By analyzing the energy landscape, we can determine the potential barriers and saddle points that may exist in the system. These barriers and saddle points represent transitions between different states, and their presence can affect the behavior of the system.

The behavior of a system is often affected by external factors or noise, which can disturb its natural state of equilibrium. However, when these external forces or noise are removed, the system tends to return to its original stable state. In other words, the system’s natural tendency is to reach a stable equilibrium point [60]. For example, one can consider the following boundary value problem:

()

We can apply implicit finite difference scheme for systems of nonlinear equations, together with upwinding scheme. The results show the convergence (Figure 1).

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

We choose the step size t = 0.001 and the number of interpolation N = 100. Result of implicit finite difference scheme converges to a numerical solution with tolerance 10⁻³ after 5178 iteration, where d = 0.001, u₀ = 1.5, and u₁ = −1. (a) shows the initial states of the system, and (b) shows the numerical solution at convergence.

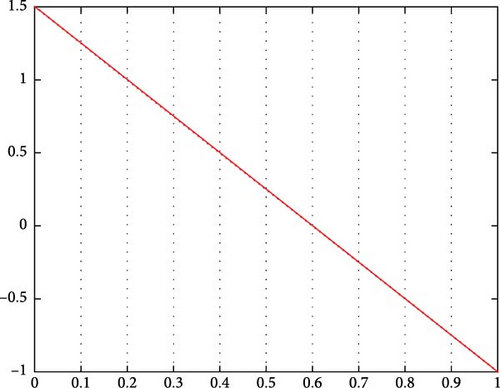
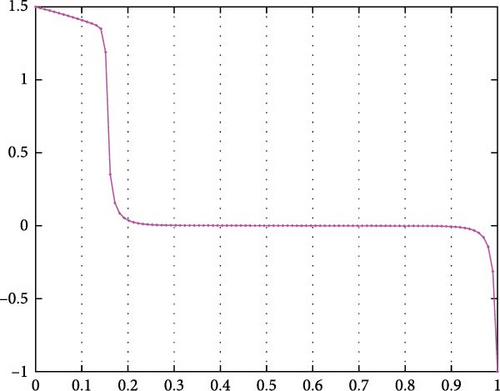
The areas around the stable equilibria are called the basin of attraction. The energy landscape description is useful in analyzing the deterministic system in Equation (29); however, when noise is present, the states of the system in Equation (29) can experience a sudden transition to another equilibrium point. In such cases, the states of the system in Equation (29) undergo an abrupt shift [61]. The concept of “stability” is no longer valid in the presence of noise, as the system jumps from one stable equilibrium to another due to the influence of noise. Therefore, the term “quasipotential” is introduced for systems with noise [61].

The mathematical SED model is built to analyze the random perturbed system. Considering the following dynamic system with random perturbations, we have the following:

()

where σ stands for the noise amplitude tensor and ξ represents a zero-mean Gaussian white noise with covariance 〈ξ_i(t)ξ_j(t^′)〉 = δ_ijδ(t − t^′). The framework of Freidlin–Wentzell [61] quasipotential gives a well-defined description of the stability of the system under the influence of random perturbation. Now, we may investigate a dynamic system with small random perturbation in Equation (31), which denote the following:

()

Equation (31) can be rewritten as the following form:

()

Applying the large deviation theory under suitable assumptions, the Freidlin–Wentzell theorem states that u satisfies the large deviation principle with a rate function as follows:

()

When the noise coefficient ɛ → 0, one can describe a path u_T that start from u₀ and end in A with certain probability:

()

In this paper, we investigate the most probable transition path for a system, described by a SED, from an initial state u₀ at time 0 to a target set A at time T. We define the quasipotential of the system as a key tool for analyzing this transition process. The minimizer u^∗ is identified as the most probable transition path, and its relationship to the quasipotential is established. Our results provide a comprehensive framework for understanding the transition behavior of the system and offer potential insights for controlling its dynamic behavior. Define the quasipotential as follows:

()

In the Freidlin–Wentzell theory, the quasipotential is equivalent to the following:

()

where

is absolutely continuous functions and u₀ and u₁ are two stable fixed points. For fixed T, analyze the following part:

()

where S_T(u) is denoted as the action functional,

()

The identification of the minimizer u^∗ as the most probable transition path and its relationship to the quasipotential offer valuable insights into the system’s transition process. The path u^∗ is known as the minimum action path (MAP), which characterizes the abrupt shift in a system under the influence of noise [62]. In various situations, such shifts are known as rare events. The MAP provides a mathematically tractable framework for analyzing these rare events. For this model (6), we have used the IMETFM to study the various forms of the PBEVC solutions. We can further take use of our solutions to calculate quasipotential between stable equilibria in terms of different solutions, which provides better understanding about the energy landscape view of the noise perturbed system.

5. Physical Interpretations of Graphs Obtained Through Computer Simulations

In this section, for further analyzing the nature and dynamic behavior in the physics of the U₁(x, t), ⋯, U₆(x, t), U₇(x, t) in the equations, we make computer simulation images. We may select some appropriate parameter values or some special functions coefficients in the following figures. The following figures are the (a) 3D, (b) 2D contour, and (c) 2D image graph of the above functions via software MATLAB 2021b.

Figure 2(a) displays the periodic wave solutions illustrating the interaction between complex solitons, as represented by the function U₁(x, t). Figure 2(b) provides a contour plot depicting the spatial distribution of U₁(x, t) over the domain. As shown in Figure 2(c) which is close to the point x = 0, detailed observations reveal distinct behaviors: when U₁(x, t) > 0, indicating the presence of a soliton, it attains its maximal amplitude at t = 0.6; conversely, when U₁(x, t) < 0, corresponding to the trough of the soliton, it reaches its minimum at t = 0.9. Furthermore, for values of U₁(x, t) lying between −1 and 0, the amplitude at t = 0.3 consistently exceeds those at t = 0.6 and t = 0.9, while the values at t = 0.6 and t = 0.9 are approximately equal. This nuanced behavior provides insights into the dynamics of the solitons. The parameters governing these solutions are , g(t) = sech(t), a(t) = csc(t), and q(t) = sin(t).

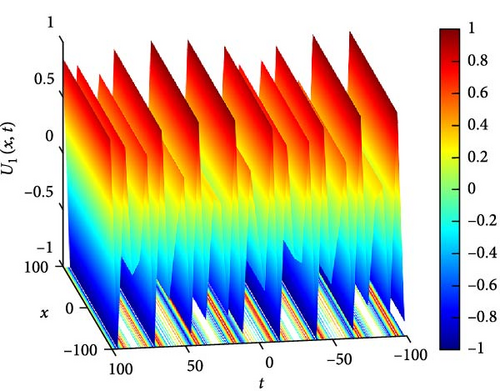
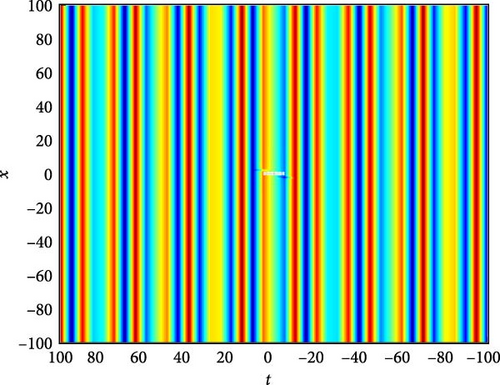
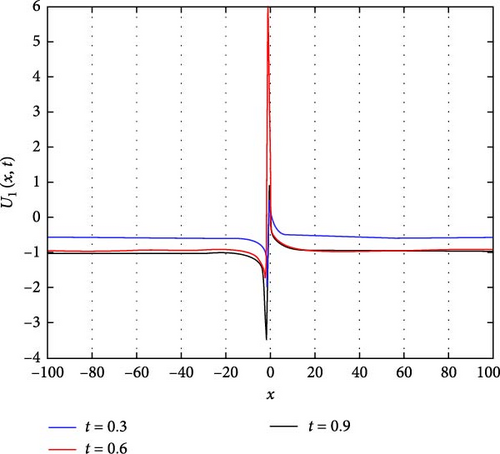
Figure 3(a) illustrates the behavior of an oscillating decaying solitary wave of U₂(x, t). In this representation, we observe the gradual dissipation of the wave over time, a characteristic of solitary waves in dissipative media. The oscillatory nature of the wave is evident as it propagates, with successive peaks and troughs becoming less pronounced as time progresses. Figure 3(b) provides further insight through a contour plot of U₂(x, t). This visualization allows us to discern the spatial distribution of U₂(x, t) at different time points, aiding in the analysis of wave propagation and decay. Figure 3(c) delves into the temporal evolution of U₂(x, t), specifically focusing on time instances t = 0.4, t = 0.8, and t = 1.2. At these time points, we observe a systematic decrease in the overall waveform of U₂(x, t), indicative of the dissipative nature of the system. Interestingly, despite the overall decay, the oscillation amplitudes of U₂(x, t) around x = 0 exhibit a notable increase. This phenomenon highlights the interplay between dissipation and localized energy concentration within the wave.

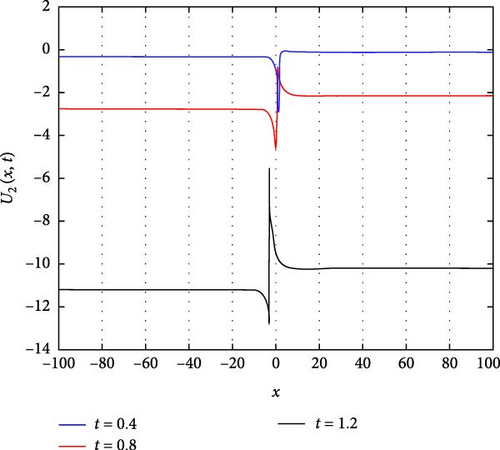
The parameters governing the system dynamics are outlined as follows: p(t), which remains constant at , g(t) characterized by the hyperbolic tangent function tanh(t), a(t) represented by the cosecant function csc(t), and q(t) determined by the polynomial function t⁴. These parameters collectively influence the behavior of U₂(x, t), shaping its evolution and characteristics over time.

Figure 4(a) depicts a singular periodic wave of U₃(x, t). This wave exhibits a repetitive pattern with distinct peaks and troughs, indicative of periodic behavior. Such waves are often encountered in systems where periodic forces or boundary conditions govern the dynamics. The singular nature of the wave suggests that it maintains its shape and characteristics unchanged over time, highlighting a stable periodicity. Figure 4(b) presents a contour plot of U₃(x, t), offering insights into its spatial distribution at different time points. This visualization aids in understanding how the wave pattern evolves and propagates throughout the domain, providing valuable information about its amplitude and phase variation. Figure 4(c) further explores the temporal behavior of U₃(x, t) at specific time instances, namely, when t takes values of −5, 0, and 5. At t = −5 and t = 5, the waveform of U₃(x, t) exhibits mirror symmetry about x = 0, indicating that the wave’s profile remains symmetrically unchanged under time reversal. At t = 0, U₃(x, t) remains constant at 0, suggesting a momentary state of equilibrium or absence of wave activity. These observations provide insights into the wave’s temporal dynamics and its relationship with the system’s boundary conditions and initial states.

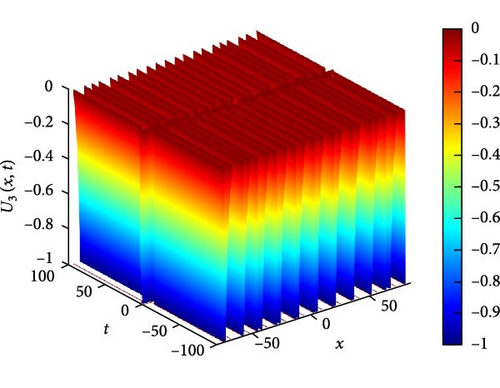
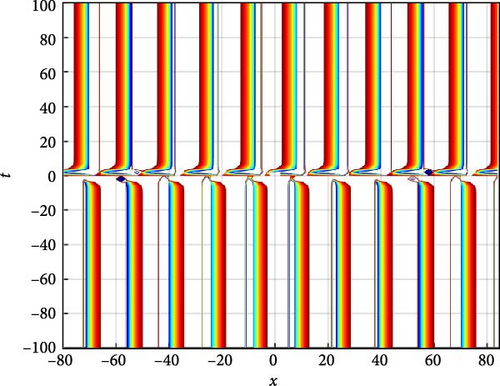
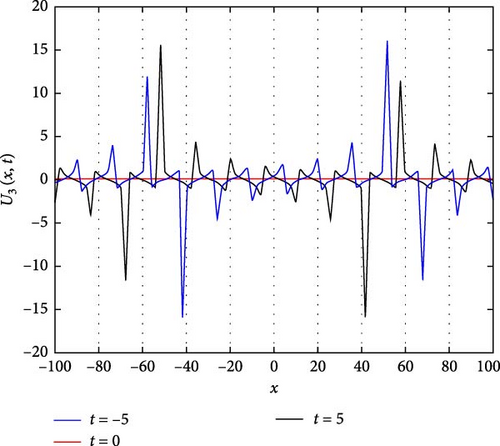
The parameters governing the system dynamics are outlined as follows: p(t) remains constant at , g(t) is characterized by the hyperbolic secant function sech(t), a(t) is represented by the hyperbolic cosecant function csch(t), and q(t) is determined by the hyperbolic tangent function tanh(t), while c₄ = 1, c₂ = 2, and c₀ = 1 contribute to the specific form of the wave equation. These parameters collectively influence the behavior of U₃(x, t), shaping its periodicity, symmetry, and overall dynamics.

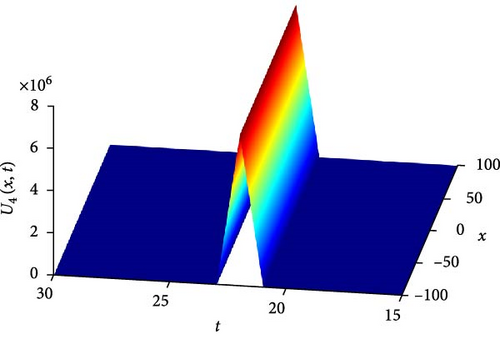
Figure 5(a) illustrates a Λ-shaped solitary wave of U₄(x, t). The Λ-shaped wave is a unique wave structure that resembles the Greek letter lambda (⋀). Solitary waves, also known as solitons, are self-reinforcing waves that propagate without changing their shape due to a balance between nonlinear and dispersive effects. In the context of the system, this solitary wave indicates a localized disturbance that maintains its profile while moving through the medium, demonstrating a stable and localized behavior. Figure 5(b) presents a contour plot of U₄(x, t), offering insights into its spatial distribution at different time points. This visualization aids in understanding how the solitary wave pattern evolves and propagates throughout the domain, providing valuable information about its amplitude and phase variation. Figure 5(c) further explores the temporal behavior of U₄(x, t) at specific time instances, namely, at t values of 0.6, 1.2, and 1.8. As t increases, the waveform of U₄(x, t) shifts downward, indicating a progressive shift in the wave pattern over time. Notably, around x = 0, a larger oscillation amplitude is observed at t = 0.6, suggesting an enhanced wave intensity at this particular time point. These observations provide insights into the wave’s temporal dynamics and its relationship with the system’s boundary conditions and initial states.

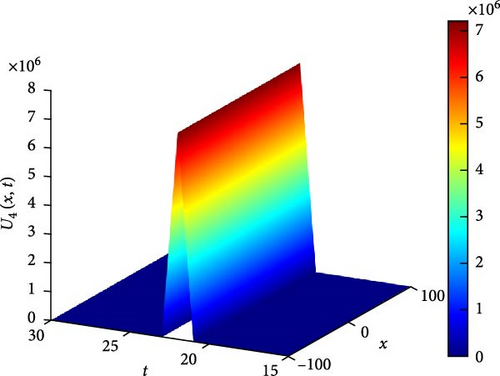
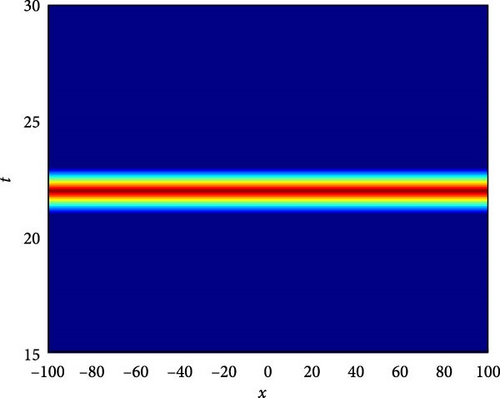
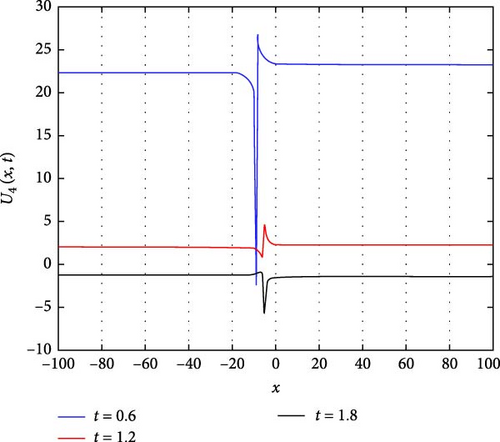
The parameters governing the system dynamics are outlined as follows: p(t) remains constant at , g(t) is characterized by the cosine function cos(t), a(t) is represented by the sine function sin(t), and q(t) is determined by the cosecant function csc(t), while , , and contribute to the specific form of the wave equation. These parameters collectively influence the behavior of U₄(x, t), shaping its solitary wave structure, amplitude, phase, and overall dynamics.

Figure 6(a) depicts a three-dimensional (3D) plot illustrating the interaction between two solitons of U₅(x, t) as solitary waves. Solitons are self-reinforcing solitary waves that propagate without changing their shape, and the interaction between them can lead to intriguing phenomena such as soliton fusion or reflection. In this representation, the 3D plot provides a visual depiction of how these solitons interact and evolve over time, showcasing their complex dynamics and mutual influence. Figure 6(b) displays a contour plot of U₅(x, t), offering insights into its spatial distribution at different time points. This visualization aids in understanding how the soliton pattern evolves and propagates throughout the domain, providing valuable information about its amplitude and phase variation. Figure 6(c) illustrates the intertwined waveform of U₅(x, t) at specific time instances, namely, at t values of 3, 6, and 9. From Figure 6(c), it can be observed that as t increases, the value of U₅(x, t) increases for x < 0, while it decreases for x > 0. This asymmetrical behavior suggests a complex interaction between the solitons, where one soliton might dominate over the other in certain spatial regions, leading to a nonuniform distribution of wave intensity.

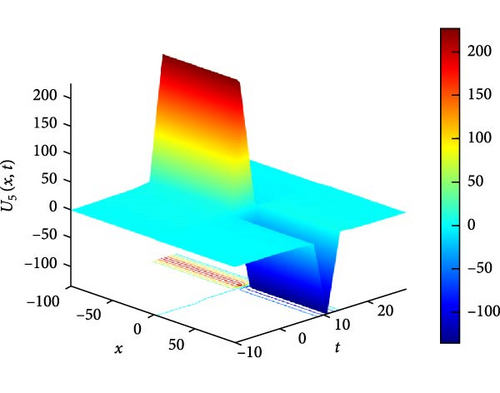
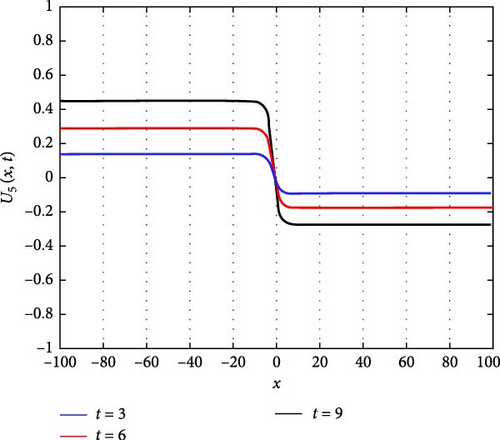
The parameters governing the system dynamics are outlined as follows: p(t) remains constant at , g(t) is characterized by the secant function sec(t), a(t) is represented by the cosecant function csc(t), q(t) is determined by the hyperbolic tangent function tanh(t), and c₂ = c₄ = 1 contribute to the specific form of the wave equation. These parameters collectively influence the behavior of U₅(x, t), shaping its soliton interaction, amplitude, phase, and overall dynamics.

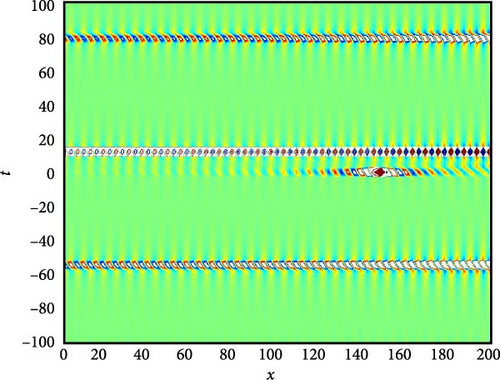
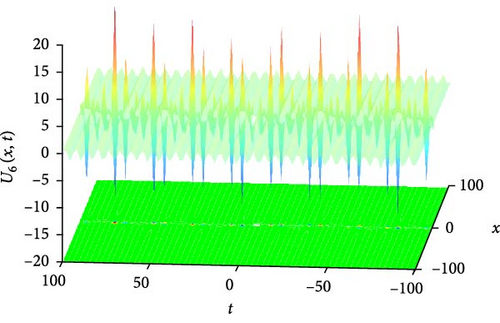
Figure 7(a) presents a 3D plot depicting the needle-shaped solitary wave soliton represented by U₆(x, t). Needle-shaped solitary waves are characterized by their narrow and elongated profile, resembling the shape of a needle. These solitons exhibit unique propagation characteristics, often associated with highly localized disturbances that maintain their shape while traveling through the medium. The 3D plot provides a visual representation of the spatial distribution of this solitary wave, offering insights into its elongated structure and propagation dynamics. Figure 7(b) showcases a 2D contour plot illustrating the profile of the needle-shaped solitary wave soliton. This visualization aids in understanding the spatial distribution of the soliton’s intensity and phase, providing valuable information about its amplitude variation along the spatial domain. Figure 7(c) represents a series of 2D graphics of U₆(x, t) at specific time instances, namely, when t takes values of −30, 30, and 90. From Figure 7(c), it can be observed that when t takes values of −30 and 30, the shape of U₆(x, t) is symmetric about x = 0, indicating a balanced distribution of wave intensity on both sides of the origin. Additionally, the oscillation amplitude of U₆(x, t) is larger around x = 0, suggesting a concentrated energy distribution at this point. However, at t = 90, the oscillation amplitude becomes smaller, indicating a change in the soliton’s intensity distribution over time.

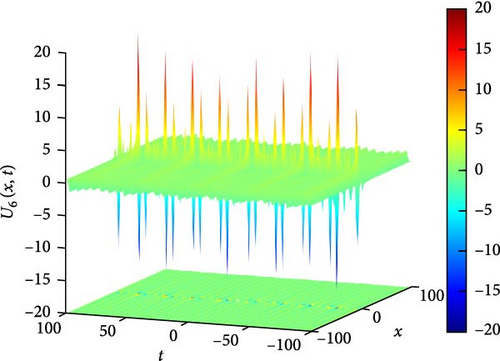
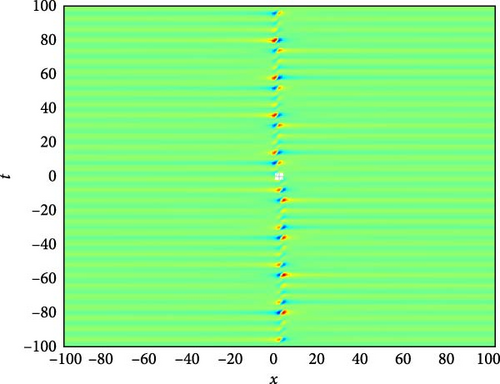
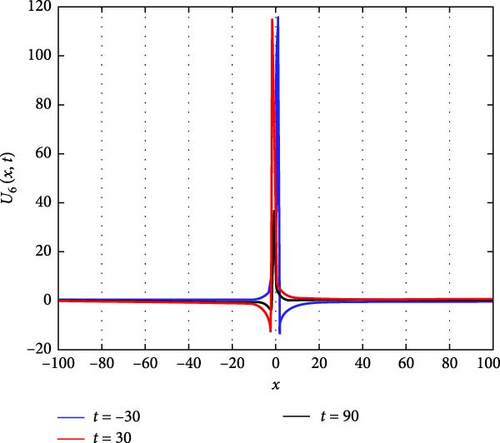
The parameters governing the system dynamics are outlined as follows: p(t) remains constant at , g(t) is characterized by the secant function sec(t), a(t) is represented by the cosecant function csc(t), and q(t) is determined by the hyperbolic tangent function tanh(t). These parameters collectively influence the behavior of U₆(x, t), shaping its needle-shaped soliton profile, amplitude, phase, and overall dynamics.

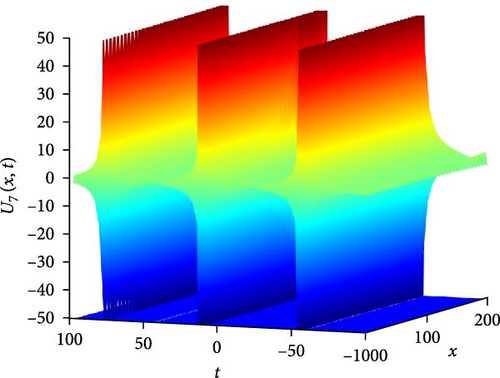
Figure 8(a) presents a 3D plot illustrating the complex interaction of solitary periodic waves represented by U₇(x, t). Solitary periodic waves are characterized by their periodic behavior and solitary nature, indicating that they maintain their shape and propagate with a periodic pattern. The 3D plot provides a visual representation of how these waves interact and evolve over time, showcasing their intricate dynamics and the interplay between different wave components. Figure 8(b) showcases a 2D contour plot depicting the profile of the complex soliton U₇(x, t). This visualization offers insights into the spatial distribution of the soliton’s intensity and phase, providing valuable information about its periodic structure and variation along the spatial domain. Figure 8(c) illustrates a curve graph displaying the absolute value of U₇(x, t) on the interval −100 ≤ x ≤ 100, showcasing the oscillatory behavior of the soliton over time. From Figure 8(c), it can be observed that at t = 30, U₇(x, t) demonstrates maximum oscillation, indicating a peak in the soliton’s intensity. Conversely, at t = 60, it shows minimum oscillation, representing a trough in the soliton’s intensity. At t = 90, it lies between these two extremes, suggesting a transitional phase in the soliton’s evolution.

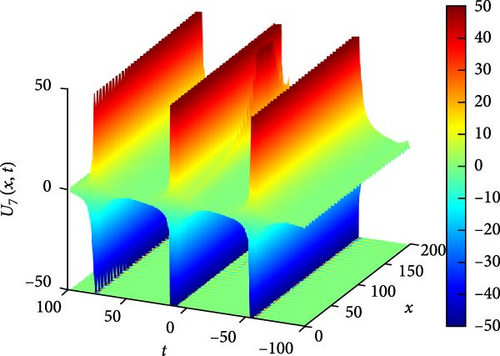
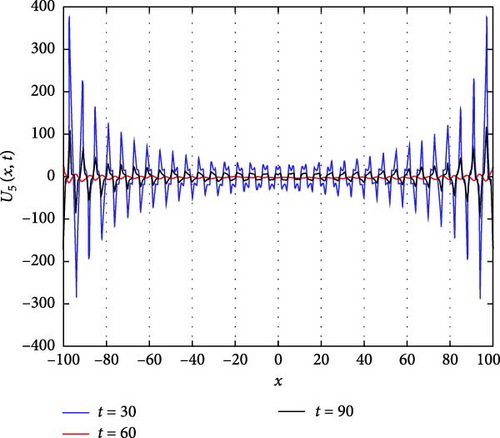
This alternating pattern of oscillations between large and small values reflects the complex dynamics of the solitary periodic waves, influenced by the interplay of various factors such as dispersion, nonlinearity, and boundary conditions. These factors collectively contribute to the intricate behavior observed in U₇(x, t), shaping its amplitude, phase, and overall evolution over time.

All physical interpretations are based on the above 3D and 2D images. We have always maintained that our conclusions can help researchers look for other new and precise solutions, which may be beneficial to researchers to explore the unknown phenomenon more precisely. Also, we trust that the above IMETFM can also be used to study several other systematic nonlinear differential equations with variable coefficients in future.

6. Pushing the Boundaries: Fusing Mathematical and Physical Visualization With Real-World Phenomena, Unleashing New Realms of Understanding

In the dynamic and ever-evolving realm of technology, innovation serves as a mere stepping stone. The essence of success rests in seamlessly integrating these revolutionary solutions into real-world applications, unlocking their full potential. This article delves into the critical endeavor of bridging the disparity between theoretical advancements and practical implementation, shedding light on vital strategies and key factors that pave the way to success. Our objective is to establish meaningful connections between the mathematical and physical visualizations we have developed and their tangible applications in the real world, enabling transformative effects on society.

The Burgers’ equation with variable coefficients is a mathematical model that describes the propagation of nonlinear waves. It has wide applications in the fields of nonlinear optics, nonlinear acoustics, and fluid mechanics. In Section 7 of the computer simulation, we randomly selected three interesting 3D plots, namely, Figures 5a, 7a, and 8a. From these plots, we depict the solitons in the analytical solutions U₄(x, t), U₆(x, t), and U₇(x, t). To establish a connection between these mathematically modeled figures and real-world phenomena, we present graphics illustrating “fiber-optic transmission under 5G technology,” “sound wave propagation in high-dimensional space,” and “waves on the ocean surface.” These graphics directly demonstrate the connection between U₄(x, t), U₆(x, t), and U₇(x, t) and their applications in the real world.

In Figure 9, we explored the behavior of the analytical solution U₄(x, t) and depicted it using a 3D mathematical model in MATLAB 2021b simulation, as shown in Figure 9a. Figure 9b illustrates the transmission of light in the fiber-optic cable in a special form of optical pulse, maintaining a relatively stable shape and energy during the propagation process, thereby revealing the characteristics of an optical soliton. Through the application of this visual representation, we forge a crucial connection between theoretical advancements and their practical applications, effectively bridging the gap that exists between these two realms. To provide a solid theoretical foundation for further research on the role of optical fiber transmission in 5G networks, fulfilling the data transmission requirements of future mobile communications.

In our endeavor to enhance the practical significance of our mathematical and physical understanding, we meticulously created a captivating visual representation demonstrating the propagation of sound waves in higher-dimensional space. This visual masterfully illustrates the intricate relationship between our mathematical model and its real-world implications. Given this scenario, Figure 10b clearly delineates the existence of sound wave solitons in higher-dimensional space, establishing a direct link to the 3D mathematical model U₆(x, t) depicted in Figure 10a, seamlessly bridging the gap between the prominently displayed 3D rendering in Figure 10a. Through these pursuits, we strive to achieve two primary objectives: first, to deepen our theoretical understanding, and second, to exemplify the profound impact of delving into mathematical solutions, unearthing captivating insights into the dynamic phenomena that unfold within the vast and interconnected tapestry of the natural world. This fusion of theoretical and real-world experiential knowledge is highly valuable as it aids in better comprehending phenomena and motivates us to explore and leverage these concepts in diverse scientific and engineering realms.

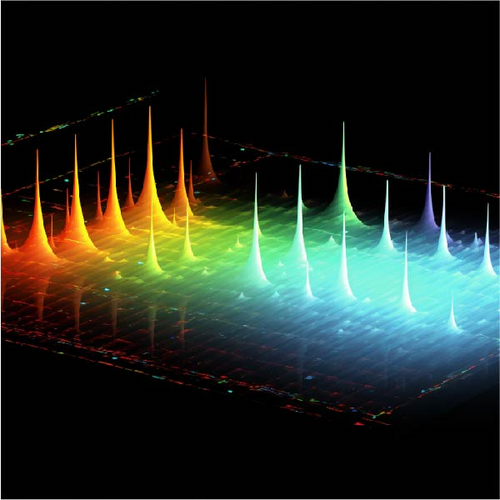
Through the study of the PBEVC, we can gain deeper insights into the wave behavior in the ocean and can predict and explain various observed phenomena, including tides, eddies, and wave interference. Figure 11a shows the 3D mathematical model of the soliton solution U₇(x, t) under computer simulation. To further relate the simulated graphics to the real world, we analyzed Figure 11b, which depicts a realistic scene of ocean surface wave fluctuations. Indeed, the ocean exhibits visual manifestations of the propagation of periodic solitary waves, and this image accurately captures the cyclic process of solitons in the ocean environment. By comparing these visual representations with real-world observations of ocean waves, we can gain deeper insights into the dynamics and behaviors of solitons, as well as their relevance in understanding and modeling similar phenomena in nature. Furthermore, the study of the PBEVC has laid a significant mathematical foundation for various fields, including ocean engineering, ocean resource development, and ocean climate simulation. The comprehension and application of these equations provide us with invaluable insights to optimize the design of oceanic structures, forecast alterations in the marine environment, and enhance the sustainable utilization of ocean resources. In summary, the study of the PBEVC presents a potent tool for augmenting our understanding of oceanic phenomena and propelling the advancement of ocean science and its associated disciplines.

7. Comparative Analysis and Discussion

Studying the interplay of stable equilibria can provide a deeper understanding of how noise perturbs the system within the energy landscape framework. By the IMETFM, we find a wealth of novel forms of exact nontraveling wave solutions for PBEVC. Many scholars, respectively, had studied the solution of PBEVC in previous papers [15, 59, 63, 64]. In 2021, Sulaiman, Yusuf, and Alquran [63] have obtained some new exact solutions for PBEVC using the knowledge of dynamics. Mohanty et al. [15] studied the exact solution of PBEVC by -extend mean in 2022. In 2023, Qi and Zhu [59] investigated the PBEVC by -extend mean and Jacobian elliptic function ideas. Gulsen et al. [64] obtained some new solutions and nonclassic symmetries of the PBEVC using the heir-equations method. Within our cognitive range, we seems firstly used the IMETFM to research the exact solutions of the PBEVC.

At the same time, in real application, noise is present because of various reasons, for example, error from experimental environment, manual error, and model error. We also consider the stochastic PBEVC under the influence of noise, which is the stochastic Burgers equations. We further discuss the energy landscape behavior of stochastic PBEVC, such as the phenomenon between stable equilibria and take use of our research which helps to analyze quasipotential of such stochastic system. This is also an another important innovation. Comparative with the previous literatures [15, 59, 63, 64], we obtain the composite form of the exponential function with the trigonometric, hyperbolic function. Therefore, the results obtained in this paper are more complex and more extensive and more diverse. To our best lore scope, a lot of new solutions are discovered which are not reported in previous paper such as U₁(x, t), U₂(x, t), U₃(x, t), U₄(x, t), U₅(x, t), U₆(x, t), and U₇(x, t).

8. Comprehensive Summary and Conclusion

This further hastened the exploration of a wide array of physical phenomena and their respective variable coefficient differential equations. The detailed important findings of this article can be summarized as follows:

1.
In this paper, using IMETFM to study Equation (6), we have found various forms of PBEVC solutions. To our best knowledge, we seem to be the first to use the IMETFM method to study PBEVC. We obtain the composite form of the exponential function with the trigonometric, hyperbolic function. A lot of new solutions have not been investigated in foregoing papers [1, 15, 59] such as U₁(x, t), ⋯, U₇(x, t). The results we obtained showed various features, such as complex solitons, oscillating and decaying solitons, singular periodic waves, Λ-shaped solitons, interacting solitons of two solitary waves, and needle-like isolated soliton solitons, among others.
2.
We also discuss the longtime behavior of stochastic PBEVC in small noise limit, and our various forms of IMETFM solution can help calculate the quasipotential between stable equilibria which helps understand noise-perturbed systemin the energy landscape view. It is obvious that with the diversity of g(t), a(t), q(t), the results of this paper contain richer and more complex solutions, which will not be listed one by one here. From the point of view of the calculation process, IMETFM is relatively complex, but more complex shape solutions can be got. We firmly believe that the IMETFM in this work may be more efficiently applied to find solutions to other nonlinear evolution equations.
3.
To establish a link between the illustrated graphs and real-world phenomena, we integrated visuals showcasing optical fiber transmission in 5G technology, the propagation of sound waves in multidimensional space, and the dynamic undulations of ocean surface waves. By incorporating real-world examples, we are able to bridge the divide between theoretical soliton behavior and practical physical phenomena, thus enriching our understanding of the significance and relevance of our discoveries.

We hope that our work will contribute to a better understanding of the physical and framework behavior in ocean models, nonlinear acoustics, and fiber-optic communications. We believe that our work has the potential to enhance our understanding and control of nonlinear effects, thereby advancing scientific research and technological progress in these fields.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This paper is supported by the Biomedical Science and Technology Support Special Project (19441914900).

Appendix A

()

Open Research

Data Availability Statement

Data sharing is not applicable to this article as no data sets were generated or analyzed during the current study.

References

1 Zayed E. M. and Abdelaziz M. A., Exact Traveling Wave Solutions of Nonlinear Variable-Coefficients Evolution Equations With Forced Terms Using the Generalized -Expansion Method, Computational Mathematics and Modeling. (2013) 24, 103–113.
10.1007/s10598-013-9163-4
Google Scholar
2 Kumar A. and Kumar S., Dynamical Behaviors With Various Exact Solutions to a (2+1)-Dimensional Asymmetric Nizhnik-Novikov-Veselov Equation Using Two Efficient Integral Approaches, International Journal of Modern Physics B. (2023) 2450064.
Google Scholar
3 Kumar S. and Kumar A., Newly Generated Optical Wave Solutions and Dynamical Behaviors of the Highly Nonlinear Coupled Davey-Stewartson Fokas System in Monomode Optical Fibers, Optical and Quantum Electronics. (2023) 55, no. 6, https://doi.org/10.1007/s11082-023-04825-6, 566.
10.1007/s11082-023-04825-6
Web of Science® Google Scholar
4 Kumar S. and Kumar A., A Study of Nonlinear Extended Zakharov-Kuznetsov Dynamical Equation in (3+1)-Dimensions: Abundant Closed-Form Solutions and Various Dynamical Shapes of Solitons, Modern Physics Letters B. (2022) 36, no. 25, https://doi.org/10.1142/S0217984922501408, 2250140.
10.1142/S0217984922501408
CAS Google Scholar
5 Kumar S. and Kumar A., Dynamical Behaviors and Abundant Optical Soliton Solutions of the Cold Bosonic Atoms in a Zig-Zag Optical Lattice Model Using Two Integral Schemes, Mathematics and Computers in Simulation. (2022) 201, 254–274, https://doi.org/10.1016/j.matcom.2022.05.009.
10.1016/j.matcom.2022.05.009
Web of Science® Google Scholar
6 Kumar S. and Kumar A., Abundant Closed-Form Wave Solutions and Dynamical Structures of Soliton Solutions to the (3+1)-Dimensional BLMP Equation in Mathematical Physics, Journal of Ocean Engineering and Science. (2022) 7, no. 2, 178–187, https://doi.org/10.1016/j.joes.2021.08.001.
10.1016/j.joes.2021.08.001
Google Scholar
7 Asghar U., Asjad M. I., Faridi W. A., and Akgül A., Novel Solitonic Structure, Hamiltonian Dynamics and Lie Symmetry Algebra of Biofilm, Partial Differential Equations in Applied Mathematics. (2024) 100653.
Google Scholar
8 Asghar U., Asjad M. I., Riaz M. B., and Muhammad T., Propagation of Solitary Wave in Micro-Crystalline Materials, Results in Physics. (2024) 58, https://doi.org/10.1016/j.rinp.2024.107550, 107550.
10.1016/j.rinp.2024.107550
Google Scholar
9 Asghar U., Asjad M. I., Faridi W. A., and Muhammad T., The Conserved Vectors and Solitonic Propagating Wave Patterns Formation With Lie Symmetry Infinitesimal Algebra, Optical and Quantum Electronics. (2024) 56, no. 4, https://doi.org/10.1007/s11082-023-06134-4.
10.1007/s11082-023-06134-4
Google Scholar
10 Asghar U., Faridi W. A., Asjad M. I., and Eldin S. M., The Enhancement of Energy-Carrying Capacity in Liquid With Gas Bubbles, in Terms of Solitons, Symmetry. (2022) 14, no. 11, 2294–2022, https://doi.org/10.3390/sym14112294.
10.3390/sym14112294
Google Scholar
11 Asghar U., Faridi W. A., Asjad M. I., Zidan A. M., and Eldin S. M., Explicit Propagating Electrostatic Potential Waves Formation and Dynamical Assessment of Generalized Kadomtsev-Petviashvili Modified Equal Width-Burgers Model With Sensitivity and Modulation Instability Gain Spectrum Visualization, Results in Physics. (2023) 44, 106167.
10.1016/j.rinp.2022.106167
Google Scholar
12 Xu T., Zhang C. Y., and Li J., et al.Symbolic Computation on Generalized Hopf-Cole Transformation for a Forced Burgers Model With Variable Coefficients From Fluid Dynamics, Wave Motion. (2007) 44, no. 4, 262–270 2007, https://doi.org/10.1016/j.wavemoti.2006.10.004, 2-s2.0-33847071172.
10.1016/j.wavemoti.2006.10.004
Web of Science® Google Scholar
13 Tang X.-Y., Liang Z.-F., and Hao X.-Z., Nonlinear Waves of a Nonlocal Modified KdV Equation in the Atmospheric and Oceanic Dynamical System, Communications in Nonlinear Science and Numerical Simulation. (2018) 60, 62–71 2018, https://doi.org/10.1016/j.cnsns.2017.12.016, 2-s2.0-85040242546.
10.1016/j.cnsns.2017.12.016
Web of Science® Google Scholar
14 Büyükaşık Ş. A. and Bozaci A., Dynamical Properties of Generalized Traveling Waves of Exactly Solvable Forced Burgers Equations With Variable Coefficients, Communications in Nonlinear Science and Numerical Simulation. (2021) 96, https://doi.org/10.1016/j.cnsns.2020.105682, 105682.
10.1016/j.cnsns.2020.105682
Google Scholar
15 Mohanty S. K., Kumar S., and Dev A. N., et al.An Efficient Technique of -Expansion Method for Modified KdV and Burgers Equations With Variable Coefficients, Results in Physics. (2022) 37, 105504.
10.1016/j.rinp.2022.105504
Google Scholar
16 Kumar S., Kumar A., and Mohan B., Evolutionary Dynamics of Solitary Wave Profiles and Abundant Analytical Solutions to a (3+1)-Dimensional Burgers System in Ocean Physics and Hydrodynamics, Journal of Ocean Engineering and Science. (2023) 8, no. 1, 1–14, https://doi.org/10.1016/j.joes.2021.11.002.
10.1016/j.joes.2021.11.002
Google Scholar
17 Burgers J. M., A Mathematical Model Illustrating the Theory of Turbulence, Advances in Applied Mechanics. (1948) 1, 171–199, https://doi.org/10.1016/S0065-2156(08)70100-5, 2-s2.0-77956834067.
10.1016/S0065-2156(08)70100-5
Google Scholar
18 Oliveri F., Painlevé Analysis and Similarity Solutions of Burgers’ Equation With Variable Coefficients, Journal of Engineering Mathematics. (1991) 25, no. 4, 317–327 1991, https://doi.org/10.1007/BF00037464, 2-s2.0-0026253684.
10.1007/BF00037464
Google Scholar
19 Wang M., Wang Y., and Zhou Y., An Auto-Backlund Transformation and Exact Solutions to a Generalized KdV Equation With Variable Coefficients and Their Applications, Physics Letters A. (2002) 303, no. 1, 45–51 2002, https://doi.org/10.1016/S0375-9601(02)00975-1, 2-s2.0-1442349436.
10.1016/S0375-9601(02)00975-1
CAS Web of Science® Google Scholar
20 Sophocleous C., Transformation Properties of a Variable Coefficient Burgers Equation, Chaos Solitons & Fractals. (2004) 20, no. 5, 1047–1057 2004, https://doi.org/10.1016/j.chaos.2003.09.024, 2-s2.0-0346094014.
10.1016/j.chaos.2003.09.024
Google Scholar
21 Abdou M. A. and Soliman A. A., Variational Iteration Method for Solving Burger’s and Coupled Burger’s Equations, Journal of Computational and Applied Mathematics. (2005) 181, no. 2, 245–251 2005, https://doi.org/10.1016/j.cam.2004.11.032, 2-s2.0-19144365030.
10.1016/j.cam.2004.11.032
Web of Science® Google Scholar
22 Vaganan B. M. and Kumaran M. S., Exact Linearization and Invariant Solutions of the Generalized Burgers Equation With Linear Damping and Variable Viscosity, Studies in Applied Mathematics. (2006) 117, no. 2, 95–108 2006, https://doi.org/10.1111/j.1467-9590.2006.00348.x, 2-s2.0-33745143554.
10.1111/j.1467-9590.2006.00348.x
Web of Science® Google Scholar
23 Cui M. and Geng F., A Computational Method for Solving One-Dimensional Variable-Coefficient Burgers Equation, Applied Mathematics and Computation. (2007) 188, no. 2, 1389–1401 2007, https://doi.org/10.1016/j.amc.2006.11.005, 2-s2.0-34248231712.
10.1016/j.amc.2006.11.005
Web of Science® Google Scholar
24 Xie S. S., Heo S., and Kimc S., et al.Numerical Solution of One-Dimensional Burgers’ Equation Using Reproducing Kernel Function, Journal of Computational and Applied Mathematics. (2008) 214, no. 2, 417–434 2008, https://doi.org/10.1016/j.cam.2007.03.010, 2-s2.0-39049173059.
10.1016/j.cam.2007.03.010
Web of Science® Google Scholar
25 Ivanova N. M., Sophocleous C., and Tracinà R., Lie Group Analysis of Two-Dimensional Variable-Coefficient Burgers Equation, Zeitschrift Fur Angewandte Mathematik Und Physik. (2010) 61, no. 5, 793–809 2010, https://doi.org/10.1007/s00033-009-0053-8, 2-s2.0-77957161417.
10.1007/s00033-009-0053-8
Google Scholar
26 Yu Y. and Ma H.-C., Exact Solutions of the Combined KdV-Burgers Equation With Variable Coefficients, Applied Mathematics and Computation. (2010) 215, no. 10, 3534–3540 2010, https://doi.org/10.1016/j.amc.2009.10.050, 2-s2.0-72749103158.
10.1016/j.amc.2009.10.050
Google Scholar
27 Ma H., Deng A., and Wang Y., Exact Solution of a KdV Equation With Variable Coefficients, Computers & Mathematics With Applications. (2011) 61, no. 8, 2278–2280 2011, https://doi.org/10.1016/j.camwa.2010.09.048, 2-s2.0-79953756069.
10.1016/j.camwa.2010.09.048
Web of Science® Google Scholar
28 Bekir A., Aksoy E., and Güner Ö., Bright and Dark Soliton Solitons for Variable Coefficient Diffusion-Reaction and Modified Korteweg-de Vries Equations, Physica Scripta. (2012) 85, no. 3, 35009–32012, https://doi.org/10.1088/0031-8949/85/03/035009, 2-s2.0-84858052896.
10.1088/0031-8949/85/03/035009
Google Scholar
29 El-Shiekh R. M., New Exact Solutions for the Variable Coefficient Two-Dimensional Burger Equation, Journal of Computational and Applied Mathematics. 2, no. 1, 21–24 2012.
Google Scholar
30 Büyükaşık Ş. A. and Pashaev O. K., Exact Solutions of Forced Burgers Equations With Time Variable Coefficients, Communications in Nonlinear Science and Numerical Simulation. (2013) 18, no. 7, 1635–1651 2013, https://doi.org/10.1016/j.cnsns.2012.11.027, 2-s2.0-84873570916.
10.1016/j.cnsns.2012.11.027
Web of Science® Google Scholar
31 Jiwari R., Mittal R. C., and Sharma K. K., A Numerical Scheme Based on Weighted Average Differential Quadrature Method for the Numerical Solution of Burgers’ Equation, Applied Mathematics and Computation. (2013) 219, no. 12, 6680–6691 2013, https://doi.org/10.1016/j.amc.2012.12.035, 2-s2.0-84873968124.
10.1016/j.amc.2012.12.035
Web of Science® Google Scholar
32 Aminikhah H. and Malekzadeh N., An Efficient Method for Systems of Variable Coefficient Coupled Burgers’ Equation With Time-Fractional Derivative, The Scientific World Journal. (2013) 2013, no. 1, 11, https://doi.org/10.1155/2013/687695, 2-s2.0-84886532714, 687695.
10.1155/2013/687695
PubMed Google Scholar
33 Zhang L.-H., Conservation Laws of the (2+1)-Dimensional KP Equation and Burgers Equation With Variable Coefficients and Cross Terms, Applied Mathematics and Computation. (2013) 219, no. 9, 4865–4879 2013, https://doi.org/10.1016/j.amc.2012.10.063, 2-s2.0-84871222715.
10.1016/j.amc.2012.10.063
Google Scholar
34 Pocheketa O. A., Popovych R. O., and Vaneeva O. O., Group Classification and Exact Solutions of Variable-Coefficient Generalized Burgers Equations With Linear Damping, Applied Mathematics and Computation. (2014) 243, 232–244 2014, https://doi.org/10.1016/j.amc.2014.05.099, 2-s2.0-84903188893.
10.1016/j.amc.2014.05.099
Google Scholar
35 Schulze-Halberg A., Burgers Equation With Time-Dependent Coefficients and Nonlinear Forcing Term: Linearization and Exact Solvability, Communications in Nonlinear Science and Numerical Simulation. (2015) 22, no. 1–3, 1068–1083 2015, https://doi.org/10.1016/j.cnsns.2014.08.029, 2-s2.0-84916618691.
10.1016/j.cnsns.2014.08.029
Web of Science® Google Scholar
36 Younis M., Ali S., and Mahmood S. A., Solitons for Compound KdV-Burgers Equation With Variable Coefficients and Power Law Nonlinearity, Nonlinear Dynamics. (2015) 81, no. 3, 1191–1196 2015, https://doi.org/10.1007/s11071-015-2060-y, 2-s2.0-84937642339.
10.1007/s11071-015-2060-y
Web of Science® Google Scholar
37 Gaur M. and Singh K., Symmetry Classification and Exact Solutions of a Variable Coefficient Space-Time Fractional Potential Burgers’ Equation, International Journal of Differential Equations. (2016) 2016, 8, https://doi.org/10.1155/2016/4270724, 2-s2.0-84991738142, 4270724.
10.1155/2016/4270724
Google Scholar
38 Pandir Y., Demiray S. T., and Bulut H., A New Approach for Some NLDEs With Variable Coefficients, Optik. (2016) 127, no. 23, 11183–11190 2016, https://doi.org/10.1016/j.ijleo.2016.08.019, 2-s2.0-84988025902.
10.1016/j.ijleo.2016.08.019
Google Scholar
39 Jima M., Shiferaw A., and Tsegaye A., Numerical Solution of the Coupled Viscous Burgers’ Equation Using Differential Quadrature Method Based on Fourier Expansion Basis, Applied Mathematics. (2018) 9, no. 7, 821–2018, https://doi.org/10.4236/am.2018.97057.
10.4236/am.2018.97057
Google Scholar
40 Seydaoğlu M., An Accurate Approximation Algorithm for Burgers’ Equation in the Presence of Small Viscosity, Journal of Computational and Applied Mathematics. (2018) 344, 473–481 2018, https://doi.org/10.1016/j.cam.2018.05.063, 2-s2.0-85048741453.
10.1016/j.cam.2018.05.063
Google Scholar
41 Huda M. A., Akbar M. A., and Shanta S. S., The New Types of Wave Solutions of the Burger’s Equation and the Benjamin-Bona-Mahony Equation, Journal of Ocean Engineering and Science. (2018) 3, no. 1, 1–10 2018, https://doi.org/10.1016/j.joes.2017.11.002.
10.1016/j.joes.2017.11.002
Web of Science® Google Scholar
42 Christov I. C., On the Numerical Solution of a Variable-Coefficient Burgers Equation Arising in Granuler Segregation, Materials Physics and Mechanics. 35, 21–27 2018.
Google Scholar
43 Gupta A. K. and Ray S. S., On the Solution of Time-Fractional KdV-Burgers Equation Using Petrov-Galerkin Method for Propagation of Long Wave in Shallow Water, Chaos Solitons & Fractals. (2018) 116, 376–380 2018, https://doi.org/10.1016/j.chaos.2018.09.046, 2-s2.0-85054194290.
10.1016/j.chaos.2018.09.046
Web of Science® Google Scholar
44 Büyükaşık Ş. A. and Bozaci A., Dirichlet Problem on the Half-Line for a Forced Burgers Equation With Time-Variable Coefficients and Exactly Solvable Models, Communications in Nonlinear Science and Numerical Simulation. (2020) 82, https://doi.org/10.1016/j.cnsns.2019.105059, 105059.
10.1016/j.cnsns.2019.105059
Google Scholar
45 Chen Y. and Zhang T., A Weak Galerkin Finite Element Method for Burgers’ Equation, Journal of Computational and Applied Mathematics. (2019) 348, 103–119 2019, https://doi.org/10.1016/j.cam.2018.08.044, 2-s2.0-85053079669.
10.1016/j.cam.2018.08.044
Web of Science® Google Scholar
46 Opanasenko S., Bihlo A., and Popovych R. O., Equivalence Groupoid and Group Classification of a Class of Variable-Coefficient Burgers Equations, Journal of Mathematical Analysis and Applications. (2020) 491, no. 1, https://doi.org/10.1016/j.jmaa.2020.124215, 124215.
10.1016/j.jmaa.2020.124215
Web of Science® Google Scholar
47 Mohammed W. W., Albosaily S., and Iqbal N., et al.The Effect of Multiplicative Noise on the Exact Solutions of the Stochastic Burgers’ Equation, Waves in Random and Complex Media. (2021) 1–13.
Google Scholar
48 Liu X.-Z., Yu J., Lou Z.-M., and Qian X.-M., A Nonlocal Variable Coefficient Modified KdV Equation Derived From a Two Layer-Fluid Systemand Its Exact Solution, Computers & Mathematics With Applications. (2019) 78, no. 6, 2083–2093 2019, https://doi.org/10.1016/j.camwa.2019.03.051, 2-s2.0-85063739125.
10.1016/j.camwa.2019.03.051
Google Scholar
49 Lan Z.-Z., Hu W.-Q., and Guo B.-L., General Propagation Lattice Boltzmann Model for a Variable-Coefficient Compound KdV-Burgers Equation, Applied Mathematical Modelling. (2019) 73, 695–714 2019, https://doi.org/10.1016/j.apm.2019.04.013, 2-s2.0-85065019564.
10.1016/j.apm.2019.04.013
Web of Science® Google Scholar
50 Wang M., Zhang J., Li E., and Xin X., The Generalized Cole-Hopf Transformation to a General Variable Coefficient Burgers Equation With Linear Damping Term, Applied Mathematics Letters. (2020) 105, https://doi.org/10.1016/j.aml.2020.106299, 106299.
10.1016/j.aml.2020.106299
Google Scholar
51 Li Z., Manafian J., and Ibrahimov N., et al.Variety Interaction Between k-Lump and k-Kink Solutions for the Generalized Burgers Equation With Variable Coefficients by Bilinear Analysis, Results in Physics. (2021) 28, https://doi.org/10.1016/j.rinp.2021.104490, 104490.
10.1016/j.rinp.2021.104490
Web of Science® Google Scholar
52 Fan E.-G., Traveling Wave Solutions for Nonlinear Equations Using Symbolic Computation, Computers & Mathematics With Applications. (2002) 43, no. 6-7, 671–680 2002, https://doi.org/10.1016/S0898-1221(01)00312-1, 2-s2.0-0036498657.
10.1016/S0898-1221(01)00312-1
Web of Science® Google Scholar
53 Fan E., Uniformly Constructing a Series of Explicit Exact Solutions to Nonlinear Equations in Mathematical Physics, Chaos Solitons & Fractals. (2003) 16, no. 5, 819–839 2003, https://doi.org/10.1016/S0960-0779(02)00472-1, 2-s2.0-0037408898.
10.1016/S0960-0779(02)00472-1
Web of Science® Google Scholar
54 Yang Z. and Hon B. Y. C., An Improved Modified Extended Tanh-Function Method, Zeitschrift Für Naturforschung A. (2006) 61, no. 3-4, 103–115 2006, https://doi.org/10.1515/zna-2006-3-401, 2-s2.0-33646873716.
10.1515/zna-2006-3-401
CAS Google Scholar
55 Mamun A. A., Ananna S. N., Gharami P. P., An T., and Asaduzzaman M., The Improved Modified Extended Tanh-Function Method to Develop the Exact Travelling Wave Solutions of a Family of 3D Fractional WBBM Equations, Results in Physics. (2022) 41, https://doi.org/10.1016/j.rinp.2022.105969, 105969.
10.1016/j.rinp.2022.105969
Google Scholar
56 Alhojilan Y. and Ahmed H. M., Novel Analytical Solutions of Stochastic Ginzburg-Landau Equation Driven by Wiener Process via the Improved Modified Extended Tanh Function Method, Alexandria Engineering Journal. (2023) 72, 269–274 2023, https://doi.org/10.1016/j.aej.2023.04.005.
10.1016/j.aej.2023.04.005
Google Scholar
57 Parkes E. J. and Duffy B. R., An Automated Tanh-Function Method for Finding Solitary Wave Solutions to Non-Linear Evolution Equations, Computer Physics Communications. (1996) 98, no. 3, 288–300 1996, https://doi.org/10.1016/0010-4655(96)00104-X, 2-s2.0-0030284901.
10.1016/0010-4655(96)00104-X
CAS Web of Science® Google Scholar
58 Fan E., Extended Tanh-Function Method and Its Applications to Nonlinear Equations, Physics Letters A. (2000) 277, no. 4-5, 212–218 2000, https://doi.org/10.1016/S0375-9601(00)00725-8, 2-s2.0-0034606149.
10.1016/S0375-9601(00)00725-8
CAS Web of Science® Google Scholar
59 Qi J. M. and Zhu Q. H., Further Results About the Non-Travelling Wave Exact Solutions of Nonlinear Burgers Equation With Variable Coefficients, Results in Physics. (2023) 46, 106285.
10.1016/j.rinp.2023.106285
Google Scholar
60 Beisner B. E., Haydon D. T., and Cuddington K., Alternative Stable States in Ecology, Frontiers in Ecology and the Environment. (2003) 1, no. 7, 376–382 2003, https://doi.org/10.1890/1540-9295(2003)001%5b0376:ASSIE%5d2.0.CO;2, 2-s2.0-84893425009.
10.1890/1540-9295(2003)001[0376:ASSIE]2.0.CO;2
Web of Science® Google Scholar
61 Kifer Y., Random Perturbations of Dynamical Systems, Nonlinear Problems in Future Particle Accelerators. (1988) 189, https://doi.org/10.1007/978-1-4615-8181-9.
10.1007/978-1-4615-8181-9
Google Scholar
62 Weinan E., Ren W., and Vanden-Eijnden E., Minimum Action Method for the Study of Rare Events, Communications on Pure and Applied Mathematics. 57, no. 5, 637–656 2004.
Google Scholar
63 Sulaiman T. A., Yusuf A., and Alquran M., Dynamics of Lump Solutions to the Variable Coefficients (2+1)-Dimensional Burger’s and Chaffee-Infante Equations, Journal of Geometry and Physics. (2021) 168, https://doi.org/10.1016/j.geomphys.2021.104315.
10.1016/j.geomphys.2021.104315
Google Scholar
64 Gulsen S., Hashemi M. S., and Alhefthi R., et al.Nonclassical Symmetry Analysis and Heir-Equations of Forced Burger Equation With Time Variable Coefficients, Computational and Applied Mathematics. (2023) 42, no. 5, 221–2023, https://doi.org/10.1007/s40314-023-02358-y.
10.1007/s40314-023-02358-y
Google Scholar

All articles

Wave Dynamics in Design: The Role of Nonlinear Potential Burgers’ Equation With Variable Coefficients

Abstract

1. Introduction

2. Apply the IMETFM to Equation (6)

3. The Exact Solution of PBEVC Is Applied in Some Concrete Examples

4. Connection to SED

5. Physical Interpretations of Graphs Obtained Through Computer Simulations

6. Pushing the Boundaries: Fusing Mathematical and Physical Visualization With Real-World Phenomena, Unleashing New Realms of Understanding

7. Comparative Analysis and Discussion

8. Comprehensive Summary and Conclusion

Conflicts of Interest

Funding

Appendix A

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Wave Dynamics in Design: The Role of Nonlinear Potential Burgers’ Equation With Variable Coefficients

Abstract

1. Introduction

2. Apply the IMETFM to Equation (6)

3. The Exact Solution of PBEVC Is Applied in Some Concrete Examples

4. Connection to SED

5. Physical Interpretations of Graphs Obtained Through Computer Simulations

6. Pushing the Boundaries: Fusing Mathematical and Physical Visualization With Real-World Phenomena, Unleashing New Realms of Understanding

7. Comparative Analysis and Discussion

8. Comprehensive Summary and Conclusion

Conflicts of Interest

Funding

Appendix A

Open Research

Data Availability Statement

References

Figures

References

Related

Information