1. Introduction

The manipulation of electron spins in semiconductors has attracted widespread interest as it plays an essential role in the design and manufacturing of spintronic devices [1–8]. To realize spintronic devices, spin splitting of energy bands is of crucial importance, which occurs in systems with asymmetric crystal potentials [9–11]. There are primarily two types of spin-orbit coupling (SOC) that are used to interpret spin splitting: Dresselhaus and Rashba SOC. The former is caused by the bulk inversion asymmetry of crystal potential (BIA) [12], while the latter originates from the structure inversion asymmetry (SIA) of the confinement potential in heterostructures [13, 14]. The SIA and Rashba spin splitting in semiconductor heterostructures can be significantly enhanced by applying internal or external electric fields that are perpendicular to the plane of the two-dimensional system [13–18] or by designing appropriate heterostructures with asymmetric geometric configurations [19–22].

Generally, there are strong spin-orbit effects in narrow-gap materials. For wide bandgap-III nitrides, it is expected that their large band gap will suppress the Rashba spin splitting. However, for AlGaN/GaN heterostructures grown along the c-axis, a large conduction band discontinuity and strong polarization effects at the interface can generate a strong built-in electric field and a high-density two-dimensional electron gas, which will increase the SIA of the heterostructures [23]. Therefore, an inherent SIA exists in the above-mentioned AlGaN/GaN heterostructures even in the absence of external electric fields, making them suitable for evaluating the Rashba spin splitting effect [9, 10, 23–25]. Previous research has investigated the Rashba coefficient and Rashba spin splitting in AlGaN/GaN heterostructures, focusing on factors such as Al content [9, 10, 24], uniaxial strain [26], well thickness [27], gate voltage [28], and conduction band nonparabolicity [29]. Additionally, the wave vector-dependent Rashba coefficient and nonlinear Rashba spin splitting in AlGaN/GaN quantum wells (QWs) [30] are also explored.

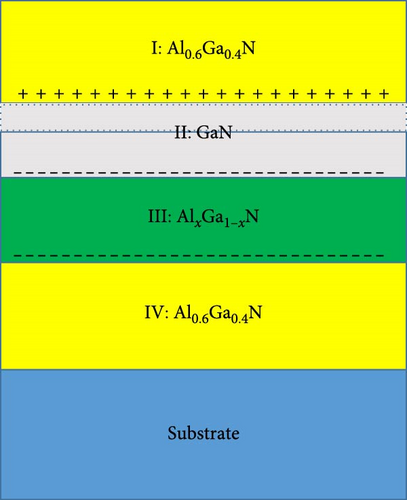
In this paper, we focus on the Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs, which are created by inserting an Al_xGa₁−_xN layer into the Al_0.6Ga_0.4N/GaN/Al_0.6Ga_0.4N QW. The schematic diagram of the structure is shown in Figure 1, and the corresponding conduction band profile and the probability density of electrons are shown in Figure 2. The insertion of the Al_xGa₁−_xN layer enhances the inherent SIA of the heterostructure. In Ref. [23], it is shown that the Rashba coefficient and the Rashba spin splitting in the Al_0.6Ga_0.4N/GaN/Al_0.3Ga_0.7N/Al_0.6Ga_0.4N QW can be modulated by changing the relative thickness of the GaN and Al_0.3Ga_0.7N layers and the external electric field. However, it remains unclear how the Al concentration in the inserted Al_xGa₁−_xN layer affects key factors, such as the polarization electric field, the Fermi level, the electron probability density, and other elements that influence the Rashba coefficient and Rashba spin splitting at the Fermi level. In this article, we found that the presence of the Al_xGa₁−_xN layer significantly affects the polarization electric field, the effective thickness of the GaN triangular potential well, and the electron probability density. Our findings indicate that the contributions to the Rashba coefficient from the left well and the left interface are dominant, and both increase with increasing x. Additionally, we observed that the contribution to the Rashba coefficient from the heterointerface is primarily determined by the electron probability density at the interface. As a result, the Rashba spin splitting at the Fermi level also increases with x due to the enhancement of the polarization electric field within the well and the movement of electrons toward the left interface. These results provide valuable insights for the design of spintronic devices.

The remainder of the paper is organized as follows. In Section 2, the method and the schematic diagram of the structure of the Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs are presented. Section 3 examines the Rashba coefficient and Rashba spin splitting for the first subband at the Fermi level of Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs, discussing in detail the individual factors that influence the Rashba coefficient and Rashba spin splitting. Finally, Section 4 gives a summary.

2. Methodology

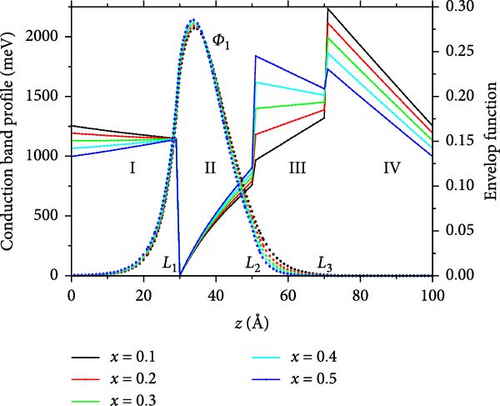
Figure 1 illustrates the schematic diagram of the structure of the calculated material, which consists of Ga (Al)-face (0001) Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs. Figure 2 displays the potential profile of the conduction band (V (z)) and the envelope function for the first confined state (Φ₁) in the Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs with x = 0.1, 0.2, 0.3, 0.4, and 0.5. As shown in Figures 1 and 2, the Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs, which are grown on top of the substrate, consist of the following regions: the left barrier region (I: LB), the left (II: LW), and right (III: RW) well regions, and the right barrier region (IV: RB). The thickness of the left and right barriers is 30 Å, while the well layer is composed of a 20 Å GaN layer (the left well) and a 20 Å inserted Al_xGa₁−_xN layer (the right well).

Material parameters are as follows. The spin-orbit split-off energy: Δ₁ = 22–80x (meV) [35], the crystal-field split energy: Δ_2,3 = 6 (meV) [36], and the interband momentum-matrix elements: $$ with E = 20 eV [9, 10].

As noted in Equation (2), the Rashba coefficient for the first subband of Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs consists of seven parts. The contributions to the Rashba coefficient from the left (Г_InterL), middle (Г_InterM), and right interfaces (Г_InterR) correspond to the first three terms. These components are proportional to the electron probability density at the left (L₁), middle (L₂), and right (L₃) heterointerfaces, respectively. They are also related to the eigenenergy E₁, potential jumps, and discontinuities in the band parameters at the heterointerfaces. The fourth term in Equation (2) is composed of four parts, where the contributions from the left and right barriers (Г_B) correspond to i = I and IV, while the contributions from the left (Г_W1) and right (Г_W2) wells correspond to i = II and III. They are all equal to the expectation value of B_iF_i over the ground state envelope function Φ₁, which is related to the position-dependent electric field (F_i), the confined energy level E₁, and the electron probability density [9, 10, 23–25, 27, 28, 31]. Therefore, the probability density of electrons significantly influences the magnitude of the Rashba coefficient. Once the Rashba coefficient α has been determined, the Rashba spin splitting at the Fermi level can be directly calculated by Δε = 2αk_F, where k_F is the Fermi wave vector, and it increases with the carrier density.

3. Results and Discussion

We will now calculate the Rashba coefficient and Rashba spin splitting for the first subband at the Fermi level of Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs. We will discuss how the Rashba spin splitting at the Fermi level varies with the Al content of the inserted layer and quantitatively explore the various factors that contribute to the Rashba coefficient and Rashba spin splitting.

As shown in Figure 2, the envelope function of the first subband peaks significantly around the left interface, and both the confining potential and the spatial distribution of electrons in the QW are asymmetric. These asymmetries are induced by the polarized electric field and the inserted Al_xGa₁−_xN layer, which will certainly result in a considerable Rashba coefficient and Rashba spin splitting.

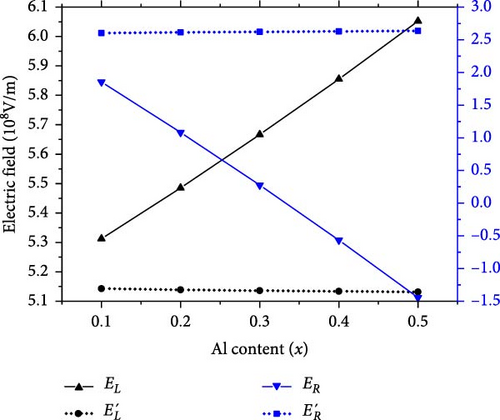
Figure 3a illustrates that when the polarization effect induced by the inserted layer is taken into account, the electric field at the left interface (E_L) increases linearly with x, while the electric field at the right interface (E_R) decreases in a similar manner. In contrast, if the polarization effect is not considered, the electric field at the left interface (E_L’) is reduced, while that at the right interface (E_R’) becomes stronger, and both will change more slowly with x. This indicates that the increase (decrease) of the electric field around the left (right) interface is primarily due to the growing polarization effect induced by the inserted layer [28]. For the Ga (Al)-face (0001) Al_xGa₁−_xN/GaN heterostructures, the polarization-induced charges at the interface are positive [24, 37–40]. Consequently, for the Ga (Al)-face (0001) Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs, the polarization charge at the left interface is positive, while the polarization charge at the middle (right) interface is negative, as illustrated in Figure 1. Additionally, if the polarization effect induced by the inserted layer is considered, with increasing x, the amount of negative charge at the middle (right) interfaces increases (decreases) [24, 37–40]. As a result, the electric field in the left well increases and the corresponding potential V (z) becomes steeper, while the electric field in the right well first decreases to zero (V (z) becomes smoother) and then reverses direction and increases in magnitude (V (z) becomes steeper). As a result, the movement of electrons towards the left interface is enhanced, as illustrated in Figure 2, and the probability density of electrons in the left well is further improved by the polarization effect induced by the inserted layer [23].

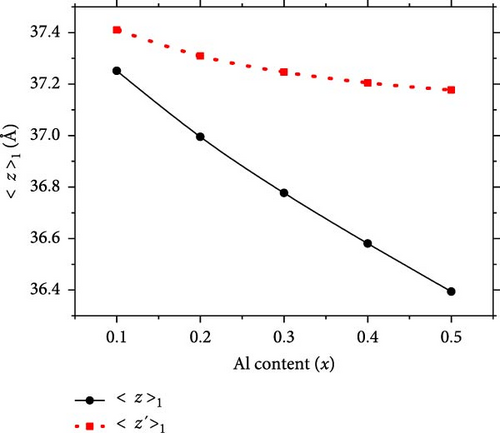
The average position of electrons in the first subband can be defined as: $$ [27, 28], with L being the thickness of the entire Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs. Figure 3b illustrates the average position of electrons in the first subband, where <z >₁ (solid lines) represents the scenario considering the polarization effect induced by the inserted layer, and <z’>₁ (dotted lines) denotes the case without this effect. As illustrated in Figure 3b, both <z>₁ and <z’>₁ gradually shift to the left side of the QW with increasing x. This observation is consistent with the findings in Ref. [31]. The reason for this shift is that the potential V (z) of the inserted Al_xGa₁−_xN layer increases with x, causing the peak of the envelope function for the first subband to move toward the left interface, as shown in Figure 2. Moreover, the polarization effect induced by the inserted layer causes the conduction band profile in the left well to become steeper, as shown in Figure 2. Consequently, the peak of the envelope function for the first subband shifts toward the left interface, as illustrated in Figure 3b. As a result, <z>₁ is smaller than <z’>₁, and <z>₁ decreases more rapidly as x decreases. This indicates that the effective thickness of the GaN triangular potential well continuously decreases.

Figure 4a illustrates the Rashba coefficient for the first subband of Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs, along with the contributions from the interfaces (Г_Inter = Г_InterL + Г_InterM + Г_InterR), the wells (Г_W = Г_W1 + Г_W2), and the barriers (Г_B) as a function of x. It is found that the magnitude of α increases linearly with x. Notably, the contribution from the wells is the largest, while that from the interfaces is slightly smaller. As can be seen in Figure 2, the probability of electrons appearing in the barrier and at the right heterointerface is relatively low, leading to minimal contributions to the Rashba coefficient from the barrier (Г_B) and the right interface (Г_InterR) [23]. Consequently, we only display the contributions to the Rashba coefficient from the left (Г_InterL) and middle (Г_InterM) interfaces, as well as from the left (Г_W1) and right (Г_W2) wells in Figure 4b.

As can be seen in Figure 4b, both Г_InterL and Г_InterM increase gradually with x, with Г_InterL being much larger than Г_InterM. To clarify this observation, Figure 4c illustrates (β_LW − β_LB), (β_RW − β_LW), and the probability density at both the left ($$) and middle ($$) heterointerfaces as a function of x. As x increases, the peak of the electron probability density shifts towards the left interface, and then the amplitude of the electron probability density at the left and middle interfaces increases, as evidenced by Figures 2 and 4c. Because the higher Al composition (x) results in a larger conduction-band offset, more electrons are transferred into the GaN triangular potential well [24, 31], as seen in Figure 2. Additionally, as shown in Figures 2 and 4c, the electron probability density at the middle interface is an order of magnitude lower than that at the left interface, so Г_InterL is much larger than Г_InterM. As x increases, (β_LW − β_LB) remains unchanged, while (β_RW − β_LW) varies rapidly, with their amplitudes being of the same order. This occurs because the material parameters near the left heterointerface remain unchanged, while those near the right heterointerface vary with x. Therefore, we can conclude that the amplitude of the electron probability density at the middle (left) interface is the dominant factor influencing the amplitude of Г_InterM (Г_InterL). What’s more, since $$ increases linearly with x, it follows that both Г_InterL and Г_Inter also increase linearly with x.

As illustrated in Figure 4b, Г_W1 gradually increases with x, while Г_W2 decreases gradually with x, and Г_W1 is much larger than Г_W2. As previously mentioned, the amplitude of Г_W1 (Г_W2) is directly proportional to the electric field and the electron probability density in the left (right) well. Figures 2 and 4c show that the electron probability density in the left well is considerably higher than that in the right well. Additionally, the electric field around the left interface is much stronger than that around the right interface, particularly when x is relatively large, resulting in a rather small amplitude of Г_W2. Moreover, as x increases, the electric field around the left heterointerface increases linearly (as illustrated in Figure 3a). Consequently, according to Equation (2), both Г_W1 and Г_W increase linearly. All these factors together result in a linear increase in α as a function of x.

Figure 5 illustrates (a) the Fermi level and the eigenenergy for the first confined state in the Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs with x = 0.1, 0.2, 0.3, 0.4, and 0.5, and (b) the corresponding Rashba spin splitting for the first subband at the Fermi level. We can see that both E_F and E₁ increase linearly with x, while their difference remains unchanged. As a result, the Fermi wave vector k_F doesn’t change. Therefore, the Rashba spin splitting for the first subband at the Fermi level of Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs increases linearly with x, as illustrated in Figure 5b.

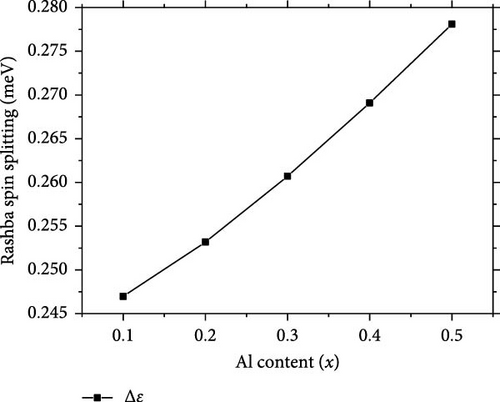
Finally, to further investigate the effects of the inserted Al_xGa₁−_xN layer, we calculate the Rashba coefficient and Rashba spin splitting for the first subband at the Fermi level of the Al_0.6Ga_0.4N/GaN/GaN/Al_0.6Ga_0.4N QW. The structural parameters of this QW are the same as those of the Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs, except that in the latter, the GaN layer in the right well is replaced by the Al_xGa₁−_xN layer. For the Al_0.6Ga_0.4N/GaN/GaN/Al_0.6Ga_0.4N QW, the Rashba coefficient is 1.1321 meV Å⁻¹, and the Rashba spin splitting is 0.2409 meV, which are both lower than those of the Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs. According to Ref. [27], the Rashba coefficient and Rashba spin splitting for the first subband at the Fermi level of the Al_0.6Ga_0.4N/GaN/GaN/Al_0.6Ga_0.4N QW decrease as the effective thickness of the GaN triangular potential well increases to a certain extent. Consequently, the effective thickness of the GaN triangular potential well in the Al_0.6Ga_0.4N/GaN/GaN/Al_0.6Ga_0.4N QW is much larger than that in the Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs. Therefore, by replacing GaN with Al_xGa₁−_xN in the right well, the effective thickness of the GaN triangular potential well in the Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs decreases as x increases.

In all, as x increases, the inserted Al_xGa₁−_xN layer brings about four main factors that enhance the Rashba spin splitting in the Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs. First, the inherent SIA of the heterostructure is enhanced. Second, the peak of the electron probability density moves towards the left interface because the potential of the inserted Al_xGa₁−_xN layer increases with x. Third, the effective thickness of the GaN triangular potential well decreases as x increases. Finally, the increasing polarization effect caused by the inserted layer leads to an increase (decrease) of the electric field around the left (right) interface.

4. Conclusions

In summary, we calculate the Rashba coefficient and Rashba spin splitting for the first subband at the Fermi level of the Al_0.6Ga_0.4N/GaN/Al_xGa₁−_xN/Al_0.6Ga_0.4N QWs. The inserted Al_xGa₁−_xN layer enhances the inherent SIA, makes the electron probability density move towards the left interface, increases the effective thickness of the GaN triangular potential well, increases the polarization effect, and increases (decreases) the electric field around the left (right) interface. As x increases, the peak of the electron probability density shifts towards the left interface, and the average electric field in the well increases. It is found that the electron probability density at the interface is the primary factor that decides the contribution to the Rashba coefficient from the heterointerfaces. Therefore, the two main contributions to the Rashba coefficient come from the left well and the left interface, and both of these contributions increase linearly with x. Moreover, as x increases, the Fermi wave vector k_F remains constant. Consequently, the Rashba spin splitting for the first subband at the Fermi level increases linearly with x. The results indicate that the inserted Al_xGa₁−_xN layer can enhance the Rashba coefficient and Rashba spin splitting in AlGaN/GaN QWs. These findings offer valuable insights for the design of spintronic devices.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research was supported by the “316” Project Plan of Xuchang University.