1. Introduction

Fractional differential equations extend integer differential equations to arbitrary orders. Unlike the local nature of integer order derivatives, fractional derivatives have global characteristics, capturing memory, and hereditary properties. For example, an integer derivative maps a parabolic curve into a straight line instantaneously, whereas a fractional derivative does so gradually to recover all the information the integer order derivative lost during the process of mapping the parabolic curve into a straight line. Because of these benefits, fractional derivatives are widely used in modeling physical problem in science and engineering as Fractional Partial Differential Equations (FPDEs).

Finding solution to FPDEs in a suitable functional space is a key focus for the members of the scientific community, especially mathematicians. Recently, few methods have been developed to obtain the solution of FPDEs. Unlike the numerical and the qualitative methods, see, for example, Barnes et al. [1] and Thalassinos et al. [2] articles, a commonly employed and highly suitable method for finding solution to FPDE is the analytic method, as it provides exact solution. One such analytic method which consistently transforms the FPDE into integral equation with the involvement of unknown Lagrangian multiplier before then generating series which finally the series converge to the exact solution is the Variational Iteration Method (VIM), for example, see articles by the authors in [3–5]. In order to use VIM to obtain the solution of FPDEs, the Lagrangian multiplier in the VIM must first be determined by applying the stationary condition before iteration. The value or the expression of the Lagrangian multiplier determines whether the series obtained will converge to exact solution of the FPDE. This Lagrangian multiplier to be determined in the VIM generates multiple values or expressions among which only one of these values or the expressions will yield a convergent series solution. Indeed, Momani and Odibat [4] applied the VIM to obtain solution to a fractional differential equation and identify four different values of the Lagrangian multiplier of which only one of these Lagrangian values yields a series which in turn yield the exact solution. In fact, there is no systematic rule for selecting the Lagrangian multiplier that will provide a series which converges to the exact solution of the fractional differential equation. However, the choice of the Lagrangian multiplier is purely guess work. This issue of multiple values of the Lagrangian multiplier in the VIM suggest that the exact solution of the fractional differential equation must be known before VIM can be used to obtain the solution of the fractional differential equation. Evidently, several researchers have made the same observation, for example, see articles by the authors in these papers [3–5]. Furthermore, He and Wu [3], observed that applying the VIM to solve the ordinary differential equation $$, together with the initial condition u(0) = 1, provided a function series which does not converge to the exact solution of the differential equation. Another analytic method which has captured the attention of researchers is the Adomian Decomposition Method (ADM) introduced by Adomian [6]. Applying the ADM to solve FPDE requires decomposing the nonlinear partial differential operator in the FPDE into Adomian polynomials, a process that is computationally difficult. With the aid of supercomputers, obtaining just one term of the series takes a significant amount of time, and computing higher order deformations and integrating the resulting polynomials is even more complex. Also, ensuring the convergence of the series emanating from the Adomian polynomials when solving the FPDE using the ADM is extremely challenging. Despite some modifications, see, Alizadeh and Effati [7–10] articles, the complexity in the computation as well as convergence remain an issue. Comparatively, He et al.[3, 5, 11] observed that the VIM has more advantages compared to ADM despite the drawbacks of the VIM. In using the Homotopy Analysis Method (HAM) to solve FPDE, a series which contains the convergence control parameter, ℏ, is obtained, see [12]. The choice of the convergence control parameter is purely based on guess work. This issue of guessing the convergence control parameter in HAM has been reported by several researchers across the globe [13–18]. How often must a researcher guess the convergence control parameter in the HAM derived series to find exact solution of the FPDE? Undoubtedly, applying the HAM to search for the exact solution of FPDE is laborious and time-consuming, which is not well received by researchers. Again, He [19] observed that applying HAM to solve a particular ODE, setting the convergence control parameter, ℏ = −1, resulted a series which converges to the exact solution. Due to this observation, He [19] named the HAM as Homotopy Perturbation Method (HPM). Using HPM to solve differential equation (whether ordinary or partial) does not always ensure convergence to the exact solution when convergence control parameter ℏ = −1. Interestingly, the HPM is not entirely different from HAM and several researchers including those in [13, 16–18] have confirmed that HPM is just a special case of HAM with the convergence control parameter ℏ = −1. The problem of guessing the value of the convergence control parameter, ℏ, remains unchanged despite the modification of the HAM, recently introduced by Odibat [20]. In addition, the Residual Power Series Method (RPSM) is a semi-analytic method for solving FPDEs which requires that one of the components of the solution to the FPDE must be known and as the iterations proceed to higher values, it becomes more tricky to compute the fractional derivatives of the residual function, see [21]. However, a combined method called the Laplace Residual Power Series Method (LRPSM) is for solving FPDEs which is tidius and combersome because the residual series is found followed by the Laplace transform of the residual series, see [22, 23]. The Fractional Power Series Method (FPSM) is a very powerful analytic method for solving FPDEs. This method involves an unknown function which is the sum of an infinite series of inner products of the independent variables in the FPDEs, see [24–27]. Addai et al. [28] modified the FPSM by replacing the polynomial function in the FPSM with the Mittag–Leffler function. The modified FPSM due to the authors in [28] is endowed with parameters which facilitate the obtaining of the solution of the FPDEs. The FPSM is improved by replacing the polynomial function in this method by the Gauss Hypergeometric Function (GHF). In this paper, the modification of the FPSM is better and provide continuum solution to the FPDEs as compared with the modified FPSM due to the authors in [28] because the Fractional Gauss Hypergeometric Power Series Method (FGHPSM) contains three parameters, Pochharmmer symbols, instead of two parameters in the improved FPSM due to authors in [28].

This paper is organized as follows: Section 1 contains introduction of the study. Section 2 introduces key concepts fundamental to the research. In Section 3, the modified FPSM is introduced and subsequently applied the modification called the FGHPSM to solve the fractional heat equation in multidimensions: two and three dimensions. In Section 4, the FGHPSM is applied to solve the fractional telegraph equation in a single dimension and the unique stable solution of the fractional heat and telegraph equations as well as the numerical results and interpretations are provided therein, while Section 5 concludes the results and findings presented in this paper.

2. Preliminary Results

In this section, we present some definitions and theorem which are used in achieving the results in this paper.

3. Main Results

In this section, we introduce the modification of the FPSM via GHF known as the FGHPSM and provide the solution steps of the modified method. Again, we solve the fractional heat equation in higher dimensions: two and three dimensions using the FGHPSM. Also, the FGHPSM is applied to solve the fractional telegraph equation. The functions obtained from solving the fractional heat and telegraph equations are derived to be in the Sobolev spaces ensuring that the functions exist and are unique in the Sobolev spaces. Again, the stability of a unique solution of both the heat and telegraph equations is provided therein.

3.5. Numerical Results

This section contains the numerical results of the findings in Subsection 3.2.1.

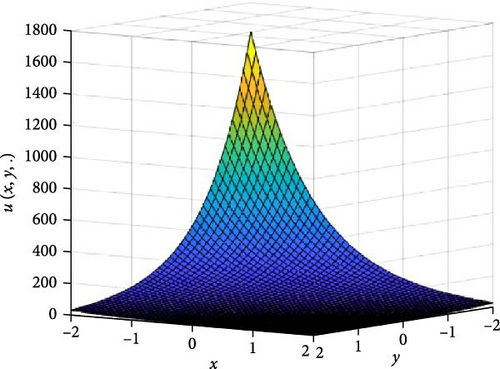
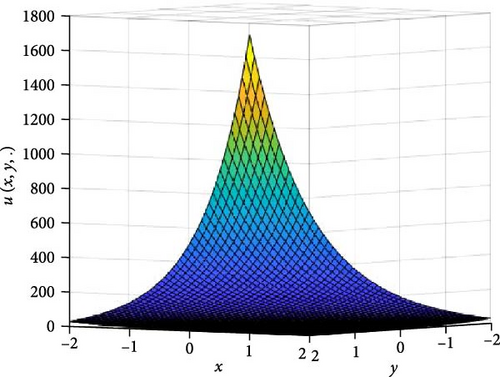
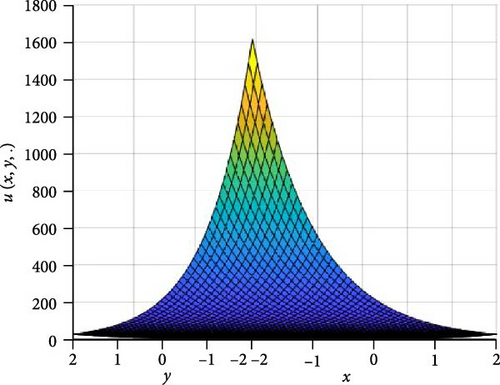
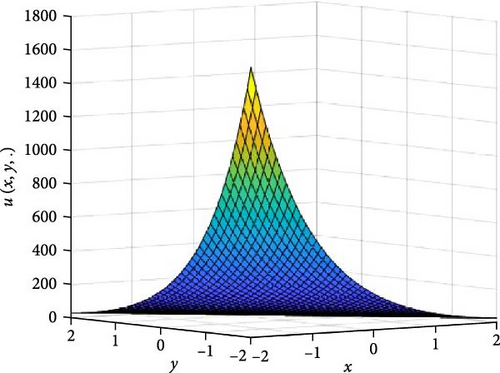
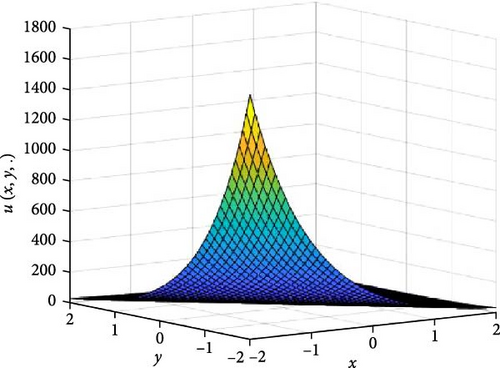
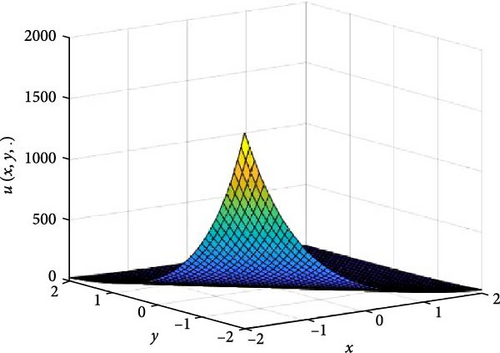
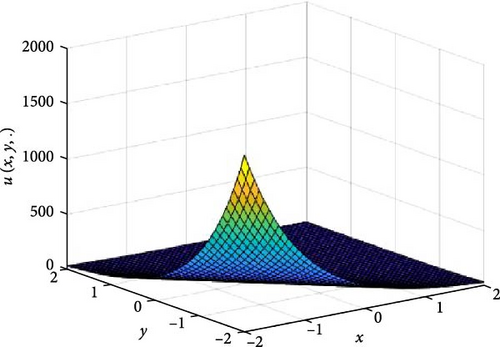
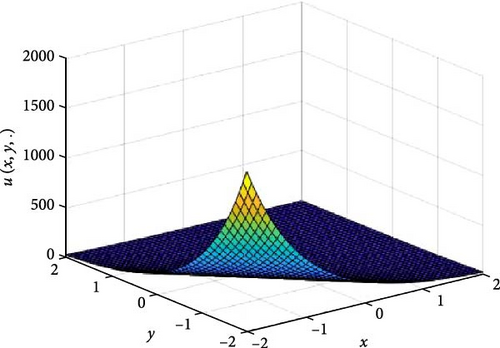
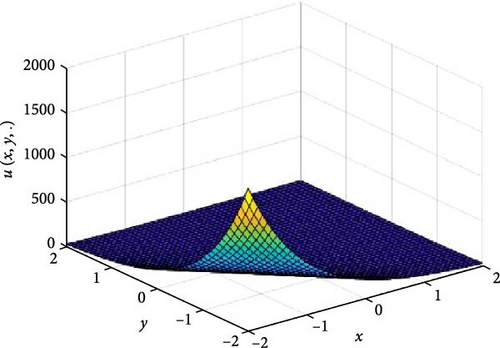
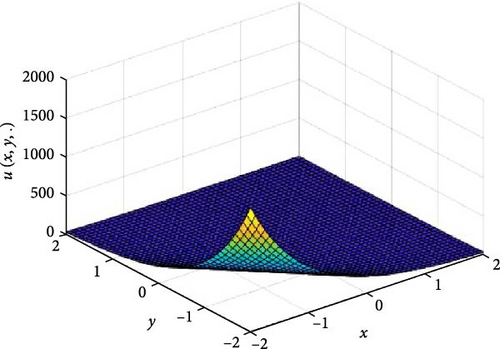
In Figures 1 and 2, the independent time, t, is suppressed by choosing t = 0.5 in order to display the graph of x and y spatial variables and u(x, y.). As α varies continuously from α = 0.1 to α = 1.0, the peak of graph flattens and the pictorial view of the coordinates become more visible, on the grounds that the stable solution, u(x, y.) in Equation (14), is inversely proportional to the value of α. As the value of α, approaches zero, the value of the stable solution, u(x, y.), peaked as shown in Figure 1a. Figure 1 consists of six graphs, and Figure 2 consists of four graphs. The six graphs in Figure 1a–f represent the stable solution u(x, y.) to the two-dimensional fractional heat equation in Equation (6) at fractional orders α = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, respectively. The four graphs in Figure 2a–d also represent the stable solution of u(x, y.) to the two-dimensional fractional heat equation in Equation (6) together with initial conditions at fractional orders α = 0.7, 0.8, 0.9, 1.0. We observed in Figures 1 and 2 that for α = 0.1, 0.2, …, 1.0, the solution is consistent and robust, as the graphs gradually stabilize toward α = 1. Thus, Figures 1 and 2 together confirm that the fractional order solution approaches the integer order solution. However, Figures 1 and 2 show that the fractional order recovers the lost information that the integer order did not capture. That is, Figures 1 and 2 clearly demonstrate the advantage of the memory and hereditary properties of the two-dimensional fractional heat equation.

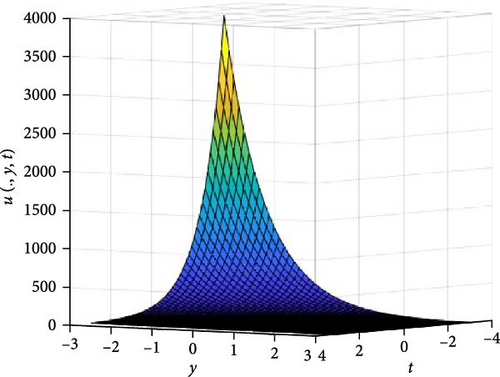
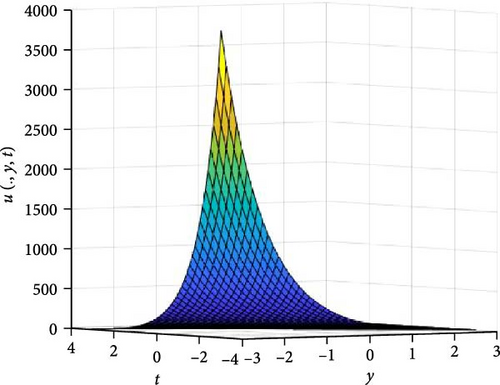
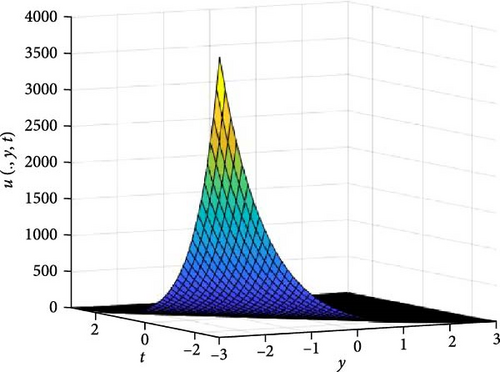
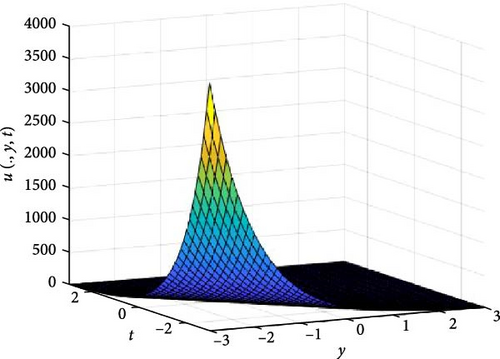
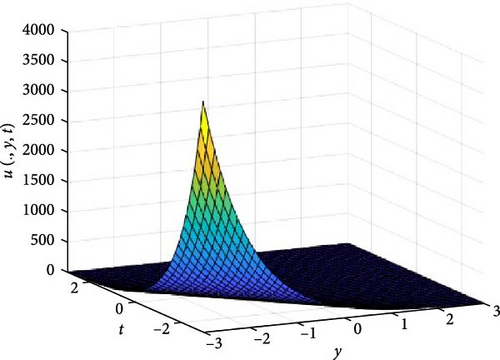
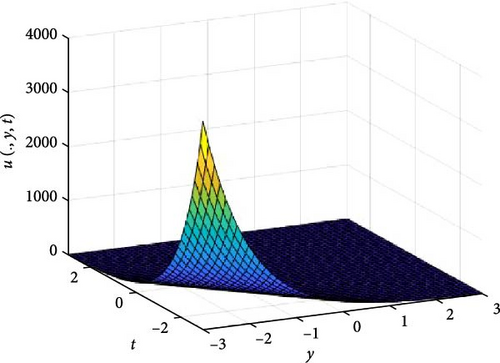
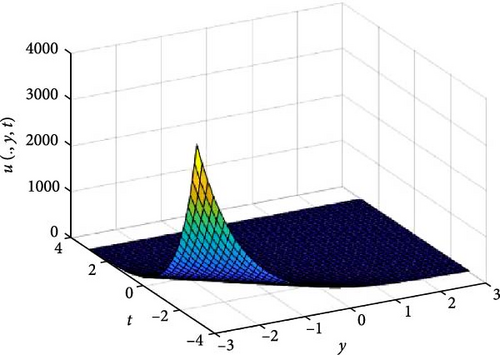
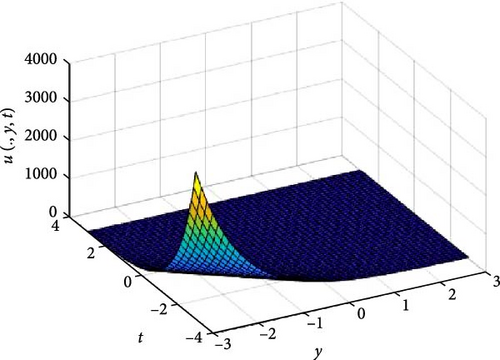
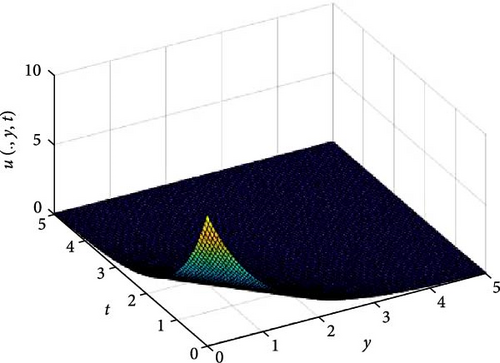
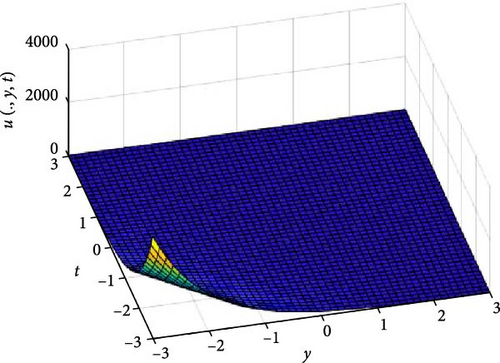
In Figures 3 and 4, the independent spatial variable, x is suppressed by choosing x = 0.5 in order to display the graph of the independent time, t and y spatial variable and u(., y, t). As α varies continuously from α = 0.1 to α = 1.0, the peak of graph flattens and the pictorial view of the coordinates become more visible on the grounds that the stable solution, u(., y, t) is inversely proportional to the value of α. As the value of α is in the neighborhood of zero, the value of the stable solution, u(., y, t), peaked as evidenced in Figure 3a. Figure 3 consists of six graphs, and Figure 4 comprises of four graphs. The six graphs in Figure 3a–f represent the solution u(., y, t) to the two-dimensional fractional heat equation in Equation (6) at fractional orders α = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, respectively. Also, the four graphs in Figure 4a–d represent the solution of u(., y, t) to the two-dimensional fractional heat equation in Equation (6) at fractional orders α = 0.7, 0.8, 0.9, 1.0. We can see in Figures 3 and 4 that for α = 0.1, 0.2, …, 1.0, the solution is consistent, as the graphs gradually approaches α = 1. Thus, Figures 3 and 4 together confirm that the fractional order solution approaches the integer order solution. However, Figures 3 and 4 show that the fractional order recovers the lost information that the integer order did not capture. Thus, the memory and hereditary properties are being captured.

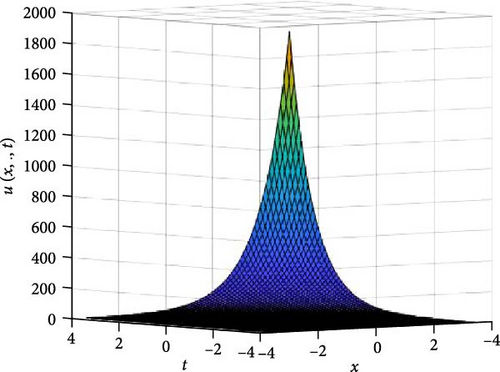
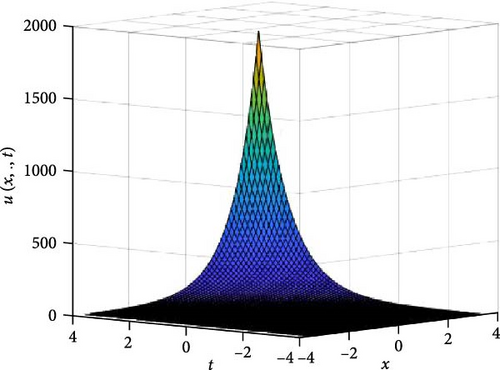
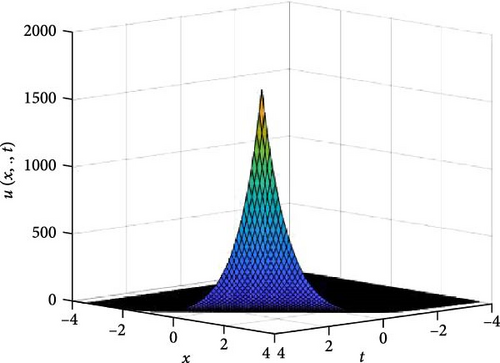
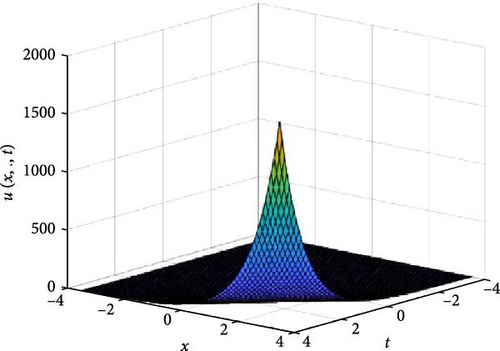
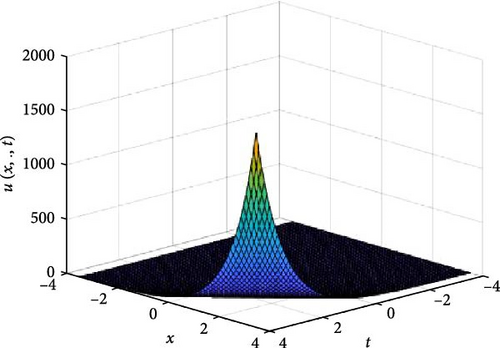
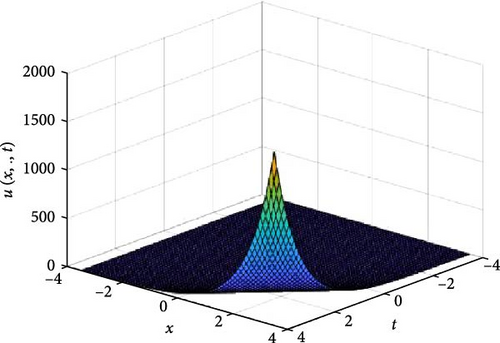
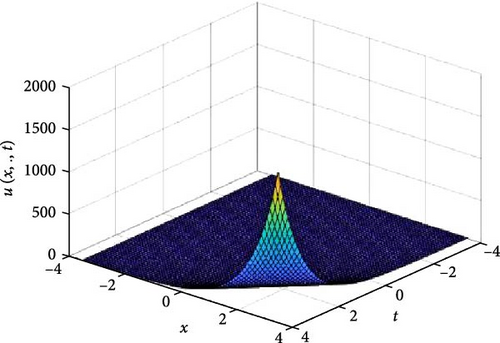
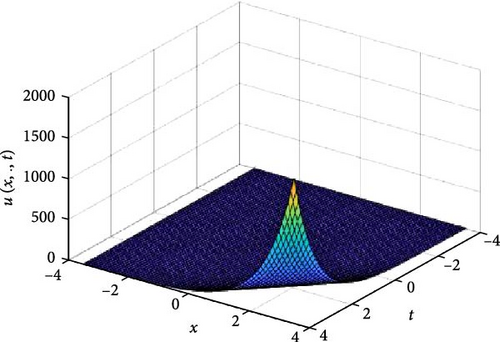
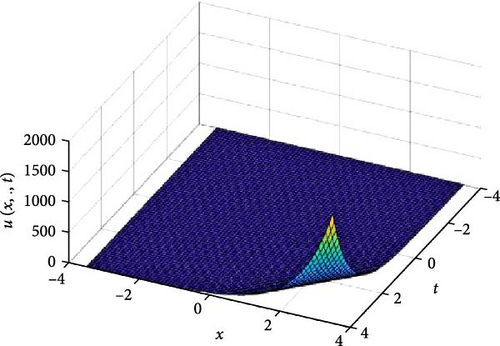
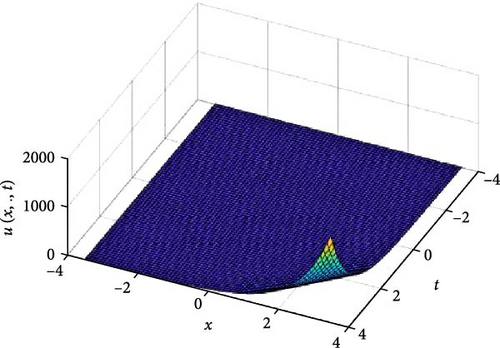
In Figures 5 and 6, the independent spatial variable, y is suppressed by choosing y = 0.5 in order to display the graph of the independent time, t and x spatial variable and u(x., t). As α varies continuously from α = 0.1 to α = 1.0, the peak of graph flattens and the pictorial view of the coordinates become more visible on the grounds that the stable solution, u(x., t) is inversely proportional to the value of α. As the value of α approaches zero the value of the stable solution, u(x., t), peaked as shown in Figure 5a. Figure 5 comprises of six graphs, and Figure 6 comprises of four graphs. The six graphs in Figure 5a–f represent the solution u(x., t) to the two-dimensional fractional heat equation in Equation (6) at fractional orders α = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, respectively. Also, the four graphs in Figure 6a–d represent the solution of u(x., t) to the two-dimensional fractional heat equation in Equation (6) at fractional orders α = 0.7, 0.8, 0.9, 1.0. We can see in Figures 5 and 6 that for α = 0.1, 0.2, …, 1.0, the solution is feasible and more consistent in the Sobolev space, as the graphs gradually approaches α = 1 from α = 0.1, 0.2, …. Thus, Figures 5 and 6 together confirm that the fractional order solution approaches the integer order solution. However, Figures 5 and 6 show that the fractional order recovers the lost information that the integer order did not capture. Thus, the advantage of the memory and hereditary properties of the fractional order are being captured.

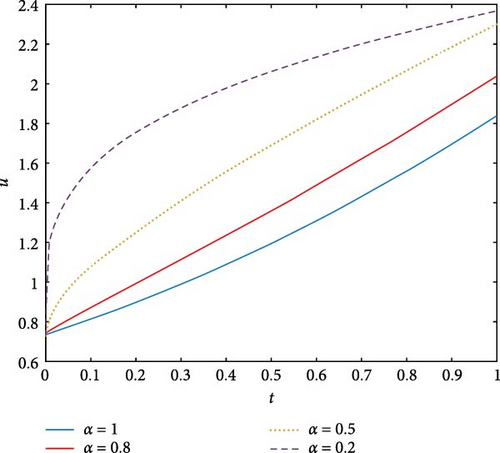
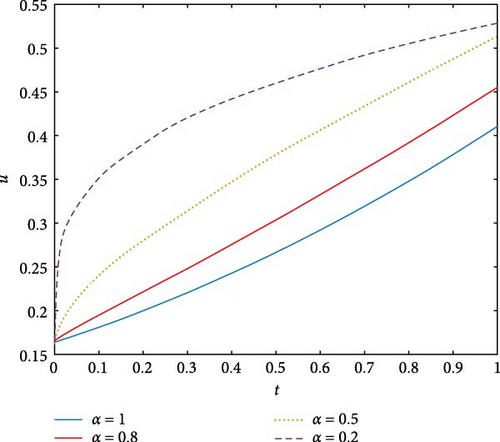
Figure 7 displays two-dimensional plots of the fractional heat equation for varying values of α (1, 0.8, 0.5, 0.2) using the FGHPSM. Specifically, for α = 0.2, 0.5, 0.8, 1, the solution for the respective fractional orders asymptotically stabilizes toward the integer solution. Consequently, the solution obtained through the FGHPSM is demonstrated to be robust and consistent, as illustrated in Figure 7.

Tables 1 and 2 depict the outcomes of the FGHPSM applied to the fractional heat equation variables. It shows the results for various values of α. It is noted that as the values of α approach an integer value, the solution remains consistent and robust in the Sobolev space.

Table 1. Results of u(x, y, t) for varying values of α = 0.1, 0.2, 0.3, 0.4, 0.5.

x	y	t	α = 0.1	α = 0.2	α = 0.3	α = 0.4	α = 0.5
1.5	0.5	0.1	0.6827	0.5781	0.4979	0.4382	0.3943
		0.2	0.7265	0.6446	0.5721	0.5111	0.4614
		0.3	0.7546	0.6908	0.6279	0.5701	0.5192
−0.5	1.5	0.1	0.1857	0.1571	1.3535	1.1911	1.0719
		0.2	1.9750	1.7522	0.5510	1.3894	1.2542
		0.3	2.0513	1.8770	1.7067	1.5496	1.4112
−2	−1.5	0.1	167.0435	141.4614	121.8363	107.2183	96.4868
		0.2	177.7803	157.7240	139.9876	125.0656	112.8990
		0.3	184.6491	169.0447	153.6503	139.4886	127.0334

Table 2. Results of u(x, y, t) using FGHPSM.

x	y	t	α = 0.6	α = 0.7	α = 0.8	α = 0.9	α = 1
1.5	0.5	0.1	0.3623	0.3388	0.3215	0.3087	0.2991
		0.2	0.4216	0.3901	0.3653	0.3457	0.3302
		0.3	0.4757	0.4393	0.4092	0.3844	0.3641
−0.5	1.5	0.1	0.9847	0.9209	0.8739	0.8390	0.8130
		0.2	1.1461	1.0604	0.9929	0.9397	0.8976
		0.3	1.2931	1.1941	1.1122	1.0449	0.9896
−2	−1.5	0.1	88.6428	82.8971	78.6648	75.5265	73.1851
		0.2	103.1657	95.4586	89.3811	84.5889	80.8017
		0.3	116.3993	107.4931	100.1210	94.0568	89.0806

3.5.1. Application of the FGHPSM for Solving Three-Dimensional Fractional Heat Equation

In this subsection, the solution of the fractional heat equation in three spatial variables is obtained using the FGHPSM.

Example 2. We consider fractional heat equation in three spatial variables together with initial conditions as follows:

$$ ()

$$ ()

$$ ()

$$ ()

where (x, y, z) ∈ R³ and s, h, r, w, p, q > 0. Setting

$$ ()

Using Equation (19), we obtain each term presented in Equation (15) as follows:

$$ ()

$$ ()

$$ ()

$$ ()

Substituting Equations (20)–(23) into Equation (15) gives the following equation:

$$

For n = 0, we have the following equation:

$$

For n = 1, we have the following equation:

$$

For n = 2, we have the following equation:

$$

It follows that:

$$ ()

Substituting Equation (24) into Equation (19), we obtain the function as follows:

$$ ()

3.7. Stable Solution of the Two-Dimensional Fractional Heat Equation

This section contains the claim that a unique solution u(x, y, z, t) of the fractional heat equation in three dimensions is asymptotically stable with respect to the initial conditions in the Sobolev spaces. To establish fact, we start by perturbing the initial conditions in Equations (16)–(18). The change in the initial conditions is obtained as follows:

$$

where 0 < ɛ < 1. We observed that $$ is bounded below by zero. The

$$

where 0 < δ < 1, but δ ≠ ɛ. We observed that $$ is bounded below by zero. Again,

$$

$$ is bounded below by zero.

We observed that the change in the initial conditions approach zero as n goes to infinity. Thus, a small perturbation in the initial conditions is bounded below by zero.

The corresponding change in the solution is as follows:

$$

where φ₁ = (x₁ + x₂) and φ₂ = (y₁ + y₂) + (z₁ + z₂). We observed that the corresponding change in the solution is bounded by $$ as n goes to infinity. Therefore, the solution u(x, y, z, t) of the fractional heat equation in three dimensions is asymptotically stable with respect to the small perturbation in the initial conditions.

3.7.1. Numerical Results

This section contains the numerical results of the findings in Subsection 3.5.1.

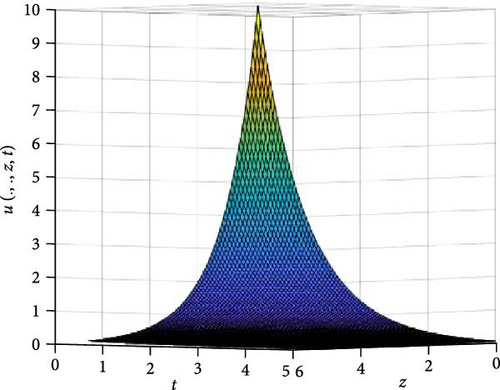
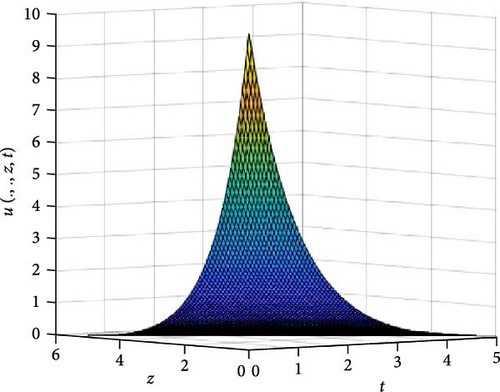
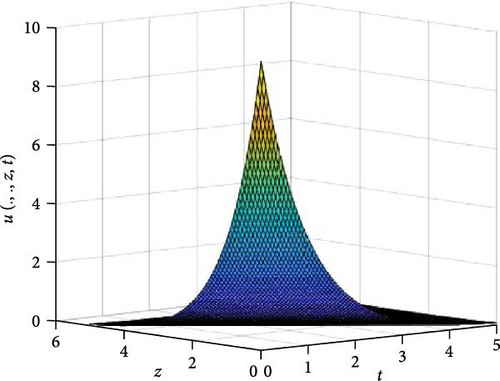
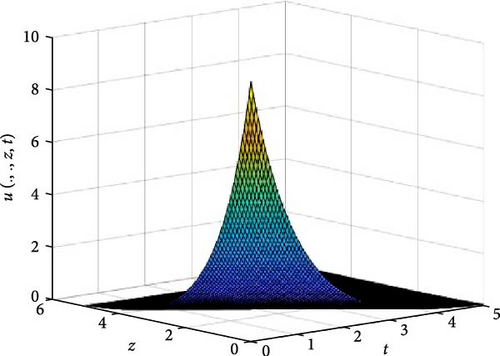
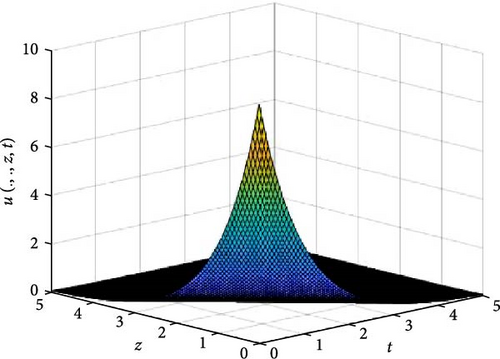
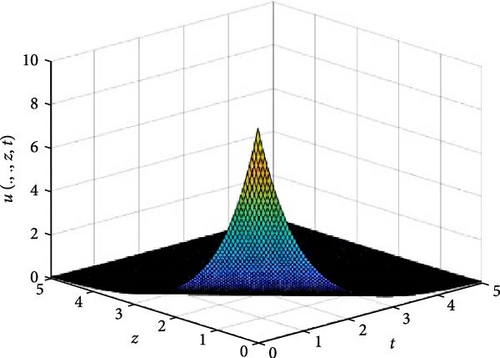
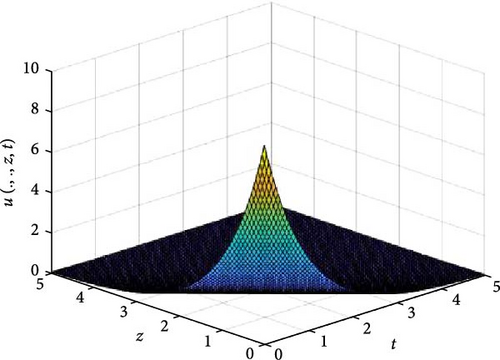
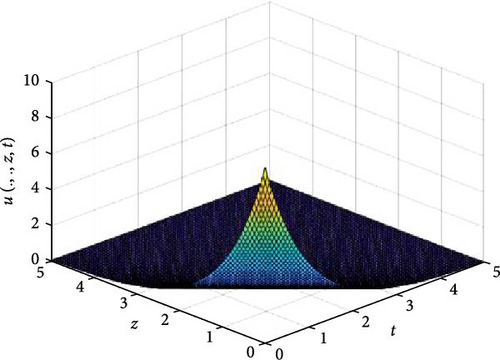
In Figures 8 and 9, the independent spatial variable, x and y are suppressed by choosing x = 0.5 and y = 0.5 in order to demonstrate the graph of the independent time, t and z spatial variable and u(.., z, t). Figure 8 consists of six graphs, and Figure 9 comprises of four graphs. The six graphs in Figure 8a–f represent the solution u(.., z, t) to the three-dimensional fractional heat equation at fractional orders α = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, respectively. Again, the four graphs in Figure 9a–d represent the solution of u(.., z, t) to the three-dimensional fractional heat equation at fractional orders α = 0.7, 0.8, 0.9, 1.0. We observed in Figures 8 and 9 that for α = 0.1, 0.2, …, 1.0, the solution is more feasible as the graphs gradually approaches α = 1. Thus, Figures 8 and 9 together confirm that the fractional order solution approaches the integer order solution. As α varies continuously from α = 0.1 to α = 1.0, the peak of graph flattens and the pictorial view of the coordinates become more visible on the grounds that the stable solution, u(.., z, t) is inversely proportional to the value of α. As the value of α approaches zero, the value of the stable solution, u(.., y, t), peaked as evidenced in Figure 8a. However, Figures 8 and 9 display that the fractional order recovers the lost information that the integer order did not capture. Thus, the memory and hereditary properties are being captured.

4. Application of the FGHPSM for Solving Fractional Telegraph Equation

In this section, the solution of the fractional telegraph equation is obtained using FGHPSM.

4.3. Numerical Results

In this subsection, we present the numerical results and interpretations of the solution fraction telegraph equation obtained using FGHPSM.

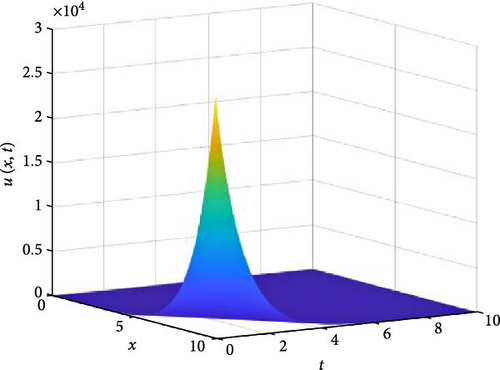
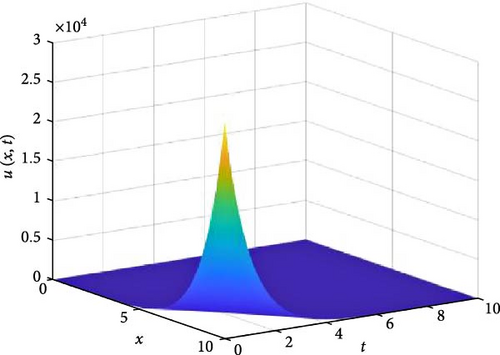
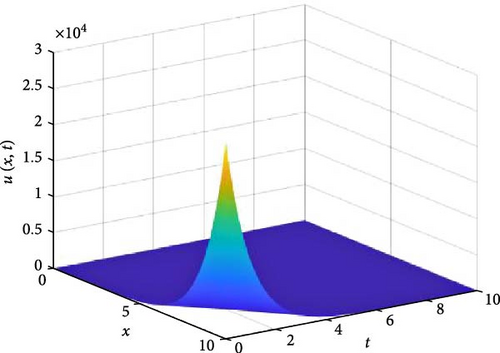
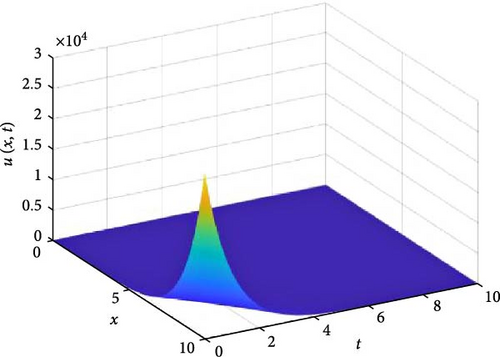
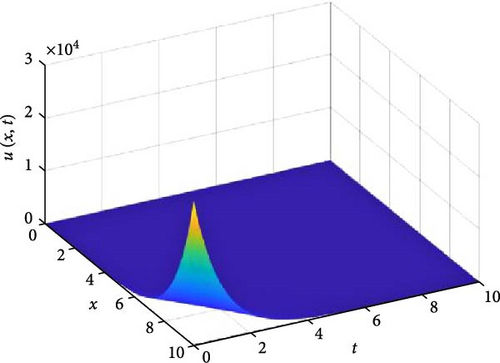
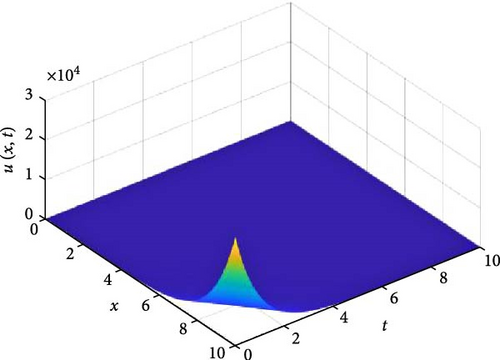
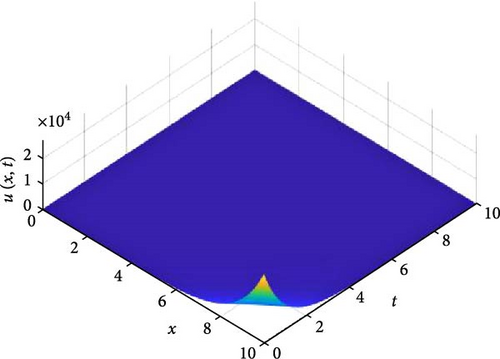
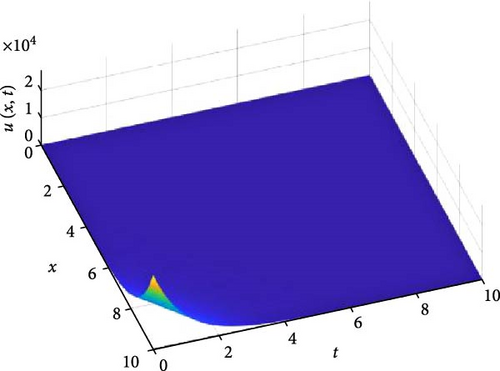
Figure 10 consists of six graphs, and Figure 11 consists of four graphs. The six graphs in Figure 10a–f represent the solution u(x, t) to the fractional telegraph equation at fractional orders α = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, respectively, using the FGHPSM. The four graphs in Figure 11a–d also represent the solution of u(x, t) to the fractional telegraph equation at fractional orders α = 0.7, 0.8, 0.9, 1.0 while maintaining β in equilibrium with β = 0.6. We observed in Figures 10 and 11 that for α = 0.1, 0.2, …, 1.0, the solution is feasible and more consistent in the Sobolev spaces, as the graphs gradually stabilize toward α = 1 from α = 0.1, 0.2, …, respectively. Thus, Figures 10 and 11 together reflect that the fractional order solution by the FGHPSM approaches the integer order solution. As α varies continuously from α = 0.1 to α = 1.0, the peak of graph flattens and the pictorial view of the coordinates become more visible on the grounds that the stable solution, u(x, t) is inversely proportional to the value of α. As the value of α is in the neighborhood of zero the value of the stable solution, u(x, t), peaked as evidenced in Figure 10a. However, Figures 10 and 11 demonstrate that the fractional order recovers the lost information that the integer order did not capture. That is, Figures 10 and 11 show the advantage of the memory and hereditary properties of the two-dimensional fractional telegraph equation.

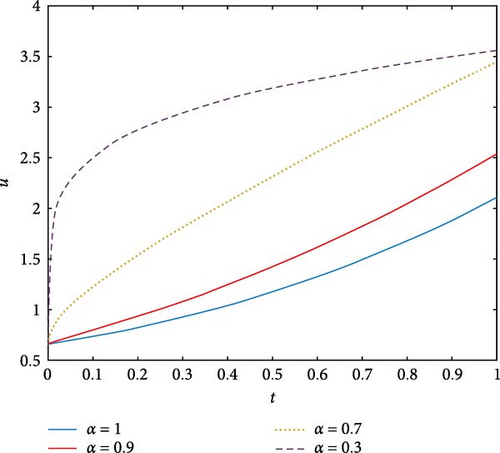
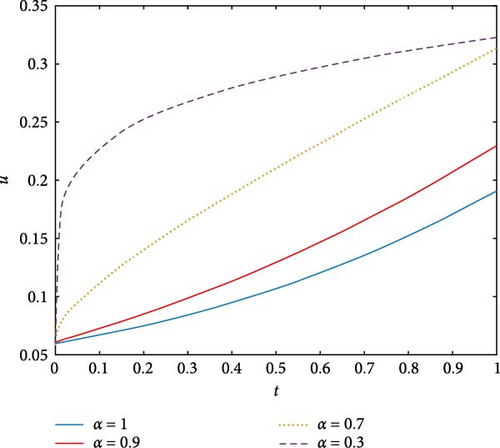
Figure 12 showcases two-dimensional plots of the fractional heat equation across various α values (1, 0.9, 0.7, 0.3) utilizing the FGHPSM. It is apparent that the FGHPSM demonstrates a more comprehensive nature, supplying information for every point in the Sobolev space where a satisfactory solution exists. Specifically, for α = 0.3, 0.7, 0.9, 1, the solution for the corresponding fractional orders asymptotically stabilizes toward the integer solution. Consequently, the solution derived from the FGHPSM is proven to be convergent, as depicted in Figure 12.

5. Conclusion

It revealed that FGHPSM yields continuum solution as compared with the FPSM. However, the solutions of the FPDEs yielded by the FGHPSM is the same as the solution of the FPDE by using the modified FPSM due to authors in [28] because the Pochhammer symbols in the FGHPSM canceled out in obtaining the solutions to the FPDEs. Surprisely, the modified FPSM containing three parameters, FGHPSM and the modified FPSM containing one parameter yield the same solutions of the FPDEs. The exact solutions for the fractional heat equation in both two and three dimensions, as well as the fractional telegraph equation in one dimension, were obtained using the FGHPSM. The solutions for the fractional heat and telegraph equations were independently derived to be in Sobolev spaces, ensuring the existence of unique solutions for the fractional heat and fractional telegraph equations, given that Sobolev spaces are complete. Also, the stable solutions for both the fractional heat equation and the fractional telegraph equation were obtained, indicating that these equations are well-posed since all the conditions for well-posedness were established in this paper. Numerical results and interpretations were obtained. However, we observed that the parameter α in the solutions of both the fractional heat equation and the fractional telegraph equation is inversely proportional to the solution u, which caused the graphs to diminish continuously from α = 0.1 to α = 1.0, by retrieving the lost information that the integer order equations lose along the path which is the memory property advantage that FPDEs have over the integer counterparts. The FGHPSM can be modified via H-function since the H-function generalizes the GHF. The modification via the H-function will provide a more general solution to the FPDE.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

There is no funding for this research.