Brucellosis remains a significant public health and economic burden, especially in developing nations where livestock–human interactions are frequent. This paper presents a partial differential equation (PDE) model to capture the transmission dynamics of brucellosis, with a focus on age-specific impacts in humans and domestic animals. Using the integrated semigroup approach, the positivity and boundedness of the model were established ensuring biologically meaningful solutions. The basic reproduction number (R₀) was derived through the Lotka–Sharpe–McKendrick integral equation, and the disease-free equilibrium (DFE) was proven to be locally asymptotically stable when R₀ < 1. Global sensitivity analysis was performed using the PAWN method to identify key parameters influencing disease dynamics. Results revealed that humans aged 0–72 years are carriers of the disease, while domestic animals, particularly those aged 0–5 and 11–15 years, act as significant reservoirs. Furthermore, environmental contamination was found to be a critical driver of transmission, emphasizing the urgent need for improved sanitation and hygiene measures. This study underscores the importance of targeting specific age groups and addressing environmental factors to enhance brucellosis control strategies, providing valuable insights for policymakers and public health practitioners.

1. Introduction

Brucellosis, also known as Malta fever, is a contagious disease of livestock that poses significant economic burdens globally [1]. It affects various animals, including cattle, swine, sheep, goats, camels, equines, and dogs, and can even extend to humans and marine mammals. The primary causative agents of brucellosis are different species of the Brucella family, B. abortus in cattle, B. melitensis in sheep and goats, B. suis in swine, and B. canis in dogs, as identified by the World Organization for Animal Health (WOAH) [2]. Transmission occurs through direct or indirect contact with infected animals, ingestion of contaminated dairy products, or inhalation of aerosols from infected animal secretions, making it a zoonotic concern for both animals and humans [3].

To mitigate the transmission of brucellosis, several interventions have been implemented, including vaccination, treatment, culling of seropositive animals, promoting proper environmental hygiene and sanitation, and personal protection [4–8]. However, these measures have proven challenging in some regions. For instance, a brucellosis control program in the Middle East showed limited implementation, with only 7% success in applying quarantine protocols [9]. While treatments have been introduced with the hope of eliminating Brucella from small ruminants and cattle, the bacteria often persist in tissues, such as lymph nodes, despite seemingly successful interventions. Additionally, the lack of extensive evaluation of published treatment regimens further complicates disease control, leading experts to generally discourage treatment [10].

Brucellosis remains a major global health concern, with an estimated 2.1 million human cases annually. However, its actual burden is often underestimated due to underreporting and diagnostic limitations [11]. While precise global prevalence and mortality rates are challenging to determine, the disease leads to significant morbidity, with a case fatality rate of ~1% [12]. In Tanzania’s Kilimanjaro Region, the reported annual incidence rates were 35 cases per 100,000 people in 2007–2008, 33 cases per 100,000 in 2012–2014, and 52 cases per 100,000 in 2020–2023, indicating its persistent occurrence. It remains endemic across Africa, with varying incidence rates, yet it is frequently underdiagnosed due to limited awareness and inadequate diagnostic infrastructure [13]. These patterns underscore the urgent need for enhanced surveillance systems, improved diagnostic tools, and strengthened public health interventions to effectively control brucellosis in endemic areas [14].

In efforts to understand and control the transmission of brucellosis, various mathematical models have been developed [6, 10, 15, 16]. These include models focusing on sheep brucellosis transmission [17], animal–human transmission dynamics in Mongolia [18], optimal control strategies [7], and time series analyses of human brucellosis [19]. Researchers have explored transmission mechanisms such as direct and indirect contact [20], vertical transmission [21], and seasonal influences [22, 23]. However, a significant limitation of many existing models lies in their assumption of homogeneous mixing populations, which restricts their applicability. In reality, individual contact probabilities and transmission risks are inherently heterogeneous. The spread of brucellosis is closely tied to host individuals’ heterogeneity, as factors like age in children, adults, or the elderly strongly influence exposure risks, clinical outcomes, and transmission pathways [14]. Integrating age-specific components into models maximize the likelihood of accurately understanding transmission dynamics and designing targeted interventions.

This paper presents a mathematical model of brucellosis transmission dynamics with a focus on age-specific factors. It examines the role of age in both the transmission and progression of brucellosis, offering insights distinct from previous models [3, 5–7, 9, 15], which did not incorporate age as a component. Unlike prior studies [2, 16, 18, 20, 23], this work employs partial differential equations (PDEs) as the mathematical framework, diverging from the more commonly used ordinary differential equations (ODEs). Although some studies have integrated age structures into their models [24, 25], the influence of age-specific variations on brucellosis transmission remains insufficiently explored in the literature. This study addresses this critical gap by developing a PDE-based age-structured model that more comprehensively captures the distinct roles of age in brucellosis transmission. Understanding age-related variations is essential, as susceptibility, transmission dynamics, and disease progression differ across age groups. For instance, children, adults, and the elderly exhibit varying exposure risks and clinical outcomes, with younger individuals more likely to experience acute symptoms and older individuals at greater risk of chronic complications. Similarly, domestic animals, as the primary reservoirs of brucellosis, display age-dependent differences young animals tend to be more susceptible to infection, while older ones shed pathogens more efficiently. By identifying these age-specific dynamics, this model provides a more refined understanding of brucellosis transmission and informs targeted public health interventions. Age-specific vaccination strategies, education campaigns, and testing programs can be optimized to enhance disease control efforts and improve resource allocation.

2. Model Formulation

The model consist of domestic animals, human, and reservoir of pathogens. At any given time t, human population are subdivided into susceptible individuals S_h(a, t), acute individuals A_h(a, t), and chronic individuals C_h(a, t) in a specific age group a ≥ 0. The total population is given by N_h(a, t) = S_h(a, t) + A_h(a, t) + C_h(a, t). The susceptible human is recruited into a population at a rate of π_h(a) > 0 by birth. They acquire the disease from infected animals and contaminated environment and transitioning into the acute class with a force of infection λ_h. In the acute stage, symptoms manifest, and treatment with antibiotics is possible and those who fail progress to chronic class at a rate of b(a). The probability of a human becoming infected is age-dependent and represented by α_h(a). Natural death occurs for all humans at a rate μ_h(a), while chronic individuals may also experience disease-induced death at the rate φ_h(a) due to complications of blood donating or bone marrow plantation. Notably, the model neglect recovery class with assumption that human who recover from the infection do not develop long-term immunity or the immunity is temporary, meaning they can become susceptible again soon after recovery.

For domestic animals, the model is subdivided into susceptible S_d(a, t) and infectious class I_d(a, t) at any given time t in specific age groups a. The total animal populations is N_d(a, t) = S_d(a, t) + I_d(a, t). The susceptible domestic animals are introduced into the population through birth and migration at a rate π_d(a) > 0. Susceptible domestic animals acquire the disease from infected animal through direct contact and contaminated environment and move to the infectious class with the force of infection λ_d. It is assumed that the probability of domestic animal to infect is α_d(a). All domestic animals experience natural death at a rate μ_d(a), and infected animals can also experience disease induced death at the rate φ_d(a) due to severe reproductive failures and other health issues. The model assume the domestic animal recovery rate is sufficiently small compared to the infection rate; the number of recovered animals remains negligible.

Infected domestic animals release pathogens into the environment at a rate ρ(a) contributing to the environmental reservoir of pathogens E(t). Pathogens decay at a rate ε(a), but Brucella species are known to survive in both environment and in animals for extended periods, allowing for long-term persistence of the bacteria [26]. It assumed that their immunity grow age-wise. The flow diagram of the model is shown in Figure 1, and the parameters used are in Table 1.

Table 1. Parameters (uniformly distributed) and their descriptions.

Parameter	Description	Values (1)	Values (2)	Source
π_h(a)	Human birth rate	0.001–0.005	0.005	[15]
α_h(a)	Human probability of getting infection	0.5–0.9	0.9	[27]
b(a)	Human transfer rate from acute class to chronic class	0.5–0.8	0.5	[12]
φ_h(a)	Human-induced death rate	0.5–0.9	0.3	[28]
μ_h(a)	Human death rate	0.1–0.9	0.4	[29]
π_d(a)	Domestic animal recruitment rate	0.0025–0.01	0.01	[3]
α_d(a)	Domestic animal probability of getting infection	0.6–1	1	[30]
φ_d(a)	Domestic animal-induced death rate	0.5–0.6	0.4	[18]
ρ(a)	Rate of concentration of bacteria	0.7–1	1	[31]
ɛ(a)	Rate of bacteria decay	0.3–0.6	0.5	[32]
μ_d(a)	Domestic animal mortality rate	0.1–0.9	0.4	[33]

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A flow chart diagram of brucellosis model for age structure.

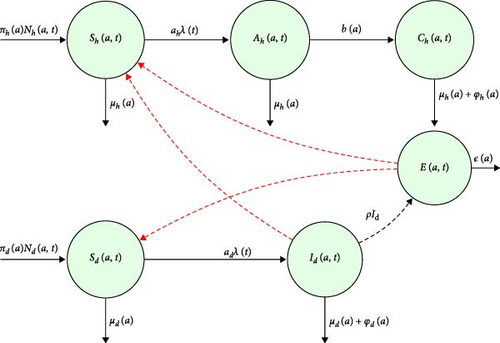
2.1. Model Equations

Based on the model description and flow diagram in Figure 1, the system of PDEs obtained is as follows:

()

The initial and boundary conditions are as follows:

where

is the total number source of infections, ϑ(a) is the domestic animal transmission rate, N_e(a, t) is the maximum carrying capacity of E(a, t), and a+ is the maximum age of an individual. The force of infection for domestic animals and humans, respectively, is as follows:

and

ϑ^∗(a) (donating blood or bone marrow).

3. Model Analysis

3.1. Normalization of the System

Consider the following total population for humans and domestic animals.

The total population for human is as follows:

The boundary and initial conditions are

and N_h(a, 0) = N_h0(a), respectively.

The total population for domestical animals is as follows:

The boundary and initial conditions are as follows:

where a₁, a₂, a₃, a₄ are the minimum age for humans, maximum age for humans, minimum age for domestic animals, and maximum age of domestic animals, respectively. This relation shows that the population dynamics are affected by the disease.

The model system shown in Equation (1) is normalized by scaling the following:

The normalized model system is as follows:

()

where

The initial and boundary values are as follows:

3.2. Existence of Positive Solution and Boundedness

The model system shown in Equation (2) shows positive solutions, and its boundedness is shown using the integrated semigroup approach [34]. Reformulate the system shown in Equation (2) into a more concise representation, commonly referred to as an abstract Cauchy problem. Consider whichdenote the set of all real-valued functions defined on an open subset such that . Also, assume X be a Banach space, defined by equipped with the norm for .

Assume Ω = {(s_h, a_h, c_h, s_d, i_d, e) ∈ X₊ | 0 ≤ s_h, a_h, c_h, s_d, i_d, e ≤ 1}, where . Consider B be a linear operator defined by .

In order to determine B₁, …, B₆, we need to neglect terms of order two and those which are multiplied by s_h, a_h, c_h, s_d, i_d, e in Equation (2), and then, we have the following:

()

Replace s_h, a_h, c_h, s_d, i_d, e by ψ₁(a), ψ₂(a), ψ₃(a), ψ₄(a), ψ₅(a), ψ₆(a) in the reduced system shown in Equation (3) to become the following:

with

, where D(B) is the domain given by the following:

and BC[0, a₊) is the set of absolutely continuous functions on [0, a₊).

Consider G be a nonlinear operator such that G : X → X by the following:

where ϕ is a bounded linear operator on L¹[0, a₊) given by

Assuming z(t) = (s_h(a, t), a_h(a, t), c_h(a, t), s_d(a, t), i_d(a, t), e(a, t)), we can rewrite the system shown in Equation (2) in an abstract Cauchy problem as follows:

()

where

According to Lotka and Sharpe and Lotka [35–37], the Cauchy problem shown in Equation (2) was formulated, and it has a solution; therefore, Equation (3) is well-posed.

3.3. Disease-Free Equilibrium (DFE)

Considering the system of Equation (2), the DFE is obtained from time independence. The DFE in an age-structured population model is obtained when time is independent because it represents a stable state where the prevalence of the disease in the population does not change over time. In this equilibrium, there are no new infections occurring, and the population is not experiencing any changes in disease transmission or progression. Equating each equation in model system as shown in Equation (2) equal to zero yields the DFE as follows:

()

3.4. Basic Reproduction Number and Local Stability of DFE

3.4.1. Basic Reproduction Number

Basic reproduction is the average number of secondary infections produced by a typical case of an infection in a population where everyone is susceptible. It is estimated within integral as the product of the rate of contacts in the host population, the probability of infection being transmitted during contact, and the duration of infectiousness. To obtain the basic reproduction number, we use the Lotka–Sharpe–Mckendrick integral equation [34, 38]. It is necessary to introduce a disturbance at DFE within the model system as shown in Equation (2); thus, we have the following:

The perturbation system is as follows:

()

with

Assume the solution of Equation (6) is in exponential form such that

The system obtained is as follows:

()

From Equation (7), we have

as the infectious class. Solving them gives as the following:

()

Substitute Equation (8) into Equation (9):

()

Substitute Equation (10) into Equation (11):

()

Substitute Equations (12), (13), and (10) into the last equation of the system as shown in Equation (7), and divide both sides by Λ ≠ 0; the obtained equations are as follows:

()

Equations (14) and (15) are called characteristic equations for the human population and domestical animal, respectively. Their right-hand sides are strictly decreasing functions of ω which assumes all the values in (0, ∞).

Denote the right-hand side of Equation (14) by M_h(ω) and define the basic reproduction number for the human population as M_h(0) = R_0h. Then, it gives the following:

()

Also, denote the right-hand side of Equation (15) by M_d(ω), and define the basic reproduction number for the domestic animal population as R_0d = M_d(0). Then, we have the following:

()

3.4.2. Local Stability of the DFE Point

Theorem 1. The DFE is locally asymptotically stable if R_0h < 1 and unstable if R_0h > 1.

Proof. , , and . Equation (12) has a unique negative real solution ω^∗ if and only if M_h(0) < 1; hence, R_0h < 1. Also, Equation (12) has a unique positive (zero) real solution if R_0h > 1. To depict that ω^∗ is the dominant real part of the roots of M_h(ω), we let ω = r + iq be an arbitrary complex solution to Equation (12); thus, 1 = M_h(ω) = |M_h(r + iq)| ≤ M_h(r), indicating that R_0h(ω) ≤ ω^∗. Then, it follows that the DFE is locally asymptotically stable if R_0h < 1 and unstable if R_0h > 1.

Theorem 2. The DFE is locally asymptotically stable if R_0d < 1 and unstable if R_0d > 1.

Proof. , , and . Equation (13) has a unique negative real solution ω^∗ if and only if M_d(0) < 1, and then R_0d < 1. In addition, Equation (13) has a unique positive (zero) real solution if R_0d > 1. To depict that ω^∗ is the dominant real part of the root of M_d(ω), let ω = x + iy be an arbitrary complex solution to Equation (13); thus, 1 = M_d(ω) = |M_d(x + iy)| ≤ M_d(x), indicating that R_0d(ω) ≤ ω^∗. Then, it follows that the DFE is locally asymptotically stable if R_od < 1 and unstable if R_od > 1.

3.4.3. Global Stability of the DFE Point

Assume ∃ a positive constant K for convenience:

Theorem 3. The DFE is globally asymptotically stable if K · R_oh < 1 and K · R_od < 1 and otherwise.

Proof. To show that

Integrating the system as in Equation (2) along the characteristics line (t − a > 0) gives the following:

()

Substituting Equation (19) into Equation (20) gives the following:

()

Substituting Equation (22) into Equation (23) gives the following:

()

Putting Equations (24), (25), and (22) into the last equation of the system as shown in Equation (2) gives Equations (26) and (27). λ(t) is for human and domestic animal, respectively:

()

Taking the limit supremum of λ(t) as t → ∞, it can be easily shown that

which implies that

It results in and . Thus, and , since we have and , which completes the proof.

3.5. Endemic Equilibrium

An endemic equilibrium is obtained from time-independent; thus,we have the following:

()

From the system of Equation (28), the following are obtained:

()

Substituting Equation (30) into Equation (31), we get Equation (35) as follows:

()

Substitute Equation (33) into Equation (34) to obtain the following:

()

Substituting Equations (35), (36), and (33) into

, we get Equations (37) and (38), respectively, as follows:

()

and

()

Assume the right-hand side of Equations (37) and (38) is denoted by R(η), respectively. If R(η) > 1, there exists an endemic equilibrium.

3.5.1. Local Stability of Endemic Equilibrium

In order to show the local stability of the endemic equilibrium, a disturbance is introduced in the model system as in Equation (2) at the endemic equilibrium as follows:

The introduced disturbance results into the following system of equations:

()

The initial conditions are .

Assume the solution of Equation (39) is in exponential form such that

Then, it gives Equation (40):

()

Assume , , , , , and .

It gives Equation (41):

()

Integrating Equation (41) gives the following:

()

Substitute Equation (46) into Equation (47):

()

Substitute Equations (43) into Equation (44):

()

Denoting the last equation of the system as shown in Equation (41) by P(σ) gives the following:

()

It follows that P (σ) is a decreasing function such that if the perturbations introduced at the endemic steady state are small. Setting σ = 0 in Equations (50) and (51), we notice that the first integral is equal to 1. From Equation (45), if the difference of , and from Equation (42), is positive if the difference of , which shows that the second integral is positive if is greater than zero and if is greater than zero. Thus, with the previous considerations, we have P(0) < 1. It follows that a unique positive real solution of P(σ = 1) exists, and as consequence [38], we have the following theorem: The endemic equilibrium state is locally asymptotically stable if R_0d > 1 and R_0h > 1.

4. Sensitivity Analysis

Sensitivity analysis is an essential tool for evaluating mathematical models, particularly in assessing the relative importance of model parameters in disease transmission and prevalence. The PAWN method, a global sensitivity analysis technique, is employed to quantify the influence of model parameters on the variability of the model’s outputs. This approach characterizes output distributions through their cumulative distribution functions (CDFs) [39, 40]. Sixteen input parameters from the brucellosis model are considered, with reference values provided in Table 1. The PAWN index used in this study is identified as the median Kolmogorov–Smirnov (KS) statistic across conditioning intervals:

A 95% confidence interval is estimated through bootstrapping. We consider four key classes acute, chronic, infected, and environmental due to their significant impact on model outputs. Figures 2–7 indicate that μ_h is the most influential parameter for the acute, chronic, and infected classes, while μ_d is the most influential for the environmental class, as shown in Figures 8 and 9. This implies that brucellosis progression and prevalence in humans are highly sensitive to the mortality rate. Specifically, disease-related mortality significantly influences the size and behavior of the acute, chronic, and infected human subpopulations. Meanwhile, the death rate of domestic animals (μ_d) directly affects pathogen load in the environment, as animal carcasses and waste products serve as significant reservoirs for Brucella bacteria. A higher μ_d could lead to increased environmental contamination.

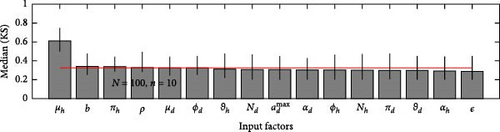
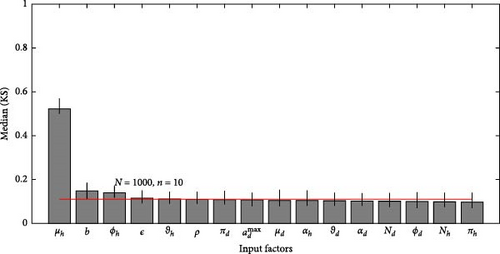
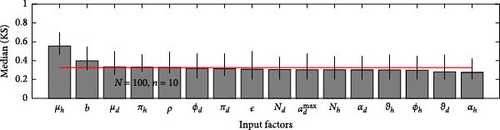
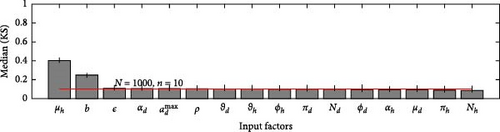
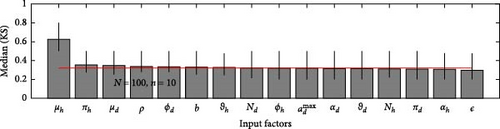
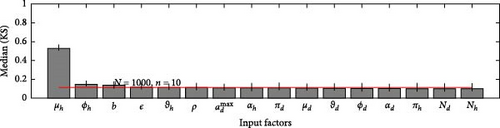
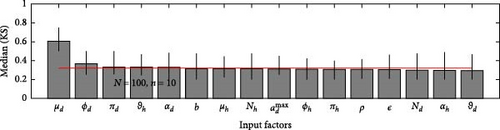
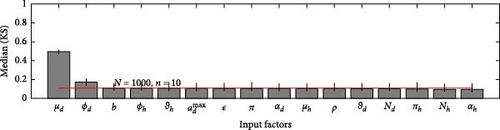
According to Figure 3, the second most influential parameters are φ_d, b, φ_h, N_d, α_h, and ɛ. These parameters form a secondary group that plays a crucial role in refining the understanding of brucellosis transmission dynamics and guiding the design of specific, secondary-level interventions to complement efforts targeting the primary influential factors. The remaining parameters exhibit average sensitivity values close to the dummy parameter, suggesting they may be uninfluential. Further analysis reveals that larger sample sizes improve the identification of highly influential parameters. For instance, Figure 5 ranks b as the second most influential parameter in the chronic class, while Figure 7 ranks φ_h and b as the second most influential parameters in the infected class. Similarly, Figure 9 identifies φ_d as the second most influential parameter in the environmental class. Together, these parameters provide valuable insights into the broader ecological and epidemiological dynamics of brucellosis. Their grouping suggests a collective influence on key factors such as human–animal interactions, the force of infection, and the basic reproduction number (R₀). This has significant implications for intervention strategies: while the first group of parameters requires immediate attention due to its overarching impact, the second group highlights specific areas for targeted intervention.

4.1. Result and Discussions

A numerical simulation was conducted using MATLAB 2016b software, employing the ODE15s solver to integrate the PDE model along characteristic lines. The ODE15s solver, which uses a combination of Euler–Riemann and backward Euler–Riemann methods, was chosen due to its robustness in handling the stiffness inherent in differential equations. To generate the initial conditions for the human (S_h, A_h, and C_h) and animal (S_d and I_d) compartments, parameter values in Equation (2) from Table 1 were applied, with the total human and domestic animal populations set at N_h = 100 and N_d = 50, respectively. The age groups investigated include 0–5, 6–10, 11–15, and 0–15 years for domestic animals and 0–18, 19–36, 37–54, 54–72, and 0–72 years for the human population.

4.1.1. Animal Population Dynamics

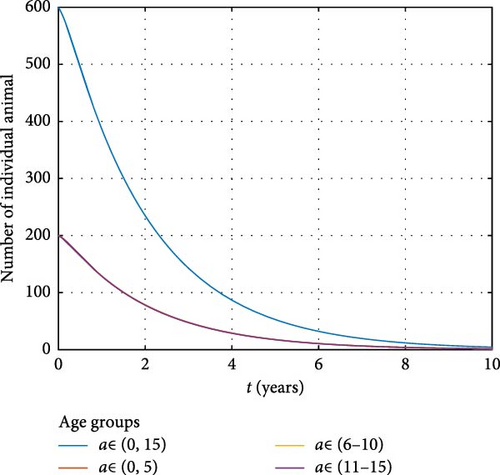
Figure 10 illustrates the total number of animals in different age groups over time. A notable decrease in the susceptible animal population is observed, which can be attributed to the high rate of Brucella pathogen release from infected animals. This pathogen contaminates the environment, contributing to further disease transmission. These findings align with previous studies that highlight the significant role of environmental contamination in the persistence of brucellosis in animal populations. For instance Ahmed et al. [41] demonstrated that environmental reservoirs of Brucella play a critical role in maintaining the infection cycle within animal populations, leading to a sustained decrease in healthy animal numbers.

4.1.2. Infection Dynamics in Animals

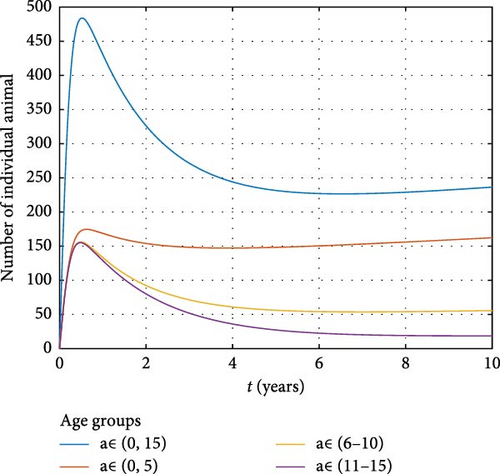
Figure 11 shows a notable increase in the number of infected animals, particularly in the newborn cohort. The high susceptibility of young animals, specifically those aged 0–5 years, makes this age group a vulnerable and high-risk population for brucellosis transmission. This persistence of brucellosis among young animals is consistent with the finding of Salmon et al. [42], who observed that younger animals are more prone to brucellosis infection due to their immature immune systems, which fail to mount a sufficient defense against the pathogen. Furthermore, the high reproductive rates among infected animals contribute to the continued transmission of the disease, as infected newborns serve as new reservoirs for the pathogen (vertical transmission).

4.1.3. Chronic Stage of Human Infections

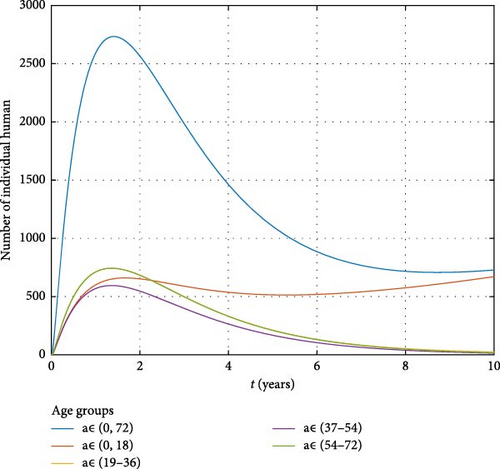
Figure 12 presents the dynamics of human populations at different stages of infection, with a specific focus on those in the chronic stage. It reveals that a significant number of individuals in the age group 0–18 are progressing to chronic infection, indicating that many are carrying the Brucella bacteria from a young age into maturity. This pattern underscores the long-term public health burden posed by brucellosis, as individuals with chronic infections can remain carriers of the pathogen for extended periods. Mangal et al. [43] similarly found that chronic brucellosis cases often stem from early-life exposure, leading to lifelong complications and the potential for transmission to new generations. The persistence of carriers in the population highlights the challenge of eradicating brucellosis and reinforces the need for early interventions and continued monitoring.

5. Conclusion

The paper presents a mathematical modeling of brucellosis transmission dynamics and its age-specific applications. A PDE model was formulated; the existence of positivity and boundedness was shown using the integrated semigroup approach. The basic reproduction number, R₀, was derived using the Lotka–Sharpe–McKendrick integral equation, and the DFE was found to be locally asymptotically stable when R₀ < 1. Global sensitivity analysis was conducted using the PAWN method, which identified the most influential parameters affecting disease transmission. Humans aged 0–72 years are identified as carriers of the disease, while domestic animals, particularly those aged 0–5 and 11–15 years, serve as critical reservoirs and transmitters of brucellosis. This highlights the need for targeted interventions in these specific age groups to control disease spread. Additionally, environmental contamination plays a significant role in sustaining transmission, emphasizing the importance of improving sanitation and hygiene practices. These results underscore the necessity for comprehensive public health measures, including enhanced testing protocols, age-specific interventions, and environmental management, to effectively mitigate the transmission of brucellosis.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Innocent Sosoma: conceptualization, formal analysis, methodology, software, writing–original draft, writing–review and editing. Eunice Mureithi: conceptualization, formal analysis, methodology, visualization, writing–review and editing. Nyimvua Shaban Mbare: conceptualization, formal analysis, methodology, writing–review and editing.

Funding

This work has been supported by the Mathematics for Sustainable Development (MATH4SDG) project, which is a research and development project running in the period 2021–2026 at Makerere University, Uganda; University of Dar es Salaam, Tanzania; and the University of Bergen, Norway, funded through the NORHED II program under the Norwegian Agency for Development Cooperation (NORAD) (Project No. 68105).

Open Research

Data Availability Statement

This study did not involve the collection of primary data. Instead, it utilized data from various secondary sources, which are appropriately cited within the manuscript. Readers may refer to the cited sources for access to the original datasets.

References

1 Seleem M. N., Boyle S. M., and Sriranganathan N., Brucellosis, A Re-Emerging Zoonosis, Veterinary Microbiology. (2010) 140, no. 3-4, 392–398, https://doi.org/10.1016/j.vetmic.2009.06.021, 2-s2.0-74249111903.
10.1016/j.vetmic.2009.06.021
PubMed Web of Science® Google Scholar
2 Sun G.-Q., Li M.-T., Zhang J., Zhang W., Pei X., and Jin Z., Transmission Dynamics of Brucellosis, Mathematical Modelling and Applications in China, Computational and Structural Biotechnology Journal. (2020) 18, 3843–3860, https://doi.org/10.1016/j.csbj.2020.11.014.
10.1016/j.csbj.2020.11.014
CAS PubMed Web of Science® Google Scholar
3 Pappas G. and Akritidis N., Modern Medicine and Ancient Hellenic Wisdom, La Maladie de la Malte Hellenic Journal of Nuclear Medicine. (2006) 9, no. 1, 8–14.
Google Scholar
4 Montiel D. O., Bruce M., Frankena K., Udo H., Van der Zijpp A., and Rushton J., Financial Analysis of Brucellosis Control for Small-Scale Goat Farming in the Bajo Region Mexico, Preventive Veterinary Medicine. (2015) 118, 247–259.
10.1016/j.prevetmed.2014.11.014
PubMed Web of Science® Google Scholar
5 Nannyonga B., Mwanga G. G., and Luboobi L. S., An Optimal Control Problem for Ovine Brucellosis With Culling, Journal of Biological Dynamics. (2015) 9, no. 1, 198–214, https://doi.org/10.1080/17513758.2015.1056845, 2-s2.0-84953372070.
10.1080/17513758.2015.1056845
CAS PubMed Web of Science® Google Scholar
6 Nkuba N., Livingstone S. L., Saul C. M., and Gabriel M. S., Mathematical Model for Brucellosis Transmission Dynamics in Livestock and Human Populations, Communications in Mathematical Biology and Neuroscience. (2020) 3, 2052–2541.
Google Scholar
7 Nyerere N., Luboobi L. S., Mpeshe S. C., and Shirima G. M., Optimal Control Strategies for the Infectiology of Brucellosis, International Journal of Mathematics and Mathematical Sciences. (2020) 2020, 1214391.
10.1155/2020/1214391
Web of Science® Google Scholar
8 Pappas G. and Papadimitriou P., Challenges in Brucellosis Control an Update, Current Opinion in Infectious Diseases, Journal of Nuclear Medicine. (2012) 25, no. 4, 365–371.
Google Scholar
9 Hegazy Y. M., Ridler A. L., and Guitian F. J., Assessment and Simulation of the Implementation of Brucellosis Control Programme in an Endemic Area of the Middle East, Epidemiology and Infection. (2009) 137, no. 10, 1436–1448, https://doi.org/10.1017/S0950268809002301, 2-s2.0-70349229687.
10.1017/S0950268809002301
CAS PubMed Web of Science® Google Scholar
10 Tumwiine J. and Robert G., A Mathematical Model for Treatment of Bovine Brucellosis in Cattle Population, Journal of Mathematical Modeling. (2017) 5, 137–152.
Google Scholar
11 Emerging Infectious Diseases, Centers for Disease Control and Prevention 2024 Global Burden of Brucellosis, 29, no. 9, 23–52.
Google Scholar
12 McDermott J. J. and Arimi S. M., Brucellosis in Sub-Saharan Africa: Epidemiology, Control and Impact, Veterinary Microbiology. (2002) 90, no. 1–4, 111–134, https://doi.org/10.1016/S0378-1135(02)00249-3, 2-s2.0-0037146715.
10.1016/S0378-1135(02)00249-3
PubMed Web of Science® Google Scholar
13 Swai E. S. and Schoonman L., The Prevalence of Brucellosis in Indigenous Cattle and Their Herders in Central Tanzania, BMC Veterinary Research. (2010) 6, 36.
PubMed Google Scholar
14 Sosoma I., Mureithi E., Alendal G., Makondo Z., and Mbare N. S., A Data-Driven Dynamical System Model for Assessing Targeted Interventions Against Brucellosis in Tanzania, Comparative Immunology, Microbiology and Infectious Diseases. (2025) 118, https://doi.org/10.1016/j.cimid.2025.102324, 102324.
10.1016/j.cimid.2025.102324
PubMed Web of Science® Google Scholar
15 Lolika P. O. and Mushayabasa S., Dynamics and Stability Analysis of a Brucellosis Model With Two Discrete Delays, Discrete Dynamics in Nature and Society. (2018) 2018, 6456107.
10.1155/2018/6456107
Web of Science® Google Scholar
16 Savini L., Candeloro L., Conte A., De Massis F., Giovannini A., and Sendiña-Nadal I., Development of a Forecasting Model for Brucellosis Spreading in the Italian Cattle Trade Network Aimed to Prioritise the Field Interventions, PLoS ONE. (2017) 12, no. 6, https://doi.org/10.1371/journal.pone.0177313, 2-s2.0-85021337836, e0177313.
10.1371/journal.pone.0177313
CAS PubMed Web of Science® Google Scholar
17 Hou Q. and Sun X.-D., Modeling Sheep Brucellosis Transmission With a Multi-Stage Model in Changling County of Jilin Province, China, Journal of Applied Mathematics and Computing. (2016) 51, no. 1-2, 227–244, https://doi.org/10.1007/s12190-015-0901-y, 2-s2.0-84931088549.
10.1007/s12190-015-0901-y
Web of Science® Google Scholar
18 Zinsstag J., Roth F., and Orkhon D., et al.A Model of Animal-Human Brucellosis Transmission in Mongolia, Preventive Veterinary Medicine. (2005) 69, no. 1-2, 77–95, https://doi.org/10.1016/j.prevetmed.2005.01.017, 2-s2.0-19344362089.
10.1016/j.prevetmed.2005.01.017
CAS PubMed Web of Science® Google Scholar
19 Yang L., Bi Z.-W., and Kou Z.-Q., et al.Time-Series Analysis on Human Brucellosis During 2004-2013 in Shandong Province, China, Zoonoses and Public Health. (2015) 62, no. 3, 228–235, https://doi.org/10.1111/zph.12145, 2-s2.0-84961369910.
10.1111/zph.12145
CAS PubMed Web of Science® Google Scholar
20 Aïnseba B., Benosman C., and Magal P., A Model for Ovine Brucellosis Incorporating Direct and Indirect Transmission, Journal of Biological Dynamics. (2010) 4, no. 1, 2–11, https://doi.org/10.1080/17513750903171688, 2-s2.0-79960511767.
10.1080/17513750903171688
PubMed Google Scholar
21 Rossetti C. A., Arenas-Gamboa A. M., Maurizio E., and Barry M., Caprine Brucellosis: A Historically Neglected Disease With Significant Impact on Public Health, PLoS Neglected Tropical Diseases. (2017) 11, no. 8, https://doi.org/10.1371/journal.pntd.0005692, 2-s2.0-85028599408, e0005692.
10.1371/journal.pntd.0005692
PubMed Web of Science® Google Scholar
22 Nkuba N., Livingstone S. L., Saul C. M., and Gabriel M. S., Modeling the Impact of Seasonal Weather Variations on the Infectiology of Brucellosis, Computational and Mathematical Methods in Medicine. (2020) 8972063.
PubMed Google Scholar
23 Yang J., Xu R., and Sun H., Dynamics of a Seasonal Brucellosis Disease Model With Nonlocal Transmission and Spatial Diffusion, Communications in Nonlinear Science and Numerical Simulation. (2021) 94, https://doi.org/10.1016/j.cnsns.2020.105551, 105551.
10.1016/j.cnsns.2020.105551
Web of Science® Google Scholar
24 Cyrille K., Gisèle M., René D., and Pascal Z., A Model for Brucellosis Disease Incorporating Age of Infection and Waning Immunity, MDPI. (2022) 10, 627.
Google Scholar
25 Yang J., Xu R., and Li J., Threshold Dynamics of An Age-Space Structured Brucellosis Disease Model With Neumann Boundary Condition, Nonlinear Analysis: Real World Applications. (2019) 50, 192–217, https://doi.org/10.1016/j.nonrwa.2019.04.013, 2-s2.0-85065640375.
10.1016/j.nonrwa.2019.04.013
Web of Science® Google Scholar
26 Corbel M. J. and Beeching N. J., Brucellosis, Harrison’s Textbook of Internal Medicine, 2004, New York, McGraw-Hill, 914–917.
Google Scholar
27 Smith G. W., Epidemics and Epizootics, The Journal of Hygiene. (1905) 5, no. 4, 363–384.
Google Scholar
28 Najm F., Yafia R., Alaoui M. A. A., and Aghriche A., Epidemic Model With Direct and Indirect Transmission Modes and Two Delays, 2022, https://doi.org/10.1101/2022.03.16.22272508.
10.1101/2022.03.16.22272508
Google Scholar
29 Rupa B., Maninder S., and Singh D. K., Status and Strategies for Control of Brucellosis—A Review, Indian Journal of Animal Sciences. (2009) 79, no. 12, 1191–1199.
Google Scholar
30 Sultana S., Hasan M., and Andallah L. S., Age-Structured Population Projection of Bangladesh by Using a Partial Differential Model With Quadratic Polynomial Curve Fitting, Open Journal of Applied Sciences. (2015) 5, no. 9, 542–551, https://doi.org/10.4236/ojapps.2015.59052.
10.4236/ojapps.2015.59052
Google Scholar
31 Paride O. L. P., Modelling the Transmission Dynamics of Brucellosis, 2018, University of Zimbabwe, PhD thesis.
Google Scholar
32 Vanessa A. F. S., José Soares F. N., and Marcos A., et al.Mathematical Modelling of Bovine Brucellosis Control Using the RB51 Vaccine, Semina Ciências Agrárias, Londrina. (2016) 37, no. 5, 3767–3776.
Google Scholar
33 Pappas G. and Papadimitriou P., Challenges in Brucella Infection, Medicine. (2013) 92, no. 6, 345–346.
Google Scholar
34 Wahid B. K. A. and Bisso S., Mathematical Analysis and Simulation of an Age-Structured Model of Two-Patch for Tuberculosis (TB), Applied Mathematics. (2016) 7, no. 15, 1882–1902, https://doi.org/10.4236/am.2016.715155.
10.4236/am.2016.715155
Google Scholar
35 Lotka A. J., Elements of Mathematical Biology, 1956, Dover Publication, New York.
Web of Science® Google Scholar
36 M’Kendrick A. G., Applications of Mathematics to Medical Problems, Proceedings of the Edinburgh Mathematical Society. (1925) 44, 98–130, https://doi.org/10.1017/S0013091500034428, 2-s2.0-84860215339.
10.1017/S0013091500034428
Google Scholar
37 Sharpe F. R. and Lotka A. J., A Problem in Age Distributions, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. (1911) 21, no. 124, 435–438, https://doi.org/10.1080/14786440408637050.
10.1080/14786440408637050
Google Scholar
38 Abba M. O., Saley B., and Benjamin M., Stability Analysis and Simulation of An Age-Structured Hepatitis B Model Without Vertical Transmission, International Journal of Differential Equations and Applications. (2015) 14, 13–41.
Google Scholar
39 Pianosi F. and Wagener T., Distribution-Based Analysis From a Generic Input-Output Sample, Environmental Modelling & Software. (2018) 108, 197–207, https://doi.org/10.1016/j.envsoft.2018.07.019, 2-s2.0-85051119871.
10.1016/j.envsoft.2018.07.019
Google Scholar
40 Saltelli A., Ratto M., and Andres T., et al. Global Sensitivity Analysis, 2008, The primer. Wiley.
Google Scholar
41 Ahmed R., Paul S., Ali A., and Karim R., Environmental Contamination as a Key Factor in the Epidemiology of Brucellosis, Journal of Veterinary Medicine and Animal Health. (2021) 13, no. 4, 112–118.
Google Scholar
42 Salmon M., Adams B., and Shabani A., Age-Structured Models of Brucellosis Transmission Dynamics in Livestock Populations, PLoS One. (2018) 13, no. 2, e0192882.
PubMed Google Scholar
43 Mangal P., Gupta N., and Singh R., Chronic Brucellosis: Epidemiological Challenges and Its Long-Term Impact on Human Health, Journal of Public Health Research. (2019) 8, no. 3, 245–252.
Google Scholar

All articles

Mathematical Modeling of Brucellosis Transmission Dynamics and Its Age-Specific Applications

Abstract

1. Introduction