Research on Hopping Routing of Periodic Multiorbit LEO Satellites
Abstract
In recent years, the low Earth orbit microsatellite network technology has experienced rapid development due to its advantages of low latency, low cost, and short development cycles. However, building an efficient and reliable satellite network routing system faces many challenges due to the characteristics of satellite networks, such as fast-changing topology, large variations in link latency, higher probabilities of node and link failures, and limited resources. Routing algorithms have a significant impact on intersatellite communication and have become a research hotspot. The current mainstream algorithms focus on reducing information propagation delays between satellites to enable faster transmission. However, many satellite networks, such as meteorological observation satellite networks, are not sensitive to propagation delays but emphasize reducing hardware costs, especially for the receiving and transmitting signal systems of satellites. This means minimizing the single-step signal transmission distance of satellites. This article proposes a routing algorithm based on time slot planning and the shortest path step length. Experimental simulation results demonstrate that this algorithm significantly reduces the step length of signal transmission and lowers hardware costs.
1. Introduction
Compared to traditional high-orbit large satellites, low Earth orbit microsatellites have remarkable advantages such as shorter development cycles, lower launch costs, and flexible launch methods. In particular, in recent years, with advancements in microelectronics technology, the development of lightweight materials, and the emergence of high-power solar cells, microsatellites have experienced rapid growth and found widespread applications in global civilian communications, remote sensing meteorology, and space science. For example, SpaceX’s Starlink program is aimed at achieving global coverage with a low Earth orbit constellation of 4425 satellites and a very low Earth orbit constellation of 7518 satellites, providing various services such as communication, meteorology, and mapping. China’s “GW” project is also expected to launch 12,992 satellites to provide more reliable and comprehensive communication services globally [1]. With the rapid development of microsatellite technology, the number of satellites in the network continues to increase, as well as the number of orbits. Due to the fast-changing topology of the satellite network, significant variations in link delays, high probabilities of node and link failures, limited resources, and dynamic changes in traffic load, the quality of routing algorithms has a tremendous impact on intersatellite communication [2].
Many effective studies have been conducted by previous researchers on this subject. Zhao, Long, and Wang considered factors such as satellite transmission capacity and intersatellite link reliability and modeled the satellite network routing problem as a selective problem of intersatellite link selection. They established a multiconstrained optimization problem and proposed an improved ant colony algorithm to solve the routing problem [3]. Wang from Beijing University of Posts and Telecommunications proposed a routing algorithm scheme for low-orbit satellite based on DDQN [4], which effectively combined the perception ability of deep learning and the decision ability of reinforcement learning. By driving the reward function and the two-hop link state perception strategy, the routing algorithm can effectively adapt to the dynamic change of satellite network traffic and select the optimal next hop according to the two-hop link state. Wang, Kishk, and Alouini [5] proposed a routing algorithm for LEO satellite networks based on stochastic geometry, which is well suited as an effective mathematical work for system-level analysis of satellite network topology. The first two algorithms are highly intelligent algorithms that are decentralized and well suited for dynamic optimization of routing, while the latter algorithm is more of a system-level analysis of the network topology from a mathematical perspective. However, for complex algorithms based on machine learning, deep learning, and other techniques, although they can plan excellent routing paths and achieve very low propagation delays, the algorithms are extremely complex. It imposes high computational and information storage requirements on each intersatellite node and does not consider the single-step distance for each hop. Therefore, it is difficult to effectively reduce hardware costs. Reference [6] proposed the ITO scheme, which utilizes digital twins to map the satellite network into virtual space and improves the efficiency of intersatellite data transfer by verifying and selecting the optimal routing paths based on the time-varying graphs in advance, in order to reduce the end-to-end ISL paths and communication delays. Inspired by this, this paper proposes a time-slice–based predictive routing algorithm. The operational time of the satellite network within one cycle is divided into multiple time slices, assuming that the relative distance between satellites does not change within each minimal time slice. The algorithm makes predictions and selects the routing path with the minimum single-step distance.
2. System Model
2.1. Model Composition
2.1.1. Basic Model
In this model, satellites are considered to be assigned to orbits with the same altitude but different inclinations, with a total of M orbit planes and N satellites in each orbit. The relative positions of satellites in orbit are fixed. These satellites are in motion all the time, and the relative positions of satellites in different orbits are changing all the time. In our study, it is assumed that the motion of the satellite is periodic, and every Q hour is a complete cycle. The m orbits are different planes, so no strict rules are made for the inclination angles of the orbits, which makes the research in this paper more universal. In this model, the first orbit can be named orbit A, the second orbit can be named orbit B, and so on for the others. However, there is a high probability that these two satellites cannot be sent directly, because they are blocked by the contour of the Earth. At this time, it is necessary to rely on the forwarding of other satellites. This paper researches the routing design of this problem. The core research topic of this paper is to reduce the transmission distance of single step.
In the table, ai_j represents the direct connection distance between No. i satellite and No. j satellite. If two satellites cannot communicate directly, the corresponding bits are represented by symbol inf, indicating that two satellites are shielded from each other and cannot be directly connected. Here, there is an orbit for satellites numbered 1 to n, an orbit for satellites numbered n + 1 to 2n, and so on. Of course, this topo list is constantly changing.
The data in the node table represents the waiting processing delay of data processed inside the node at that time. Of course, the data in the table is also constantly changing.
2.2. Contrast Algorithm
As shown in Figure 1, this is a schematic diagram of a low Earth orbit satellite constellation system, which includes multiple operational orbits.
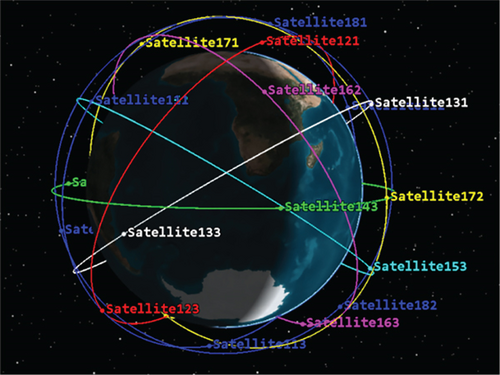
In order to compare and evaluate the algorithm proposed in this paper, two other typical algorithms are selected for comparison. One is the flooding algorithm that traverses all possible paths, which calculates the path with the shortest delay, and the other is the fixed gateway node routing algorithm, which is currently widely used because of its high practicality.
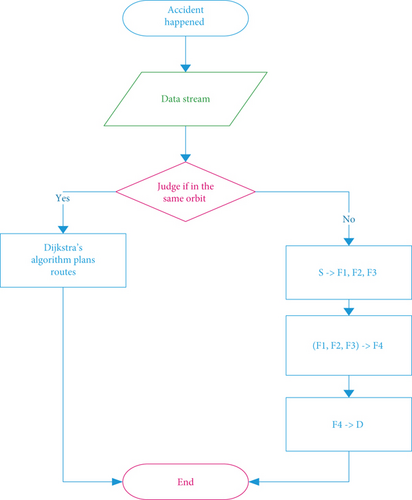
2.2.1. Fixed Gate Node Routing Algorithm
- 1.
Three gateway node satellites are fixed in each orbit. Communication between different orbits is possible only using the gateway node satellites, and only gateway nodes can communicate with each other. The gateway node satellites store information about their communications with gateway nodes in other orbits.
- 2.
When both the source satellite and the destination satellite are in the same orbit, the Dijkstra algorithm is used to calculate the route directly. The path here is the path of the signal transmission, which is a straight-line distance.
- 3.
When the source node and destination node are not in the same orbit, the source node (S) first sends data to the three gateway nodes (F1, F2, and F3) within the orbit. After all three passing nodes receive data, they start to determine whether the data can be sent within the time range. If this is the time period that a pass node can send, then it will be sent to the passing node of another orbit. The other two gateway nodes discard information directly. When the information is transmitted to the gateway node (F4) of the target node’s orbit, the information is sent to the target node (D) through the Dijkstra algorithm [7–9].
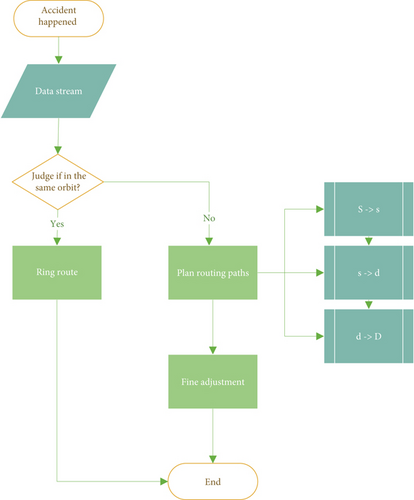
2.2.2. A Time-Slice–Based Predictive Estimation Routing Algorithm
- 1.
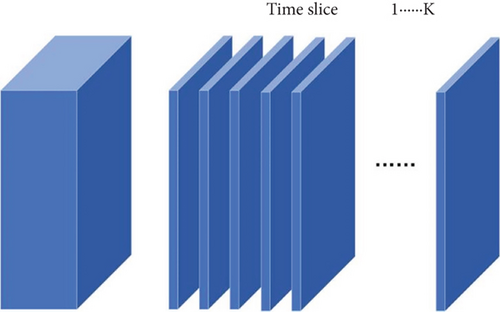
Split time slice: The time during a motion cycle of a satellite is cut into many uniform time slices. The relative positions of the satellites do not change during the time slices.
- 2.
In-orbit algorithm: If both the source node and the destination node are within the orbit, at this time, it is only necessary to calculate a short path according to the idea of ring routing algorithm and pass it along other satellite nodes one by one until the target node.
- 3.
Routing design of nodes of different orbits:
Step 1. The source node needs to find the three pairs of nodes closest to the two orbits where the source node Sand destination node D are located according to the data in the time slice at this time. All three pairs can be used as transit nodes, so there are three alternative paths. The transit nodes of the orbit where the source node S is located are denoted as s1, s2, and s3, respectively, and the corresponding is that the transit nodes of the orbit where the destination node D is located are denoted as d1, d2, and d3. The reason for choosing three alternate paths here is that it is possible that the message encounters congestion during intraorbital transmission, and by the time it is transmitted to the intended s2, the link between s2 and d2 is no longer the closest link between the two orbits. At this point, the alternative paths can be enabled and adjusted in both directions when three alternative paths are available. It is also stated that in the few specific cases where there are only two alternative paths, the procedure is the same as when there are three alternative paths. Considering that satellites may fail, more alternative paths are beneficial to enhance the robustness of the network.
Step 2. The source node needs to calculate and select the best from the three alternative paths.
- 1.
S⟶⋯⟶s1⟶d1⟶⋯⟶D
- 2.
S⟶⋯⟶s2⟶d2⟶⋯⟶D
- 3.
S⟶⋯⟶s3⟶d3⟶⋯⟶D
Considering the transmission time of the message between the nodes of the satellite, by the time the message is transmitted between two different orbits, it may not be in the current time slice; the algorithm needs to account for this time and predict the time slice to select the best path:
Step 3. Fine adjustment: If the relay node s finds that due to a small deviation in the estimate, it is no longer the two closest satellites between the two orbits. At this time, the relay node s that has received the information will calculate the estimate and choose to send left or right to a satellite near itself.
2.2.3. Flooding Algorithm
For source and destination nodes, traverse all paths. However, some paths that pass through too many forwarding nodes are discarded for the sake of efficiency, because a path that passes through too many forwarding nodes is basically unlikely to be the best path. Compare among them and select the best path [10, 11].
3. Analysis and Results
In this section, the algorithms are analyzed at two levels. This includes analyzing the complexity of each algorithm and the actual simulation performance of each algorithm [12].
3.1. Complexity Analysis
In this portion, we will discuss the computational complexity of the algorithm. This is discussed in two parts; one is the comparison of the amount of information that needs to be stored in the satellite itself, and the other is the comparison of the amount of computation involved in implementing the algorithm [13].
3.1.1. Node Storage Information Analysis
This section analyzes the basic information that nodes need to store for route calculation under different algorithms. Note that the amount of information is quantified here. For example, if a node stores information about its location and distance from another node, that is a piece of information. Suppose there are N satellite nodes per orbit and M orbits, and time is cut into K time slices in one period. The amount of information is denoted by S.
3.1.1.1. Fixed Gate Node Routing Algorithm
For fixed node routing algorithm, it is divided into two cases: whether it is a gateway node or not.
Not gateway node:
In this case, p means the number of gateway nodes in the orbit, so that the source node knows where to send the information.
In addition to the information that ordinary nodes need to store, gateway nodes also need to store additional information (q) with other orbit’s gateway nodes.
3.1.1.2. A Time-Slice–Based Predictive Estimation Routing Algorithm
The first item here is the location information of this node and the nodes in other orbits, recording K time slices. The second term is the position information with other nodes in this orbit; because this is relatively stable, there is no need to record K time slices. The third item is the queued processing delay of each node in the system, which usually needs to record more than one cycle of data.
3.1.1.3. Flooding Algorithm
To summarize the above analysis, in the algorithm proposed in this paper, the time within a cycle is cut into K time slices, but in the algorithm to complete the flooding, the data needed for each time slot will be more, which is generally said to be divided into smaller time slices, the need for massive data, far more than the amount of K time slices, so this paper uses exponential times. In the above formula, the former term is the amount of information to store the relative position information between this node and other nodes, and the latter term is the processing delay within the storage node. Because the relative position and distance of the satellite change periodically, while the processing delay within the node is not strictly in accordance with the periodic change, more data is needed to build the model, so here β > α. Therefore, from this metric, the highest complexity is flooding algorithm, followed by the algorithm proposed in this paper, and the lowest is fixed gate node routing algorithm.
3.1.2. Algorithm Complexity Analysis
This section analyzes the amount of computation involved in implementing the above three algorithms. When analyzing the complexity of the amount of computation, it will be divided into two cases whether the source and destination nodes are in the same orbit or not [14].
3.1.2.1. Fixed Gate Node Routing Algorithm
According to the Dijkstra algorithm, N − 1 operations are to be performed on N nodes.
The first item is that the source node needs to send a message to p gateway nodes at the same time and perform the routing computation of the Dijkstra algorithm. The second term is the computation of the attempted docking between the p gateway nodes that received the message and the p nodes in the other orbit. The third item is the routing process from the gateway node that received the message to the destination node in the other orbit.
3.1.2.2. A Time-Slice–Based Predictive Estimation Routing Algorithm
In-orbit routing is calculated using ring routing algorithm.
Here, 3 · ((N − 1)/2 + 1) is the amount of computation needed to calculate to the three target nodes, and N2 is traversing the two orbits to find the three pairs of satellites that are relatively close to each other.
3.1.2.3. Flooding Algorithm
The flooding algorithm is to traverse each path and choose the best one, but the actual experiments will only traverse paths that pass through a relatively small number of nodes, so here is only a mathematical demonstration of the theory.
3.2. Algorithm Analysis
- 1.
Number of junction points
- 2.
Total path length
- 3.
Maximum step length
- 4.
Total path latency
The total path latency refers to the total message transfer time spent.
In order to generalize the study in this paper, it is assumed here that the delay within the node conforms to normal distribution (μ, σ2). In the following analysis, whether the source node and the destination node are in the same orbit will be discussed. The following are theoretical estimates.
3.2.1. Fixed Gate Node Routing Algorithm
- 1.
Number of junction points:
- 2.
Total path length:
- 3.
Maximum step length:
- 4.
Total path latency:
c is the speed of the light.
3.2.2. A Time-Slice–Based Predictive Estimation Routing Algorithm
- 1.
Number of junction points:
- 2.
Total path length:
- 3.
Maximum step length:
- 4.
Total path latency:
3.2.3. Flooding Algorithm
Objectively speaking, since the flooding algorithm traverses all possible paths, the above four indexes must be optimal. Because it is extremely difficult to analyze these metrics of the flooding algorithm specifically from a mathematical point of view and is not the focus of this paper, it will not be analyzed too much here [17].
3.3. Simulation and Analysis
In the simulation, the four indicators mentioned in Section 3.2 are simulated. In this experiment simulation, there are a total of 60 satellites, distributed in four orbits; each orbit has 15 satellites. The four orbits are named as A, B, C, and D. The parameter information of the four orbits is shown in Table 1.
| Orbit | Inclination | Eccentricity | Altitude | Cycle |
|---|---|---|---|---|
| A | 0° | 0 | 1675 km | 2 h |
| B | 45° | 0 | 1675 km | 2 h |
| C | 90° | 0 | 1675 km | 2 h |
| D | 135° | 0 | 1675 km | 2 h |
The experiments conducted covered various nodes communicating with each other for a total of 3600 communications.
Note that under the simulation of the fixed node routing algorithm, we set the number of gateway nodes per orbit to three. In the subsequent simulation experiments, Algorithm 1 represents the fixed node routing algorithm and sets the number of gateway nodes per orbit to three, Algorithm 2 represents a time-slice-based predictive estimation routing algorithm proposed in this paper, and Algorithm 3 represents the flooding algorithm.
The first is the simulation of the number of passing nodes.
As can be seen from Figure 5, Algorithm 3 passes through the least number of nodes, while Algorithm 2 passes through the most. From the simulation results, the algorithm proposed in this paper is required to go through more nodes to forward, and more forwarding nodes are used in order to reduce the step length of a single step. Then, the next index is average simulated path length.
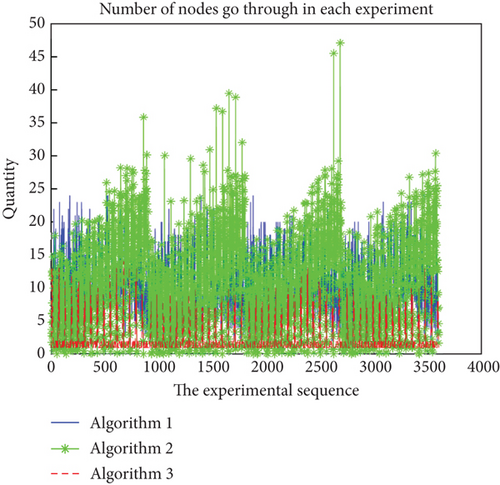
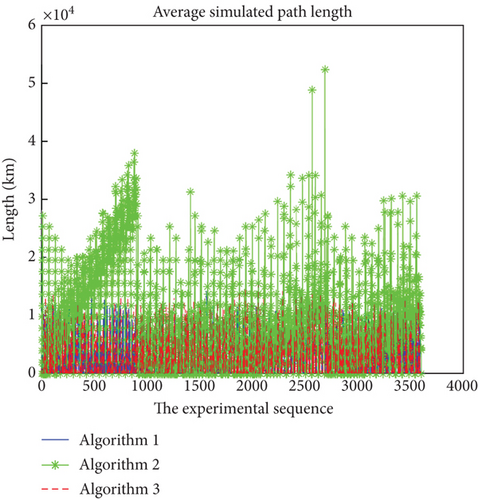
From the simulation (Figure 6), the routing path calculated by Algorithm 2 is the longest and significantly longer than the other two algorithms, while Algorithm 1 and Algorithm 3 are more similar, with Algorithm 1 being a bit longer. It shows that the algorithm proposed in this paper has a disadvantage in the metric of routing path length because the algorithm has to go through a lot of forwarding nodes and the algorithm within the orbit uses a ring routing algorithm, so it increases the length of the routing path. Algorithm 1 uses the Dijkstra algorithm within the orbit, which is very beneficial in reducing the total routing path length. Algorithm 3 would have traversed almost all the paths, and the resulting total path length is surely optimal.
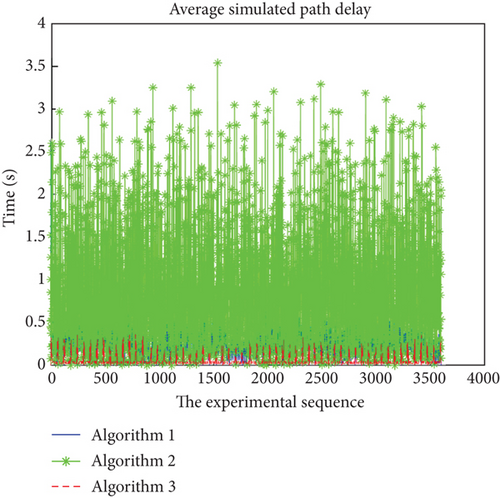
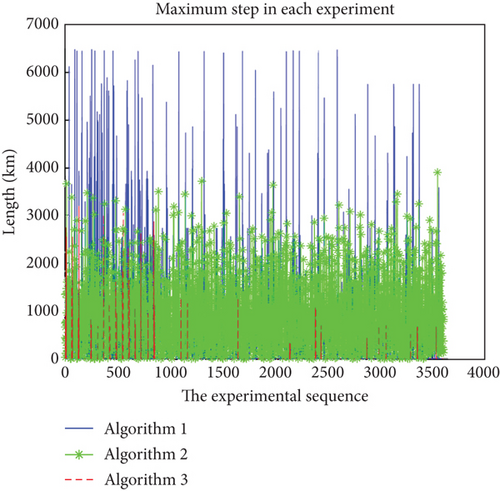
Finally, the simulation is performed for the single-step maximum step length and the total delay.
As can be seen from Figures 7 and 8, compared with the other two algorithms in terms of main indicators, the algorithm proposed in this paper has an excellent performance in the maximum step length of a single step and a mediocre performance in other aspects. This means that the algorithm proposed in this paper can indeed largely reduce the maximum step length of a single step of the planned routing path and reduce the requirements for hardware devices such as transmitter–receiver. However, the other three indicators do not perform as well as the other two algorithms. The algorithm proposed in this paper is suitable for constellation projects with small information transmission load and low requirements for delay but sensitive to economy.
3.4. Hardware Cost Analysis
Here, d is the propagation distance in meters. f is the transmission frequency in hertz. c is the speed of light.
If the propagation distance (d) is increased, FSPL will increase, causing Pr to decrease. In order to keep Pr constant, Pt must increase to compensate for the higher FSPL. If the distance is doubled, the FSPL increases by an amount equal to about 6 dB, which means that the transmit power needs to be increased by a factor of 4 in order to maintain the same receive power.
This formula illustrates that path loss is expressed in dB, which increases proportionally to the logarithm of the distance. The loss of signal power is proportional to the square of the propagation distance.
The increase in transmit power required with increasing distance also implies higher energy consumption and requires more expensive components such as transmit antennas and power amplifiers, which take up more space and weight. Therefore, reducing the transmitting distance in a single step has great significance in reducing the hardware cost.
4. Further Optimization for Algorithm
Although the above simulations show that the algorithm proposed in this paper has a large advantage in key metrics, it is still explored in this section to improve the algorithm and increase the balance of the algorithm. There are two optimization directions. One direction is to partially sacrifice the maximum single-step length and change the in-orbit algorithm from the original ring routing algorithm to the Dijkstra algorithm. Another direction is to further simplify the algorithm and introduce notification mechanism [18, 19].
4.1. In-Orbit Algorithm Optimization
In the algorithm proposed in the previous part of this paper, the routing algorithm inside the orbit is a ring routing algorithm, where information is relayed by neighboring nodes in pursuit of the minimum single-step length. The advantages of this algorithm are obvious, but the disadvantages are also obvious, which will increase many transit nodes and the routing path becomes longer. Therefore, this section tries to change the original ring routing algorithm within the orbit to the Dijkstra algorithm to improve the performance in other aspects and improve the algorithmic balance. It is worth emphasizing that in-orbit here does not mean that the source and destination nodes are in the same orbit, but simply means planning routes within an orbit [20].
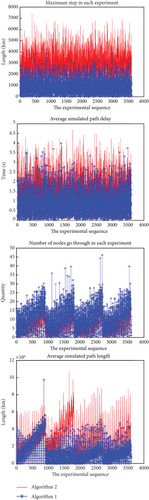
Therefore, with exactly the same conditions as the other experiments in the previous section, the comparison is between the algorithm before optimization and the algorithm after this optimization, and the simulation diagram is as follows.
In the following simulation, Algorithm 1 is unoptimized and Algorithm 2 is optimized.
As can be seen from Figure 9, the calculation path of the algorithm is optimized to a large extent after the change, and the single-step length increases slightly. This shows that the optimized algorithm can indeed improve the algorithm performance to a large extent and can be a beneficial supplement in some scenario.
4.2. Simplification of Algorithm Complexity
Then, we try to simplify the algorithm further by introducing a notification mechanism. In the model presented in this paper, all satellite nodes are in motion from time to time. Moreover, this paper introduces the concept of time slice. For two orbits, in some adjacent time slices, there are two fixed nodes in the two orbits, the distance between them is the closest, and each satellite node has the chance to become the closest node between the two orbits [21].
The flow of improved algorithm is as follows: (1) Each satellite node stores the information when it is the closest node between two orbits, including the docking node, the corresponding time slice, and the distance. (2) Each node has a system that broadcasts its information to the whole network several time slices in advance when it is about to become the closest node between two orbits. (3) When each node receives such information, it will know where to send the information for the next orbital communication.
Next, calculate the length of the time slice for the advance broadcast. There are N satellites in each orbit, and the satellites that need to be broadcast in advance will broadcast in both clockwise and counterclockwise directions to satellites throughout the orbit. There may be at most [(N − 1)/2] + 1 satellites broadcasting passes in one direction (brackets represent rounded numbers). In order to ensure that early broadcasting is reliable, we need to consider the most extreme cases.
The final satellite that receives the broadcast takes the same amount of time to send the message back to the satellite that sent the broadcast at the source.
The complexity of the improved algorithm is analyzed next. The amount of information required to store is as follows:
Here, N · (N − 1) in the equation represents all the satellite node information within this orbit that needs to be stored within the node, and ω refers to the time slices in which the node is acting as the nearest node of this orbit to other orbits.
Computational complexity:
Obviously, it can be easily seen from the above equation that the complexity of the improved algorithm is greatly reduced compared to the previous one.
Therefore, with exactly the same conditions as the other experiments in the previous section, the comparison is between the algorithm before optimization and the algorithm after this optimization, and the simulation diagram is as follows.
In the following simulation, Algorithm 1 is unoptimized and Algorithm 2 is optimized.
From the simulation (Figure 10), the optimized algorithm performs a little worse in the overall index relative to the previous one, but the gap is very small overall except for the index average simulated path length, which is still very promising for application relative to the significant optimization of the computational complexity. Next is a summary of the pros and cons.
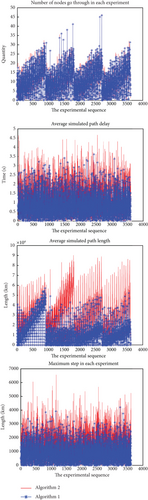
The advantages of this approach are obvious. (1) The storage pressure of each node is less, and only the information of each node in the same orbit needs to be stored, which greatly reduces the storage pressure. (2) When calculating node routing, the calculation amount is greatly reduced, and no more complicated calculation is needed to determine the two closest nodes between two tracks.
The disadvantage is as follows: (1) The accuracy of the algorithm will be slightly decreased, because there is a certain lag. This is because when a node receives a broadcast and sends the signal to the corresponding node according to the information in the broadcast, some nodes may be busy in the middle, leading to a large delay. By the time the signal is sent to the corresponding node, the corresponding node is no longer the nearest node in the two tracks needed. It also increases the burden of link processing, because signals need to be broadcast on the network as a whole, occupying more tape resources.
5. Conclusion
- 1.
Simulation results show that the algorithm proposed in this paper has obvious advantages in the index of maximum single-step path length. This can greatly reduce the requirements of satellite node transmission power and other indicators and reduce the cost of satellite hardware.
- 2.
In the second part of this paper, the algorithm is further optimized. Optimizing the route calculation method on the track can greatly reduce the number of passing nodes and delays, while slightly increasing the step size. The second optimization direction is the introduction of notification mechanism, which greatly reduces the computing power requirements for satellite nodes, and the small number of paths added is almost negligible. The application scenarios of this algorithm are enriched.
- 3.
In general, the algorithm proposed in this paper can effectively reduce the hardware cost of intersatellite nodes, has good adaptability, and can be used as a useful supplement to the existing satellite networking algorithms.
Nomenclature
-
- M
-
- the number of orbits
-
- N
-
- the number of satellite in each orbit
-
- Q
-
- the time of a complete cycle
-
- K
-
- the number of time slices
-
- a
-
- the direct connection distance between two satellite nodes
-
- b
-
- internal wait delay of a node
-
- S
-
- the amount of information stored in the node
-
- p
-
- the number of gateway nodes in each orbit
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
The authors acknowledge the financial support provided by Micro-Satellite Research Center, Zhejiang University, and National Natural Science of China (62073289 and U21A20443).
Acknowledgments
The authors acknowledge the financial support provided by the National Natural Science of China (62073289 and U21A20443).
Open Research
Data Availability Statement
The numerical data used to support the findings of this study are included within the article.




