Transfemoral amputees rely on prosthetic devices to restore their mobility and maintain their independence. However, the design and performance of these devices can significantly affect the amputee’s gait and overall functionality. In this study, we investigate the knee torque dynamics of a single-leg transfemoral prosthetic during walking using a mathematical model that takes into consideration knee friction force (β₂), the horizontal component of the ground reaction force (F₁), and the vertical component of the ground reaction force (F₂). By carrying out model simulation in the MATLAB tool, along with Simulink, we derived the tracking error between the generated knee torque of the transfemoral prosthesis and the knee torque trajectory for a normal human leg. This error was evaluated using the normalized root mean square error (NRMSE) method. Our results show that when β₂ = 0.3 N.s.m⁻¹, F₁ = 320 N, and F₂ = 800 N, a tracking error of NRMSE = 0.342868% occurs. A comparison between the simulated knee torque and a desired knee torque trajectory for a normal leg study in the literature suggests that the tracking error generated will force the amputee to use higher metabolic energy to minimize discomfort while walking. These findings highlight the importance of optimizing the design and performance of transfemoral prosthetic devices to improve the knee torque dynamics and overall functionality of amputees. Our mathematical model provides a useful tool for future research in this field, which could help develop more effective prosthetic devices for transfemoral amputees.

1. Introduction

Lower limb amputations become frequent in the whole world due to various reasons such as accidents, civil wars, explosives, gunshots, diabetes mellitus, peripheral vascular diseases, neuropathy, trauma, and cancer [1, 2]. In fact, the loss of the lower limb causes a lot of inconveniences in the daily life of amputee patients. These peoples face frequent health issues, have lower economic, social, academic participation, and performance rates than people without disabilities [3]. In general, the rehabilitation of an amputee is typically achieved via therapy and prescription of a prosthesis [4]. Indeed, depending on the type and severity of leg amputations, amputee patients need to use a specific type of artificial leg prosthesis. However, most prosthetic devices available on the market cause pain and discomfort to the amputee. Smoother movements are usually hampered by inactivity and by the lack of adaptivity of the prosthetic device to the movement pattern of the patient. Among different types of lower limb prosthetic devices, a transfemoral prosthetic is more commercialized due to the highest number of transfemoral amputees. The prosthetic knee adapted to this type of amputation can be classified into three different types depending on the knee structures [5]. There are purely passive transfemoral prostheses, variable damping, active, and dynamic semiactive prostheses [6]. Indeed, the performance of passive transfemoral prostheses knee joints is limited, due to the fact that transfemoral amputees often have asymmetrical gait and have to walk more slowly than healthy people [7]. This requires the amputee to generate more metabolic energy to compensate for the lost muscles [8]. Variable damping prosthetic knees have internal intrinsically passive actuators and, therefore, they can change dynamically. For instance, it is reported in Refs. [9, 10], that the dynamical behavior of the microprocessor-controlled variable damping prosthetic knee relies on the control of a magneto-rheological damper. This type of prosthetic produces the required breaking knee torque during walking and, therefore, allows the knee to adapt to the gait pattern [11]. It improves gait symmetry and reduces musculoskeletal degeneration of transfemoral amputees to one degree [12]. The research group of Professor Goldfarb’s at Vanderbilt University created a low-extremity prosthesis in 2006, which produced a maximum torque of 86 Nm and was powered by a pneumatic pump. Two years later, they developed another low-extremity prosthesis with a maximum torque of 75 Nm, which used a 150 W BLDC motor and a ball screw. In 2012, they made modifications to the design, incorporating a 200 W class BLDC motor and a three-stage pulley-belt type, resulting in a prosthesis with a maximum torque of 85 Nm [13–19]. Their studies showed that an active prosthesis could be helpful for amputees while moving on stairs or steep slopes. In 2011, the research group of Professor Herr’s at MIT developed a knee prosthesis that could generate 130 Nm of torque and 58 RPM, using a series of elastic mechanisms and cable pulleys. In 2014, they incorporated a 200 W class BLDC motor into the existing series elastic mechanism, resulting in a peak output performance of 120 Nm and a maximum speed of 112 RPM. These advancements opened up the possibility of commercializing an active prosthesis [20–22]. The University of Michigan has developed the Open Source Leg [13], which is capable of delivering a torque up to 120 Nm using an aeronautical rotor, despite its low reduction ratio of (42 : 1). In this model, assembling the actuator is rapid and easy, making this a highly convenient option. This prosthetic limb is fully active and can produce up to 80 Nm of knee joint torque with more than 40 RPM (240 deg/s), enabling amputees to smoothly walk on stairs and steep slopes [23]. Despite its impressive functionality, the prosthetic’s heavy weight and its limited battery life of only 1 or 2 hours have prevented it from being widely commercialized. Indeed, most amputees prefer a lighter prosthetic limb that causes less muscle fatigue, even if its functionality is limited. In fact, dynamically active transfemoral prostheses can inject power in order to provide ankle push-off generation and reduce the extra metabolic energy consumption, as presented in [24–28]. However, the active prosthetic knee is energy-intensive and requires a large actuator, which increases the weight of the prosthetic knee and reduces the battery life. Therefore, there is reluctance among people to adopt a fully active prosthetic limb that weighs more than 4 kg limited battery life [13].

In general, the biological knee provides active and passive torque during walking [29]. However, active or passive microprocessor-controlled prosthetic knees cannot simulate the semiactive model. To address this challenge, recent research efforts have been focused on developing prosthetic limbs that are lighter and can be used for longer periods of time. To achieve these objectives, researchers have been exploring the use of passive components such as springs and hydraulic cylinders in their designs [30, 31]. As walking on level ground or low slopes is the norm for most amputees, with stairs or steep slopes, a transfemoral prosthetic knee with a semiactive dynamic is a solution to improve the walking performance of transfemoral amputees. While analyzing the gait of individuals with transfemoral prostheses, multiple approaches are utilized, including kinematic and kinetic analysis, electromyographic (EMG) measurements, and other techniques [32]. Electromyographic (EMG) measurements require a time-consuming process of attaching skin markers and electrodes to the body of the examined patient. Hence, combining kinematic and kinetic analyses could have a considerable advantage in analyzing the dynamic of transfemoral leg prosthetics. In fact, it is reported in [33] that, when kinematic and kinetic analyses are combined, inverse dynamics can then be utilized to obtain variables such as torques in individual joints of lower limbs. Generally, the term gait in prosthesis leg movement analysis describes the style of walking, rather than the walking process itself [34]. At present, there are two approaches to analyzing the dynamics of lower limb prostheses. The first one is a neuromuscular model, which is based on muscle mechanics and the second one is a mathematical model, which is based on the prosthesis parameters. In fact, in Ref. [35], a neuromuscular model of human motion is proposed and a prosthesis controller using muscle reflex and local feedback is designed. Numerical simulation of this model has shown that the neuromuscular control model results in a more robust gait than the one obtained by the impedance control method and improves the amputee’s movement. However, neuromuscular models are not suitable for transfemoral prostheses because of the need to consider coordinated movement between muscles due to serious muscle loss of transfemoral amputees. In general, the Lagrange formalism is the main method to derive the mathematical model of prosthesis devices. In concrete terms, the Lagrangian formulation describes the behavior of a dynamic system in terms of kinetic and potential energy stored in the system rather than of the forces and moments of the individual members involved. The forces (i.e., constraint forces), that restrict the motion of the knee joint within the prosthesis do not appear in the formulation of the Lagrangian dynamic equations. In [36], for example, the motion equations that describe the dynamic of Active Knee Prosthesis are derived through the Euler–Lagrange formalism. In addition to this, a knowledge-based fuzzy inference system is established using the lower limb data to control the dynamic motion of the active knee prosthesis. Researchers in Ref. [37] designed a robot to test transfemoral prostheses. Then, the Lagrange method was used to establish the mathematical model of the robot. Moreover, the authors have shown that the signals of hip displacement and thigh angle can be applied to the robot, and the sliding mode controller can track the position of the hip joint. In [38], the method to describe the forward kinematics of prosthesis has been proposed using a combination of Lie group, Lie algebra, and Lagrange equation to derive a mathematical model of the transfemoral prosthesis. Furthermore, switching control rules were designed to help amputees have normal gait at different phases.

2. Methods

The key improvement of the transfemoral prosthetic knee is to include ground reaction forces and knee friction and to simulate the knee torque. Moreover, combining kinematic and kinetic analyses could have a considerable advantage in analyzing the knee torque trajectory. Moreover, when kinematic and kinetic analyses are combined, inverse dynamics can then be utilized to obtain the torque in the knee joint of the transfemoral prosthetic.

2.1. Parameterized Model of the Transfemoral Prosthetic

As shown in Figure 1, a parameterized model of the transfemoral prosthetic was adopted to simulate the knee torque trajectory. In this model, the transfemoral prosthetic is represented by a two-segment single-axis knee joint.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Model of transfemoral prosthetic limb [39].

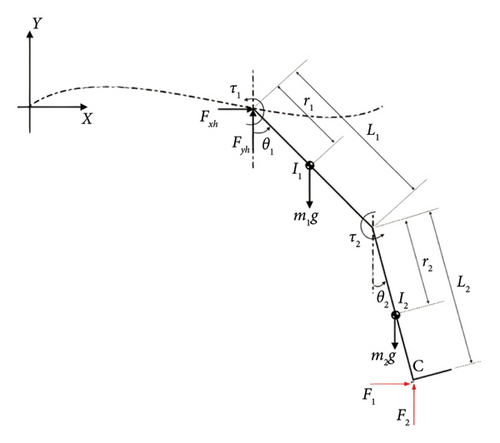
Subscripts i = 1 and i = 2 denote the thigh and shank, respectively, such as m_i are the masses, r_i represent the distances of the mass centers from the respective proximal joints; I_i are the moments of inertial; L_i are lengths; θ_i are the absolute angular displacement of the thigh and shank from the vertical; τ_i represents the torques applied to the hip and knee; and F_i are the ground reaction forces. Also, (x_h, y_h) are the coordinates of the hip with respect to the global reference frame XY. To be more specific, x_h represents the horizontal movement of the hip, and y_h is the vertical movement of the hip while F_xh and F_yh are the forces acting at the hip joint by the socket.

In general, to derive the torque generated at the hip and knee joints, the following steps are used that is: (i) determine the number of degrees of freedom in the system and select appropriate independent generalized coordinates; (ii) derive the velocity for the center of mass of each body in terms of the generalized coordinate position and velocity; (iii) identify both conservative and nonconservative forces; (iv) derive the kinetic and potential energy in term of the generalized coordinate position and velocity; and (v) substitute these quantities into Lagrange’s equation and solve for the equations of motion to obtain the torque generated at the hip and knee joints. Without loss of generality, in the present investigation, we assumed that:

(1)
The transfemoral prosthetic and the remaining part of a natural leg are both considered as two rigid segments linked to the amputee’s body with two pin joints.
(2)
The model only considers the sagittal plane motion.
(3)
The ankle joint is considered to be fixed.
(4)
The hip joint is assumed to be actively controlled by the patient.

2.2. Inverse Dynamics of the Transfemoral Prosthetic

Inverse dynamics is the most comprehensive method, giving access to net forces and torques as a function of the evolution of joint coordinates and their derivatives. In this method, the Euler–Lagrange formalism is used to find the equation of motion of the transfemoral prosthetic. Indeed, from Figure 1, the coordinates of the center of mass of each link, (x₁, y₁) and (x₂, y₂) are determined in the global coordinate system (XY) as

(1)

(2)

The use of the inverse dynamics method plays an important role in this research to derive the equations of motion for transfemoral single-leg prostheses due to its global nature and ability to provide detailed insights into the biomechanics of the system. In addition, it is sensitive to input data such as inertial parameters, kinematic derivatives, joint center positions, and center of pressure [40]. To be more explicit, this method calculates the net forces and torques at each joint, using the coordinates of the center of mass of each link (x₁, y₁) and (x₂, y₂) given by equations (1) and (2). By exploiting known kinematic data, such as joint angles and their derivatives, inverse dynamics can accurately trace the movements and performance of the prosthetic limb. This method effectively deals with the complex interactions between the hip and knee, described by the angles θ₁ and θ₂.

Before following the ultimate goal of the present research, it is crucial to note that in equations (1) and (2), all angular and linear positions depend on time. However, t is omitted and the time derivative of each time-dependent variable for instance dv/dt, is denoted by

, for simplicity. Furthermore, instead of considering the unknown applied forces F_xh and F_yh in deriving equations of motion for the stance phase, the known kinematic parameters of point

are utilized. Therefore, in the following calculations F_xh and F_yh are not involved. The time derivative of the coordinates of the center of mass for each link is calculated using equations (1) and (2). It follows from this that the linear velocity of the first link is

(3)

and the linear velocity of the second link is also calculated as

(4)

The total kinetic energy of the system is given as

(5)

The two first terms in equation (5) represent the total kinetic energy of the first link due to the linear and angular velocity of the center of mass of this link (i.e., thigh). The last two terms denote the total kinetic energy of the second link (i.e., shank). Replacing equations (3) and (4) into (5) yields:

(6)

Furthermore, the gravitational potential energy P of the system is the sum of the potential energy of each link PE(θ) = m₁gy₁ + m₂gy₂ calculated as

(7)

The Lagrangian density L of the whole system is defined as the difference between the total kinetic energy and the total gravitational potential energy given as

(8)

Using the Euler–Lagrange formulation [41], the generalized displacement of the hip joint and the knee joint is obtained as

(9)

where

represents the nonconservative generalized forces. However, except the gravity, constraints forces, and internal forces all other forces and moments applying on two links are considered as the generalized forces [42]. In this study, the generalized forces are obtained via the theory of virtual work given by

(10)

where D_i is the Rayleigh dissipation function [41] defined as

from which the generalized hip friction force and knee friction force can be calculated as

(11)

where β_i is the direction-dependent friction coefficient. To be more specific, β₁ is a hip coefficient of friction and β₂ is a knee coefficient of friction. The parameter J_e is the kinematic Jacobian relative to the point of application of the ground reaction forces. In fact, the coordinates of the point of application of the ground reaction forces is given by

(12)

Using (12), the Jacobian matrix J_e appearing in (10) is calculated as

(13)

Using this expression, (9) can be written in the matrix form as

(14)

Substituting (8) into (14), the applied torques at each joint are derived as

(15)

(16)

Using (15) and (16), the dynamic of the transfemoral prosthetic is given by

(17)

where M(θ) is the inertial matrix,

are the Centripetal and Coriolis forces, G(θ) is the gravity vector, B(θ) is the hip acceleration term, f_m is the joint’s friction forces and ground reaction forces terms while the vector τ is the aggregated hip and knee torques generated. θ₁ and θ₂ are the corresponding absolute angles of thigh and shank, respectively, from the vertical.

It is important to note that the model (17) is represented as the robotic pendulum model, as considered in previous works [43–48] that address various control strategies and perturbation attenuation techniques for similar systems.

2.3. Comparison of the Developed Model with the Old Model

The model developed in the present study emanates from the previous model proposed in [39], where a transfemoral prosthetic leg is modeled as a single axis of two segmental prosthetic knees implemented with a magneto-rheological (MR) damper as a variable damping element. By carrying out a dynamic analysis of the knee of the transfemoral prosthetic via the inverse dynamic approach, the authors reported that the dynamic model of the transfemoral prosthetic can predict the kinetic and kinematic performances, which can help to trace the desired knee torque trajectory. However, in their work, they did not consider the effects of ground reaction forces as well as the effect of the friction generated by the blade rotation located within the knee joint. In this respect, we extended their model to the realistic context by considering that the friction of the blade generated during the rotation of the center of the knee joint axis, and ground reaction forces are relevant. This consideration incurs three additional terms in the time evolution equation for the transfemoral prosthetic knee torque (see (16) for instance), in contrast to the one proposed in Ref. [39]. These terms are, namely, knee friction force, horizontal ground reaction force, and vertical ground reaction force. To our knowledge, this is the first theoretical work aimed at understanding the impact of these parameters on knee torque dynamics. The presence of these parameters can guide prosthesis designers in selecting appropriate actuators for use in the transfemoral prosthesis knee to improve performance and reduce energy expenditure for the user.

3. Results and Discussion

3.1. Variation of Steady State Knee Torque with Shank Angular Displacement in the Presence of Ground Reaction Forces

As stressed above, we will follow our assumption which states that the patient can actively control his or her hips and only pay attention to the differential (16) of the knee joint’s motion in the presence of friction and ground reaction forces. The data for the prosthetic leg used in the simulation is shown in Table 1 and the inputs to the model such as thigh, and shank angular displacements, their derivatives, as well as hip joint accelerations, are obtained from winter [49]. The whole weight of the prosthesis is around 2.5 kg as reported in [39].

Table 1. Experimental data needed for the computation, adopted from [39, 49].

Parameters	Values
Body weight	80 kg
Body height	1.75 m
m₂	3.46 kg
I₂	0.108 kg·m²
L₁	0.314 m
L₂	0.425 m
r₂	0.2576 m
g	9.81 m/s²

To start, we analyzed the system dynamics at the steady state walking regime, with the aim to probe the effect of shank angular displacement on the knee torque dynamics. It should be noted that the steady state walking regime here represents the states where the friction force does not influence the movement of the knee. Knowing that the steady state is a state of a system that does not change in time broadly, in (16) we set,

and

, which gives rise to

(18)

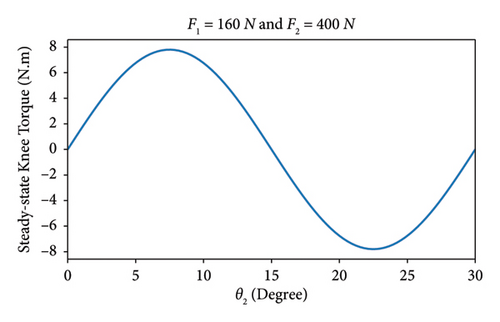
The expression of τ₂ given in formula (18) does not include the knee friction coefficient β₂, but rather it is primarily controlled by the shank angular displacement θ₂. Therefore, to investigate the relationship between the knee torque τ₂ and the shank angular displacement θ₂, we have chosen to plot their respective values for fixed forces F₁ = 160N and F₂ = 400N, using the parameter values specified in Table 1. It is worth mentioning that the decision to assign a greater magnitude to the vertical ground reaction force F₂ compared to the horizontal component F₁ is based on experimental evidence, which demonstrates that the vertical ground reaction force plays a more significant role in knee joint movement than the horizontal component. By analyzing the resulting curve in Figure 2, we observe that as the shank angular displacement θ₂ increases, the steady-state knee torque trajectory follows a natural gait pattern. Notably, during the increasing phase of θ₂, the knee movement remains stable. This insight holds significant physical relevance, as it indicates that within the range of θ₂ values at the steady state, the knee torque trajectory facilitates smooth transitions between flexion and extension, thereby ensuring stability and preventing falls or stumbling.

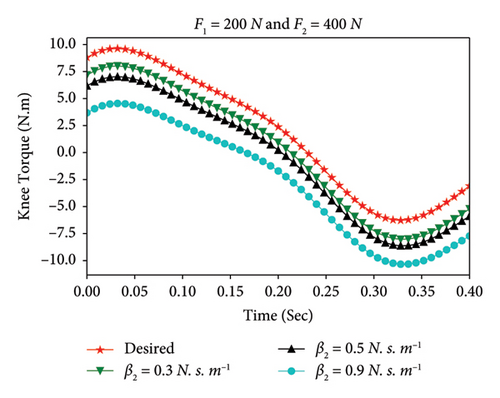
Using implementations under MATLAB and the Simulink toolbox and the differential equation of motion given by (16), the torque provided by the transfemoral prosthetic knee is simulated. The results are shown in Figures 3 and 4 for different values of prosthetic knee friction coefficient and ground reaction forces. Figure 3 represents the variations of the prosthetic knee torque, τ₂, as a function of time, for different values of prosthetic knee friction coefficient (β₂). In this case, the ground reaction forces have been fixed to F₁ = 200 N and F₂ = 400 N. According to Figure 3, when β₂ is increased in relatively large values, τ₂ decreases in time, and the tracking errors between the desired knee torque pattern and the simulated torque trajectory of the transfemoral prosthetic knee increases. To be more explicit, the damping phenomena induced by the blade rotation incorporated into the knee center of rotation of the prosthetic during the dynamic process of the knee are clinically relevant. In fact, this limits the prosthetic knee’s ability to produce optimal knee flexion-extension. Consequently, amputees may need to expend high metabolic energy to modify their gait to walk, leading to modifications in gait patterns that can result in a slower and less symmetrical gait in the swing phase.

In the context of the present study, the knee torque trajectory of a transfemoral prosthesis can be improved by varying F₁ and F₂ while keeping β₂ = 0.3 N.s/m. To do this, we first analyzed the effect of varying the horizontal component of the ground reaction force F₁ while fixing F₂ = 400N and β₂ = 0.3 N.s/m. In this respect, we considered three different values of F₁ such as 320N, 350N, and 400N. The effect of varying this parameter on the knee torque dynamics is shown in Figure 5 and the results show that by taking F₁ = 320N, the simulated knee torque trajectory is close to the normal knee torque trajectory with a tracking error of 5.63867%. Concretely, Figure 5 suggests that this tracking error can lead to several issues for the amputee patient during walking, including reduced gait efficiency and increased energy expenditure, discomfort and potential pain in the residual limb, compromised balance and stability, abnormal stress on other joints leading to pain. To mitigate these effects, it is crucial to look at the impact of the contribution of the vertical component of the ground reaction force F₂ on the knee torque dynamics while keeping β₂ fixed at 0.3 N.s/m and F₁ at 320 N. To follow the goal of the present investigation, the key parameter F₂ is varied, and the results presented in Figure 4 suggest that when F₂ = 800 N the tracking error between the simulated knee torque and the normal knee torque dynamics is reduced to = 0.342868%. Despite this improvement, the extension of the transfemoral prosthetic knee remains limited due to the friction force induced by the blade rotation located at the knee center. To be more explicit, Figure 4 demonstrates that to achieve the desired knee torque trajectory reported in ref. [49], the transfemoral prosthetic knee’s friction coefficient should be set to

(19)

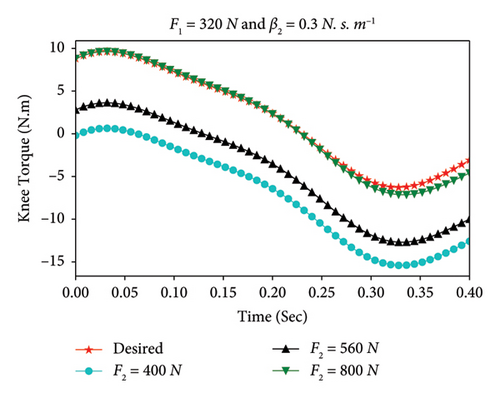
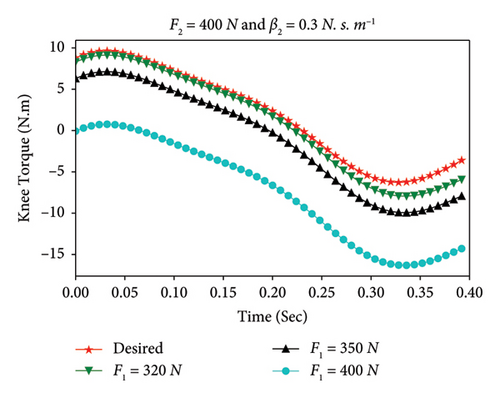
The quantity β_2(th) represents a threshold value for the friction coefficient, above which the transfemoral prosthetic knee torque tracking error may occur.

However, for comparison purposes, the errors between a desired knee torque (i.e. for the normal human leg), and the simulated knee torque presented in this work are calculated to indicate the effects of the prosthetic knee friction and ground reaction forces. These errors are evaluated through the normalized root mean square error (NRMSE) method as evidenced by

(20)

In (20), τ₂(t) denotes the predicted data point, with τ_2(desired)(t) as a reference, N is the total number of data points of which t (i.e., time) indicates one specific data point. max(τ_2(desired)(t)) and min(τ_2(desired)(t)) are the maximum and minimum values of desired knee torque. Using formula (20), the results summarized in Table 2 clearly show that the combination of the values of the following parameters β₂ = 0.3 N.s.m⁻¹, F₁ = 320 N, and F₂ = 800 N makes it possible to reduce the knee torque tracking errors of the amputee patient during locomotion.

Table 2. Summary of tracking errors generated by the transfemoral prosthetic knee.

F₁	F₂	β₂	NRMSE (%)
200	400	0.3	1.00966
		0.5	1.48975
		0.9	2.77402

320	400	0.3	5.63867
	560		3.83856
	800		0.342868

It is important to note that, the desired knee torque (i.e., in red color), shown in Figures 3 and 4 is plotted based on the experimental data provided in Ref. [49] for the normal leg. This corresponds to the case where β₂ = 0, F₁ = 0, and F₂ = 0 in the present work. Indeed, these variables represent specific conditions in which the knee joint is not subject to any friction and external forces.

4. Conclusions

The dynamics of the knee joint of a transfemoral prosthetic leg were investigated, with a focus on the effects of prosthetic knee friction and ground reaction forces on the temporal profiles of the prosthetic knee torque. The mathematical model of the transfemoral prosthetic knee torque was derived using the inverse dynamics method. Simulation results have demonstrated that incorporating knee friction and ground reaction forces in the model proposed in Ref. [39] leads to tracking errors (see Table 2 for instance) in the prosthetic knee torque trajectory, which results in increased metabolic energy costs for the amputee. To this end, an optimal control problem must be formulated for the three parameters to avoid tracking errors in the knee torque dynamics.

Disclosure

The responsibility for the content of this publication lies with the author.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This paper is based on the DAAD project 57611107 that has received funding from the Federal Ministry of Education and Research (BMBF). The first author wishes to thank the German Academic Exchange Service (DAAD) and the Institute for Automation and Systems Engineering at the Technische Universität Ilmenau, Germany, for a visit during which part of this work was completed. The second author would like to express his sincere gratitude to Alexander von Humboldt and the German Academic Exchange Service (DAAD) for their generous support, which has been instrumental in the successful completion of this research project. The two authors would also like to thank the organizing committee of the conference: International African Conference on Machine Learning, Optimization, and Applications (MLOA) (July 2023), which enabled them to present the first version of this work.

Open Research

Data Availability

The processed data used to support the findings of this study are included within the present article. The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.

References

1 Pana C. F., Manta L. F., Vladu I. C., Cismaru s.I., Petcu Besnea F. L., Cojocaru D., and Bizdoaca N., The design of a smart lower-limb prosthesis supporting people with transtibial amputation-A data acquisition system, Applied Sciences. (2022) 12, no. 13, https://doi.org/10.3390/app12136722.
10.3390/app12136722
Google Scholar
2 Walter N., Alt V., and Rupp M., Lower limb amputation rates in Germany, Medicina (Kaunas). (2022) 58, no. 1, https://doi.org/10.3390/medicina58010101.
10.3390/medicina58010101
Google Scholar
3 Yepes J. C., Rúa S., Osorio M., Pérez V. Z., Moreno J. A., Al-Jumaily A., and Betancur M. J., Human-robot interaction torque estimation methods for a lower limb rehabilitation robotic system with uncertainties, Applied Sciences. (2022) 12, no. 11, https://doi.org/10.3390/app12115529.
10.3390/app12115529
Google Scholar
4 Andrysek J., Michelini A., Eshraghi A., Kheng S., Heang T., and Thor P., Gait performance of friction-based prosthetic knee joint swing-phase controllers in under-resourced settings, Prosthesis. (2022) 4, no. 1, 125–135, https://doi.org/10.3390/prosthesis4010013.
10.3390/prosthesis4010013
Google Scholar
5 Zhang Z., Yu H., Cao W., Wang X., Meng Q., and Chen C., Design of a semi-active prosthetic knee for transfemoral amputees: gait symmetry research by simulation, Applied Sciences. (2021) 11, no. 12, https://doi.org/10.3390/app11125328.
10.3390/app11125328
Google Scholar
6 Liang W., Qian Z., Chen W., Song H., Cao Y., Wei G., Ren L., Wang K., and Ren L., Mechanisms and component design of prosthetic knees: a review from a biomechanical function perspective, Frontiers in Bioengineering and Biotechnology. (2022) 10, 950110–954185, https://doi.org/10.3389/fbioe.2022.950110.
10.3389/fbioe.2022.950110
PubMed Web of Science® Google Scholar
7 Theeven P. J., Hemmen B., Geers R. P., Smeets R. J., Brink P. R., and Seelen H. A., Influence of advanced prosthetic knee joints on perceived performance and everyday life activity level of low-functional persons with a transfemoral amputation or knee disarticulation, Journal of Rehabilitation Medicine. (2012) 44, no. 5, 454–461, https://doi.org/10.2340/16501977-0969, 2-s2.0-84861088328.
10.2340/16501977-0969
PubMed Google Scholar
8 Waters R. L., Perry J., Antonelli D., and Hislop H., Energy cost of walking of amputees: the influence of level of amputation, The Journal of Bone and Joint Surgery. (1976) 58, no. 1, 42–46, https://doi.org/10.2106/00004623-197658010-00007, 2-s2.0-0017253701.
10.2106/00004623-197658010-00007
CAS PubMed Web of Science® Google Scholar
9 Jung-Hoon K. and Jun-Ho O., Development of an above-knee prosthesis using MR damper and leg simulator, Proceedings ICRA. IEEE International Conference on Robotics and Automation (Cat. No.01CH37164) 4, 2001, 3686–3691.
10.1109/ROBOT.2001.933191
Google Scholar
10 Herr H. and Wilkenfeld A., User-adaptive control of a magnetorheological prosthetic knee, Industrial Robot: International Journal. (2003) 30, no. 1, 42–55, https://doi.org/10.1108/01439910310457706, 2-s2.0-0037265402.
10.1108/01439910310457706
Web of Science® Google Scholar
11 Lansade C., Chiesa G., Paysant J., Vicaut E., Cristina M. C., and Ménager D., Impact of C-LEG on mobility, satisfaction and quality of life in a multicenter cohort of femoral amputees, Annals of physical and rehabilitation medicine. (2021) 64, no. 1, 101386, https://doi.org/10.1016/j.rehab.2020.03.011.
10.1016/j.rehab.2020.03.011
PubMed Google Scholar
12 Thiele J., Schöllig C., Bellmann M., and Kraft M., Designs and performance of three new microprocessor-controlled knee joints, Biomedizinische Technik. Biomedical engineering. (2019) 64, no. 1, 119–126, https://doi.org/10.1515/bmt-2017-0053, 2-s2.0-85042163994.
10.1515/bmt-2017-0053
CAS PubMed Google Scholar
13 Shin H., Park J., Lee H., Jung S., Jeon M., and Park S., Selective passive/active switchable knee prosthesis based on multifunctional rotary hydraulic cylinder for transfemoral amputees, Actuators. (2023) 12, no. 3, https://doi.org/10.3390/act12030118.
10.3390/act12030118
PubMed Google Scholar
14 Shields B. L., Fite K. B., and Goldfarb M., Design, control, and energetic characterization of a solenoid-injected monopropellantpowered actuator, IEEE/ASME Transactions on Mechatronics. (2006) 11, no. 4, 477–487, https://doi.org/10.1109/tmech.2006.878531, 2-s2.0-33947138101.
10.1109/TMECH.2006.878531
Google Scholar
15 Sup F., Varol H. A., Mitchell J., Withrow T., and Goldfarb M., Design and control of an active electrical knee and ankle prosthesis, Proceedings of the 2nd IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics, March 2008, Scottsdale, AZ, USA, 523–528, https://doi.org/10.1109/BIOROB.2008.4762811, 2-s2.0-63049100904.
10.1109/BIOROB.2008.4762811
Google Scholar
16 Lawson B. E., Huff A., and Goldfarb M., A preliminary investigation of powered prostheses for improved walking biomechanics in bilateral transfemoral amputees, Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, December 2012, San Diego, CA, USA, 4164–4167, https://doi.org/10.1109/EMBC.2012.6346884, 2-s2.0-84880941357.
10.1109/EMBC.2012.6346884
Google Scholar
17 Lawson B. E., Mitchell J., Truex D., Shultz A., Ledoux E., and Goldfarb M., A robotic leg prosthesis: design, control, and implementation, IEEE Robotics and Automation Magazine. (2014) 21, no. 4, 70–81, https://doi.org/10.1109/MRA.2014.2360303, 2-s2.0-84919599273.
10.1109/MRA.2014.2360303
Web of Science® Google Scholar
18 Sup F., Varol H. A., and Goldfarb M., Upslope walking with a powered knee and ankle prosthesis: initial results with an amputee subject, IEEE Transactions on Neural Systems and Rehabilitation Engineering. (2011) 19, no. 1, 71–78, https://doi.org/10.1109/TNSRE.2010.2087360, 2-s2.0-79951657383.
10.1109/TNSRE.2010.2087360
PubMed Web of Science® Google Scholar
19 Ledoux E. D. and Goldfarb M., Control and evaluation of a powered transfemoral prosthesis for stair ascent, IEEE Transactions on Neural Systems and Rehabilitation Engineering. (2017) 25, no. 7, 917–924, https://doi.org/10.1109/TNSRE.2017.2656467, 2-s2.0-85029595114.
10.1109/TNSRE.2017.2656467
PubMed Google Scholar
20 Martinez-Villalpando E. C. and Herr H., Agonist-antagonist active knee prosthesis: a preliminary study in level-ground walking, Journal of rehabilitation research and development. (2009) 46, no. 3, 361–373, https://doi.org/10.1682/jrrd.2008.09.0131, 2-s2.0-70349289953.
10.1682/JRRD.2008.09.0131
PubMed Web of Science® Google Scholar
21 Martinez-Villalpando E. C., Mooney L., Elliott G., and Herr H., Antagonistic active knee prosthesis. A metabolic cost of walking comparison with a variable-damping prosthetic knee, 2011, Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, December 2011, Boston, MA, USA, 8519–8522, https://doi.org/10.1109/IEMBS.2011.6092102, 2-s2.0-84861665607.
10.1109/IEMBS.2011.6092102
Google Scholar
22 Rouse E. J., Mooney L. M., and Herr H. M., Clutchable series-elastic actuator: implications for prosthetic knee design, The International Journal of Robotics Research. (2014) 33, no. 13, 1611–1625, https://doi.org/10.1177/0278364914545673, 2-s2.0-84910081493.
10.1177/0278364914545673
Web of Science® Google Scholar
23 Azocar A. F., Mooney L. M., Hargrove L. J., and Rouse E. J., Design and characterization of an open-source robotic leg prosthesis, Proceedings of the 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), June 2018, Enschede, The Netherlands, 111–118, https://doi.org/10.1109/BIOROB.2018.8488057, 2-s2.0-85056604086.
10.1109/BIOROB.2018.8488057
Google Scholar
24 Sup F., Bohara A., and Goldfarb M., Design and control of a powered transfemoral prosthesis, The International Journal of Robotics Research. (2008) 27, no. 2, 263–273, https://doi.org/10.1177/0278364907084588, 2-s2.0-38649089762.
10.1177/0278364907084588
PubMed Web of Science® Google Scholar
25 Sup F., Varol H. A., Mitchell J., Withrow T., and Goldfarb M., Design and control of an active electrical knee and ankle prosthesis, Proceedings of the EMBS International Conference on Biomedical Robotics and Biomechatronics, December 2008, Scottsdale, AZ, USA, 523–528, https://doi.org/10.1109/BIOROB.2008.4762811, 2-s2.0-63049100904.
10.1109/BIOROB.2008.4762811
Google Scholar
26 Unal R., Behrens S. M., Carloni R., Hekman E. E. G., Stramigioli S., and Koopman H. F. J. M., Prototype design and realization of an innovative energy-efficient transfemoral prosthesis, Proceedings of the EMBS International Conference on Biomedical Robotics and Biomechatronics, July 2010, Tokyo, Japan, 191–196, https://doi.org/10.1109/BIOROB.2010.5626778, 2-s2.0-78650385753.
10.1109/BIOROB.2010.5626778
Google Scholar
27 Dejan P., Rajko T., Dejan T., and Laszlo S., Control aspects of active above-knee prosthesis, International Journal of Man-Machine Studies. (1991) 35, no. 6, 751–767, https://doi.org/10.1016/S0020-7373(05)80159-2, 2-s2.0-0012082692.
10.1016/S0020-7373(05)80159-2
Google Scholar
28 Awad M. I., Dehghani-Sanij A. A., Moser D., and Zahedi S., Inertia properties of a prosthetic knee mechanism, Towards Autonomous Robotic Systems. (2015) 9287, 38–43, https://doi.org/10.1007/978-3-319-22416-9_5, 2-s2.0-84947086885.
10.1007/978-3-319-22416-9_5
Google Scholar
29 Elery T., Rezazadeh S., Reznick E., Gray L., and Gregg R. D., Effects of a powered knee-ankle prosthesis on amputee hip compensations: a case series, IEEE Transactions on Neural Systems and Rehabilitation Engineering. (2020) 28, no. 12, 2944–2954, https://doi.org/10.1109/TNSRE.2020.3040260.
10.1109/TNSRE.2020.3040260
PubMed Google Scholar
30 Tran M., Gabert L., Cempini M., and Lenzi T., A lightweight, efficient fully powered knee prosthesis with actively variable transmission, IEEE Robotics and Automation Letters. (2019) 4, no. 2, 1186–1193, https://doi.org/10.1109/LRA.2019.2892204, 2-s2.0-85064635644.
10.1109/LRA.2019.2892204
Google Scholar
31 Lenzi T., Cempini M., Hargrove L., and Kuiken T., Design, development, and testing of a lightweight hybrid robotic knee prosthesis, The International Journal of Robotics Research. (2018) 37, no. 8, 953–976, https://doi.org/10.1177/0278364918785993, 2-s2.0-85052084485.
10.1177/0278364918785993
Web of Science® Google Scholar
32 Gross R., Delporte L., Arsenault L., Revol P., Lefevre M., Clevenot D., Boisson D., Mertens P., Rossetti Y., and Luauté J., Does the rectus femoris nerve block improve knee recurvatum in adult stroke patients? A kinematic and electromyographic study, Gait and Posture. (2014) 39, no. 2, 761–766, https://doi.org/10.1016/j.gaitpost.2013.10.008, 2-s2.0-84892822399.
10.1016/j.gaitpost.2013.10.008
CAS PubMed Google Scholar
33 Vaverka F., Elfmark M., Svoboda Z., and Janura M., System of gait analysis based on ground reaction force assessment, Acta Gymnica. (2015) 45, no. 4, 187–193, https://doi.org/10.5507/ag.2015.022, 2-s2.0-84957899295.
10.5507/ag.2015.022
Google Scholar
34 Al-Hayali N. K., Nacy S. M., Chiad J. S., and Hussein O., A Mathematical model of the human lower limb during a complete gait cycle and its various phases, Journal of Mechanical Engineering Research and Developments. (2021) 44, no. 8, 392–405.
Google Scholar
35 Thatte N. and Geyer H., Toward balance recovery with leg prostheses using neuromuscular model control, IEEE Transactions on Biomedical Engineering. (2016) 63, no. 5, 904–913, https://doi.org/10.1109/TBME.2015.2472533, 2-s2.0-84966737899.
10.1109/TBME.2015.2472533
PubMed Google Scholar
36 Wiem A., Rahma B., and Bel Hadj Ali Naoui S., An adaptive TS fuzzy-PID controller applied to an active knee prosthesis based on Human walk, Proceedings of the International Conference on Advanced Systems and Electric Technologies, June 2018, 22–27, https://doi.org/10.1109/aset.2018.8379828, 2-s2.0-85050008928.
10.1109/aset.2018.8379828
Google Scholar
37 Richter H., Simon D., Smith W. A., and Samorezov S., Dynamic modeling, parameter estimation and control of a leg prosthesis test robot, Applied Mathematical Modelling. (2015) 39, no. 2, 559–573, https://doi.org/10.1016/j.apm.2014.06.006, 2-s2.0-84922619803.
10.1016/j.apm.2014.06.006
Web of Science® Google Scholar
38 Chen Y., Xuan B., Geng Y., Ding S., and Chen L., Modeling and control of knee-ankle-toe active transfemoral prosthesis, IEEE Access. (2020) 8, no. 1, 133451–133462, https://doi.org/10.1109/ACCESS.2020.3010636.
10.1109/ACCESS.2020.3010636
Web of Science® Google Scholar
39 Chandramohan S., Radhe S., and Hemantha K., Semi-active control of a swing phase dynamic model of transfemoral prosthetic device based on inverse dynamic model, Journal of the Brazilian Society of Mechanical Sciences and Engineering. (2020) 42, no. 6, 16785878, https://doi.org/10.1007/s40430-020-02387-2.
10.1007/s40430-020-02387-2
Google Scholar
40 Dumas R., Cheze L., and Frossard L., Loading applied on prosthetic knee of transfemoral amputee: comparison of inverse dynamics and direct measurements, Gait and Posture. (2009) 30, no. 4, 560–562, https://doi.org/10.1016/j.gaitpost.2009.07.126, 2-s2.0-70349335356.
10.1016/j.gaitpost.2009.07.126
CAS PubMed Web of Science® Google Scholar
41 Richter H., Simon D., Smith W. A., and Samorezov S., Dynamic modeling, parameter estimation and control of a leg prosthesis test robot, Applied Mathematical Modelling. (2015) 39, no. 2, 559–573, https://doi.org/10.1016/j.apm.2014.06.006, 2-s2.0-84922619803.
10.1016/j.apm.2014.06.006
Web of Science® Google Scholar
42 Borjian R., Design, Modeling, and Control of an Active Prosthetic Knee, 2008, University of Waterloo, Canada.
Google Scholar
43 de Jesús Rubio J., Hernandez M. A., Rosas F. J., Orozco E., Balcazar R., and Pacheco J., Genetic high-gain controller to improve the position perturbation attenuation and compact high-gain controller to improve the velocity perturbation attenuation in inverted pendulums, Neural Networks. (2024) 170, 32–45, https://doi.org/10.1016/j.neunet.2023.11.029.
10.1016/j.neunet.2023.11.029
PubMed Google Scholar
44 de Jesús Rubio J., Bat algorithm based control to decrease the control energy consumption and modified bat algorithm based control to increase the trajectory tracking accuracy in robots, Neural Networks. (2023) 161, 437–448, https://doi.org/10.1016/j.neunet.2023.02.010.
10.1016/j.neunet.2023.02.010
PubMed Google Scholar
45 Xie X., Wei C., Gu Z., and Shi K., Relaxed resilient fuzzy stabilization of discrete-time takagi–sugeno systems via a higher order time-variant balanced matrix method, IEEE Transactions on Fuzzy Systems. (2022) 30, no. 11, 5044–5050, https://doi.org/10.1109/tfuzz.2022.3145809.
10.1109/TFUZZ.2022.3145809
Web of Science® Google Scholar
46 de Jesús Rubio J., Orozco E., Cordova D. A., Hernandez M. A., Rosas F. J., and Pacheco J., Observer-based differential evolution constrained control for safe reference tracking in robots, Neural Networks. (2024) 175, https://doi.org/10.1016/j.neunet.2024.106273, 106273.
10.1016/j.neunet.2024.106273
PubMed Google Scholar
47 Qiu J., Wang T., Sun K., Rudas I. J., and Gao H., Disturbance observer-based adaptive fuzzy control for strict-feedback nonlinear systems with finite-time prescribed performance, IEEE Transactions on Fuzzy Systems. (2022) 30, no. 4, 1175–1184, https://doi.org/10.1109/tfuzz.2021.3053327.
10.1109/TFUZZ.2021.3053327
Web of Science® Google Scholar
48 García-Chávez R. E., Silva-Ortigoza R., Hernández-guzmáN V. M., Marciano-Melchor M., Orta-Quintana Á. A., García-Sánchez J. R., and Taud H., A robust sliding mode and PI-based tracking control for the MIMO “DC/DC buck converter–inverter–DC motor” system, IEEE Access. (2023) 11, 119396–119408, https://doi.org/10.1109/access.2023.3327425.
10.1109/ACCESS.2023.3327425
Google Scholar
49 Winter D. A., Biomechanics and Motor Control of Human Movement, 2009, Publishing House: John Wiley &Sons, Canada, Inc.
10.1002/9780470549148
Google Scholar

All articles

Investigation of Knee Torque Dynamics in Single-Leg Transfemoral Prosthetic during Walking Using Mathematical Modeling

Abstract

1. Introduction

2. Methods

2.1. Parameterized Model of the Transfemoral Prosthetic

2.2. Inverse Dynamics of the Transfemoral Prosthetic

2.3. Comparison of the Developed Model with the Old Model

3. Results and Discussion

3.1. Variation of Steady State Knee Torque with Shank Angular Displacement in the Presence of Ground Reaction Forces

4. Conclusions

Disclosure

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Investigation of Knee Torque Dynamics in Single-Leg Transfemoral Prosthetic during Walking Using Mathematical Modeling

Abstract

1. Introduction

2. Methods

2.1. Parameterized Model of the Transfemoral Prosthetic

2.2. Inverse Dynamics of the Transfemoral Prosthetic

2.3. Comparison of the Developed Model with the Old Model

3. Results and Discussion

3.1. Variation of Steady State Knee Torque with Shank Angular Displacement in the Presence of Ground Reaction Forces

4. Conclusions

Disclosure

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information