A Novel Approach with Comparative Computational Simulation of Analytical Solutions of Fractional Order Volterra Type Integral Equations
Abstract
The main purpose of this article is to reconsider the theory of variational iteration method and embed it with Laplace transform to construct the conjoined technique variational iteration Laplace transform method. And then, by using the proposed method we solve a class of integral equations, especially fractional order Volterra type integro-partial-differential equations occurring in different fields of natural and social sciences. For this, we first turn to some prelude concepts and different types of equations especially integral equations of different kinds from the literature. Then, we will present step by step the embedded technique. Next, some fractional order model integral equations will be tackled using the proposed method along with some existing techniques, like the Adomian decomposition method and successive approximations method. The efficacy and authentication of the proposed technique will be analysed with the help of the obtained results and graphical exhibitions of the particular solved examples. Finally, use of the initiated method in the future for different types of equations occurring in different fields of science will be presented.
1. Introduction
The use of mathematical models in different fields of natural sciences is indispensable. Because for the description of any physical circumstance some sort of mathematics which may be in the form of mathematical logic or some types of equations is required. Mathematical logic is rather easy to interpret, understand, and easily solvable [1, 2]. On the other hand, a model in the form of complex equations, for example, algebraic equations (AE) [3], transcendental equations (TEs) [4], ordinary differential equations (ODEs) [5, 6], partial differential equations (PDEs) [7], fractional order partial differential equations (FOPDEs) [8], and integral equations (IEs) [9, 10] needs some sort of mathematical manipulations for their solutions and future employments. Some of the mathematical techniques are, quadratic formula for quadratic equations in one variable [11] and the matrix inversion method for a system of linear equations [12]. Also, iterative methods like Newton–Raphson formula (NRF) [13, 14], Jacobi’s method, finding the integrating factors and the method of separation of variables for ODEs as well as PDEs [15–17] and [18, 19] are referred for FOPDEs. Also note that the successive approximation method and Adomian decomposition method (ADM) are successfully applicable to IEs [20].
The above mentioned mathematical techniques are analytical, numerical, and iterative in nature and we have observed in mathematical literature that in some cases these techniques also fail to find the exact answer of the problem or not easily applicable. So, in such situations, some other techniques are manipulated that may give the approximate answer or such approximations may converge to the exact solution of the problem. For this, the interested reader is referred to [21–25]. A large number of physical models in the fields of physics [26], astronomy [27], biophysics [28], plasma physics [29], and applied mathematics are in the form of integral equations as may be seen in [30, 31]. To predict the behaviour, hereditary and memory effects of the physical models in these fields and the entail for more decisive results, the ordinary IEs are converted into FOIEs.
The structure of the article is that first we give brief description of the IEs, related terminologies, different methods for the solution of IEs, their drawbacks, some definitions, proposed embedded technique, applications of the proposed method to particular FOIEs, conclusions, future directions and at the end references are given.
1.1. Integral Equations
- (i)
If in (1), then the IE (1) is homogeneous otherwise nonhomogeneous.
- (ii)
If the unknown function under the integral sign is in linear form, then the IE is linear otherwise nonlinear.
- (iii)
If both the limits of integration are constants in (1) and (2) then the resulting IE is called Fredholm type IEs.
- (iv)
On the other hand, if at least one or both the limits of integration are variable, then the corresponding IE is of Volterra type.
- (v)
If both limits or at least one of them is infinite that is the integral is improper then the IE is singular IE.
- (vi)
Similarly, if at certain points in the range of integration limits, the kernel does not exist, then also the IE is singular.
There have been developed many techniques for the solution of IEs, for example, Adomian decomposition method (ADM), successive approximation method (SAM), direct computation method (DCM), method of successive substitution (MSS), series solution method (SSM), variational iteration method (VIM), and method of regularization (MOR). Some of these methods were applicable only for the solution of ODEs but work also for the IEs. The ADM and SAM may be applicable directly almost for all types of IEs except for the IEs in which kernel is undefined at some points in the range of limits of integration. Moreover, while solving an IE by ADM, one faces the problem of finding the Adomian polynomials which is not an easy task. Also, to apply VIM on an IE first it is converted into the corresponding integro-differential form and then is solved.
Calculation of Lagrange’s multiplier in the VIM is also a cumbersome task. So, keeping in mind all these points, in the ongoing section, we will modify the classical VIM by embedding it with Laplace transform to develop the coupled technique variational iteration Laplace transform method (VILTM). Then, we will solve some Volterra type fractional order integral equations (FOIEs) with the help of ADM, SAM, and the proposed technique VILTM. We will see that the initiated method is much easier to understand and apply than the ordinary ADM, SAM, and Laplace transform. Because we have not to find the general Lagrange’s multiplier for each particular numerical example as we are to find it in the classical VIM. So, in the upcoming section, we will present the VILTM for general FOIEs and put it in to solve some particular FOIEs for checking the efficacy and suitability of VILTM. But let us review some definitions before we discuss VIM and Laplace transform.
Definition 1. Fractional order integral equation
The general form of FOIE is, [32],
Definition 2. Laplace transform
Consider a real valued piecewise continuous function, in the interval [0, ∞], then its Laplace transform denoted as and is given by
The Laplace transform of the derivative of a function is as follows:
Substituting different values of n, we have the Laplace transform of corresponding derivative, for example, if n = 1, 2, then (6) is
Definition 3. Leibniz derivative rule of an integral
Let and , that is given function and its partial derivative w. r. t. are continuous in both and , in some region of -plane. Also, are in that region with , , and continuous in the region , then
The formula is known as the general form of the Leibniz derivative rule an integral.
1.2. Variational Iteration Method
2. Variational Iteration Laplace Transform Method
3. Examples
To understand the proposed technique VILTM, we apply it on some particular Volterra type FOIEs, the results, and their graphical analysis will show the efficacy and authenticity of the method.
Example 1. As a first particular example, consider the following Volterra type IE:
Now, we solve (19) by using ADM, SAM, and the proposed method VILTM.
-
Case-I: Adomian decomposition method
-
Here, we solve (19) using ADM for this, let us say and put it in the relation:
() -
For n = 0, 1, 2, … we get the following iterations:
() -
The final solution may be written as
() -
that gives as the exact solution of (19). Next, we solve (19) using SAM.
-
Case-II: Successive approximation method
-
Let and solve the relation
() -
for n = 0, 1, 2, … to get the following iterations:
() -
that gives the final solution of (19) as .
-
Case-III: Variational iteration Laplace transform method
-
Now, we solve (19) with the help of the proposed method VILTM, and for this, the corresponding integro-partial-differential equation using (8) is
() -
Hence, the iterative relation for the above FOIE (19) according to (17) is
() -
Now, for n = 0, 1, 2, …., we get the following iterations:
() -
that gives as the final solution of (19). This is in complete agreement with the solution obtained by the other methods, like, ADM or SAM, etc., for ordinary as well as FOIEs, showing that the proposed technique is not only reliable but much efficient and easier to apply for Volterra type fractional IEs.
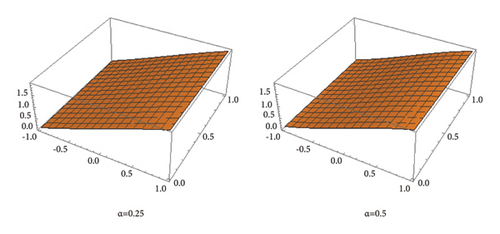
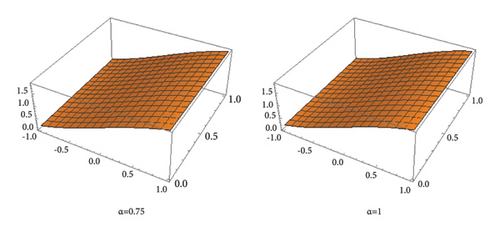
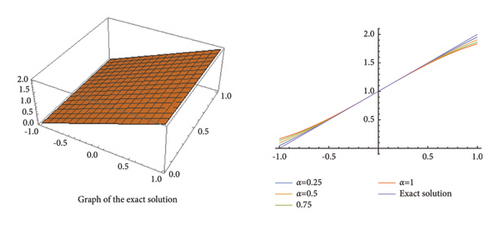
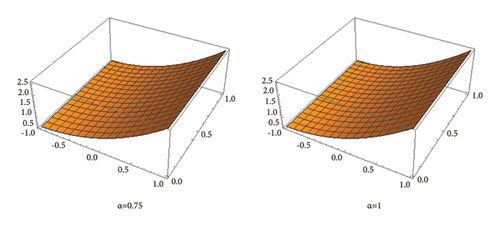
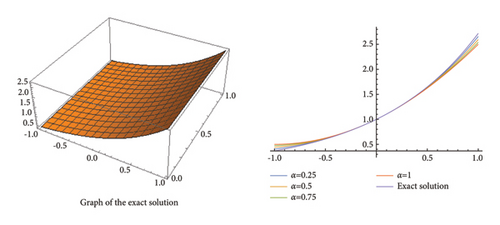
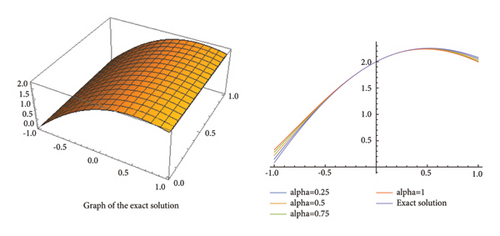
Now, in the Figures 1, 2, 3, we give the graphical representations of the exact solution and the approximated solution by using equation (26) for n = 0, and α = 0.25, 0.5, 0.75 , 1, converging to the exact solution. Also, table 1 represents the numerical values of the exact solution and the approximated solution.
Example 2. To become more familiar with the proposed scheme, let us solve another particular Volterra type IE by using the proposed VILTM. So, consider
Here, we solve (29) with the help of ADM, SAM, and VILTM as in the first example.
-
Case-I: Adomian decomposition method
-
To solve (29) with the help of ADM, let us suppose and solve the relation
() -
For n = 0, 1 , 2, …, we get the following iterations:
() -
The final solution may be written as
() -
that gives as the exact solution of (29).
-
Case-II: Successive approximation method
-
Now, we solve (29) by using SAM for this let us again say and put in the relation for SAM,
() -
for n = 0, 1, 2, …, we get the following iterations:
() -
hence, we get the exact solution of (29) as .
-
Case-III: Variational iteration Laplace transform method
-
To solve (29) by using the proposed method VILTM, first we get the differential form of (29) by using (8) which is
() -
Hence, the iterative relation according to (17) for the above IE is
() -
Substituting the values of n = 0, 1, 2, …., we get the following successive iterations,
() -
and the final solution is written as
() -
which turns out to be
() -
which exactly satisfies the given IE and shows the effectiveness and reliability of the proposed technique.
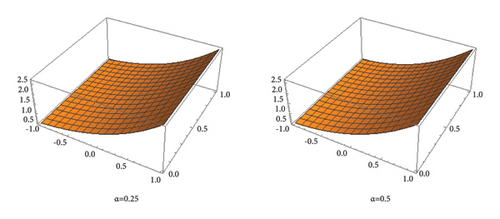
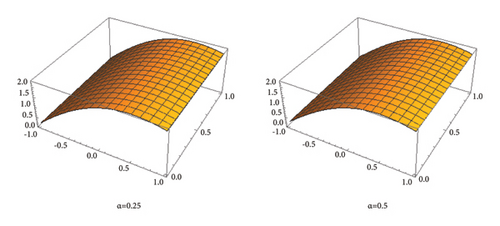
Now, observe the graphical depiction of the exact solution and the approximated solution with the help of (36) converging to the exact solution, in the Figures 4, 5, 6. Also study Table 2 for particular numerical values.
Example 3. Consider the following Volterra type IE as a third particular numerical example,
We solve (41) with the help of ADM, SAM, and by the proposed method VILTM.
-
Case-I: Adomian decomposition method
-
Let us suppose and substitute in the relation,
() -
Hence, for n = 0, 1, 2…, we get the iterations
() -
The final solution is written as
() -
which gives as the exact solution of (41).
-
Case-II: Successive approximation method
-
Next, we solve (41) by using the SAM for this let us again say and on solving the equation:
() -
for n = 0, 1, 2…, we get the iterations:
() -
that gives the exact solution of equation (41) as .
-
Case-III: Variational iteration Laplace transform method
-
To apply the proposed scheme VILTM on (41), we first write its integro-differential form with the help of (8) as
() -
Hence, the iterative relation according to (17) for the above equation becomes
() -
Now, for n = 0, 1, 2, …, the successive iterations may be obtained as
() -
and the final solution may be found as
() -
which turns out to
() -
which in all respect satisfies equation (41).
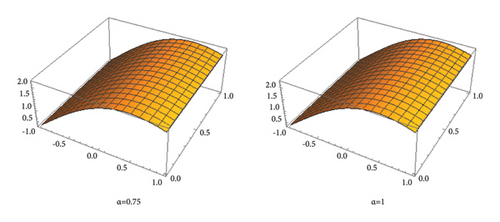
In Table 3, we give the numerical values of the exact and approximated solutions and in the Figures 7, 8, 9, we give the graphical description of the exact solution and the successive iterations obtained from (48) for n = 0 and converging to the exact solution.
Example 4. Consider the fourth and the last Volterra type IE,
Let us solve (53) with the help of ADM, SAM, and VILTM as in the previous examples.
-
Case-I: Adomian decomposition method
-
To solve (53) using ADM, let us say and put it in the relation,
() -
For n = 0, 1, 2, …, we get the following iterations:
() -
The final solution is written as
() -
which gives as the exact solution of (53).
-
Case-II: Successive approximation method
-
Now, we solve (53) by using SAM, for this again, let us say and solve the following relation:
() -
for n = 0, 1, 2, … to get the following iterations:
() -
The final solution is written as
() -
that converges to as the exact solution of (53).
-
Case-III: Variational iteration Laplace transform method
-
To solve (53) by using the proposed method VILTM, for this, the integro-differential form using (8) is
() -
Hence, the iterative relation according to (17) for the above equation becomes
() -
Now, for n = 0, 1, 2, …., the following successive iterations may be obtained:
() -
And the final solution may be found as
() -
which turns out to be
() -
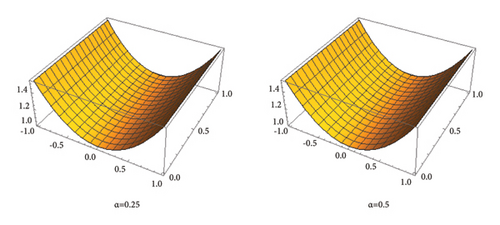
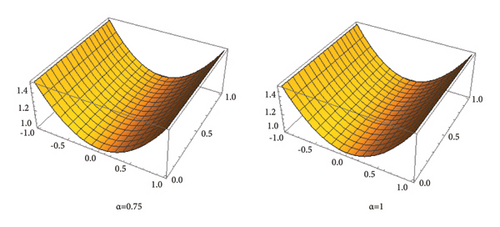
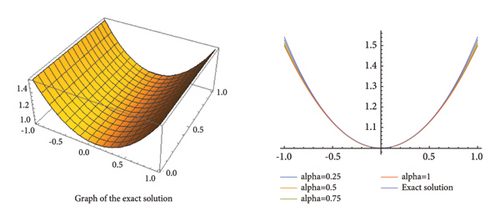
which in all respects satisfies equation (53). In the Figures 10, 11, 12, we present the graphical description of the exact solution and the approximated solution with the help of (61) for n = 0, α = 0.25, 0.5, 0.75, 1, and , also, observe the Table 4 for numerical calculations.
4. Conclusions
The results of the examples, either analytical or graphical shown in Section 3, suggests that the proposed method VILTM is not only authentic but also much faster than the existing techniques in the literature for the solutions of Volterra type FOIEs. As we proceed towards the successive iterations by neglecting the squares and higher powers of α and , the previous iteration is contained in the next one. Also, particular numerical examples show that if we neglect the squares and higher powers of α and as well as their products, the difference between any two consecutive terms is negligible. Then, Tables 1, 2, 3, and 4 contain the numerical values of the exact and the approximated solutions for different values of and α. In this way, we get close and close to the exact solution. Easy calculation of the general Lagrange’s multiplier is the key point of the method for all Volterra type FOIEs and a lot of time may be saved which is consumed in the calculation of Lagrange’s multiplier.
| c1 | c2 | c3 | c4 | c5 | c6 |
|---|---|---|---|---|---|
| α = 0.25 | α = 0.5 | α = 0.75 | α = 1 | Exact solution | |
| −1 | 0.046 | 0.094 | 0.136 | 0.167 | 0 |
| −0.5 | 0.506 | 1.512 | 0.517 | 0.521 | 0.5 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 0.5 | 1.494 | 1.488 | 1.483 | 1.479 | 1.5 |
| 1 | 1.954 | 1.906 | 1.864 | 1.833 | 2 |
| c1 | c2 | c3 | c4 | c5 | c6 |
|---|---|---|---|---|---|
| α = 0.25 | α = 0.5 | α = 0.75 | α = 1 | Exact solution | |
| −1 | 0.404 | 0.442 | 0.476 | 0.500 | 0.368 |
| −0.5 | 0.612 | 0.617 | 0.622 | 0.625 | 0.607 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 0.5 | 1.642 | 1.635 | 1.629 | 1.625 | 1.649 |
| 1 | 2.658 | 2.595 | 2.540 | 2.500 | 2.718 |
| c1 | c2 | c3 | c4 | c5 | c6 |
|---|---|---|---|---|---|
| α = 0.25 | α = 0.5 | α = 0.75 | α = 1 | Exact solution | |
| −1 | 0.149 | 0.220 | 0.282 | 0.328 | 0.0866 |
| −0.5 | 1.262 | 1.270 | 1.276 | 1.281 | 1.255 |
| 0 | 2 | 2 | 2 | 2 | 2 |
| 0.5 | 2.251 | 2.246 | 2.242 | 2.240 | 2.255 |
| 1 | 2.057 | 2.032 | 2.010 | 1.995 | 2.081 |
| c1 | c2 | c3 | c4 | c5 | c6 |
|---|---|---|---|---|---|
| α = 0.25 | α = 0.5 | α = 0.75 | α = 1 | Exact solution | |
| −1 | 1.52919 | 1.51570 | 1.50793 | 1.50000 | 1.54308 |
| −0.5 | 1.12565 | 1.12389 | 1.12548 | 1.12500 | 1.12763 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 0.5 | 1.12565 | 1.12389 | 1.12548 | 1.12500 | 1.12763 |
| 1 | 1.52919 | 1.51570 | 1.50793 | 1.50000 | 1.54308 |
The sequence of successive iterations in each presented example in Section 3, converging to the exact solution that is the fixed point of the problem, makes a strong connection with the fixed point theory. This leads the interested researcher to further investigate about the stability and the rate of convergence of the proposed method using the techniques of the fixed point techniques. Graphical representations of the exact solution along with a comparative diagram of the approximated solution with the help of VILTM for different types of integral equations are given by Figures 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12. Final comments may be to say that the proposed method provides us a step-by-step procedure to get close to the exact solution through iterative approximations.
The successful application of the scheme VILTM to the Volterra type FOIEs in the preceding section is clearly a beacon of light for the interested readers in the field of FOIEs and after analysing the method, they will also be able to invent and discover more new methods or re-establish the already existing methods for the solution of FOIEs. In practice, the results obtained here can be applied to random fractal process surveys.
4.1. Future Directions
- (i)
Whether one may apply the proposed VILTM for the solution of more other types of FOIEs, for example, nonlinear Volterra type FOIEs and singular FOIEs.
- (ii)
One may check the efficacy, authentication, and fast convergence towards the exact solution by using VILTM for different types of FOIEs as compared to the existing semianalytical, numerical methods, like the Adomian decomposition method and ordinary variational iteration method.
- (iii)
Interested new incumbents may also further generalize the VILTM for higher dimensional IEs existing in the literature.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Open Research
Data Availability
No underlying data were collected or produced in this study.




