International Journal of Aerospace Engineering

Volume 2024, Issue 1 7955020

Research Article

Open Access

L1 Adaptive Fault-Tolerant Attitude Tracking Control of UAV Systems Subject to Faults and Input Saturation

Yan Zhou,

Corresponding Author

Yan Zhou

[email protected]

orcid.org/0000-0003-4998-2490

School of Electronic and Electrical Engineering , Zhaoqing University , Zhaoqing , 526061 , Guangdong , China , zqu.edu.cn

Search for more papers by this author

Huiying Liu,

Huiying Liu

School of Automation , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

Huijuan Guo,

Huijuan Guo

School of Information Engineering , Suqian University , Suqian , 223800 , Jiangsu , China , en.squ.edu.cn

Search for more papers by this author

Yongjian Chen,

Yongjian Chen

School of Computer Science and Software , Zhaoqing University , Zhaoqing , 526061 , Guangdong , China , zqu.edu.cn

Search for more papers by this author

Yan Zhou,

Corresponding Author

Yan Zhou

[email protected]

orcid.org/0000-0003-4998-2490

School of Electronic and Electrical Engineering , Zhaoqing University , Zhaoqing , 526061 , Guangdong , China , zqu.edu.cn

Search for more papers by this author

Huiying Liu,

Huiying Liu

School of Automation , Northwestern Polytechnical University , Xi’an , 710129 , China , nwpu.edu.cn

Search for more papers by this author

Huijuan Guo,

Huijuan Guo

School of Information Engineering , Suqian University , Suqian , 223800 , Jiangsu , China , en.squ.edu.cn

Search for more papers by this author

Yongjian Chen,

Yongjian Chen

School of Computer Science and Software , Zhaoqing University , Zhaoqing , 526061 , Guangdong , China , zqu.edu.cn

Search for more papers by this author

First published: 11 July 2024

https://doi.org/10.1155/2024/7955020

Academic Editor: Gang Wang

Share a link

Email
Wechat
Bluesky

Abstract

This paper investigates an adaptive fault-tolerant control scheme for an unmanned aerial vehicle (UAV) attitude control system in the presence of multiple faults, input saturation, and external disturbances. The attitude control system of a UAV is divided into an outer loop consisting of attitude angles and an inner loop consisting of attitude angle velocities. The nonlinear dynamic inversion (NDI) method based on sliding mode surface is used to construct the outer loop controller to ensure fast response and accurate attitude tracking. The treatment of the inner loop with multiple faults, input saturation, and external disturbances is more complex. First, input saturation and sensor faults are converted successively for ease of analysis. After the conversion and reorganization of such uncertainties including actuator faults, sensor faults, input saturation, and external disturbances, a nonlinear uncertain system model is developed. Second, a L1 neural network adaptive fault-tolerant controller is designed to deal with uncertainties, where radial basis function neural networks (RBFNNs) are applied to approximate the nonlinear function in the system model. The L1 adaptive fault-tolerant controller includes three parts: state predictor, adaptive law, and control law. Adaptive laws based on the projection operator estimate and update the unknown parameters in the system and transfer them to the control law and the state predictor to compensate for the effects of uncertainties. The control law with a low-pass filter also eliminates the high-frequency oscillations caused by a high adaptive gain in conventional adaptive algorithms, which guarantee the robustness and fast self-adaptation. Finally, simulation results are given to verify the effectiveness and feasibility of the proposed controller.

1. Introduction

Unmanned aerial vehicles (UAVs) have been used progressively in many applications due to their mobility, versatility, and lowered casualty in recent years. Along with that, the accident rate of UAVs is also inevitably rising year by year. These accidents occur mainly in actuators, sensors, and other constituent parts of UAV systems such as the engine and wings. The faults of actuators and sensors are the most common among them. There has been a proliferation of research results dealing with actuator faults or sensor faults, especially the former. A finite-time sliding mode fault-tolerant control method and a neural network-based adaptive fault-tolerant control scheme are investigated for actuator faults in [1, 2], respectively. The predictive descriptor observer is designed in [3] to deal with sensor faults and compensate large delay. Researchers have continued to be concerned about simultaneous faults of actuators and sensors [4–8]. These research results of actuator and sensor faults rely mainly on fault information obtained from fault detection or estimation, which may make the structure of fault-tolerant controllers more complex.

Input saturation is a physical limitation prevalent in the actual actuator mechanism, which is a nonlinear constraint. It has been studied for a long time, and many effective methods are applied to compensate for performance degradation caused by input saturation and environmental constraints [9–13]. In [14], a sigmoid-type function is applied to tackle the input saturation, and a discrete-time disturbance observer is proposed to ensure the boundedness of virtual control signal. The problem of actuator saturation nonlinearity is solved by an improved Gaussian function and an auxiliary compensation system in [15]. For attitude tracking problem of quadrotor UAVs with input saturation and disturbances, a low-computation adaptive neural network technology and an auxiliary system are introduced to deal with external disturbances and input saturation in [16, 17]. Similarly, an auxiliary system is constructed to compensate for the effects of input saturation in [18–20]. For uncertain quadrotor systems with thrust saturation, [21, 22] utilize a differentiable function to design the translational thrust so that it is maintained within a predesigned boundary. In addition to function approximation and auxiliary systems, designing antisaturation controllers is also a well-proven method [23].

The attitude control system is the foundation and key part of the whole flight control system. Its reliability and safety directly affect whether the UAV can fulfill the flight mission normally. In order to avoid coupling between state variables and reduce the design difficulty, the dual-loop design of the attitude control system is a simple and effective method [24–26]. In addition, the attitude control of aircraft under faults has also been paid more and more attention. The attitude tracking problem of multiple UAVs with nonaffine nonlinear faults is investigated in [27], where the neural networks and the Butterworth low-pass filter are introduced to deal with unknown nonlinearities and actuator faults. The fault-tolerant attitude tracking controllers are proposed in [28, 29] to solve the problem of actuator faults and input saturation. Based on the consideration of actuator faults, external disturbances, and measurement errors of attitude angles and angle velocities of rigid-flexible coupled spacecraft, an adaptive fault-tolerant attitude tracking control is investigated in [30]. Looking at the existing research results on fault-tolerant control of attitude tracking systems, it is easy to see that most of these researches are limited to one or a few abnormal conditions. When anomalies outside the scope of coverage arise, the controller may reduce efficiency or even fail completely. The scenarios of actuator faults, sensor faults, input saturation, and external disturbances are possible anomalies of the UAV systems, which are very likely to occur at the same time. Therefore, the fault-tolerant control of UAV systems under multiple faults, input saturation, and external disturbances plays a crucial role in enhancing the reliability and safety of the systems. However, dealing with numerous anomalies at the same time is quite a difficult issue because of the different generation mechanisms, coupling, and influence. Nowadays, fault-tolerant control methods based on fault detection or estimation are widely used. External disturbances are mostly handled in the similar way. It is difficult to design so many observers or estimators when actuator faults, sensor faults, and external disturbances occur simultaneously. Not to mention the need to consider the role of input saturation. Based on the above considerations, a new fault-tolerant control scheme for UAV attitude control systems is proposed in this paper. The dual-loop control structure consists of a sliding mode nonlinear dynamic inverse controller in the outer loop and a L1 neural network adaptive controller (L1NNAC) in the inner loop. The nonlinear dynamic inverse control based on the sliding mode surface ensures the fast response and precise attitude tracking. Through transformation and reorganization, input saturation, sensor faults, actuator faults, and external disturbances are regarded as a lumped uncertainty and the L1 adaptive controller is designed to compensate its effects. The L1 adaptive control algorithm is a deformation of the model reference adaptive control (MRAC). By introducing a low-pass filter in the control law, the L1 adaptive controller can not only handle the uncertainties of systems effectively but also eliminate the high-frequency oscillations due to high gains. In recent years, the L1 adaptive control algorithm has been increasingly used in fault-tolerant control to ensure fast adaptation and robustness of the closed-loop system [31–34].

Compared with the existing research results on fault-tolerant tracking control of aircraft, the main contributions of this paper are summarized as follows:

1.
Compared with [2–4, 28–30] dealing with a few types of faults, this paper investigates a more encompassing fault-tolerant control scheme that addresses most of the aircraft anomaly conditions, including actuator faults, sensor faults, external disturbances, and input saturation.
2.
Unlike the direct or indirect estimation of faults and external disturbances in [1, 3, 5, 6], this paper views faults and external disturbances as a lumped uncertainty with the help of a low-pass filter and the state expansion approach and utilizes L1 adaptive to compensate for the effects of the uncertainty. The entire fault-tolerant controller does not require the values of faults and external disturbances. This advantage makes the fault-tolerant controller simple in structure, since there is no need to design observers or estimators for faults and disturbances.
3.
In contrast to the auxiliary system or saturation dynamic filter approaches in [10, 18–20, 23], the input saturation problem in this paper is solved by a combination of nonlinear function approximation and the median theorem, which better integrates and simplifies the design process of the adaptive fault-tolerant controller. Meanwhile, the steady-state and transient performance analysis of the closed-loop system is accomplished by introducing a L1 reference system, which provides a theoretical basis for improving the system performance.

The rest of this paper is organized as follows: the problem formulation is described in Section 2. In Section 3, the design of a dual-loop controller for a UAV attitude tracking system is presented. Performance analysis of the fault-tolerant controller is given in Section 4. Simulation results are shown in Section 5. Finally, some conclusions are given in Section 6.

2. Problem Formulation

According to the principle of time-scale separation, the state variables of a UAV attitude control system can be divided into slow variables consisting of attitude angles and fast variables consisting of attitude angle velocities. Consider the following model of UAV attitude control system with actuator faults, sensor faults, and external disturbances:

(1)

(2)

where x₁ = [ϕ, θ, ψ]^T, x₂ = [p, q, r]^T, and

y₁ and y₂ are the outputs of the outer and inner loops. g₁, g₂ and f are nonlinear functions related to the attitude angles and aerodynamic parameters. ω_a = diag(ω_i)(i = 1, 2, 3) denotes the multiplicative faults of actuators: (1) ω_i = 1, no fault; (2) 0 < ω_i < 1, a loss of effectiveness fault; (3) ω_i = 0, a drift fault. σ_a, Δ_f and d indicate the additive actuator faults, offset sensor faults, and external disturbances, respectively, which are bounded. u(v), v are control inputs with saturated nonlinearity and actual control inputs in which

(3)

where u_m indicates the boundary of the input signal v.

The goal of this paper is to design a fault-tolerant controller such that the output y₁ can track the given input signals of attitude angles in presence of faults, input saturation, and external disturbances.

To design the fault-tolerant controller, the following assumptions and lemma are needed:

Assumption 1. There exists B_f > 0, such that |f(t, 0)| ≤ B_f(t ≥ 0).

Assumption 2. For arbitrary δ > 0, there exist , and the partial derivatives of f(t, x₂) are semiglobal uniform bounded:

( )

Assumption 3. There exists a constant L₀ > 0 such that hold uniformly in t ≥ 0.

Remark 1. f represents the system nonlinearity from (2). Assumption 1 indicates that this nonlinearity is bounded, and the piecewise continuity and boundedness of its partial differentials are demonstrated in Assumption 2. These two assumptions are reasonable because the system nonlinearity depends on the aerodynamic parameters, whereas all parameters are continuous and bounded when the UAV is flying normally within the flight envelope. Assumption 3 is the Lipschitz condition, which is needed later to derive the performance boundaries of the closed-loop system.

For a stable proper MIMO system H(s) with input r(t) and output y(t), there exists an arbitrary time , such that .

3. The Design of Fault-Tolerant Controller

In this section, a dual-loop adaptive fault-tolerant controller is designed to counteract various uncertainties in UAV attitude control systems, including an outer-loop nonlinear dynamic inversion (NDI) controller based on a sliding mode control (NDI-SMC) and an inner-loop L1NNAC. The fault-tolerant controller structure is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Fault-tolerant control structure diagram of UAV attitude control system.

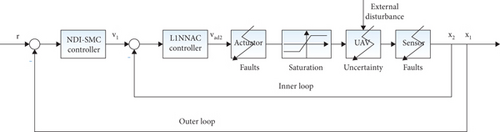
3.1. Design of the Outer Loop Controller

The NDI algorithm is a frequently applied feedback linearization method, which is characterized by simplicity, effectiveness, and fast response. However, the existence of various uncertainties in UAV systems makes it difficult to achieve optimal control with conventional NDI. Therefore, here, the conventional NDI algorithm is improved by introducing the control law based on an integral sliding mode surface to enhance the robustness.

Consider the following control law of conventional NDI [25]:

(4)

where v₁ denotes the control output of the outer loop. ω₁ and e₁ = r − x₁ represent the bandwidth and the tracking error of the outer loop, respectively.

Design the integral sliding mode surface as follows:

(5)

By differentiating Equation (5), we get

(6)

The following exponential convergence law is chosen:

(7)

By substituting the definition of tracking error e₁ into (6) and combining with (7), one obtains

(8)

Therefore, the control law of NDI in (4) can be rewritten as follows:

(9)

where k₀, k₁, and k₂ are the parameters to be designed. sign(s) is a symbolic function with

( )

Remark 2. In general, intelligent algorithms, neural networks, and fuzzy logic systems are common methods for tuning parameters. Considering the timeliness of fault-tolerant control, this paper selects the parameters in advance by simulation experiments. It has been observed that k₀, k₂ generally affects the performance of the system in terms of overshoot, oscillation, steady-state error and others. At the same time, larger k₁ causes stronger system oscillations, so k₁ is usually set to a smaller value.

3.2. Design of the Inner Loop Controller

A L1NNAC algorithm is applied to construct the inner loop controller. Due to the presence of nonlinearities and input saturation, the inner loop nonlinear model in (2) is first linearized here. A function approximation approach is employed to deal with the input saturation function.

Considering the ability of the hyperbolic tangent function to approximate the saturation function, a hyperbolic tangent function is designed as follows:

(10)

And then, the Lagrange median theorem is applied to decouple the hyperbolic tangent function (10). For ∀v^∗ ∈ (0, v), we have

(11)

It is clear from (10) that h(0) = 0. Define

, so h(v) is rewritten as follows:

(12)

Define the approximation error as e = sat(v) − h(v). It is obvious from (3) and (10) that the approximation error e is bounded and its boundary can be derived as follows: |e| = |sat(v) − h(v)| ≤ u_m(1 − tanh(1)). Combining the above discussions, the saturation function sat(v) is rewritten as

(13)

It can be seen from (13) that the input saturation function is transformed into a time-varying system with parameter uncertainties and disturbances based on a function approximation approach and the Lagrange median theorem.

Define the control law of the inner loop as follows:

(14)

where

is a linear control law to ensure desired dynamic characteristics. v_ad2 is an adaptive control law to be designed.

Substituting (14) into (2), and combining (13) and the Erzberger model full tracking condition [36], one yields

(15)

where

is a lumped uncertainty. A_m2 denotes the system matrix of reference model. A₂, B_m2 are the linear segments of the system matrix and input matrix in (2).

represents a compound impact factor of multiplicative actuator fault and input saturation, which can be estimated by the adaptive law designed later.

There are sensor faults in the system (2) in addition to input saturation and actuator faults. In order to be easily handled together with actuator faults, sensor faults are here converted to pseudoactuator faults using the expanded state-variable method.

Consider the following low-pass filter:

(16)

Substituting the output equation of (2) into (16) gives

(17)

Consider the equation of state in (15), this can be derived:

(18)

Let

( )

So, (18) can be rewritten as

(19)

Note that the presence of nonlinear function

in (19), a RBFNN, is used here to approximate it. Consider the following RBFNN:

(20)

where W is an unknown weight matrix. ε is the bounded approximation error with

. Φ is the activation function, and it is generally a Gaussian function Φ(x) = exp(−(‖x − a‖²/2b²)) in which a, b are the preselected center point vector and width vector.

From (19) and (20), a state predictor is designed as

(21)

where

are estimates of the unknown parameters

, respectively.

Design the following projection-based adaptive laws for (21) as follows:

(22)

where

is the prediction error. P₂ is a symmetric positive solution matrix satisfying

, in which Q₂ is also a symmetric positive matrix. Γ is an adaptive gain.

The control law with a low-pass filter is proposed as

(23)

where

and

. r(t) is a given bounded reference signal.

is a low-pass filter to be designed.

In summary, the L1NNAC for the inner loop has been designed, which is composed of the state predictor in (21), adaptive laws in (22), and the control law in (23).

Remark 3. For C₂(s) in (23), it should be a strictly proper system with C₂(0) = 0. The design of low-pass filters in L1 adaptive control is an open problem. Some effective methods are used to construct low-pass filters such as optimization methods [37] and fuzzy logic systems [38]. For simplicity, C₂(s) is defined as [35]

(24)

where ϖ > 0 is an important parameter to be designed such that C₂(s) satisfies the following L1-norm condition.

Remark 4. Define, and γ_δ is an arbitrary positive constant. To guarantee the stability of the closed-loop system, C₂(s) are also designed to satisfy that, for a given ρ₀, there exists ρ_r > ρ₀ such that the following L1-norm condition holds:

(25)

where

is the upper boundary of the nonlinear function

. Note that this condition (25) is essential to guarantee the boundedness of the state variables of the following reference system in Lemma 2.

Meanwhile, the L1-norm condition (25) can be further simplified based on Assumption 2 to facilitate the selection of the low-pass filter parameters. Define and combine with the L1-norm condition in (25) that, for all x₂ ∈ Rⁿ, the relationship holds: and the L1-norm condition (25) can be simplified to . By substituting the low-pass filter (24) into the above one, the boundary of ϖ can be estimated, and then, the appropriate parameter value can be selected by means of experimental simulation.

Remark 5. k_g is designed according to the principle of MRAC. Consider the following ideal reference model for the system (19): , its frequency domain form is . It is obvious that when s⟶0, k_g can be chosen as in order to achieve .

4. Analysis of Fault-Tolerant Controller

To analyze the steady-state and transient performance of the closed-loop system, a L1 reference system is introduced:

(26)

where κ_ref(s) is the Laplace transformation of

Rewrite the state equation of (26) into the frequency domain form and substitute the reference control law to get

(27)

where G(s), H(s) and

are introduced in (25).

The following Lemma 2 proves that the L1 reference system is stable.

Consider the L1 reference system (26) subject to the L1-norm condition in (25), if , then

(28)

where ρ_r is introduced in (25), and ρ_vr is defined as

( )

From (19) and (21), the prediction error equation is got:

(29)

where

The minimum estimation error of RBFNN is defined as

(30)

where

is the optimal estimation of the weights of RBFNN.

So, (29) can be rewritten as

(31)

From (20), (31) is organized as

(32)

where

Theorem 1. For the closed-loop system ((19)) with a L1 adaptive fault-tolerant controller consisting of ((21)), ((22)), and ((23)), subject to the L1-norm condition ((25)), if

(33)

then

(34)

where γ₀ is an arbitrary positive constant.

Proof 1. The Lyapunov function is chosen as follows:

(35)

By calculation, is obtained as

(36)

From (32) and (22), the upper bound of is derived:

(37)

where P₂, Q₂ are introduced in (22), and

is the minimum eigenvalue of Q₂.

When P₂ in the adaptive law (22) is designed, is easy to realize. Therefore, (37) can be rewritten as follows:

(38)

From the continuity of V, one can be obtained:

(39)

Considering (33) and Barbalat’s lemma [40], one gets

(40)

Equation (40) implies that the estimation error of is bounded, so (34) can be deduced. Next, the following theorem explores the performance bounds of the closed-loop system.

Theorem 2. For the given system ((19)) and the L1 adaptive fault-tolerant controller consisting of ((21)), ((22)), and ((23)), subject to the L1-norm condition ((25)), and the L1 reference system ((26)), if , then

(41)

(42)

(43)

(44)

where

( )

in which c₀ should be chosen so that H₁(s) is a proper and stable system.

are introduced in (25). γ₀ and

are arbitrary positive constants.

Proof 2. Suppose (42) and (43) do not hold, then consider and the continuity of and v_ad2, there exist τ > 0, such that

(45)

(46)

Equations (45) and (46) imply that

(47)

Recalling Lemma 2, the following relationship is derived:

(48)

where ρ = ρ_r + γ₂, ρ_v = ρ_vr + γ₃, γ₂, and γ₃ are arbitrary positive constants. ρ_r and ρ_vr are raised in (25) and (28).

It follows from Theorem 1 that (41) is proved.

The control law of (23) can be derived as

(49)

where

are the Laplace transform of κ = W^TΦ + ε and

in which

and

By further sorting out (49), one gets

(50)

Combining with (20), the frequency domain form of the state equation of (19) is obtained as

(51)

It is yield from (29) and the definition of in (49):

(52)

Subtract (51) and (27) to get

(53)

From Lemma 1, (53) can be rewritten as

(54)

From Assumption 3 and (25), it gets

(55)

By substituting (55), (54) can be further derived as

(56)

Combining (41) and the definition of , (42) is proved.

It is from (50) and the control law in (26) that

(57)

Considering the definition of H₁(s), the following relationship is yield:

(58)

From Lemma 1 and Assumption 3, (57) is derived

(59)

So, (43) is proved. From the closed-loop system (19) and the L1 reference system (26), one has that

(60)

Combining with (42), it is clear that (44) is proved.

Remark 6. Noted that the L1 reference system in (26) is not realizable due to the use of the unknown input gain and the unknown lumped uncertainty . The L1 reference system is introduced only for the derivation of stability and performance bounds of the closed-loop system in Theorems 1 and 2.

5. Simulation Examples

In this section, the simulation of a UAV is implemented, and the initial simulation conditions are set: x₁ = [0, 0, 0]^Tdeg, x₂ = [0, 0, 0]^Trad/s. The mass and moment of inertia matrix of the UAV are set to be m = 425 kg and J = [52723, 0, 8435; 0, 6314, 0; 8435, 0, 58771](kg · m²). The disturbances in the inner loop are sin(t). The given attitude angles are r = [5⁰, 5⁰, 5⁰]. The RBFNNs are designed as a 6-5-1 structure, and the center point vector a and width b are chosen to be

( )

The parameters of the outer loop controller are designed:

( )

The parameters of the L1 adaptive controller are designed as

( )

In order to verify the effectiveness of the proposed controller, the following four scenarios are carried out. Scenario 1 shows the simulation of the UAV subjected to input saturation and external disturbances, when the actuators and sensors are in normal operation. Scenarios 2 to 4 demonstrate the simulation of the UAV subject to input saturation and external disturbances under three fault modes: sensor faults, actuator faults, and simultaneous sensor faults and actuator faults. In order to highlight the fault tolerance of the proposed L1 adaptive controller (denoted as L1), Scenarios 2 to 4 add a comparison with the attitude angle tracking performance of the MRAC.

5.1. Scenario 1: No Fault

In this scenario, actuators and sensors are working normally, and the UAV suffers from input saturation and external disturbances. The simulation results are shown in Figures 2, 3, and 4.

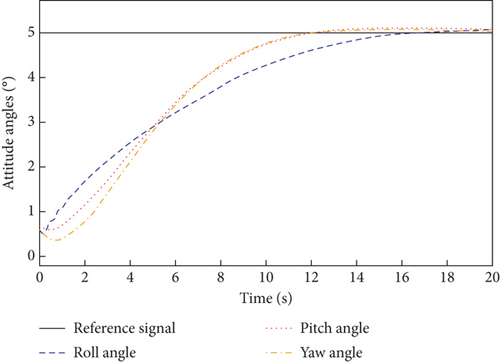
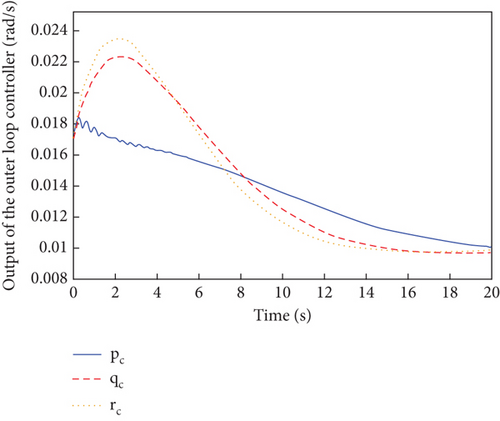
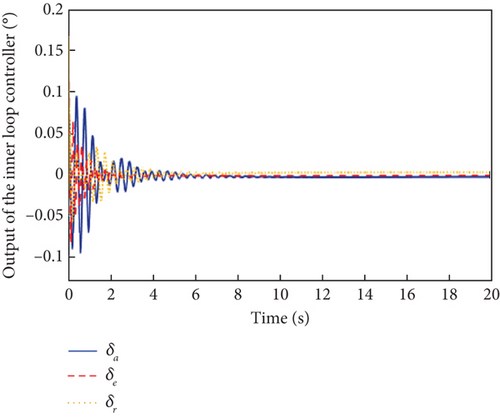
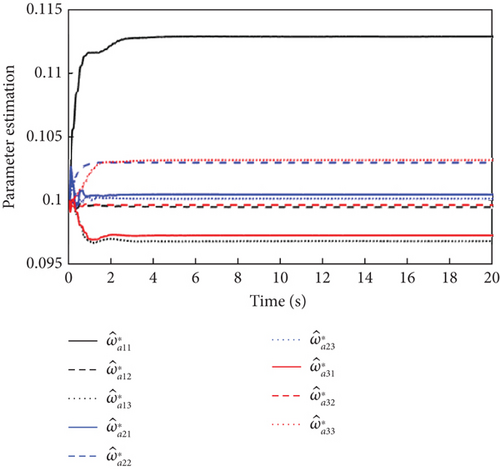
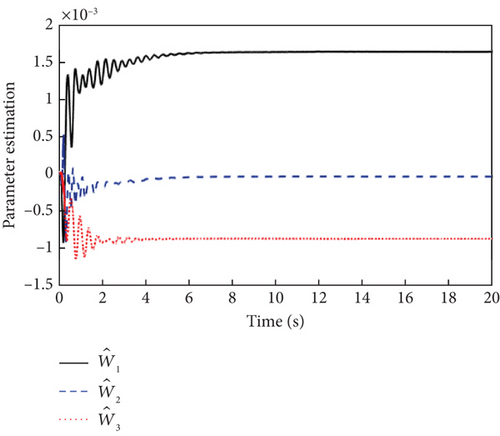
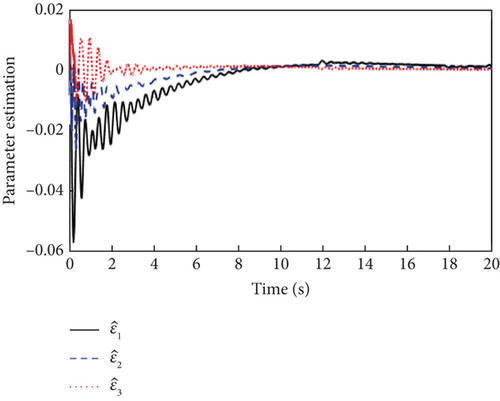
Figures 2, 3, and 4 show the attitude angle tracking, the outputs of inner and outer loop controller, and the parameter estimation curves of L1 adaptive controller, respectively. From Figure 2, it is seen that the attitude tracking performance in the presence of input saturation and external disturbances is good, with small overshoot and fast response. The control outputs of both the outer and inner loops in Figure 3 are smooth and convergent. As can be seen from Figure 4, bounded and fast estimation of adaptive parameter and ε are achieved by projection operators.

Based on the above simulations, the following three scenarios are designed for simulation to verify the fault tolerance of the proposed controller: sensor faults, actuator faults, and simultaneous sensor faults and actuator faults.

5.2. Scenario 2: Sensor Faults

The sensor faults are considered Δ_f = [0.01, 0.01, 0.01]^T, and the simulation results are shown in Figures 5, 6, and 7.

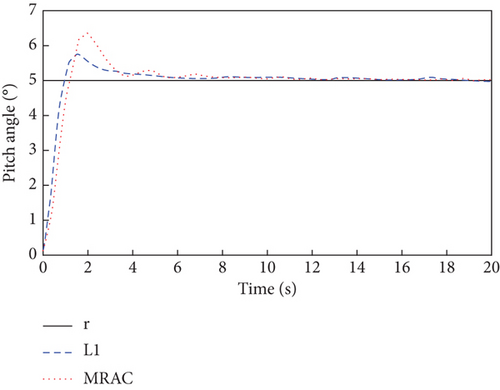
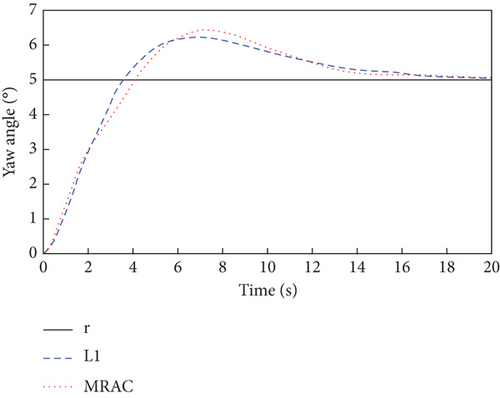
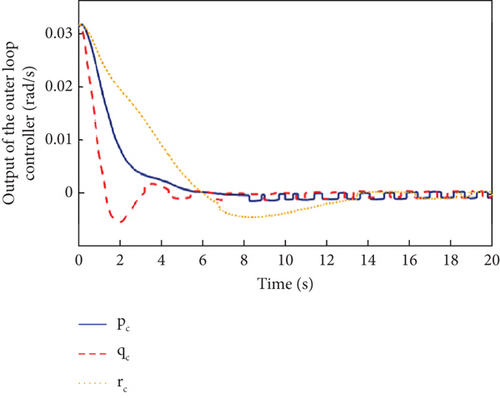
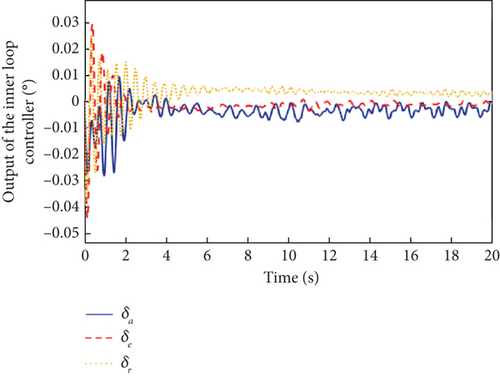
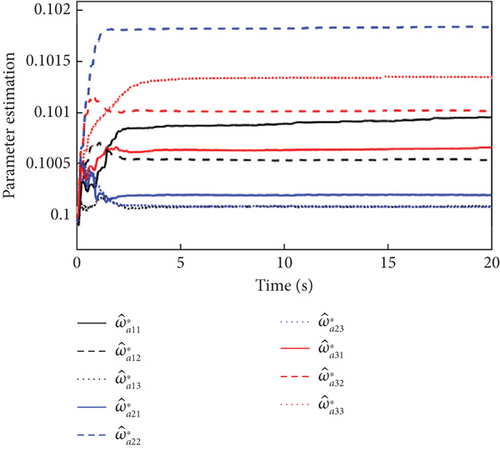
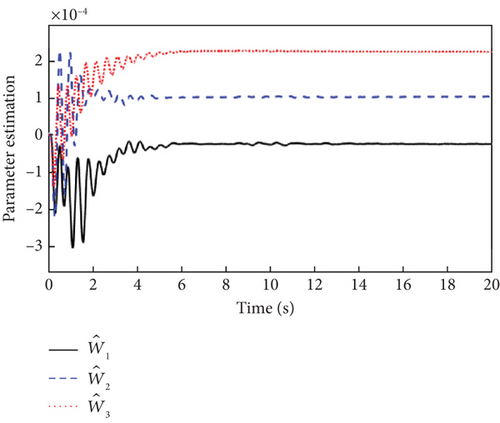
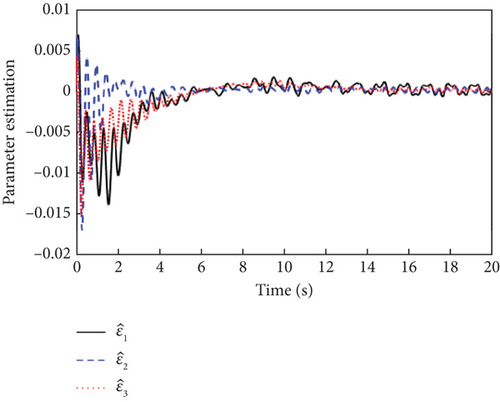
It can be seen from Figure 5 that both the L1 adaptive controller and the MRAC controller have good attitude tracking performance even under the effect of sensor faults. Compared with the MRAC controller, the proposed L1 adaptive controller has the advantages of low overshoot, fast response, and convergence, which has better dynamic performance. As can be seen from Figure 6, the output signals of the inner and outer loop controllers fluctuate more than that without fault due to the existence of sensor faults. From the response curves of parameter estimation in Figure 7, it can be seen that all the adaptive parameters maintain boundedness and fast convergence even in the case of sensor fault.

5.3. Scenario 3: Actuator Faults

The actuator faults are designed as ω = diag(0.3, 0.5, 0.2t).

It shows that the aileron and elevator channels have constant multiplicative actuator faults, while the rudder channel has time-varying multiplicative actuator faults. The simulation results are shown in Figures 8, 9, and 10.

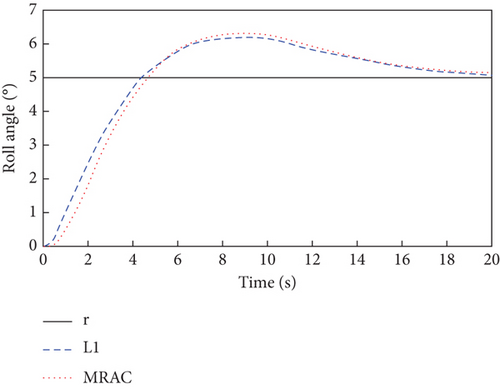
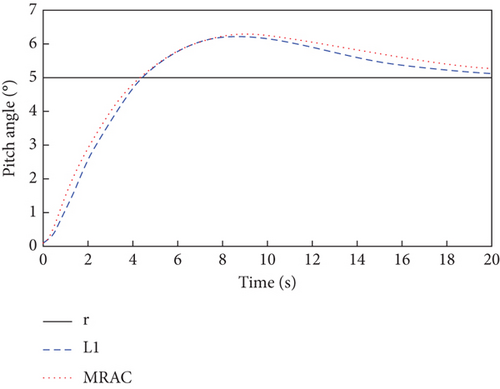
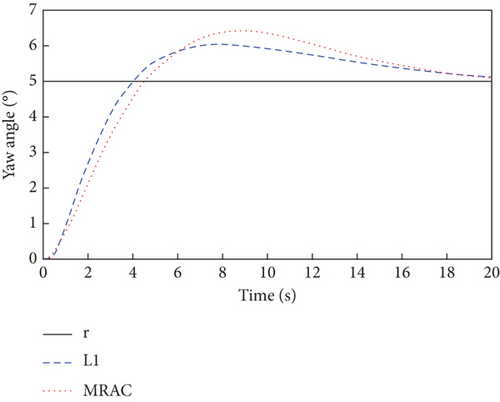
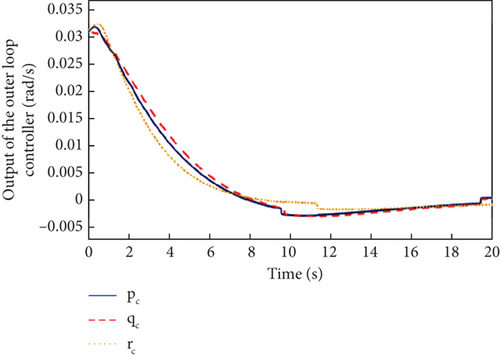
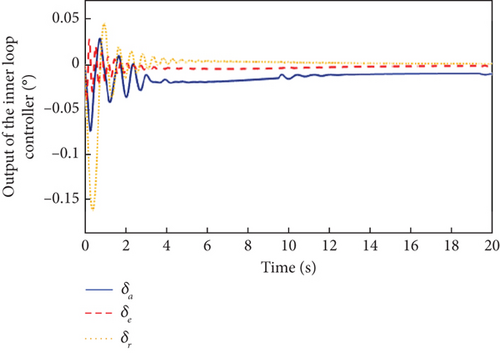
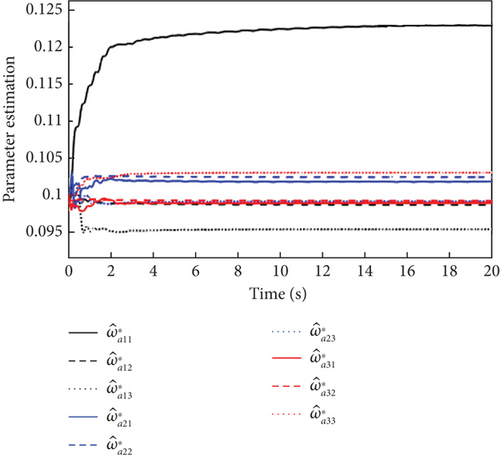
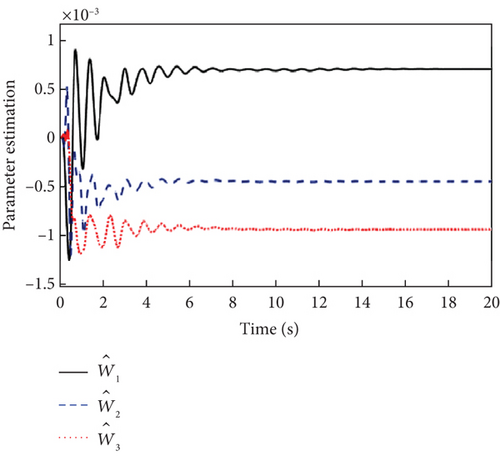
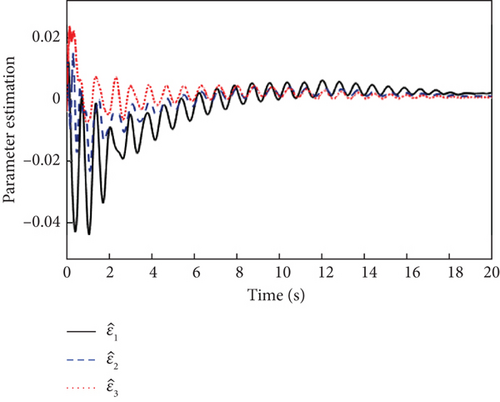
As can be seen in Figure 8, due to the presence of actuator faults, the closed-loop system has a greater overshoot compared to when there are no faults in Figure 2. However, with the inner and outer loop controllers of Figure 9, the three attitude angles are close to a given reference value with fast convergence and small steady-state error. It is also clear from Figure 8 that the proposed L1 adaptive controller has better attitude tracking performance compared to the MRAC controller. Meanwhile, the outputs of the inner and outer loop controllers in Figure 9 and the estimation curves of adaptive parameters in Figure 10 show that the L1 adaptive controller has good stability and fault tolerance.

5.4. Scenario 4: Actuator Faults and Sensor Faults

The actuator faults are considered as follows:

( )

The sensor faults are considered as follows:

( )

Obviously, the actuator works normally when t < 8. However, the multiplicative and additive actuator faults are introduced at t = 8. The sensor works normally when t < 7 and the constant offset sensor faults occur at t = 7. The simulation results are shown in Figures 11, 12, and 13.

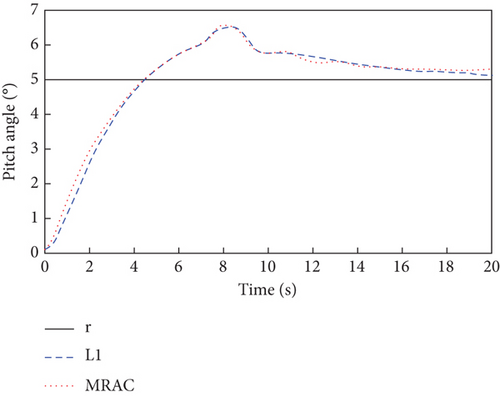
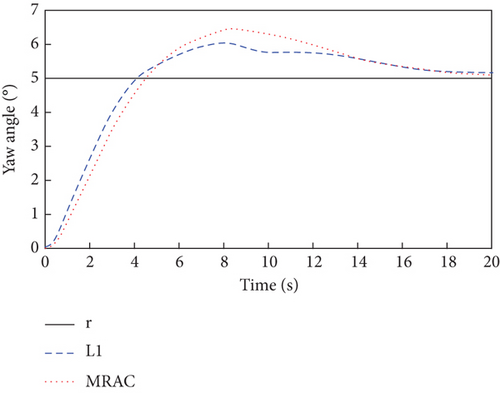
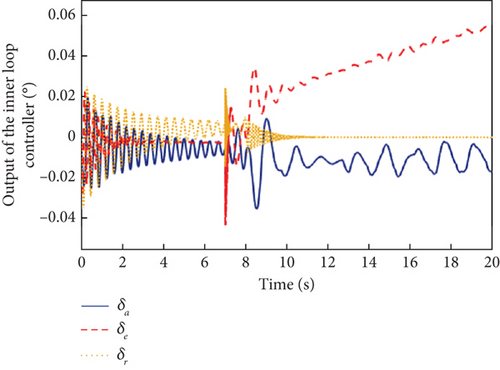
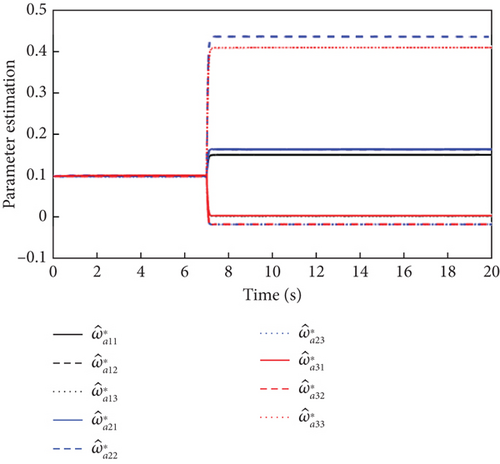
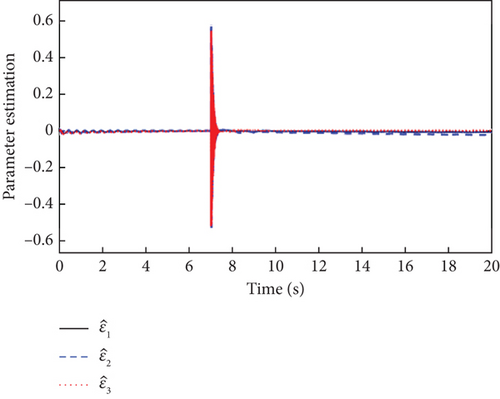
From Figure 11, it is obvious that due to the need for the controller to compensate for the effects of actuator faults and sensor faults, the output signals of the attitude angles are significantly more overshooting than in the case of a single fault mode with sensor faults or actuator faults in Figures 5 and 8. Moreover, the attitude angle tracking curves of the L1 adaptive controller possess a smaller overshoot, faster convergence, and smaller steady-state error than that of the MRAC controller. It can be seen from Figures 12 and 13 that the simultaneous occurrence of actuator faults and sensor faults makes the L1 adaptive controller’s output signals and the estimation curves of the adaptive parameters oscillate more significantly compared to a single fault mode of sensor faults or actuator faults in Figures 6, 7, 9, and 10. Nevertheless, it can be seen from Figures 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, and 13 that the L1 adaptive controller has good attitude tracking ability, strong robustness, and fault tolerance.

6. Conclusion

This paper explored a dual-loop fault-tolerant control for a UAV attitude tracking system in the presence of multiple faults, input saturation, and external disturbances. The outer loop controller adopted a NDI algorithm based on integral sliding mode control, which was used to ensure the fast response and improve the robustness. Input saturation was converted into system uncertainties and disturbances by means of function approximation and the median theorem. With the method of state-variable expansion, multiple faults including actuator faults and sensor faults are treated as a single actuator fault. On this basis, the L1 adaptive control based on RBFNN could be applied to the inner loop to counteract the effects of uncertainties. Simulation results showed that the dual-loop fault-tolerant controller achieved good attitude tracking and guaranteed uniform boundedness of all input and output signals. Next, other adaptive fault-tolerant control methods for multiple faults and input saturation will be a future research direction, such as antisaturation controllers and fault estimators.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by key fields special project of Guangdong Provincial Colleges and Universities under Grant 2021ZDZX1082.

Acknowledgments

This work was supported by key fields special project of Guangdong Provincial Colleges and Universities under Grant 2021ZDZX1082.

Open Research

Data Availability Statement

The data (system parameters and simulation parameters) used to support the findings of this study are included within the article.

References

1 Tang P., Zhang F. B., Ye J. C., and Lin D. F., An integral TSMC-based adaptive fault-tolerant control for quadrotor with external disturbances and parametric uncertainties, Aerospace Science and Technology. (2021) 109, article 106415, https://doi.org/10.1016/j.ast.2020.106415.
10.1016/j.ast.2020.106415
Web of Science® Google Scholar
2 Song Y. D., He L., Zhang D., Qian J. Y., and Fu J., Neuroadaptive fault-tolerant control of quadrotor UAVs: a more affordable solution, IEEE Transactions on Neural Networks and Learning Systems. (2019) 30, no. 7, 1975–1983, https://doi.org/10.1109/TNNLS.2018.2876130, 2-s2.0-85056150257, 30403643.
10.1109/TNNLS.2018.2876130
PubMed Web of Science® Google Scholar
3 Wang C. Y., Dong W., Wang J. N., and Ding Z. T., Predictive descriptor observer design for a class of linear time-invariant systems with applications to quadrotor trajectory tracking, IEEE Transactions on Industrial Electronics. (2021) 68, no. 10, 10019–10028, https://doi.org/10.1109/TIE.2020.3028803.
10.1109/TIE.2020.3028803
Web of Science® Google Scholar
4 Yu Z. Q., Zhang Y. M., Jiang B., Su C. Y., Fu J., Jin Y., and Chai T. Y., Fractional-order adaptive fault-tolerant synchronization tracking control of networked fixed-wing UAVs against actuator-sensor faults via intelligent learning mechanism, IEEE Transactions on Neural Networks and Learning Systems. (2021) 32, no. 12, 5539–5553, https://doi.org/10.1109/TNNLS.2021.3059933.
10.1109/TNNLS.2021.3059933
PubMed Web of Science® Google Scholar
5 Zhu X. D., Li W. Q., and Xia Y. Q., Finite-time fault estimate and fault-tolerant control for discrete-time Markov jump systems with actuator and sensor faults, International Journal of Robust and Nonlinear Control. (2023) 33, no. 11, 6233–6249, https://doi.org/10.1002/rnc.6694.
10.1002/rnc.6694
Web of Science® Google Scholar
6 Ashraf M. A., Ijaz S., Javaid U., Hussain S., Anwaar H., and Marey M., A robust sensor and actuator fault tolerant control scheme for nonlinear system, IEEE Access. (2022) 10, 626–637, https://doi.org/10.1109/ACCESS.2021.3137388.
10.1109/ACCESS.2021.3137388
Web of Science® Google Scholar
7 Yu D. X., Yang M., Liu Y. J., Wang Z., and Chen C. L. P., Adaptive fuzzy tracking control for uncertain nonlinear systems with multiple actuators and sensors faults, IEEE Transactions on Fuzzy Systems. (2023) 31, no. 1, 104–116, https://doi.org/10.1109/TFUZZ.2022.3182746.
10.1109/TFUZZ.2022.3182746
Web of Science® Google Scholar
8 Xia Z. L. and He S. P., Finite-time asynchronous H_∞ fault-tolerant control for nonlinear hidden Markov jump systems with actuator and sensor faults, Applied Mathematics and Computation. (2022) 428, article 127212.
Web of Science® Google Scholar
9 Liang H. J., Liu G. L., Huang T. W., Lam H. K., and Wang B. H., Cooperative fault-tolerant control for networks of stochastic nonlinear systems with nondifferential saturation nonlinearity, IEEE Transactions on Systems Man Cybernetics-Systems. (2022) 52, no. 3, 1362–1372, https://doi.org/10.1109/TSMC.2020.3020188.
10.1109/TSMC.2020.3020188
Web of Science® Google Scholar
10 Zhu L., Li X. F., Huang D. Q., Dong H. R., and Cai L. C., Distributed cooperative fault-tolerant control of high-speed trains with input saturation and actuator faults, IEEE Transactions on Intelligent Vehicles. (2023) 8, no. 2, 1241–1251, https://doi.org/10.1109/TIV.2022.3168550.
10.1109/TIV.2022.3168550
Google Scholar
11 Ma L., Zong G. D., Zhao X. D., and Huo X., Observed-based adaptive finite-time tracking control for a class of nonstrict-feedback nonlinear systems with input saturation, Journal of the Franklin Institute-Engineering and Applied Mathematics. (2020) 357, no. 16, 11518–11544, https://doi.org/10.1016/j.jfranklin.2019.07.021, 2-s2.0-85072831709.
10.1016/j.jfranklin.2019.07.021
Web of Science® Google Scholar
12 Li Y. L., Niu B., Zong G. D., Zhao J. F., and Zhao X. D., Command filter-based adaptive neural finite-time control for stochastic nonlinear systems with time-varying full-state constraints and asymmetric input saturation, International Journal of Systems Science. (2022) 53, no. 1, 199–221, https://doi.org/10.1080/00207721.2021.1943562.
10.1080/00207721.2021.1943562
Web of Science® Google Scholar
13 Wang G., Yang W. X., Zhao N., Ji Y. F., Shen Y. T., Xu H., and Li P., Distributed consensus control of multiple UAVs in a constrained environment, Proceedings of 2020 IEEE International Conference on Robotics and Automation (ICRA), 2020, Paris, France, 3234–3240.
Google Scholar
14 Shao S. Y., Chen M., Hou J., and Zhao Q. J., Event-triggered-based discrete-time neural control for a quadrotor UAV using disturbance observer, IEEE/ASME Transactions on Mechatronics. (2021) 26, no. 2, 689–699, https://doi.org/10.1109/TMECH.2021.3051835.
10.1109/TMECH.2021.3051835
Web of Science® Google Scholar
15 Liu K., Yang P., Jiao L., Wang R. J., Yuan Z. P., and Li T., Observer-based adaptive finite-time neural control for constrained nonlinear systems with actuator saturation compensation, IEEE Transactions on Instrumentation and Measurement. (2024) 73, article 7502516.
Web of Science® Google Scholar
16 Liu K., Yang P., Wang R. J., Jiao L., Li T., and Zhang J., Observer-based adaptive fuzzy finite-time attitude control for quadrotor UAVs, IEEE Transactions on Aerospace and Electronic Systems. (2023) 59, no. 6, 8637–8654, https://doi.org/10.1109/TAES.2023.3308552.
10.1109/TAES.2023.3308552
Web of Science® Google Scholar
17 Liu K., Yang P., Jiao L., Wang R. J., Yuan Z. P., and Dong S. F., Antisaturation fixed-time attitude tracking control based low-computation learning for uncertain quadrotor UAVs with external disturbances, Aerospace Science and Technology. (2023) 142, article 108668, https://doi.org/10.1016/j.ast.2023.108668.
10.1016/j.ast.2023.108668
Web of Science® Google Scholar
18 Sun Y. Z., Liu J. X., Gao Y. B., Liu Z., and Zhao Y., Adaptive neural tracking control for manipulators with prescribed performance under input saturation, IEEE-ASME Transactions on Mechatronics. (2023) 28, no. 2, 1037–1046, https://doi.org/10.1109/TMECH.2022.3213441.
10.1109/TMECH.2022.3213441
Web of Science® Google Scholar
19 Yang C. G., Huang D. Y., He W., and Cheng L., Neural control of robot manipulators with trajectory tracking constraints and input saturation, IEEE Transactions on Neural Networks and Learning Systems. (2021) 32, no. 9, 4231–4242, https://doi.org/10.1109/TNNLS.2020.3017202.
10.1109/TNNLS.2020.3017202
PubMed Web of Science® Google Scholar
20 Liu K., Wang R. J., Wang X. D., and Wang X. X., Anti-saturation adaptive finite-time neural network-based fault-tolerant tracking control for a quadrotor UAV with external disturbances, Aerospace Science and Technology. (2021) 115, article 106790, https://doi.org/10.1016/j.ast.2021.106790.
10.1016/j.ast.2021.106790
Web of Science® Google Scholar
21 Wang G., Yang W. X., Zhao N., Li P., Shen Y. T., and Wang C. L., An approximation-free simple control scheme for uncertain quadrotor systems: theory and validations, Proceedings of 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2019, Macau, China, 3078–3083, https://doi.org/10.1109/IROS40897.2019.8967666.
10.1109/IROS40897.2019.8967666
Google Scholar
22 Wang G., Yang W. X., Zhao N., Shen Y. T., and Wang C. L., An approximation-free simple controller for uncertain quadrotor systems in the presence of thrust saturation, Mechatronics. (2020) 72, article 102450, https://doi.org/10.1016/j.mechatronics.2020.102450.
10.1016/j.mechatronics.2020.102450
Web of Science® Google Scholar
23 Wei Y. L., Sheng L., Gao M., and Ma Y. H., Anti-saturation fault-tolerant control for Markov jump nonlinear systems with unknown control coefficients and unmodeled dynamics, Nonlinear Analysis-Hybrid Systems. (2023) 50, article 101384, https://doi.org/10.1016/j.nahs.2023.101384.
10.1016/j.nahs.2023.101384
Web of Science® Google Scholar
24 Zhu C. J., Chen J. C., and Zhang H., Attitude control for quadrotors under unknown disturbances using triple-step method and nonlinear integral sliding mode, IEEE Transactions on Industrial Electronics. (2023) 70, no. 5, 5004–5012, https://doi.org/10.1109/TIE.2022.3189086.
10.1109/TIE.2022.3189086
Web of Science® Google Scholar
25 Nie B., Liu Z. T., Guo T. H., Fan L. T., Ma H. X., and Sename O., Design and validation of disturbance rejection dynamic inverse control for a tailless aircraft in wind tunnel, Applied Sciences-Basel. (2021) 11, no. 4, https://doi.org/10.3390/app11041407.
10.3390/app11041407
Web of Science® Google Scholar
26 Nie L., Cai B., Zhu Y. M., Yang J. N., and Zhang L. X., Switched linear parameter-varying tracking control for quadrotors with large attitude angles and time-varying inertia, Optimal Control Applications & Methods. (2021) 42, no. 5, 1320–1336, https://doi.org/10.1002/oca.2729.
10.1002/oca.2729
Web of Science® Google Scholar
27 Zheng X. H., Li H. Y., Ahn C. K., and Yao D. Y., NN-based fixed-time attitude tracking control for multiple unmanned aerial vehicles with nonlinear faults, IEEE Transactions on Aerospace and Electronic Systems. (2023) 59, no. 2, 1738–1748.
Web of Science® Google Scholar
28 Shao X. D., Hu Q. L., Shi Y., and Jiang B. Y., Fault-tolerant prescribed performance attitude tracking control for spacecraft under input saturation, IEEE Transactions on Control Systems Technology. (2020) 28, no. 2, 574–582, https://doi.org/10.1109/TCST.2018.2875426, 2-s2.0-85055726806.
10.1109/TCST.2018.2875426
Web of Science® Google Scholar
29 Mei Y. F., Liao Y., and Gong K. J., Adaptive fuzzy dynamic surface fault-tolerant control for coupled spacecraft with actuator faults and saturation, Advances in Space Research. (2023) 71, no. 11, 4843–4859, https://doi.org/10.1016/j.asr.2023.01.053.
10.1016/j.asr.2023.01.053
Web of Science® Google Scholar
30 Xiao Y., de Ruiter A., Ye D., and Sun Z. W., Adaptive fault-tolerant attitude tracking control for flexible spacecraft with guaranteed performance bounds, IEEE Transactions on Aerospace and Electronic Systems. (2022) 58, no. 3, 1922–1940, https://doi.org/10.1109/TAES.2021.3123295.
10.1109/TAES.2021.3123295
Web of Science® Google Scholar
31 Li Z. Y., Shi S., and Liu H., Trajectory tracking of tail-sitter aircraft by L1 adaptive fault tolerant control, Journal of Systems Engineering and Electronics. (2021) 32, no. 6, 1477–1489.
10.23919/JSEE.2021.000125
Web of Science® Google Scholar
32 Souanef T., Multiple model L1 adaptive fault-tolerant control of small unmanned aerial vehicles, Journal of Aerospace Engineering. (2024) 37, no. 1, article 04023103, https://doi.org/10.1061/JAEEEZ.ASENG-4427.
10.1061/JAEEEZ.ASENG-4427
Web of Science® Google Scholar
33 Zhang L., Mu J., Ma H. T., Dai G. C., and Tong S. X., Research on fault-tolerant control of combined airframe damage of electric aircraft, Aerospace. (2023) 10, no. 7, https://doi.org/10.3390/aerospace10070611.
10.3390/aerospace10070611
Web of Science® Google Scholar
34 Li Y., Liu X. X., Ming R. C., Zhu H. Y., and Zhang W. G., A cascaded nonlinear fault-tolerant control for fixed-wing aircraft with wing asymmetric damage, ISA Transactions. (2023) 136, 503–524, https://doi.org/10.1016/j.isatra.2022.10.021, 36379760.
10.1016/j.isatra.2022.10.021
PubMed Web of Science® Google Scholar
35 Cao C. Y. and Hovakimyan N., Design and analysis of a novel adaptive control architecture with guaranteed transient performance, IEEE Transactions on Automatic Control. (2008) 53, no. 2, 586–591, https://doi.org/10.1109/TAC.2007.914282, 2-s2.0-41849088862.
10.1109/TAC.2007.914282
Web of Science® Google Scholar
36 Durham W. C. and Lutze F. H., Perfect explicit model-following control solution to imperfect model-following control problems, Journal of Guidance Control and Dynamics. (1991) 14, no. 2, 391–397, https://doi.org/10.2514/3.20651, 2-s2.0-0026122358.
10.2514/3.20651
Web of Science® Google Scholar
37 Jafarnejadsani H., Sun D. L., Lee H. M., and Hovakimyan N., Optimized L1 adaptive controller for trajectory tracking of an indoor quadrotor, Journal of Guidance Control and Dynamics. (2017) 40, no. 6, 1415–1427, https://doi.org/10.2514/1.G000566, 2-s2.0-85019436316.
10.2514/1.G000566
Web of Science® Google Scholar
38 Maiti R., Das Sharma K., and Sarkar G., Adaptive fuzzy low-pass filter based L1 adaptive controller design for twin rotor MIMO system, 2019 IEEE Region 10 Symposium (TENSYMP), 2019, Kolkata, India, 744–749, https://doi.org/10.1109/TENSYMP46218.2019.8971315.
10.1109/TENSYMP46218.2019.8971315
Google Scholar
39 Cao C. Y. and Hovakimyan N., L1 adaptive controller for a class of systems with unknown nonlinearities: part I, 2008 American Control Conference, 2008, Seattle, Washington, USA, 4093–4098, https://doi.org/10.1109/ACC.2008.4587134, 2-s2.0-52449108358.
10.1109/ACC.2008.4587134
Google Scholar
40 Khalil H. K., Nonlinear systems, 2002, 3rd edition, Prentice-Hall, Englewood Cliffs, NJ.
Web of Science® Google Scholar

All articles

L1 Adaptive Fault-Tolerant Attitude Tracking Control of UAV Systems Subject to Faults and Input Saturation

Abstract

1. Introduction

2. Problem Formulation

3. The Design of Fault-Tolerant Controller

3.1. Design of the Outer Loop Controller

3.2. Design of the Inner Loop Controller

4. Analysis of Fault-Tolerant Controller

5. Simulation Examples

5.1. Scenario 1: No Fault

5.2. Scenario 2: Sensor Faults

5.3. Scenario 3: Actuator Faults

5.4. Scenario 4: Actuator Faults and Sensor Faults

6. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

L1 Adaptive Fault-Tolerant Attitude Tracking Control of UAV Systems Subject to Faults and Input Saturation

Abstract

1. Introduction

2. Problem Formulation

3. The Design of Fault-Tolerant Controller

3.1. Design of the Outer Loop Controller

3.2. Design of the Inner Loop Controller

4. Analysis of Fault-Tolerant Controller

5. Simulation Examples

5.1. Scenario 1: No Fault

5.2. Scenario 2: Sensor Faults

5.3. Scenario 3: Actuator Faults

5.4. Scenario 4: Actuator Faults and Sensor Faults

6. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information