International Journal of Aerospace Engineering

Volume 2024, Issue 1 7780558

Research Article

Open Access

Aeroelastic Stability Analysis of a Laminated Composite Sandwich Panel With a Magnetorheological Fluid Core Under Yawed Supersonic Airflow

Jian Zhou

orcid.org/0000-0001-5621-329X

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Liang Li,

Liang Li

orcid.org/0009-0003-9877-8549

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Minglong Xu,

Corresponding Author

Minglong Xu

[email protected]

orcid.org/0009-0000-3340-4632

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Jian Zhou,

Jian Zhou

orcid.org/0000-0001-5621-329X

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Liang Li,

Liang Li

orcid.org/0009-0003-9877-8549

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

Minglong Xu,

Corresponding Author

Minglong Xu

[email protected]

orcid.org/0009-0000-3340-4632

State Key Laboratory for Strength and Vibration of Mechanical Structures , School of Aerospace Engineering , Xi’an Jiaotong University , Xi’an , China , xjtu.edu.cn

Search for more papers by this author

First published: 26 September 2024

https://doi.org/10.1155/2024/7780558

Academic Editor: Paolo Gasbarri

Share a link

Email
Wechat
Bluesky

Abstract

In this study, we conducted an aeroelastic stability analysis of a laminated composite magnetorheological fluid (MRF) sandwich panel in supersonic airflow for varying yawed angles. The aeroelastic equations for a rectangular sandwich panel (MRF core layer and composite cross-ply laminate constraining and host layers) were established using a MIN3 plate element. Aerodynamic forces for different yawed angles would result in different coupled flutter boundaries of the panel. The first-order piston theory with a flow-yawed angle was employed. The flutter dynamic pressure was obtained through eigenvalue analysis. The effects of various parameters such as the magnetic field intensity, MRF core and constraining layer thicknesses, ply orientation, and yawed flow angle on the flutter dynamic pressure were studied for the simple- and fixed-support boundary conditions. Our results demonstrated that the flutter dynamic pressure of the laminated composite MRF sandwich panel (i) increased for increasing magnetic field intensity and constraining layer thickness; (ii) initially decreased and then increased with the increasing MRF core thickness; and (iii) was strongly influenced by the ply orientation and yawed flow angle.

1. Introduction

Traditional sandwich panel structures have been used for many applications in structural engineering such as airplanes, helicopter blade, space vehicles, wind turbine blade, and high-speed train. These panel structures have some limitations such as constant frequency and damping properties. Under the action of aerodynamic loads, a self-excited vibration behavior named panel flutter will occur. Panel flutter is an aeroelastic instability phenomenon caused by the coupling effect of aerodynamic, inertial, and elastic forces on the skin structure. Especially in supersonic aircraft [1], it seriously affects flight safety and, therefore, has received widespread attention from aeroelasticity experts [2]. In most previous studies, the flutter boundary and nonlinear response characteristics of the panel were mainly studied from the perspectives of structure, aerodynamics, and boundary conditions [3–6]. To improve stealth and aerodynamic performance, modern supersonic aircraft extensively use relatively large skinned panels, flattening the overall panels. Complex and harsh mechanical environments, such as high-speed airflow and aerodynamic heating, can inevitably lead to insufficient structural stiffness and strength margins and, hence, an increased risk of panel flutter. By changing the structural stiffness, damping, and mass properties, the flutter characteristics of the panel may be improved.

Piezoelectric actuators [7–9], constrained damping [10, 11], and nonlinear absorbers [12, 13] can change the structure properties or behavior to improve the flutter boundary of the panel. In recent years, among smart materials that have damping properties, materials such as electrorheological fluids (ERF) and magnetorheological fluids (MRF) [14] with controllable rheological attributes, are set as the viscoelastic cores in sandwich structures. They can modify the shear stress and viscoelastic damping of fluids through the action of electric and magnetic fields, thereby altering the structural characteristics of sandwich panels.

ERFs have been long used as core layers for vibration suppression in beam/plate structures. Yeh and Chen [15–17] established the equations of motion for an orthotropic sandwich plate with an ERF core layer and analyzed its ability for varying natural frequencies, loss factors, and static buckling loads. Mohammadi and Sedaghati [18] and Aboutablebi et al. [19] developed the nonlinear equations of motion for an ERF sandwich shell and plate structures and investigated the effects of small and large displacements, core thickness ratio, electric field intensity, and boundary conditions on their nonlinear vibration behavior. Gholamzadeh Babaki and Shakouri [20] and Shahali, Haddadpour, and Shakhesi [21] investigated the effects of functionally graded component ratios on the dynamic behavior of sandwich plates and shells with functionally graded face layers and an ERF core. Rahiminasab and Rezaeepazhand [22] examined the aeroelastic stability of ERF core sandwich plates in supersonic airflow and studied the influences of electric field intensity and the constraining and ERF layer thicknesses on the flutter dynamic pressure. They revealed the capability of the ERF core layer to shift the system flutter instability. Hasheminejad and Motaaleghi [23] investigated the aeroelastic response control of a simply supported two-dimensional sandwich panel with a tunable ERF core layer, resting on an elastic foundation and exposed to supersonic airflow.

Compared to ERF, MRF has been widely applied for its higher yield strength and invariance with temperature [24]. Sun, Zhou, and Zhang [25] studied the relationship between the magnetic field and the complex shear modulus of magnetorheological (MR) materials. They further examined the vibration characteristics of an adaptive beam for varying magnetic field intensities using a structural dynamic modeling approach. These studies illustrate the vibration control capability of MRF materials. Yeh and Shih [26] established a theoretical model of an MRF-based adaptive beam under an axial harmonic load and analyzed the influences of the magnetic field, beam length, and core thickness ratio on its loss factor, dynamic instability, buckling load, and natural frequency. Lara-Prieto et al. [27] experimentally investigated the vibration characteristics controllability of MRF-based cantilever sandwich beams. Rajamohan, Rakheja, and Sedaghati [28–30] investigated the vibration responses of a partially treated multilayer MRF beam. They revealed that the transverse displacement response and natural frequencies of the partially treated MRF beams are strongly affected by the applied magnetic field intensity, along with the fluid pocket location and length. Additionally, they (i) combined finite element analysis with optimization algorithms based on sequential quadratic programming (SQP) and a genetic algorithm (GA) to identify optimal locations for MRF treatment and achieve maximum modal damping corresponding to the first five modes of flexural vibration (individually and simultaneously) and (ii) formulated an optimal control strategy based on the linear quadratic regulator (LQR) and a full state dynamic observer to suppress the beam vibration. Li et al. [31] established the mathematical model of a sandwich plate with MRF using the finite element method and studied the natural frequencies and loss factors for varying parameters. Manoharan et al. [32] investigated the effect of a laminated composite MRF sandwich plate ply orientation on (i) the variation of natural frequencies and loss factors and (ii) the dynamic response of the sandwich plate under harmonic force excitations for varying magnetic fields. Eshaghi, Sedaghati, and Rakheja [33] numerically and experimentally investigated the vibration characteristics of a partially treated sandwich plate considering different boundary conditions and magnetic flux intensities. The GA was used to identify optimal locations for MRF treatments to maximize the variations in natural frequencies and damping ratios in response to that in the magnetic field. Aboutalebi et al. [34] performed postyield MRF characterization and studied the nonlinear vibration behavior of MRF-based sandwich plates undergoing large amplitude oscillations. Asgari et al. [35, 36] studied the aeroelastic characteristics of a sandwich beam with a partially treated MRF core in supersonic airflow and showed that the critical nondimensional aerodynamic pressure of the sandwich beam is strongly influenced by the core and constraining layer thickness, magnetic field intensity, and core configuration. Eshaghi [37] investigated the effect of plate parameters, boundary conditions, and magnetic field intensity on sandwich MR plate flutter boundaries. Houshangi et al. [38] focused on the supersonic flutter characteristics of truncated sandwich conical shells with an MRF core. They studied the effects of various parameters, such as total thickness, length, semivertex angle, magnetic field intensity, and MRF core thickness on the shell stability regions.

Although these previous works provided excellent contributions, to the best of our knowledge, no studies have been conducted on the aeroelastic characteristics of a sandwich panel with an MRF core, laminated composite host, and constraining layers in supersonic airflow with a yawed angle. Therefore, in this study, we investigated a rectangular laminated composite sandwich panel with an MRF core in supersonic airflow with a yawed angle.

The rest of the article is structured as follows: The aeroelastic equations for the MRF core are established in Section 2; program code validation is demonstrated in Section 3; analysis of the aeroelastic characteristics of the laminated composite MRF sandwich panel is illustrated in Section 4; and the conclusion is presented in Section 5.

2. MRF Core Aeroelastic Equations

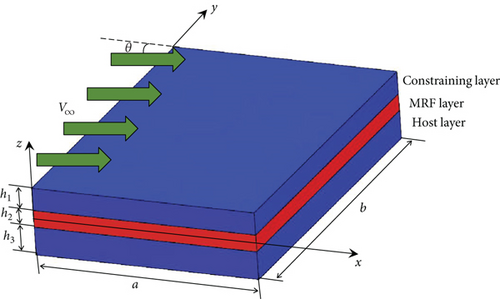
A rectangular sandwich panel with an MRF core layer and composite cross-ply laminates as the host and constraining layers under a supersonic airflow is shown in Figure 1. Here, a and b are the length and width of the panel, respectively; h₁, h₂, and h₃ are the heights of the constraining, MRF, and host layers, respectively; V_∞ is the supersonic flow speed; and θ is the yawed flow angle between the airflow direction and the x-axis. Both the constraining and host layers consisted N composite layers.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) Three-dimensional and (b) side-view of the MRF composite sandwich panel under a supersonic airflow.

2.1. Element Model and Shape Function

A there-node Mindlin plate element (MIN3) was used to establish the aeroelastic equations for a laminated composite sandwich panel with MRF core under yawed supersonic airflow. The MIN3 could solve the shear locking problem and could be applied to linear and nonlinear analysis of composite laminates [39]. Each node has five degrees of freedom, including their degrees of displacement(u, v, and w) and two degrees of rotational freedom(θ_x and θ_y). θ_x and θ_y are the rotations in the xy− and yz− planes, respectively. And u, v, and w denote the displacements in the x, y, and z directions, respectively. A MIN3 element has 15 degrees of freedom, which can be expressed as

()

where

()

The displacement field of a MIN3 element can be obtained by interpolating the displacement of nodes.

()

[H_w], [H_wθ], [H_θx], [H_θy], [H_u], and [H_v] are the displacement interpolation functions represented by area coordinates, as shown in Appendix A.

2.2. Constitutive Equations

To construct the sandwich panel mathematical model, we assumed that the MRF core normal stress is negligible and no slipping occurs between the composite and MRF layers. The strain-displacement relationship of the constraining (i = 1) and host (i = 3) faces can be expressed as

()

where

()

The shear strain-displacement relationship of the MRF layer (i = 2), γ₂, can be expressed as

()

In the general case of a composite lamina, the constitutive relations of constraining and host layers with respect to the x and y axes can be expressed as

()

where k = 1⋯ (N is the total number of composite layers for the ith face). The expressions for Q₁₁, Q₁₂, Q₂₁, Q₂₂, Q₄₄, Q₅₅, Q₆₆, T_σ, and T_s are provided in Appendix B.

The shear stress of the MRF core layer can be expressed as

()

where G^∗ = G^′ + jG^″ is the complex shear modulus of the MRF, G^′ is the storage modulus, G^″ is the loss modulus, and

. We fixed

and

are in this study, where G_a is the magnetic field intensity (Gauss).

The bending moments, M_i, in-plane forces, N_i, and shear forces, R_i, for the constraining and host faces can be expressed as

()

where

()

where A_i, B_i, D_i, and A_si are the extensional, coupling, bending, and shear stiffness matrices of constraining and host faces, respectively. The shear stiffness of the MRF core layer, R₂, can be expressed as

()

2.3. First-Order Piston Theory Aerodynamics With a Flow-Yawed Angle

Piston theory has sufficient accuracy to calculate supersonic aerodynamic loads, and its physical meaning is clear and the expression is concise [40]. For panel flutter under a supersonic airflow, we can usually employ the first-order piston theory with a flow-yawed angle [41]. The aerodynamic pressure, p_a, is written in this case as

()

where

; V_∞ is the airflow speed; ρ_a is the airflow density; M_a is the Mach number; and

is the Prandtl–Glauert parameter. The dimensionless aerodynamic pressure, λ, and aerodynamic damping, g_a, can be defined as follows

()

where D₁₁ is the first entry of the bending stiffness matrix of the laminated composite MRF sandwich panel. Furthermore, we have

()

Using the Equation (13), we finally obtain

()

The aerodynamic force vector on the MIN3 element node can be derived from Equation (3) and Equation (13):

()

2.4. Governing Equations

The governing equations for the laminated composite MRF sandwich panel can be derived using the Hamilton principle, which implies

()

where T and U represent the kinetic and potential energies, respectively; and ψ is the work done by the aerodynamic pressure. The kinetic energies of the constraining face (i = 1), host face (i = 3), and the MRF core (i = 2) can be expressed as

()

where S is the panel area; ρ_i and ρ₂ are the face and core densities, respectively; and

. Therefore, the total kinetic energy becomes

()

The potential energies of the constraining (i = 1), host (i = 3), and MRF (i = 2) layers can be expressed as

()

where α_s denotes the shear correction factor. The total potential energy can then be obtained as

()

Work done due to the supersonic-flow-induced aerodynamic pressure can be written as

()

By introducing Equations (19), (22), and (23) in Equation (16), the governing equation for a MIN3 element can be expressed as

()

where m, c_a, k₀, k_a, and w are the MIN3 element mass matrix, damping matrix, structural stiffness matrix, aerodynamic stiffness matrix, and displacement vector. The expressions are provided in Appendix C.

The motion equation of the overall structure obtained through finite element assembly is

()

where M, C_a, K₀, K_a, and W are the overall mass matrix, damping matrix, structural stiffness matrix, aerodynamic stiffness matrix, and displacement vector obtained from the finite element assembly, respectively. Equation (25) can be then obtained in state-space form.

()

Let us assume

()

Substituting Equation (27) into Equation (26), it can be obtained that

()

where Ω = Ω_R ± iΩ_I, with Ω_R and Ω_I being the real and imaginary parts of the complex eigenvalue of Equation (28).

The natural frequency and flutter dynamic pressure, λ_cr, can be determined by the eigensystem described by Equation (28). When λ = 0, Ω_I is the natural frequency of the MRF sandwich panel; Panel flutter occurs for Ω_R > 0 . The D₁₁ component varies with changes in the geometrical parameters of the composite lamina. To better represent the flutter dynamic pressure, we defined and used .

3. Methodology Verification

Since, to the best of our knowledge, no studies have been conducted on the aeroelastic stability of a composite laminated MRF sandwich panel, structure and aerodynamic load programs were validated separately. To verify the structure program, we compared the values of the first three natural frequencies of a composite laminated MRF sandwich panel at a magnetic field intensity of G_a = 400G (derived in the present analysis and those reported in [32]; Table 1). The results had good consistency, so, it verified the accuracy of the mass and stiffness matrices of the computed structure.

Table 1. Natural frequencies of a composite laminated MRF sandwich panel.

	Present analysis (Hz)			Manoharan et al. [32] (Hz)
	Mode No.
	1	2	3	1	2	3
0.5	127.2	190	262	129.2	191.7	266.3
1.0	107.4	160	222.8	108.1	160	222.5
1.5	97.1	144.7	200	97.6	144.2	198.7
2.0	90.4	135	184	90.6	134.5	181.1
2.5	85.5	128.1	172.8	85.3	127.5	170.6

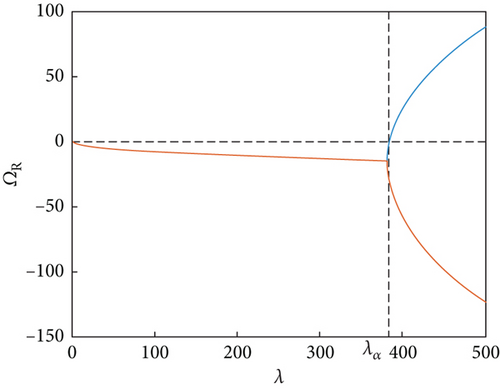
In order to validate the aerodynamic load calculation, we performed a flutter dynamic pressure analysis of a simple-support [−40°/40°/−40°] composite panel [41]. The flutter dynamic pressure value was computed to be λ_cr = 382.4 (Figure 2), which was approximately the same as the previously reported value of λ_cr = 382[40]. Owing to the program accuracy verification, we employed it to study the flutter characteristics of the composite laminated MRF sandwich panel.

4. Results and Discussion

For the composite MRF sandwich panel, we used two types of boundary conditions, namely, four-sided fixed-support (CCCC) and four-sided simple-supported (SSSS). The properties of the constraining and host layers are mentioned as follows: E₁ = 131GPa; E₂ = E₃ = 10.34GPa; G₁₂ = G₂₃ = 6.895GPa; G₁₃ = 6.205GPa; υ₁₂ = υ₁₃ = 0.22; υ₂₃ = 0.49; and ρ₁ = ρ₃ = 1627kgm⁻³. The MRF layer density was fixed at ρ₂ = 3500 kgm⁻³. The base model parameters were fixed as follows: The length and width of the base model were a = 380 mm, and b = 350 mm, respectively; the flow-yawed angle was θ = 0^°; the ply orientation of the constraining and host layers was [0°/90°/0°/MRF/0°/90°/0°]; h₁/h₃ = 1 and h₂/h₁ = 1.2.

4.1. Flutter Boundary Analysis

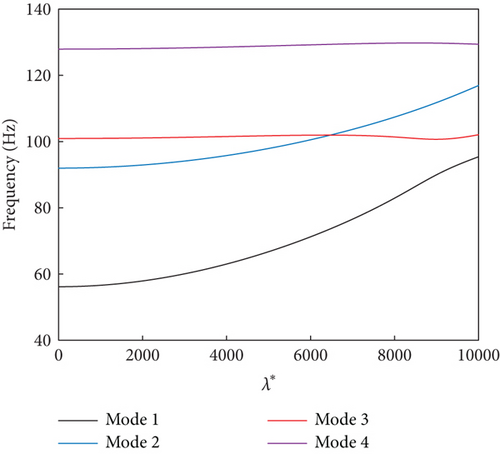
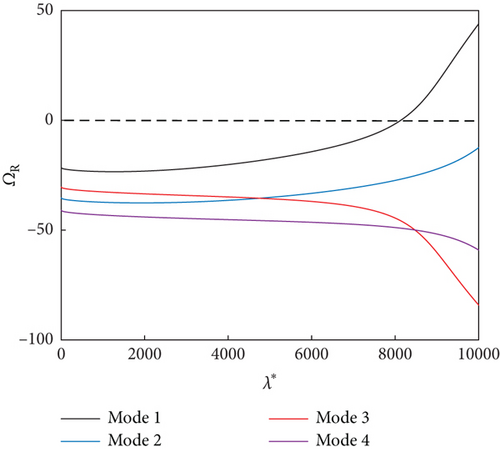
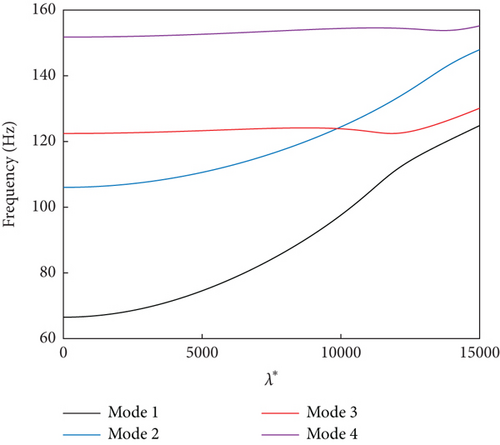
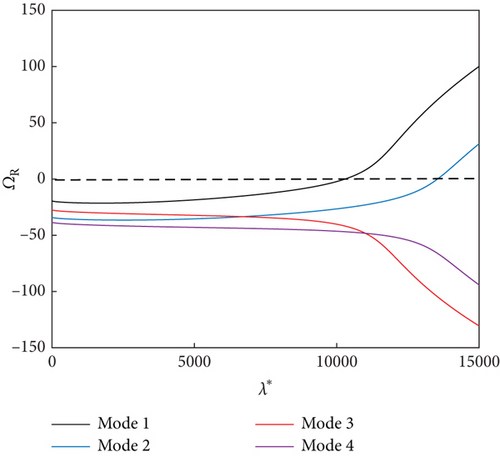
For a magnetic field intensity of 400 G on the MRF sandwich panel, we analyzed the variation of the real and imaginary parts of the eigenvalues with the dynamic pressure under the simple-support (Figure 3) and fixed-support (Figure 4) boundary conditions. When the real part of the first characteristic root switched from a negative to a positive value, the panel experienced unstable(flutter) dynamic pressure. When the panel experiences flutter, the first and third modal frequencies are close to each other but do not overlap due to the presence of aerodynamic and MRF damping. The panel experiences flutter due to the coupling of the first and third modes (mode-coupled flutter). Although coupled flutter also occurs for the second and fourth modes at higher dynamic pressures, the flutter boundary is only the dynamic pressure corresponding to the smallest unstable point. It was also observed that the flutter dynamic pressure at the fixed-support boundary was greater than that at the simple-support boundary.

4.2. Influence of the Magnetic Field Intensity

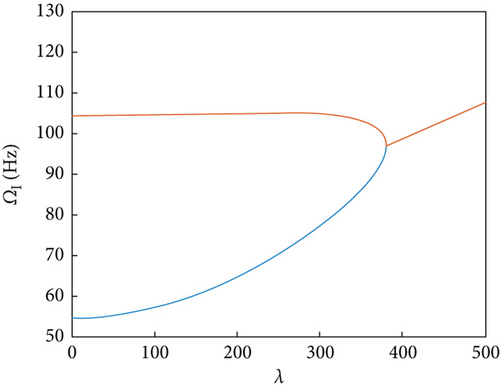
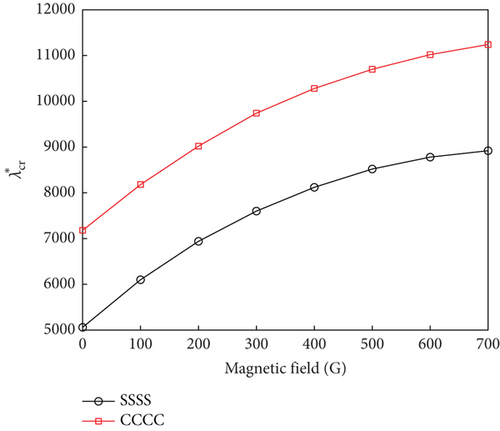
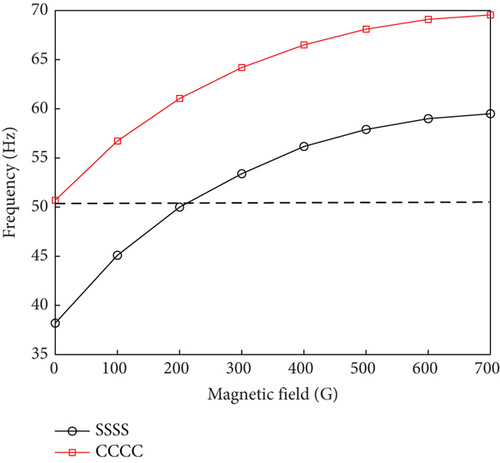
We further analyzed the influence of the magnetic field intensity on the flutter dynamic pressure and first-order modal frequency of the MRF sandwich panels under the simple- and fixed-support boundary conditions (Figure 5). From the figure, it can be seen that as the magnetic field intensity increased, the flutter dynamic pressure of the MRF sandwich panel increased as shown in Figure 5(a). This is mainly because as the magnetic field intensity increased, the stiffness characteristics of the MRF sandwich panel increased, manifested as an increase in the first-order modal frequency as shown in Figure 5(b), thereby increasing the flutter dynamic pressure. When the magnetic field intensity was increased from 0 to 700 G, the flutter dynamic pressure increased by (i) 76.3% for the simple-support panel and (ii) 56.5% for the fixed-support panel. However, the rate of increase in flutter dynamic pressure for both cases decreased with increasing field intensity. This is mainly determined by the relationship between the MRF and the magnetic field intensity. As the magnetic field intensity increases, the shear stiffness of MRF rises rapidly at the initial stage; and the higher the magnetic field intensity is, the smaller the rate of increase of the MRF shear stiffness will become.

4.3. Influence of MRF Core Thickness

We further investigated the variation characteristics of flutter dynamic pressure with respect to the h₂/h₃ ratio for different values of h₁/h₃ (Figure 6). With increasing h₂/h₃, the flutter dynamic pressure is initially reduced followed by an increase. However, for smaller values of h₁/h₃, the flutter dynamic pressure decreases very slightly with the increase of h₂/h₃ at very small values of the ratio. Increasing the thickness of the MRF core is manifested by increasing the damping and stiffness characteristics of the panel. For smaller MRF core thicknesses, the damping characteristics (light damping) play a dominant role. According to the works by Lottati [42], for lightly damped nonconservative systems, adding small structural damping can significantly reduce the instability boundary of the system. The lower the damping, the more reduction in instability boundary. In this condition, slightly increasing the damping reduces the flutter dynamic pressure. As a result, the flutter dynamic pressure decreases with the increase of h₂/h₃ for small h₂/h₃ values. As the MRF core thickness increases, the panel stiffness increases and starts playing a more decisive role. This results in an increase in the flutter dynamic pressure with the increasing h₂/h₃.

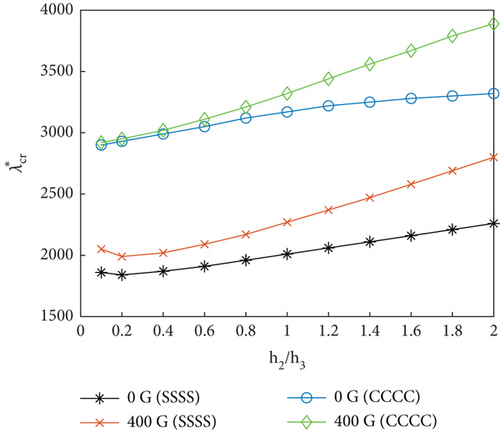
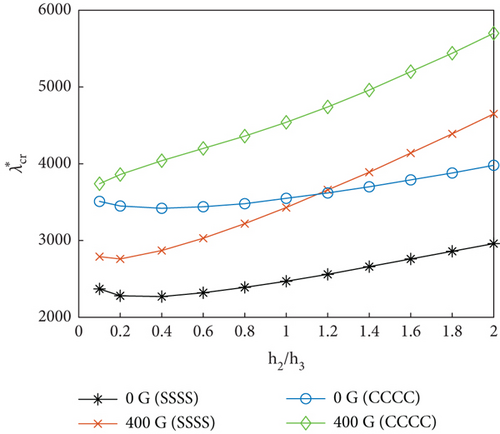
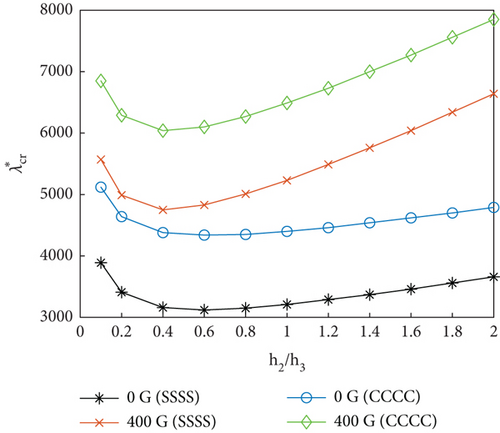
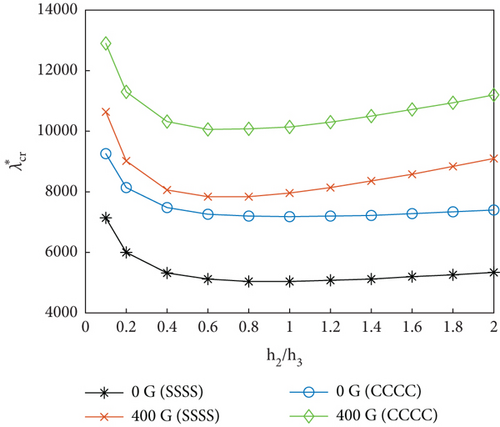
As the MRF core thickness increases, the magnetic field intensity strongly influences the panel flutter. Additionally, as the constraining layer thickness increases, the MRF sandwich panel stiffness also increases, leading to an increase in the flutter dynamic pressure (Figure 6).

4.4. Influence of Ply Orientation and Yawed Flow Angle

The influence of ply orientation and yawed flow angle on the flutter dynamic pressure of the MRF sandwich panels was studied by simulating seven different ply orientations (, , , , , and ) and five different yawed flow angles (0^∘, 30^∘, 45^∘, 60^∘, and 90^∘). Figure 7 shows the variations of the flutter dynamic pressure of MRF sandwich panels with magnetic field intensity under different ply orientations and yawed flow angles for both simple- and fixed-support boundary conditions. Irrespective of the yawed flow angles, ply orientations, and boundary conditions, the flutter dynamic pressure increased with the increasing magnetic field intensity. For a fixed magnetic field intensity, the flutter dynamic pressure was affected by ply orientation (Figure 8) and the yawed flow angle (Figure 9). When the yawed flow angle is 0^∘, the flutter dynamic pressure decreases with the increase of the ply orientation, the main reason is that the stiffness of the panel in the airflow direction decreases with the increase of the ply orientation. As the yawed flow angle increases, the flutter dynamic pressure of the panel first increases and then decreases with the increase of the ply orientation. When the yawed flow angle is 90^∘, the flutter dynamic pressure increases with the increase of the ply orientation. Similar conclusions can be drawn regarding the influence of yawed flow angle. When the ply orientation is , the flutter dynamic pressure decreases with the increase of the yawed flow angle. As the ply orientation increases, the flutter dynamic pressure of the panel first increases and then decreases with the increase of the yawed flow angle. When the ply orientation is , the flutter dynamic pressure increases with the increase of the yawed flow angle.

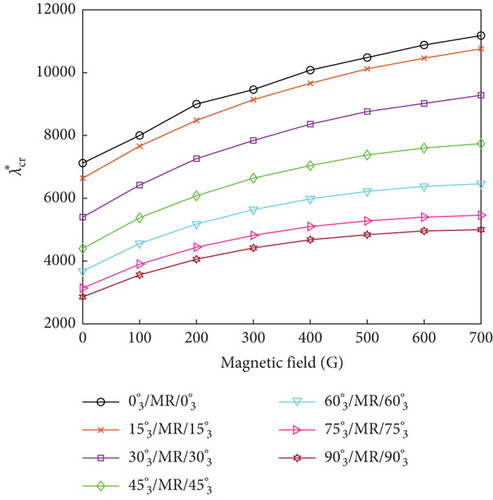
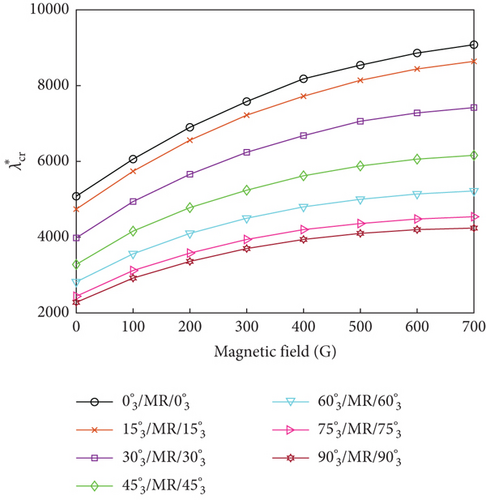
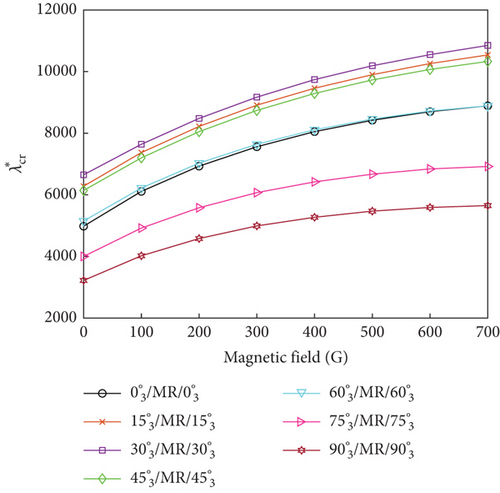
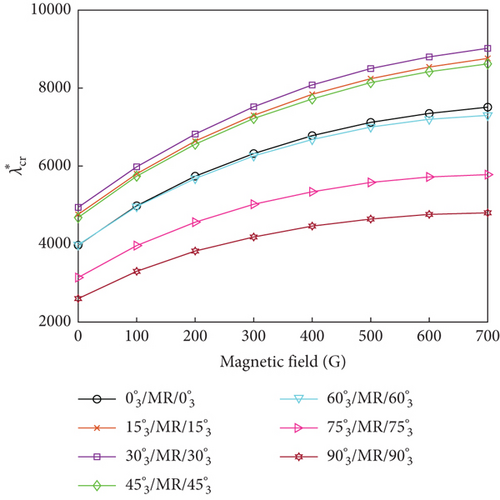
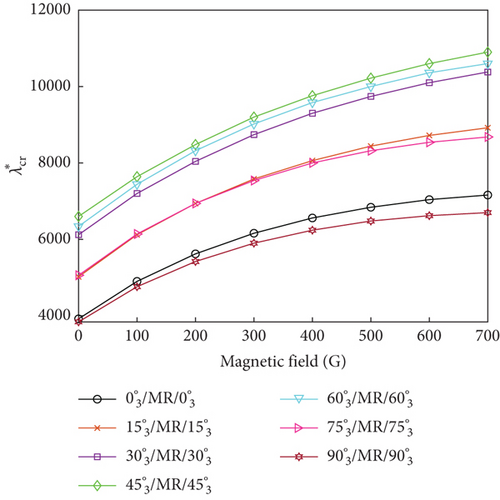
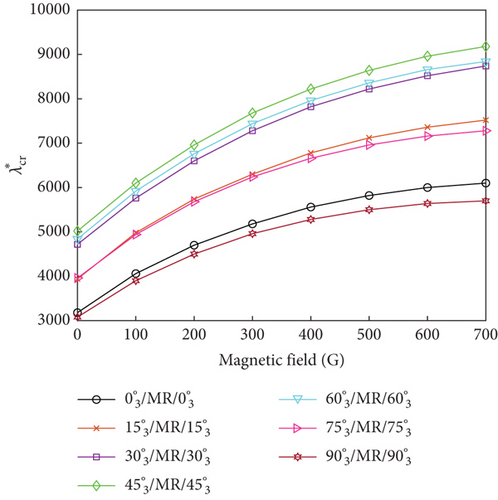
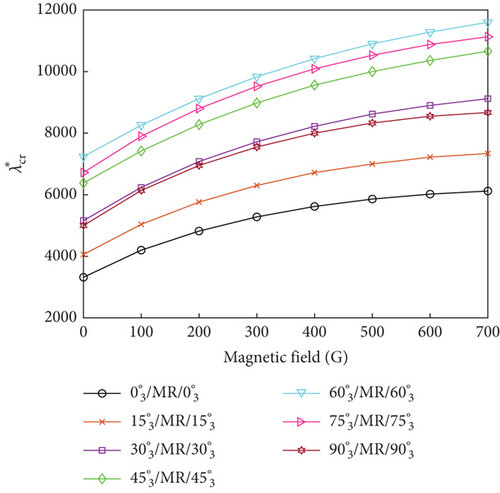
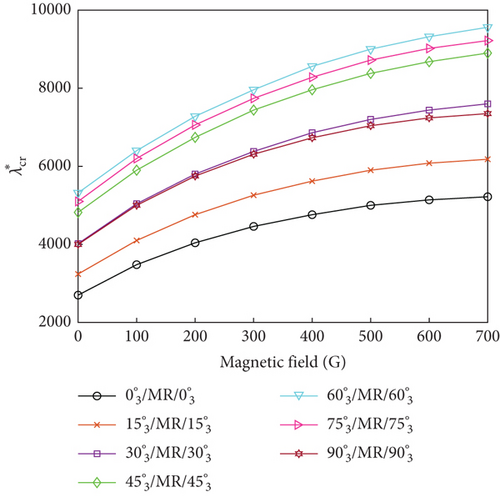
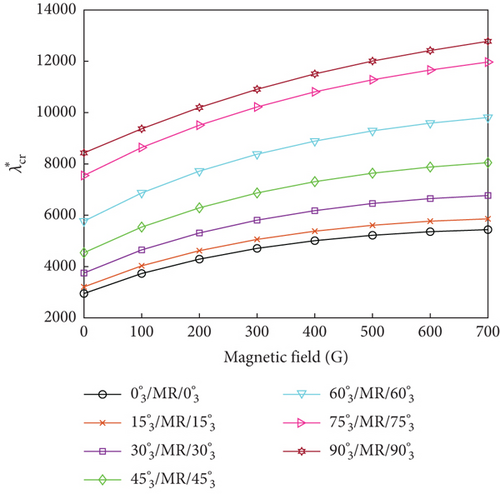
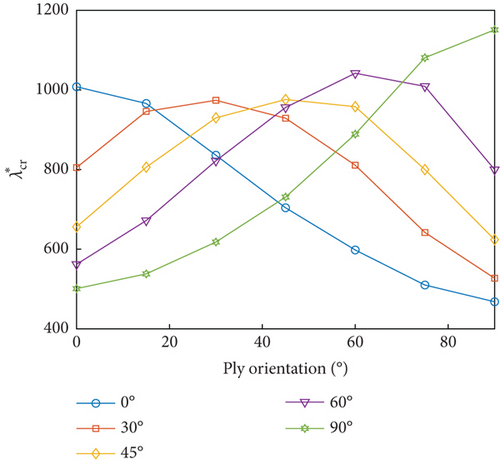
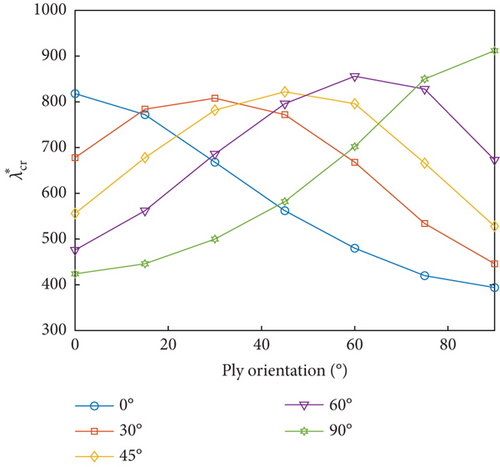
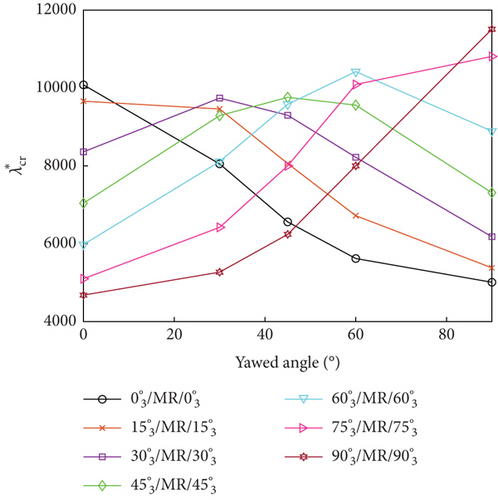
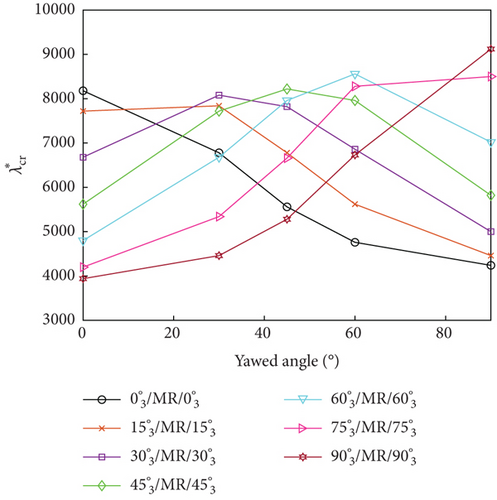
In summary, the maximum flutter dynamic pressure was obtained when the ply orientations of the constraining and host layers were aligned with the yawed flow angle, as the panel bending stiffness reached its maximum value for this condition.

5. Conclusion

In this study, we conducted the aeroelastic stability analysis of a laminated composite MRF sandwich panel in supersonic airflow for varying yawed flow angles. The influence of various parameters, such as MRF core, magnetic field intensity and constraining layer thicknesses, ply orientation, and yawed flow angle on the flutter dynamic pressure was studied. The primary conclusions of this study are presented as follows:

1.
With the increasing magnetic field intensity, the flutter dynamic pressure of the MRF sandwich panel gradually increases, but its rate of increase decreases. The influence of magnetic field intensity on the dynamic pressure of the MRF sandwich panel with a simple-support boundary was higher than that with the fixed-support boundary.
2.
The flutter dynamic pressure initially decreases and then increases with the increasing MRF core thickness, which also enhances the influence of the magnetic field intensity on the panel flutter. Additionally, an increase in the constraining layer thickness also increases the flutter dynamic pressure.
3.
The peak flutter dynamic pressure is obtained when the ply orientations of the constraining and host layers are aligned with the yawed flow angle.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This study was funded by the Natural Science Basic Research Program of Shaanxi (Program No. 2023-JC-QN-0019) and the National Natural Science Foundation of China (No. 11872050).

Acknowledgments

This study was funded by the Natural Science Basic Research Program of Shaanxi (Program No. 2023-JC-QN-0019) and the National Natural Science Foundation of China (No. 11872050).

Appendix A. [H_w], [H_wθ], [H_θx], [H_θy], [H_u], and [H_v]

()

where

()

The relationship between the coordinates of the three nodes can be found in [39].

Appendix B. Q₁₁,Q₁₂, Q₂₁, Q₂₂, Q₄₄, Q₅₅, Q₆₆_, and T_σ,T_s

()

β is the ply angle of the composite lamina.

Appendix C. m, c_a, k₀, k_a, and w

()

Open Research

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Mei C., Abdel-Motagaly K., and Chen R., Review of nonlinear panel flutter at supersonic and hypersonic speeds, Applied Mechanics Reviews. (1999) 52, no. 10, 321–332, https://doi.org/10.1115/1.3098919, 2-s2.0-0000454291.
10.1115/1.3098919
Google Scholar
2 Norouzi H. and Younesian D., Fluid-structure interactions in nonlinear plates subjected to sub and supersonic airflow: a review, Thin-Walled Structures. (2023) 192, https://doi.org/10.1016/j.tws.2023.111144.
10.1016/j.tws.2023.111144
Google Scholar
3 Zhou H., Wang G., Li Q. Z., and Liu Y., Numerical study on the nonlinear characteristics of shock induced two-dimensional panel flutter in inviscid flow, Journal of Sound and Vibration. (2023) 564, https://doi.org/10.1016/j.jsv.2023.117893.
10.1016/j.jsv.2023.117893
Google Scholar
4 Zhou J., Xu M. L., Zhang Z. J., and Tian Z., Vibration and aeroelastic stability analysis of hexagonal honeycomb core sandwich panels in supersonic airflow, Thin-Walled Structures. (2022) 180, article 109746, https://doi.org/10.1016/j.tws.2022.109746.
10.1016/j.tws.2022.109746
Google Scholar
5 An X. M., Deng B., Feng J. Y., and Qu Y. W., Analysis of nonlinear aeroelastic response of curved panels under shock impingements, Journal of Fluids and Structures. (2021) 107, article 103404, https://doi.org/10.1016/j.jfluidstructs.2021.103404.
10.1016/j.jfluidstructs.2021.103404
Google Scholar
6 Chai Y. Y., Li F. M., Song Z. G., and Zhang C. Z., Influence of the boundary relaxation on the flutter and thermal buckling of composite laminated panels, Aerospace Science and Technology. (2020) 104, article 106000, https://doi.org/10.1016/j.ast.2020.106000.
10.1007/978-981-13-9845-2
Google Scholar
7 Swain P. K., Tiwari P., Maiti D. K., Singh B. N., and Maity D., Active flutter control of delaminated composite plate using active fiber composite patches, Thin-Walled Structures. (2022) 172, https://doi.org/10.1016/j.tws.2021.108856.
10.1016/j.tws.2021.108856
Google Scholar
8 Zhou J., Xu M. L., and Yang Z. C., Aeroelastic stability analysis of curved composite panels with embedded macro fiber composite actuators, Composite Structures. (2019) 208, 725–734, https://doi.org/10.1016/j.compstruct.2018.10.035, 2-s2.0-85055347896.
10.1016/j.compstruct.2018.10.035
Web of Science® Google Scholar
9 Song Z. G. and Li F. M., Flutter and buckling characteristics and active control of sandwich panels with triangular lattice core in supersonic airflow, Composite Part B. (2017) 108, 334–344, https://doi.org/10.1016/j.compositesb.2016.10.013, 2-s2.0-84992092183.
10.1016/j.compositesb.2016.10.013
Web of Science® Google Scholar
10 Mahmoudkhani S. and Laghaie K. S., Flutter analysis of sandwich panel with the constrained viscoelastic layer considering the effects of the imperfection and the core thickness deformation, Thin-Walled Structures. (2022) 173, https://doi.org/10.1016/j.tws.2022.108980.
10.1016/j.tws.2022.108980
Google Scholar
11 Yang X. D., Yu T. J., Zhang W., Qian Y. J., and Yao M. H., Damping effect on supersonic panel flutter of composite plate with viscoelastic mid-layer, Composite Structures. (2016) 137, 105–113, https://doi.org/10.1016/j.compstruct.2015.11.020, 2-s2.0-84947926506.
10.1016/j.compstruct.2015.11.020
Web of Science® Google Scholar
12 Zhou J., Xu M. L., Yang Z. C., and Gu Y. S., Suppression of panel flutter response in supersonic airflow using a nonlinear vibration absorber, International Journal of Non-Linear Mechanics. (2021) 133, article 103714, https://doi.org/10.1016/j.ijnonlinmec.2021.103714.
10.1016/j.ijnonlinmec.2021.103714
Google Scholar
13 Pacheco D. R. Q., Marques F. D., and Ferreira A. J. M., Panel flutter suppression with nonlinear energy sinks: numerical modeling and analysis, International Journal of Non-Linear Mechanics. (2018) 106, 108–114, https://doi.org/10.1016/j.ijnonlinmec.2018.08.009, 2-s2.0-85053766104.
10.1016/j.ijnonlinmec.2018.08.009
Web of Science® Google Scholar
14 Eshaghi M., Sedaghati R., and Subhash R., Dynamic characteristics and control of magnetorheological/electrorheological sandwich structures: a state-of-the-art review, Journal of Intelligent Material Systems and Structures. (2016) 27, no. 15, 2003–2037, https://doi.org/10.1177/1045389X15620041, 2-s2.0-84984891090.
10.1177/1045389X15620041
CAS Web of Science® Google Scholar
15 Yeh J. Y. and Chen L. W., Vibration of a sandwich plate with a constrained layer and electrorheological fluid core, Composite Structures. (2004) 65, no. 2, 251–258, https://doi.org/10.1016/j.compstruct.2003.11.004, 2-s2.0-2642544763.
10.1016/j.compstruct.2003.11.004
Web of Science® Google Scholar
16 Yeh J. Y. and Chen L. W., Dynamic stability of a sandwich plate with a constraining layer and electrorheological fluid core, Journal of Sound and Vibration. (2005) 285, no. 3, 637–652, https://doi.org/10.1016/j.jsv.2004.08.033, 2-s2.0-18844407029.
10.1016/j.jsv.2004.08.033
Google Scholar
17 Yeh J. Y. and Chen L. W., Finite element dynamic analysis of orthotropic sandwich plates with an electrorheological fluid core layer, Composite Structures. (2007) 78, no. 3, 368–376, https://doi.org/10.1016/j.compstruct.2005.10.010, 2-s2.0-33845207935.
10.1016/j.compstruct.2005.10.010
Web of Science® Google Scholar
18 Mohammadi F. and Sedaghati R., Nonlinear free vibration analysis of sandwich shell structures with a constrained electrorheological fluid layer, Smart Materials and Structures. (2012) 21, no. 7, article 075035, https://doi.org/10.1088/0964-1726/21/7/075035, 2-s2.0-84863679023.
10.1088/0964-1726/21/7/075035
Google Scholar
19 Aboutalebi R., Eshaghi M., Taghvaeipour A., and Bakhtiari-Nejad F., Post-yield characteristics of electrorheological fluids in nonlinear vibration analysis of smart Sandwich panels, Mechanics Based Design of Structures and Machines. (2023) 51, no. 4, 1944–1963, https://doi.org/10.1080/15397734.2021.1886946.
10.1080/15397734.2021.1886946
Google Scholar
20 Gholamzadeh Babaki M. H. and Shakouri M., Free and forced vibration of sandwich plates with electrorheological core and functionally graded face layers, Mechanics Based Design of Structures and Machines. (2021) 49, no. 5, 689–706, https://doi.org/10.1080/15397734.2019.1698436.
10.1080/15397734.2019.1698436
Google Scholar
21 Shahali P., Haddadpour H., and Shakhesi S., Dynamic analysis of electrorheological fluid sandwich cylindrical shells with functionally graded face sheets using a semi-analytical approach, Composite Structures. (2022) 295, article 115715, https://doi.org/10.1016/j.compstruct.2022.115715.
10.1016/j.compstruct.2022.115715
Google Scholar
22 Rahiminasab J. and Rezaeepazhand J., Aeroelastic stability of smart sandwich plates with electrorheological fluid core and orthotropic faces, Journal of Intelligent Material Systems and Structures. (2012) 24, no. 5, 669–677.
10.1177/1045389X12470306
Google Scholar
23 Hasheminejad S. M. and Motaaleghi M. A., Aeroelastic analysis and active flutter suppression of an electro-rheological sandwich cylindrical panel under yawed supersonic flow, Aerospace Science and Technology. (2015) 42, 118–127, https://doi.org/10.1016/j.ast.2015.01.004, 2-s2.0-84922062402.
10.1016/j.ast.2015.01.004
Web of Science® Google Scholar
24 Weiss K. D., Carlson J. D., and Nixon D. A., Viscoelastic properties of magneto- and electro-rheological fluids, Journal of Intelligent Material Systems and Structures. (1994) 5, no. 6, 772–775, https://doi.org/10.1177/1045389X9400500607, 2-s2.0-0028546175.
10.1177/1045389X9400500607
Web of Science® Google Scholar
25 Sun Q., Zhou J. X., and Zhang L., An adaptive beam model and dynamic characteristics of magnetorheological materials, Journal of Sound and Vibration. (2003) 261, no. 3, 465–481, https://doi.org/10.1016/S0022-460X(02)00985-9, 2-s2.0-0037468845.
10.1016/S0022-460X(02)00985-9
Web of Science® Google Scholar
26 Yeh Z. F. and Shih Y. S., Dynamic characteristics and dynamic instability of magnetorheological material-based adaptive beams, Journal of Composite Materials. (2006) 40, no. 15, 1333–1359, https://doi.org/10.1177/0021998306059715, 2-s2.0-33745939394.
10.1177/0021998306059715
CAS Web of Science® Google Scholar
27 Lara-Prieto V., Parkin R., Jackson M., Silberschmidt V., and Kesy Z., Vibration characteristics of MR cantilever sandwich beams: experimental study, Smart Materials and Structures. (2010) 19, no. 1, article 015005, https://doi.org/10.1088/0964-1726/19/1/015005, 2-s2.0-75649121784.
10.1088/0964-1726/19/1/015005
Google Scholar
28 Rajamohan V., Rakheja S., and Sedaghati R., Vibration analysis of a partially treated multi-layer beam with magnetorheological fluid, Journal of Sound and Vibration. (2010) 329, no. 17, 3451–3469, https://doi.org/10.1016/j.jsv.2010.03.010, 2-s2.0-77951112270.
10.1016/j.jsv.2010.03.010
Web of Science® Google Scholar
29 Rajamohan V., Sedaghati R., and Rakheja S., Optimum design of a multilayer beam partially treated with magnetorheological fluid, Smart Materials and Structures. (2010) 19, no. 6, article 065002, https://doi.org/10.1088/0964-1726/19/6/065002, 2-s2.0-77951652136.
10.1088/0964-1726/19/6/065002
Google Scholar
30 Rajamohan V., Sedaghati R., and Rakheja S., Optimal vibration control of beams with total and partial MR-fluid treatments, Smart Materials and Structures. (2011) 20, no. 11, https://doi.org/10.1088/0964-1726/20/11/115016, 2-s2.0-80155156953.
10.1088/0964-1726/20/11/115016
Google Scholar
31 Li Y. H., Fang B., Li F. M., Zhang J. Z., and Li S., Dynamic analysis of sandwich plates with a constraining layer and a magnetorheological fluid core, Polymers & Polymer Composites. (2011) 19, no. 4-5, 295–302, https://doi.org/10.1177/0967391111019004-507.
10.1177/0967391111019004-507
CAS Web of Science® Google Scholar
32 Manoharan R., Vasudevan R., and Jeevanantham A. K., Dynamic characterization of a laminated composite magnetorheological fluid sandwich plate, Smart Materials and Structures. (2014) 23, no. 2, article 025022, https://doi.org/10.1088/0964-1726/23/2/025022, 2-s2.0-84892384803.
10.1088/0964-1726/23/2/025022
Web of Science® Google Scholar
33 Eshaghi M., Sedaghati R., and Rakheja S., Vibration analysis and optimal design of multi-layer plates partially treated with the MR fluid, Mechanical Systems and Signal Processing. (2017) 82, 80–102, https://doi.org/10.1016/j.ymssp.2016.05.008, 2-s2.0-84973558707.
10.1016/j.ymssp.2016.05.008
Web of Science® Google Scholar
34 Aboutalebi R., Eshaghi M., Hemmatian M., and Sedaghati R., Post-yield characteristics of magnetorheological fluids; from modelling to large-amplitude vibration analysis of Sandwich plates using nonlinear finite element method, Aerospace Science and Technology. (2021) 110, article 106508, https://doi.org/10.1016/j.ast.2021.106508.
10.1016/j.ast.2021.106508
Google Scholar
35 Asgari M. and Kouchakzadeh M. A., Aeroelastic characteristics of magneto-rheological fluid sandwich beams in supersonic airflow, Composite Structures. (2016) 143, 93–102, https://doi.org/10.1016/j.compstruct.2016.02.015, 2-s2.0-84958533753.
10.1016/j.compstruct.2016.02.015
Google Scholar
36 Asgari M., Rokn-Abadi M. R., Yousefi M., and Haddadpour H., Aeroelastic analysis of a sandwich panel with partially treated magneto-rheological fluid core, Journal of Intelligent Material Systems and Structures. (2019) 30, no. 1, 140–154, https://doi.org/10.1177/1045389X18803462, 2-s2.0-85058617180.
10.1177/1045389X18803462
Google Scholar
37 Eshaghi M., The effect of magnetorheological fluid and aerodynamic damping on the flutter boundaries of MR fluid sandwich plates in supersonic airflow, European Journal of Mechanics/A Solids. (2020) 82, article 103997, https://doi.org/10.1016/j.euromechsol.2020.103997.
10.1016/j.euromechsol.2020.103997
Google Scholar
38 Houshangi A., Jafari A. A., Haghighi S. E., and Nezami M., Supersonic flutter characteristics of truncated sandwich conical shells with MR core, Thin-Walled Structures. (2022) 173, article 108888, https://doi.org/10.1016/j.tws.2022.108888.
10.1016/j.tws.2022.108888
Google Scholar
39 Tessler A. and Hughes T. J. R., A three-node Mindlin plate element with improved transverse shear, Computer Methods in Applied Mechanics and Engineering. (1985) 50, no. 1, 71–101, https://doi.org/10.1016/0045-7825(85)90114-8, 2-s2.0-0022097749.
10.1016/0045-7825(85)90114-8
Web of Science® Google Scholar
40 Cheng G. F. and Mei C., Finite element modal formulation for hypersonic panel flutter analysis with thermal effects, AIAA Journal. (2004) 42, no. 4, 687–695, https://doi.org/10.2514/1.9553, 2-s2.0-2342616844.
10.2514/1.9553
Web of Science® Google Scholar
41 Abdel-Motagaly K., Chen R., and Mei C., Nonlinear flutter of composite panels under yawed supersonic flow using finite elements, AIAA Journal. (1999) 37, no. 9, 1025–1032, https://doi.org/10.2514/2.818, 2-s2.0-0033197385.
10.2514/2.818
Google Scholar
42 Lottati I., The role of damping on supersonic panel flutter, AIAA Journal. (1985) 23, no. 10, 1640–1642, https://doi.org/10.2514/3.9141, 2-s2.0-0022146053.
10.2514/3.9141
Google Scholar

All articles

Aeroelastic Stability Analysis of a Laminated Composite Sandwich Panel With a Magnetorheological Fluid Core Under Yawed Supersonic Airflow

Abstract

1. Introduction