1. Introduction

As a high-precision measurement platform, the drag-free satellite cannot install moving parts to meet the hardware design requirements for being a rigid body. Therefore, the microthruster is generally used to be the main executive mechanism of drag-free satellites in space. Thrust and torque produced by microthrusters should compensate for the nonconservative force and torque accurately so as to keep relatively static between the satellite and the internal test mass without contraction. The failure or damage of the thruster could occur in the long-term operation, which may lead to the instability of the control system and even the failure of the mission.

In order to avoid the above problem, one method is the master/replica actuator configuration. In 2015, the European Space Agency launched a satellite Laser Interferometer Space Antenna (LISA) Pathfinder (LPF) [1, 2]. LPF is equipped with the main and backup cold gas microthrusters as the execution system to operate safely and reliably in the halo orbit of the Lagrange L1 point in the Sun–Earth system. And the key technologies of drag-free control in space gravitational wave detection have been verified. Apart from the main backup method, the failure of the thruster can also be figured out by the redundant thruster configuration. The redundant thruster layout means that the thrusters used in the satellite are more than the degrees of freedom required for the control mission to make the system have a certain fault tolerance. In this research, Crawford [3] determined the relationship between the number of thrusters in the redundant configuration and the degrees of freedom of the satellite. For the LISA program [4, 5] in the future, the redundant microthruster configuration is proposed to complete the mission of drag-free control. In addition, Taiji-1 [6], a drag-free satellite launched by the Chinese Academy of Sciences in 2019, installed four radiofrequency ion thrusters and four Hall electric thrusters, which were used in single-degree-of-freedom drag-free control.

Most high-performance satellites could be equipped with redundant actuators in the control system to complete the control task. Xia et al. [7] extracted the design parameters of the GEO satellite thruster layout and optimized the process through programming to reduce the design iteration cycle and improve design efficiency. Gazzino et al. [8] introduced a control scheme to realize the satellite equipped with electric thrusters to minimize fuel consumption while maintaining position using four electric thrusters. Li et al. [9] designed a fault detection algorithm and developed two efficient station-keeping strategies in full and failure modes. The eight thrusters are used in normal mode, and the specified four thrusters are used in fault mode. However, apart from station-keeping, attitude control is also necessary for the system to be stable. Weiss, Kalabić, and Cairano [10] proposed a model predictive control strategy, which used six electrically powered thrusters and three axially symmetric reaction flywheels as actuators for orbit control and attitude control, respectively. In addition, Wei et al. [11] proposed a novel electric thruster configuration design combined with the 4-DOF robotic arm, which can provide flexible thrust in space to reduce propellant. Besides, to solve the problem of thruster failure, Faure et al. [12] studied the optimal layout of spacecraft (SC) thrusters under the constraints of fault diagnosability and fault recoverability.

Thrusters are more suitable for satellite models close to rigid body dynamics than robot arms and reaction flywheels. And the redundant thruster layout entails fewer thrusters at a lower cost than the master/replica actuator configuration because they could change the center of mass of the satellite. However, it should be noted that the redundant thruster layout could lead to unique thrust instructions. Many scholars proposed diverse solutions, such as the direct allocation method [13], daisy chain control allocation [14], and generalized inverse allocation methods [15]. Johansen and Fossen [16] summarized common methods under the nonlinear and linear models of actuators under different application backgrounds. Although varieties of algorithms can be used to obtain the proper instructions, the SC equipped with redundant thrusters still produce allocation errors in the control process, which will affect the control stability of the whole system [17]. Buffington and Enns [14] conducted a study on the stability of control systems with control allocation. To reduce the allocation error, the method based on mathematical programming [16] sets the minimum error as the objective function of the control allocation. Besides, Yang et al. [18] presented an optimization strategy for high-precision attitude control using the solid propellant microthruster array. Doman and Oppenheimer [19] proposed a closed-loop feedback control method to improve the stability of the system with control allocation, considering the effects of the efficiency matrix error caused by the installation deviation. Besides, the microthruster applied to a drag-free satellite needs an extremely strict thrust resolution. To decrease the actuator output deviation, Ma et al. [20] developed the radiofrequency ion microthruster μRIT-1 by optimizing the key structural components, which could make thrust output continuously adjustable. Moreover, Yang [21] developed the cold gas microthruster with an extremely strict thrust resolution to decrease output deviation.

Many researches only consider the relation between the thruster number and the orbit control or the attitude control. But the orbit control and the attitude control must be performed in the drag-free control process. And the design of the thruster layout for the drag-free control needs to take many factors into consideration, including the thruster number, position, and orientation. Moreover, a high microgravity level of drag-free control leads to high requirements for designing the thruster layout. But optimization algorithms and hardware optimization are unsuitable for the design of thruster layout to decrease errors. It is complex and difficult to design a suitable layout to optimize the thruster layout, considering allocation errors. Therefore, it is necessary for high-precision drag-free control to do research on designing the redundant thruster layout.

To realize the high precision attitude and orbit control, the paper proposes a design method for redundant thruster layout to reduce the distribution error generated by various influence factors. First, the main components of allocation error are derived from theoretical analysis. And the thruster configuration factor (TCF) is determined to represent the position and angle of the thrusters involved in the allocation error. In addition, the design criterion of minimum required thrusters is derived to be applied to the satellite model with the orbit control and the attitude control. The criterion is put forward to balance the thruster number and fault tolerance. On this basis, an optimization model is developed to reduce allocation error and improve the availability of layout design. Finally, the simulation results of the gravitational wave detection satellite show that the design of redundant thrusters can reduce the allocation error and improve the fault tolerance of the control system. It demonstrates the feasibility of the proposed method. This work is expected to provide a reference for the redundant thruster configuration design of the drag-free satellite or other satellites in the future.

The paper is organized as follows: Section 2 shows mathematical descriptions of thrust allocation. Section 3 presents the deduction of the optimization principle and method. Section 4 provides the application of the layout design and simulation strategy. Section 5 discusses the results. Section 6 presents the conclusions.

2. Mathematical Model of Thrust Allocation

The expected control quantity F_c is the generalized active control force. T is the thrust column vector. $$, where T_i represents the thrust generated by the i-th thruster. A is the control efficiency matrix, which is determined by the direction, position, and number of thrusters.

The installation of one thruster is determined in the xyz-coordinate system, as shown below.

In Figure 1, O is the origin of the satellite body coordinate system. C is the center of mass of the satellite. T is the installation position of the thruster. The xyz-coordinate system is parallel to the x_by_bz_b-coordinate system. θ is the angle between the thruster direction and the x-y plane. φ is the angle between the projection of the thruster in the x-y plane and the x-axis.

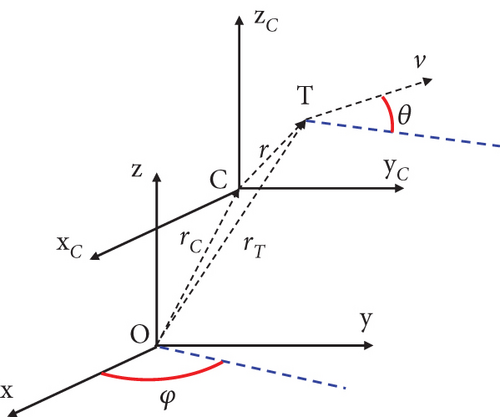
There are m installation positions of thrusters. In Figure 1, r represents the position vector of the thruster in the x_by_bz_b-coordinate system. $$ moment efficiency matrix L = (r₁ × v₁ ⋯ r_j × v_i ⋯ r_m × v_n).

The disturbing force measured is taken as the desired control vector F_c. The optimal solution T is calculated considering specific constraints subject to the thrust limits. T represents the lower limit of thrust, and $$ represents the upper limit of thrust. Based on Formula (6), the allocation errors of thruster configuration could be analyzed.

3. The Design Method of Thruster Layout

The advantage of a redundant thruster layout is that it could effectively solve problems such as failure or damage of thrusters. However, there exist errors between the actual result F and the desired control vector F_c, called the allocation error. To reduce allocation errors, the number and the installation orientation of thrusters are designed in this paper.

4. Designs of Redundant Thruster Layout

According to the above method of designing redundant thruster layout, the corresponding whole simulation strategy is shown in Figure 2. And the drag-free satellite LPF [23] is taken as an example for designing the thruster layout in this paper. A series of calculations would be performed to verify the redundancy of the thruster layout.

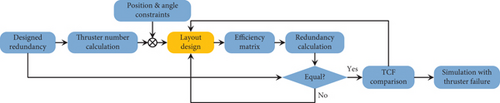
4.1. The Model of Redundant Thruster Layout

The satellite model is shown in Figure 3.

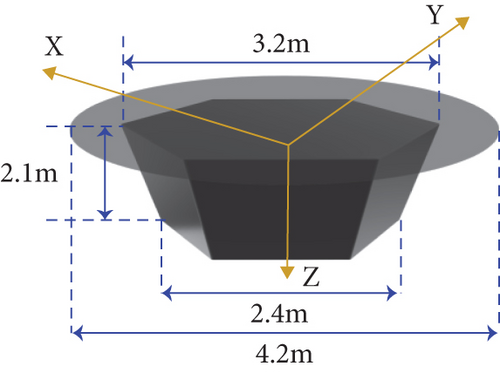
In order to reduce design parameters, paired thrusters are applied to each position, and as few installation positions as possible are used. The designed redundancy is set to be zero or one. Seven layouts are designed on the satellite model, as shown in Figure 4.

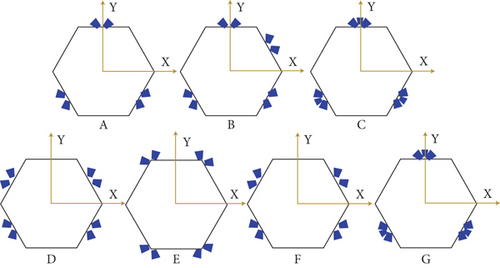
Layouts a, b, and c are designed to compare the effect of thruster number on Δ. Different from the first layout, the latter two layouts add two and three thrusters, respectively, to compare the TCF of the corresponding layout. In addition, layouts d and e are arranged to contrast the influence of the installation position of thrusters on Δ with layout b on the basic of the same thrusters. Besides, the difference between layout f and layout d is the installation angle, the same as the difference between layout c and layout g.

4.2. Results of Redundancy

According to the redundancy calculation method given in Section 3.4.1, the calculation process of the redundancy is shown in Figure 5.

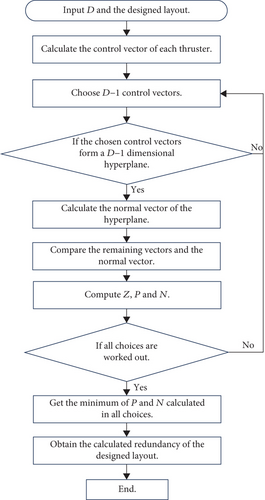
The designed layout determines the efficiency matrix A, which can be calculated by Equations (2)–(4). Efficiency matrices corresponding to all designed layouts in the previous section can be calculated. But with more factors taken into consideration, designing a redundant thruster layout is more complex. Using the paired thrusters can decrease the installation positions. And the design criterion minimum required thrusters can limit the number of thrusters.

Each unit vector applied on layout a is shown in Tables 1, 2, 3, 4, 5, and 6.

Table 1. Unit vectors of each thruster of layout a.

No.	vx	vy	vz
T1	−0.078310	−0.864364	0.496732
T2	−0.787716	0.364364	0.496732
T3	0.787716	0.364364	0.496732
T4	0.078310	−0.864364	0.496732
T5	−0.709406	0.500000	0.496732
T6	0.709406	0.500000	0.496732

Table 2. The extra unit vectors of layout b compared to layout a.

No.	vx	vy	vz
T7	0.787716	−0.364364	0.496732
T8	0.078310	0.864364	0.496732

Table 3. The extra unit vectors of layout c compared to layout a.

No.	vx	vy	vz
T7	0.433013	0.250000	0.866025
T8	−0.433013	0.250000	0.8660254
T9	0	−0.500000	0.866025

Table 4. Unit vectors of layout d and layout e.

No.	vx	vy	vz
T1	−0.078310	−0.864364	0.496732
T2	−0.787716	0.364364	0.496732
T3	0.787716	−0.364364	0.496732
T4	0.078310	0.864364	0.496732
T5	0.787716	−0.364364	0.496732
T6	0.078310	0.864364	0.496732
T7	−0.787716	−0.364364	0.496732
T8	−0.078310	0.864364	0.496732

Table 5. Unit vector of layout f.

No.	vx	vy	vz
T1	0.669550	−0.602866	0.433884
T2	−0.187322	0.881281	0.433884
T3	0.187322	0.881281	0.433884
T4	−0.669550	−0.602866	0.433884
T5	−0.669550	0.602866	0.433884
T6	0.187322	−0.881281	0.433884
T7	−0.187322	−0.881281	0.433884
T8	0.669550	0.602866	0.433884

Table 6. The extra unit vectors of layout g compared to layout c.

No.	vx	vy	vz
T7	0.813798	0.469846	0.342020
T8	−0.813798	0.469846	0.342020
T9	0	-0.939693	0.342020

Then, the installation positions of the thrusters should be determined. The installation positions of layouts c and g are the same as layout a. The position vectors of the corresponding installation place to the satellite centroid coordinate system are r₁ = (−1.05, −0.61, 0.62), r₂ = (1.05, −0.61, 0.62), and r₃ = (0, 1.21, 0.62).

Different from layout a, the additional position vector of layout b is r₄ = (1.05, 0.61, 0.62).

Layout d is the same as layout f. And the position vectors of each installation placed in the satellite centroid coordinate system are r₁ = (−1.05, −0.61, 0.62), r₂ = (1.05, −0.61, 0.62), r₃ = (1.05, 0.61, 0.62), and r₄ = (−1.05, 0.61, 0.62).

The position vectors of Layout e are r₁= (-0.7, -1.21, 0.62), r₂= (0.7, -1.21, 0.62), r₃= (0.7, 1.21, 0.62) and r₄= (-0.7, 1.21, 0.62).

Throughout the use of Equation (4), the efficiency matrix A corresponding to each thruster layout is deduced, which is input into the redundancy calculation. In addition, D = 6. Thus, the calculation results are shown in Table 7.

Table 7. The checking calculation results of redundancy.

Layout	a	b	c	d	e	f	g
The calculated redundancy	−1	−1	−1	−1	−1	−1	−1
The actual redundancy	0	1	1	1	1	1	1

The difference between the calculated redundancy and the actual redundancy is caused by the virtual thruster produced by solar radiation pressure. Because the solar radiation pressure exerted on the drag-free satellite is a relatively stable force with respect to the SC, it can be regarded as a virtual thruster T_v, as shown in Figure 6.

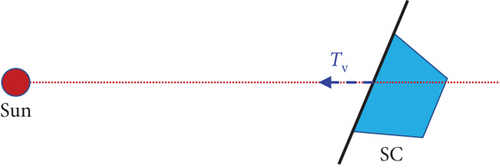
The position vector of the virtual thruster T_v is r = (0, 0, −0.4 m). θ = 60^°. φ of T_v in the SC body coordinate system varies with the satellite position in the orbit. The actual redundancy of each layout should be computed with the virtual thruster, which is reliable. Consequently, the actual redundancy of each thruster in Table 7 can fulfill the design requirement for six degrees of freedom.

5. Simulation

According to the simulation strategy and the control allocation model, a series of simulations of the above layouts are completed to evaluate the relationship between Δ and TCF. Besides, the propellant consumption of each layout is figured out, and the fault tolerance can be verified.

5.1. Simulation of the Orbit

The orbits of the Taiji Project [24] are taken for simulation test in this paper, as shown in Figure 7.

In the above figure, three SCs (SC1, SC2, and SC3) in an equilateral triangle formation [25] are behind the Earth at a certain angle γ (γ = 20^°). The arm length l between each other is 3 × 10⁶ km. The satellite formation is in the Earth’s orbit around the sun (ɑ = 1A.U.). The angle ϕ between the plane of the satellite formation and the ecliptic plane is 60° (ϕ = 60^°). i represents the orbital inclination of SC1, expressed as

$$ ()

The semimajor axis ɑ of the orbit satisfies the following equation:

$$ ()

Besides, the expression of e is as follows:

$$ ()

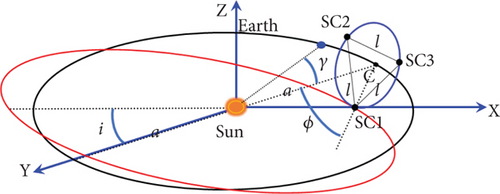
l = 3 × 10⁶ km. And the results of i and e are about 0.009968838702433 and 0.005839000853703, respectively.

The relation among the longitude of ascending node Ω, the argument of pericenter ω, and the mean anomaly M is

$$ ()

The results are shown in Table 8.

Table 8. The values of Ω, ω, and M.

Satellite	Ω	ω	M
SC1	270°	270°	180°
SC2	150°	270°	300°
SC3	30°	270°	60°

The formula of the eccentric anomaly E is

$$ ()

And true anomaly θ_a can be calculated.

$$ ()

Hence, the corresponding values of θ_a are 180° 299.5636083225304° and 60.436391677469594°, respectively.

Based on the above results, the orbits are simulated through MATLAB software and the TU Delft Astrodynamics Toolbox (TUDAT). The mass of each satellite model is 1500 kg. The diameter of the sail is 4.2 m. The operation time is 2 years. The step size is 1000 s. The simulation orbits are shown in Figure 8.

5.2. Simulation of the Disturbing Force

The dynamics of the drag-free satellite around the sun is

$$ ()

q_sc is the generalized displacement of the satellite. M_sc is the generalized mass of the satellite. f_d is the generalized disturbing force applied to the satellite. F_c is the desired control force. The SC needs to become a static and stable platform. f_d and F_c should satisfy the following equation:

$$ ()

5.2.1. Simulation of the Solar Radiation Pressure

The generalized disturbing force f_d acting on the satellite mainly comes from solar radiation pressure [5]. Combined with the solar radiation pressure model [26], the perturbation force model f_srp in this paper is

$$ ()

The speed of light in vacuum is c = 299792458 m/s. 1A.U. = 1.495978707 × 10¹¹ m. The standard solar constant is W₀ = 1361 W/m² [27]. R_l is the relative distance between the satellite and the sun. S_z is the solar sail area. R_a is the absorption coefficient. R_d is the diffuse reflection coefficient. R_s is the specular reflection coefficient. These three coefficients satisfy R_a + R_d + R_s = 1. z is the unit vector of the z-axis. s is the unit direction vector of the satellite pointing towards the sun.

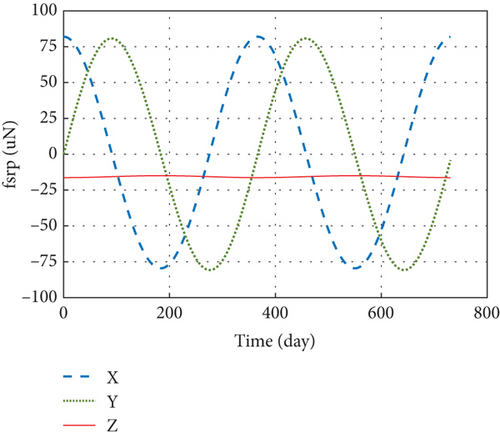
Three drag-free satellites construct an equilateral triangular formation. The calculation of the disturbing force acting on SC1 is the same as the other two. Assuming R_s = 0 and R_a = 0.14 [28], the calculation results of f_srp in the ecliptic coordinate system are obtained, as shown in Figure 9.

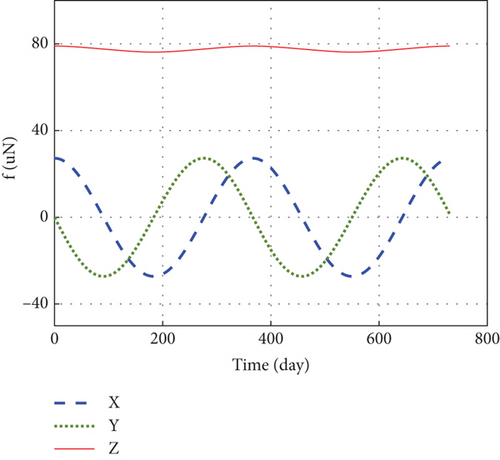
5.2.2. Enter Instruction of Control Allocation

Results in Figure 9 show the axial components of solar radiation perturbation exerted on the satellite in the heliocentric ecliptic coordinate system. But Equation (6) is established in the satellite centroid coordinate system. Therefore, the coordinate system needs to be transformed by the coordinate transformation matrix.

$$ ()

The force f in the generalized disturbing force f_d is calculated, as shown in Figure 10.

The calculation of the torque l is as follows:

$$ ()

r_c = (0, 0,−0.4 m)^Т. The torque l in the generalized disturbing force f_d is calculated, shown in Figure 11.

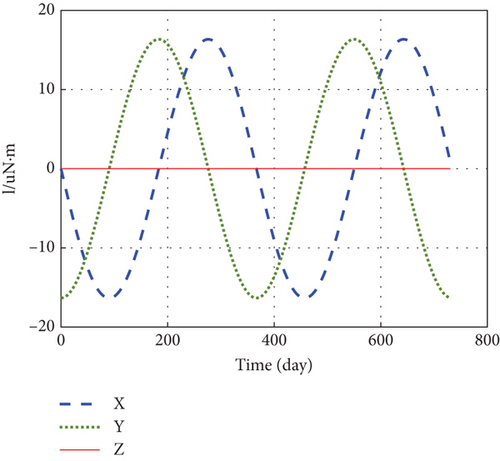
f and l compose f_d. According to Equation (51), F_c can be figured out and used as the enter instruction to calculate the thrust distribution of each thruster at each time point.

5.4. Simulation Results and Analysis

Because of a larger thrust range and lower noise [21], the cold gas microthruster is chosen as the actuator. The limited range of T_i in Equation (6) is set as [1 μN, 100 μN]. Different simulations of all layouts in normal mode are compared to find the relationship between the TCF of each layout and Δ of the counterpart. And the simulation in thruster failure mode is performed to verify the fault tolerance of the redundant thruster layout.

5.4.1. Simulation Results of All layouts

In order to simulate the thrust output error, a random value taken from 0 to 0.1 μN is added to each element of the distribution result T. The actual thrust results of all layouts are shown in Figure 12.

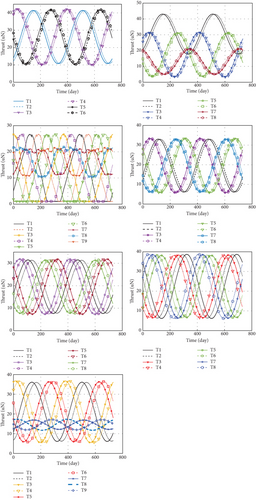
From top to bottom and left to right, the seven pictures represent the thrust results of layouts a, b, c, d, e, f, and g. All the figures show that the actual thrust of each thruster in each picture fluctuates periodically within the restricted range, which meets the constraint condition. The smooth curves indicate that the correspondent thrusters are barely assigned a constant value equal to the lower limit or upper limit of thrust. In addition, if the thrust is in a flat line, the output of the thruster must be equal to the limits of the thrust.

Throughout the use of the above results, we can obtain the actual control forces and torques, which constitute the actual control vector. And the allocation error Δ is the difference between the actual control vector and the desired control vector. The results of Δ are shown in Figure 13.

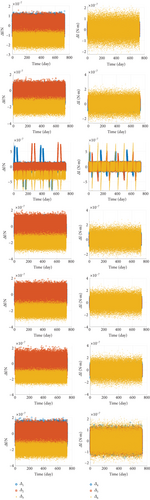
Two pictures at each line in Figure 13 represent Δ of the correspondent layout. The left picture shows the error Δ of each control force. The right picture shows the error Δ of each control torque. The results show that the allocation error in all pictures is at the level of 10⁻⁷. The difference in pictures in the third line implies that thrust redistribution is executed in the simulation of layout c. With the increase in thruster number, thrust redistribution could be more likely to occur in the control process. But given the possibility of thruster failure, we should keep the balance between thruster number and allocation error.

5.4.2. Analysis of Allocations

The main source of noise is allocation error. And the influence of TCF on allocation error is studied by frequency spectrum analysis to obtain the ability to restrain the error of each layout. The spectrum of Δ corresponding to each layout is shown in Figure 14.

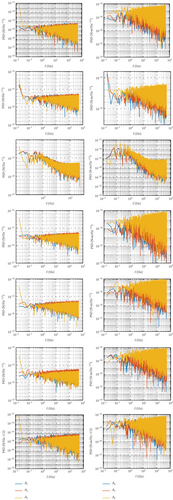
The left picture in each row represents the control force noise, and the right picture in each row represents the control torque noise. Except for layout c, the results of other layouts show that the noise from 0.1 to 1000 Hz is between 16 and 17 orders of magnitude. The results of layouts c and g with the same thrusters reveal that thrust redistribution also influences the error, which belongs to the algorithm error. Subsequently, the variance of Δ is calculated to compare the data from different layouts intuitively. And the sum of varΔ_i is worked out. The value of TCF corresponding to each layout is computed. The calculations are shown in Table 9.

Table 9. The variance of Δ of each layout.

Layout	a	b	c	d	e	f	g
varΔi/10−15	1.88	2.40	16.17	2.09	2.09	1.62	3.00
	1.89	2.63	16.19	2.90	2.94	3.77	2.98
	1.24	1.63	11.12	1.62	1.66	1.27	1.53
	0.70	0.98	8.23	1.10	1.21	1.61	1.95
	0.69	0.89	8.17	0.75	1.07	1.10	1.94
	3.71	4.94	31.36	5.00	6.59	7.14	3.70
Sum/10−15	10.1	13.5	91.2	13.5	15.6	16.5	15.1
TCF	12.1	16.2	20.7	16.2	18.6	19.9	18.1

It can be seen that TCF is positively associated with thruster number, derived from the data in Columns 1, 2, and 3 corresponding to layouts a, b, and c. It verifies the validity of the deduction in Section 3.3.1. And from the data in Columns 2, 4, 5, and 6 in the table, it can be found that the sum of varΔ_i augments with the increase of TCF on the condition of the same thrusters. In addition, because cov(Δ_i, Δ_i) = varΔ_i, the sum of varΔ_i is equal to tr(covΔ). Thus, it can be found that TCF is proportional to tr(covΔ), which demonstrates the deduction of Equation (26). Moreover, the sum of varΔ_i of layout c is the maximum among all results. It illustrates that thrust redistribution could lead to an increase in the sum. The limitation of the obtained results is that the relation between TCF and allocation error must be evaluated on the condition of the same number of thrusters. It can be found that the TCF of layout g is smaller than the TCF of layouts e and f, while the thrusters of layout g are more than the thrusters of layouts e and f. But if the extra thrusters are added to the designed layout, TCF can be compared between them. For example, the results of layouts a, b, c, and g show that the TCF of layout c error is the biggest, as well as the allocation.

5.4.3. Analysis of Fuel Consumption and Fault Tolerance

On the basics of the above thrust distribution results, the total impulse consumed in 2 years can be calculated through the time integral of thrust. Assuming that the specific impulse I_sp of the cold gas microthruster is 60 s (N₂) and g is 9.8 N/kg, the total mass corresponding to each layout is shown in Table 10.

Table 10. Propellant consumption of each thruster layout.

Layout	Total impulse /N·s	Mass/kg	TCF
a	9878.85	16.80	12.1
b	9885.18	16.81	16.2
c	7494.40	12.75	20.7
d	9885.06	16.81	16.2
e	9855.10	16.81	18.6
f	11313.31	19.24	19.9
g	10742.96	18.27	18.1

The above results show that the fuel consumption of redundant thrusters is related not only to the number of thrusters but also to thruster configuration. And it can be seen that layouts a, b, and e consume almost the same mass of fuel, while they have different values of TCF. Besides, four layouts with eight thrusters indicate that fuel consumption has some relationship with thruster configuration. A reasonable configuration could balance thruster number, allocation error, and fuel consumption.

A redundant thruster layout could improve the fault tolerance caused by the permission of R failure thrusters. R of layout a is 0. Hence, one of the redundant thrusters designed in other layouts is chosen to be invalid. The results are shown in Figure 15.

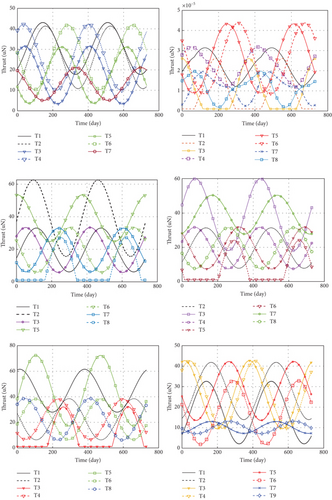
Based on the calculation of the actual redundancy corresponding to each layout, all layouts but layout a can perform simulation experiments with one thruster failure. All the above pictures show the distribution results of each redundant thruster layout. The missing curve T7 in the first picture indicates that the Thruster 7 is out of use. The same goes for other pictures. Compared with the former simulation without failed thrusters, the latter results reveal that the redundant thruster layout has a certain fault tolerance, which could use other thrusters to compensate for the effect of the failed thruster on control stability. It demonstrates the feasibility of the designed layout with redundant thrusters.

6. Conclusion

This paper presents a design method for the redundant thruster layout to improve the control stability of the satellite and reduce the allocation error. In the proposed method, the TCF of redundant thruster layout is put forward and derived through theoretical analysis. The simulation results can verify that TCF can be set as the key criterion for evaluating the allocation error of the attitude and orbit control systems. And the geometric relationship between the thrusters should be designed to reduce the allocation error with a smaller TCF. In addition, the minimum number of thrusters satisfying the redundancy requirement is defined in the layout design. The calculation method for thruster redundancy is provided in this paper. The results of the layouts with one failed thruster verify the validity of the design criterion of minimum required thrusters. And the advantage of a redundant thruster layout is that it can effectively solve problems such as failure or damage of thrusters. Moreover, the simulation results can verify the feasibility and effectiveness of the proposed design method for attitude and orbit control and show the influence of thruster layout on fuel consumption. Future work will be to consider establishing the relation between fuel consumption and requests for allocation error to seek a more suitable design method for the redundant thruster layout for a wider practical application.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the Ministry of Science and Technology of China (grant number 2021YFC2202604).