This paper studies the salvo attack problem for multiple unmanned aerial vehicles (UAVs) against a maneuvering target, and a guidance scheme based on distributed model predictive control (DMPC) is presented to achieve cooperative interception with constraints of terminal impact angle and no-fly zone (or obstacle) avoidance. Firstly, for guaranteeing the synchronization of UAVs in calculating their acceleration commands, the assumed predictive trajectories are introduced, whose deviation from the actual state trajectories is limited by the designed compatibility constraints. Secondly, based on the velocity-obstacle model, the obstacle avoidance constraints are presented, and for guaranteeing the convergence of impact time and impact angles, the auxiliary controller and terminal ingredients are developed, which complete the design of DMPC cooperative guidance scheme. Subsequently, the rigorous proof for the convergence of the proposed guidance scheme is provided. Based on the above design, a complete implementation process of the guidance scheme is presented, in which each UAV uses the particle swarm optimization algorithm to solve the preprocessed local optimization problem, and only the shared information among neighbors is utilized for calculation. Finally, the numerical simulations are conducted under diverse cases, which demonstrate the effectiveness of the proposed guidance scheme when solving cooperative interception problems with terminal angle and obstacle avoidance constraints.

1. Introduction

As an ideal choice for performing dangerous and tedious tasks, UAVs have been widely used in various fields [1], which brings along the rapid development of the cooperative guidance technique [2–4]. Meanwhile, with the advancement of anti-interception methods and target’s maneuverability, reaching the consensus on the impact time is no longer the only requirement for cooperative guidance, the coordination in intercept angles and the no-fly zone avoidance have also attracted attention for the purpose of maximizing the damage effect [5–7] and improving the survivability of UAVs in the presence of enemy radars or antiair weapons. Therefore, proposing a method that can meet all the above requirements is of great significance from both theoretical and practical viewpoints.

For the cooperative guidance with impact time constraints, researchers have made outstanding contributions. As the pioneering research in this field, the authors of ref. [8] proposed an impact-time-control guidance (ITCG) law for salvo attack of multiple missiles, which required a predetermined impact time as the global information for all the missiles. Due to the absence of communication among missiles, however, ITCG is not considered as a cooperative guidance law in its real sense by some researchers. For this concern, Zhao and Zhou [9] introduced coordination algorithms into the guidance of multiple missiles and presented a two-level hierarchical cooperative guidance architecture, which can be implemented in either centralized or distributed communication topology. Motivated by ref. [9], the authors of ref. [10] proposed a cooperative proportional navigation (CPN) law which uses the time-varying navigation gain for eliminating the difference in impact times among multiple missiles. Zhao et al. [11] extended CPN to three-dimensional situation and presented different coordination strategies. Because of the utilization of the local guidance law such as PN, this kind of cooperative guidance is easy to implement. However, due to the fact that most of the above methods are based on the assumption that the velocities of UAVs are constants, the applicability of them is limited to some extent. For this reason, some researchers have managed to introduce the consistency theory into cooperative guidance [12, 13] and divide the design of the guidance law into two stages [14]. The first stage is to design the acceleration command along the direction of the line of sight using the consistency theory, to ensure the consensus on the impact time. The second stage is to design the acceleration command normal to the line of sight for guaranteeing that each UAV precisely hits the target. This idea of design is adopted by lots of researchers [15, 16] and has implications for studies on cooperative guidance with both impact time and impact angle constraints.

The cooperative guidance with impact time and impact angle constraints is widely concerned in recent years [17–20] for achieving the best destroying effect on the target. The authors of ref. [21] presented a novel closed-form guidance law for salvo attack of antiship missiles, based on the biased proportional navigation guidance (BPNG) law. It utilizes the error between the time-to-go and its designated value for feedback control and adds another biased term to BPNG, thereby satisfying both impact time and impact angle constraints. However, the communication among the UAVs is not needed for this method. Enlightened by ref. [14], Dong et al. [16] proposed a fixed-time cooperative guidance law to simultaneously attack a maneuvering target at desired terminal angles. It uses the consistency protocol, fixed-time control theory, and integral sliding mode control to design the tangential acceleration command and normal acceleration command, respectively. In ref. [18], researchers proposed the time- and angle-constrained cooperative guidance law based on the finite-time sliding mode control and the super-twisting control algorithm. Most of the above researches adopted the design idea in ref. [14] and achieved satisfactory guidance effects; however, there are still limitations in some aspects. First, the maneuver of the UAV is achieved through the acceleration command perpendicular to or along its velocity. Most of the above researches failed to take the saturation constraints of normal or tangential acceleration (with respect to velocity) into account. Second, the design in line-of-sight coordinate system is only intended to complete the interception task, while how to avoid entry into no-fly zones or collision with obstacles remains unresolved for the above studies.

No-fly zone (or obstacle) avoidance is one of the hotspots in UAV path planning, and some latest progress has been made on the basis of existing algorithms such as hybrid A∗ algorithm [22] and artificial potential field method [23]. Despite the great significance of obstacle avoidance in improving the survivability of UAVs when performing interception tasks, only a few studies on guidance or cooperative guidance have taken obstacle avoidance into consideration. Among them, the authors of ref. [24] presented a time-constrained guidance approach for multimissiles attacking a stationary target based on model predictive control (MPC), which achieved no-fly zone avoidance by adding a safe distance-based penalty term to the local cost function. The authors of ref. [25] proposed a three-dimensional guidance approach for maneuvering target interception and handled obstacle avoidance constraints by decomposing the optimization problem into two subproblems, thus enabling the UAV to avoid obstacles while ensuring the guidance effect. The above researches introduced MPC into guidance and provided new ideas for solving such problems.

As an emerging control theory, MPC is able to handle control problems with multiple constraints and has been employed into cooperative guidance in recent years [26]. Besides the aforementioned ref. [24, 25], Zhao and Zhou [27] presented a cooperative guidance approach based on distributed model predictive control (DMPC), which could coordinate the impact time of a group of UAV missiles against the stationary target. Kang et al. [28] reformulated the impact time coordination as a consensus on the ranges and range rates of the missiles and presented a MPC-based cooperative guidance law. However, the optimization problem formulated in ref. [28] is solved in a centralized manner. The authors of ref. [29] designed a cooperative guidance algorithm with impact angle constraints based on distributed MPC, which could be applied to salvo attack against a stationary or low-speed maneuvering target. Although there are precedents indicating the successful use of MPC for cooperative guidance, some crucial issues have not yet been resolved, such as the design of terminal ingredients and compatibility constraints; they are all essential for guaranteeing the recursive feasibility and the convergence of the overall system [30, 31]. In addition, up to now, it is still challenging to develop a cooperative guidance approach that simultaneously achieves maneuvering target interception, consensus on the impact time, coordination in impact angles, and obstacle avoidance (for the sake of comparison, all the existing studies on MPC-based cooperative guidance are listed in Table 1).

Table 1. Comparison of existing studies on MPC-based cooperative guidance.

Reference	Target type	Consensus on impact time	Coordination in impact angles	No-fly zone or obstacle avoidance	Convergence guarantee
[24]	Stationary	Yes	No	Yes	No
[27]	Stationary	Yes	No	No	No
[28]	Stationary	Yes	No	No	No
[29]	Low-speed maneuvering	Yes	Yes	No	No

Therefore, aiming at addressing the issues listed above, we develop a DMPC-based cooperative guidance scheme. The main contributions of this study are as follows.

(1)
Compared to refs [14, 16, 18] which separately design the acceleration commands normal to and along the LOS, we simultaneously design the normal and tangential acceleration commands in virtue of DMPC, and take the saturation of acceleration into consideration
(2)
Compared with refs [24, 27, 29], we further ensure the convergence of the multi-UAV system under DMPC by developing the compatibility constraints and the terminal ingredients. Different from designing a state-related constraint as in refs [32, 33], we derive an obstacle avoidance constraint applied to the control input of each UAV. This work ensures successful obstacle avoidance without reducing the feasible region of solution
(3)
To the best of our knowledge, it is the first time in cooperative guidance that maneuvering target interception, consensus on the impact time, coordination in impact angles, and obstacle avoidance are all achieved. Besides, different from ref. [28], all the UAVs participating in guidance share the information only with their neighbors and synchronously solve the optimization problem to obtain the acceleration commands

The remainder of this paper is organized as follows. In Section 2, the preliminaries about planar cooperative guidance geometry and DMPC are provided. In Section 3, the detailed design and convergence analysis are conducted for the DMPC-based cooperative guidance scheme. In Section 4, the complete implementation process of DMPC cooperative guidance scheme using particle swarm optimization algorithm is introduced. In Section 5, the numerical simulations are carried out under diverse cases, in which the proposed DMPC cooperative guidance scheme is compared with other methods. Finally, in Section 6, the conclusions are drawn.

2. Preliminary

In this section, some preliminaries about planar cooperative guidance geometry and distributed model predictive control are provided. For simplicity, the following assumptions are adopted in the research process.

Assumption 1. The UAVs and the target are considered as the geometric points in the plane.

Assumption 2. The autopilot dynamics of the UAVs are fast enough that the lag can be neglected.

2.1. Cooperative Guidance Geometry

The planar engagement geometry of multiple UAVs attacking a single maneuvering target is depicted in Figure 1, where M_i(i = 1, 2, ⋯, N_M) and T denote the UAV and the target, respectively; obs_l(l = 1, 2, ⋯, N_obs) denotes the obstacle or the no-fly zone, which is modelled as a circle with a radius of R_obs l; and M_iXY and M_iX_LY_L represent the inertial reference frame and the line-of-sight (LOS) reference frame, respectively. Meanings of other symbols are given as follows: θ_Mi and θ_T are the flight path angles of M_i and T, v_Mi and v_T are the velocities of M_i and T, q_i is the line-of-sight (LOS) angle with respect to M_i and T, r_i is the relative distance between each UAV and the target, q_obs il is the LOS angle with respect to M_i and obs_l, and d_il is the distance between M_i and obs_l. All the above angles are positive in the counterclockwise direction.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Planar cooperative guidance geometry.

Assuming that all the UAVs are thrust controllable, the acceleration of M_i in inertial frame can be decomposed into a_Mi and u_Mi, where a_Mi is the normal acceleration and changes the direction of v_Mi and u_Mi is the tangential acceleration changing the magnitude of v_Mi, while the target is assumed to be passive vehicle with only direction of velocity controllable. Then, the relative motion between M_i and T can be described using Eq. (1), with Eq. (2) describing that between M_i and obs_l.

()

Here,

()

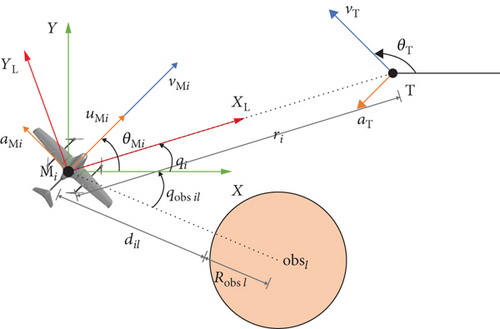
Remark 3. For the UAV equipped with radar seeker and inertial navigation system, θ_Mi, v_Mi, r_i, q_i, and q_obs il can be acquired in real time. Using this information, , , and can be directly calculated.

For ease of design, we define

, and

()

Take the derivative of

and

. Applying (4) and (5) yields

()

To estimate the remaining impact time of each UAV, we introduce a new variable called time-to-go, formulated as

()

Supposing that the desired terminal LOS angle of each UAV is q_di (commonly, there is q_di ≠ q_dj when i ≠ j), the state variables for the guidance system are selected as

()

Then, we can get a nonlinear system

()

In order to control all the UAVs to simultaneously hit the target at their respective terminal LOS angles without colliding with obstacles, the control objectives of each UAV are described as

()

where t_fi is the final time of guidance of each UAV, which satisfies

To achieve all the control objectives of UAVs, a cooperative guidance scheme based on the synchronous distributed model predictive control (DMPC) will be proposed below.

2.2. Distributed Model Predictive Control

With lower computational cost and more structural flexibility [31], DMPC has the potential to solve complex control problems of large-scale systems. Compared to traditional centralized MPC [28], DMPC requires each UAV to independently solve the constrained optimization problem and obtain their control actions, without the need for a central controller to complete all the calculations for all the UAVs.

Among several update strategies of DMPC (sequential DMPC [34], iterative DMPC [35], and synchronous DMPC [30–32, 36, 37]), the synchronous DMPC requires the least communication and computation resources, as it allows all the UAVs to synchronously calculate the control actions and communicate only with their neighbors. Therefore, the synchronous DMPC strategy is a preferred choice for a cooperative guidance problem with multiple constraints.

Prior to designing the cooperative guidance scheme, the basic model of DMPC is given in this subsection. Consider the DMPC problem as follows.

Problem 4. At sampling instant t_k, given the current state of M_i, i.e., x_i(t_k), the predictive state trajectories of the neighbors of M_i, i.e., x_i−(τ|t_k), τ ∈ [t_k, t_k + T], the predictive disturbances w_i(τ|t_k), find the optimal control inputs

()

subject to system equation (9),

()

In Problem 4, t_k = t₀ + kδ, k = 0, 1, ⋯, δ denotes the sampling period, T represents the control horizon. L_i(τ|t_k, x_i, x_i−, u_i, w_i) is the stage cost given as in (17), which is established based on the control objectives of each UAV. g_i(x_i(t_k + T|t_k)) is the terminal cost, and

is the admissible set of the control inputs, whose specific form is given as (18). It should be noted that the terminal cost and the other terminal ingredients are essential in guaranteeing the convergence of the multi-UAV system and will be specifically designed in Section 3.2.

()

In Eq. (17), ℕ_i is the neighbor index set of M_i, and λ_1i and λ_2i are the weighting scalars given beforehand.

By solving the above constrained optimization problem, each UAV will obtain its real-time guidance command

, τ ∈ [t_k, t_k+1). As the system states evolve along the dynamic equation (9) from t_k to t_k+1, the above problem will be renewed, which ensures the real-time feedback and correction of DMPC. However, considering that the future system states are currently unknown, the following issues should be addressed before solving Problem 4:

(1)
The actual state trajectories of neighbors x_i−(τ|t_k) cannot be acquired in advance
(2)
The exact value of disturbance w_i(τ|t_k) cannot be obtained beforehand

For the former issue, we introduce the assumed predictive state trajectories replacing actual ones and employ the compatibility constraints to limit the deviation between the two trajectories, thereby ensuring the convergence of the overall multi-UAV system. For the latter issue, we propose a prediction method to estimate the target’s states within the control horizon, which helps to compensate the disturbances caused by target maneuvering. All detailed analysis and design will be presented in the next section.

3. Design and Analysis of DMPC Cooperative Guidance Scheme

Based upon the previous studies on how to implement synchronous DMPC in cooperative guidance [24, 27, 29], in this section, we further present the associated constraints and terminal ingredients to ensure the convergence of the overall multi-UAV system. Additionally, our work also achieves both obstacle avoidance and cooperative interception, which has not yet been addressed in relevant researches.

3.1. Assumed Predictive State Trajectories and Prediction for System Disturbances

In order to synchronously calculate the control action, each UAV needs to know the predictive state trajectories of its neighbors according to (14) and (17). However, since any UAV cannot obtain its actual state trajectory before solving the optimization problem (Problem 4), an assumed predictive state trajectory is needed as a substitute.

To distinguish the two different trajectories, we denote the actual (optimal) control inputs as and the assumed control inputs as . The actual predictive state trajectory [30] refers to the system state trajectory obtained by implementing the optimal control inputs and is denoted as , while the assumed predictive state trajectory is obtained by implementing .

The assumed control inputs are constructed as (19), which consist of the optimal control inputs at the previous sampling instant, i.e.,

, and the virtual control inputs generated by the auxiliary controller, i.e.,

. The auxiliary controller is the crucial guarantee of the system stability and will be designed in Section 3.2.

()

Accordingly, the assumed predictive state trajectory can be represented as

()

In which, is the system state obtained by implementing .

Applying the assumed state trajectories, UAVs are able to synchronously compute control actions as long as their neighbors send the assumed trajectories to them in advance; accordingly, the stage cost will be rewritten as follows:

()

However, the introduction of assumed state trajectories induces the uncertain deviation from the actual ones; in order for eliminating the effect of such deviation and ensuring the convergence of the overall system, a compatibility constraint will be given in the following.

According to (21), the only assumed state variable involved in stage cost is x_i2; thus, the deviation between the assumed predictive state trajectory and the actual one is defined as

. Then, the compatibility constraint is given by

()

Wherein |N_i| is the number of the neighbors of M_i, , , and γ_i ∈ (0, 1) is the preset scalar.

By employing compatibility constraints, the action taken by the UAV will not deviate significantly from that it planned and told its neighbors, and the role of which in ensuring the convergence of the overall system will be detailed in Section 3.3.

Due to the absence of interaction like that between the UAV and its neighbors, the UAV is unable to receive the predictive state trajectory from the target, so the only means to acquire the future states of the target is via prediction. From equations (1) and (5), the disturbances in system (9) are caused by the change of the target’s flight path angle; hence, the prediction object is chosen as e = θ_T.

For the prediction object, we assume the following.

Assumption 5. e is N-order differentiable on interval [t_k−N+1, t_k + T].

Assumption 6. e and its arbitrary-order derivatives are bounded.

Applying Assumptions 5 and 6, the following theorem can be derived.

Theorem 7. Given (t_k−N+1, e(t_k−N+1)),⋯,(t_k, e(t_k)), there exist α₀, α₁, ⋯, α_N−1 such that, for any i = 0, 1, ⋯, N − 1, and , where

()

whose proof follows.

Proof of Theorem 7. Using Taylor’s mean value theorem and Assumption 5, for ∀τ ∈ [t_k−N+1, t_k + T], there holds

()

Here, is the N − 1-order Lagrange remainder, and is a certain value between τ and t_k.

Let Δ_i = t_k−i − t_k, i = 0, 1, ⋯, N − 1. Constructing matrix

()

and vectors

()

yields

()

Let

()

Then, we obtain Ξ · α − e = Ξ · Ξ⁻¹e − e = 0; that is, for any i = 0, 1, ⋯, N − 1,

. Moreover, constructing

yields e(τ) = τ · β + R_N−1(τ − t_k) and

()

Applying Assumption 6, we get ; thus, Theorem 7 holds.

From Theorem 7, if T is set small, (26) and (31) can be used for predicting the value of e within the control horizon, and the derivative of e can be predicted with

()

Then, using (1), (3), and (5), we can calculate the predictive disturbances w_i(τ|t_k).

Remark 8. According to Theorem 7, by updating the observation data in the manner of sliding window, the above designed prediction method can provide a relatively accurate estimation and offset the effect induced by the disturbances within a short horizon. Therefore, the estimation error and the associated robustness constraints [38] will not be discussed specifically in the following sections.

3.2. Design of the Auxiliary Controller, Terminal Ingredients, and Obstacle Avoidance Constraints

Avoidance of obstacles or no-fly zones is the primary assurance for safely accomplishing the interception tasks. Nevertheless, it is rarely studied in previous literature on cooperative guidance, which is mainly because the associated problem cannot be integrated into the framework of the traditional control theory. In this subsection, we tackle this issue by employing the obstacle avoidance constraints under DMPC.

According to the traditional VO model depicted in Figure 2, the UAV is able to avoid the obstacle as long as its flight path angle meet:

()

Based on (34), we define

()

and provide the following theorem.

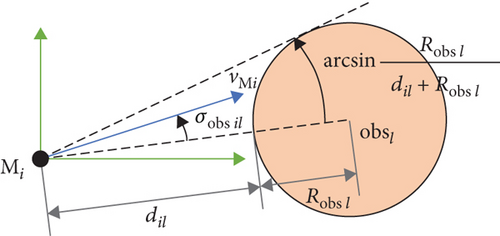
Theorem 9. Suppose there exists t^∗ > t such that d_il(t^∗) = 0. If there are d_il(τ) > 0 and f_il(τ) < 0 for any τ ∈ [t, t^∗), then the sufficient condition for the UAV to successfully avoid obstacles at t^∗ is as follows: holds for any τ ∈ [t, t^∗).

Proof of Theorem 9. Under the condition of Theorem 9, there is

()

Integrating (36) from τ to t^∗ yields

()

Namely,

()

Following the monotonicity of ln(·) and applying f_il(τ) < 0 yields

()

According to (34), the UAV is able to avoid the obstacle at t^∗, which completes the proof.

Based on Theorem 9, the obstacle avoidance constraint and its triggering condition are derived as follows:

()

where

()

Figure 3 shows the difference between the obstacle avoidance constraints adopted by refs. [32, 33] and those designed in this paper. By employing the latter ones, the feasible region is significantly augmented, and the saturation of normal acceleration is alleviated. Besides, according to (40), the obstacle avoidance constraint is directly imposed on the control input a_Mi, so we can redefine the admissible set of the control inputs as

()

Obviously,

is a compact set, and we suppose

()

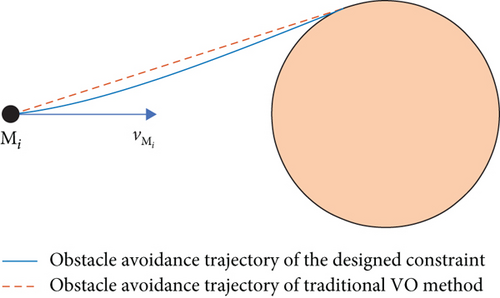
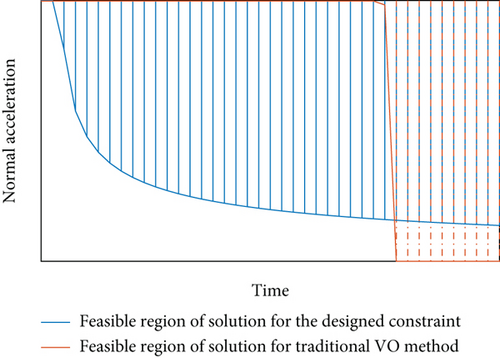
Thereupon, the design of obstacle avoidance constraints is completed.

For a conventional MPC problem, the auxiliary controller and other terminal ingredients are of great significance in ensuring the recursive feasibility and system stability; nonetheless, in most studies on DMPC cooperative guidance [27–29], their development remains a challenging issue.

For the auxiliary controller and terminal ingredients, the following requirements should be satisfied [30, 31].

Definition 10. The terminal set Ω_i(t_k) and the auxiliary controller are such that for any x_i(t|t_k) ∈ Ω_i(t_k) and τ ≥ t, by implementing

()

In Definition 10, conditions (45)–(47) represent the positive invariance, control input admissibility, and local convergence, respectively. Based on the above, we design the terminal ingredients and the auxiliary controller as follows.

The terminal cost is defined as

()

where x_ri(τ) is the reference trajectory, selected as

()

The terminal set is given as

()

The auxiliary controller is designed in the form of

()

Remark 11. In this paper, the local convergence of each UAV subsystem is mainly guaranteed by the terminal cost and the auxiliary controller, so the terminal region can be determined conservatively by setting Λ_1i and Λ_2i large. If a less conservative terminal region is required, Λ_1i and Λ_2i should be properly determined adopting methods proposed in ref. [36, 37]. Besides, different from ref. [39] which adopts dual-mode MPC strategy, our strategy is the same as ref. [30]; i.e., the control action will be obtained by solving the optimization problem regardless of whether the states are inside the terminal region or not, rather than applying the auxiliary controller as the actual control action.

In order for making the above items meet the conditions in Definition 10, the following assumption is required.

Assumption 12. Given weighting scalars λ_1i and λ_2i (in stage cost (17)) and μ_i (in terminal cost (48)), there exist positive scalars ρ_1i, ρ_2i, k_1i, and k_2i such that (53)–(55), and there always exists an auxiliary controller satisfying for any x_i(τ|t_k) ∈ Ω_i(t_k).

()

Remark 13. In some cases, the above assumption may not hold due to the contradiction between (46) and (54), especially when the obstacle avoidance constraints in (40) are triggered. The priority in these cases is to ensure that condition (46) is met, while as a cost, the convergence of the overall system may be broken and restored soon after the above contradiction disappears.

Now, the design of auxiliary controller and terminal ingredients is completed. By substituting the terminal, compatibility, and obstacle avoidance constraints into Problem 4, the optimization problem to be solved by each UAV can be expressed as follows.

Problem 14. At sampling instant t_k, given the current state of M_i, i.e., x_i(t_k), the assumed predictive state trajectories of the neighbors of M_i, i.e., , τ ∈ [t_k, t_k + T], the predictive disturbances w_i(τ|t_k), find the optimal control inputs.

()

subject to dynamic equation (9), compatibility constraint (22), admissibility constraint of control inputs (considering obstacle avoidance) (57), and terminal set constraint (58).

()

wherein,

()

3.3. Convergence Analysis of the Multi-UAV System under DMPC

As Problem 14 is constructed following the common practices of MPC, the convergence analysis of the multi-UAV system adopting DPMC cooperative guidance scheme will be carried out in two steps:

(1)
Analysis of recursive feasibility: under auxiliary controller (51) and (52) and with Assumption 5, all the conditions in Definition 10 will be satisfied, and the optimization problem (Problem 14) is feasible at each sampling instant (see Theorem 15)
(2)
Analysis of closed-loop stability: employing compatibility constraint (22) and condition (47), the multi-UAV system using , τ ∈ [t_k, t_k+1) as the real-time guidance command is exponentially stable (see Theorem 16)

The associated theorems and their proofs are given as follows.

Theorem 15. Let the terminal cost and terminal set be given as in (48) and (50); suppose Assumption 12 holds, x_i(t|t_k) ∈ Ω_i(t_k), and Problem 14 is feasible at t_k−1. Then, using auxiliary controller (51), (52), and assumed control inputs (19),

(a)
for any τ ≥ t, the requirements in Definition 10 are satisfied
(b)
the optimization problem (Problem 14) is feasible at t_k

Proof of Theorem 15 (for ease of derivation, we omit “(τ)” or “(τ|tk)” in (60)–(66)). According to Assumption 12, the auxiliary controller belongs to the admissible set of control inputs, so condition (46) is met.

Under auxiliary controller (51) and (52), according to dynamic equation (9), there are

()

Applying (54), (60), and (61) yields

()

Thus, for any τ ≥ t, condition (45) is met.

Applying inequality

()

the condition (47) holds if

()

Substituting (55), (62), and (63) into yields

()

According to (66), inequality (65) holds, and condition (47) is satisfied. Thereupon, conclusion (a) holds.

Since the optimization problem (Problem 14) is feasible at t_k−1, the optimal control inputs and the optimal terminal states at t_k−1 are such that and .

Consider the assumed control inputs at t_k, whose corresponding predictive state trajectory satisfies (20). It implies that, for any τ ∈ [t_k, t_k−1 + T), by implementing inputs (following the invariance property of , Ω_i(t_k)), there are

()

Then, according to Definition 10, for any τ ∈ [t_k−1 + T, t_k + T), by implementing auxiliary controller , (57), (58), and (69) hold; that is, for the assumed control inputs , τ ∈ [t_k, t_k + T), all the constraints in Problem 14 are satisfied; thus, is a feasible solution of Problem 14 at t_k, and conclusion (b) holds.

Theorem 16. For the multi-UAV system, each UAV solves the optimization problem (Problem 14) at sampling instant t_k. Suppose Theorem 15 holds for any sampling instant after t_k. Then, by implementing the real-time guidance commands , the guidance error, the angle tracking error, and the consistency error for multi-UAV system will converge to zero.

Proof of Theorem 16. For the multi-UAV system, the Lyapunov function is selected as

()

If we choose as a transitional solution at t_k+1, then, following (20), there is

()

Applying condition (47) with x_i(t|t_k) being , then, (72) holds for any τ ≥ t_k + T

()

Integrating (72) from t_k + T to t_k+1 + T yields

()

Define . Employing compatibility constraint (22), we can obtain inequality (74) and (75) (“(τ|t_k)” and “(t_k)” are omitted)

()

Ulteriorly,

()

Substituting (73) and (76) into (71) yields

()

Thus, if Theorem 15 holds for any sampling instant after t_k, the multi-UAV system is exponentially stable, and Theorem 16 holds.

Thereupon, we have completed the design and analysis of the cooperative guidance scheme based on DMPC. The next section will mainly focus on the implementation of the proposed cooperative guidance scheme.

4. Implementation of DMPC Cooperative Guidance Scheme

In this section, the particle swarm optimization (PSO) algorithm is introduced to solve the optimization problem (Problem 14), and then, the detailed implementation process of DMPC cooperative guidance scheme is presented.

4.1. Solving Procedure Based on Particle Swarm Optimization Algorithm

Unlike traditional control methods with analytical expressions for the control inputs, DMPC is an optimization-based control method which relies on an efficient optimization algorithm to find the optimal control actions at each sampling instant.

However, due to the constraint of nonlinear system dynamic (9), the solving procedure of Problem 14 involves large amounts of integral operations, and therefore, appropriate simplification is needed. To this end, the approximation of the system dynamic is carried out based on explicit Euler’s method.

Suppose N_c = T/δ and N_c ∈ ℤ⁺, where ℤ⁺ is the positive integer set. Then, the system within control horizon can be approximated by

()

Equation (78) implies that the system evolves in the manner of zero-order holding over each sampling interval within the control horizon; thus, the control inputs and the disturbances can be represented in the form of sequences:

()

Applying the approximation of the actual system (78), the objective function of Problem 14 is approximately equal to

()

where X_i(t_k) = [x_i(t_k+1|t_k), x_i(t_k+2|t_k), ⋯, x_i(t_k + T|t_k)].

All the constraints of Problem 14 can be approximated in a same manner and further transformed into the constraints imposed on

. Take the compatibility constraint as an example, which can be transformed into the constraint given by

()

where the upper and lower bounds of

, i.e.,

and

, can be derived from (22) and dynamic equation (9).

()

Similarly, the terminal set constraint can be transformed into

()

with

and

being calculated in the same manner as shown in (83) and (84). In summary, for any l = 0, 1, ⋯, N_c − 1,

is constrained by

()

where

()

with

and

being −∞ and +∞, respectively.

Based on the above processing, each UAV solves Problem 14 at sampling instant t_k using particle swarm optimization (PSO) algorithm. PSO algorithm is a heuristic optimization algorithm widely used in UAV decision-making problems [40], whose iterative process relies on the searching experience of all the particles in the swarm, with no need for calculating the gradient of each optimization variable.

In PSO, each particle corresponds to a solution of the optimization problem, whose position can be represented as with the same dimension as U_i(t_k). denotes the j, l-th element of .

In the same manner, the velocity of the particle is denoted as

, which determines the updating direction and step size of each particle in a single iteration, as shown in

()

Commonly, the velocity of the particle is simultaneously affected by its ever-reached best position

, the global best position P^gb, and its current velocity, which is formulated as

()

where ω represents the inertia weight, which can be preset or adjusted in iteration; η₁ and η₂ are the acceleration constants given a priori; and ξ₁ and ξ₂ are the random numbers within (0, 1).

and P^gb satisfy

and

, respectively.

is the fitness function defined as (90), for evaluating the fitness of each particle at its current position.

()

The velocity of each particle is also limited by the maximum velocity, and there is

()

Additionally, in order to guarantee the feasibilities of particles in each iteration, we need to check the positions of the particles to prevent them from violating constraints as given in (57), (84), and (85). The check and correction will be made as follows.

In Algorithm 1,

and u_i(t_k+l|t_k) are corrected using the saturation function as follows:

()

where

()

Thereupon, the complete pseudocode of the PSO algorithm for Problem 14 is given as follows.

Algorithm 1: Pseudocode of the position correction for each particle.

1: for l:= 0 to N_c − 1do
2: Calculate σ_Mi(t_k+l|t_k) and using (3) and (4)
3: Calculate ,,,,
,
, according to (40)~(44) and ~(87)
4: Correct applying , where
,
5: Recalculate u_i(t_k+l|t_k) according to (4)
6: Correct u_i(t_k+l|t_k) applying , where
,
7: Let , j = 1, 2 be the corrected u_i(t_k+l|t_k)
8: Calculate x_i(t_k+l+1|t_k) applying (78).
9: end for
10: Return the corrected and X_i(t_k)

Using Algorithm 2, we can obtain the optimal control inputs and the real-time guidance command of M_i at sampling instant t_k. Based on which, the complete implementation process of the DMPC cooperative guidance scheme will be presented in the next subsection.

Algorithm 2: Pseudocode of PSO algorithm.

1: // Initialization
2: Set the parameters of the algorithm: ω, η₁, η₂, V^max(j, l), population size Ps, the maximum number of iterations K, and maximum number of invalid iterations K^′.
3: Randomly generate the initial positions of particles , h = 1, 2, ⋯, Ps, which include the assumed control input sequence .
4: Randomly generate the initial velocities of particles .
5: Initialize the current iteration as iter = 0 and number of invalid iterations as iter^′ = 0.
6: // Main loop
7: while iter < K∧iter^′ < K^′do
8: for h:= 1 to Psdo
9: Correct using (91)
10: Correct and obtain x_i(t_k+l|t_k), l = 1, ⋯, N_c with algorithm 1
11: Calculate using (90)
12: Determine the individual best position
13: end for
14: Determine the global best position P^gb
15: Record the global best fitness value at current iteration Rec^(iter) = F^gb
16: if iter > 1∧Rec^(iter) = Rec^{(iter − 1)}then
17: iter^′ = iter^′ + 1
18: else
19: iter^′ = 0
20: for h:= 1 to Psdo
21: Update the position of particle as , using (88)
22: Update the velocity of particle as , using (89)
23: end for
24: Update the current iteration as iter = iter + 1
25: end while
26: Determine the optimal control input sequence at t_k as
27: //Results
28: return

4.2. Implementation of DMPC Cooperative Guidance Scheme

In order to improve the terminal guidance effect of each UAV, we adopt two strategies as follows.

(a)
Variable control horizon

As the final time approaches, the control horizon of each UAV will be adjusted as

()

(b)
Variable sampling period

If the time-to-go is smaller than the current sampling period, then, in order to obtain the actual guidance effect at final time, we let sampling period be

()

The DMPC cooperative guidance scheme is implemented in two stages, as follows.

Now the implementation of the DMPC cooperative guidance scheme is completed.

5. Numerical Simulation

In order to demonstrate the effectiveness of the DMPC cooperative guidance scheme, the numerical simulations are conducted in this section. The simulation scenario is set as four UAVs with fixed communication topology attacking a single maneuvering target, and in different cases, the target adopts diverse maneuvering strategies. The simulations will be carried out in the cases with obstacles and cases without obstacles, and the methods proposed in recent studies [16, 24] will be used for comparison.

In all of simulations, the communication topology among the UAVs is shown in Figure 4, the initial positions, velocities, and the admissible inputs of the UAVs are given in Table 2, and the initial position and flight path angle of the target are set to x_T(0) = 15000 m, y_T(0) = 15000 m, and θ_T(0) = −135^∘; all the scalars and parameters of Algorithm 2 and Algorithm 3 are given as follows.

Table 2. Initial states of UAVs.

Index	Initial position (m)	Initial velocity (m/s)	Initial flight path angle (°)	Maximum and minimum normal overload (m·s^-2)	Maximum and minimum tangential acceleration (m·s^-2)
1	(-6000, 0)	400	45	200, -200	200, -200
2	(0, -6000)	400	45	200, -200	200, -200
3	(6000, -6000)	400	67.5	200, -200	200, -200
4	(-6000, 6000)	400	22.5	200, -200	200, -200

Algorithm 3: DMPC cooperative guidance scheme.

Offline stage: For each UAV M_i, give (initial) sampling period δ, control horizon T, maximum data size of the observation data N, weighting scalars for stage cost: λ_1i, λ_2i, weighting scalars for terminal cost: ρ_1i, ρ_2i, μ_i, scalars for terminal set constraint and compatibility constraint: Λ_1i, Λ_2i, γ_i, and parameters for auxiliary controller: k_1i, k_2i. Those scalars or parameters are supposed to satisfy assumption 12.
Online stage: At the initial time t₀, each UAV M_i sets as and as , initializes the observation data for the target as e(t₀) = θ_T(t₀), sends to the neighbors and receives from them, τ ∈ [t₀, t₀ + T).
(I) At sampling instant t_k, k ≥ 0, for each UAV M_i
(a) predict w_i(τ|t_k), τ ∈ [t_k, t_k + T) using the method proposed in section 3.1.
(b) compute υ_i(t_k) according to (23), (24).
(c) solve optimization problem 14 using algorithm 2, to obtain , τ ∈ [t_k, t_k + T).
(II) Over time interval t ∈ [t_k, t_k+1), for each UAV M_i
(a) implement the real-time guidance command , t ∈ [t_k, t_k+1) and sample the system states.
(b) update the observation data, by adding e(t_k+1) = θ_T(t_k+1). If there is k + 1 ≥ N, then delete e(t_k+1−N).
(c) calculate the assumed control inputs and the corresponding state trajectories, τ ∈ [t_k+1, t_k+1 + T), according to (19), (51), (52), and (20).
(d) sends to M_j and receives from M_j, j ∈ ℕ_i
(III) Return to (I), update T and δ using (94) and (95). If the updated δ is smaller than the preset one, then stop control and sample system states at t_k + δ.

For Algorithm 2, Ps = 5, K = 20, K^′ = 5, η₁ = η₂ = 0.1, ω_max = 0.8, ω_min = 0.2, and ω = ω_max − iter²(ω_max − ω_min)/(K²).

For Algorithm 3, (initial) δ = 0.1 s, (initial) T = 0.3 s, N = 8, λ_1i = 1, λ_2i = 1, ρ_1i = 10, , μ_i = 2, Λ_1i = 25, Λ_2i = 25, γ_i = 0.1, k_1i = 0.36, and k_2i = 2.

5.1. Scenario I: Without Obstacles

In this subsection, the comparison simulations are carried out in cases (Cases 1 and 2) without no-fly zones or obstacles. To validate the advantages of the DMPC cooperative guidance scheme (DMPC-CG), it will be compared with the fixed-time cooperative guidance law (FxTCG) proposed in [16]. The velocities and the maneuvering inputs of the target in Case 1 and Case 2 are given as follows.

Case 1. v_T = 200 m/s, and a_T(t) = 0 m/s².

Case 2. v_T = 500 m/s, and a_T(t) = 5tcos(0.4t) m/s².

Case 1 simulates the scenario of intercepting a low-speed, nonmaneuvering target, while Case 2 simulates the interception scenario against a high-speed target that adopts snake maneuvering tactics.

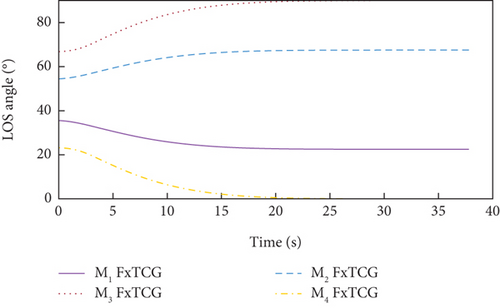
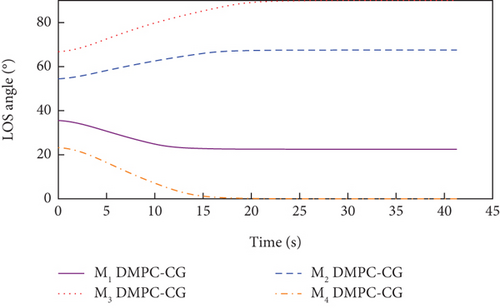
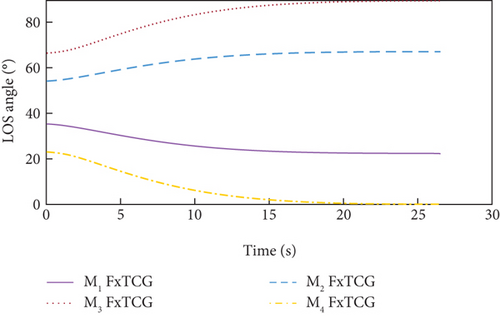
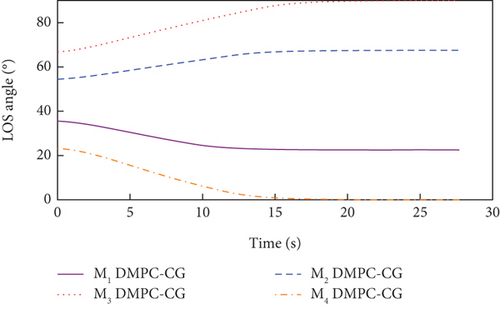
In both cases, the desired LOS angles of the UAVs are set to q_d1 = 22.5^∘, q_d2 = 67.5^∘, q_d3 = 90^∘, and q_d4 = 0^∘, respectively.

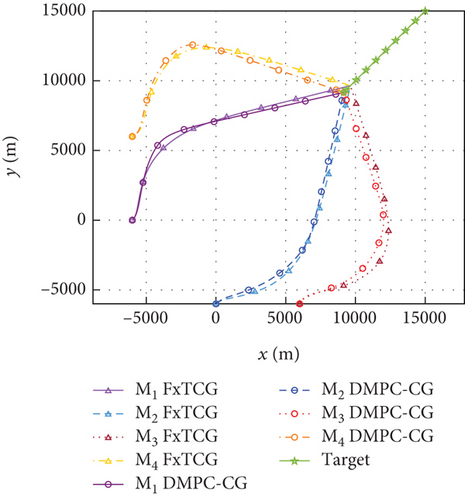
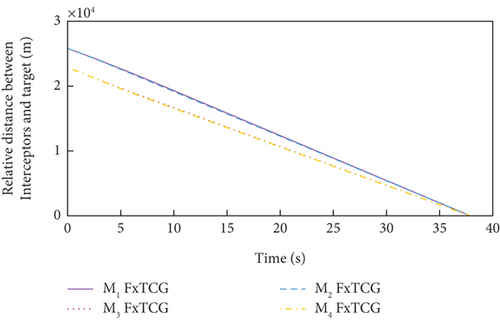
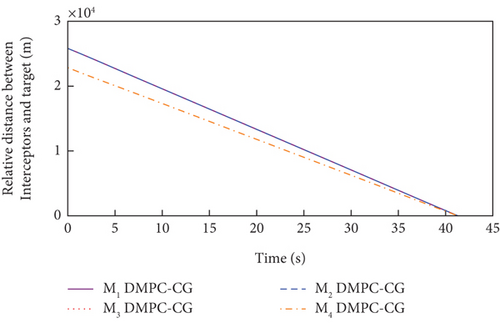
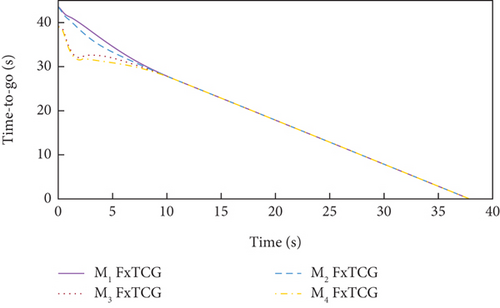
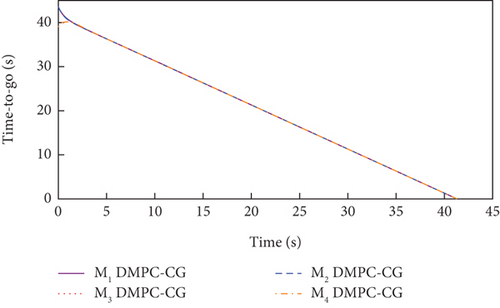
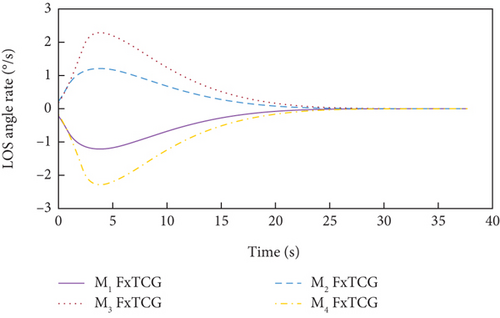
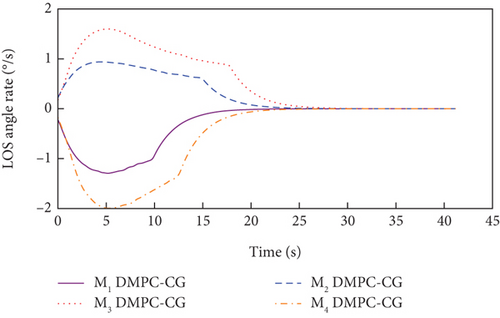
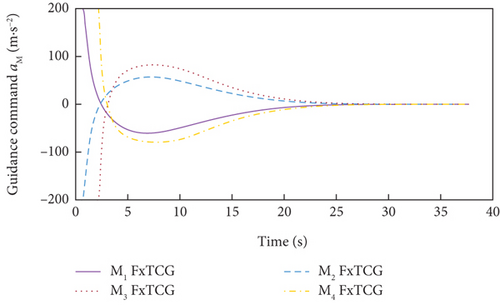
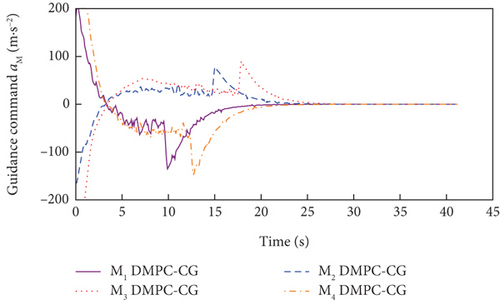
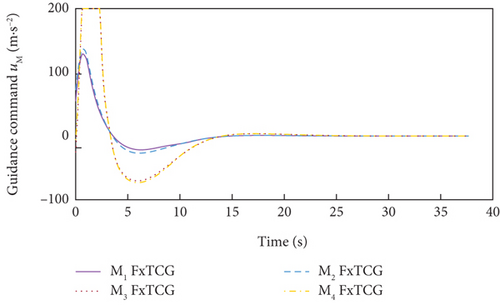
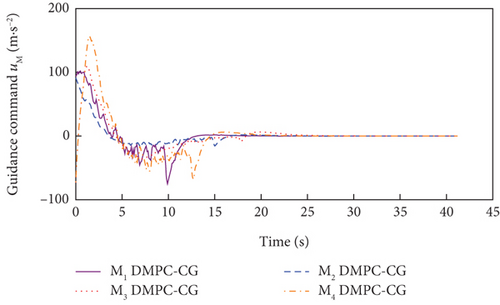
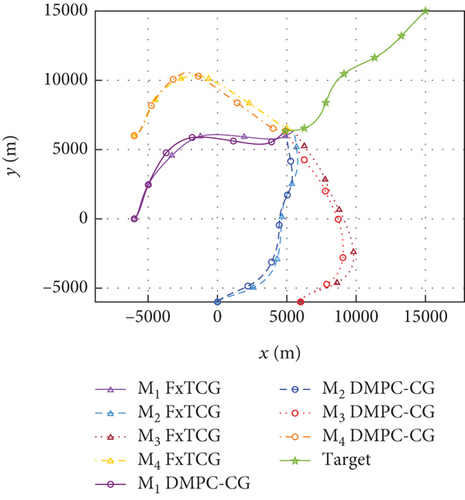
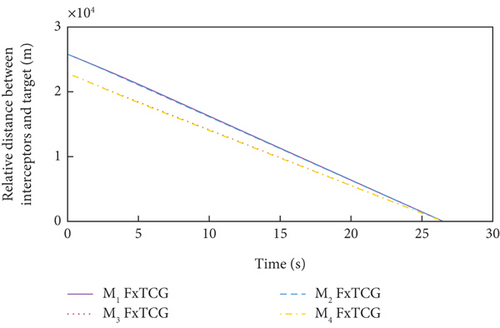
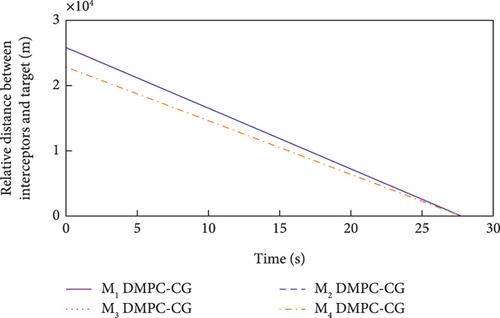
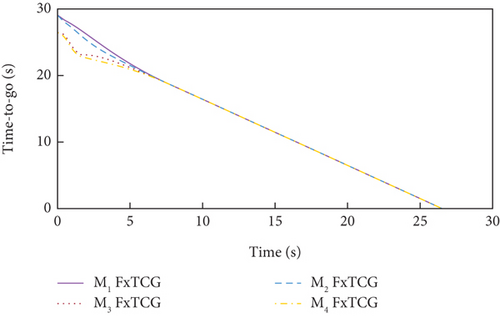
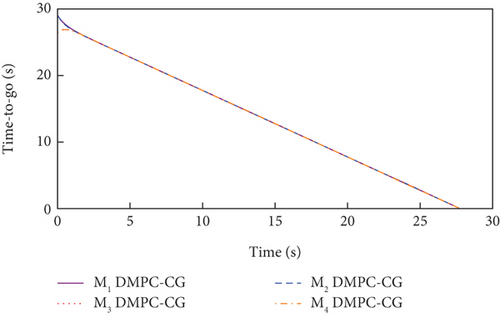
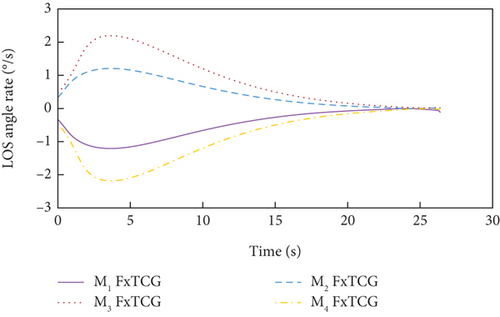
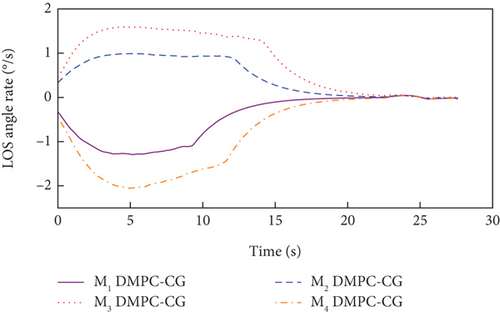
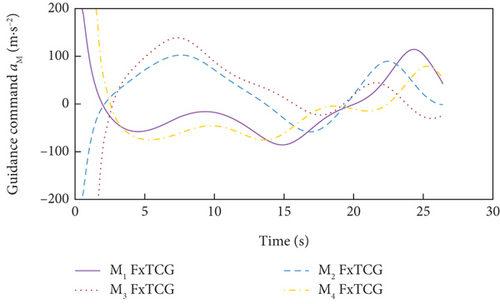
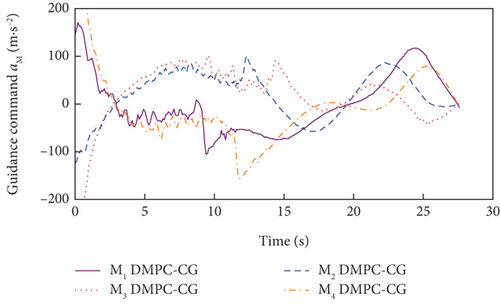
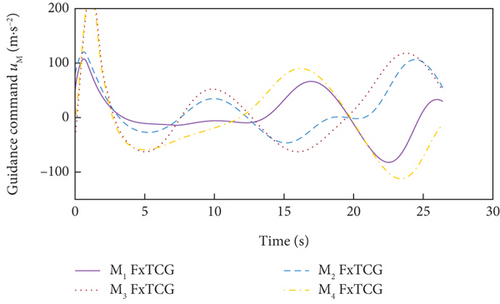
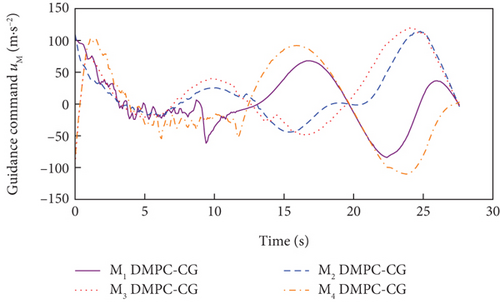
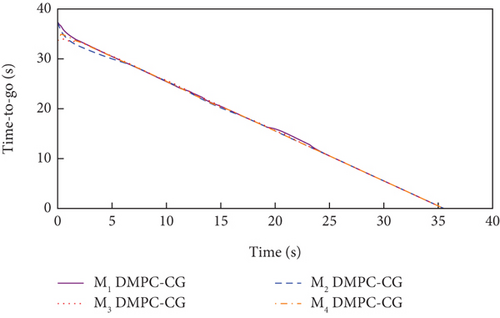
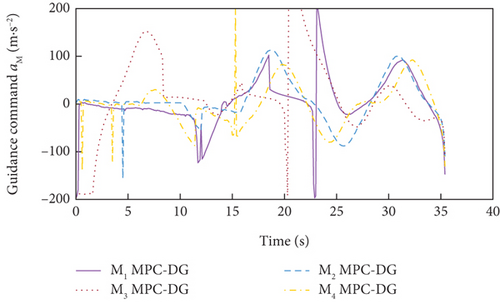
Simulation results under Case 1 and Case 2 are shown in Figure 5 and Table 3 and Figure 6 and Table 4, respectively. From Figures 5(a)–5(c) and 6(a)–6(c), it can be seen that using either method, all the UAVs hit the target with smooth flight trajectories. However, significant differences between the two methods can be observed from Figures 5(d)–5(m) and 6(d)–6(m). Figures 5(d)–5(g) and 6(d)–6(g) show that, with either method, the time-to-go of all the UAVs can reach a consensus within a finite time, and the LOS angles ultimately converge to their desired values. However, under DMPC-CG, the time spent before reaching the consensus is about 2 s, which is shorter than that under FxTCG. In Figures 5(j)–5(m) and 6(j)–6(m), the guidance commands exhibit rapid changes in the initial phase of guidance under DMPC-CG, but the duration of acceleration saturation is largely shortened. In contrast, under FxTCG, the saturation of acceleration lasts longer, though the curves of guidance commands are smoother. Besides, according to Tables 3 and 4, the DMPC-CG achieves smaller miss distances and convergence errors in LOS angles than the FxTCG in both cases. Therefore, the proposed DMPC cooperative guidance scheme can achieve cooperative interception with advantageous performance than the fixed-time cooperative guidance law in cases without obstacles.

Table 3. Simulation results for Case 1.

Index	FxTCG			DMPC-CG
Index	Miss distance (m)	Error of LOS angle (°)	Interception time (s)	Miss distance (m)	Error of LOS angle (°)	Interception time (s)
1	7.07 × 10⁻⁴	1.57 × 10⁻⁴	37.8654	1.17 × 10⁻⁶	4.94 × 10⁻⁵	41.3079
2	7.03 × 10⁻⁴	1.57 × 10⁻⁴	37.8654	1.08 × 10⁻⁵	7.57 × 10⁻⁶	41.3079
3	5.32 × 10⁻⁵	2.62 × 10⁻⁴	37.8654	4.09 × 10⁻⁵	4.59 × 10⁻⁵	41.3079
4	6.20 × 10⁻⁵	2.61 × 10⁻⁴	37.8654	6.44 × 10⁻⁶	3.16 × 10⁻⁵	41.3079

Table 4. Simulation results for Case 2.

Index	FxTCG			DMPC-CG
Index	Miss distance (m)	Error of LOS angle (°)	Interception time (s)	Miss distance (m)	Error of LOS angle (°)	Interception time (s)
1	0.0210	0.127	26.5123	3.97 × 10⁻³	9.49 × 10⁻³	27.7539
2	2.20 × 10⁻³	0.0352	26.5122	4.12 × 10⁻⁴	6.27 × 10⁻³	27.7539
3	3.85 × 10⁻³	0.0517	26.5123	1.76 × 10⁻³	5.64 × 10⁻³	27.7539
4	5.82 × 10⁻³	0.0542	26.5124	4.23 × 10⁻³	0.0251	27.7539

5.2. Scenario II: With Obstacles

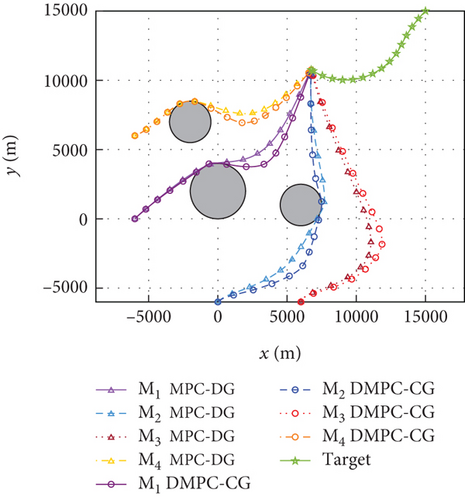
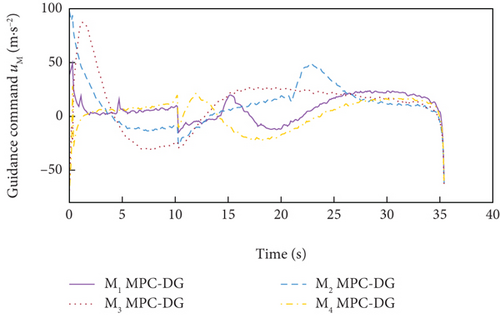
In order to further demonstrate the effectiveness of the proposed DMPC cooperative guidance scheme in the presence of obstacles, simulations are conducted in this subsection (Cases 1 and 2). The proposed DMPC-CG will be compared with another MPC-based distributed guidance method (MPC-DG) [24]. As MPC-DG is designed to achieve time-constrained guidance in consideration of obstacle avoidance, the comparison will mainly focus on the performance of guidance, coordination of impact times, and obstacle avoidance. The control of LOS angles will be analyzed as an additional property of DMPC-CG.

In Cases 1 and 2, the obstacles are randomly dispersed, as shown in Table 5. The desired LOS angles of UAVs are set to q_d1 = 45^∘, q_d2 = 67.5^∘, q_d3 = 90^∘, and q_d4 = 22.5^∘, and the velocities and maneuvering inputs of the target are given as follows.

Case 1. v_T = 300 m/s

()

Case 2. v_T = 300 m/s, and a_T(t) = 100cos(0.5t) m/s².

Table 5. Obstacles’ positions and radiuses.

Index of case	Index of obstacle	Center position (m)	Radius (m)
3	1	(0, 2000)	2000
	2	(6000, 1000)	1500
	3	(-2000, 7000)	1500

4	1	(1000, 0)	1400
	2	(5000, 1000)	1000
	3	(7500, -1000)	1500
	4	(-1000, 2000)	1000
	5	(0, 7000)	800
	6	(4000, 5000)	1200
	7	(11000, 1000)	900

For ease of comparison, the objective function designed in ref. [24] is given as follows:

()

In (97), and are the weighting scalars of the stage cost, while is the weighting scalar of the terminal cost. The sampling period, prediction horizon, and other parameters are set to be the same as those in ref. [24].

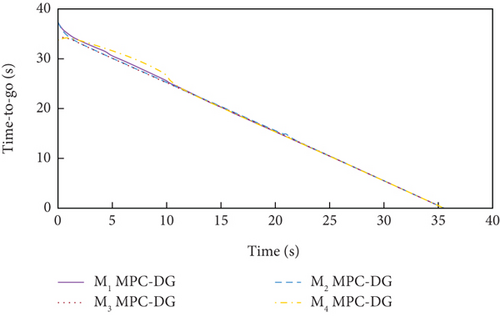
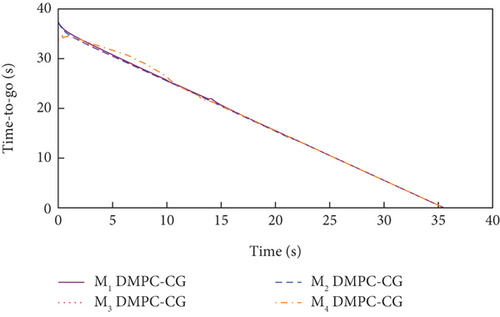
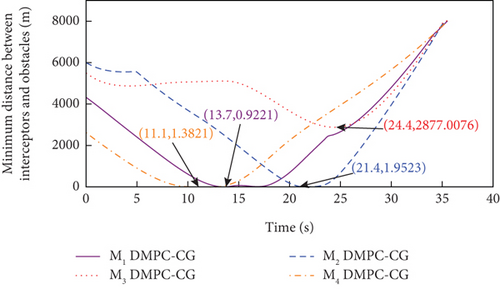
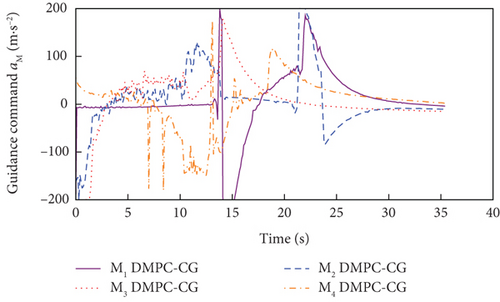
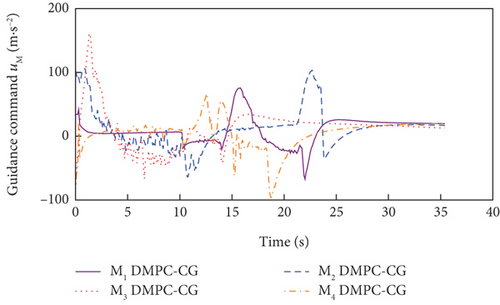
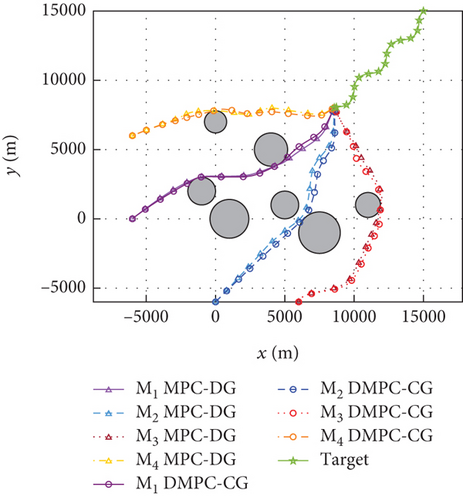
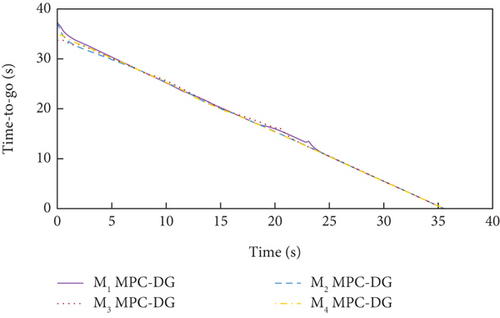
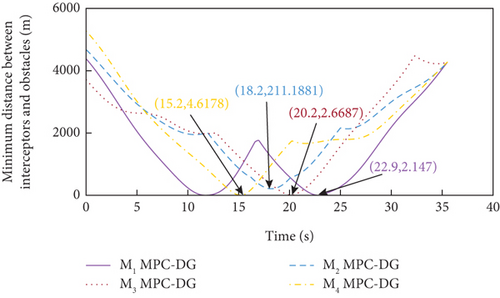
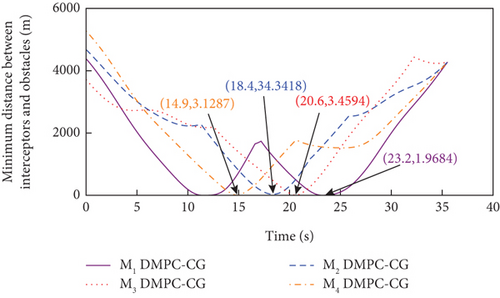
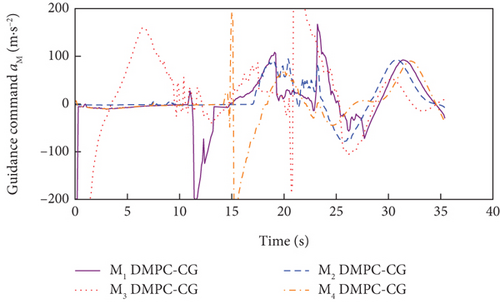
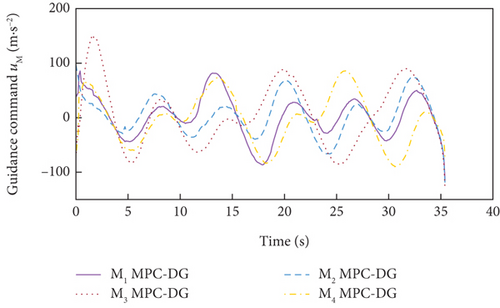
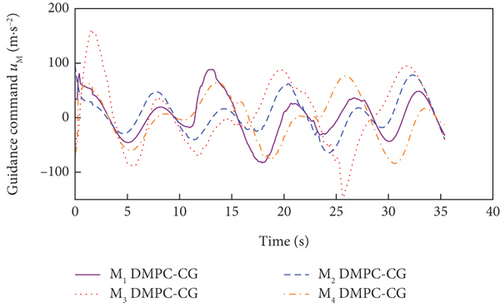
Simulation results for Case 1 and Case 2 are shown in Figure 7 and Table 6 and Figure 8 and Table 7, respectively. From Figures 7(a), 7(d), and 7(e) and 8(a), 8(d), and 8(e), it can be observed that using these two methods, all the UAVs successfully avoid collisions with obstacles and fly towards the target with smooth trajectories. From Figures 7(b) and 7(c) and 8(b) and 8(c), it can be seen that once a UAV takes a maneuver to avoid obstacles, the consensus on time-to-go is briefly broken, but under either method, the consensus will soon be restored and maintained for most of the time during guidance. Although both methods basically meet the requirements of the time-constrained cooperative guidance with obstacle avoidance based on the above analysis, there are still differences in guidance performance between the two methods. According to Tables 6 and 7, the DMPC-CG achieves smaller miss distance and consistency errors in impact time for both cases, which largely depends on the rational design of the objective function and the related constraints.

Table 6. Simulation results for Case 1.

Index	MPC-DG			DMPC-CG
Index	Miss distance (m)	Error of LOS angle (°)	Interception time (s)	Miss distance (m)	Error of LOS angle (°)	Interception time (s)
1	2.2121	—	35.5212	1.25 × 10⁻³	0.0216	35.5241
2	2.4485	—	35.5210	3.50 × 10⁻³	8.49 × 10⁻³	35.5241
3	2.1738	—	35.5199	4.19 × 10⁻⁴	4.13 × 10⁻³	35.5241
4	2.3300	—	35.5215	6.71 × 10⁻⁴	0.0166	35.5242

Table 7. Simulation results for Case 2.

Index	MPC-DG			DMPC-CG
Index	Miss distance (m)	Error of LOS angle (°)	Interception time (s)	Miss distance (m)	Error of LOS angle (°)	Interception time (s)
1	2.6746	—	35.5210	0.0146	0.0117	35.5243
2	2.3191	—	35.5213	2.91 × 10⁻³	0.0316	35.5242
3	2.6041	—	35.5219	8.86 × 10⁻³	0.0182	35.5242
4	1.9049	—	35.5184	7.34 × 10⁻⁴	0.0185	35.5245

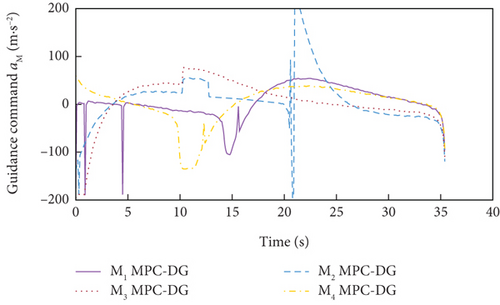
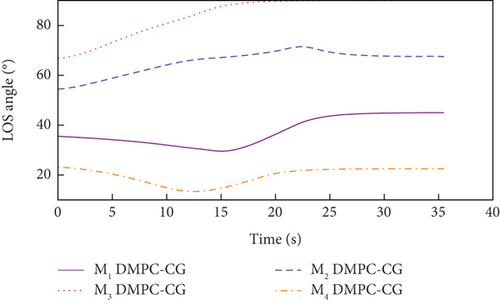
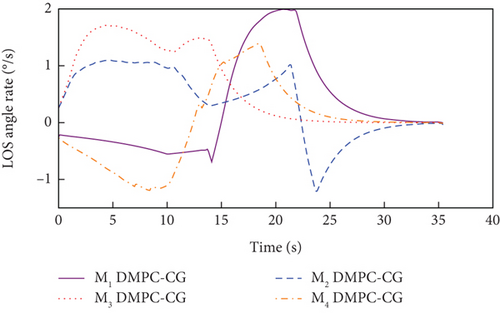
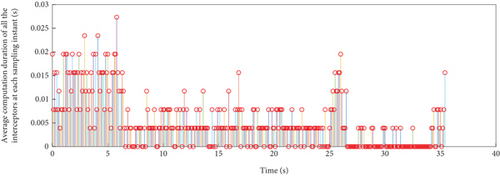
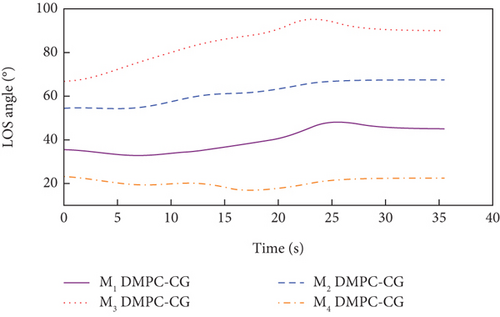
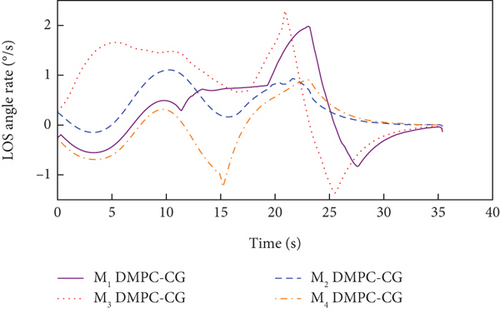
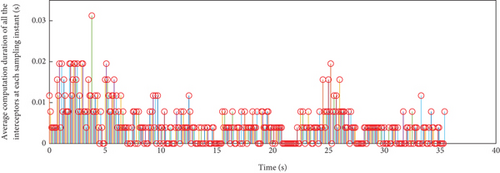
In addition, the curves of LOS angles and LOS angle rates are separately depicted for DMPC-CG in Figures 7(j) and 7(k) and 8(j) and 8(k). It can be seen that the LOS angles and angular rates deviate significantly from their desired values at the beginning and exhibit fluctuations during the guidance process. However, by adopting DMPC-CG, all of them eventually converge to the desired values. Figures 7(l) and 8(l) show the average computation duration under DMPC-CG. At each sampling instant, all the UAVs are able to complete calculations within 0.032 s, with most calculations lasting less than 0.01 s. These results show that the proposed DMPC cooperative guidance scheme is capable of achieving time and angle-constrained cooperative guidance in the presence of obstacles or no-fly zones.

6. Conclusion

This study is concerned with the salvo attack problem for controllable thrust UAVs against a maneuvering target. The guidance scheme is presented based on distributed model predictive control to achieve simultaneous interception at the desired impact angle and no-fly zone avoidance. The guidance scheme proposed in this study is advanced as follows:

(1)
By introducing assumed predictive trajectories, all the UAVs are able to synchronously figure out their acceleration commands utilizing the shared information among the neighbors
(2)
By designing the prediction method and associated constraints, both obstacle avoidance and maneuvering target interception are achieved
(3)
By employing compatibility constraints, terminal set constraints, and auxiliary controller, the convergence of the multi-UAV system is guaranteed
(4)
Using PSO algorithm, the computation efficiency of the optimal acceleration commands is improved

The effectiveness of the method is verified through the numerical simulation. In the next step of our work, the DMPC will be applied to three-dimensional cooperative interception problem with the constraints of terminal angle and obstacle avoidance, and the disturbance observer-based robust DMPC scheme for cooperative guidance against maneuvering target will also be studied.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This research was funded by the Shandong Natural Science (ZR2020MF090).

Open Research

Data Availability

The data used to support the findings of this study are included within the article.

References

1 Gao X., Wang L., Yu X., Su X., Ding Y., Lu C., Peng H., and Wang X., Conditional probability based multi-objective cooperative task assignment for heterogeneous UAVs, Engineering Applications of Artificial Intelligence. (2023) 123, article 106404, https://doi.org/10.1016/j.engappai.2023.106404.
10.1016/j.engappai.2023.106404
Web of Science® Google Scholar
2 Chen Y., Wang J., Shan J., and Xin M., Cooperative guidance for multiple powered missiles with constrained impact and bounded speed, Journal of Guidance, Control, and Dynamics. (2021) 44, no. 4, 825–841, https://doi.org/10.2514/1.G005578.
10.2514/1.G005578
Web of Science® Google Scholar
3 Kumar S. R. and Mukherjee D., Terminal time-constrained nonlinear interception strategies against maneuvering targets, Journal of Guidance, Control, and Dynamics. (2021) 44, no. 1, 200–209, https://doi.org/10.2514/1.G005455.
10.2514/1.G005455
Web of Science® Google Scholar
4 Long T., Cao Y., Sun J., and Xu G., Adaptive event-triggered distributed optimal guidance design via adaptive dynamic programming, Chinese Journal of Aeronautics. (2022) 35, no. 7, 113–127, https://doi.org/10.1016/j.cja.2021.08.005.
10.1016/j.cja.2021.08.005
Web of Science® Google Scholar
5 He S. and Lin D., Adaptive nonsingular sliding mode based guidance law with terminal angular constraint, International Journal of Aeronautical and Space Sciences. (2014) 15, no. 2, 146–152, https://doi.org/10.5139/IJASS.2014.15.2.146, 2-s2.0-84903639862.
10.5139/IJASS.2014.15.2.146
Web of Science® Google Scholar
6 Park B. G., Kwon H. H., Kim Y. H., and Kim T. H., Composite guidance scheme for impact angle control against a nonmaneuvering moving target, Journal of Guidance, Control, and Dynamics. (2016) 39, no. 5, 1132–1139, https://doi.org/10.2514/1.G001547, 2-s2.0-84964832614.
10.2514/1.G001547
Web of Science® Google Scholar
7 Zhao J., Shi S., Chong Y., Feng M., and You H., Distributed cooperative guidance law for multiple missiles with impact angle constraint, Journal of Chinese Inertial Technology. (2018) 26, no. 4.
Google Scholar
8 Jeon I.-S., Lee J.-I., and Tahk M.-J., Impact-time-control guidance law for anti-ship missiles, IEEE Transactions on Control Systems Technology. (2006) 14, no. 2, 260–266, https://doi.org/10.1109/TCST.2005.863655, 2-s2.0-33244497367.
10.1109/TCST.2005.863655
Web of Science® Google Scholar
9 Shiyu Z. and Rui Z., Cooperative guidance for multimissile salvo attack, Chinese Journal of Aeronautics. (2008) 21, no. 6, 533–539, https://doi.org/10.1016/S1000-9361(08)60171-5, 2-s2.0-58149234073.
10.1016/S1000-9361(08)60171-5
Web of Science® Google Scholar
10 Jeon I. S., Lee J. I., and Tahk M. J., Homing guidance law for cooperative attack of multiple missiles, Journal of Guidance, Control, and Dynamics. (2010) 33, no. 1, 275–280, https://doi.org/10.2514/1.40136, 2-s2.0-73949138438.
10.2514/1.40136
Web of Science® Google Scholar
11 Zhao J., Zhou R., and Dong Z., Three-dimensional cooperative guidance laws against stationary and maneuvering targets, Chinese Journal of Aeronautics. (2015) 28, no. 4, 1104–1120, https://doi.org/10.1016/j.cja.2015.06.003, 2-s2.0-84938741483.
10.1016/j.cja.2015.06.003
Web of Science® Google Scholar
12 Sinha A., Kumar S. R., and Mukherjee D., Cooperative integrated guidance and control design for simultaneous interception, Aerospace Science and Technology. (2022) 120, https://doi.org/10.1016/j.ast.2021.107262.
10.1016/j.ast.2021.107262
Web of Science® Google Scholar
13 Li K., Wang J., Lee C. H., Zhou R., and Zhao S., Distributed cooperative guidance for multivehicle simultaneous arrival without numerical singularities, Journal of Guidance, Control, and Dynamics. (2020) 43, no. 7, 1365–1373, https://doi.org/10.2514/1.G005010.
10.2514/1.G005010
Web of Science® Google Scholar
14 Song J., Song S., and Xu S., Three-dimensional cooperative guidance law for multiple missiles with finite-time convergence, Aerospace Science and Technology. (2017) 67, 193–205, https://doi.org/10.1016/j.ast.2017.04.007, 2-s2.0-85018495353.
10.1016/j.ast.2017.04.007
Web of Science® Google Scholar
15 Liu S., Yan B., Zhang T., Dai P., Liu R., and Yan J., Three-dimensional cooperative guidance law for intercepting hypersonic targets, Aerospace Science and Technology. (2022) 129, https://doi.org/10.1016/j.ast.2022.107815.
10.1016/j.ast.2022.107815
Web of Science® Google Scholar
16 Dong W., Wang C., Wang J., Zuo Z., and Shan J., Fixed-time terminal angle-constrained cooperative guidance law against maneuvering target, IEEE Transactions on Aerospace and Electronic Systems. (2022) 58, no. 2, 1352–1366, https://doi.org/10.1109/taes.2021.3113292.
10.1109/TAES.2021.3113292
Web of Science® Google Scholar
17 Zhao J. and Zhou R., Unified approach to cooperative guidance laws against stationary and maneuvering targets, Nonlinear Dynamics. (2015) 81, no. 4, 1635–1647, https://doi.org/10.1007/s11071-015-2096-z, 2-s2.0-84938966685.
10.1007/s11071-015-2096-z
Web of Science® Google Scholar
18 Zhang S., Guo Y., Liu Z., Wang S., and Hu X., Finite-time cooperative guidance strategy for impact angle and time control, IEEE Transactions on Aerospace and Electronic Systems. (2021) 57, no. 2, 806–819, https://doi.org/10.1109/taes.2020.3037958.
10.1109/TAES.2020.3037958
Web of Science® Google Scholar
19 Yu H., Dai K., Li H., Zou Y., Ma X., Ma S., and Zhang H., Three-dimensional adaptive fixed-time cooperative guidance law with impact time and angle constraints, Aerospace Science and Technology. (2022) 123, https://doi.org/10.1016/j.ast.2022.107450.
10.1016/j.ast.2022.107450
Web of Science® Google Scholar
20 Liu S., Yan B., Liu R., Dai P., Yan J., and Xin G., Cooperative guidance law for intercepting a hypersonic target with impact angle constraint, The Aeronautical Journal. (2022) 126, no. 1300, 1026–1044, https://doi.org/10.1017/aer.2021.117.
10.1017/aer.2021.117
Web of Science® Google Scholar
21 Zhang Y., Ma G., and Liu A., Guidance law with impact time and impact angle constraints, Chinese Journal of Aeronautics. (2013) 26, no. 4, 960–966, https://doi.org/10.1016/j.cja.2013.04.037, 2-s2.0-84883135579.
10.1016/j.cja.2013.04.037
Web of Science® Google Scholar
22 Wang X., Li B., Su X., Peng H., Wang L., Lu C., and Wang C., Autonomous dispatch trajectory planning on flight deck: a search-resampling-optimization framework, Engineering Applications of Artificial Intelligence. (2023) 119, https://doi.org/10.1016/j.engappai.2022.105792.
10.1016/j.engappai.2022.105792
Web of Science® Google Scholar
23 Li X., Wang L., Wang H., Tao L., and Wang X., A warm-started trajectory planner for fixed-wing unmanned aerial vehicle formation, Applied Mathematical Modelling. (2023) 122, 200–219, https://doi.org/10.1016/j.apm.2023.05.035.
10.1016/j.apm.2023.05.035
Web of Science® Google Scholar
24 Zhao J., Zhou S., and Zhou R., Distributed time-constrained guidance using nonlinear model predictive control, Nonlinear Dynamics. (2016) 84, no. 3, 1399–1416, https://doi.org/10.1007/s11071-015-2578-z, 2-s2.0-84952668334.
10.1007/s11071-015-2578-z
Web of Science® Google Scholar
25 Jiang Z., Yang X., Zhang Y., Wang C., and Yu H., Three-dimensional guidance approach with obstacle avoidance against maneuvering targets, International Journal of Aerospace Engineering. (2023) 2023, 25, https://doi.org/10.1155/2023/8872166, 8872166.
10.1155/2023/8872166
Web of Science® Google Scholar
26 Jiang H., An Z., Chen S., and Xiong F., Cooperative guidance with multiple constraints using convex optimization, Aerospace Science and Technology. (2018) 79, 426–440, https://doi.org/10.1016/j.ast.2018.06.001, 2-s2.0-85048799365.
10.1016/j.ast.2018.06.001
Web of Science® Google Scholar
27 Zhao J. and Zhou R., Distributed three-dimensional cooperative guidance via receding horizon control, Chinese Journal of Aeronautics. (2016) 29, no. 4, 972–983, https://doi.org/10.1016/j.cja.2016.06.011, 2-s2.0-84979257054.
10.1016/j.cja.2016.06.011
Web of Science® Google Scholar
28 Kang S., Wang J., Li G., Shan J., and Petersen I. R., Optimal cooperative guidance law for salvo attack: an MPC-based consensus perspective, IEEE Transactions on Aerospace and Electronic Systems. (2018) 54, no. 5, 2397–2410, https://doi.org/10.1109/TAES.2018.2816880, 2-s2.0-85044062226.
10.1109/TAES.2018.2816880
Web of Science® Google Scholar
29 Cong M., Cheng X., Zhao Z., and Li Z., Studies on multi-constraints cooperative guidance method based on distributed MPC for multi-missiles, Applied Sciences. (2021) 11, no. 22, https://doi.org/10.3390/app112210857.
10.3390/app112210857
Google Scholar
30 Wang P. and Ding B., Distributed RHC for tracking and formation of nonholonomic multi-vehicle systems, IEEE Transactions on Automatic Control. (2014) 59, no. 6, 1439–1453, https://doi.org/10.1109/TAC.2014.2304175, 2-s2.0-84901441972.
10.1109/TAC.2014.2304175
Web of Science® Google Scholar
31 Dai L., Cao Q., Xia Y., and Gao Y., Distributed MPC for formation of multi-agent systems with collision avoidance and obstacle avoidance, Journal of the Franklin Institute. (2017) 354, no. 4, 2068–2085, https://doi.org/10.1016/j.jfranklin.2016.12.021, 2-s2.0-85009352894.
10.1016/j.jfranklin.2016.12.021
Web of Science® Google Scholar
32 Qin M., Wang Z., Li H., and Liu X., DMPC for formation of multi-UAV with collision/obstacle avoidance, Journal of Beijing University of Aeronautics and Astronautics. (2022) https://doi.org/10.13700/j.bh.1001-5965.2022.0509.
10.13700/j.bh.1001-5965.2022.0509
Google Scholar
33 Vargas S., Becerra H. M., and Hayet J. B., MPC-based distributed formation control of multiple quadcopters with obstacle avoidance and connectivity maintenance, Control Engineering Practice. (2022) 121, article 105054, https://doi.org/10.1016/j.conengprac.2021.105054.
10.1016/j.conengprac.2021.105054
Web of Science® Google Scholar
34 Kim H., Shim H., and Seo J. H., Output consensus of heterogeneous uncertain linear multi-agent systems, IEEE Transactions on Automatic Control. (2011) 56, no. 1, 200–206, https://doi.org/10.1109/tac.2010.2088710, 2-s2.0-78651313706.
10.1109/TAC.2010.2088710
CAS Web of Science® Google Scholar
35 Camponogara E. and De Oliveira L. B., Distributed optimization for model predictive control of linear-dynamic networks, IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans. (2009) 39, no. 6, 1331–1338, https://doi.org/10.1109/TSMCA.2009.2025507, 2-s2.0-77955087766.
10.1109/TSMCA.2009.2025507
Google Scholar
36 Chen W. H., Ballance D. J., and O′Reilly J., Optimisation of attraction domains of nonlinear MPC via LMI methods, 4, Proceedings of the 2001 American Control Conference. (Cat. No.01CH37148), June 2001, Arlington, VA, USA, 3067–3072, https://doi.org/10.1109/acc.2001.946387, 2-s2.0-0034842132.
10.1109/acc.2001.946387
Google Scholar
37 Yu S. Y., Chen H., Zhang P., and Li X. J., An LMI optimization approach for enlarging the terminal region of MPC for nonlinear systems, Acta Automatica Sinica. (2008) 34, no. 7, 798–804, https://doi.org/10.3724/SP.J.1004.2008.00798, 2-s2.0-48549104630.
10.3724/SP.J.1004.2008.00798
Google Scholar
38 Liu X., Shi Y., and Constantinescu D., Robust distributed model predictive control of constrained continuous-time nonlinear systems using two-layer invariant sets, Journal of Dynamic Systems, Measurement, and Control. (2016) 138, no. 6, article 061004, https://doi.org/10.1115/1.4032829, 2-s2.0-84963864872.
10.1115/1.4032829
Web of Science® Google Scholar
39 Li H. and Shi Y., Robust distributed model predictive control of constrained continuous-time nonlinear systems: a robustness constraint approach, IEEE Transactions on Automatic Control. (2014) 59, no. 6, 1673–1678, https://doi.org/10.1109/tac.2013.2294618, 2-s2.0-84898894228.
10.1109/TAC.2013.2294618
Web of Science® Google Scholar
40 Wang X., Wang Y., Su X., Wang L., Lu C., Peng H., and Liu J., Deep reinforcement learning-based air combat maneuver decision-making: literature review, implementation tutorial and future direction, Artificial Intelligence Review. (2024) 57, no. 1, https://doi.org/10.1007/s10462-023-10620-2.
10.1007/s10462-023-10620-2
PubMed Web of Science® Google Scholar

All articles

Multi-UAV DMPC Cooperative Guidance with Constraints of Terminal Angle and Obstacle Avoidance

Abstract

1. Introduction

2. Preliminary

2.1. Cooperative Guidance Geometry

2.2. Distributed Model Predictive Control

3. Design and Analysis of DMPC Cooperative Guidance Scheme

3.1. Assumed Predictive State Trajectories and Prediction for System Disturbances

3.2. Design of the Auxiliary Controller, Terminal Ingredients, and Obstacle Avoidance Constraints

3.3. Convergence Analysis of the Multi-UAV System under DMPC

4. Implementation of DMPC Cooperative Guidance Scheme

4.1. Solving Procedure Based on Particle Swarm Optimization Algorithm

4.2. Implementation of DMPC Cooperative Guidance Scheme

5. Numerical Simulation

5.1. Scenario I: Without Obstacles

5.2. Scenario II: With Obstacles

6. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Multi-UAV DMPC Cooperative Guidance with Constraints of Terminal Angle and Obstacle Avoidance

Abstract

1. Introduction

2. Preliminary

2.1. Cooperative Guidance Geometry

2.2. Distributed Model Predictive Control

3. Design and Analysis of DMPC Cooperative Guidance Scheme

3.1. Assumed Predictive State Trajectories and Prediction for System Disturbances

3.2. Design of the Auxiliary Controller, Terminal Ingredients, and Obstacle Avoidance Constraints

3.3. Convergence Analysis of the Multi-UAV System under DMPC

4. Implementation of DMPC Cooperative Guidance Scheme

4.1. Solving Procedure Based on Particle Swarm Optimization Algorithm

4.2. Implementation of DMPC Cooperative Guidance Scheme

5. Numerical Simulation

5.1. Scenario I: Without Obstacles

5.2. Scenario II: With Obstacles

6. Conclusion

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information