Volume 2024, Issue 1 6769271

Research Article

Open Access

Ideal Parameter Estimation of Photocatalysis Process to Boost Amoxicillin Degradation Efficiency Using Marine Predators Optimization Algorithm

Mohamed K. Hassan

orcid.org/0000-0002-5353-3578

Mechanical Engineering Department , College of Engineering and Islamic Architecture , Umm Al-Qura University , Makkah , 21955 , Saudi Arabia , uqu.edu.sa

Search for more papers by this author

Daniel T. Cotfas,

Corresponding Author

Daniel T. Cotfas

[email protected]

orcid.org/0000-0002-9606-8442

Electronics and Computers Department , Transilvania University of Brasov , Brasov , Romania , unitbv.ro

Search for more papers by this author

Hegazy Rezk,

Hegazy Rezk

orcid.org/0000-0001-9254-2744

Department of Electrical Engineering , College of Engineering in Wadi Alddawasir , Prince Sattam bin Abdulaziz University , Al-Kharj , 11942 , Saudi Arabia , psau.edu.sa

Search for more papers by this author

H. Youssef,

H. Youssef

orcid.org/0000-0003-4919-2966

Mechanical Engineering Department , College of Engineering and Islamic Architecture , Umm Al-Qura University , Makkah , 21955 , Saudi Arabia , uqu.edu.sa

Search for more papers by this author

Ahmed S. Shehata,

Ahmed S. Shehata

orcid.org/0000-0001-9984-8295

Marine Engineering Department , College of Engineering and Technology , Arab Academy for Science, Technology, and Maritime Transport , Alexandria , P.O. Box 1029, Egypt , aast.edu

Search for more papers by this author

Alaa A. El-Bary,

Alaa A. El-Bary

orcid.org/0000-0002-8846-0487

Basic and Applied Science Institute , Arab Academy for Science , Technology and Maritime Transport , P.O. Box 1029, Alexandria , Egypt , aast.edu

National Committee for Mathematics , Academy of Scientific Research and Technology , Alexandria , Egypt , asrt.sci.eg

Council of Future Studies and Risk Management , Academy of Scientific Research and Technology , Alexandria , Egypt , asrt.sci.eg

Search for more papers by this author

Mohamed K. Hassan,

Mohamed K. Hassan

orcid.org/0000-0002-5353-3578

Mechanical Engineering Department , College of Engineering and Islamic Architecture , Umm Al-Qura University , Makkah , 21955 , Saudi Arabia , uqu.edu.sa

Search for more papers by this author

Daniel T. Cotfas,

Corresponding Author

Daniel T. Cotfas

[email protected]

orcid.org/0000-0002-9606-8442

Electronics and Computers Department , Transilvania University of Brasov , Brasov , Romania , unitbv.ro

Search for more papers by this author

Hegazy Rezk,

Hegazy Rezk

orcid.org/0000-0001-9254-2744

Department of Electrical Engineering , College of Engineering in Wadi Alddawasir , Prince Sattam bin Abdulaziz University , Al-Kharj , 11942 , Saudi Arabia , psau.edu.sa

Search for more papers by this author

H. Youssef,

H. Youssef

orcid.org/0000-0003-4919-2966

Mechanical Engineering Department , College of Engineering and Islamic Architecture , Umm Al-Qura University , Makkah , 21955 , Saudi Arabia , uqu.edu.sa

Search for more papers by this author

Ahmed S. Shehata,

Ahmed S. Shehata

orcid.org/0000-0001-9984-8295

Marine Engineering Department , College of Engineering and Technology , Arab Academy for Science, Technology, and Maritime Transport , Alexandria , P.O. Box 1029, Egypt , aast.edu

Search for more papers by this author

Alaa A. El-Bary,

Alaa A. El-Bary

orcid.org/0000-0002-8846-0487

Basic and Applied Science Institute , Arab Academy for Science , Technology and Maritime Transport , P.O. Box 1029, Alexandria , Egypt , aast.edu

National Committee for Mathematics , Academy of Scientific Research and Technology , Alexandria , Egypt , asrt.sci.eg

Council of Future Studies and Risk Management , Academy of Scientific Research and Technology , Alexandria , Egypt , asrt.sci.eg

Search for more papers by this author

First published: 16 September 2024

https://doi.org/10.1155/2024/6769271

Citations: 1

Academic Editor: Umapada Pal

Share a link

Email
Wechat
Bluesky

Abstract

This paper presents a methodology for determining the optimal parameters of a photocatalysis process for treating pharmaceutical wastewater. Three parameters are considered: pH value, catalyst dosages, and reaction time to boost the amoxicillin degradation efficiency (ADE). The proposed methodology contains two stages: fuzzy modelling and a parameter determination process using the marine predators algorithm (MPA). Firstly, based on the experimental dataset of ADE in terms of pH value, catalyst dosages, and reaction time, a robust fuzzy model is produced to model the photocatalysis/ozonation process. The target is reducing the root mean square error (RMSE) between the actual data and the experimental dataset. Using fuzzy, the RMSE decreased from 2.0248 using ANOVA to 0.3148 using fuzzy (decreased by 84%). Next, using the MPA, the optimal parameters of pH value, catalyst dosages, and reaction time corresponding to maximum ADE are determined. The suggested strategy boosted the ADE from 88.23% to a rate of 11.68% compared with the experimental and RSM approaches. Under this condition, the optimal solutions are 11, 384 mg/L, and 33.615 min, respectively, for pH, catalyst dosages, and reaction time.

1. Introduction

Securing fresh water and clean energy are the top priorities of all nations [1–3]. While securing freshwater resources from water desalination seems the best choice worldwide, it needs a lot of energy. Wastewater treatment is considered a valid option for decreasing water stress when applying a proper treatment method, such as those relying on solar energy [4, 5] or innovative methods such as microbial fuel cells [6–8]. Antibiotics are widely utilized in human, veterinary, and aquaculture medicine to treat microbial infection or control disease [9–12]. β-Lactam antibiotics, that is, amoxicillin, account for 65% of all antibiotic types used globally [13]. Antibiotics reach the aquatic environment from various sources, including laboratory activities, hospital effluents, and the pharmaceutical industry [14]. Moreover, human and livestock waste, where 30%–90% of these chemicals are found [15, 16]. As a result, these chemicals are found in various environments like the ocean, soil, surface and groundwater sources, sediment, effluents from wastewater treatment plants, and, moreover, sometimes in drinking water [17, 18]. Concerns about environmental pollution from antibiotics such as amoxicillin have received increasing attention. These compounds should be eliminated from discharged effluents to avoid their possible negative effects on humans and animals [19, 20].

In wastewater and water sectors, adsorption, membrane filters, and AOPs (advanced oxidation processes) are usually used to remove pharmaceutical chemicals [21–23]. AOP techniques, including photo-Fenton processes, ozonation, and UV irradiation, are typically regarded as the most successful way for the elimination of nonbiodegradable organic matters, hazardous, and refractory due to their high efficiency, low cost, easy operation, and mineralization ability [24, 25]. During ozonation, ozone assaults organic molecules and oxidizes them directly or indirectly at low or high pH, respectively, through a chain reaction mechanism to form the •HO (hydroxyl radical). The catalyst in AOPs boosts the formation of •OH, pollutant removal, and the rate of reaction rate, as well as decreasing the hazardous intermediates in the effluent [26]. MgO (magnesium oxide), TiO₂ (titanium oxide), and ZnO (zinc oxide) have been employed as catalysts in AOPs [27–30]. Among them, MgO is considered a heterogeneous catalyst that has been shown to be effective in the treatment of water and wastewater and effluents as it is nontoxic, cheap, ecofriendly, contains a high concentration of active sites, and has the ability to remove a wide range of organic pollutants [20, 31, 32]. The amalgamation of photocatalysis with ozonation is an auspicious strategy for reducing pollution [33]. When excited electrons come into contact with ozone molecules or oxygen molecules, respectively, ozonide radicals and •O2− radicals are produced via photocatalytic ozonation [34]. After a series of reactions, these free radicals break down organic contaminants, generating •HO radicals. A hierarchy grey relational analysis (GRA) was developed by applying GRA and AHP (analytic hierarchy process) for accelerating the associated environmental decision-making approach by taking into account the multiobjective and unpredictable aspects comprised in selecting an appropriate wastewater treatment solution [35].

A design of experiments (DoE) was used to optimize ozonation procedures to remove pharmaceutical products, including diazepam, bromazepam, and clonazepam, from municipal wastewater treatment plants in Rio de Janeiro City, Brazil [36]. RSM (response surface methodology) was employed to optimize the photocatalytic ozonation to remove furosemide from wastewater using ZnO supported on ion-exchanged clinoptilolite as a nanophotocatalyst [37]. The influence of various operational parameters, including reaction time, pollutant concentration, catalyst loading, and initial ozone concentration, on the degradation of furosemide was investigated, as was the interaction between them. The degradation of antibiotic amoxicillin from wastewater was also examined using a photocatalysis-ozonation technique based on MgO catalyst; moreover, the process was optimized by applying RSM based on BBD (Box–Behnken design) [20].

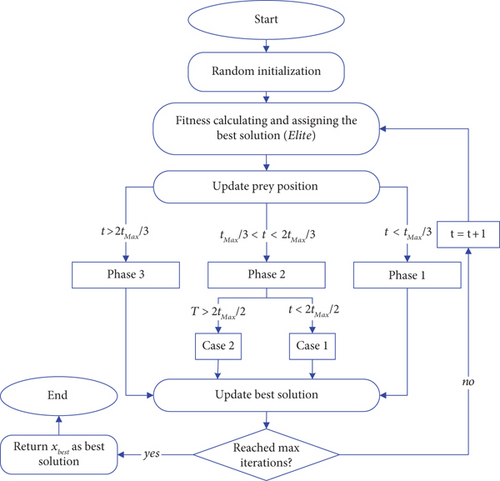
This study determines the optimal parameters of a photocatalysis/ozonation process to treat wastewater. Three parameters are considered: pH value, catalyst dosages, and reaction time to boost the amoxicillin degradation efficiency (ADE). The proposed methodology involves fuzzy modelling and parameter estimation process working marine predators algorithm (MPA). MPA is an optimization algorithm inspired by nature, specifically the optimal foraging strategy and encounter rate policy observed in predator–prey dynamics within marine ecosystems. It incorporates a Lévy approach for environments with scarce prey concentrations while employing Brownian movement in areas abundant with prey [37]. To prove the superiority of MPA, the results are compared with SMA (slime mould algorithm), PSO (particle swarm optimization), HHO (Harris hawks optimization), GWO (grey wolf optimization) algorithm, and EESHHO (hybrid elite evolutionary strategy [EES] HHO).

The contributions of the paper can be outlined as follows:

1.
Developing an accurate fuzzy model of the photocatalysis/ozonation process to treat wastewater
2.
Defining the optimal values of pH value, catalyst dosages, and reaction time
3.
Carrying out comprehensive comparisons to prove the proposed strategy
4.
Boosting the ADE

2. Dataset

The dataset used in this study is taken from an open access previously published article [20]. One gram of amoxicillin powder was dissolved in 1 L of distilled water to produce a stock solution of 1000 mg/L amoxicillin. This solution was then diluted with distilled water to produce solutions with the desired concentration (100 mg/L amoxicillin). The amoxicillin solution and a definite amount of MgO powder (250–750 mg/L) were put into a bench-size reactor. The amoxicillin solution’s pH was then adjusted using sodium hydroxide and diluted sulfuric acid. The suspension of amoxicillin was magnetically agitated for 30 min at room temperature in the dark to ensure that the adsorption/desorption equilibrium had been achieved on the catalyst surface. The photocatalytic process involved irradiating a suspension with light using a 6W OSRAM “low-pressure mercury lamp” inside a quartz tube reactor. As part of the photocatalytic ozonation procedure, 200 mg of ozone per hour was bubbled into the reactor from a 5 L/min ozone generator. The concentration of amoxicillin was measured using a UV-vis spectrophotometer set at 228 nm after 5 mL of the suspension had been removed, centrifuged for 20 min at 6000 rpm to remove the catalyst, and then analyzed (maximum absorbance wavelength). To calculate how efficient amoxicillin’s degradation process is, we used Equation (1). All experiments were carried out on a lab bench at a constant 25°C. More experimental details are found in [20].

()

where C_i and C_f denote the initial and final amoxicillin concentration, respectively [20, 38].

3. Methodology

As explained in Figure 1, the proposed method includes two stages: the first stage is the fuzzy-based model of ADE, whereas the second one is the parameter identification of the photocatalysis/ozonation process.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Main steps of the methodology.

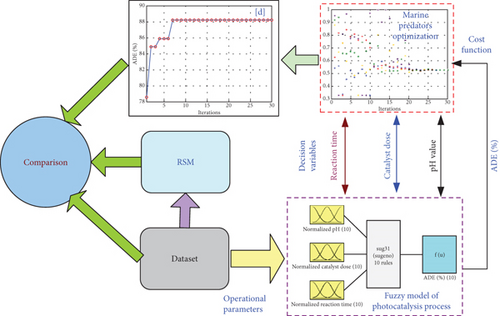
3.1. First Stage: Fuzzy-Based Model of ADE

Membership functions (MFs) are employed in the fuzzification process to nonlinearly map the inputs. The inference engine stage encompasses the generation of fuzzy rules, evaluation of the rules’ outputs, and aggregation of the activated rules to generate the output [39]. Subsequently, the output is converted to a crisp form through the defuzzification phase. In fuzzy logic (FL), the relationship between input and output is expressed through IF-THEN rules. An illustrative instance of a fuzzy rule is provided below.

IF x is A₁ and y is B₁, then f₁ = g₁(x, y)where the A₁ and B₁ denote MFs of inputs.

The output of the f is estimated as follows:

(output layer)

Evaluating and (defuzzification layer)

and (N layer)

and (π layer)

where , , , and are the MF values of inputs.

3.2. Second Stage Parameter Identification Using MPA Optimizer

The aim of the parameter identification process is to determine the optimal values of pH value, catalyst dosages, and reaction time corresponding to the maximum value of the ADE. In this work, MPA is used. It is a metaheuristic algorithm, and its core idea is extracted from laws that control a marine creature’s ideal foraging behavior and encounter rate policy. MPA employs the Lévy strategy in environments where prey concentration is low but switches to Brownian movement in areas where prey is abundant. When the velocity ratio is low, the optimal strategy for a predator is to use the Lévy strategy, regardless of whether the prey is moving according to Brownian or Lévy patterns. However, in scenarios where the velocity ratio is unity and the prey moves according to Lévy patterns, the best strategy for a predator is to use Brownian movement. Conversely, when the velocity ratio is high, the most effective strategy for a predator is to remain stationary. In such cases, whether the prey exhibits Brownian or Lévy movement, the predator takes advantage of its excellent memory to remember its companions and successful foraging locations. More details about the mathematical model of MPA can be found in [37]. The step size and updating process during the low-velocity ratio can be represented as follows:

()

where S_i denotes the step size, R_B is a vector comprising randoms based on the normal distribution on behalf of the Brownian motion, and R is a random value. The step size and updating process during the low-velocity ratio can be represented as follows:

()

where R_L is a vector generated using Lévy motion’s distribution. If t (iteration number) is greater than half of t_Max (maximum number of iterations), this phase can be expressed as

()

The step size and updating process during the high-velocity ratio can be represented as follows:

()

The MPA process is shown in Figure 2.

In sum, the parameter identification method aims to determine the ideal pH values, catalyst dosages, and reaction times to increase the efficiency of amoxicillin degradation. MPA was employed after developing a consistent fuzzy model to get the ideal values for three input parameters. An evaluation of MPA’s performance compared to SMA, PSO, HHO, GWO, and EESHHO is conducted. The following can be used to describe the case study’s optimization challenge.

()

where x is the three input parameters.

4. Results and Discussion

4.1. Fuzzy Model of ADE

The number of samples employed to construct the fuzzy model is 17 points. The points are divided into two factions. The first one has 11 points. It has been employed for training the model, while the rest points have been used to test the model. The fuzzy model is trained with a hybrid approach, applying least squares estimation (LSE) in the forward direction and backpropagation in the backward direction. The subtractive clustering is adopted to create the fuzzy rules in the case study 10 rules. Then, these models were trained until a minimum RMSE value was attained. The statistical evaluation of the fuzzy-based model is displayed in Table 1.

Table 1. Numerical assessment of fuzzy-based model of ADE.

	Train	Test	All	Train	Test	All
	RMSE			R-squared
Fuzzy	0.1897	0.4634	0.3148	0.9815	0.9334	0.9605
ANOVA	NA	NA	2.0248

Regarding Table 1, the RMSE values for the ADE-based fuzzy model come in at 0.1897 and 0.4634, respectively, for the training and testing data. When it comes to training and testing, the R-squared values come in at 0.9815 and 0.9334, respectively. The RMSE was reduced by fuzzy in comparison to ANOVA by an 84% margin, going from 2.0248 when using ANOVA [20] to 0.3148 when using fuzzy. In conclusion, the fuzzy model’s low RMSE and high R-squared values indicate the successful completion of the modelling stage. The structure of the fuzzy model is depicted in Figure 3 and consists of three inputs and one output. Figure 4 illustrates the various forms that the Gaussian MFs can take; for pH, see Figure 4(a); for catalyst dose, see Figure 4(b); and for reaction time, see Figure 4(c).

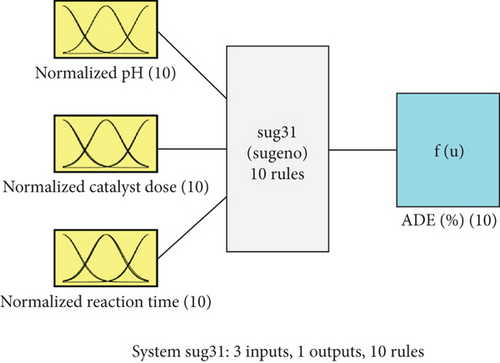
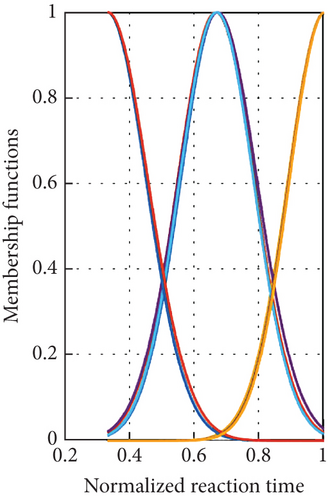
Figure 5 points out the spatial explanation from a 3D surface of the parameters. The maximum point of the output goes to dark red, but the minimum point goes to dark blue. As the figure shows, the ADE is low at low pH values and increases with increasing pH values, especially at pH values higher than 7. It is also clear that the optimum pH value (to obtain the highest ADE) is dependent on the catalyst dose. For instance, at a low catalyst dose, a high pH value of around 10 is necessary to get the best removal efficiency, while the required pH value at a higher catalyst dose is decreased until it has a pH value of 7 at the highest catalyst dose of 750 mg/L, as can be seen in Figure 5(a). The same behavior was recorded in the case of the effect of the pH at the different reaction times, where high pH values of around 10 are required to obtain the highest ADE at a low reaction time of 30 min and lower pH values are required to get the highest ADE at longer reaction times that reach a pH value of around 7 at the highest reaction time of 90 min, as can be seen in Figure 5(b). Figure 5(c) shows the effect of both the reaction time and catalyst dose on the ADE. As is clear from the figure, a high catalyst load of around 750 mg/L is required at a shorter reaction time of 30 min, and the required catalyst load for the highest ADE removal is decreased to around 500 mg/L at longer reaction times (Figure 5(c)).

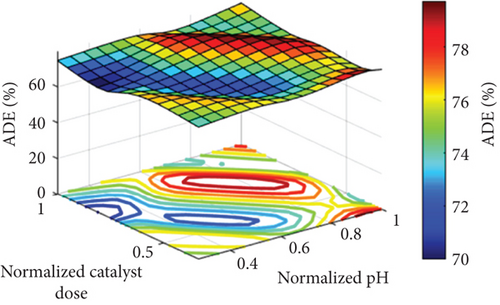
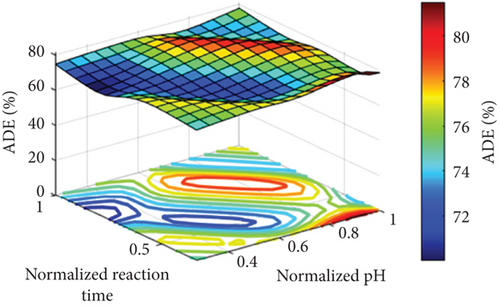
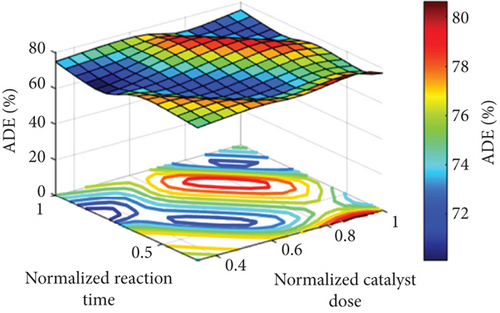
The pH effect on amoxicillin degradation was linked to the characteristics of the catalyst and the pollutant. The catalyst used is MgO with a zero-point charge at a pH value of 12.4 [20]; therefore, it will have a positive charge in the whole pH range used in the current study (pH 3–11), while the pollutant (amoxicillin) is a zwitterionic molecule with both acidic and basic and has three pKa values (3, 7, and 11). At low pH (around 3), both the pollutant and the catalyst have the same charge (positive); therefore, a repulsion happens, and thus, ADE is low. Generally, the increase in the pH value would result in increasing the hydroxyl radical and the reaction of the pollutant, that is, amoxicillin, with the generated holes (h+) [20]. The optimum value of the catalyst dosage around 500 mg/L would be related to the shortage in the photocatalytic active sites at a low catalyst dosage of 250 mg/L that increased with the increase in the catalyst dosage to 500 mg/L. However, the further increase in the catalyst dosage to 750 mg/L decreased the performance. The decrease in the ADE at a high catalyst dosage of 750 mg/L would be related to the excess number of catalyst nanoparticles that restricted the through of the light, and thus photodegradation decreased as verified in similar photocatalytic processes as reported in [15, 40, 41]. The improved ADE with time was related to the increase in the degradation of the amoxicillin with time; therefore, ADE is increased with time.

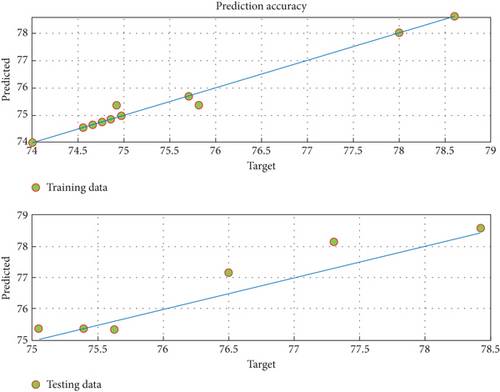
Reaching a precise model of the electrochemical oxidation process encourages the constructed fuzzy model to predict ADE. This is seen from mapping the predicted outputs of fuzzy with the measured dataset, as shown in Figure 6. The experimental and fuzzy data agree. Additionally, the graphs of the predictions around the line of 100% accuracy are shown in Figure 7 for the training and testing phases.

4.2. Parameter Identification

Using measured data, RSM methodology, and the MPA, Table 2 shows the ideal values for pH value, catalyst doses, and reaction time. The efficiency of amoxicillin degradation was improved when fuzzy and MPA were combined. In comparison to measured data and RSM methodology, the ADE has increased to 88.23% with a rate of 11.68%.

Table 2. Optimal parameters applying different methods.

Method	pH	Catalyst dose (mg/L)	Reaction time (min)	ADE (%)	Change (%)
Exp. [20]	11	500	90	79.0	0.00
RSM [20]	11	500	90	78.7	−0.38
MPA and FL	1	0.512	0.3735	88.23	11.68
MPA and FL	11	384	33.615	88.23	11.68

To avoid arbitrary results, each optimisation algorithm under consideration has been used 30 times to test its resilience. Table 3 compares the algorithms that were taken into consideration. Algorithms were used to maintain constant populations (five) and iterations (100) throughout the comparison to ensure fairness. Table 4 shows that MPA is superior to SMA, PSO, HHO, GWO, and EESHHO. MPA achieves the lowest standard deviation (STD) score of 1.9408, while PSO achieves the highest STD of 2.8827. The MPA method yields the best mean cost function, 87.2606, while the PSA method yields the worst cost, 82.8008. This illustrated how successful the suggested approach was. Figure 8 depicts the convergence of the particles during the optimization process. The ideal answers are 0.512 and 0.3735. While Figure 9 presents the details of the 30 runs.

Table 3. Comparison between considered algorithms.

	SMA	PSO	HHO	GWO	EESHHO	MPA
Best (maximum)	88.231	88.2312	88.2302	88.2314	88.2302	88.2315
Worst (minimum)	83.3812	79.5097	79.7196	79.6759	80.9085	82.6787
Mean	87.1228	82.8008	85.9653	86.8629	85.8279	87.2606
Median	88.227	81.1108	88.2023	88.2283	88.2086	88.2294
Variance	4.0053	8.3101	8.1799	6.5599	7.9032	3.7666
STD	2.0013	2.8827	2.8601	2.5612	2.8113	1.9408

Table 4. Details of 30 runs for different optimizers (ADE [percentage]).

Run	SMA	PSO	HHO	GWO	EESHHO	MPA
1	88.221	88.231	88.23	88.23	83.551	88.226
2	83.548	81.094	85.885	88.225	83.54	88.23
3	88.225	81.098	88.227	88.231	88.22	88.216
4	88.228	81.108	82.679	88.231	83.551	88.23
5	83.536	81.104	83.837	82.679	83.519	88.23
6	83.552	79.51	80.726	88.23	88.209	83.552
7	88.213	81.101	88.227	88.225	88.221	88.23
8	88.229	81.105	88.227	88.231	88.22	88.231
9	88.225	81.113	88.227	88.23	81.111	83.552
10	88.23	81.111	82.679	88.229	88.227	88.23
11	88.228	79.548	79.72	88.229	82.679	83.552
12	88.228	81.109	88.178	79.676	82.679	88.229
13	88.225	81.105	88.23	88.227	83.54	88.222
14	88.221	81.11	88.151	88.224	88.227	88.231
15	83.479	81.092	82.679	88.23	81.105	83.552
16	88.231	82.679	88.228	88.231	88.206	88.222
17	88.23	81.101	87.485	88.227	88.208	88.231
18	88.227	88.231	88.229	83.545	82.679	88.226
19	88.231	88.23	88.23	88.23	82.679	88.228
20	88.231	81.101	88.229	88.228	88.228	88.23
21	83.448	88.23	88.227	88.221	88.23	88.228
22	88.228	81.111	88.228	88.231	88.227	83.449
23	83.381	81.109	82.804	83.5	88.211	82.679
24	88.231	83.549	88.228	88.23	88.214	88.231
25	88.221	88.23	82.679	82.679	88.227	88.23
26	88.228	83.523	82.679	88.228	88.215	88.229
27	83.523	83.499	82.679	88.23	88.228	88.23
28	88.23	88.229	88.227	88.23	80.909	88.231
29	88.227	83.551	82.679	81.087	83.551	88.226
30	88.227	81.114	88.23	83.464	88.229	88.23

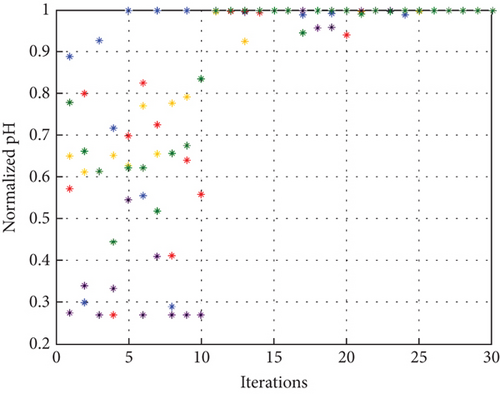
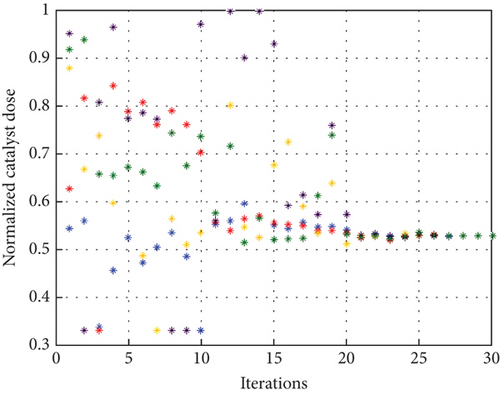
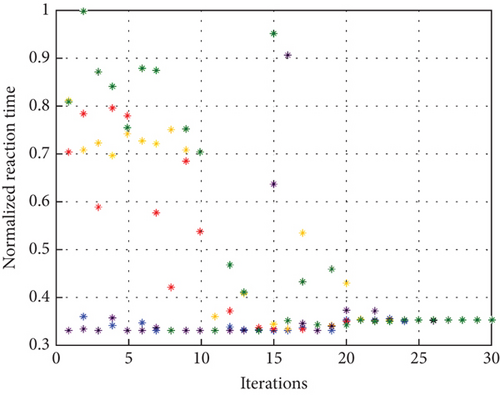
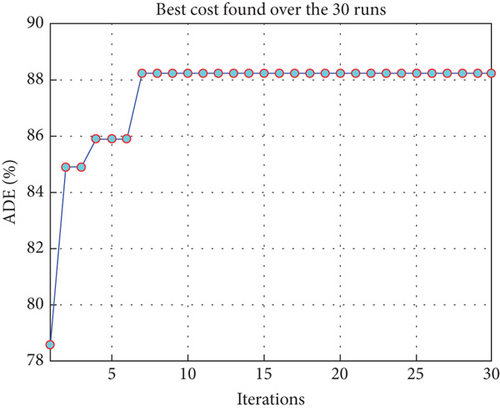
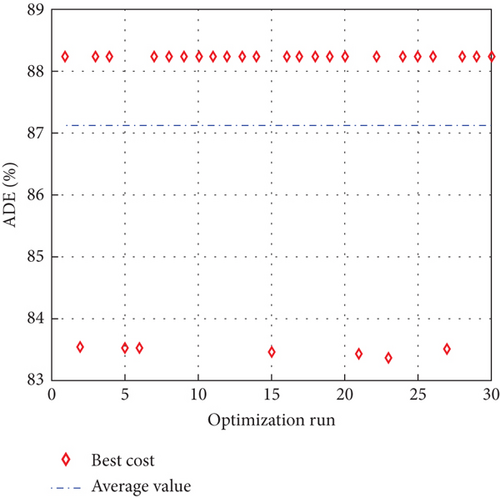
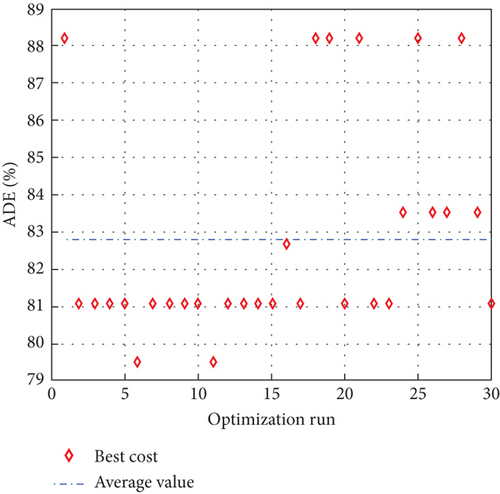
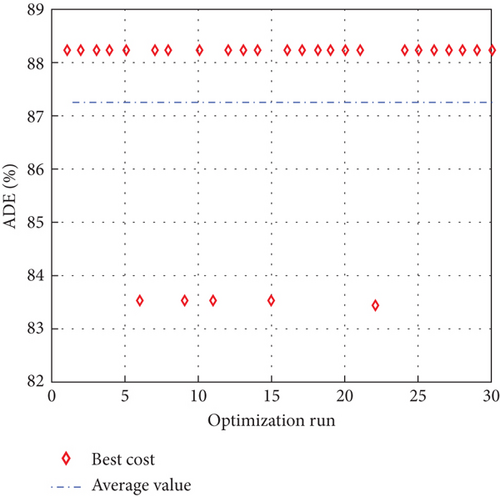
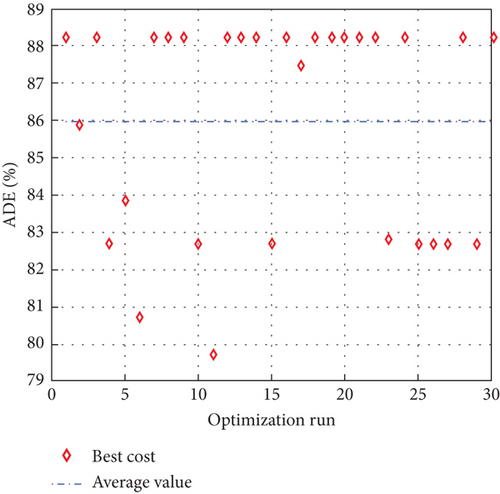
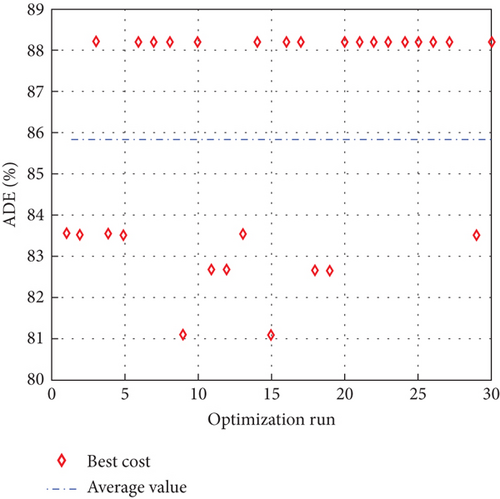
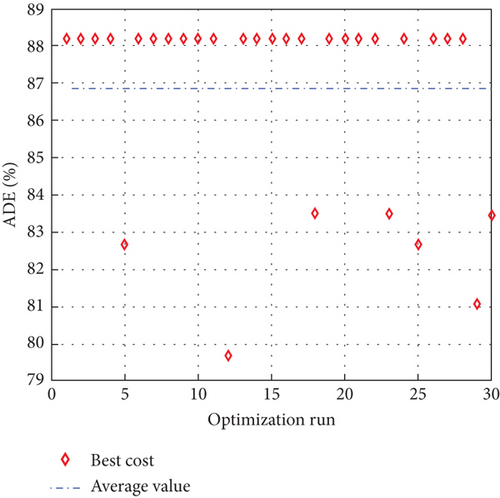
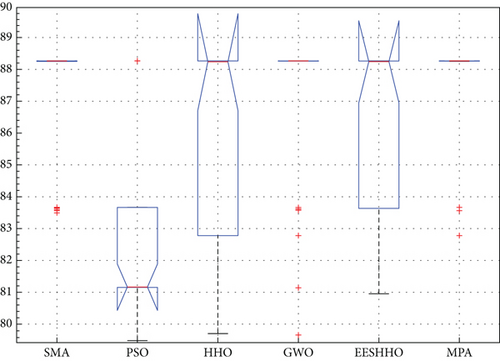
Table 5 displays the ANOVA test results, and Figure 10 displays the corresponding graphical ranking. The p value in the table is much lower than the F value, affirming the variation between both the results obtained. As shown in Figure 11, SMA, GWO, and MPA provided higher mean fitness with lower variance. Tukey’s test will be performed to investigate their performance deeply. On the other hand, the PSO provided the worst performance. Hence, it will be excluded from the Tukey test.

Table 5. ANOVA results (for control).

Source	SS	df	MS	F	p value > F
Columns	415.67	4	83.1363	12.45	2.4552e − 10
Error	1161.75	145	6.6767
Total	1577.42	149

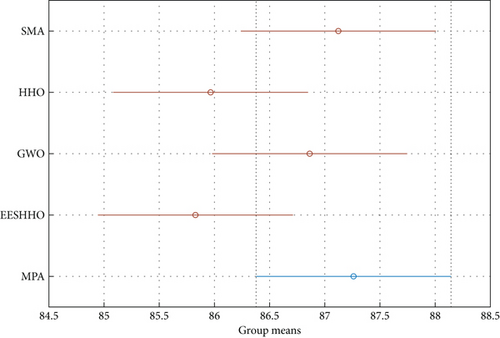
After excluding the PSO due to its poor performance, the Tukey HSD (honestly significant difference) test is used to further clarify the ANOVA test results. The results are shown in Figure 9. The MPA has a higher mean fitness, indicating that it can successfully solve this problem. The SMA performance is extremely competitive, and the GWO closely follows them.

5. Conclusion

The main target of this work is modelling and optimizing the performance of the photocatalysis/ozonation process for treating wastewater. The goal has been accomplished by applying artificial intelligence and MPAs. The proposed methodology integrates fuzzy-based modelling and parameter identification by MPA. Three parameters are considered: pH value, catalyst dosages, and reaction time to boost the ADE. Using the fuzzy modelling, the RMSE values are 0.1897 and 0.4634 for training and testing data. The R -squared values are 0.9815 and 0.9334, respectively, for training and testing. Using fuzzy, the RMSE diminished from 2.0248 (ANOVA) to 0.3148 (decreased by 84%). In sum, the fuzzy model’s low RMSE and the high R-squared values reveal a successful modelling stage. For the optimization phase, the combination of fuzzy and MPA increased ADE from 88.23% to the rate of 11.68% in comparison with the experimental dataset. The optimal solutions are 11, 384 mg/L, and 33.615 min, respectively, for pH, catalyst dosages, and reaction time. To prove the superiority of MPA, the results were compared with SMA, PSO, HHO, GWO, and EESHHO. MPA achieves the minimum STD value of 1.9408, whereas PSO obtains the maximum STD of 2.8827. MPA obtains the highest mean objective function of 87.2606, whereas PSO obtains the worst value of 82.8008. This confirmed the effectiveness of the proposed strategy.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The authors thank the Deanship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number IFP22UQU4361238DSR078.

Acknowledgments

The authors thank the Deanship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number IFP22UQU4361238DSR078.

Open Research

Data Availability Statement

Data used to support this study are available from the corresponding author upon request.

References

1 Azni M. A., Md Khalid R., Hasran U. A., and Kamarudin S. K., Review of the effects of fossil fuels and the need for a hydrogen fuel cell policy in Malaysia, Sustainability. (2023) 15, no. 5, https://doi.org/10.3390/su15054033.
10.3390/su15054033
Web of Science® Google Scholar
2 Zakaria Z., Kamarudin S. K., and Wahid K. A. A., Fuel cells as an advanced alternative energy source for the residential sector applications in Malaysia, International Journal of Energy Research. (2021) 45, no. 4, 5032–5057, https://doi.org/10.1002/er.6252.
10.1002/er.6252
CAS Web of Science® Google Scholar
3 Salameh T., Olabi A. G., Abdelkareem M. A., Masdar M. S., Kamarudin S. K., and Sayed E. T., Integrated energy system powered a building in Sharjah Emirates in the United Arab Emirates, Energies. (2023) 16, no. 2, https://doi.org/10.3390/en16020769.
10.3390/en16020769
PubMed Web of Science® Google Scholar
4 Soltani S., Gacem A., Choudhary N., Yadav V. K., Alsaeedi H., Modi S., Patel A., Khan S. H., Cabral-Pinto M. M. S., Yadav K. K., and Patel A., Scallion peel mediated synthesis of zinc oxide nanoparticles and their applications as nano fertilizer and photocatalyst for removal of organic pollutants from wastewater, Water. (2023) 15, no. 9, https://doi.org/10.3390/w15091672.
10.3390/w15091672
Web of Science® Google Scholar
5 Lu M., Dong J., Hu M., Cheng G., and Lv J., Perovskite LaMnO3 composite graphene carbon nitride g-C3N4 improves the photocatalytic performance of tetracycline degradation, Water. (2023) 15, no. 8, https://doi.org/10.3390/w15081627.
10.3390/w15081627
Web of Science® Google Scholar
6 Rusli S. F. N., Abu Bakar M. H., Loh K. S., and Mastar M. S., Review of high-performance biocathode using stainless steel and carbon-based materials in microbial fuel cell for electricity and water treatment, International Journal of Hydrogen Energy. (2019) 44, no. 58, 30772–30787, https://doi.org/10.1016/j.ijhydene.2018.11.145, 2-s2.0-85058675503.
10.1016/j.ijhydene.2018.11.145
CAS Web of Science® Google Scholar
7 Rusli S. F. N., Daud S. M., Abu Bakar M. H., Loh K. S., and Masdar M. S., Biotic cathode of graphite fibre brush for improved application in microbial fuel cells, Molecules. (2022) 27, no. 3, https://doi.org/10.3390/molecules27031045, 35164309.
10.3390/molecules27031045
PubMed Web of Science® Google Scholar
8 Basri S. and Kamarudin S. K., Microbial fuel cell (MFC) variants, Waste to Sustainable Energy. (2019) 15, https://doi.org/10.1201/9780429448799-2.
10.1201/9780429448799-2
Google Scholar
9 Malakootian M., Yaseri M., and Faraji M., Removal of antibiotics from aqueous solutions by nanoparticles: a systematic review and meta-analysis, Environmental Science and Pollution Research. (2019) 26, no. 9, 8444–8458, https://doi.org/10.1007/s11356-019-04227-w, 2-s2.0-85060953389, 30706272.
10.1007/s11356-019-04227-w
CAS PubMed Web of Science® Google Scholar
10 Balarak D. and McKay G., Utilization of MWCNTs/Al₂O₃ as adsorbent for ciprofloxacin removal: equilibrium, kinetics and thermodynamic studies, Journal of Environmental Science and Health, Part A. (2021) 56, no. 3, 324–333, https://doi.org/10.1080/10934529.2021.1873674.
10.1080/10934529.2021.1873674
CAS Google Scholar
11 Kalli M., Noutsopoulos C., and Mamais D., The fate and occurrence of antibiotic-resistant bacteria and antibiotic resistance genes during advanced wastewater treatment and disinfection: a review, Water. (2023) 15, no. 11, https://doi.org/10.3390/w15112084.
10.3390/w15112084
Web of Science® Google Scholar
12 Obón J. M., Fernández-López J. A., Alacid M., and Angosto J. M., Spinning submerged filter adsorber versus packed bed adsorber for the continuous removal of antibiotics from wastewater with activated carbon, Water. (2023) 15, no. 9, https://doi.org/10.3390/w15091726.
10.3390/w15091726
Web of Science® Google Scholar
13 Samadi M. T., Shokoohi R., Araghchian M., and Tarlani Azar M., Amoxicillin removal from aquatic solutions using multi-walled carbon nanotubes, Journal of Mazandaran University of Medical Sciences. (2014) 24, no. 117, 103–115.
Google Scholar
14 de Ilurdoz M. S., Sadhwani J. J., and Reboso J. V., Antibiotic removal processes from water & wastewater for the protection of the aquatic environment-a review, Journal of Water Process Engineering. (2022) 45, article 102474, https://doi.org/10.1016/j.jwpe.2021.102474.
10.1016/j.jwpe.2021.102474
Google Scholar
15 Elmolla E. S. and Chaudhuri M., Photocatalytic degradation of amoxicillin, ampicillin and cloxacillin antibiotics in aqueous solution using UV/TiO₂ and UV/H₂O₂/TiO₂ photocatalysis, Desalination. (2010) 252, no. 1-3, 46–52, https://doi.org/10.1016/j.desal.2009.11.003, 2-s2.0-74649084798.
10.1016/j.desal.2009.11.003
CAS Web of Science® Google Scholar
16 Liu H., Liu W., Zhang J., Zhang C., Ren L., and Li Y., Removal of cephalexin from aqueous solutions by original and Cu(II)/Fe(III) impregnated activated carbons developed from lotus stalks kinetics and equilibrium studies, Journal of Hazardous Materials. (2011) 185, no. 2-3, 1528–1535, https://doi.org/10.1016/j.jhazmat.2010.10.081, 2-s2.0-78649924130.
10.1016/j.jhazmat.2010.10.081
CAS PubMed Web of Science® Google Scholar
17 Cuerda-Correa E. M., Alexandre-Franco M. F., and Fernández-González C., Advanced oxidation processes for the removal of antibiotics from water. An overview, Water. (2020) 12, no. 1, https://doi.org/10.3390/w12010102.
10.3390/w12010102
Web of Science® Google Scholar
18 Alnajrani M. N. and Alsager O. A., Removal of antibiotics from water by polymer of intrinsic microporosity: isotherms, kinetics, thermodynamics, and adsorption mechanism, Scientific Reports. (2020) 10, no. 1, https://doi.org/10.1038/s41598-020-57616-4, 31964938.
10.1038/s41598-020-57616-4
PubMed Web of Science® Google Scholar
19 Bombaywala S., Mandpe A., Paliya S., and Kumar S., Antibiotic resistance in the environment: a critical insight on its occurrence, fate, and eco-toxicity, Environmental Science and Pollution Research. (2021) 28, no. 20, 24889–24916, https://doi.org/10.1007/s11356-021-13143-x, 33765260.
10.1007/s11356-021-13143-x
CAS PubMed Web of Science® Google Scholar
20 Norabadi E., Panahi A. H., Ghanbari R., Meshkinian A., Kamani H., and Ashrafi S. D., Optimizing the parameters of amoxicillin removal in a photocatalysis/ozonation process using Box-Behnken response surface methodology, Desalination and Water Treatment. (2020) 192, no. 192, 234–240, https://doi.org/10.5004/dwt.2020.25728.
10.5004/dwt.2020.25728
CAS Web of Science® Google Scholar
21 Mohammadi R., Massoumi B., and Rabani M., Photocatalytic decomposition of amoxicillin trihydrate antibiotic in aqueous solutions under UV irradiation using Sn/TiO₂ nanoparticles, International Journal of Photoenergy. (2012) 2012, 11, 514856, https://doi.org/10.1155/2012/514856, 2-s2.0-84859772522.
10.1155/2012/514856
Web of Science® Google Scholar
22 Astuti M. P., Rangsivek R., and Padhye L. P., Laboratory and pilot-scale UV, UV/H₂O₂, and granular activated carbon (GAC) treatments for simultaneous removal of five chemicals of emerging concerns (CECs) in water, Journal of Water Process Engineering. (2022) 47, article 102730, https://doi.org/10.1016/j.jwpe.2022.102730.
10.1016/j.jwpe.2022.102730
Google Scholar
23 Elmolla E. S. and Chaudhuri M., Degradation of amoxicillin, ampicillin and cloxacillin antibiotics in aqueous solution by the UV/ZnO photocatalytic process, Journal of Hazardous Materials. (2010) 173, no. 1-3, 445–449, https://doi.org/10.1016/j.jhazmat.2009.08.104, 2-s2.0-71749086081, 19773120.
10.1016/j.jhazmat.2009.08.104
CAS PubMed Web of Science® Google Scholar
24 Panahi A. H., Ashrafi S. D., Kamani H., Khodadadi M., Lima E. C., Mostafapour F. K., and Mahvi A. H., Removal of cephalexin from artificial wastewater by mesoporous silica materials using Box-Behnken response surface methodology, Desalination and Water Treatment. (2019) 159, 169–180, https://doi.org/10.5004/dwt.2019.24109, 2-s2.0-85068701337.
10.5004/dwt.2019.24109
CAS Web of Science® Google Scholar
25 Kıdak R. and Doğan Ş., Medium-high frequency ultrasound and ozone based advanced oxidation for amoxicillin removal in water, Ultrasonics Sonochemistry. (2018) 40, no. Part B, 131–139, https://doi.org/10.1016/j.ultsonch.2017.01.033, 2-s2.0-85011409955, 28169126.
10.1016/j.ultsonch.2017.01.033
CAS PubMed Web of Science® Google Scholar
26 Wang J. and Chen H., Catalytic ozonation for water and wastewater treatment: recent advances and perspective, Science of the Total Environment. (2020) 704, article 135249, https://doi.org/10.1016/j.scitotenv.2019.135249.
10.1016/j.scitotenv.2019.135249
Google Scholar
27 Hayati F., Isari A. A., Anvaripour B., Fattahi M., and Kakavandi B., Ultrasound-assisted photocatalytic degradation of sulfadiazine using MgO@ CNT heterojunction composite: effective factors, pathway and biodegradability studies, Chemical Engineering Journal. (2020) 381, article 122636, https://doi.org/10.1016/j.cej.2019.122636.
10.1016/j.cej.2019.122636
Google Scholar
28 Calcio Gaudino E., Canova E., Liu P., Wu Z., and Cravotto G., Degradation of antibiotics in wastewater: new advances in cavitational treatments, Molecules. (2021) 26, no. 3, https://doi.org/10.3390/molecules26030617, 33504036.
10.3390/molecules26030617
PubMed Web of Science® Google Scholar
29 Sansenya T., Masri N., Chankhanittha T., Senasu T., Piriyanon J., Mukdasai S., and Nanan S., Hydrothermal synthesis of ZnO photocatalyst for detoxification of anionic azo dyes and antibiotic, Journal of Physics and Chemistry of Solids. (2022) 160, article 110353, https://doi.org/10.1016/j.jpcs.2021.110353.
10.1016/j.jpcs.2021.110353
Google Scholar
30 Malesic-Eleftheriadou N., Evgenidou E. N., Kyzas G. Z., Bikiaris D. N., and Lambropoulou D. A., Removal of antibiotics in aqueous media by using new synthesized bio-based poly (ethylene terephthalate)-TiO₂ photocatalysts, Chemosphere. (2019) 234, 746–755, https://doi.org/10.1016/j.chemosphere.2019.05.239, 2-s2.0-85067613258, 31238270.
10.1016/j.chemosphere.2019.05.239
CAS PubMed Web of Science® Google Scholar
31 Zheng X., Wang K., Huang Z., Liu Y., Wen J., and Peng H., MgO nanosheets with N-doped carbon coating for the efficient visible-light photocatalysis, Journal of Industrial and Engineering Chemistry. (2019) 76, 288–295, https://doi.org/10.1016/j.jiec.2019.03.053, 2-s2.0-85064153382.
10.1016/j.jiec.2019.03.053
CAS Web of Science® Google Scholar
32 Wang B., Xiong X., Ren H., and Huang Z., Preparation of MgO nanocrystals and catalytic mechanism on phenol ozonation, RSC Advances. (2017) 7, no. 69, 43464–43473, https://doi.org/10.1039/C7RA07553G, 2-s2.0-85029482357.
10.1039/C7RA07553G
CAS Web of Science® Google Scholar
33 Valério A., Wang J., Tong S., de Souza A. A. U., Hotza D., and González S. Y. G., Synergetic effect of photocatalysis and ozonation for enhanced tetracycline degradation using highly macroporous photocatalytic supports, Chemical Engineering and Processing - Process Intensification. (2020) 149, article 107838, https://doi.org/10.1016/j.cep.2020.107838.
10.1016/j.cep.2020.107838
Google Scholar
34 Mecha A. C. and Chollom M. N., Photocatalytic ozonation of wastewater: a review, Environmental Chemistry Letters. (2020) 18, no. 5, 1491–1507, https://doi.org/10.1007/s10311-020-01020-x.
10.1007/s10311-020-01020-x
CAS Web of Science® Google Scholar
35 Zeng G., Jiang R., Huang G., Xu M., and Li J., Optimization of wastewater treatment alternative selection by hierarchy grey relational analysis, Journal of Environmental Management. (2007) 82, no. 2, 250–259, https://doi.org/10.1016/j.jenvman.2005.12.024, 2-s2.0-33751199693, 16635543.
10.1016/j.jenvman.2005.12.024
CAS PubMed Web of Science® Google Scholar
36 Cunha D. L., da Silva A. S. A., Coutinho R., and Marques M., Optimization of ozonation process to remove psychoactive drugs from two municipal wastewater treatment plants, Water, Air, & Soil Pollution. (2022) 233, no. 2, https://doi.org/10.1007/s11270-022-05541-9.
10.1007/s11270-022-05541-9
Web of Science® Google Scholar
37 Faramarzi A., Heidarinejad M., Mirjalili S., and Gandomi A. H., Marine predators algorithm: a nature-inspired metaheuristic, Expert Systems with Applications. (2020) 152, article 113377, https://doi.org/10.1016/j.eswa.2020.113377.
10.1016/j.eswa.2020.113377
Web of Science® Google Scholar
38 Wang Q., Zhang L., Guo Y., Shen M., Wang M., Li B., and Shi J., Multifunctional 2D porous g-C₃N₄ nanosheets hybridized with 3D hierarchical TiO₂ microflowers for selective dye adsorption, antibiotic degradation and CO₂ reduction, Chemical Engineering Journal. (2020) 396, article 125347, https://doi.org/10.1016/j.cej.2020.125347.
10.1016/j.cej.2020.125347
Google Scholar
39 Rezk H., Olabi A. G., Abdelkareem M. A., Maghrabie H. M., and Sayed E. T., Fuzzy modelling and optimization of yeast-MFC for simultaneous wastewater treatment and electrical energy production, Sustainability. (2023) 15, no. 3, https://doi.org/10.3390/su15031878.
10.3390/su15031878
Web of Science® Google Scholar
40 Khodadadi M., Ehrampoush M. H., Ghaneian M. T., Allahresani A., and Mahvi A. H., Synthesis and characterizations of FeNi₃@SiO₂@TiO₂ nanocomposite and its application in photo- catalytic degradation of tetracycline in simulated wastewater, Journal of Molecular Liquids. (2018) 255, 224–232, https://doi.org/10.1016/j.molliq.2017.11.137, 2-s2.0-85041443394.
10.1016/j.molliq.2017.11.137
CAS Web of Science® Google Scholar
41 Rashid J., Barakat M. A., Ruzmanova Y., and Chianese A., Fe₃O₄/SiO₂/TiO₂ nanoparticles for photocatalytic degradation of 2-chlorophenol in simulated wastewater, Environmental Science and Pollution Research. (2015) 22, no. 4, 3149–3157, https://doi.org/10.1007/s11356-014-3598-9, 2-s2.0-84925463069, 25239108.
10.1007/s11356-014-3598-9
CAS PubMed Web of Science® Google Scholar

Citing Literature

All articles

Ideal Parameter Estimation of Photocatalysis Process to Boost Amoxicillin Degradation Efficiency Using Marine Predators Optimization Algorithm

Abstract

1. Introduction

2. Dataset

3. Methodology

3.1. First Stage: Fuzzy-Based Model of ADE

3.2. Second Stage Parameter Identification Using MPA Optimizer

4. Results and Discussion

4.1. Fuzzy Model of ADE

4.2. Parameter Identification

5. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Ideal Parameter Estimation of Photocatalysis Process to Boost Amoxicillin Degradation Efficiency Using Marine Predators Optimization Algorithm

Abstract

1. Introduction

2. Dataset

3. Methodology

3.1. First Stage: Fuzzy-Based Model of ADE

3.2. Second Stage Parameter Identification Using MPA Optimizer

4. Results and Discussion

4.1. Fuzzy Model of ADE

4.2. Parameter Identification

5. Conclusion

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Related

Information