This paper presents a multistrategy fusion particle swarm optimization model for dynamic economic dispatching of renewable energy in distribution networks. The objective is to minimize active network losses and system voltage deviation while considering the integration of distributed energy sources and static reactive power compensators. The algorithm incorporates specific strategies, including a particle position change strategy based on the midpipeline convergence approach, a strategy for generating exploding particles near the optimal particles, and a particle velocity update strategy relying on the global optimal particle position. The inertia weights and particle position update methods of the simplified particle swarm optimization algorithm are also utilized. Simulation experiments are conducted on an IEEE 33 bus radial distribution system, demonstrating the effective optimization of system losses while ensuring system voltage stability. This research contributes to the scientific understanding of renewable energy integration in distribution networks and its economic dispatching.

1. Introduction

Renewable energy sources are being actively promoted to replace fossil fuels, as part of efforts to achieve comprehensive green transformation in economic and social development [1]. The shift towards clean and low-carbon energy consumption is accelerating, driving the energy industry towards high-quality development. The rapid and stable economic growth has led to increased energy demand and consumption [2]. To meet this demand while reducing power losses and emissions, renewable energy-based power generation technologies, in the form of distributed generation (DG), are being integrated into existing power networks to supply electricity to local customers [3–5].

Various studies have been conducted by researchers worldwide to optimize the siting and capacity planning of DG from different perspectives. For example, Song et al. [6] improved the genetic algorithm for distributed power planning using a multiobjective optimization model. Abo El-Ela et al. [7] enhanced the gray wolf algorithm by incorporating chaotic sequences and considering multiple objectives. Karunarathne et al. [8] applied a chaotic search strategy in the cat swarm algorithm to minimize system losses and power purchase costs. Balu and Mukherjee [9] improved the particle swarm algorithm for determining the optimal location and capacity of DG.

The integration of renewable energy sources, such as wind and solar, presents challenges due to their variability and uncertainty, leading to imbalances in power generation and consumption [10–14]. The economic operation of renewable energy sources has become a major research focus. Several optimization models and algorithms have been proposed, including those considering wind-heat systems [15], optimal power system dispatch under combined uncertainty of wind power [16], and real-time economic dispatch models accounting for renewable energy variations [17].

While these solutions have shown promise, there is still a need to improve their stability and adaptability. Particle swarm optimization (PSO) algorithms, known for their simplicity and efficiency, have been widely used for optimization problems. They suffer from limitations such as premature convergence and low convergence accuracy. To address these issues, researchers have explored various improvements to the PSO algorithm, such as adjusting inertia weights [18], enhancing population diversity [19, 20], and incorporating other algorithms [21].

In this paper, a multistrategy fusion particle swarm model is proposed for dynamic economic dispatch of renewable energy. The objective is to minimize active network losses and voltage deviations, while considering the operating limits of the AC distribution network. The effectiveness of the proposed model is demonstrated using the IEEE 33 node bus radial distribution system.

2. Methodology

2.1. Optimization Model of Distribution Network System with Distributed Renewable Energy

For distribution networks connected with distributed generation (DG), the control of active network losses involves optimizing the reactive power of the system while simultaneously optimizing the node voltage. The mathematical model consists of an objective function, power constraints, and equations for control variables.

To classify additional methods for integrating distributed renewable energy into the grid, this paper refers to existing equivalent calculation schemes. The paper categorizes these methods into three groups.

(1)
UV access method for distributed renewable energy

For distributed renewable energy sources that operate with a constant power factor, such as doubly fed wind turbines and static var compensators (SVCs), this paper considers them as UV nodes. In the system load flow calculation, they are typically treated as loads with negative power output. The equivalent model for the load flow calculation can be expressed as

(1)

where U and V are the active power and reactive power equivalent to the load of the power supply model and U_ms and V_s are the rated active and reactive power output from distributed renewable energy sources such as doubly fed wind turbines and SVCs with constant power factor operation.

(2)
Distributed renewable energy UQ access method

For asynchronous wind turbine-type distributed energy connected to the grid through an inverter, this paper treats it as UQ node.

(3)
Distributed renewable energy UX access method

For distributed renewable energy connected by DC current control inverter of PV plant type, it can be treated as UX node. Such nodes can be processed as follows in the tidal current calculation:

(2)

where n is the number of iterations, V_solar(n) is the reactive power of the n-iteration of distributed renewable energy of the photovoltaic power station type, U_solar is the active power of a photovoltaic power station, X_solar is the amplitude of current injected into the distribution network, and P_solar(n − 1) is the node voltage calculated at (n − 1) iteration. Then, the UX node can be transformed into UV node function by the above equation.

(3)

Active network loss is a crucial economic and technical parameter in distribution networks, and optimizing it is essential for improving equipment operation from an economic perspective. Simultaneously, nodal voltage deviation is an important indicator that impacts the efficiency and working condition of power equipment, and it should be taken into consideration.

In this paper, the objective function is established with the active loss and nodal voltage deviation of the distribution network system, considering distributed renewable energy, as the control targets. The control objective prioritizes the optimization of active network loss and voltage deviation control. The expressions are as follows:

(4)

(5)

(6)

(7)

where F₁ is the active network loss control objective function, F₂ is the voltage deviation control objective function, t is the total network tributary, U_a is the total active power input, U_DA,x is the active power input of the distributed power supply at each node, U_L represents each active load of the distribution network, ΔQ_x is the threshold deviation of node voltage, Q_xmax and Q_xmin are the maximum and minimum voltage values allowed at the node, and λ₁ and λ₂ are the weight coefficients of the objective function, which can be adjusted according to the control target bias.

When ΔQ_x ≥ Q_xmax, ΔQ_x = ΔQ_x − Q_xmax. When ΔQ_x ⩽ Q_xmin, ΔQ_x = Q_xmin − ΔQ_x. When Q_xmin ⩽ ΔQ_x ⩽ Q_xmax, ΔQ_x = 0. In this paper, λ₁ = 0.7, and λ₂ = 0.3. η is the penalty coefficient of the control voltage deviation, which is expressed according to the oscillatory dispersion penalty coefficient treatment as

(8)

where z₁ is the constrained gravitational increasing coefficient, n is the number of iterations, n^′ is the oscillatory divergence period length, and z₂ is the gravitational decreasing coefficient. It is designed to guarantee convergence. In this paper, z₁ = 0.2, z₂ = 0.02, and N^′ = 300.

For this reactive optimization model, each node must satisfy the active power and reactive power balance; i.e., the condition of equation (9) is satisfied.

(9)

where U_Lx and V_L,x are the active and reactive power loads at node x, V_xSVC is the reactive power output of the SVC connected to node x, θ_xy is the voltage phase angle difference between nodes x and y, and A_xy and H_xy are the node conductance and conductance.

In the actual model, the voltage and reactive power compensation capacity of each node are limited to a certain range to ensure power quality and investment control. After the distribution network is connected to DG, the node voltage amplitude is controlled by the access of SVC equipment, and the variable constraints are shown in equation (10).

(10)

where V_xSVCmin and V_xSVCmax are the minimum and maximum allowable power output values of the static reactive power compensation device connected to node x.

2.2. Improved Particle Swarm Algorithm for Multistrategy Fusion

2.2.1. Convergence Strategy of the Midperm Algorithm

Midperpendicular algorithm (MA) is a new swarm intelligent optimization algorithm. The algorithm makes use of the property of the middle vertical line in geometry: the distance between any point on the middle vertical line and the two ends of the line segment that is bisected is equal. As shown in Figure 1, it is assumed that there is only one optimal point U in a sufficiently small range (the inner region of the outer rectangle) in two-dimensional space, there are random points G and H, and the midvertical of the line segment connecting the two points is L. The distance from G to U is less than the distance from H to U, because any point on L is the same distance from G and H. But if |UG| < |UH|, U must exist in the region near G side of L. MA replaces the distance from the optimal point with the fitness of the point; that is, in Figure 1, the fitness of point G is superior to that of point H, and P has the best fitness. Taking Figure 1 as a specific case, the convergence process of MA is as follows:

(1)
MA determines that the region where the optimal value U exists must be located in the region of the midpipeline against the G side (the yellow region in Figure 1), and U must not be located in the region of L against the H side
(2)
MA discards the original point H and generates a new random point H^′ in the region of L against G
(3)
Make G and H^′ form the midline of the line L^′, as shown in Figure 1. At this point, H^′ is closer to point U; that is, H^′ is better adapted, so MA determines that the optimal value must exist in the region of L^′ against H^′ (the orange grid region in Figure 1)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Principle diagram of the midpipeline algorithm.

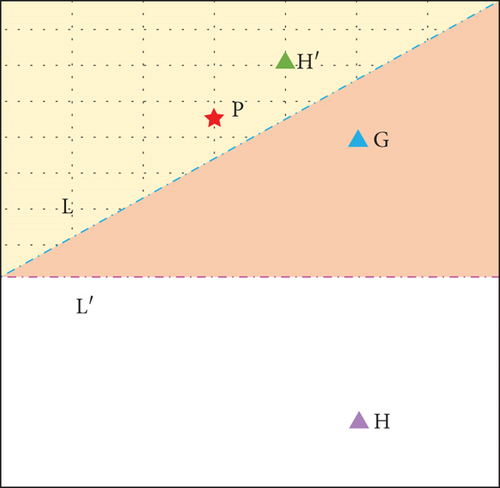
A new point G is generated in the area where the optimal point is likely to exist, and then, the space where the optimal point is located can be narrowed down by the midpipeline determination method. Repeat the above steps to find the optimal point.

2.2.2. Particle Position Change Strategy Incorporating Convergence Strategy of Midpipeline Algorithm

The standard PSO adjusts the velocity of each particle by the relationship between the current best particle position abest and the historical best position ubest of each particle and the current particle position i. The specific adjustment method is as follows.

(11)

(12)

where m is the inertia factor, c₁ is the individual learning rate, and c₂ is the population learning rate. This strategy allows each particle to be influenced by the population optimal position and the individual historical optimal position, so as to find the optimal solution. Relying only on particle velocity to regulate the position of particles is likely to lead to slow convergence of PSO.

If a random particle C is added in Figure 1, C is located in the region of H side of the middle good line, as shown in Figure 2. If the particle position update strategy of PSO is used to update the positions of points H and C, it must take several iterations to reach the region of the midpipeline on the G side. To address this problem, this paper proposes to move particles H and C to H^′ and C^′ before using the particle velocity and position update strategy of PSO. The particles H and C are moved to the vertical foot which is perpendicular to L^′ past point B or C. And then, the particle velocity and position update strategy of PSO is used to change the particle positions. The above strategy algorithm is implemented as follows. The evaluation involves determining whether the particle is located in the region of the midpipeline against the H side and setting it accordingly.

(13)

Then, if a particle x is located in the region near the H side of the vertical line, the y-th dimension variable of i satisfies the following inequality.

(14)

where

(15)

To improve the global optimization performance of the algorithm, the particle x only needs to have any two-dimensional variables that do not meet the above conditions. That is, it is determined that the position of the particle is located in the small good line against the G side region, and the position of the particle does not use the above strategy. If it is determined that the particle is located in the region of the middle vertical line against the H side, the y-th and (y + l)-th dimensional variables of i_x are updated as follows.

(16)

(17)

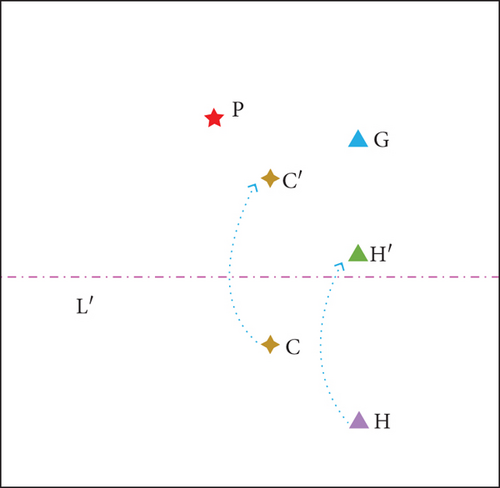
Figures 3 and 4 show the variation of particles when finding the minimum of the function for the improved PSO algorithm incorporating the above strategies.

From the comparison of particle position variation in Figures 3 and 4, it can be seen that the improved particle position variation approach incorporating the convergence strategy of the midpipeline algorithm has the following advantages and problems.

(a)
When facing a single extremum problem, the slow displacement of particles that are in the region judged by the MA convergence strategy as impossible to exist at the best advantage can be effectively avoided. This helps to accelerate the convergence accuracy of the algorithm. Compared with the convergence strategies of the particle swarm algorithm, genetic algorithm, and whale algorithm, the convergence strategy of MA has great advantages in convergence accuracy and speed
(b)
When facing a complex optimization problem with multiple extremes, the convergence strategy of the midpipeline algorithm may cause the particle swarm algorithm to directly discard the optimal point range and search in the minimal value range. As the population of the algorithm increases, the probability of occurrence of this situation decreases significantly. At the same time, as the algorithm’s extreme value points increase, the probability that the distance between the optimal points G and H determined at each iteration is greater will be greater, and the range of optimal points determined by the convergence strategy of MA will be greater, causing a further reduction in the probability of the above problem. The convergence strategy of the midpipeline algorithm will cause a reduction in the global merit-seeking performance of the algorithm, but the reduction is not significant
(c)
Despite the appeal problem, if the region where the optimal point exists as determined by the previous MA convergence strategies is correct, all particles will be searched in the correct region. This can greatly enhance the global optimal search performance of the algorithm in that region

2.2.3. Optimal Particle Explosion Strategy

When the optimal particle abest of traditional PSO updates the velocity of a particle according to equation (11), the particle position of the next generation generated will often be inferior to that of the previous moment, relying only on the historical information of that particle. The role of the optimal particle is not fully explored causing the algorithm’s optimization-seeking accuracy and speed to decrease. To address this problem, this paper proposes an optimal particle explosion strategy to generate a certain number of particles around the optimal particles. These particles are generated in the following way.

(18)

The y-th dimensional variable of the t-th exploded particle ei_t is generated in equation (18). These particles are generated around the optimal particle, and the range of generated particles is 1/4 of the difference between the dimensions of the optimal particle abest (i.e., point G) and point H.

2.2.4. Improved Particle Velocity Update Strategy

The traditional particle swarm algorithm affects the velocity of particles by the historical best position of each particle. After adopting the midpipeline strategy, if the historical position information of the particles is used, the particles will return to the position on the H side of the midpipeline, which will affect the convergence speed of the algorithm. The following particle velocity update strategy is used.

(19)

If the total number of population particles is w and t exploding particles are generated around the optimal particles, then the number of traditional particles that need position updating is (w–t). To enhance the ability of the algorithm to jump out of the local optimum, the population of traditional particles is divided into two parts. Let a part of the traditional particles update their positions according to equation (19), and the proportion of this part to the total number of particles is α. To ensure that most of the particles keep approaching, the optimal value set α = [0.6,1]. The remaining conventional particles update the particle velocity according to

(20)

That is, the velocity of particle i_x is influenced by the explosive particle ei_t, making the particle converge to the explosive particle ei_t. The x-th conventional particle i_x is chosen to converge to the t-th explosive particle ei_t with equal probability. After the velocity update using equations (19) and (20), the position change of different particles is shown in Figure 5. The particle with velocity update by equation (19) will be close to the current optimal point abest. The particle with velocity update by equation (20) will be close to the particle ei_t produced by the explosion of abest.

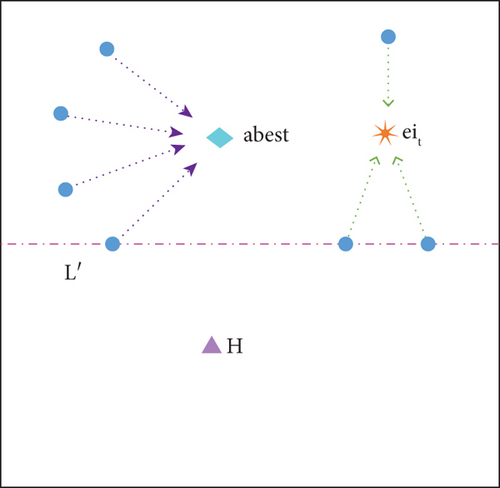
Using this strategy has these advantages: (a) part of the particles updated by the speed of equation (19) can ensure that part of the algorithm constantly converge to the optimal point, which helps the algorithm to stabilize. (b) The velocity update of some particles according to equation (20) can make some of the particles in the algorithm positioned close to the exploding particles around the optimal particles. This can enhance the diversity of particle populations and enhance the global optimization finding ability of the algorithm.

2.2.5. Improved Particle Position Update Strategy

In this paper, a particle position update strategy is proposed using the following equation, and its effectiveness in improving the global optimization-seeking capability of the algorithm is demonstrated.

(21)

2.2.6. Inertia Weight Update Strategy

A nonlinearly varying inertia weight based on logistic mapping is also proposed, which is defined as follows.

(22)

where m_min = 0.9 and m_max = 0.4. The nonlinear inertia adjustment method of equation (22) using logistic mapping is more likely to make the algorithm jump out of the local optimum, the inertia weight update method is described in equation (22). The variation of inertia weights with increasing number of iterations is shown in Figure 6.

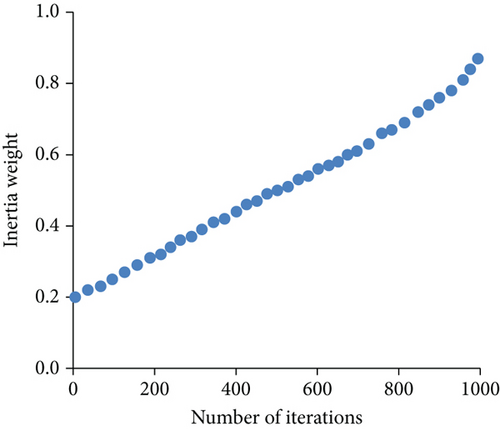
2.2.7. Algorithm Implementation Steps

According to the above introduction, the implementation of the improved multistrategy fusion particle swarm optimization algorithm in this paper can be obtained.

Algorithm 1: Multistrategy fusion particle swarm algorithm.

Input: same initial values for variables, fitness function, maximum number of iterations, problem dimension.
Output: best fitness value, optimal particles.
1) Initialize parameters: population learning rate, particle velocity parity, number of exploding particles t, total population w, m_min and m_max.
2) Initialize the population of traditional particles by generating (w − t) particles and calculate the fitness for each particle.
3) Set the particle with the best fitness as abest (point G) and the particle with the second-best fitness as point H.
4) Generating inertia weights m with equation (22).
5) Generating t exploding particles by equation (18).
6) Update the velocities of α × (t − w) random conventional particles using equation (19).
7) Update the velocities of the remaining traditional particles using equation (20).
8) Update the positions of traditional particles using equation (21).
9) Calculate the fitness of all traditional particles.
10) Update the values of abest (point G) and point H.
11) Check if the end condition of the algorithm is met. If so, terminate the algorithm; otherwise, go to step 4.

By fusing these strategies together, the proposed algorithm combines the exploration capability of exploding particles, the exploitation capability of conventional particles, and the update strategies based on particle velocities and positions. The algorithm dynamically adjusts the particle velocities and positions, using both global and historical information, to guide the search towards better solutions. This fusion of strategies enables proposed method to effectively balance exploration and exploitation, leading to improved optimization performance and the identification of optimal solutions.

3. Result Analysis and Discussion

3.1. Experimental Setup

To verify the superiority and feasibility of the proposed algorithm, this paper carries out the analysis of the algorithm based on the IEEE 33 node distribution network model with enhanced distributed generation. The experimental analysis is performed using Python 2.7 environment, and the implementation platform is a standalone Intel Xeon E5-2650 processor. In this experiment, the number of populations is 200, the maximum number of iterations is 250, and the experimental results are averaged. The algorithm of this paper was tested on an IEEE 33 bus radial distribution system (see Figure 7).

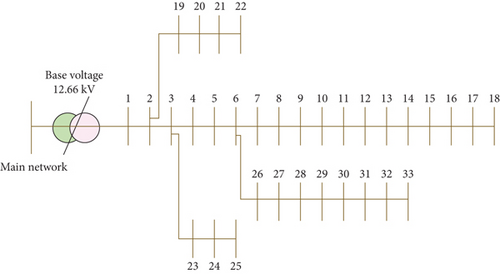
3.2. Analysis of Simulation Results

3.2.1. Analysis of Network Loss Impact

Minimal value seeking is performed on the normalized objective function after normalization. Literatures [22, 23] are used to compare with the algorithm in this paper, and the results are shown in Figure 8.

As can be seen from Figure 8, in the scheme where DG is not connected to the distribution network, the active power loss of the system can reach about 2012.1 kWh. After the DG is connected to the distribution network, the active power loss is reduced from 2012.1 kW to 957.3 kW by using the proposed model. Literature [22] and literature [23] are smaller than the optimization results of the proposed algorithm. The experiments prove that the optimized model of this paper has significantly improved the system absorption and support capacity and enhanced the power transmission capacity of the distribution network.

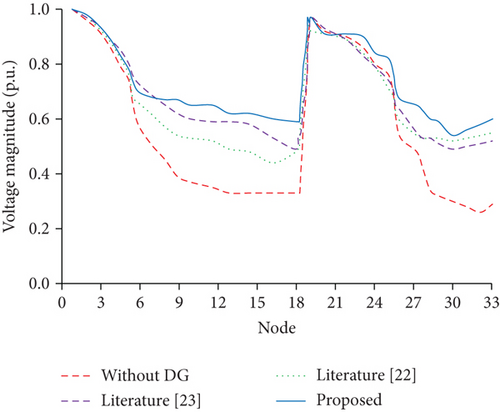
3.2.2. Node Voltage Impact Analysis

Figure 9 shows the voltage scaling values of each node before and after the access to DG with different optimization models for siting and capacity determination. From the figure, it can be seen that the minimum values of node voltages have been increased after accessing DG. When the distribution network is not connected to DG, the minimum value of system voltage is around 0.265 p.u. at node 32. In literature [22], the lowest node voltage amplitude was found at node 16 with 0.442 p.u. after the optimization of the model. In literature [23], the lowest node voltage amplitude occurs at node 18, which is about 0.496 p.u. The lowest node voltage amplitude occurs at node 30 after the input of the model optimization strategy in this paper, reaching a minimum voltage of 0.545 p.u. at the node. The results indicate that the overall boost voltage level is the best. In summary, in terms of voltage magnitude, the model in this paper has the best improvement on the system voltage, the model in literature [23] has the second-best improvement, and the model in literature [22] is the worst.

3.2.3. Comparative Analysis of Algorithm Effect

To demonstrate the optimization effect of the improved particle swarm algorithm, the improved algorithm in this paper and two other comparative algorithms are used to optimize under the same network. The results are shown in Figure 10 and Table 1.

Table 1. Comparison of optimization results of different algorithms.

Algorithm	Literature [22]	Literature [23]	Proposed
Minimum net loss (kWh)	1257.16	1392.72	957.33
Average number of iterations	131	175	71
Average time (s)	17.9	25.5	15.3

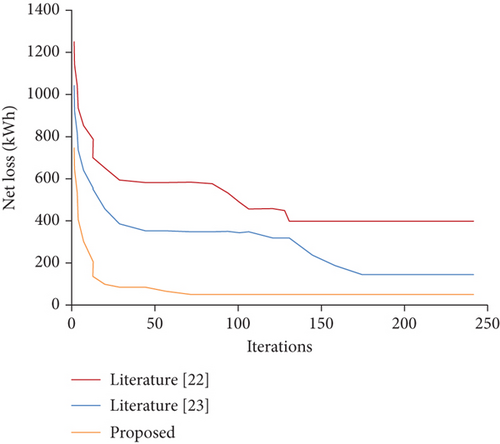
It can be seen from Figure 10 that the proposed algorithm has the smallest value of network loss. The improved PSO optimization algorithm access in this paper plays a significant role in the network loss reduction of the distribution network system. It shows that the algorithm improves the individual location optimization of the population and is effective, and the distributed power supply is connected from the lowest voltage node of the distribution network, which can raise the voltage of the accessed point and slow down the tidal current movement on the feeder, reducing the net loss to some extent. Since the results are better than other algorithms from the beginning, the convergence speed will be faster during the next optimal solution fine-tuning strategy.

Table 1 reveals that the three algorithms exhibit similar iteration accuracy, yet the enhanced PSO optimization algorithm presented in this paper demonstrates superior optimization accuracy. Regarding optimization efficiency, this algorithm achieves an average of 71 iterations, while the other two algorithms require 131 and 175 iterations. The improved algorithm in this paper exhibits the lowest number of iterations. Upon conducting 100 runs for each of the three algorithms, the algorithm proposed in this paper showcases the highest optimization efficiency, the shortest average time consumption, and superior optimization accuracy and efficiency.

Based on the experimental results, the proposed multistrategy fusion particle swarm optimization model demonstrates superior performance compared to other state-of-the-art optimization algorithms in several key aspects:

(1)
Network loss impact: the proposed algorithm significantly reduces network losses in the IEEE 33 node distribution network model, surpassing other state-of-the-art algorithms
(2)
Node voltage impact: the proposed algorithm effectively improves node voltage levels, leading to enhanced system voltage magnitude
(3)
Comparative analysis of algorithm effect: the proposed algorithm achieves the smallest network loss value compared to other algorithms. It also demonstrates superior optimization accuracy and efficiency with the fewest iterations required

The proposed algorithm exhibits clear superiority in terms of network loss reduction, node voltage improvement, optimization accuracy, convergence speed, and time consumption. These findings validate its effectiveness and competitiveness in optimizing the dynamic economic dispatch of renewable energy sources.

The proposed algorithm addresses the variability of renewable energy sources, such as wind and solar power, through dynamic economic dispatch strategies. It incorporates real-time optimization and forecasting techniques to account for the uncertain and fluctuating nature of these energy sources. By optimizing the scheduling and allocation of power generation, the algorithm effectively utilizes renewable energy while meeting load requirements. It adjusts power generation levels based on real-time measurements and feedback, ensuring efficient integration into the power grid. The proposed algorithm enables the effective utilization of renewable energy and reduces reliance on conventional sources.

4. Conclusion

This paper presents a multistrategy fusion-improved particle swarm algorithm for grid-connected optimization in distributed renewable energy systems. The algorithm focuses on minimizing network losses and enhancing node voltage stability, providing significant scientific value and practical applicability. By integrating the convergence strategy of the midperpendicular algorithm and the optimal particle explosion strategy, the algorithm achieves faster convergence with maintained accuracy. Simulation results demonstrate its effectiveness in reducing active power loss and voltage fluctuation, thereby improving power quality in distribution networks. Comparative analysis against traditional optimization algorithms verifies its superior performance in power loss reduction and voltage distribution. This study addresses specific optimization challenges in distributed renewable energy systems, showcasing its novelty. The extended application of this approach to systems incorporating renewable energy sources contributes to sustainable energy management. Additionally, the algorithm’s applicability in dynamic pricing for energy markets, considering environmental factors, presents new opportunities for efficient and ecofriendly energy systems. While the study demonstrates promising results, it is important to acknowledge limitations and potential challenges. Further investigation is needed to address scalability, parameter tuning, and handling the dynamic nature of renewable energy sources. Resolving these challenges will enhance the real-world implementation of the proposed algorithm.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

Authors’ Contributions

Feng Wu contributed to the writing of the manuscript and data analysis. Yueying Li supervised the work and designed the study. All the authors have read and agreed the final version to be published.

Acknowledgments

This work is supported by the Xinyang Agriculture and Forestry University.

Open Research

Data Availability

The labeled data set used to support the findings of this study is available from the corresponding author upon request.

References

1 Kandpal R. and Singh R., Renewable energy sources – a review, ECS Transactions. (2022) 107, no. 1, 8133–8140, https://doi.org/10.1149/10701.8133ecst.
10.1149/10701.8133ecst
CAS Google Scholar
2 Shan Y., Guan D., Zheng H., Ou J., Li Y., Meng J., Mi Z., Liu Z., and Zhang Q., China CO₂ emission accounts 1997–2015, Scientific Data. (2018) 5, no. 1, 1–14, https://doi.org/10.1038/sdata.2017.201, 2-s2.0-85040953060.
10.1038/sdata.2017.201
PubMed Web of Science® Google Scholar
3 Badran O., Mekhilef S., Mokhlis H., and Dahalan W., Optimal reconfiguration of distribution system connected with distributed generations: a review of different methodologies, Renewable and Sustainable Energy Reviews. (2017) 73, 854–867, https://doi.org/10.1016/j.rser.2017.02.010, 2-s2.0-85012013297.
10.1016/j.rser.2017.02.010
Web of Science® Google Scholar
4 Jafar-Nowdeh A., Babanezhad M., Arabi-Nowdeh S., Naderipour A., Kamyab H., Abdul-Malek Z., and Ramachandaramurthy V. K., Meta-heuristic matrix moth–flame algorithm for optimal reconfiguration of distribution networks and placement of solar and wind renewable sources considering reliability, Environmental Technology & Innovation. (2020) 20, https://doi.org/10.1016/j.eti.2020.101118.
10.1016/j.eti.2020.101118
Web of Science® Google Scholar
5 Galiveeti H. R., Goswami A. K., and Dev Choudhury N. B., Impact of plug-in electric vehicles and distributed generation on reliability of distribution systems, Engineering Science and Technology, an International Journal. (2018) 21, no. 1, 50–59, https://doi.org/10.1016/j.jestch.2018.01.005, 2-s2.0-85044079114.
10.1016/j.jestch.2018.01.005
Web of Science® Google Scholar
6 Song P., Lei Y., and Fu Y., Multi-objective optimization and matching of power source for PHEV based on genetic algorithm, Energies. (2020) 13, no. 5, https://doi.org/10.3390/en13051127.
10.3390/en13051127
Web of Science® Google Scholar
7 Abo El-Ela A. A., Allam S. M., Shaheen A. M., and Nagem N. A., Optimal allocation of biomass distributed generation in distribution systems using equilibrium algorithm, International Transactions on Electrical Energy Systems. (2021) 31, no. 2, article e12727, https://doi.org/10.1002/2050-7038.12727.
10.1002/2050-7038.12727
Web of Science® Google Scholar
8 Karunarathne E., Pasupuleti J., Ekanayake J., and Almeida D., Optimal placement and sizing of DGs in distribution networks using MLPSO algorithm, Energies. (2020) 13, no. 23, https://doi.org/10.3390/en13236185.
10.3390/en13236185
Web of Science® Google Scholar
9 Balu K. and Mukherjee V., Siting and sizing of distributed generation and shunt capacitor banks in radial distribution system using constriction factor particle swarm optimization, Electric Power Components and Systems. (2020) 48, no. 6-7, 697–710, https://doi.org/10.1080/15325008.2020.1797935.
10.1080/15325008.2020.1797935
Web of Science® Google Scholar
10 Li H., Liu Y., and Yang J., A novel FCS-MPC method of multi-level APF is proposed to improve the power quality in renewable energy generation connected to the grid, Sustainability. (2021) 13, no. 8, https://doi.org/10.3390/su13084094.
10.3390/su13084094
Web of Science® Google Scholar
11 Naderipour A., Abdul-Malek Z., Noorden Z. A., Davoudkhani I. F., Nowdeh S. A., Kamyab H., Chelliapan S., and Ghiasi S. M. S., Carrier wave optimization for multi-level photovoltaic system to improvement of power quality in industrial environments based on Salp swarm algorithm, Environmental Technology & Innovation. (2021) 21, https://doi.org/10.1016/j.eti.2020.101197.
10.1016/j.eti.2020.101197
Web of Science® Google Scholar
12 Hasanien H. M., Whale optimisation algorithm for automatic generation control of interconnected modern power systems including renewable energy sources, IET Generation, Transmission & Distribution. (2018) 12, no. 3, 607–614, https://doi.org/10.1049/iet-gtd.2017.1005, 2-s2.0-85041523929.
10.1049/iet-gtd.2017.1005
Web of Science® Google Scholar
13 Moghaddam S., Bigdeli M., and Moradlou M., Optimal design of an off-grid hybrid renewable energy system considering generation and load uncertainty: the case of Zanjan city, Iran, SN Applied Sciences. (2021) 3, no. 8, 1–15, https://doi.org/10.1007/s42452-021-04718-x.
10.1007/s42452-021-04718-x
Web of Science® Google Scholar
14 Jahannoosh M., Nowdeh S. A., Naderipour A., Kamyab H., Davoudkhani I. F., and Klemeš J. J., New hybrid meta-heuristic algorithm for reliable and cost-effective designing of photovoltaic/wind/fuel cell energy system considering load interruption probability, Journal of Cleaner Production. (2021) 278, https://doi.org/10.1016/j.jclepro.2020.123406.
10.1016/j.jclepro.2020.123406
Web of Science® Google Scholar
15 Yang X., Ye T., and Zhang Y., A novel optimization model for combined wind power accommodation and electric boiler with thermal storage, International Journal of Energy Research. (2019) 43, no. 12, 6494–6509, https://doi.org/10.1002/er.4525, 2-s2.0-85064511623.
10.1002/er.4525
Web of Science® Google Scholar
16 Li Z., Wang C., Li B., Wang J., Zhao P., Zhu W., Yang M., and Ding Y., Probability-interval-based optimal planning of integrated energy system with uncertain wind power, IEEE Transactions on Industry Applications. (2020) 56, no. 1, 4–13, https://doi.org/10.1109/tia.2019.2942260.
10.1109/TIA.2019.2942260
Web of Science® Google Scholar
17 Shakrina Y. and Margossian H., A Stackelberg game-inspired model of real-time economic dispatch with demand response, International Transactions on Electrical Energy Systems. (2021) 31, no. 11, article e13076, https://doi.org/10.1002/2050-7038.13076.
10.1002/2050-7038.13076
Web of Science® Google Scholar
18 Yu H., Gao Y., Wang L., and Meng J., A hybrid particle swarm optimization algorithm enhanced with nonlinear inertial weight and Gaussian mutation for job shop scheduling problems, Mathematics. (2020) 8, no. 8, https://doi.org/10.3390/math8081355.
10.3390/math8081355
Web of Science® Google Scholar
19 Yang Q., Zhu Y., Gao X., Xu D., and Lu Z., Elite directed particle swarm optimization with historical information for high-dimensional problems, Mathematics. (2022) 10, no. 9, https://doi.org/10.3390/math10091384.
10.3390/math10091384
Web of Science® Google Scholar
20 Boehnlein A., Diefenthaler M., Sato N., Schram M., Ziegler V., Fanelli C., Hjorth-Jensen M., Horn T., Kuchera M. P., Lee D., Nazarewicz W., Ostroumov P., Orginos K., Poon A., Wang X. N., Scheinker A., Smith M. S., and Pang L. G., Colloquium: machine learning in nuclear physics, Reviews of Modern Physics. (2022) 94, no. 3, article 031003, https://doi.org/10.1103/RevModPhys.94.031003.
10.1103/RevModPhys.94.031003
Web of Science® Google Scholar
21 Zhang L., Oh S.-K., Pedrycz W., Yang B., and Wang L., A promotive particle swarm optimizer with double hierarchical structures, IEEE Transactions on Cybernetics. (2022) 52, no. 12, 13308–13322, https://doi.org/10.1109/TCYB.2021.3101880.
10.1109/TCYB.2021.3101880
PubMed Web of Science® Google Scholar
22 Zhao F., Yuan J., and Wang N., Dynamic economic dispatch model of microgrid containing energy storage components based on a variant of NSGA-II algorithm, Energies. (2019) 12, no. 5, https://doi.org/10.3390/en12050871, 2-s2.0-85062669512.
10.3390/en12050871
Web of Science® Google Scholar
23 Mahmoud K., Abdel-Nasser M., Mustafa E., and Ali Z. M., Improved salp–swarm optimizer and accurate forecasting model for dynamic economic dispatch in sustainable power systems, Sustainability. (2020) 12, no. 2, https://doi.org/10.3390/su12020576.
10.3390/su12020576
Web of Science® Google Scholar

Citing Literature

All articles

Multistrategy Fusion Particle Swarm for Dynamic Economic Dispatch Optimization of Renewable Energy Sources

Abstract

1. Introduction

2. Methodology

2.1. Optimization Model of Distribution Network System with Distributed Renewable Energy