In this paper, an efficient new technique is used for solving nonlinear fractional problems that satisfy specific criteria. This technique is referred to as the double conformable fractional Laplace-Elzaki decomposition method (DCFLEDM). This approach combines the double Laplace-Elzaki transform method with the Adomian decomposition method. The fundamental concepts and findings of the recently suggested transformation are presented. For the purpose of assessing the accuracy of our approach, we provide three examples and introduce the series solutions of these equations using DCLEDM. The results show that the proposed strategy is a very effective, reliable, and efficient approach for addressing nonlinear fractional problems using the conformable derivative.

1. Introduction

Recent studies have shown that fractional calculus (FC) is needed to model many real-life situations in engineering and sciences. It has been widely employed in mathematics, mechanics, chemical engineering, and other scientific and technical disciplines [1–3]. According to recent research studies, fractional calculus can more effectively reflect some nonlinear effects. Fractional derivatives have been defined in a number of ways in the literature, like Caputo, Hadamard, Riesz, Weyl, Atangana-Baleanu-Caputo, Caputo-Fabrizio, conformable derivatives, M-truncated derivatives, and beta derivatives [4–9]. Most of these definitions referred to above lack some basic properties for the case of integer order, such as the property that not all of them follow the chain rule, the product rule, and the quotient rule of two functions, and the conformable derivative among them still fulfills the classical properties of integer derivatives. So, it is simple to use to solve linear and nonlinear fractional differential equations (NFDEs). Khalil et al. [4] developed the conformable derivative (CD), a more recent development of the conventional limit definition for the derivative of a function. This new derivative has been used with other methods [10–13] in a lot of different situations because it is so simple to use. Hashemi [10] established the invariant subspace approach for obtaining accurate solutions to a variety of conformable time fractional differential equations. Osman et al. [11] came up with a new way to solve singular fractional pseudohyperbolic and pseudoparabolic equations using a modified double conformable Laplace transform. A lot of NPDEs with conformable derivatives were solved using the conformable double Laplace-Sumudu iterative approach [12]. Bhanotar and Kaabar [13] came up with the conformable triple Laplace transform decomposition technique to solve NFPDEs analytically.

Various methods for transforming new double integrals have been successfully developed in recent years [14–17], where definitions and results have been provided and many different types of differential equations have been solved. Al-Sook and Amer [14] utilized the Laplace-Elzaki transform to solve the integral and partial differential equations. Elzaki and Iashag [15] obtained the solution of the telegraph equation by the Elzaki-Laplace transform. Ahmed et al. [16, 17] created the Laplace-Sumudu transform to solve a variety of fractional and partial differential equations.

George Adomian introduced the Adomian decomposition method (ADM) [18–23] in 1980, which is an effective approach for finding numerical and exact solutions to a broad class of differential equations that are either linear or nonlinear. This approach has the benefit of generating results quickly since it gives analytic series solutions to the target equations without the need for any constrained assumptions, transformations, or discretization. The double transformation techniques have some advantages over other strategies in that they have faster convergence to the solution. Regrettably, this transformation, like other transformations, lacks the ability to handle nonlinear situations. So, in this work, we have proposed a novel strategy that combines the double conformable Laplace-Elzaki transform with the decomposition method (DM) called the double conformable Laplace-Elzaki decomposition method (DCLEDM). The DCLEDM approach allows speedy convergence of the precise solution without making any restrictive assumptions about the answer. This is one advantage of employing the decomposition method in conjunction with the DCLET approach.

The following components comprise the study’s overall construction: Section 2 contains some essential definitions and theorems for conformable fractional derivatives (CFDs). Section 3 presents fundamental DCLET definitions, features, and theorems. Section 4 talks about the model and steps for using the DCLET and decomposition methods to solve the NCFPDEs that were mentioned analytically. Three hypothetical scenarios are given in Section 5 to illustrate the recommended approach’s liability, convergence, and efficacy. The statistical findings are given in Section 6. Section 7 includes conclusions.

2. Conformable Fractional Derivative (CFD)

To achieve our significant results, we now define the CFD and its fundamental qualities, which are described below.

Definition 1 (see [4].)Given that a function ψ : (0, ∞)⟶R is a real-valued function, then the CFD of ψ order ϑ₂ ∈ (0, 1] is defined by

(1)

Definition 2 (see [24].)Given that a function ψ(u, v): R × (0, ∞)⟶R, the conformable space and time fractional partial derivative for the function ψ(u, v) of orders ϑ₁ and ϑ₂, respectively, is given as follows:

(2)

(3)

where u, v > 0, 0 < ϑ₁, ϑ₂ ≤ 1,

, and

are referred to as FDs of order ϑ₁ and ϑ₂, respectively.

Proposition 3. Suppose 0 < ϑ₁, ϑ₂ ≤ 1, c, d, λ, and μ ∈ ℝ; then

(4)

3. Double Conformable Laplace-Elzaki Transform (DCLET)

In this part, we present the DCLET and some of its features that can be used to solve some NCFPDEs in the future. The reader can get more details about the proposed transformation in [14, 15].

Definition 4. Let ψ(u, v) be a function of two variables u, v ∈ ℝ⁺.

(i)
The CLT of ψ(u, v) with respect to u of exponential of order ϑ₁ is denoted by and defined as

(5)

The CET of ψ(u, v) with respect to v of exponential of order ϑ₂ is denoted by and defined as

(6)

(ii)
The DCLET of function ψ(u, v) of exponential of orders ϑ₁ and ϑ₂ is denoted by and defined as

(7)

where q, w ∈ ℂ, 0 < ϑ₁, ϑ₂ ≤ 1,

and

It is worth mentioning that if ψ(u, v) meets the essential requirements [25], then

(8)

and so,

(9)

The inverse double conformable Laplace-Elzaki transform (IDCLET) is defined by

(10)

Theorem 5 (see [26].)Assume ψ : ℝ × (0, ∞)⟶ℝ such that exists, then

(11)

where

Theorem 6 (see [14], [15].)The DCLET for a few functions is provided below.

Proof. Here, we provide evidence for results (1) and (3).

(1)

(3)

The same procedure may be used to illustrate the remaining outcomes.

Theorem 7 (see [26], [27] DCL-DCLE duality.)If the DCLET of ψ(u, v) exists, then

(12)

where

Theorem 8. Assume and ; then,

(i)
(ii)
(iii)
(iv)

Proof.

(i)
It is simple to verify (i) by using the definition of the CDSET
(ii)

Put s = (q/(1 + c₂q)); then,

(13)

(iii)
Suppose γ = λw and η = μv; then,

(14)

(iv)
Here, by combining Theorem 7 with Theorem 2.1 from [28], we obtain

(15)

Theorem 9 (see [14].)Suppose that ψ(u, v) is a function of exponential order a and b defined on the intervals (0, U) and (0, V); then, DLET of ψ(u, v) is well defined for all w and 1/q supplied Re[w] > a and Re[1/q] > b.

Theorem 10 (see [29].)If , then the DCLET of the FPDs and can be represented as follows: 0 < ϑ₁, ϑ₂ ≤ 1

(16)

The findings described above may be broadly expanded as follows:

(17)

Theorem 11 (convolution theorem). Assume that ψ(u, v) and ξ(u, v) are two functions of the CDSET; then,

(18)

where

Proof. Using Theorem 7 and Theorem 2.2 in [29], we obtain

(19)

The CDLET for certain essential functions is summarized in Table 1.

Table 1. DCLET for some functions of two variables [14, 15].

Sr. no
1	c
2	, m, n ∈ ℤ⁺
3
4
5
6
7
8

4. Descriptions of the Method

Utilizing the DCLET method and the decomposition method, this section looks at the general solution to the NPDEs of the conformable derivative type in the following form:

(20)

with the ICs

(21)

and the BCs

(22)

where

and

are linear and nonlinear operators, respectively, and

is the source term.

Operating the DCLET on both sides of Eq. (20), we get

(23)

Applying Theorem 10 in Eq. (23) yields

(24)

Using the CLT for the criteria (2) and the CET for the BCs (3), one can obtain

(25)

Substituting Eq. (25) into Eq. (24) yields the simplified

(26)

Taking the

on both sides of Eq. (26), we get

(27)

Here, we are assuming the existence of the

for all terms on the right side of Eq. (27).

The DCLEDM proposes an infinite series solution for the function

in infinite series:

(28)

Also, the nonlinear term

can be defined as

(29)

There are a few terms of the Adomian polynomial for A_i that go as follows:

(30)

We put the equations ((28) and (29)) into Eq. (27), to obtain

(31)

Now there is a general form of method, as follows:

(32)

(33)

4.1. Convergence of the Proposed Method

The method suggests that the solution is expressed in the form of an infinite series. Therefore, the concerned series rapidly converges to the solution. For more information about the convergence of the proposed method, you can refer to [30–33].

5. Numerical Applications

In this part, DCLEDM is applied to the following classes of NFPDs of the conformable derivative type to demonstrate the capability and effectiveness of DCLEDM.

Example 1. Consider the following NCFPD:

(34)

with the IC

(35)

and the BC

(36)

Solution: operating the DCLET on both sides of Eq. (34), we get

(37)

Applying the CLT for the IC (35) and the CET for the BC (36), one can obtain

(38)

Substituting Eq. (38) into Eq. (37) yields the simplified

(39)

By applying the on both sides of Eq. (39), we have

(40)

Now, by DCLEDM

(41)

The nonlinear term can be defined as

(42)

With

(43)

We put the equations ((41) and (42)) into Eq. (40), and then, we get

(44)

Some components of the Adomian polynomial A_i are given as follows:

(45)

and so on. As a result, the zeroth component from Eq. (44) is as follows:

(46)

Also, we can obtain the other components in the following form:

(47)

Thus, if we substitute Eq. (45) into Eq. (47), we get

(48)

Hence, we obtain the following series solution to Eq. (34):

(49)

If ϑ₁ = ϑ₂ = 1, we get

(50)

In the following example, we will discuss the solution of the KdV equation, which has many physical applications, including an approximate description of long water waves, acoustic wave propagation in plasma, long internal waves in density, and shallow water waves.

Example 2. Consider the fourth order KdV problem of NCFPD:

(51)

with IC

(52)

and BCs

(53)

Solution: by implementing the DCLET for both sides of Eq. (51), the CLT for Eq. (52), and the CET for Eq. (53), we get

(54)

(55)

According to equations ((31)–(33)), the first three terms are derived as follows:

(56)

Consequently, we derive the subsequent series solution for Eq. (51):

(57)

The exact solution, if ϑ₁ = ϑ₂ = 1, is

(58)

Example 3. Consider the following NCFPD:

(59)

with IC

(60)

Solution: by applying the DCLET to both sides of Eq. (59) and the CLT to Eq. (60), we get

(61)

By applying the on both sides of Eq. (61), we have

(62)

The DCLEDM proposes an infinite series solution for the function in infinite series:

(63)

Also, the nonlinear terms

and

can be defined by

(64)

where

(65)

We put the equations ((63) and (64)) into Eq. (62); then, we get

(66)

Some components of the Adomian polynomials A_i and B_i are given as follows:

(67)

(68)

As a result, the zeroth component from Eq. (59) is as follows:

(69)

Now, we can obtain the other components in the following general form:

(70)

Thus, substituting Eqs. (67) and (68) into Eq. (70), we get

(71)

Hence, we obtain the following series solution to Eq. (59).

(72)

The exact solution, if ϑ₁ = ϑ₂ = 1, is

(73)

6. Results and Discussion

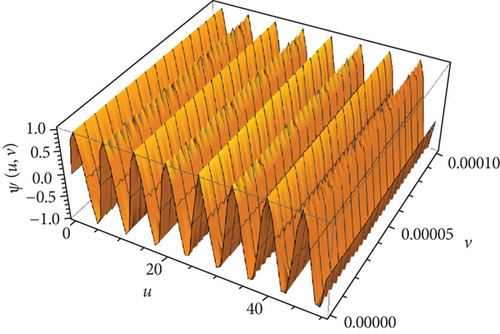
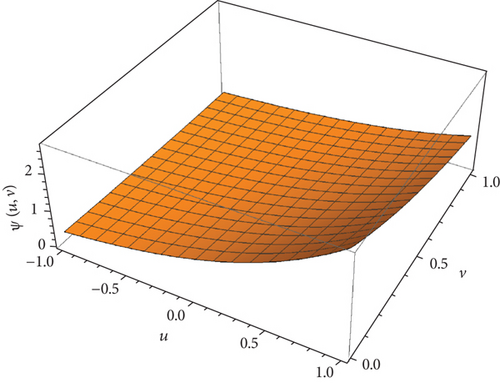
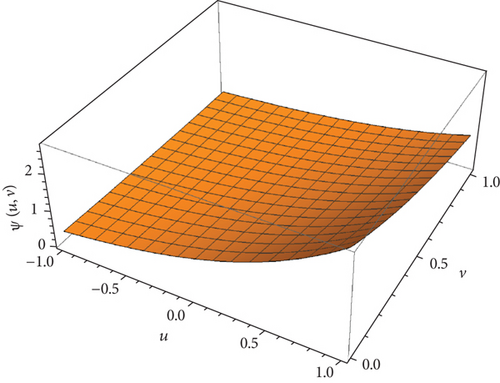
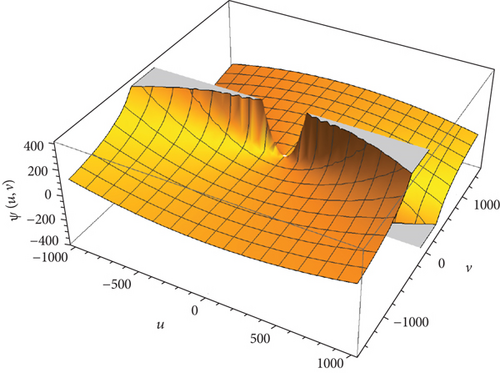
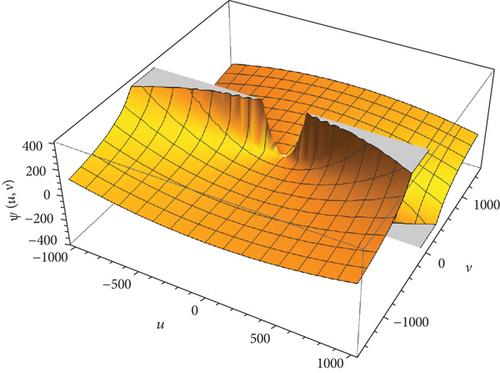
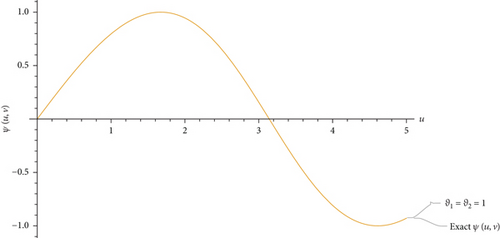
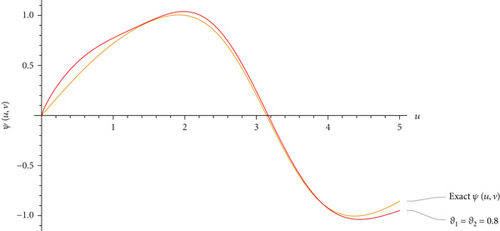
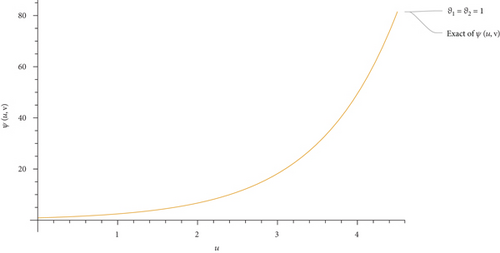
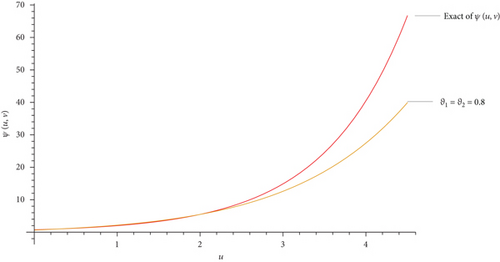
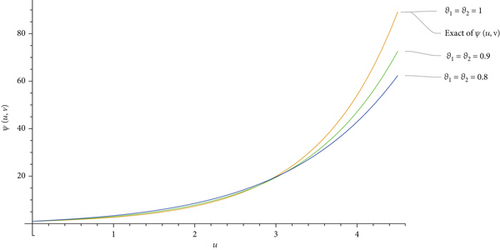
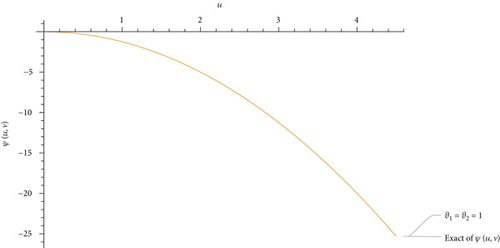
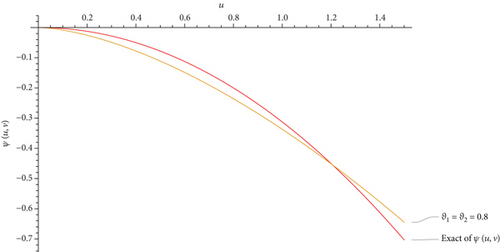
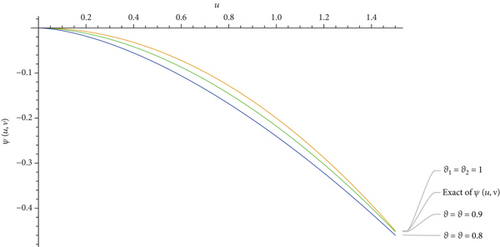
This part evaluates the precision and efficacy of the suggested method by comparing the approximate and exact results using graphical representations and tables. Figures 1-3 display the 3D plot of approximate solutions found using the current approach. These solutions are compared with the exact solutions for ϑ₁ = ϑ₂ = 1 in Examples 1–3. These figures show how well the precise answers and the DCLEDM approximations match up. These pictures (Figures 4-6) show lines that show how the proposed method’s approximation solutions compare to the exact answers from Examples 1–3. These comparisons are conducted for different values of the variable v as well as the fractional-order variables ϑ₁ and ϑ₂. The line plots of the estimated series solution using DCLEDM actually match those of the exact solution, as seen in the figures. Moreover, the solution obtained using the current method converges to the exact answer with greater accuracy as the order of approximation increases and the fractional values ϑ₁ and ϑ₂ approach one. Tables 2–4 compare the exact and approximate solutions for each example in relation to the absolute error at u = 1, ϑ₁ = ϑ₂ = 0.8,0.9, and 1 for various values of the variable v. Based on the data shown in the figures and tables, our solution technique demonstrates rapid convergence towards an accurate solution.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The 3D approximate solution of Example 3 to Eq. (49) was produced using the (a) DCLEDM with the (b) precise answer at ϑ₁ = ϑ₂ = 1.

Table 2. The analysis of the absolute error of

for Example 1.

u	v	ϑ₁	ϑ₂	CDLEDM ϑ₁ = ϑ₂ = 0.8,0.9	Exact ϑ₁ = ϑ₂ = 1	\|ψ_Exact − ψ_CDLEDM\| ϑ₁ = ϑ₂ = 0.8,0.9
1	0.01	0.8	0.8	0.939317	0.836932	1.02385 × 10⁻¹
	0.02			0.931822	0.832409	9.94127 × 10⁻²
	0.03			0.924856	0.827904	9.69516 × 10⁻²

1	0.01	0.9	0.9	0.889163	0.836932	5.22308 × 10⁻²
	0.02			0.883036	0.832409	5.06267 × 10⁻²
	0.03			0.877195	0.827904	4.92913 × 10⁻²

Table 3. The analysis of the absolute error of

for Example 2.

u	v	ϑ₁	ϑ₂	CDLEDM ϑ₁ = ϑ₂ = 0.8,0.9	Exact ϑ₁ = ϑ₂ = 1	\|ψ_Exact − ψ_CDLEDM\| ϑ₁ = ϑ₂ = 0.8,0.9
1	0.01	0.8	0.8	3.38245	2.69123	6.91219 × 10⁻¹
	0.02			3.30465	2.66446	6.40198 × 10⁻¹
	0.03			3.23615	2.63794	5.98208 × 10⁻¹

1	0.01	0.9	0.9	2.98471	2.69123	2.93471 × 10⁻¹
	0.02			2.93953	2.66446	2.75074 × 10⁻¹
	0.03			2.8973	2.63794	2.59351 × 10⁻¹

Table 4. The analysis of the absolute error of

for Example 3.

u	v	ϑ₁	ϑ₂	CDLEDM ϑ₁ = ϑ₂ = 0.8,0.9	Exact ϑ₁ = ϑ₂ = 1	\|ψ_Exact − ψ_CDLEDM\| ϑ₁ = ϑ₂ = 0.8,0.9
1	0.01	0.8	0.8	1.92519	1.06383	8.61359 × 10⁻¹
	0.02			2.32518	1.13636	1.18882
	0.03			2.86009	1.21951	1.64058

1	0.01	0.9	0.9	1.38042	1.06383	3.16593 × 10⁻¹
	0.02			1.53777	1.13636	4.01402 × 10⁻¹
	0.03			1.72426	1.21951	5.04744 × 10⁻¹

7. Conclusion

In this paper, the DCLEDM is introduced, along with a verification of its key features. Selected NCFPDEs are then solved using the DCLEDM. Additionally, graphical representations and tables are provided for the results of applying the DCLEDM, along with examples for various values of ϑ₁ and ϑ₂. We can conclude that this method can be a highly effective tool for solving a variety of fractional PDEs with conformable derivatives that arise in the fields of physics, chemistry, and engineering. In the future, the author also wants to look into resolutions for NCFPDEs by using DCLEDM and other noninteger fractional derivatives and then comparing the results with other methods to demonstrate the effectiveness of the method.

Conflicts of Interest

The authors declare that there are no conflicts of interest.

Open Research

Data Availability

The findings of this study are readily available from the author upon request for supporting data. Please contact the author with any data requests.

References

1 Miller K. S. and Ross B., An Introduction to the Fractional Calculus and Fractional Differential Equations, 1993, John Wiley & Sons, New York, USA.
Google Scholar
2 Podlubny I., Fractional Differential Equations, 1999, Academic Press, San Diego.
Web of Science® Google Scholar
3 Kilbas A. A., Srivastava H. M., and Trujillo J. J., Theory and Applications of Fractional Differential Equations, 2006, Elsevier, Amsterdam.
10.1016/S0304-0208(06)80001-0
Google Scholar
4 Khalil R., Al-Horani M., Yousef A., and Sababheh M., A new definition of fractional derivative, Journal of Computational and Applied Mathematics. (2014) 264, 65–70, https://doi.org/10.1016/j.cam.2014.01.002, 2-s2.0-84893186929.
10.1016/j.cam.2014.01.002
Web of Science® Google Scholar
5 Abdeljawad T., On conformable fractional calculus, Journal of Computational and Applied Mathematics. (2015) 279, 57–66, https://doi.org/10.1016/j.cam.2014.10.016, 2-s2.0-84911406110.
10.1016/j.cam.2014.10.016
Web of Science® Google Scholar
6 Tajadodi H., Khan A., Gómez-Aguilar J. F., and Khan H., Optimal control problems with Atangana-Baleanu fractional derivative, Optimal Control Applications and Methods. (2021) 42, no. 1, 96–109, https://doi.org/10.1002/oca.2664.
10.1002/oca.2664
Web of Science® Google Scholar
7 Bedi P., Kumar A., and Khan A., Controllability of neutral impulsive fractional differential equations with Atangana-Baleanu-Caputo derivatives, Chaos, Solitons & Fractals. (2021) 150, article 111153, https://doi.org/10.1016/j.chaos.2021.111153.
10.1016/j.chaos.2021.111153
Web of Science® Google Scholar
8 Ur Rahman R., Al-Maaitah A. F., Qousini M., Az-Zo’bi E. A., Eldin S. M., and Abuzar M., New soliton solutions and modulation instability analysis of fractional Huxley equation, Results in Physics. (2023) 44, article 106163, https://doi.org/10.1016/j.rinp.2022.106163.
10.1016/j.rinp.2022.106163
Web of Science® Google Scholar
9 Ur Rahman R., Faridi W. A., El-Rahman M. A., Taishiyeva A., Myrzakulov R., and Az-Zo’bi E. A., The sensitive visualization and generalized fractional solitons construction for regularized long-wave governing model, Fractal and Fractional. (2023) 7, no. 2, https://doi.org/10.3390/fractalfract7020136.
10.3390/fractalfract7020136
Web of Science® Google Scholar
10 Hashemi M. S., Invariant subspaces admitted by fractional differential equations with conformable derivatives, Chaos, Solitons and Fractals. (2018) 107, 161–169, https://doi.org/10.1016/j.chaos.2018.01.002, 2-s2.0-85041350011.
10.1016/j.chaos.2018.01.002
Web of Science® Google Scholar
11 Osman W. M., Elzaki T. M., and Siddig N. A. A., Modified double conformable Laplace transform and singular fractional pseudo-hyperbolic and pseudo-parabolic equations, Journal of King Saud University–Science. (2021) 33, no. 3, article 101378, https://doi.org/10.1016/j.jksus.2021.101378.
10.1016/j.jksus.2021.101378
Web of Science® Google Scholar
12 Ahmed S. A., Qazza A., Saadeh R., and Elzaki T., Conformable double Laplace–Sumudu iterative method, Symmetry. (2023) 15, no. 1, https://doi.org/10.3390/sym15010078.
10.3390/sym15010078
PubMed Web of Science® Google Scholar
13 Bhanotar S. A. and Kaabar M. K. A., Analytical solutions for the nonlinear partial differential equations using the conformable triple Laplace transform decomposition method, International Journal of Differential Equations. (2021) 2021, 18, 9988160, https://doi.org/10.1155/2021/9988160.
10.1155/2021/9988160
Web of Science® Google Scholar
14 Al-sook A. A. S. and Amer M. M., Laplace–Elzaki transform and its properties with applications to integral and partial differential equations, Journal of Natural Sciences, Life and Applied Sciences. (2019) 3, no. 2, 110–196, https://doi.org/10.26389/AJSRP.S130219.
10.26389/AJSRP.S130219
Google Scholar
15 Elzaki T. and Iashag A. A., Solution of telegraph equation by Elzaki-Laplace transform, African Journal of Engineering & Technology. (2022) 2, no. 1, 1–7, https://doi.org/10.47959/AJET.2021.1.1.8.
10.47959/AJET.2021.1.1.8
Google Scholar
16 Ahmed S. A., Elzaki T., Elbadri M., and Mohamed M. Z., Solution of partial differential equations by new double integral transform (Laplace-Sumudu transform), Ain Shams Engineering Journal. (2021) 12, no. 4, 4045–4049, https://doi.org/10.1016/j.asej.2021.02.032.
10.1016/j.asej.2021.02.032
Web of Science® Google Scholar
17 Elzaki T., Ahmed S., Areshi M., and Chamekh M., Fractional partial differential equations and novel double integral transform, Journal of King Saud University-Science. (2022) 34, no. 3, article 101832, https://doi.org/10.1016/j.jksus.2022.101832.
10.1016/j.jksus.2022.101832
Web of Science® Google Scholar
18 Adomian G., Nonlinear Stochastic Operator Equation, 1986, Academic Press, San Diego.
Google Scholar
19 Adomian G., Solution of physical problems by decomposition, Computers and Mathematics with Application. (1994) 27, no. 9-10, 145–154, https://doi.org/10.1016/0898-1221(94)90132-5, 2-s2.0-0000244996.
10.1016/0898-1221(94)90132-5
Web of Science® Google Scholar
20 Adomian G. and Rach R., Noise terms in decomposition solution series, Applied Mathematics and Computers. (1992) 24, no. 11, 61–64, https://doi.org/10.1016/0898-1221(92)90031-C, 2-s2.0-0002095007.
10.1016/0898-1221(92)90031-C
Google Scholar
21 Adomian G. and Rach R., Modified Adomian polynomials, Mathematical and Computer Modeling. (1996) 24, no. 11, 39–46, https://doi.org/10.1016/S0895-7177(96)00171-9, 2-s2.0-0030437455.
10.1016/S0895-7177(96)00171-9
Web of Science® Google Scholar
22 Az-Zo’bi E. A., Construction of solutions for mixed hyperbolic elliptic Riemann initial value system of conservation laws, Applied Mathematical Modelling. (2013) 37, no. 8, 6018–6024, https://doi.org/10.1016/j.apm.2012.12.006, 2-s2.0-84874563618.
10.1016/j.apm.2012.12.006
Web of Science® Google Scholar
23 Az-Zo’bi E. A., Modified Laplace decomposition method, World Applied Sciences Journal. (2012) 18, no. 11, 1481–1486.
Google Scholar
24 Thabet H. and Kendre S., Analytical solutions for conformable space-time fractional partial differential equations via fractional differential transform, Chaos Solitons Fractals. (2018) 109, 238–245, https://doi.org/10.1016/j.chaos.2018.03.001, 2-s2.0-85043306088.
10.1016/j.chaos.2018.03.001
Web of Science® Google Scholar
25 Love E., Changing the order of integration, Journal of the Australian Mathematical Society. (1970) 11, no. 4, 421–432, https://doi.org/10.1017/S1446788700007904, 2-s2.0-84974399433.
10.1017/S1446788700007904
Google Scholar
26 Eltayeb H. and Mesloub S., A note on conformable double Laplace transform and singular conformable pseudoparabolic equations, Journal of Function Spaces. (2020) 2020, 12, https://doi.org/10.1155/2020/8106494, 8106494.
10.1155/2020/8106494
Web of Science® Google Scholar
27 Elzaki T. M., Elzaki S. M., and Elnour E. A., On the new integral transform “Elzaki transform” fundamental properties investigations and applications, Global Journal of Mathematical Sciences. (2012) 4, no. 1, 1–13.
Google Scholar
28 Zkan O. and Kurt A., On conformable fractional double Laplace transform and its applications to fractional partial integro-differential equations, Journal of Fractional Calculus and Applications. (2020) 11, 70–81.
Google Scholar
29 Zkan O. and Kurt A., On conformable double Laplace transform, Optical and Quantum Electronics. (2018) 50, no. 2, 1–9, https://doi.org/10.1007/s11082-018-1372-9, 2-s2.0-85041542089.
10.1007/s11082-018-1372-9
Web of Science® Google Scholar
30 Kaya D. and Inan I. E., A convergence analysis of the ADM and an application, Applied Mathematics and Computation. (2005) 161, no. 3, 1015–1025, https://doi.org/10.1016/j.amc.2003.12.063, 2-s2.0-10644229158.
10.1016/j.amc.2003.12.063
Web of Science® Google Scholar
31 El-Kalla I., Convergence of the Adomian method applied to a class of nonlinear integral equations, Applied Mathematics Letters. (2008) 21, no. 4, 372–376, https://doi.org/10.1016/j.aml.2007.05.008, 2-s2.0-40149084513.
10.1016/j.aml.2007.05.008
Web of Science® Google Scholar
32 Eltayeb H., Mesloub S., and Kilicxman A., Application of double Laplace decomposition method to solve a singular one-dimensional pseudohyperbolic equation, Advances in Mechanical Engineering. (2017) 9, no. 8, 168781401771663, https://doi.org/10.1177/1687814017716638, 2-s2.0-85028339593.
10.1177/1687814017716638
Web of Science® Google Scholar
33 Habib U., Zeb S., Shah K., and Hussain S. M., KdV equation solution by double Laplace Adomian decomposition method and its convergence analysis, Mathematical Problems in Engineering. (2022) 2022, 8, https://doi.org/10.1155/2022/1132557, 1132557.
10.1155/2022/1132557
Google Scholar

Citing Literature

All articles

An Efficient New Technique for Solving Nonlinear Problems Involving the Conformable Fractional Derivatives

Abstract

1. Introduction

2. Conformable Fractional Derivative (CFD)

3. Double Conformable Laplace-Elzaki Transform (DCLET)

4. Descriptions of the Method

4.1. Convergence of the Proposed Method

5. Numerical Applications

6. Results and Discussion

7. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

An Efficient New Technique for Solving Nonlinear Problems Involving the Conformable Fractional Derivatives

Abstract

1. Introduction

2. Conformable Fractional Derivative (CFD)

3. Double Conformable Laplace-Elzaki Transform (DCLET)

4. Descriptions of the Method

4.1. Convergence of the Proposed Method

5. Numerical Applications

6. Results and Discussion

7. Conclusion

Conflicts of Interest

Open Research

Data Availability

References

Citing Literature

Figures

References

Related

Information