A Mathematical Analysis of the Impact of Immature Mosquitoes on the Transmission Dynamics of Malaria
Abstract
This study delves into the often-overlooked impact of immature mosquitoes on the dynamics of malaria transmission. By employing a mathematical model, we explore how these aquatic stages of the vector shape the spread of the disease. Our analytical findings are corroborated through numerical simulations conducted using the Runge–Kutta fourth-order method in MATLAB. Our research highlights a critical factor in malaria epidemiology: the basic reproduction number . We demonstrate that when is below unity , the disease-free equilibrium exhibits local asymptotic stability. Conversely, when surpasses unity , the disease-free equilibrium becomes unstable, potentially resulting in sustained malaria transmission. Furthermore, our analysis covers equilibrium points, stability assessments, bifurcation phenomena, and sensitivity analyses. These insights shed light on essential aspects of malaria control strategies, offering valuable guidance for effective intervention measures.
1. Introduction
Plasmodium is the parasite that causes malaria, which is a protozoan disease. The female Anopheles mosquito, which has an estimated lifespan of at least 5 months, is the carrier of this parasite. The typical lifespan of their male counterparts is barely 6–7 days. The Plasmodium parasite causing malaria in humans is typically divided into four kinds. We have the vivax, falciparum, malariae, and ovale. Ninety-five percent of incidences come from the first two [1]. Malaria is usually transmitted after a female Anopheles mosquito carrying the parasite stings a victim. High fever, headache, sweating, chills, and shivering with a drop in body temperature are all signs of malaria. In severe cases, there is anaemia, enlarged liver and spleen, and general ill health. Malaria has been globally considered a problem. The World Health Organization approximated that about 178 million infections were confirmed [2]. Out of this, African countries contributed 171 million, and Ghana, almost 7 million cases. An attempt to control and eliminate pathogens responsible for the spread of communicable diseases has been of great interest in the field of public health as far back as the early 1950s. In the 1960s, there were indications of hope from the practices that seemed to eliminate these diseases. Improved sanitation and the use of antibiotics were contributing factors to the elimination of most infectious diseases. Nonetheless, these agents, with time, get adapted to the control strategies and resurface in probably different forms [3]. Organisms’ medical resistance resulting in the growth of new forms of microorganisms and diseases is usually related to population growth, climate change, increased urbanization, and increased travel. A lot of research has been conducted employing mathematical modelling to understand the dynamics of diseases and strategies for combatting them [4–10]. Malaria has been a menace and sometimes fatal epidemic disease that affects about half or a greater portion of the world’s populace. The World Health Organization estimated a total of 168 million confirmed cases of malaria were recorded in 2016, which rose to 241 million cases in 2020 [2]. Whitty and Ansah [11] estimated that the number of deaths resulting from malaria stood at 435,000 in 2019. Malaria stands fifth in the world in terms of infectious diseases leading to death while being second in Africa. Due to this, a number of research has been made by a whole lot of researchers interested in the eradication of the disease. Oke et al. [12] formulated a mathematical model for malaria, taking into consideration control measures such as treated bed nets, medication, and insecticide spray. Their study revealed that the combination of treatment and treated bed nets is the best control measure. Further, Abioye et al. [13] proposed a malaria model incorporating four control strategies: insecticide-treated bed net control, infected human treatment control, sterile mosquito technique control, and use of control on pregnant women and newborn births. They concluded that if the controls are well managed and implemented, then it would curb or limit the transmission of malaria between vector–host–related populations. Iboi, Gumel, and Taylor [14] presented a new mathematical model for assessing the impact of sterile insect technology (SIT) and seasonal variation in local temperature on the population abundance of malaria mosquitoes in an endemic setting. These research works were based on adult mosquitoes.
In a study of Layie et al. [15], an agent-based model (ABM) was proposed to assess and examine the impact of mosquito’s aquatic habitat (AH) destruction program and also bring out guidelines for larval source management (LSM) by AH destruction. They also took into account the questing–resting to represent the number of infectious bites in our ABM which had not yet been carried out until now. Also, Koutou, Traoré, and Sangaré [16] proposed the vector population dynamic model including autoregulation phenomena of eggs, larvae, and pupae. Their results showed that the effect of immature stages is very important in the mosquito’s population proliferation. Traoré, Koutou, and Sangaré [17] formulated a deterministic mathematical model of malaria transmission by incorporating seasonality. They took into account the four distinct mosquito metamorphic stages. It was coupled with two submodels, namely, the model of mosquito population and the model of malaria parasite transmission due to the interaction between mosquitoes and humans. Very few work has been done considering the immature stages (egg, larva, and pupa) of the vector as cited above, yet these stages of mosquitoes play a major role in the transmission of malaria. They grow into infected adult mosquitoes, and the spread of the disease continues when they could have been economically controlled. Olaniyi et al. [18] presented a model to control malaria transmission dynamics while considering the social classes of the human population and their interaction with the mosquito population. They further classified each social class into three compartments. That is, susceptible, infectious, and recovered with temporal immunity. They also divided the vector population into susceptible and infectious. Their model could not account for the impact of immature mosquitoes on the transmission dynamics and control. Also, Tchoumi et al. [19] proposed a malaria model with an age structure consisting of SEIS for individuals below the age of 5 years and then SEIRS for those aged 6 years and above. The vector population was also put under three compartments, that is, susceptible, exposed, and infectious. The principal objective of their study was to verify if it was justifiable to place emphasis on fighting malaria in children below the age of 5 and also to determine if the preventive measures taken affect the general endemicity of the disease in the human population positively. Their results showed that controlling malaria in children below the age of 5 years when stepped up could eradicate the disease completely. The works of Tchoumi et al. [19] coupled with that of Olaniyi et al. [18] serve as motivation to restructure the human population by adding the vaccinated class to the human population and also the immature stages of the vector to improve the understanding of the transmission dynamics and control of malaria.
This research therefore seeks to present a mathematical epidemiological model that will help investigate the impacts of immature mosquitoes and vaccination on the transmission dynamics of malaria. The paper is divided into the following sections: Section 2 entails the formulated proposed model, while analytical analysis is presented in Section 3. Numerical simulations performed in support of previous sections are captured in Section 4. Finally, Section 5 consists the conclusion.
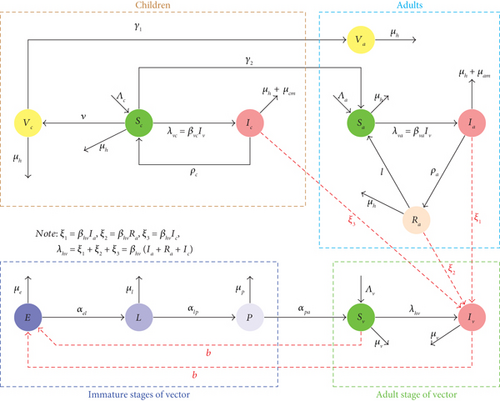
2. Model Formulation
The life cycle of the vector (female Anopheles) passes through four different developmental stages. These include the egg, larval, pupal, and adult stages. The first three stages are considered immature and usually aquatic, while the last stage is arboreal [20, 21]. Blood is sucked when an infected adult female mosquito bites a human. These female mosquitoes feed on the blood of the exposed human, which is then utilized to produce eggs. When conditions are favorable, the eggs that are laid on the surfaces of water hatch into larvae a few days afterwards. In unfavourable conditions such as drought, the eggs may take several months to hatch. The larvae are very small in size. They usually depend on organic matter and algae for food [22, 23]. Larvae are considered cannibal because, under adverse conditions, they feed on earlier-stage larvae. After the larvae have undergone complete moulting, they become pupae. The pupal stage is regarded as the resting and dormant developmental phase. This is a period when the pupae grow into the adult-stage mosquito. Here, the skin of the pupa sheds, and the adult mosquito develops [24, 25]. Therefore, in the model, the mosquito population is divided into two stages, immature and mature stages. The immature compartments at any given time (t) are further divided into eggs (E), larvae (L), and pupae (P), while the adult (A) mosquito is subdivided into two groups: susceptible mosquitoes (Sv) and infectious mosquitoes (Iv). The total adult vector population is given by Nv(t) = Sv(t) + Iv(t).
| Parameter | Description |
|---|---|
| ν | Vaccination rate among children |
| μh/μv | Natural death rate in humans/vectors |
| μe | Failure rate of eggs to hatch |
| μl | Failure rate of larvae to develop into pupa |
| μp | Failure rate of pupae to develop into adult mosquitoes |
| αel | Rate of transition from egg stage to larva stage |
| αlp | Rate of transition from larva stage to pupa stage |
| αpa | Rate of transition from pupa stage to susceptible mosquito |
| βhv | Probability of infection per contact with infected human |
| βvc(βva) | Probability of infection among children (adults) per contact with infectious mosquito |
| b | Egg-laying rate in vectors |
| Λc/Λa/Λv | Recruitment rate into children/adult/vector population |
| γ1(γ2) | Transition rate of vaccinated (unvaccinated) children into adults |
| ρc, (ρa) | Rate of recovery from malaria among children (adults) |
| μcm, (μam) | The mortality rate attributed to malaria in children (adults) |
| ℓ | Rate of waning of postmalaria recovery immunity in adults |
| ξ1,2,3 | Rate of acquisition of protozoan from human reservoirs (Ia, Ra, and Ic, respectively) |
3. Basic Properties of the Model
3.1. Positivity of Solution
Theorem 1. Given the initial conditions of the state equations being nonnegative (thus E(0) ≥ 0, L(0) ≥ 0, P(0) ≥ 0, Sv(0) ≥ 0, Iv(0) ≥ 0, Sc(0) ≥ 0, Vc(0) ≥ 0, Ic(0) ≥ 0, Sa(0) ≥ 0, Ia(0) ≥ 0, Ra(0) ≥ 0, and Va(0) ≥ 0), then the future solutions are also nonnegative (i.e., E(t) ≥ 0, L(t) ≥ 0, P(t) ≥ 0, Sv(t) ≥ 0, Iv(t) ≥ 0, Sc(t) ≥ 0, Vc(t) ≥ 0, Ic(t) ≥ 0, Sa(t) ≥ 0, Ia(t) ≥ 0, Ra(t) ≥ 0, and Va(t) ≥ 0) for all t > 0.
Proof 1. Given t > 0 as the initial time such that E(t) = 0. Then, from the first equation, we have dE/dt = bNv ≥ 0. Hence, E(t) ≥ 0 ∀ t > 0.
Also, at a positive time t, if Sv(t) = 0, then the fourth equation becomes Svt = Λc + ρcIc ≥ 0, which shows that Sv(t) ≥ 0 and ∀t > 0. It is clear that the rest of the state variables can similarly be proven as nonnegative at any positive time. This concludes the proof.
3.2. Boundedness and Feasible Region of Solutions of Model
In this section, it is demonstrated that the model can be thoroughly examined within a specific area. We have provided the circumstances in the theorem below.
Theorem 2. All solutions of Model (1) are uniformly bounded and contained in the feasible region defined by , where and This implies that the region is positively invariant under the flow defined by Model (1).
Proof 2. If the total adult vector and human populations are identified by Nv and Nh, then Nv = Sv + Iv and Nh = Sc + Vc + Ic + Sa + Ia + Ra + Va, respectively. Then, we have Nvt = Λv − Nvμv and Nht = Λc + Λa − Nhμh − (μcmIc + μamIa).
From Nvt, we have Nvt ≤ Λv − Nvμv.
By standard comparison theorems [26], we have so that .
Also, from Nvt, we have , where Λ = Λc + Λa.
Hence, all solutions are uniformly bounded.
Let and .
Then, the region is positively invariant under Model (1). Hence, the model is mathematically and epidemiologically well posed, and therefore, it is sufficient to study the model in . This concludes the proof.
3.3. Equilibrium Points
- 1.
The model has a unique endemic equilibrium whenever Φ0 < 0 (equivalently ).
- 2.
The model has two endemic equilibria whenever Φ0 > 0 (equivalently ) and Φ1 < 0.
3.4. Local Stability Analysis of Equilibrium Points
Here, the indirect Lyapunov method is used to analyze the local stability of the malaria-free and malaria-persistent equilibrium points. With this approach, an equilibrium point x∗ of a model xt = f(x) is considered as locally asymptotically stable if all eigenvalues of the Jacobian of the model evaluated at x∗ have negative real parts.
From Routh–Hurwitz stability conditions, the malaria-free equilibrium point is said to be locally asymptotically stable if the following conditions hold.
Condition 1.
Condition 2. .
Substituting the expressions for and simplifying shows that Condition (1) holds always. Condition (2) holds only when . The following result is therefore established.
Theorem 3. The disease-free equilibrium point is locally asymptotically stable whenever and unstable otherwise.
3.5. Global Stability of the Malaria-Free Equilibrium Point
3.6. Sensitivity Analysis of
Sensitivity analysis helps understand how small adjustments in parameter values impact disease transmission. In this study, the sensitivity of malaria transmission to parameter changes was assessed using the basic reproduction number , which indicates whether the disease might be eliminated or persist. The analysis utilized the normalized forward sensitivity index.
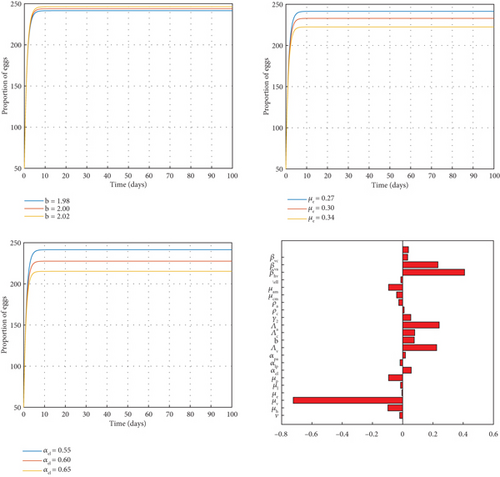
The sensitivity indices for concerning the model parameters are computed and detailed in Table 2, utilizing the parameter values specified in Table 3. These sensitivity indices illustrate the percentage alteration in a model’s output due to a percentage shift in the model parameter. A positive (negative) sensitivity index of a parameter signifies that a percentage rise (decline) in the model parameter leads to an increase (decrease) in . Conversely, a negative 100 sensitivity index suggests that an increase (decrease) in the parameter’s value will induce a decrease (increase) in . The corresponding Latin hypercube plot is represented in Figure 2.
| Parameter | Numerical sensitivity index | Parameter | Numerical sensitivity index |
|---|---|---|---|
| αel | −0.2222 | μp | 0.2500 |
| αlp | −0.2857 | μh | −0.9201 |
| αpa | −0.2500 | μcm | −0.0099 |
| βhv | 0.5000 | μam | −0.0635 |
| βva | 0.4316 | μv | −0.3334 |
| βvc | 0.0684 | ν | −4.1759 × 10−4 |
| Λv | 1/2 | γ2 | 8.9708 × 10−5 |
| Λc | 0.0685 | ρa | 3.6437 × 10−06 |
| Λa | 0.4315 | ρc | −0.0062 |
| μe | 0.2222 | b | −0.6666 |
| μl | 0.2857 | l | −2.4706 × 10−7 |
| Parameter | Value per day | Source |
|---|---|---|
| ν | 0.01 | Assumed |
| μh | 1.6300 | [29] |
| μv | 0.119 | Assumed |
| μe | 0.3 | [24] |
| μl | 0.3 | [24] |
| μp | 0.15 | [24] |
| αel | 0.60 | [24] |
| αlp | 0.40 | [24] |
| αpa | 0.25 | [24] |
| Λv | 5.000 | Assumed |
| b | 2.0 | [24] |
| Λc | 10 | Assumed |
| Λa | 20 | Assumed |
| γ1 | 0.10 | [29] |
| γ2 | 0.001 | [29] |
| ρc | 0.1930 | Assumed |
| ρa | 0.0001 | Assumed |
| μcm | 0.3100 | [29] |
| μam | 0.2810 | [29] |
| ℓ | 0.0155 | Assumes |
| βhv | 0.0452 | Assumed |
| βva | 0.0320 | Assumed |
| βvc | 0.0114 | Assumed |
3.7. Bifurcation Analysis
The center manifold theory as described in Theorem 4.1 of [30] is used for the bifurcation analysis.
Clearly, a < 0 and b > 0, and hence following Theorem 4.1 of [30], the following result is established.
Theorem 4. Bifurcation at .
- 1.
Whenever , then the malaria-free equilibrium is locally asymptotically stable, and there is no endemic equilibrium.
- 2.
Whenever , then the malaria-free equilibrium is unstable, and a stable endemic equilibrium appears.
- 3.
The Malaria Model (1) exhibits forward bifurcation at .
4. Numerical Simulation
In this section, we carried out numerical simulations to illustrate some analytical conclusions and to analyze the impact of some model parameters on the dynamics of malaria. MATLAB software with the Runge–Kutta fourth-order method was used in the numerical simulation for the model of Equation (1). The values of the parameters are given in Table 3 and the initial conditions E(0) = 50, L(0) = 40, P(0) = 30, Sv(0) = 55, Iv(0) = 45, Sc(0) = 50, Sa(0) = 200, Ic(0) = 500, Ia(0) = 350, Vc(0) = 30, Ra(0) = 400, and Va(0) = 20.
From Figure 2, the rate of growth of egg numbers is proportional to the egg-laying rate in vectors (b). An increase or decrease in the growth of eggs results in a corresponding change of b. This therefore increases the population of the larva (L) class. Failure rate of eggs to hatch (μe) and rate of transfer from egg stage to larva stage (αel) are inversely proportional to the rate of growth of the egg population. That is, an increase in μe or αel leads to a decrease in the population of the egg compartment and consequently a decrease in the larva population.
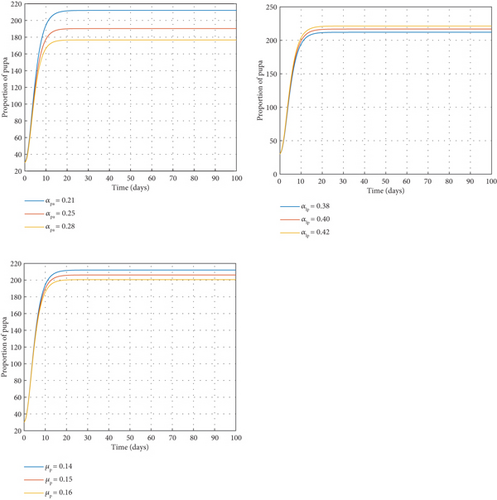
Figure 3 shows a negative correlation between the rate of transfer from the pupa stage to susceptible mosquitoes (αpa) and the pupal population. It means an increase in one quantity leads to a decrease in another and subsequently a decrease in the population of the next compartment, that is, the susceptible mosquitoes. When the rate of transfer from larva stage to the pupa stage (αlp) increases, it results in a corresponding increment in the population of the pupal class and vice versa. This obviously will result in an increase in the larval population. The graph also indicates an indirect proportion between the parameter and the variable. For this reason, an increase in the failure rate of pupae to develop into adult mosquitoes (μp) will yield a reduction in the number of pupa.
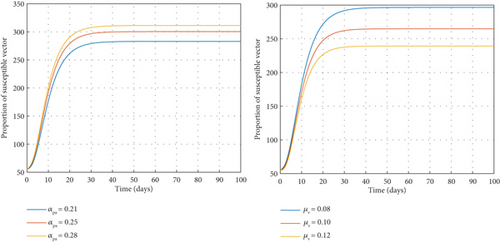
A decrease in the rate of transfer from the pupa stage to susceptible mosquitoes (αpa) always results in a corresponding decrease in the population of susceptible vectors and vice versa, as seen in Figure 4. An increase in the natural death rate in adult vectors (μv) will lead to a decrease in the susceptible vector population and eventually a decline in the population of the infected vector compartment.
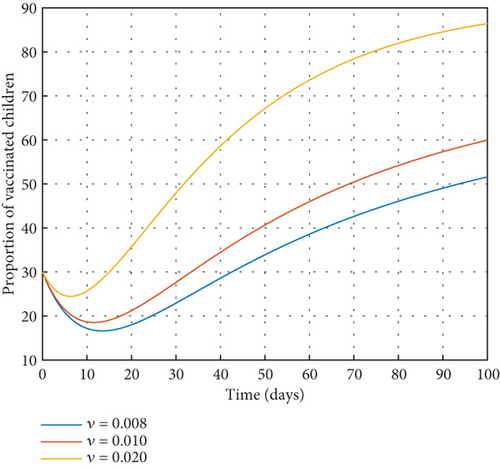
Increasing or decreasing the vaccination rate among children (ν) results in an initial fall in the number of vaccinated children as displayed in Figure 5. But then, after some days, there is a great increment in the vaccinated children population. It is clear that increasing ν will result in the growth of the proportion of vaccinated children.
5. Conclusions
In this research, we proposed a mathematical model to study the impact of immature mosquitoes and vaccination on the transmission dynamics of malaria. The basic reproduction number is computed to measure the potential of the disease. The disease-free and endemic equilibrium points are shown to be asymptotically stable whenever and , respectively. The sensitivity analysis and numerical simulations performed confirmed that parameters with positive sensitivity indices should be decreased, while the parameters that are inversely related to the basic reproduction number should be increased so as to minimise the transmission of malaria. The analysis further showed that in the management of malaria, immature mosquitoes are essential. It therefore suggests that individuals, the general public, and the government must strengthen activities and campaigns and formulate policies to control the immature stages of the vector at all levels (homes, markets, institutions, and firms) to eradicate malaria completely. These findings are supported by [16]. The use of vaccines in newborn babies also helps in mitigating malaria, as shown in the analysis.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
There is no funding from any institution or organization.
Appendix A
Open Research
Data Availability Statement
All data used to support the findings of this study are included within the article.




