Fractional Derivative Technique for Modeling the Dynamics of Social Media Impacts
Abstract
The advent of social media (SM) platforms has transformed communications, information dissemination, and interpersonal relationships on a global scale. As SM continues to evolve and proliferate, its impact on various aspects of society has become increasingly complex and multifaceted. For this reason and over the past decades, several controversies have been held about whether SM is good or bad. However, the mathematical modeling technique inculcating SM impacts (positive and negative) has not been studied in the existing works. This article considers a mathematical model approach using the ABC-fractional derivative technique to study the dynamics of SM impacts. We provide the various definitions and the properties needed to study the model. Also, we use the fixed point theorem and a nonlinear analytic approach to demonstrate the theoretical solutions of the existence of solutions for the proposed model. Furthermore, the fundamental reproduction number is computed, and the stability of the model is achieved using the Ulam–Hyers (HU) criteria. We again perform a sensitivity study for the SM impact model and the effects of the sensitive parameters are presented in 3D and contour plots. In addition, a numerical algorithm of the predictor–corrector type of the Adams–Bashforth method for determining the approximate solution of the model is developed and the results are discussed. The effects of the most sensitive parameters on affected individuals in the model with a constant fractional order are shown and discussed. The simulation results indicate that as individuals become aware of the negative impacts of SM, the number of positively impacted individuals rises.
1. Introduction
Social media (SM) has significantly changed the entire world in recent times. The most common technology that receives widespread attention and shapes a society’s or an individual’s interaction with communication is SM. According to [1], SM influences people in both positive and negative ways. People utilize SM in a variety of fields which are not limited to entertainment industries, health sectors, business environment, and educational systems [2, 3]. People also use SM platforms like Google to acquire information that piques their interest. Other individuals establish new or old acquaintances, generate money, present their work, create advertising items, and trade their commodities through SM platforms like Facebook, Instagram, TikTok, and YouTube. Twitter users can play games from various programs and communicate pieces of information easily [4–6].
Students who use networking sites perform noticeably better academically, partly because they may interact with one another for outside-of-class collaboration projects and schoolwork tasks. For instance, Facebook enables students to congregate outside of class to discuss assignments [7]. SM’s user base is expanding at an exponential rate, so businesses use this channel to advertise their products while promoting their brands, highlighting their benefits, and raising awareness. SM helps users feel linked to each other [8], which could help people who feel less socially isolated. SM provides a range of channels for communication with individuals who are close and those who are not [9]; it also has a big impact on how people of all ages use their sense of community [10].
An increasing body of research highlights SM as a new communication channel [8, 11]. SM can be crucial in building one’s presence, identity, and reputation, which in turn helps with social interaction, relationship building and maintenance, and idea sharing [12]. It is interesting to note that recent studies (e.g. [11, 13]) have indicated that the effect of smartphone use on psychological well-being relies on the amount of time users spend using each type of application and the activities they carry out. This paper [14] explored the impact of SM on psychological well-being, using a quantitative study of 940 users from Mexico. The study discovered that using SM had a beneficial indirect effect, mostly because it facilitated social capital bridging and bonding.
Even though SM is now a part of our daily lives and we have shown above some of the significance emanating from the use of SM, it can adversely impact the lives of individuals or society in general. As a result, there are more worries about the potential negative effects of SM [15, 16]. The adverse impacts of SM can be viewed in three main domains: It promotes a false sense of online “connections” and superficial friendships resulting in emotional and psychological challenges, easy addiction, and wasting family and personal time with the effect of diminishing interpersonal skills and causing antisocial behavior, and finally, SM is now acting as a tool for criminals, predators, and terrorists allowing them to commit illegal acts [17]. According to the National Children’s Home study, one in four children in Britain reported experiencing online bullying which has left teenagers with lasting psychological damage contributing to teen suicides [7].
SM addiction is one of the important factors contributing to severe negative effects. People who devote their time to SM in their daily lives and get nervous when they cannot visit a site are referred to as having SM addiction [18, 19]. In reality, addiction to SM is a form of addiction similar to psychological issues with drinking, smoking, video game addiction, etc. [20]. SM, according to [21], robs us of self-control and the capacity to think for ourselves and instead makes us naive enough to join any group that posts abnormal statements that touch our ears and amuse our senses without weighing the repercussions.
The intense nature of the online environment, which necessitates frequent interaction, however, fosters a level of self-awareness that in some individuals may lead to despair. Like those who experience depression offline, those who experience depression on Facebook run the danger of social exclusion and occasionally seek out harmful websites and blogs for “help” that may encourage substance misuse, unsafe sexual behavior, and aggressive and self-destructive actions [22]. Social isolation, anxiety, loneliness, and depression have all been linked to SM use [23], as well as “phubbing,” which refers to the use of or distraction from a smartphone while engaging in face-to-face conversation with others [24–26].
The creation of mathematical models is essential for comprehending how these problems behave dynamically. For example, the authors of [27, 28] created a mathematical model that correctly projected the methamphetamine epidemic in South Africa. The authors [29] used psychological addicts to investigate the stability of epidemic models for the spread of synthetic medications. Additionally, the authors [30] examined the global stability and backward bifurcation of a synthetic drug transmission model with therapy. Further recommended readings include an alcoholism model incorporating treatment and Twitter’s impact [30], an online game addiction model [31], and a mathematical model of Bangladesh’s smoking pandemic [32].
The application of Liouville–Caputo fractional-order derivative (LC), Caputo–Fabrizio fractional-order derivative (CF), and others has recently been applied to mathematical models in recent times. For the fractional-order models, we recommend the reader explore the following references and the references therein [33–42]. Additionally, a few mathematicians have used the fractional-order derivative to address social-related problems. Conventional integer differential equations are unable to offer information between two integer values while fractional differential equations can help make this information clear [43]. The authors [44] investigated the fractional model of SM addiction utilizing the Caputo differential operator. The authors [45] studied a fractional model for giving up smoking dynamics using CF. An alcoholism model of the CF type with fractional order and a fixed point theorem was provided in [46]. Modeling of LC tobacco smoking has been developed and studied in [47]. Among the most well-known operators for fractional derivatives is Atangana–Baleanu–Caputo which was originally accomplished in [48]. The authors in [49] have used fractional-order derivative to study polycystic ovarian syndrome disease including medication and treatment mechanisms for infertility in women. The authors in [50] have analyzed the chaotic behavior of a fish farming model with singular and nonsingular kernels. A fractional model of the effect of awareness programs by media on the binge drinking model with Mittag-Leffler kernel is studied in [51]. The authors in [52] have investigated the E-cigarette smoking model with the Mittag-Leffler kernel. The authors [53] have used mathematical analysis and simulation of a giving up smoking model employing a nonsingular derivative. Mathematical analysis and numerical simulation for a smoking model with Atangana–Baleanu derivative were studied in [54]. The authors in [55] used the Legendre wavelet method–based solution of fractional-order prey–predator model in a type-2 fuzzy environment. In many practical applications, the ABC-fractional derivative produces better results. The authors [56–65] have used ABC-fractional derivatives that produced novel results.
Fractional derivatives of SM addiction have been formulated and studied [33, 66, 67]. However, none of these studies have included the impacts of SM despite its tremendous influence on individuals. It is therefore prudent to fill this gap that has not been studied in the existing literature. Hence, our research incorporates the positive and negative impacts of SM on individuals, expanding upon the model put forward in [20]. In this research, a fractional-order derivative is defined in ABC sense known to exhibit a more accurate description of the crossover behavior and the memory effect in the model.
In Section 2 of the paper, we present the SM compartmental model that we will study. Parameter descriptions and the nonlinear order fractional differential equations governing the study will also be presented in this section. Section 3 of this paper discusses the preliminaries that will be used throughout this paper. In Section 4, we ascertain the invariant region, and the points of equilibrium and the basic reproduction number are computed. We further present the existence and uniqueness of the SM impact model using Banach’s fixed point theorems and the stability of the model using the Ulam–Hyers (HU) approach, and sensitivity analysis is also performed in this section. Section 5 presents the numerical results to support the analytical solution. This paper finishes with discussions and conclusions with possible future research directions in Section 6.
2. The Fractional-Order Model
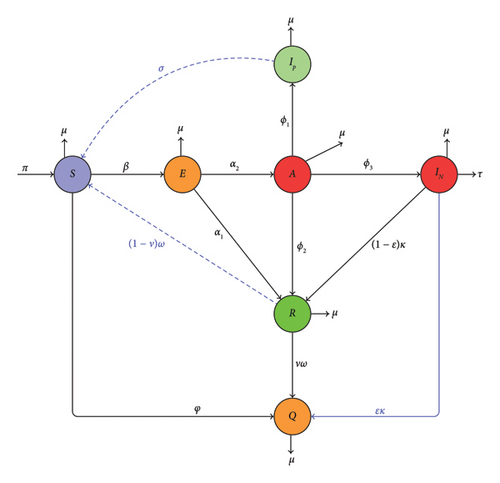
The model partitions the total population into seven compartments: susceptible individuals S, exposed individuals E, addiction individuals A, individuals affected by SM positively IP, individuals affected by SM negatively IN, recovered individuals R, and individuals who have permanently stopped using SM Q. Detailed descriptions of these variables are shown in Table 1. Hence, the entire populace N(t) is denoted as N(t) = S(t) + E(t) + A(t) + IP(t) + IN(t) + R(t) + Q(t). We describe the parameters in the model as follows: Πϱ is the rate of recruiting susceptible individuals into the population. βϱ is the interaction rate of the recruited susceptible individuals with the probability of becoming exposed at ηϱ. A portion of the susceptible population who are not interested in SM joins the permanently stop compartment at the rate φϱ. and are the rates at which exposed individuals recover or become addicted, respectively. , and represent the rates of the addicted individuals benefiting positively, joining the recovered class, or are negatively impacted, respectively.
| Variable | Description |
|---|---|
| S | Individuals who have not experienced SM impacts but are prone to SM usage |
| E | Individuals who do not use SM often and have not reached the stage of impacts |
| A | Individuals who have fully blown with SM usage and can experience SM impacts |
| IP | Individuals positively impacted by SM through addiction |
| IN | Individuals negatively impacted by SM through addiction and can die through psychological trauma or even commit suicide |
| R | Individuals who do not show interest in SM usage after being exposed, addicted, or negatively impacted |
| Q | Individuals who quit social media usage completely |
A portion of positively impacted individuals move to the susceptible compartment at the rate σϱ. A portion of the negatively impacted individuals join the permanently stopped individuals at εϱκϱ or move to the recovered compartment through the treatment (1 − εϱ)κϱ. One dies through psychological trauma, suicide, or other means due to the negative impact of SM at the rate τϱ. υϱωϱ is the proportion of the recovered individuals stopping SM usage permanently or becoming susceptible again at (1 − υϱ)ωϱ. The natural mortality rate is denoted by μϱ. Detailed descriptions of the defined parameters can be seen in Table 2. The diagrammatic representation of the SM impact process is shown in Figure 1.
| Parameter | Description |
|---|---|
| Π | Recruitment rate of the susceptible individuals |
| β | The transmission rate of addiction to the susceptible |
| σ | Rate of positively impacted individuals becoming susceptible |
| η | Contact rate of susceptible individuals with addicted |
| υ | Rate of the recovered individuals quitting |
| ω | Proportion of the recovered individuals becoming susceptible |
| φ | Rate of susceptible individuals permanently quitting |
| α1 | Rate of exposed individuals recovering |
| α2 | Rate of exposed individual becoming addicted |
| μ | Natural mortality rate |
| ϕ1 | Rate of addicted positively impacted |
| ϕ2 | Rate of addicted recovering |
| ϕ3 | Rate of addicted individuals negatively impacted |
| κ | Rate of negatively impacted individuals recovering |
| τ | Death rate through negative impact |
| ε | Rate of negatively impacted individuals quitting |
3. The Preliminary Results
In this section, we present the basic results necessary for the analysis of the problem in the work. We rely on definitions and lemma from [33, 48, 70].
Definition 1 (see [48], [70].)The fractional derivative of order ϱ according to the Liouville–Caputo (LC) concept is defined as
Definition 2 (see [48].)The fractional derivative of order ϱ according to the Caputo–Fabrizio (CF) concept is given as
Definition 3 (see [48].)Atangana–Baleanu derivative defined in the Caputo sense (ABC-derivative):
Definition 4 (see [48].)The crucial fractional integral of the Atangana–Baleanu defined in Caputo’s sense:
Lemma 1 (see [33], [70].)The following inequality satisfied the Lipschitz condition by the ABC-fractional derivative for two functions h1, h2 ∈ C1(m, n), with n greater than m:
Lemma 2 (see [71].)For every h(t) in , and letting with ϱ ∈ (0, 1], then for any t ∈ [m, n], there exist u ∈ [m, t] such that
One can easily see in Lemma 2 that for every h(t) in , , , and for all t in (m, n] with ϱ ∈ (0, 1], then h(t) is nondecreasing function. On the other hand, if , and for all t in (m, n] with ϱ ∈ (0, 1], then h(t) is nonincreasing for all t ∈ [m, n].
4. Analysis of the Fractional-Order Model
4.1. The Invariant Region
We determine the feasible zone of the solutions to the system of equations (1) with initial data that have non-negative values. We demonstrate that the feasible area is positively invariant with respect to model (1).
Theorem 1. The closed set
Proof. Let N(t) = S + E + A + IP + IN + R + Q represent the whole population, and let the set (S, E, A, IP, IN, R, Q) have any solution of the SM fractional derivative model (1); then from Lemma 2, we show
It is verified that N(t)⟶(Πϱ/μϱ) as t⟶∞.
Therefore, the solutions of the fractional SM model (1) holds true for all values of t greater than 0. In light of the above, the fractional system (1) is, therefore, a positively invariant zone.
4.2. Existence and Uniqueness Results
In order to prove our results, we assume the following : The functions under consideration are continuous such that ‖S(t)‖ ≤ C1, ‖E(t)‖ ≤ C2, ‖A(t)‖ ≤ C3, ‖I‖p(t) ≤ C4, ‖I‖N(t) ≤ C5, ‖R(t)‖ ≤ C6, ‖Q(t)‖ ≤ C7.
Theorem 2. The solution of the ABC-fractional SM impact model is unique for all t ∈ [0, k] if and only if
Proof. Because the functions S(t), E(t), A(t), Ip(t), IN(t), R(t), Q(t) are bounded and we have that equations (26) and (27) hold, then in the same way, (34) approaches
Therefore, this establishes a unique solution of system (36).
4.3. Stability Analysis of the SM Impact Model
This section studies the stability of the SM impact model (1) as changes may occur in the neighborhood of the solutions to the model. We therefore carry out a stability analysis of the model in discussion by employing the HU stability criteria. This stability criterion can deal with models that even have approximated solutions [72]. We therefore state categorically the HU definition to ascertain that model (1) is HU stable.
Hence, we assume that the model (1) is HU stable.
Definition 5 (see [61].)The ABC-fractional SM impact model (1) is HU stable if for σi > 0, (i = 1, 2, ⋯7, i ∈ N7) and ηi > 0, we have
Theorem 3. Based on assumption , we can conclude that the fractional-order model (1) exhibits HU stability.
Proof. Using Theorem 3, system (10) has a unique solution {S(t), E(t), A(t), IP(t), IN(t), R(t), Q(t)}. Let be an approximate solution of the model (1) which satisfies system (40). Then, we have
Therefore, we have proved that model (1) is HU stable.
4.4. Equilibrium Points and Basic Reproduction Number
In compartmental modeling, similar to epidemiological modeling techniques, the basic reproduction number is observed to be the most important variable. It is an important indicator in analyzing the stability of the equilibrium points and it can be obtained via the next-generation matrix method.
SM impact–free equilibrium will occur when , indicating the absence of infection. This implies that only susceptible individuals and those who have quit SM permanently will remain, while the rest will vanish.
Theorem 4. The equilibrium of the absence of SM impact model is locally asymptotically stable when and unstable otherwise.
Proof. Firstly, the model (1) Jacobian matrix is presented as
Here, a, −μϱ, c, d, and −(μϱ + σϱ) are the negative eigenvalues of the Jacobian matrix , and the other two eigenvalues can be demonstrated to be negative if . When , the SM-free equilibrium is therefore locally asymptotically stable, proving the theorem.
4.5. Sensitivity Analysis
Sensitivity analysis is widely utilized to assess the robustness of model predictions regarding the values of parameters because there are frequent errors in collecting information and expected values of parameters. It is employed to determine parameters that have significant effects on the basic reproduction number. This will help to identify the intervention techniques that should be addressed. Sensitivity analysis provides information about how important each parameter is to SM dynamics. This knowledge is vital not just for experimentation but also for data assimilation and simplification of complicated nonlinear systems [73].
We can quantify the relative change in a variable when a parameter changes by using sensitivity indices. The normalized forward sensitivity index of a variable with respect to a parameter is the proportion of the relative change in that variable to the proportionate change in the value of the parameter.
Parameters whose sensitivity indices are negative decrease the value of as their values increase while those with positive signs increase the value of as their values increase. The parameters with the most sensitive indices in this model are β, Π, η, α2, and μ. For example, the results in Table 3 show that increasing (or decreasing) the values of β, Π, and η by 10% increases (or decreases) the value of by 10% and increases the value of α2 by 10% increases the value of by 3.636%. In the same way, increasing (or decreasing) the value of μ by 10% increases (or decreases) the value of by 9.121%.
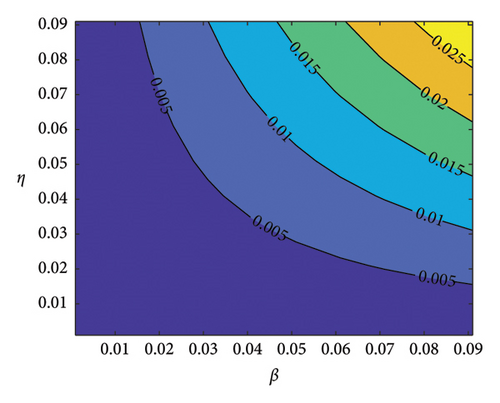
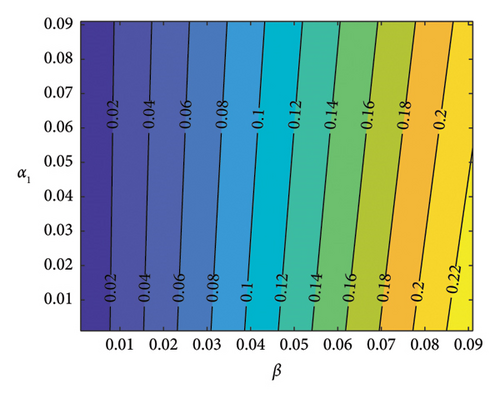
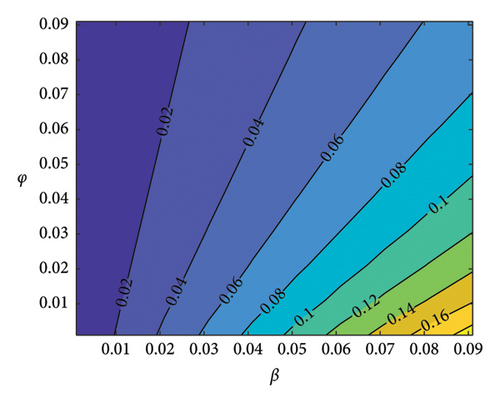
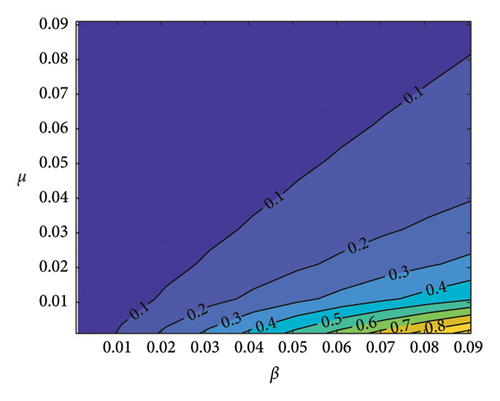
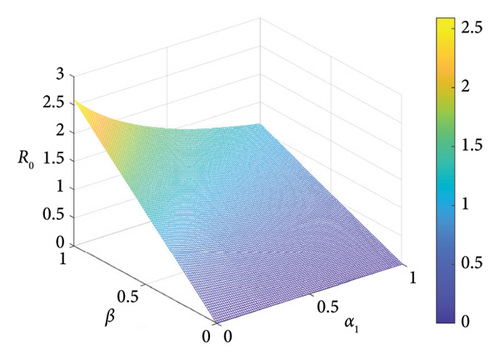
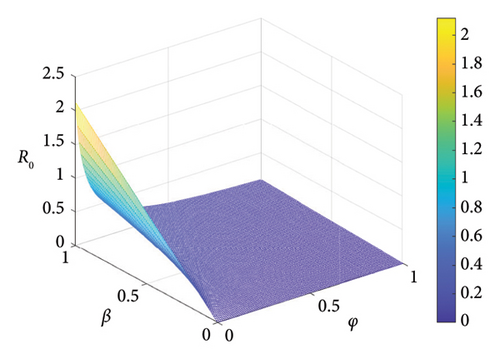
Figure 2 indicates the contour plots in support of the sensitivities of some key parameters in Table 4. It can be observed in Figures 2(a), 2(b), 2(c), and 2(d) that β and η increase SM addiction when their values are increased while φ, α1, and μ decrease SM addiction when their values are increased. Also, the 3D graph in Figure 3 shows the impacts of β, φ, and α1 on . It can be seen in Figures 3(a) and 3(b) that the value increases as the value of the transmission rate (β) increases. Also, the value of decreases as the value of the recovery rates α1 and φ increases. In order to control SM addiction, the value of the transmission rate (β) must be decreased. This can be achieved through self-control on the part of the user, turning off SM notifications, spending more time with friends offline, and freezing SM accounts. The values α1 and φ can also be increased to ensure SM addiction control. This can also be achieved by treatment through education and counseling.
| Parameters | Sensitivity value |
|---|---|
| β | 1.0000 |
| Π | 1.0000 |
| η | 1.0000 |
| φ | −0.1667 |
| α1 | −0.3131 |
| α2 | 0.3636 |
| μ | −0.9121 |
| ϕ1 | −0.1333 |
| ϕ2 | −0.4667 |
| ϕ3 | −0.3667 |
5. Numerical Simulations
5.1. Numerical Scheme
Here, we adapt the predictor–corrector type of the Adams–Bashforth method to ascertain the numerical approximation of the ABC-fractional nonlinear differential derivatives. We assumed the solution is closed under the interval [0, T], where T is the upper bound. We then set L = T/M such that tn = Ln, where n = 0, 1, 2, …, M and L = h.
5.2. Numerical Results
This section presents the computational results for the fractional SM model (1) with Table 3 showing the parameter values used in this study. In the case where N = 100 days, (S0, E0, A0, Ip,0, IN,0, R0, Q0) = (8, 5, 3, 2, 2, 1, 3). It is observed in Figures 4(a) and 4(b) that as the number of recovering individuals rises, the exposed and addicted individuals recover and decline to zero. Also, when the addicted transmission rate is halted, we observed that the number of exposed individuals, addicted positive individuals, and negatively affected individuals rapidly increases and gradually diminishes to zero. Moreover, as the number of individuals who abstain from SM permanently increases rapidly and eventually drops to zero, the number of susceptible and recovered individuals increases while the number of addicted individuals declines. However, susceptible and addicted individuals dropped as fewer people chose to use SM exclusively, increasing the number of high-quality individuals. More importantly, the various plots show that the negatively impacted compartment diminishes faster than the positively impacted compartment. It can be observed in Figures 4, 5, and 6 that as more people become aware of the negative impact of SM, they tend to use SM positively, and this increases the number of positive impact individuals than the negatively affected individuals and vice versa.
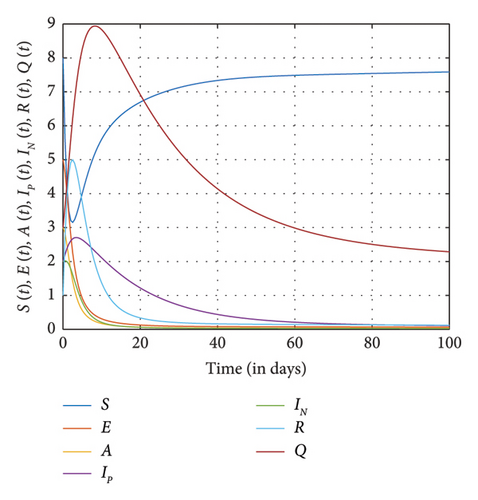
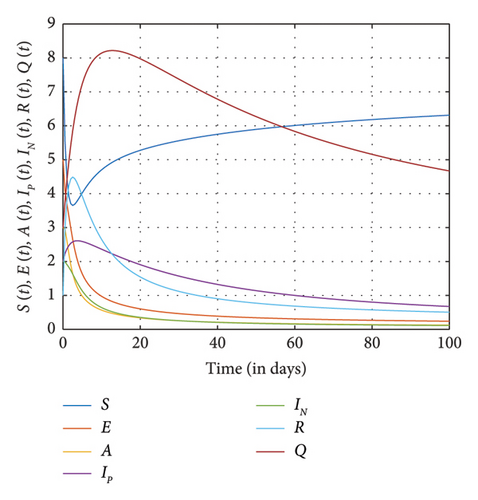
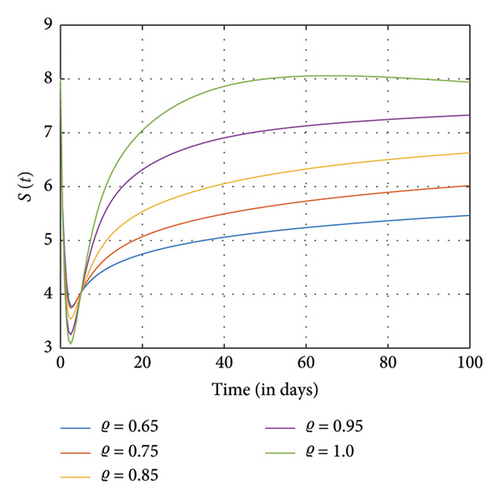
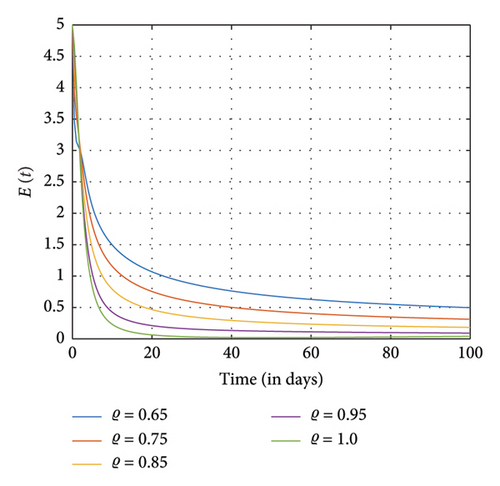
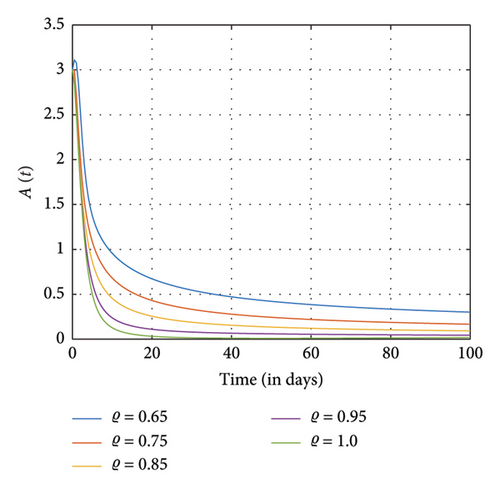
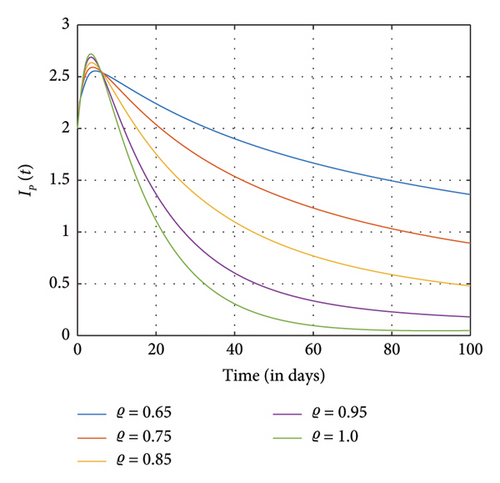
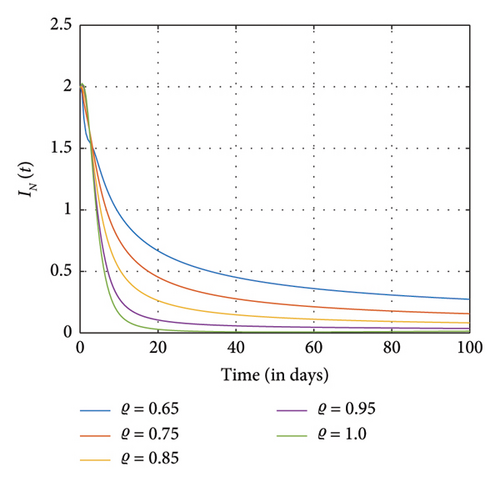
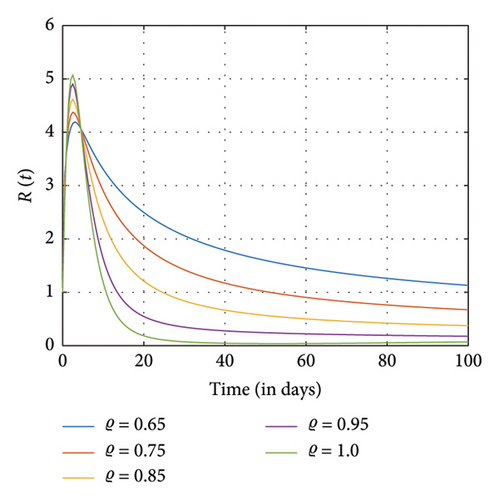
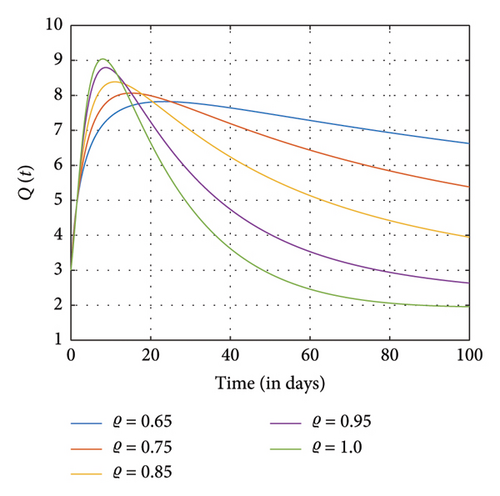
In Figures 5 and 6, exposure to SM and addiction from SM to certain groups increase considerably, marking the addiction’s peak and subsequent stabilization in transmission. The recovered population also grows, declines, and stabilizes in accordance with the decline in exposed and addicted individuals. Furthermore, individuals abandoning SM usage are permanently declining as individuals affected by SM addiction and exposure are beginning to recover. However, as the number of individuals who are susceptible to SM usage decreases, becomes stable, and then marginally rises, more people are exposed to SM usage and choose to give it up permanently.
Further simulations show that individuals who are exposed to and engaged in addiction as well as those positively and negatively impacted individuals rise and fall quickly as different fractional orders ϱ diminish and eventually approach one. The dynamics of the recovery individuals and those who have permanently stopped using SM are depicted as they grow and shrink at different fractional orders ϱ, eventually nearing 1.
Figures 7, 8, and 9 show the effects of sensitive parameters in Table 3 on the model with a constant fractional order ϱ = 0.98. For instance, we observed in Figure 7(d) that as the recruitment rate increases, more individuals enter the positive impact compartment as compared to the number of individuals who enter the negative impact compartment in Figure 7(e) at the final time. As a result of awareness of the negative impact of SM usage, people therefore tend to utilize it judiciously. Moreover, as more people enter the susceptible class, the exposed individuals, the addicted individuals, and the negative and the positive individuals also increase as observed in Figures 7(a), 7(b), 7(c), 7(d), and 7(e), respectively.
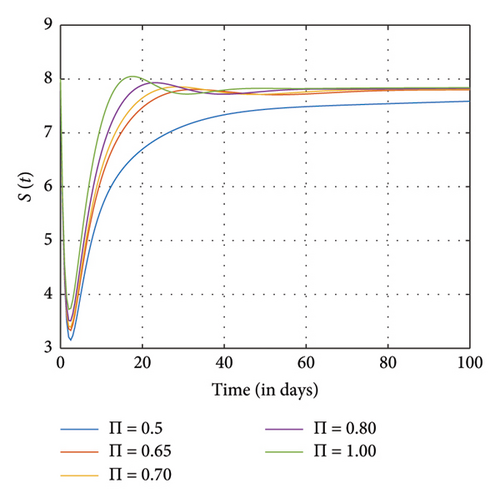
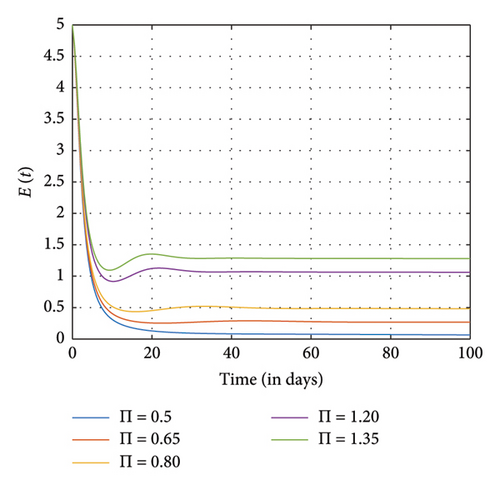
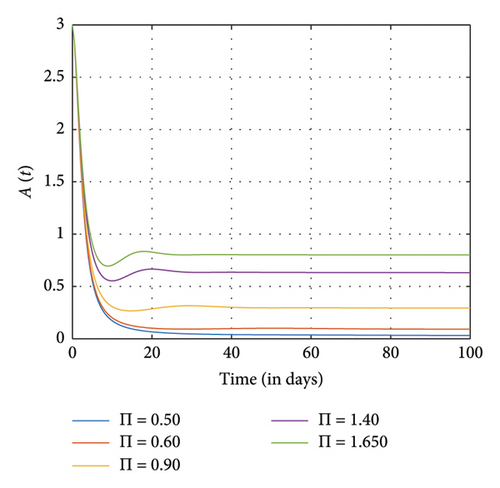
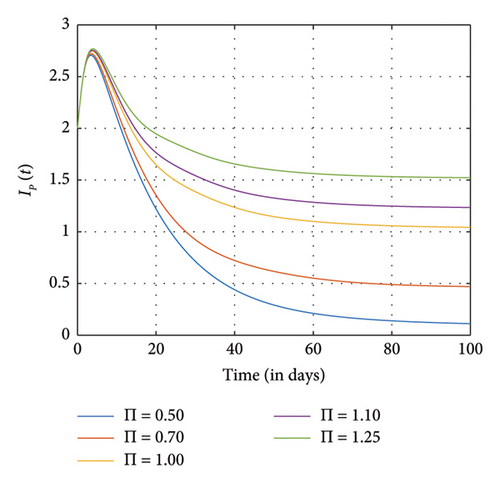
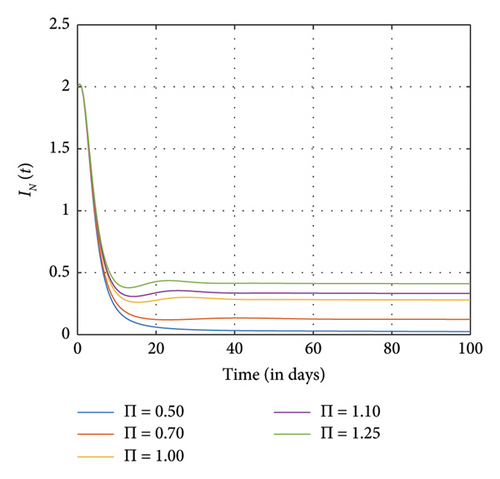
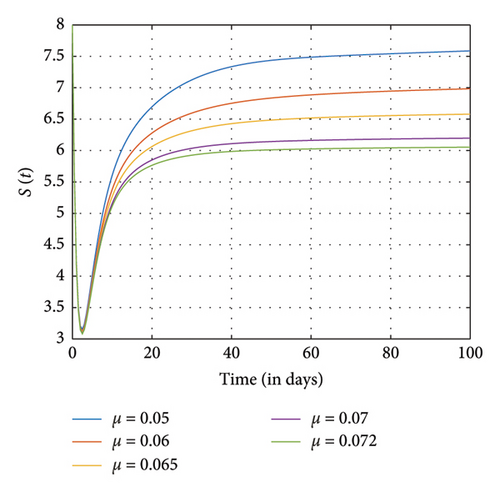
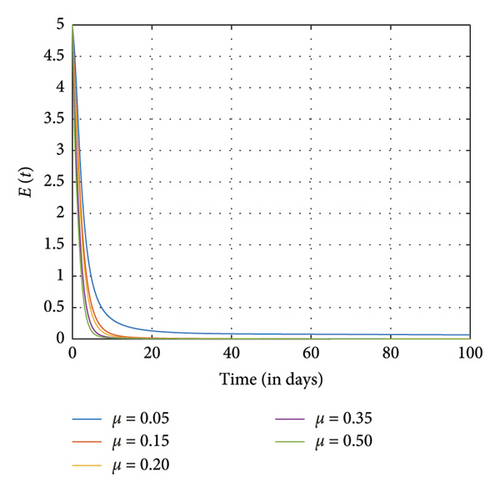
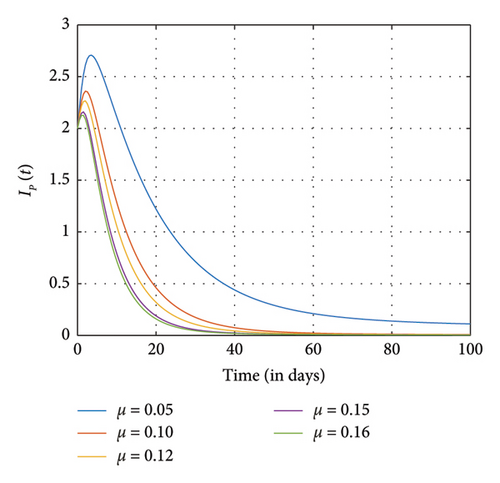
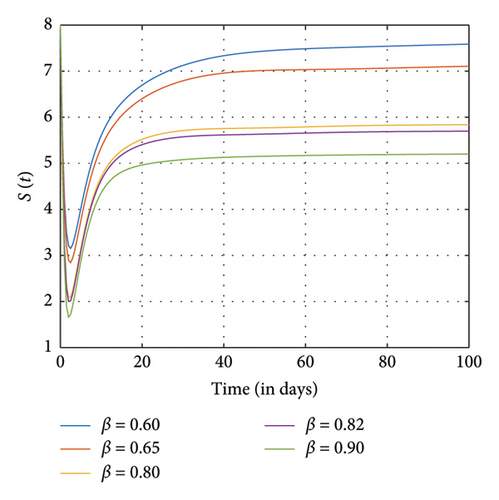
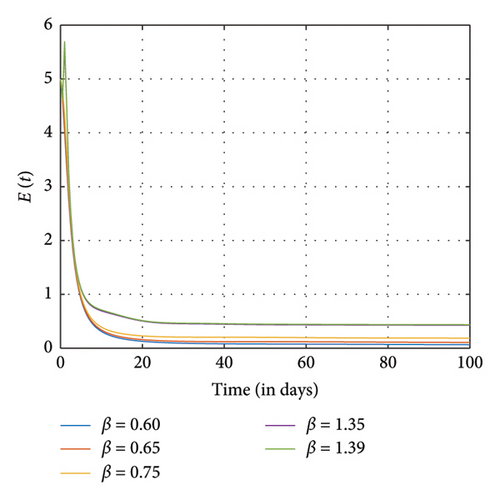
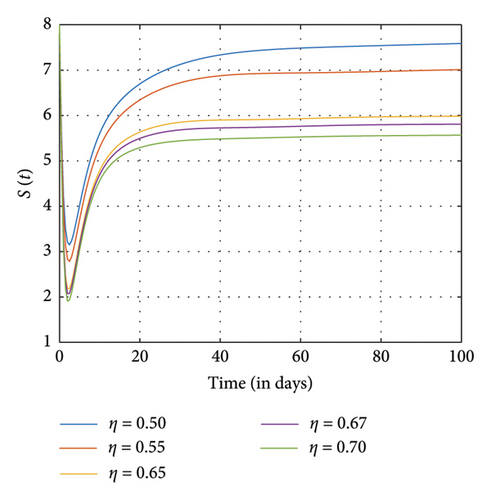
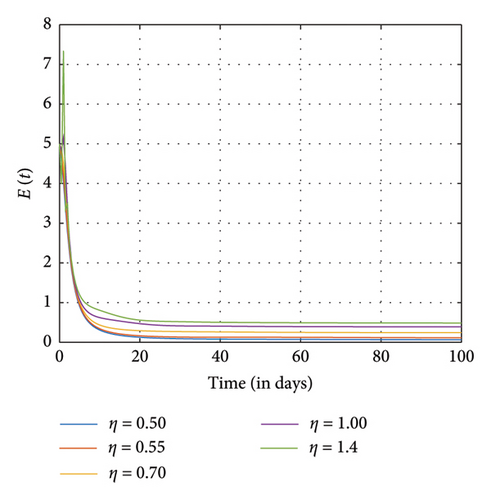
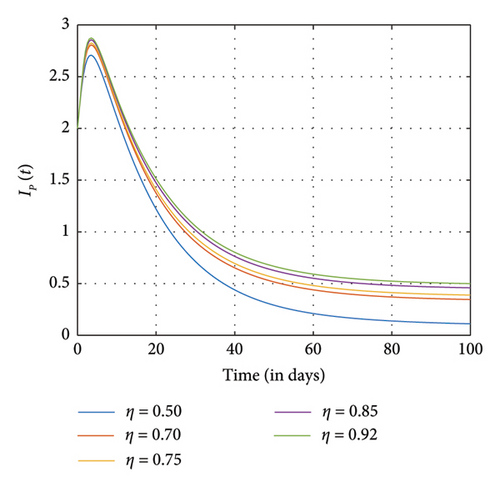
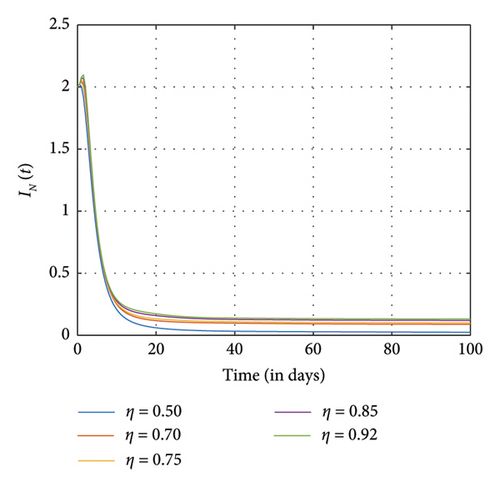
Figure 8 shows the effects of increasing the natural death rate μ on the susceptible, exposed, and negative impact individuals and the interaction rate β on the susceptible and the exposed individuals, respectively, with a constant ϱ = 0.98 and the final time N = 100. One can observe in Figures 8(a), 8(b), 8(c), 8(d), and 8(e) that as the natural death rate and the interaction rate increase, the susceptible, exposed, and negative impact individuals also decline in proportion to the increase in values of μ and β at the final time, respectively. In Figure 9, we observed that when the probability of susceptible individuals being exposed to SM η increases, the susceptible individuals drop quickly and rise at an increasing rate and eventually drop at the final time in proportion to the increase in the η values. Here, the positively impacted individuals rise quickly and drop at a decreasing rate and eventually increase in proportion to the increase in the values of η. However, when the fractional order is decreased, there is a reduction in the rate at which susceptible individuals become addicted, indicating a positive impact on controlling the spread of SM impact within the population. Also, it can be seen that when the fractional order is decreased, there is an increase in exposed, addicted, addicted positively and negatively, recovered, and those who have permanently stopped using SM. This suggests that more individuals will become addicted to SM. SM presents serious problems for society; by comprehending these consequences and putting management plans in place, we may reduce the negative impacts and maximize the benefits of SM.
6. Conclusion
In this paper, we have investigated the impacts of SM dynamics in the context of fractional order, ϱ, specifically, the ABC-derivative approach. The points of equilibrium and the basic reproduction number are computed. Also, we have established the existence and uniqueness of the SM impact model using Banach’s fixed point theorems. We performed the stability analysis of the model using the HU approach. Furthermore, the sensitivity analysis, 3D graphs, and contour plots of the most sensitive parameters of the basic reproduction number are discussed. The numerical results to support the analytical solutions have been discussed extensively. Approximations for the various fractional orders ϱ are obtained using the numerical technique of the predictor–corrector method of Adams and Bashforth. We studied the fractional SM impacts dynamics behavior as ϱ gets closer to 1. Simulations of the SM impact model with different fractional order values ϱ = 0.65, 0.75, 0.85, 0.95 on the various compartments have been carried out. The system responses were determined at several orders of fractional derivatives, and it was shown that small modifications did not affect the behavior of the function overall, but mainly on numerical simulations. As individuals become aware of the negative impacts of SM, the number of positively impacted individuals rises and the reverse is true. There must be control measures such as public education and personal protection from the negative impacts of SM. Therefore, we recommended optimal control strategies in the future direction.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
The authors did not receive any funding for this study.
Open Research
Data Availability Statement
No data were used. All the parameter values used in the work are duly cited and referenced.




