International Journal of Aerospace Engineering

Volume 2024, Issue 1 5546122

Research Article

Open Access

Dynamics and Control of Noncooperative Space Target Capture Using a Flexible Manipulator

Kang-Hao Wang

State Key Laboratory of Ocean Engineering , Key Laboratory of Hydrodynamics of Ministry of Education , Shanghai Jiao Tong University , Shanghai , 200240 , China , sjtu.edu.cn

Search for more papers by this author

Ru-Hao Wang,

Ru-Hao Wang

State Key Laboratory of Ocean Engineering , Key Laboratory of Hydrodynamics of Ministry of Education , Shanghai Jiao Tong University , Shanghai , 200240 , China , sjtu.edu.cn

Search for more papers by this author

Xiao-Feng Liu,

Corresponding Author

Xiao-Feng Liu

[email protected]

orcid.org/0000-0002-7880-7344

State Key Laboratory of Ocean Engineering , Key Laboratory of Hydrodynamics of Ministry of Education , Shanghai Jiao Tong University , Shanghai , 200240 , China , sjtu.edu.cn

Search for more papers by this author

Yu-Lei Fu,

Yu-Lei Fu

Shanghai Institute of Ceramics , Chinese Academy of Sciences , Shanghai , 200050 , China , cas.cn

Search for more papers by this author

Guo-Ping Cai,

Guo-Ping Cai

orcid.org/0000-0003-1248-3700

State Key Laboratory of Ocean Engineering , Key Laboratory of Hydrodynamics of Ministry of Education , Shanghai Jiao Tong University , Shanghai , 200240 , China , sjtu.edu.cn

Search for more papers by this author

Kang-Hao Wang,

Kang-Hao Wang

State Key Laboratory of Ocean Engineering , Key Laboratory of Hydrodynamics of Ministry of Education , Shanghai Jiao Tong University , Shanghai , 200240 , China , sjtu.edu.cn

Search for more papers by this author

Ru-Hao Wang,

Ru-Hao Wang

State Key Laboratory of Ocean Engineering , Key Laboratory of Hydrodynamics of Ministry of Education , Shanghai Jiao Tong University , Shanghai , 200240 , China , sjtu.edu.cn

Search for more papers by this author

Xiao-Feng Liu,

Corresponding Author

Xiao-Feng Liu

[email protected]

orcid.org/0000-0002-7880-7344

State Key Laboratory of Ocean Engineering , Key Laboratory of Hydrodynamics of Ministry of Education , Shanghai Jiao Tong University , Shanghai , 200240 , China , sjtu.edu.cn

Search for more papers by this author

Yu-Lei Fu,

Yu-Lei Fu

Shanghai Institute of Ceramics , Chinese Academy of Sciences , Shanghai , 200050 , China , cas.cn

Search for more papers by this author

Guo-Ping Cai,

Guo-Ping Cai

orcid.org/0000-0003-1248-3700

State Key Laboratory of Ocean Engineering , Key Laboratory of Hydrodynamics of Ministry of Education , Shanghai Jiao Tong University , Shanghai , 200240 , China , sjtu.edu.cn

Search for more papers by this author

First published: 18 October 2024

https://doi.org/10.1155/2024/5546122

Academic Editor: Gang Wang

Share a link

Email
Wechat
Bluesky

Abstract

The capture of noncooperative space targets is an important research topic in the aerospace field. Although a lot of research has been done, capturing remains a significant challenge, particularly when using a flexible manipulator. In this paper, the dynamic modeling and control problems of capturing a noncooperative spacecraft using a long-span flexible manipulator are investigated. Firstly, a modified model is presented to describe the flexibility of the manipulator arising from both its links and joints, in which the flexibility of the joint is considered as an elastic constraint of links. Additionally, we provide the frequency and mode functions of this model and derive the dynamic equations of the flexible manipulator based on the floating frame of reference formulation. Secondly, this paper employs the position–based damping control method to design the capturing controller. A simulation example of capturing a tumbling spacecraft in three dimensions is presented. The simulation results show that the designed control method can quickly eliminate vibration and achieve stable contact retention for at least 3 s when capturing noncooperative spacecraft.

1. Introduction

A space station, an advanced facility positioned in outer space, functions as a pivotal center for scientific research, international collaboration, and exploration beyond Earth’s atmosphere. To ensure its uninterrupted long-term operation, the space station requires regular resupply missions conducted by various spacecraft, including unmanned cargo spacecraft equipped with fully autonomous docking systems. In the event of failures during autonomous docking, the cargo supply mission will be unable to be completed, necessitating a relaunch to provide the space station with the necessary supplies. Utilizing the space station’s long-span flexible manipulator for capturing a malfunctioning cargo spacecraft holds significant economic value. Yet, this task presents significant challenges due to the risk of collision during the capture operation. Such an impact could disengage the target from the capture effector and potentially cause damage to the flexible manipulator. Therefore, further research into controlling flexible space manipulators for safe and efficient on-orbit capture tasks is imperative.

Flexible space manipulators are pivotal in on-orbit assembly, testing, and maintenance, with notable examples being the shuttle and International Space Station arms (Canadarm and Canadarm 2) [1]. Their flexibility arises from lightweight links and joints, posing challenges such as reduced accuracy and excessive vibrations [2], particularly in capturing noncooperative targets. Scholars have extensively investigated the dynamics modeling and simulation of flexible spacecraft manipulators during the capturing process. For instance, Cyril et al. [3, 4] delved into postcapture dynamics deeply. Kövecses and Cleghorn [5] introduced an impulsive constraints-based approach to describe capturing impact, utilizing Jourdain’s principle to derive dynamic equations. Liu, Wu, and Lu [6] researched the impact dynamics and control of a flexible dual-arm spacecraft capturing an object, revealing substantial impact effects on system dynamics when capturing objects at specific velocities. Felicetti et al. [7] utilized ADAMS to build a capture dynamic model. Yu et al. [8] proposed a simplified model for simulating flexible manipulators to analyze capturing impact. Wei et al. [9] investigated an adaptive model-free constrained prescribed performance control approach for flexible spacecraft with unknown captured objects, considering various complexities such as elastic vibration and external disturbances. Stolfi, Gasbarri, and Misra [10] derived a dynamics model for a two-arm flexible space manipulator system with nonlinear formulation for the rigid-body motions and linear for the elastic dynamics. Additionally, Ma et al. [11] proposed a parametric modeling method for flexible space manipulators and analyzed their dynamic behavior during the docking and capturing process.

The research reviewed above shows that the impact of capturing can generate significant adverse effects to the capturing task. To reduce these adverse impacts, various methodologies and strategies have been proposed. For instance, Yoshida et al. [12–14] introduced an impedance match control method based on conventional impedance control to prevent the grasper from moving away after collision. Their approach involves adjusting collision behavior by manipulating collision mass. Uyama et al. [15, 16] proposed a modified impedance control method, aiming to set the coefficient of restitution to zero by controlling the relative motion between the end-effector (EE) and the target. Stolfi et al. [17, 18] augmented the EE with a compliant wrist to mitigate collision impact and employed an impedance controller to drive the robotic arm. In contrast to Uyama et al.’s research [16], the compliant wrist was utilized specifically to prolong contact duration. Moreover, Flores-Abad et al. [19] introduced a disturbance-observer–based impedance controller to extend contact time during capturing, demonstrating enhanced controller robustness against uncertainties through simulation results. Wu et al. [20] developed a generic frictional contact model and designed a resolved motion admittance control method to realize tracking for a tumbling target. Han et al. [21, 22] proposed a dual-integral sliding mode (DISM) control method based on the reconfiguration of the reaction wheels and designed a compliant controller to ensure stability in the contact force of a dual-arm spacecraft. Wang et al. [23] adapted the hybrid force/position controller to manage contact force during the capture task. Furthermore, Raina et al. [24] used an adaptive reactionless control strategy for capturing objects with unknown parameters after the impact. In our prior works [25, 26], we proposed two damping control methods to reduce the collision impact effect and analyzed the dynamic behaviors of rigid spacecrafts during capture tasks.

In the aforementioned research, scholars have proposed diverse control methods aimed at enhancing capturing success by mitigating collision impact. However, while these methods have been shown to be effective for capturing tasks using a rigid manipulator, their suitability for use with a flexible manipulator remains unanswered. Although some researchers, such as Cyril, Jaar, and Misra [27] and Liu, Wu, and Lu [6], have studied the capturing control problem using a flexible manipulator, the capturing object they only considered is a floating lightweight cylinder. Obviously, when the captured object is a floating spacecraft, the difficulty of control will increase significantly. Given the importance of the capture task using a flexible manipulator, this paper studied the dynamics and control problems of that task in depth. Firstly, a modified model is introduced to characterize the flexibility of both the link and joint, where joint flexibility is considered an elastic constraint of the links. The model’s frequency and mode are outlined, establishing the dynamic equation of the flexible manipulator based on the floating frame of reference formulation. Subsequently, this paper designed a position–based damping–capturing controller for the flexible manipulator. Finally, diverse simulations are executed to assess the efficacy of the designed controller and analyze the influence of control parameters on performance.

The structure of this paper is organized as follows: Section 2 briefly introduces the dynamic modeling of spacecraft and capture, including the use of an improved modeling method of a flexible joint link manipulator. In Section 3, a position–based damping control algorithm is described, and the overall strategy and related mathematical principles are presented. In Section 4, several numerical results are given, and the parameter selection and performance are analyzed. Section 5 reports the final conclusions.

2. Dynamic Modeling of a Flexible Space Manipulator

In this paper, the flexible space manipulator refers to the long-span manipulator, whose flexibility mainly comes from lightweight links and joints. In previous studies focused on capturing dynamics, the consideration has mainly been on the flexibility of the links, neglecting the joint’s flexibility. However, Ma et al.’s work [11] has demonstrated the impact of joint flexibility on the manipulator’s dynamic behavior during capturing. For a more accurate simulation of real capturing conditions, it is essential to incorporate both link and joint flexibility in the dynamics modeling.

2.1. Description of Capturing System

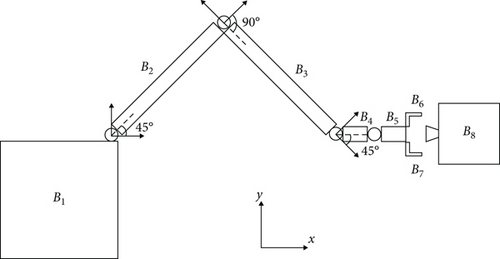
In this paper, we employ the capturing system shown in Figure 1 to study the dynamics and control of capturing a noncooperative spacecraft using a flexible manipulator. As depicted in Figure 1, the capturing system consists of a base, a long-span manipulator, and a free-floating noncooperative spacecraft. The long-span manipulator includes two flexible links (B₂ and B₃) and two rigid links (B₄ and B₅). The joints of the manipulator are revolute joints, and only the flexibility of Joint 2 (H₂) and Joint 3 (H₃) are considered. This section addresses the dynamics modeling problem by initially introducing a modified link model that accounts for the flexibility of both links and joints. Here, joint flexibility is treated as an elastic constraint of the flexible link. The utilization of this modified flexible link model reduces the number of variables and facilitates the analysis of vibration effects during capturing. Subsequently, we establish the dynamic equation of the flexible manipulator using the floating frame of reference formulation. This equation integrates the mode of link flexibility to describe the contribution of deformation. Further details regarding this modeling approach will be provided in the following sections.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Spacecraft and the noncooperative target.

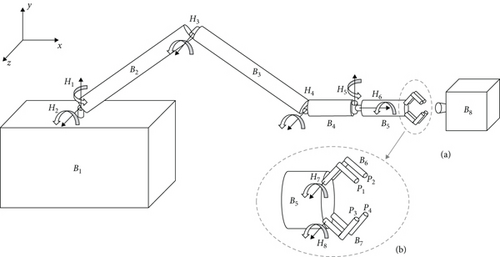
2.2. Description of a Flexible Link With a Flexible Revolute Joint

In most research on the dynamic modeling of the manipulator with the flexible link and flexible joint, the flexibility of the link and joint is considered separately. The flexible link is regarded as a deformable cantilever beam, and the flexible revolute joint is represented by a real revolute joint and a virtual revolute joint with a torsional spring. The latter joint is used to represent the joint flexibility. According to the structural dynamics theory [28], however, the introduction of a virtual revolute joint with a torsional spring is unnecessary, and the elastic constraint can describe the joint flexibility. Hence, the flexible link connected with a flexible revolute joint can be simplified as a supported-free deformable beam with an elastic revolute constraint as shown in Figure 2. Since this study employs the assumed mode method to describe the contribution of flexibility to the dynamics of the capturing system, we present the mode function of the modified flexible link in this subsection.

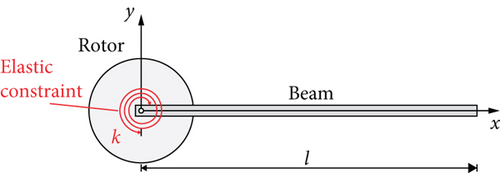
For clarity, notations (∗)^′ = ∂(∗)/∂x, (∗)^′′ = ∂²(∗)/∂x², (∗)^′′′ = ∂³(∗)/∂x³, (∗)⁽⁴⁾ = ∂⁴(∗)/∂x⁴, , and are used throughout this paper.

The beam shown in Figure 2 is assumed as a uniform Euler–Bernoulli beam, whose bending free vibration equation in y direction is

()

where E is Young’s modulus, I is the sectional moment of inertia, ρ is the density of the beam, and A is the sectional area. According to the structural dynamics theory, the solution of y is

()

where ϕ_i(x) and q_i(t) are the ith mode function and ith mode coordinate, respectively.

Considering that the energy proportion of high-order modes is too low, high-order modes have little impact on structural vibration. Usually, we only consider the vibration of the first N-order modes. Due to the orthogonality of the mode functions, we can separate and discuss the modes of each order. Therefore, the main vibration function can be expressed as

()

Substituting Equation (3) into Equation (1) gives

()

where λ is a constant. We can obtain two equations

()

The mode coordinate q(t) is assumed to be harmonic with frequency ω and thus λ = ω². q(t) will be solved in system dynamics equations in the next section. Set the weighted frequency β by

()

Thus, Equation (6) can be rewritten as

()

The general solution of Equation (8) can be expressed as

()

where the weighted frequency β and three of the four constants C₁, C₂, C₃, and C₄ will be determined by the boundary conditions.

For the flexible beam shown in Figure 2, since the bending moment and the shearing force at the free end are both zero, while the bending moment of the beam must be equal to the elastic torque of the torsional spring and the deflection is zero at the elastic constraint end, the corresponding boundary conditions can be given as

()

where k is the stiffness of the torsion spring and θ_r is the deformation of the torsional spring.

Substituting θ_r = y^′(0, t) and Equation (3) into Equation (10) gives

()

Similarly, by substituting Equation (9) into Equation (11), the unknown coefficients C₁, C₂, C₃, and C₄ can be expressed in the following form:

()

Equation (12) has a nonzero solution for each coefficient only if the determinant of the coefficient matrix is zero, simplifying to obtain the following equation about β:

()

where the solutions of β_i(i = 1, 2, 3⋯) in Equation (13) can be calculated by numerical methods.

According to the relation (Equation 7), the natural frequency of the system is

()

Substituting Equation (12) and the solutions of β_i into the mode function in Equation (9) gives

()

where

()

As a result, the mode functions (Equation 15) and the natural frequencies (Equation 14) of the flexible beam with an elastic constraint have been obtained.

2.3. Dynamic Modeling of Capturing System

As shown in Figure 1, the capturing system consists of a service spacecraft with flexible manipulators and a noncooperative spacecraft. This study employs the multibody dynamic method based on the floating frame [29] to model the dynamic equation of the capturing system. The L-N model [30] is used to describe the collision force between and manipulator and the noncooperative spacecraft.

Based on Jourdain’s velocity variation principle [31], the dynamics equation of the system can be expressed as

()

where v_i is the vector of configuration velocity of the ith body;

denotes the acceleration-dependent inertia force acting on the ith body;

is the velocity-dependent inertia force acting on the ith body;

is the external force of system acting on the ith body;

is the elastic force acting on the ith body (if the ith body is a rigid body,

will be a zero vector); ΔP is the sum of virtual power of the inner forces of system.

Based on the assumed mode method, the elastic force

can be expressed as

()

where a_i is the modal coordinate vector of the ith body;

are the modal damping and stiffness matrices of the ith body, s denotes the highest order of the model chosen,

and

are the mode function vector and the mode frequency vector of the ith body, respectively.

In matrix form, Equation (17) can be written as

()

where

is the configuration velocity of the system; M = diag(M₁, ⋯, M_n) is the mass matrix;

, and

are the velocity-dependent inertia force, the external force, and the elastic force, respectively.

The relation of v and the independent generalized coordinate vector y is [32]

()

And the relation of v and the independent generalized coordinate vector y is

()

where the expression of G and g can be found in the relative reference [32],

is an N-dimensional vector with all elements being 1.

Using Equation (16) and Equations (17) and (19) can be written as

()

where Z = G^TMG, z = G^T(f^u + f^ω − Mg1_N), h = G^Tf^o, and f^ey is the vector of the generalized force of the system.

Since all the elements of y are independent, Equation (22) can be written as

()

This formula is the dynamic equation of a multibody system. The derivation details can be found in our previous work [31].

3. Capturing Control

In the process of capturing, the grasper of the manipulator inevitably collides with the surface of the noncooperative spacecraft. The impact of collision could push the grasper away from the target spacecraft. Avoiding this situation is a prerequisite for completing the capturing mission. In order to address this issue, scholars proposed various control methods for operating the manipulator. However, it is noteworthy that the effectiveness of these methods has primarily been demonstrated on short-span rigid–type manipulators. Until now, few studies have focused on the capturing control of the long-span flexible manipulator. In this study, we employed the position-based damping control scheme to design the capturing controller, which was proposed for the rigid manipulator in our previous work [25, 26]. The control objective of the position–based damping control scheme converts the manipulator into a damper. Consequently, the impact of collision on the grasper will be absorbed by the manipulator during capturing. Meanwhile, the reactive force acting on the grasper will prevent it from moving away from the noncooperative spacecraft. As shown in Figure 3, the position–based damping control scheme primarily comprises a damping motion planner and a motion controller. The role of the damping motion planner is to generate the desired trajectory for the grasper incorporating damping forces. Meanwhile, the motion controller is responsible for guiding the manipulator to ensure that the grasper accurately follows the specified trajectory. Generating the desired trajectory for the grasper is the key issue of the position–based damping control scheme, which determines whether the manipulator can be converted to a damper. Next, this section will present the details of the motion planner and the motion-tracking controller.

According to the second Newton’s law, the dynamic equation of the grasper including a damping force and the contact force is

()

where

is the acceleration of the grasper in the body-fixed frame of the noncooperative spacecraft, respectively; m_grasper is the mass of the grasper, c is the control damping coefficient, and F_c is the contact force.

Integrating Equation (24) gives

()

Integrating

yields

()

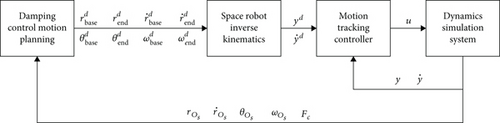
During capturing, , , , and are expected to equal to y_grasper(0), , z_grasper(0), , respectively. And the direction cosine matrix of the grasper in the body-fixed frame of the noncooperative spacecraft is expected to equal to A_grasper(0). Moreover, the position and orientation of the service spacecraft are expected to remain unchanged. After the motion of the noncooperative spacecraft is obtained by sensors, such as cameras or lasers, the inverse kinematics of the manipulator, ignoring its own flexibility, is employed to its desired motion in the joint space.

Our original approach [25, 26] employed the computed torque method (CTM) to design a motion-tracking controller. This method can compensate for the effects of inertial forces and gravity on the control but cannot compensate for the effects of the elastic force. Therefore, the CTM is hard to obtain ideal control performance. In this paper, the elastic force generated by the deformation of the flexible space robot is regarded as an unknown disturbance force on the space robot. In order to realize the desired control goals, we employed the disturbance observer (DOB)–based method [33] to design the motion tracking controller. Considering the disturbances, the dynamic Equation (23) could be rewritten as

()

where

and

are the estimated values of Z(y) and

, respectively. w is regarded as the lumped disturbance from the external disturbance and inertia uncertainties.

Define an auxiliary variable vector as [33].

()

where

is the estimate of w and

could be determined as

To estimate the lumped disturbance, the dynamics of the DOB is given by [33].

()

where L is the observer gain matrix.

Based on the DOB, the controller is designed as [33]

()

where e_s is the control error and is defined as e_s = y_d − y and D and K are the derivative and proportional gain matrices, respectively.

Compared to classical CTM, the DOB controller can compensate for this flexibility as a disturbance term in the control, thereby improving the performance of the controller to a certain extent. The effectiveness of the controllers was compared in Section 4.3.

4. Numerical Results

In this section, numerical simulations are carried out to verify the correctness of our dynamic modeling method, evaluate the effectiveness of the damping control scheme, and provide a detailed analysis of its performance.

4.1. Simulation Settings

The structures of the service spacecraft and the noncooperative spacecraft are shown in Figure 1 before, while their physical parameters are presented in Table 1.

Table 1. Physical parameters of the spacecraft.

Body	Mass (kg)	I_xx (kg·m²)	I_yy (kg·m²)	I_zz (kg·m²)	EI (N·m²)	GJ (N·m²)	EA (N)
B₁	1 × 10⁵	5 × 10⁶	5 × 10⁶	5 × 10⁶
B₂	138	0.397	470.90	470.90	4.04 × 10⁶	2.040 × 10⁶	2.8 × 10⁹
B₃	138	0.397	470.90	470.90	4.04 × 10⁶	2.040 × 10⁶	2.8 × 10⁹
B₄	18.38	0.023	0.149	0.149
B₅	18.38	0.023	0.149	0.149
B₆	1.486	1.5 × 10⁻²	9 × 10⁻³	9.8 × 10⁻³
B₇	1.486	1.5 × 10⁻²	9 × 10⁻³	9.8 × 10⁻³
B₈	2000	300	350	250

The lengths of the bodies B₂–B₅ are 6.4, 6.4, 0.3, and 0.3 m, respectively. The base B₁ and the target spacecraft B₈ are cubes with sides of 1 and 0.5 m. The sample time of control is 5 ms. As initial conditions, the manipulator of the spacecraft is already deployed which joint angles are chosen as . The initial position and attitude of the target are shown in Figure 4. The center of the grasper mass is aligned along the x inertial axis with the target center of mass. During the collision control phase, the grasper is locked at 90°. After this phase, the spacecraft state stabilizes, and the grasper begins to close.

4.2. Dynamic Model Verification

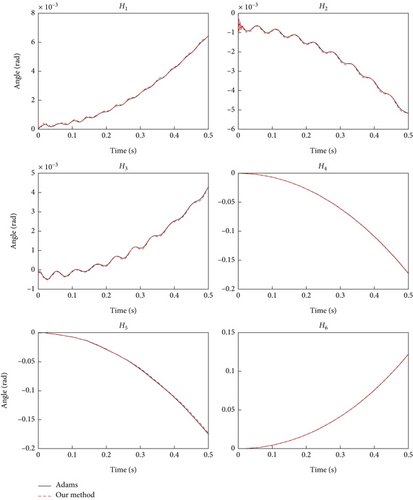
To validate our modified dynamic model, we conducted a numerical simulation using both Adams and our proposed method. In this simulation, torque is applied to the joints to alter the configuration of the space manipulator. Initially, the entire capturing system is static, with the manipulator set at initial joint angles of . Constant driving torques are applied to each joint, given by f^ey = [500 N · m,−500 N · m,−100 N · m,−10 N · m, 0.5 N · m, 0.1 N · m]^T. The time histories of rotation angles for each joint, calculated using both our method and Adams, are depicted in Figure 5. It is evident from the figure that the simulation results of our model align with those obtained from Adams, affirming the validity of our proposed model.

4.3. Effectiveness of the Position–Based Damping Control

This subsection shows performance in a collision scenario to evaluate the effectiveness of the damping collision control scheme. We employ the L-N model [30] to describe the contact force, whose expression is

()

where Δx is the penetration depth and k_c is the contact stiffness depending on the material and contact surface curvature. The exponent α depends on the topology characteristics of contact surfaces, which is set to be α = 1.5 according to the Hertzian contact approach. The hysteretic damping coefficient μ is defined as [30]

()

where

is the value of

at the beginning of the collision and e ∈ [0, 1] is the restitution coefficient.

In the simulation case, the translational velocity components with respect to the inertial reference frame are assumed as [−0.2 m/s, 0, 0]^T with an angular velocity around its center of mass of [0, 0, −0.1 rad/s]^T shown in Figure 6. The applicable damping coefficient is C = 4000, and the control parameters of the motion controller are chosen as K_p = diag(40,40,40,40,40,40) and K_d = diag(25,25,25,25,25,25). Given that the problem of flexible manipulator capture is still in the research phase and there is no consensus on the optimal material for end effector design, we use the contact stiffness k_c = 1 × 10⁶ N · m^–1.5 and the collision coefficient of restitution e = 0.8 in this section to preliminarily evaluate the effectiveness of the control strategy and assess whether the introduction of the new DOB motion tracking control can improve performance. In Section 4.5, we will simulate captures using various contact stiffness values to further evaluate the operational boundaries of the capture control strategies. The results of this research can provide valuable references for the design of end effectors.

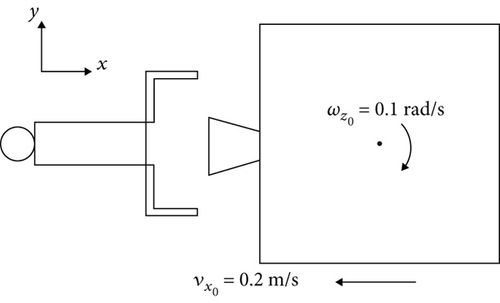
Figure 7 shows that when the servicing spacecraft is not controlled, the contact time is very short, only about 70 ms (note: a positive penetration depth indicates there is contact, while a negative or zero value means there is no contact). In contrast, when the service spacecraft is controlled with both CTM and DOB controllers, the contact time of all grasper contact points is significantly extended to at least 3 s as shown in Figure 8, indicating that the damping control scheme prevents separation from the target, effectively forming a stable contact after the collision. Meanwhile, after using the DOB controller, the contact oscillation of the upper gripper was significantly reduced, and the contact depth was more consistent with that of the lower gripper, indicating that the attitude control effect of the gripper has been improved. Therefore, the numerical simulations in the following sections are all based on the DOB controller. The DOB gain is set as 5.

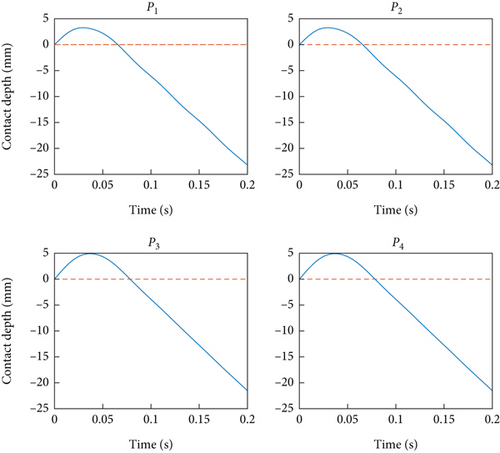
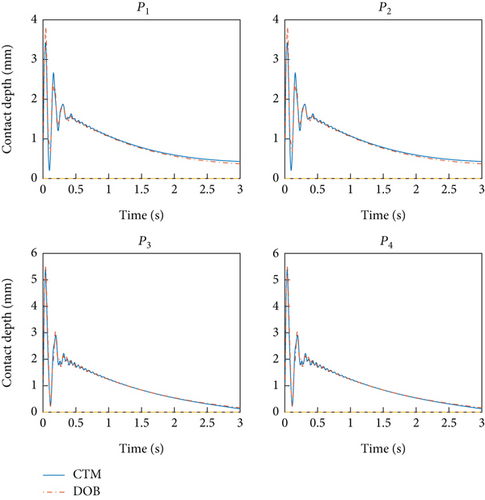
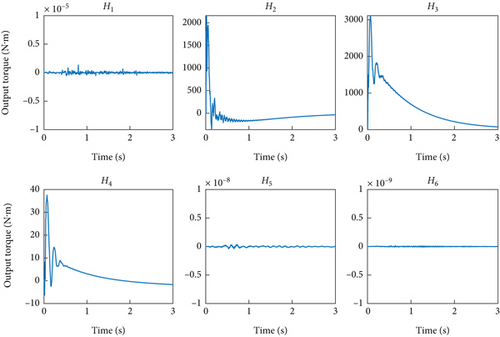
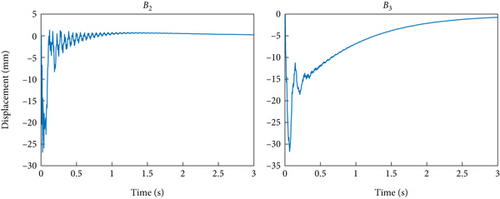
Figure 9 shows the control torque used in the damping control scheme, with a maximum torque not exceeding 3000 N·m and a rapid decrease over time, indicating that our method can achieve control at a controllable energy cost. Figure 10 depicts the vibration of the end of the flexible manipulator in the y-direction. After the collision, the robotic arm will produce relatively obvious vibrations, but after using the damping control scheme, the vibrations will be significantly suppressed and become stable. Considering that the flexible arm is 6.4 m long, subsequent vibrations are negligible.

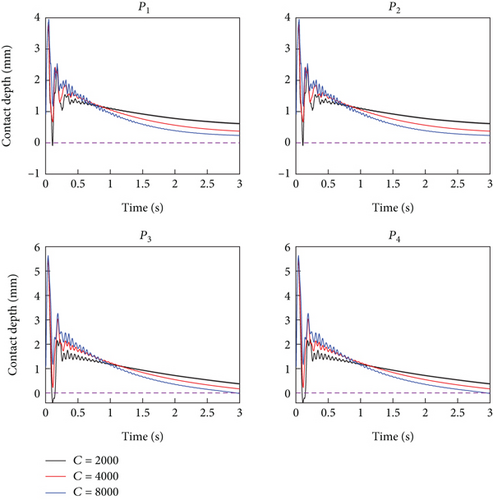
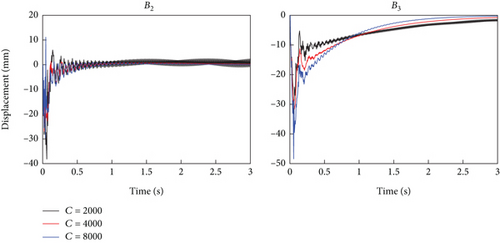
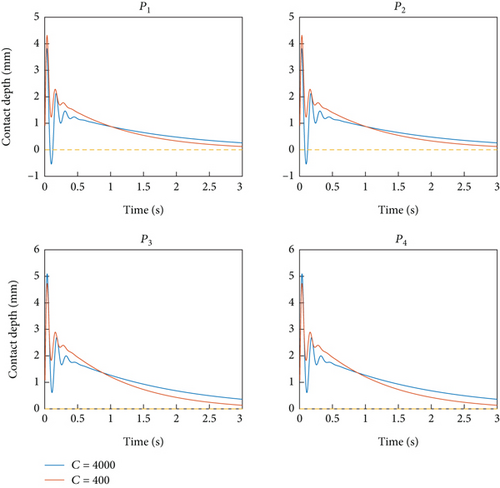
The above simulation results have verified the effectiveness of the proposed control scheme. Next, three new simulations are conducted to evaluate the impact of different control damping coefficients on the control results. Here, we take three damping coefficients of 2000, 4000, and 8000 as examples. Except for the damping coefficient, all other parameters are consistent with the above simulations. As shown in Figure 11, a smaller damping coefficient results in a shorter duration of separation but can achieve a longer contact duration. In contrast, larger damping will increase the duration of oscillation. Figure 12 shows that as the damping increases, the vibration duration of B₂ and B₃ decreases, the initial vibration amount of B₂ decreases, and the initial vibration amount of B₃ increases, both of which are controllable. In summary, the damping coefficient has little effect on the overall effectiveness of the control scheme. Our method has high parameter adaptability and can achieve good control effects on the system over a large range.

4.4. Influence of the Manipulator’s Flexibility Manipulator on the Control

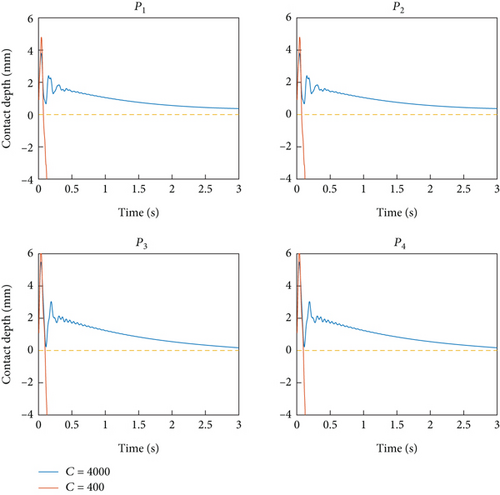
This section will carry out two sets of simulations to illustrate the influence of the manipulator’s flexibility on the control outcomes. The simulations involve the operation of the same controller on both a rigid manipulator and a flexible manipulator to accomplish the capture task. The inertia parameters and geometry parameters for the rigid manipulator are identical to those of the flexible manipulator. In the first set of simulations, the damping control coefficient C is set to 400, while the motion control parameters K_p and K_d are chosen as diag(500,500,500,500,500,500) and diag(300,300,300,300,300,300). In the other set, all control parameters remain the same as those in Section 4.3. Figure 13 shows that the rigid manipulator can stably contact the target after a collision under different control parameters. However, Figure 14 shows that the flexible manipulator can only stably contact the target when C is larger and K_p and K_d are smaller. These results indicate that controlling the flexible manipulator is more challenging and highlight the necessity of choosing larger C and smaller K_p and K_d to effectively control the flexible manipulator.

The analysis of the damping control [26] indicates that the effective mass involved in collisions affects the damping control gain. Specifically, as the effective mass decreases, the required damping control gain increases. This is because a reduction in the effective mass of the space robot makes the EE more susceptible to being pushed away by collision forces. To counteract this tendency, the space robot must apply greater control to the EE, necessitating a higher damping control gain. Unlike rigid space manipulators, flexible space manipulators deform and absorb impact energy upon collision. This deformation can be modeled as a spring connecting the base and the EE, meaning the base does not fully engage in the collision. Consequently, the effective collision mass of a flexible space robot is smaller than that of a rigid one. This explains why a larger damping control gain is required when using a flexible manipulator to capture a noncooperative object.

Additionally, due to the influence of deformation, the response of a flexible manipulator is slower compared to that of a rigid manipulator under the same control force. Therefore, using large K_p and K_d parameters can significantly increase overshoot, leading to substantial oscillations in the system. To achieve better control results, it is necessary to use smaller K_p and K_d values when controlling a flexible manipulator.

4.5. Robustness of the Damping Control Scheme to Uncertainty

In the actual capture mission, the inertial parameters of the target and initial collision conditions of the captured target may not be accurately known. Hence, whether the damping control scheme can maintain robustness under different conditions deserves further analysis.

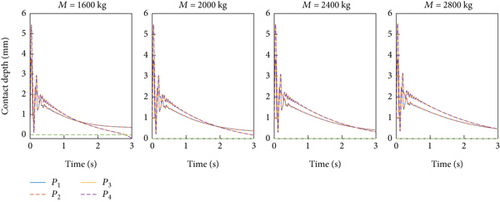
Initially, we assess the robustness of the damping control for different target inertia parameters outlined in Table 2. The remaining simulation settings align with those described in Section 4.3. As depicted in Figure 15, our damping control scheme effectively establishes stable contact between the grasper and different targets using the same control parameters, even in the presence of varying inertia parameters. This observation underscores the robustness of the damping control scheme in mitigating uncertainties related to the target’s inertia parameters.

Table 2. Inertial parameters of the noncooperative target.

Case	Mass (kg)	I_xx (kg·m²)	I_yy (kg·m²)	I_zz (kg·m²)
1	1600	250	300	200
2	2000	300	350	250
3	2400	350	400	300
4	2800	400	450	350

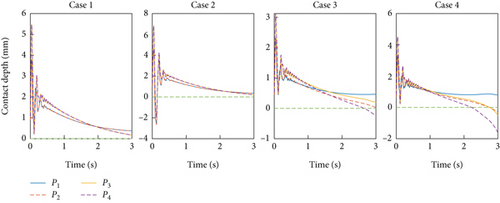
The second set of simulations explores different initial target velocities, as indicated in Table 3. The other settings are the same as those in Section 4.3. The results shown in Figure 16 indicate that the control strategy successfully extended the contact duration of the target in various initial states to varying degrees, although there may be brief separation phenomena. This observation highlights the robustness of the damping control scheme in the face of uncertainties in the target’s initial velocity, without necessitating alterations to the control parameters.

Table 3. Initial velocities of the noncooperative target.

Case	v_x (m/s)	ω_x (rad/s)	ω_y (rad/s)	ω_z (rad/s)
1	−0.2	0	0	−0.1
2	−0.24	0	0	−0.12
3	−0.1	0.01	−0.01	−0.05
4	−0.15	0.02	−0.02	−0.1

The third set of simulations involves different contact stiffness coefficients: 1 × 10⁵, 1 × 10⁶, and 1 × 10⁷. The remaining settings are consistent with those outlined in Section 4.3. Figure 17 illustrates that, when the contact stiffness is less than 1 × 10⁷, the contact rapidly stabilizes, preventing separation between the grasper and the target. As the contact stiffness becomes 1 × 10⁷, the initial stage shows more noticeable oscillations in contact depth, indicating that the grasper and the target experience a “contact-separation” state. Despite this, after multiple occurrences of contact separation, the controller establishes stable contact between the grasper and the target, prolonging the contact duration. Thus, without changing the control parameters, the results in Figure 17 demonstrate the robustness of the damping control scheme to the uncertainties of the contact stiffness.

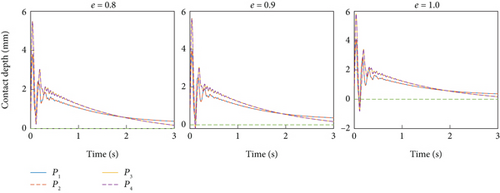
In the final set of simulations, various coefficients of restitution were considered. The results of these simulations are presented in Figure 18. As depicted in the figure, it is evident that, without altering the control parameters, the damping control scheme can consistently achieve the control objectives across different coefficients of restitution.

5. Concluding Remark

In this paper, we investigate the dynamic modeling and control challenges associated with capturing a noncooperative spacecraft using a flexible manipulator. We introduce an improved modeling method tailored for a flexible link with a flexible revolute joint. This approach accounts for joint flexibility without adding extra degrees of freedom, thereby improving solution efficiency and simplifying controller implementation. Subsequently, we apply a position–based damping control scheme to address control challenges. Significantly, the control scheme, originally devised for rigid manipulators, is extended to accommodate the flexibility of the manipulator. Numerical simulations are conducted to assess the efficacy of the modified dynamics modeling method and the adopted control scheme. The simulation results showcase the effectiveness of both the modeling method and the control scheme. Through an analysis of the influence of manipulator flexibility on control outcomes, we observe that a larger damping control gain and smaller control parameters in the motion controller are necessary when dealing with a flexible manipulator. Moreover, the simulation results underscore the high robustness of the damping control scheme in the presence of uncertainties.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 12172214 and 12172215).

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author, Xiao-Feng Liu, upon reasonable request.

References

1 Scott M. A., Gilbert M. G., and Demeo M. E., Active vibration damping of the space shuttle remote manipulator system, Journal of Guidance, Control, and Dynamics. (1993) 16, no. 2, 275–280, https://doi.org/10.2514/3.56598, 2-s2.0-0027557813.
10.2514/3.56598
Google Scholar
2 Flores-Abad A., Ma O., Pham K., and Ulrich S., A review of space robotics technologies for on-orbit servicing, Progress in Aerospace Sciences. (2014) 68, 1–26, https://doi.org/10.1016/j.paerosci.2014.03.002, 2-s2.0-84899458942.
10.1016/j.paerosci.2014.03.002
Web of Science® Google Scholar
3 Cyril X., Jaar G. J., and Misra A. K., The effect of payload impact on the dynamics of a space robot, Proceedings of 1993 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS′93), 1993, 3, IEEE, 2070–2075.
10.1109/IROS.1993.583916
Google Scholar
4 Cyril X., Misra A. K., Ingham M., and Jaar G. J., Postcapture dynamics of a spacecraft-manipulator-payload system, Journal of Guidance, Control, and Dynamics. (2000) 23, no. 1, 95–100, https://doi.org/10.2514/2.4491, 2-s2.0-0033905768.
10.2514/2.4491
Web of Science® Google Scholar
5 Kövecses J. and Cleghorn W. L., Finite and impulsive motion of constrained mechanical systems via Jourdain′s principle: discrete and hybrid parameter models, International Journal of Non-Linear Mechanics. (2003) 38, no. 6, 935–956, https://doi.org/10.1016/S0020-7462(02)00039-2, 2-s2.0-0037411977.
10.1016/S0020-7462(02)00039-2
Google Scholar
6 Liu S., Wu L., and Lu Z., Impact dynamics and control of a flexible dual-arm space robot capturing an object, Applied Mathematics and Computation. (2007) 185, no. 2, 1149–1159, https://doi.org/10.1016/j.amc.2006.07.035, 2-s2.0-33847296545.
10.1016/j.amc.2006.07.035
Web of Science® Google Scholar
7 Felicetti L., Gasbarri P., Pisculli A., Sabatini M., and Palmerini G. B., Design of robotic manipulators for orbit removal of spent launchers’ stages, Acta Astronautica. (2016) 119, 118–130, https://doi.org/10.1016/j.actaastro.2015.11.012, 2-s2.0-84948783541.
10.1016/j.actaastro.2015.11.012
Google Scholar
8 Yu S., Qu Z., Zheng S., and Han J., Capture dynamics modeling and simulation of the space flexible manipulator, Theory, Methodology, Tools and Applications for Modeling and Simulation of Complex Systems: 16th Asia Simulation Conference and SCS Autumn Simulation Multi-Conference, AsiaSim/SCS AutumnSim 2016, Beijing, China, October 8-11, 2016, Proceedings, Part I 16, 2016, Springer, 296–307.
10.1007/978-981-10-2663-8_32
Google Scholar
9 Wei C., Luo J., Dai H., and Yuan J., Adaptive model-free constrained control of postcapture flexible spacecraft: a Euler–Lagrange approach, Journal of Vibration and Control. (2018) 24, no. 20, 4885–4903, https://doi.org/10.1177/1077546317736965, 2-s2.0-85043491544.
10.1177/1077546317736965
Google Scholar
10 Stolfi A., Gasbarri P., and Misra A. K., A two-arm flexible space manipulator system for post-grasping manipulation operations of a passive target object, Acta Astronautica. (2020) 175, 66–78, https://doi.org/10.1016/j.actaastro.2020.04.045.
10.1016/j.actaastro.2020.04.045
Google Scholar
11 Ma X., Li N., Zhang C., Chen M., Ju X., Wu S., and Zou H., Modeling and analysis of force-closure properties for the flexible space manipulator during docking and capturing process, International Conference on Mechanism and Machine Science, 2022, Springer, Singapore, 1755–1767.
Google Scholar
12 Yoshida K. and Nakanishi H., Impedance matching in capturing a satellite by a space robot, Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), 2003, Las Vegas, NV, USA, 3059–3064, https://doi.org/10.1109/IROS.2003.1249626.
10.1109/IROS.2003.1249626
Google Scholar
13 Yoshida K., Nakanishi H., Ueno H., Inaba N., Nishimaki T., and Oda M., Dynamics, control and impedance matching for robotic capture of a non-cooperative satellite, Advanced Robotics. (2004) 18, no. 2, 175–198, https://doi.org/10.1163/156855304322758015, 2-s2.0-1642376214.
10.1163/156855304322758015
Web of Science® Google Scholar
14 Yoshida K., Dimitrov D., and Nakanishi H., On the capture of tumbling satellite by a space robot, 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2006, Beijing, China, IEEE, 4127–4132, https://doi.org/10.1109/IROS.2006.281900, 2-s2.0-34250672877.
10.1109/IROS.2006.281900
Google Scholar
15 Uyama N., Hirano D., Nakanishi H., Nagaoka K., and Yoshida K., Impedance-based contact control of a free-flying space robot with respect to coefficient of restitution, 2011 IEEE/SICE International Symposium on System Integration (SII), 2011, Kyoto, Japan, IEEE, 1196–1201, https://doi.org/10.1109/SII.2011.6147619, 2-s2.0-84857577330.
10.1109/SII.2011.6147619
Google Scholar
16 Uyama N., Nakanishi H., Nagaoka K., and Yoshida K., Impedance-based contact control of a free-flying space robot with a compliant wrist for non-cooperative satellite capture, 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2012, Vilamoura-Algarve, Portugal, IEEE, 4477–4482, https://doi.org/10.1109/IROS.2012.6386082, 2-s2.0-84872297321.
10.1109/IROS.2012.6386082
Google Scholar
17 Stolfi A., Gasbarri P., and Sabatini M., A combined impedance-PD approach for controlling a dual-arm space manipulator in the capture of a non-cooperative target, Acta Astronautica. (2017) 139, 243–253, https://doi.org/10.1016/j.actaastro.2017.07.014, 2-s2.0-85024099435.
10.1016/j.actaastro.2017.07.014
Web of Science® Google Scholar
18 Stolfi A., Gasbarri P., and Sabatini M., Performance analysis and gains tuning procedure for a controlled space manipulator used for non-cooperative target capture operations, Aerotecnica Missili & Spazio. (2018) 97, no. 1, 3–12, https://doi.org/10.1007/BF03404759.
10.1007/BF03404759
Google Scholar
19 Flores-Abad A., Crain A., Nandayapa M., Garcia-Teran M. A., and Ulrich S., Disturbance observer-based impedance control for a compliance capture of an object in space, 2018 AIAA Guidance, Navigation, and Control Conference, 2018, Kissimmee, Florida, https://doi.org/10.2514/6.2018-1329, 2-s2.0-85044617039.
10.2514/6.2018-1329
Google Scholar
20 Wu S., Mou F., Liu Q., and Cheng J., Contact dynamics and control of a space robot capturing a tumbling object, Acta Astronautica. (2018) 151, 532–542, https://doi.org/10.1016/j.actaastro.2018.06.052, 2-s2.0-85049434887.
10.1016/j.actaastro.2018.06.052
Web of Science® Google Scholar
21 Han D., Huang P., Liu X., and Yang Y., Combined spacecraft stabilization control after multiple impacts during the capture of a tumbling target by a space robot, Acta Astronautica. (2020) 176, 24–32, https://doi.org/10.1016/j.actaastro.2020.05.035.
10.1016/j.actaastro.2020.05.035
Google Scholar
22 Han D., Liu Z., and Huang P., Capture and detumble of a non-cooperative target without a specific gripping point by a dual-arm space robot, Advances in Space Research. (2022) 69, no. 10, 3770–3784, https://doi.org/10.1016/j.asr.2022.02.039.
10.1016/j.asr.2022.02.039
Google Scholar
23 Wang Z., Zou L., Su X., Luo G., Li R., and Huang Y., Hybrid force/position control in workspace of robotic manipulator in uncertain environments based on adaptive fuzzy control, Robotics and Autonomous Systems. (2021) 145, article 103870, https://doi.org/10.1016/j.robot.2021.103870.
10.1016/j.robot.2021.103870
Google Scholar
24 Raina D., Gora S., Maheshwari D., and Shah S. V., Impact modeling and reactionless control for post-capturing and maneuvering of orbiting objects using a multi-arm space robot, Acta Astronautica. (2021) 182, 21–36, https://doi.org/10.1016/j.actaastro.2021.01.034.
10.1016/j.actaastro.2021.01.034
Web of Science® Google Scholar
25 Liu X.-F., Cai G.-P., Wang M.-M., and Chen W.-J., Contact control for grasping a non-cooperative satellite by a space robot, Multibody System Dynamics. (2020) 50, no. 2, 119–141, https://doi.org/10.1007/s11044-020-09730-4.
10.1007/s11044-020-09730-4
Google Scholar
26 Liu X.-F., Zhang X.-Y., Cai G.-P., and Wang M.-M., A collision control strategy for detumbling a non-cooperative spacecraft by a robotic arm, Multibody System Dynamics. (2021) 53, no. 3, 225–255, https://doi.org/10.1007/s11044-021-09793-x.
10.1007/s11044-021-09793-x
Google Scholar
27 Cyril X., Jaar G. J., and Misra A. K., Dynamical modelling and control of a spacecraft-mounted manipulator capturing a spinning satellite, Acta Astronautica. (1995) 35, no. 2-3, 167–174, https://doi.org/10.1016/0094-5765(94)00262-K, 2-s2.0-0010871562.
10.1016/0094-5765(94)00262-K
Google Scholar
28 Bottega W. J., Engineering Vibrations, 2014, CRC Press, https://doi.org/10.1201/b17886.
10.1201/b17886
Google Scholar
29 Likins P. W., Finite element appendage equations for hybrid coordinate dynamic analysis, International Journal of Solids and Structures. (1972) 8, no. 5, 709–731, https://doi.org/10.1016/0020-7683(72)90038-8, 2-s2.0-0015331830.
10.1016/0020-7683(72)90038-8
Google Scholar
30 Lankarani H. M. and Nikravesh P. E., A contact force model with hysteresis damping for impact analysis of multibody systems, Journal of Mechanical Design. (1990) 112, no. 3, 369–376, https://doi.org/10.1115/1.2912617, 2-s2.0-84990847021.
10.1115/1.2912617
Web of Science® Google Scholar
31 Liu X., Li H., Wang J., and Cai G., Dynamics analysis of flexible space robot with joint friction, Aerospace Science and Technology. (2015) 47, 164–176, https://doi.org/10.1016/j.ast.2015.09.030, 2-s2.0-84943797834.
10.1016/j.ast.2015.09.030
Web of Science® Google Scholar
32 Xu W., Meng D., Chen Y., Qian H., and Xu Y., Dynamics modeling and analysis of a flexible-base space robot for capturing large flexible spacecraft, Multibody System Dynamics. (2014) 32, no. 3, 357–401, https://doi.org/10.1007/s11044-013-9389-0, 2-s2.0-84920256118.
10.1007/s11044-013-9389-0
Google Scholar
33 Mohammadi A., Tavakoli M., Marquez H. J., and Hashemzadeh F., Nonlinear disturbance observer design for robotic manipulators, Control Engineering Practice. (2013) 21, no. 3, 253–267, https://doi.org/10.1016/j.conengprac.2012.10.008, 2-s2.0-84872391084.
10.1016/j.conengprac.2012.10.008
Web of Science® Google Scholar

All articles

Dynamics and Control of Noncooperative Space Target Capture Using a Flexible Manipulator

Abstract

1. Introduction