Islanding Detection and Power Quality Diagnosis of Wind Power Integrated Microgrid with Reduced Feature Trained Novel Optimized Random Decision Forest
Abstract
Distributed generations (DGs) have been increasingly addressing the ongoing power deficit in the electricity market. However, a significant concern in DG-integrated microgrids is the detection of accidental islanding. To tackle this issue, this article proposes a cost-friendly, novel data-driven passive islanding detection scheme named EEMD-HOBRC, combining noise-assisted ensemble empirical mode decomposition (EEMD) and a hybrid optimization-based random forest classifier (HOBRFC). The detection scheme employs a diverse set of features extracted from both raw and EEMD decomposed signals. Essential features are selected using the binary grey wolf optimizer (BGWO) to reduce computational burden. To further improve classification accuracy, the parameters of the random forest classifier are optimized through a hybrid particle swarm and reformed grey wolf optimization (PSRGWO) technique with Cohen’s kappa index as the cost function. The proposed technique is rigorously validated in two different multi-DG environments, encompassing islanding and various nonislanding events. The results demonstrate the effectiveness of the approach in terms of enhanced accuracy, detection time, and performance under both noisy and noise-free conditions. The accuracy of detection under ideal and high noise scenarios is found to be 99.88% and 99.2%, respectively, with maximum detection time of 34.27 ms. Comparative analysis with other algorithms also supports the superiority of the proposed technique. Finally, the method is successfully applied to shrink the nondetection zone (NDZ) with minimal power mismatch, further enhancing its utility in practical applications.
1. Introduction
Distributed generators (DGs) are proving to be the best solution to match the ongoing demand for electricity. Since every solution is equipped with new problem(s), the DGs are equipped with the challenge of unintentional islanding. In simple terms, islanding is such a scenario where the DG(s) of an area is/are kept on supplying power to the nearby loads even though the central grid is no longer connected. This occurrence should be detected within 2 sec as per IEEE 1547 [1] norms. The conventional strategies of islanding detection [2–5] have a common concern that is reducing the nondetection zone (NDZ). By definition, NDZ is a power mismatch region where the islanding is remained undetected due to supply-demand equilibrium. Several research works have already proposed to conquer the NDZ issue by applying signal processing approach (SPA) to the conventional passive detection techniques [6, 7]. But still, these have issues like computational complexity, affected by noise interference, and unapplicable to nonlinear and nonstationary signals. Hence, the necessity of further research is essential in this particular field. Eventually, mode decomposition- (MD-) oriented SPAs are gaining popularity that brings forward empirical MD (EMD) [8], variational MD (VMD) [9], and empirical wavelet transform (EWT) [10] into the limelight. But these MD techniques basically suffer from mode mixing issues. This major drawback is wonderfully eliminated by a recently proposed noise-assisted technique called ensemble EMD (EEMD) [11] by taking the mean of an aggregate of trials that comprises of signal and finite amplitude white noise. It has also displayed significant results in detecting differential protection [12], load forecasting [13], wind speed prediction [14], etc. Thus, EEMD is chosen as the base SPA in this work.
Disturbance detection only with SPA brings thresholding challenges in front. Setting such critical thresholds is a tough job. A suitable alternative is to go for machine learning classifiers (MLCs) that detect the class of event by training-testing approach [15]. Such an application utilizes the inherent features of a signal. Since there are lot of simple as well as complex features can be obtained from any signal, it is important to look for an effective feature selection technique (FST) so as to reduce the time complexity and thereby increasing the efficacy of the MLC with least number of features. Many researchers have already suggested several FSTs where the feature selection process is considered as a combinatorial problem [16]. But the classical FSTs have some flaws which can be overcame by evolutionary optimization techniques [17–20] those can be of two types, namely, continuous and discrete (binary). As the decision variable of feature selection varies in binary space, a binary optimization algorithm can be chosen to deal with this [21–23]. But it is essential to look for an algorithm that maintains a proper balance between exploration and exploitation. One of the recent bioinspired techniques is grey wolf optimization (GWO) that is gaining popularity due to its smooth transition between exploration and exploitation [24, 25]. A binary variant of GWO has been proposed by Ahmadipour et al.[26] which has shown significant result for feature selection problems. That is why BGWO has been chosen for feature selection. Once the features are obtained, then it is required to look for a classifier. A number of MLCs are already implemented in several research works starting from consensus-based intelligent control [27], machine faults [28–30], and islanding detection [31–35], which have their own uniqueness and limitations. Eventually, ensemble machine learning paradigms are stepping ahead with the concept of combining more than one learner together to bolster the classification rate. One of such learners is random forest (RF) which ensembles the decision trees (DTs). RF possesses the advantages like well performance with less parameters, hardly affected by fitting issues, and has better generalizing capability [36]. Furthermore, the efficacy of RF is tested under public data [37], and it has observed that RF is displaying significant result among the MLCs. Hence, RF is considered as the base classifier in this study. But before implementing RF classifier, it is necessary to look through two major factors; those are DTs inside forest and cardinality of feature subset. These two deciding factors also called hyperparameters can be evaluated by implementing any optimization algorithm. A hybrid optimization algorithm combining the social behaviour like swarm etiquettes and grey wolf hunting is proposed in this study to extremize the major hyperparameters of RF which can enhance the robustness and classification capability of the classifier. Moreover, for solving any optimization problem, it is required to define an objective function. Here, the objective function can be the classification accuracy or some other criterion that might consider the best trade-off between attribute extraction, computational burden, and efficiency. For instant, evaluating the performance of any classifier only considering the number of misclassifications may be deceitful [38], if there is prediction failure obtained for one or more features. Hence, a different statistical measure is suggested in this study for assessing the classification accuracy called Cohen’s kappa. The kappa index is generally a measure of inter-rater agreement that indemnifies the possibility of classification by chance [39]. Further, it is unrealistic to rate all the error as identical. For example, an islanding event if misclassified as capacitor switching is much more destructive than a transformer switching misclassified as capacitor switching. Thus, for cost sensitive classifications, the preliminary job is to ensure that the errors are free of constraints, assumptions, and biasing which can be achieved by estimating Cohen’s kappa.
Furthermore, integration of multiple DG units with the exiting grid is creating added complexity, which is to be addressed. The generated voltage out of any DG unit can be AC or DC depending on the nature of the source. It has to be converted first to the nominal voltage and frequency with the nominal parameters before feeding to the grid. For that reason, transformers and/or inverters are usually used while DG-GRID integration. Hence, DGs can be classified into two major categories such as inverter-based DG and rotating machine DG which have separate impact individually on the associated system. For an instant, when a wind power generation unit is disconnected from grid, the voltage of the system will swell up for few cycles due to the sudden drop in reactive power of the system. On the contrary, the outage of a PV unit certainly brings some fluctuation in frequency along with voltage amplitude that resembles a flicker. Hence, it is highly desired to detect the PQ events arising because of these DGs along with other PQ events and islanding [40].
Briefly, the work focuses on islanding and power quality disturbance classification from the BGWO reduced feature dataset that fed into the novel particle swarm and reformed grey wolf optimization (PSRGWO) random forest classifier. Further, the proposed approach is validated with two different multi-DG systems under ideal and noisy conditions. The descriptive information of all the concepts is discussed in the Section 2. Section 3 is dedicated to microgrid system under consideration whereas Section 4 explains about feature extraction and data collection. The methodology part is covered in Section 5, and the results are analyzed in Section 6. At last, the study is concluded in Section 7.
- (i)
Application of EEMD on extracted signals to decompose into different IMFs and most informative IMF is chosen to extract multiple features, and some of the features are extracted from raw signal
- (ii)
Maidan application of binary grey wolf optimization to select optimal informative features
- (iii)
A novel hybrid PSRGWO optimization algorithm has been formulated to optimize the parameters of the proposed random forest classifier, i.e., termed as hybrid optimization-based random forest classifier (HOBRFC)
- (iv)
Kappa statics is used as objective function for the optimization problem to eradicate the possibility of classification by chance
- (v)
The proposed method is used for classifying the islanding and other power quality disturbances
- (vi)
The efficacy of the proposed classifier is tested for two different test systems for ideal and noisy scenarios
- (vii)
Finally, the reduction of nondetection zone is validated with a separate dataset of very small power mismatch
2. Theoretical Background
2.1. Binary Grey Wolf Optimization
The grey wolves are preferring to stay in a pack by maintaining a social hierarchy where the alpha wolves lead the pack followed by beta and delta wolves. The movement of the wolves in GWO algorithm took place stochastically in the search space. There are problems, whose solutions are restricted to binary 0/1 or true/false type that inspires to go for a special variant of optimization technique, i.e., binary optimization algorithms. Thus, BGWO comes into picture as an FST. In BGWO, the conventional grey wolf optimization is carried out initially and the position updating equation is forced to be binary.
Here, , , and .
2.2. Ensemble Empirical Mode Decomposition (EEMD)
Mode decomposition is eventually gaining enormous interest both in the community of researchers as well as industrialists. EMD is the start point of such signal preprocessors and has already used in wide range of applications. The descriptive explanation of EMD can be found in [14]. It simply divides the original signal into several intrinsic mode functions. But the major problem arises here is the mixing of modes which can be eliminated by implementing a noise-assisted method called EEMD that collaborate the different scale signals to their respective band of IMFs.
Here, each of the observation is impersonated by appending different realization of white noise to a single observation c(t). Even though the white noise inclusion brings about the drop in signal-to-noise ratio, but it comes up with relatively uniform distribution of reference scale which actually eradicates the problem of mode mixing. Hence, EEMD determines the true IMF by calculating the average on ensemble of trails where each trail consists of a signal and finite amplitude white noise. Figure 1 represents a flow diagram for the implementation of EEMD.

- (i)
The cluster of white noises abandons each other in an ensemble mean that only left out the components of original signal
- (ii)
The finite amplitude noise actually facilitates the inhabitation of different scale signal into the corresponding IMF which makes the ensemble mean much more worthwhile
Moreover, EEMD introduces an element of randomness to the decomposition process by incorporating white noise into the disturbance signal. This results in the generation of multiple slightly varied realizations of the signal. The IMFs from these realizations are then averaged, providing a stronger illustration of each IMF. The ensemble averaging technique proves effective in mitigating the mode mixing problem. Because the added noise in each realization is random, the mixing effects tend to cancel out when combining results from multiple realizations. Additionally, EEMD follows statistical process to address mode mixing, leveraging the law of large numbers. With an increasing number of realizations, the signal’s statistical properties become more evident, leading to a more reliable decomposition process [11, 14].
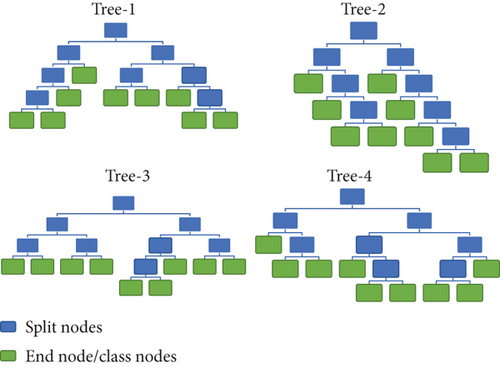
2.3. Random Decision Forest Classifier
Here, xrand is the random feature set at each node split, and crand is the subset of classes a tree can predict.
Furthermore, the limitation of RF is high variance and biasing that arises fitting issues. That means a delta amount of change in training data is supposed to create a completely different variant of decision trees. However, the problem of underfitting and overfitting is effectively addresses through two primary strategies: bagging and random feature selection. Bagging entails creating multiple subsets of the training data by sampling with replacement. Each subset undergoes training with a decision tree. This approach diminishes the model’s variance, reducing its sensitivity to noise or outliers in the data. Another important strategy is random feature selection, where instead of using all features at each split of the decision tree, a random subset of features is chosen. This helps minimize the correlation among trees and boosts the model’s resilience to irrelevant or redundant features. By combining these two techniques, the random decision forest achieves a well-balanced trade-off between bias and variance, effectively managing challenges related to underfitting and overfitting issues [41, 42].
3. Systems under Study
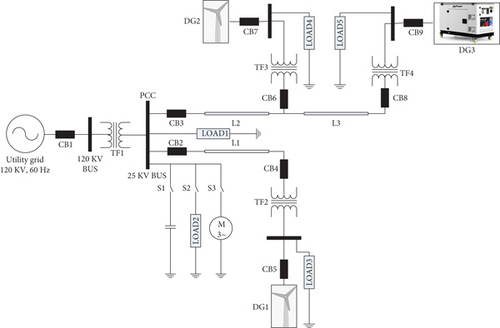
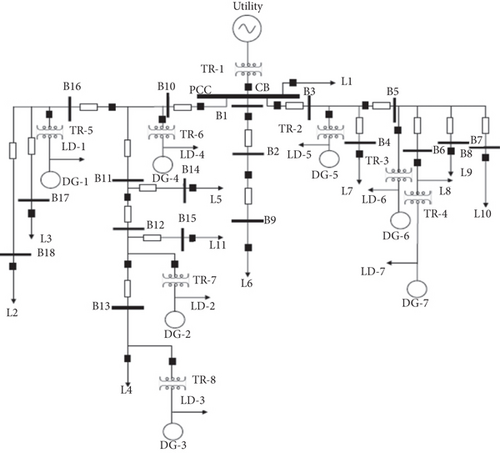
In this study, the validations are made with two separate test systems, namely, TS-I and TS-II, to ensure the dynamism of the proposed work. The first microgrid TS-I [40] is connected to a central grid at 120 kV bus which can be intentionally islanded by operating circuit breaker 1 (CB1). The related TS-I parameters are summarized in Table 1. The main transformer TF1 steps down the voltage from 120 kV to 25 kV and connected to the PCC at the low voltage end. Figure 2 shows the one-line diagram of TS-I that comprises of 3 DGs at separate location. On the other hand, the TS-II is consisting of 7 numbers of DGs where DG-1,2,7 are wind farms, DG-3,5,6 are diesel generators deployed in the time of emergency, and DG-4 is alone a PV unit. It is shown in Figure 3. The specifications of TS-II are presented in [43].
| Parameters | Specification |
|---|---|
| Utility grid | 120 kV, 60 Hz |
| DG1, DG2 | 9 MW wind system, 6 units of 1.5 MW, 60 Hz, 575 V |
| DG3 | 3.125 MVA synchronous diesel engine, 60 Hz, 575 V |
| Switching capacitor (C) | 25 kV, 2 MVAR |
| Induction motor (M) | 6 MVA |
| TF1 | 25 MVA, 120 kV/25 kV star-delta |
| TF2, TF3 | 12 MVA, 25 kV/575 V delta-star |
| TF4 | 5 MVA, 25 kV/575 V delta-star |
| L1, L2, L3 | 22 km, 60 Hz, 3-phase π-section line |
| LOAD3,4 | 8 MW, 1.75 MVAR |
| LD5 | 2.5 MW, 0.75 MVAR |
| LOAD1,2 | 6 MW, 1.4 MVAR |
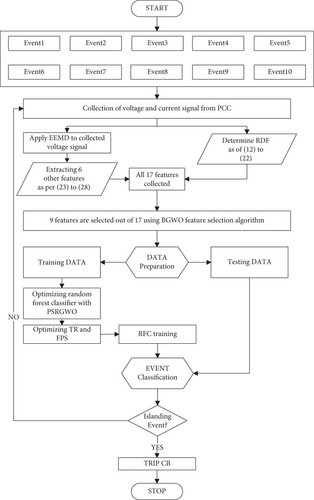
4. Data Collection and Feature Extraction
- (a)
The voltage and current signals form the PCC are collected from few cycles and saved as time series data
- (b)
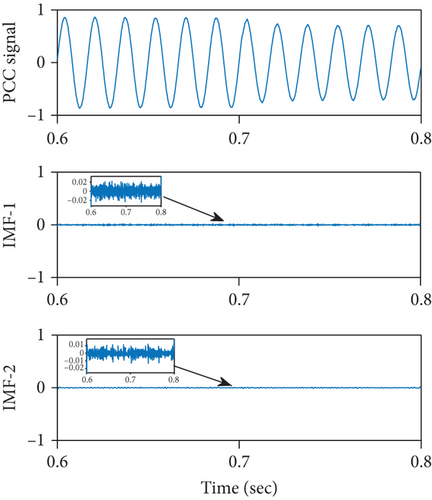
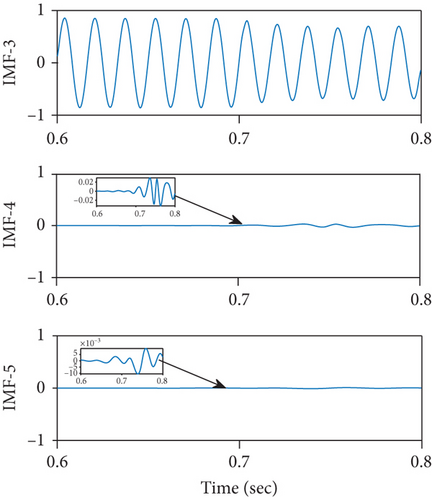
The signals are sampled uniformly at 2.4 kHz, and data samples are stored within a time frame of 0.6 to 0.8 seconds as disturbance is intentionally occurred within this interval. This can be seen in Figures 4(a) and 4(b)
- (c)
From the retrieved signals, 2 types of features are extracted, namely, raw signal features (RSFs) and decomposed signal features (DSFs)
5. Methodology
| Event classes | Name of event | Description | Samples |
|---|---|---|---|
| EC-1 | Islanding | CB1 opening | 800 |
| EC-2 | Outage of DG | DG-1 | 800 |
| EC-3 | DG-2 | 800 | |
| EC-4 | Capacitor switching | S1 switching | 800 |
| EC-5 | Line switching | CB3 opening | 800 |
| EC-6 | Induction motor switching | S3 switching | 800 |
| EC-7 | Load switching | S2 switching | 800 |
| EC-8 | Fault | LG, LLG, LLL, LLLG | 200 |
| EC-9 | Voltage sag | At target DG | 800 |
| EC-10 | Voltage swell | At target DG | 800 |
| IMFi | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 |
|---|---|---|---|---|---|
| PERCC | 0.0173 | 0.0392 | 0.9137 | 0.1733 | 0.0851 |
Next, the compressed dataset undergoes data preparation stage where the data is get divided into training and testing data to fed into RFC. But with the focus on improving the efficacy of this classifier, a hybrid optimization technique, namely, PSO with reformed-GWO (PSRGWO), has been proposed in this paper. This hybrid optimizer is basically going to optimize two parameters. The detailed information regarding the application of PSRGWO is presented in the next subsection.
5.1. Hybrid PSO and Reformed GWO Algorithm (PSRGWO)
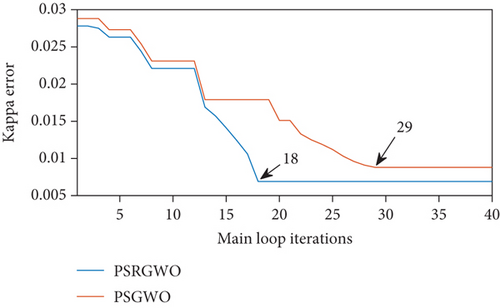
In this section, a hybrid algorithm is suggested combining the traditional particle swarm optimization with a reformed version of grey wolf optimization so as to strengthen the exploration capabilities. Here, within a single iteration of main loop, there exist few iterations of PSO followed by a few iterations of GWO. At the end of every loop, the outcomes of PSO and GWO are compared to save the best value till that particular iteration. As a result, the modified GWO will ensure the reduction in probability of PSO to get trapped in local extrema. The workflow of the proposed algorithm is shown in Figure 6.
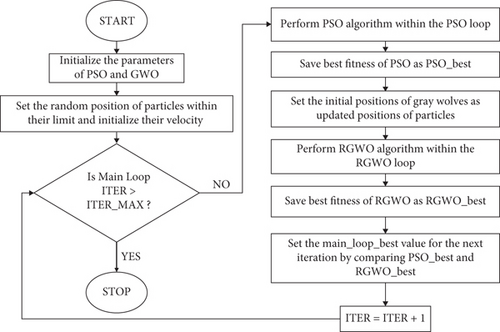
Here, ₭error represents the kappa error, and ₭ represents the actual kappa index. These are function of number of trees (TR) in the forest and feature involved in each split (FPS) of any tree construction.
6. Result Analysis
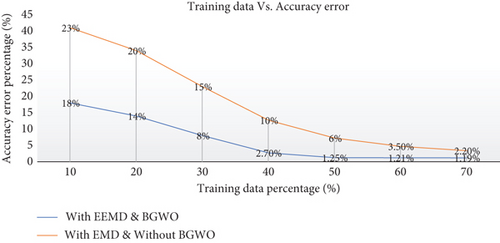
The proposed system is simulated in MATLAB (version 2018a) software running in a Lenovo personal computer with INTEL core-i5 8th generation 2.3 GHz processor and 8 GB RAM. The performance will be evaluated using the feature optimized dataset consisting of 9 distinct features (column wise) that holds 10 sets of event classes (row wise) to form an 8000 × 9 data vector. The collection of data samples is made under a wide range of power mismatch condition for both I&NI occurrences which results in a diversified dataset that have the seldom possibility of redundancy and biasing. Here, half of the data are taken for training and the remaining half for testing to verify the hybrid optimization-based random forest classifier (HOBRFC). Normally, a higher percentage of data (70 to 80%) are taken to train any classifier to ensure higher accuracy, but purity and clarity of data abstraction can play a vital role to amplify the performance indices of any classifier. A “training data percentage” versus “accuracy error” graph in Figure 7 can well describe the meaning of the previous statement. It can be observed that the reduced dataset can attain maximum prediction level even with 50% of training data. This signifies the unmatched data abstraction ability of EEMD as well as the unbiased feature selection capability of BGWO.
6.1. Optimal Parameter Selection for HOBRFC
RF classifier’s performance is based on the decision of several DTs whose branch division is carried out with a random subset of features. Training such type of models requires the dimensionality definition of both of these two elements which can be achieved using optimization. As we are optimizing TR and FPS, the preliminary requirement is to set the lower and upper limits of these two. The default FPS [42] in an RFC is chosen as , where p is the maximum number of available features. In this case, p = 9 so the lower limit of FPS is taken as 3. On the other side setting, the max value as the upper limit, certainly going against the core definition of the term “random” as this signifies any node of a DT inside the RF is subdivided into further branches using a random subset of features.
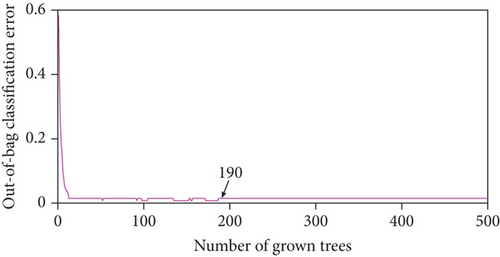
The parameters used during the implementation of proposed optimization algorithm are presented in Table 4. It can be seen from Figure 10 that PSRGWO’s performance is proving better both in terms of a number of iterations and error margin. While the PSGWO is taking 29 iterations to get the least converged error, on the other hand, the proposed PSRGWO is only taking 18 iterations to achieve an even low error margin. Finally, the optimum values of FPS (OFPS) and TR (OTR) are found to be 4 and 141, respectively, after taking the modes of 100 trails.
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Max iteration of main loop | 40 | Search agents | 20 |
| Max iteration of PSO loop | 15 | Max iteration of GWO loop | 15 |
| Range of split features | [3 8] | Range of trees | [9 200] |
6.2. Performance Indices
Performance indices (PIs) are the measures to analyze the prediction capability of a classifier once it is trained. It may sound a little weird if the formulae of different indices are directly stated over here. But it will be much easier to understand the PIs once after understanding the concept of the confusion matrix (CM). Simply, CM is a square matrix datasheet that estimates the performance of any ML classification model.
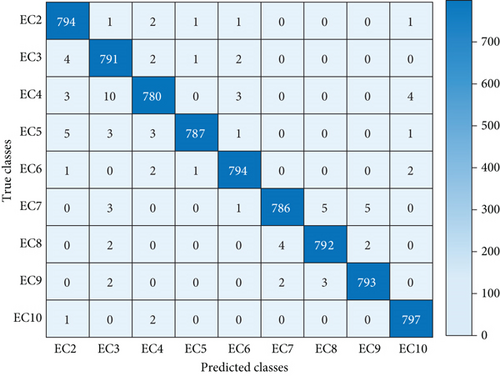
The core of the random forest machine learning model is decision trees, and each decision tree will train with random subset of features. Furthermore, the end nodes of these trees are the event classes. Therefore, a model trained with 10 classes will one islanding, and 9 PQ events (case 1) have separate tree structures than that of a model trained with only 9 PQ event classes (case 2). For this reason, the proposed model is tested with both the conditions.
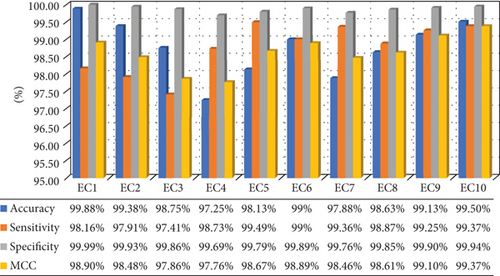
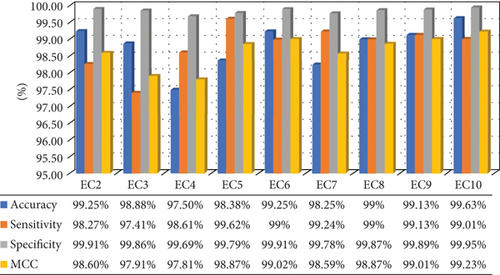
In Figure 11(a), the confusing matrix is obtained for the model trained with case 1, where 800 events per class are predicted using the proposed detection technique. It is found that the method shows 99.88% accuracy in detecting the islanding scenarios as 799 islanding cases are truly detected out of 800 classes. Apart from that, other nonislanding events are also showing promising accuracy of detection. Here, classes EC-1 to EC-10 are mapped as 1 to 10. Similarly, in Figure 11(b), only the case 2 events are considered. The proposed classifier also displays much accuracy for nonislanding events alone where EC-10 has highest accuracy rate of 99.63% since 797 events have predicted truly out of 800. Here, classes EC-2 to EC-10 are mapped as 1 to 9. The figures are represented as heatmaps. The darker color of the diagonal elements reflecting the elegant performance of the classifier. Now the above statement can be verified mathematically with the help of several PIs.

6.3. Noise Tolerance Evaluation
Noise is a nonavoidable part of any system, thus also visible in power system. The companionship of communication lines with power lines creates electromagnetic interference which is the main reason for noise existence in collected signal.
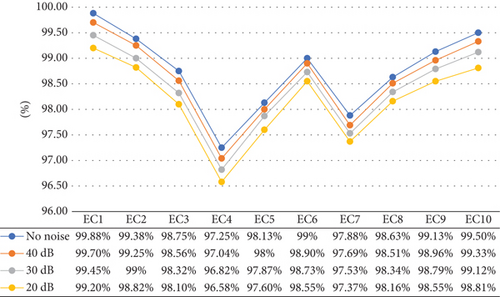
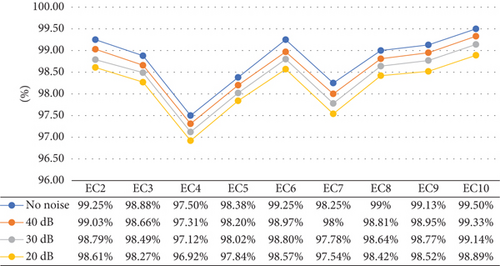
The proficiency of the suggested approach under noisy conditions can be contemplated in Figures 13(a) and 13(b). It is observed that the noise-free accuracy of important islanding events (EC-1) is reaching 99.88% whereas it is hitting 99.2% even under the dense noise of 20 dB. Similarly, the mean accuracies of the other events under islanding conditions represented by EC-2 to EC-10 are maintained at 98.79%, 98.58%, 98.39%, and 98.18% for 40 dB, 30 dB, and 20 dB SNR, respectively.
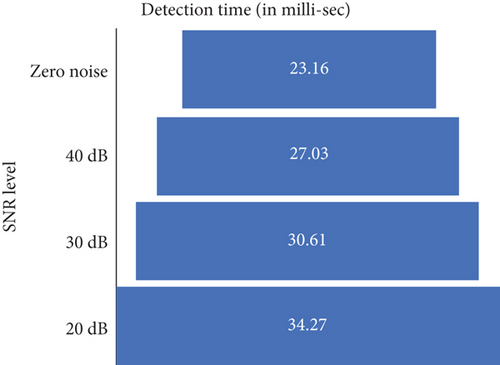
Additionally, the proposed EEMD-HOBRFC also provides faster detection of all the events, and it is noted to be only 23.16 msec under the ideal situation. The exceptional ability of the technique makes it to elapse almost same time to detect any type of trained event. But the performance is stagnated with the introduction of noise. A series of 500 disturbance cases is taken for each SNR level, and the mean time of detection is illustrated in Figure 14.
6.4. Performance Assessment in TS-II
The extraordinary efficacy of the EEMD-HOBRFC is already seen in the previous subsections for test system 1. However, it is essential to verify whether it is performing in the same manner or not for a different system. So as to validate it, a separate test system is taken into consideration as shown in Figure 3. A 400 number of cases are extracted for each event class only having the BGWO optimized prediction variables (9 numbers of features) from test system 2. This extraction has taken place in both islanding and nonislanding scenarios. The confusion matrix in relation to both the scenarios can be seen in Figures 15(a) and 15(b). It can be seen from Figure 15(a) that the method shows 100% accuracy in detecting the islanding scenarios as all the 400 cases are truly detected. Here, classes EC-1 to EC-10 are mapped as 1 to 10. On the other hand, the proposed classifier also displays much accuracy for nonislanding events alone where EC-15 has highest accuracy rate of 99.5% since 398 events have predicted truly out of 400. Here, classes EC-2 to EC-10 are mapped as 1 to 9.
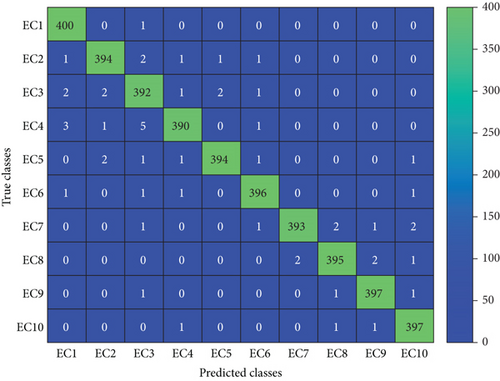
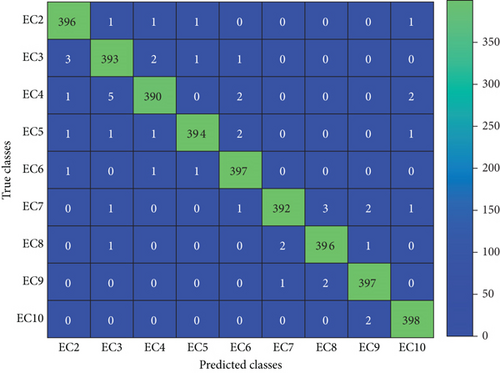
It can be noted that, under islanding condition (Figure 15(a)), the method of EEMD-HOBRFC successfully detected all the 400 islanding events. In addition, it is also displayed its detection capability for the other events with and without islanding occurrences. Hence, the proposed method is found to be effective even in other microgrid structures.
6.5. Comparative Study
This section covers up the comparative study of the proposed EEMD-HOBRFC method with several other methods. Firstly, both EMD and EEMD are combined with simple unoptimized RF and latterly clubbed with HOBRFC for 3 different SNR levels as presented in Table 5. The resulting accuracy data can well define the dominancy of the proposed method that reaching 99.2% under substantial noise (20 dB) and 99.88% without any noise. Moreover, Table 6 unveils its supremacy over other ML tools. It can be noticed that the EEMD-HOBRFC is displaying appreciable accuracy with respect to all these MLTs with maintaining a mean accuracy of 98.75%.
| Techniques | Zero noise | SNR level | ||
|---|---|---|---|---|
| 40 dB | 30 dB | 20 dB | ||
| EMD-RF | 97.6% | 97.4% | 97.1% | 96.6% |
| EMD-HOBRFC | 98.6% | 98.42% | 98.24% | 97.97% |
| EEMD-RF | 99.1% | 98.87% | 98.69% | 98.4% |
| EEMD-HOBRFC | 99.88% | 99.7% | 99.45% | 99.2% |
| Classes | NB | ELM | KNN | SVM | DT | Proposed |
|---|---|---|---|---|---|---|
| EC-1 | 93.58% | 98.65% | 98.81% | 99.02% | 99.3% | 99.88% |
| EC-2 | 92.95% | 98.11% | 98.25% | 98.47% | 98.81% | 99.38% |
| EC-3 | 92.78% | 97.6% | 97.77% | 98.01% | 98.33% | 98.75% |
| EC-4 | 91% | 96.07% | 96.23% | 96.43% | 96.78% | 97.25% |
| EC-5 | 91.72% | 96.95% | 97.09% | 97.31% | 97.6% | 98.13% |
| EC-6 | 92.53% | 97.76% | 97.93% | 98.15% | 98.48% | 99% |
| EC-7 | 91.47% | 96.63% | 96.8% | 97.03% | 97.34% | 97.88% |
| EC-8 | 92.39% | 97.5% | 97.64% | 97.87% | 98.17% | 98.63% |
| EC-9 | 92.75% | 97.89% | 98.03% | 98.26% | 98.61% | 99.13% |
| EC-10 | 93.04% | 98.18% | 98.36% | 98.55% | 98.98% | 99.50% |
| Mean | 92.421% | 97.534% | 97.691% | 97.91% | 98.24% | 98.75% |
Further, the analysis is extended in terms of detection time, detection accuracy, and performance under noisy conditions. The time required for islanding detection for different preproposed techniques with their references can be seen in Table 7. The maximum detection time taken is around 55 ms for a transient monitoring [45] based detection system which is more than twice of the detection time of the proposed one. Besides that, the performance of the EEMD-HOBRFC is evaluated against other prepublished work in Table 7. Furthermore, in Table 8, it can be noticed that, although [48, 52] delivering an accuracy level of 100%, still they are underperforming in the presence of noise. But the proposed method has built up with both noise-assisted signal processing technique and noise robust machine learning technique that is why performing at towering level of accuracy in all three noisy conditions.
| Sl no. | Published work | Accuracy | |||
|---|---|---|---|---|---|
| Noise free | 20 dB | 30 dB | 40 dB | ||
| 1 | [26] | 98.8% | 98.3% | 97.5% | 97% |
| 2 | [34] | 99.09% | 91.51% | 96.96% | — |
| 3 | [48] | 100% | 97.66% | — | — |
| 4 | [49] | 98.19% | — | — | — |
| 5 | [50] | 98% | — | — | — |
| 6 | [51] | — | — | 98.3% | — |
| 7 | [52] | 100% | 90% | 98.78% | — |
| 8 | [53] | 99.33% | — | — | — |
| 9 | [54] | 98% | 94.2% | — | — |
| 10 | Proposed | 99.88% | 99.2% | 99.45% | 99.7% |
6.6. Nondetection Zone Validation
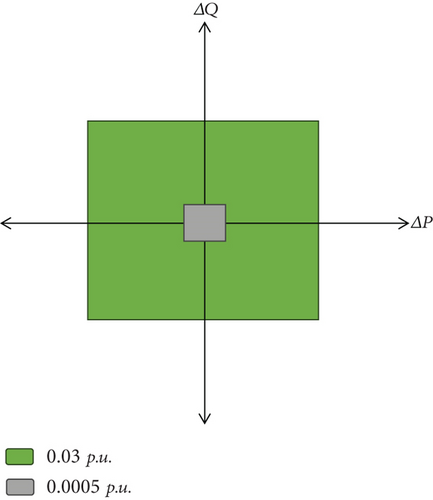
The contraction of NDZ can be validated by considering a mix of 500 diversified islanding data samples within a power mismatch range of 0.0005 pu to 0.03 pu with 30 dB SNR. Even in such a narrow range, the EEMD-HOBRFC is still capable of detecting 498 islanding event classes. The other two are detected falsely as DG outage and capacitor switching. The outcomes not only indicate the impact of the proposed method under low power mismatch conditions but also replicate the efficacy under the noisy situations. That means it can be well implemented in practical environment. The result of this test is given in Table 9, and the contracted region of nondetection is shown in grey color in Figure 16.
| True class | Predicted class | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EC-1 | EC-2 | EC-3 | EC-4 | EC-5 | EC-6 | EC-7 | EC-8 | EC-9 | EC-10 | |
| EC-1 | 498 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
7. Conclusion
The manuscript presents an islanding detection scheme, namely, EEMD-HOBRFC, that can identify and classify the islanding as well as nonislanding power quality events. In the proposed approach, some of the features are retrieved from the raw signal to retain the original characteristics of the signal and the rest of the features are extracted from the decomposition of noise-assisted signal preprocessor called EEMD to capture the inherent characteristics.
Moreover, the least correlated features are filtered with BGWO and then fed to a PSRGWO optimized random forest classifier. The proposed technique is validated with a system consisting of multi-DG system with high wind energy penetration, and accuracy of islanding detection under ideal condition is found to be 99.88%.
Its performance is not worsening under noisy condition and maintained at 99.2% even in the dense noise of 20 dB because both EEMD and RF are noise robust in nature. Additionally, the detection time is found to be as low as 23.16 ms with no noise and 34.27 ms at heavier noise.
Lastly, the method is also able to detect islanding event in real scenario (30 dB SNR) alongside a power mismatch range of 0.03 pu to 0.005 pu with an appreciable accuracy of 99.6%. Hence, the method is found to be very competitive with reference to the related research works of recent past. From rigorous simulation study, it is found that the proposed EEMD-HOBRFC is able to detect and classify the islanding and nonislanding event classes efficiently.
Abbreviations
-
- BGWO:
-
- Binary grey wolf optimization
-
- CM:
-
- Confusion matrix
-
- DG:
-
- Distributed generator
-
- DSF:
-
- Decomposed signal feature
-
- DT:
-
- Decision tree
-
- EC:
-
- Event class
-
- EEMD:
-
- Ensemble empirical mode decomposition
-
- EMD:
-
- Empirical mode decomposition
-
- EWT:
-
- Empirical wavelet transform
-
- FPS:
-
- Feature per split
-
- FST:
-
- Feature selection tool
-
- GWO:
-
- Grey wolf optimization
-
- HOBRFC:
-
- Hybrid optimization-based random forest classifier
-
- I&NI:
-
- Islanding and nonislanding
-
- IMF:
-
- Intrinsic mode function
-
- MCC:
-
- Matthew’s correlation coefficient
-
- MLC:
-
- Machine learning classifier
-
- NDZ:
-
- Nondetection zone
-
- OAE:
-
- Overall accuracy error
-
- OBCE:
-
- Out-of-bag classification error
-
- PCC:
-
- Point of common coupling
-
- PERCC:
-
- Pearson’s correlation coefficient
-
- PI:
-
- Performance index
-
- PSRGWO:
-
- Particle swarm and reformed grey wolf optimization
-
- RF:
-
- Random forest
-
- RSF:
-
- Raw signal feature
-
- SPA:
-
- Signal processing approach
-
- TR:
-
- Number of tress in forest
-
- TS:
-
- Test system
-
- VMD:
-
- Variational mode decomposition.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA, for funding this research work through the project number NBU-FPEJ-2024-2484-01; also, the authors declare that this article has been produced with the financial support of the European Union under the REFRESH—Research Excellence For Region Sustainability and High-Tech Industries project number CZ.10.03.01/00/22_003/0000048 via the Operational Program Just Transition, and the paper was supported by the following project TN02000025 National Centre for Energy II.
Open Research
Data Availability
There are no data to mention.




