Discrete Dynamics in Nature and Society
Volume 2024, Issue 1 4930326
Research Article
Open Access

Observer-Based Exponential Stabilization for Conformable Polynomial Fuzzy Systems With Time Delay

Imen Iben Ammar, 

Imen Iben Ammar

GREAH Laboratory , Department of Electronics, Electrical Energy and Automation , UFR Sciences and Technology , Le Havre Normandy University , 75 Rue Bellot, Le Havre , 76600 , France

Search for more papers by this author
Hamdi Gassara, 

Hamdi Gassara

Laboratory of Sciences and Techniques of Automatic Control and Computer Engineering , Department of Electrical Engineering , National Engineering School of Sfax , University of Sfax , PB 1173, Sfax , 3038 , Tunisia , fss.rnu.tn

Search for more papers by this author
Mohamed Rhaima, 

Mohamed Rhaima

Department of Statistics and Operations Research , College of Science , King Saud University , P.O. Box 2455, Riyadh , 11451 , Saudi Arabia , ksu.edu.sa

Search for more papers by this author
Lassaad Mchiri, 

Lassaad Mchiri

Department of Mathematics , University of Panthéon Assas Paris-2 , Paris , France

Search for more papers by this author
Abdellatif Ben Makhlouf, 

Corresponding Author

Abdellatif Ben Makhlouf

Department of Mathematics , Faculty of Sciences , Sfax University , BP 1171, Sfax , Tunisia , uss.rnu.tn

Search for more papers by this author
First published: 07 November 2024
https://doi.org/10.1155/2024/4930326
Academic Editor: Mouquan Shen

Abstract

This paper focuses on solving the challenge of observer-based exponential control (O-BC) regarding conformable fuzzy polynomial models with time delay. In this work, polynomial matrices with unmeasurable states are considered to enhance the practicality of the model in the design problem. The proposed approach guarantees the existence of the polynomial controller and observer gains by satisfying sufficient conditions based on the sum-of-squares (S-O-S) approach. The stability conditions of the addressed system are solved using MATLAB SOSTOOLS, and the effectiveness of the proposed control scheme is evaluated through the presentation of simulation results from a numerical example and a mass-spring-damper system.

1. Introduction

Due to its ability to efficiently model nonlinear systems and produce many standard theoretical results, the Takagi–Sugeno fuzzy (T–SF) model has attracted increasing interest since 1985 [1]. Through the utilization of the linear matrix inequalities (LMIs) method alongside the Lyapunov theory, T–SF models have been widely employed in analyzing and achieving control outcomes for nonlinear systems, e.g., asymptotic stability (AS) [2, 3], exponential stability (ES) [4] and observer-based control (O-BC) [5, 6]. The designing of observers to estimate unmeasured system states remains an active and dynamic field of research. Recently, a sequence of iterative proportional-integral observers has been developed to estimate state variables and unknown disturbances of linear discrete-time systems [7]. In addition, the work in [8] has addressed the tracking control problem for Markov T–SF models with disturbance and mismatched faults. A collection of novel iterative proportional-integral observers was designed by fully using system outputs to enhance estimation accuracy. By adopting a nonquadratic Lyapunov functional, a proportional multi-integral observer is designed in [9] for T–SF models with unmeasurable premise variables in the presence of external disturbances. In 2007 [10], Tanaka and al. have extended T–SF models to polynomial fuzzy (PF) models by exploiting a software tool which has been appeared in 2002 [11], called SOSTOOLS. The main difference between T–SF models and PF models lies in the representation of the nonlinear system. Indeed, the T–SF models contain, in the consequence part of each fuzzy If-Then rule, a linear local model, while the PF models present a polynomial model which allows us to have a more precise approximation of the system. Another major advantage is that the number of fuzzy rules in PF models is generally fewer than the number of fuzzy rules in T–SF models [12]. However, the LMI approach is not suitable for handling PF models due to the polynomial nature of the matrices describing the system. In this case, the LMI toolbox [13] is replaced by SOSTOOLS [14], which provides the capability to efficiently manage polynomial inequalities. Considerable research has been conducted to address the analysis and control challenges of PF models, with an emphasis on presenting design results through the lens of sum-of-squares (S-O-S) conditions, e.g., AS [12], OB-C [15], fuzzy tracking control [16], and fault tolerant control [17].

It is essential to highlight that all previous results are discussed in the context of nonlinear systems without delay and with integer-order derivatives. In the following paragraphs, we will explore two themes: (i) the widespread occurrence of delays within systems and (ii) the alternative approach provided by conformable derivatives (CDs), which offer a more flexible and intuitive method for modeling some dynamic systems.

On one hand, incorporating time delay considerations is crucial for accurately modeling and controlling practical systems such as long transmissions lines, mechanical systems, and chemical processes. In this context, Razumikhin [18] and Krasovskii [19] have proposed fundamental theories to address time delay equations by extending Lyapunov’s theory from 1892. The two previous works, particularly that of Krasovskii, have found widespread application in the analysis and control synthesis of many classes of models with time delay. In [20], the authors introduced the initial effort to extend T–SF models to accommodate delay systems. Since the publication of this work in 2000, T–SF models with delay have attracted the attention of researchers, leading to many significant discoveries, e.g., AS [21] and ES [22]. Similarly, PF models have been improved while taking into account temporal delay, giving rise to several relevant results in this area, e.g., AS [23], ES [24], and O-BC [25].

On the other hand, the significance of the CD lies in its ability to offer a more flexible and intuitive approach to modeling dynamic systems [26, 27], particularly in scenarios where traditional derivatives may not accurately capture the behavior of complex phenomena. For instance, a comparative study aiming to ascertain the precision of various derivatives in modeling supercapacitors reveals that the CD yields the highest accuracy, closely subsequently the Caputo fractional derivative [28]. Wu et al. in [29] have proposed an optimized time power–based gray model into the conventional model by using the CD. Ali, Ahmad, and Javed in [30] discussed the stability of novel complex solutions to the conformable malaria model. Shahen et al. in [31] studied the numerical solutions of low-pass electrical transmission line conformable model. There has been limited progress in the literature concerning the analysis and control design of conformable systems (CSs), with few new results emerging. As an illustration, the issue of designing fault detection observers for Lipschitz continuous systems is addressed in [32], focusing on H∞/H− criteria. Sadek et al. in [33] have studied the observability, controllability, and linear-quadratic problem for CS. Cuchta, Poulsen, and Wintz in [34] have proposed the linear quadratic tracker for CS. Kharrat et al. in [35] have studied the practical ES for a class of CS with delay.

According to the authors’ knowledge, most research has concentrated on PF model-based control systems. However, very few studies have addressed conformable polynomial model-based control systems, and there are no findings discussing the exponential O-BC of conformable PF systems. This forms the motivation of our study.

This study focuses on conformable PF systems with time delay, aiming to develop innovative methods and techniques for their analysis and synthesis. We address the problem of exponential stabilization to enhance the stability of the closed-loop system under O-BC. A conformable PF model is employed to represent the nonlinear system with time delay. The design challenge of the observer-based polynomial controller is tackled to ensure the ES of the resulting closed-loop system and the convergence of state estimation errors and their estimated values. Furthermore, stability conditions based on S-O-S are derived to assess the system’s stability. Finally, a design example is provided to demonstrate the effectiveness of the proposed approach. The structure of the paper unfolds as follows. Section 2 delves into preliminaries concepts, while Section 3 scrutinizes the problem formulation. In Section 4, we present our theoretical results. In Section 5, we present two illustrative examples to showcase the practical applicability of the theoretical results.

1.1. Notations

, ℏ, ℵ, and ℧ denote the sets of orthogonal matrices, symmetric positive constant matrices, polynomial matrices, and S-O-S, respectively. For a matrix , , means that the dimension of is n × n.

2. Preliminaries

All definitions and lemmas provided in the following will be useful for next developments.

Definition 1 (see [36].)Let . The CD of Ψ is defined by

(1)
for every κ > c, 0 < ς < 1. If exists, ∀κ ∈ (c, e) for some e > c and exists; therefore, by definition,
(2)

Definition 2 (see [36].)Let ς ∈ (0, 1). The conformable integral of Ψ is given by

(3)

Remark 1. If c = 0, the conformable integral and derivative reduced to the definitions proposed in [37].

In the rest of the paper, we note and .

Let us consider the CS,

(4)
where , τ > 0, and .

Definition 3. System (4) is called exponentially stable, if there are scalars R1 > 0 and R2 > 0 such that

(5)
where and ‖ϑ‖ = supκ∈[−τ, 0]‖ϑ(κ)‖.

Definition 4 (see [11].)Let H1(Ψ(κ)) ≥ 0 be a polynomial function, where . H1(Ψ(κ)) ∈ ℧ if there exist polynomials m1(Ψ(κ)), m2(Ψ(κ)), …, mg(Ψ(κ)) such that

(6)

It is clear that H1(Ψ(κ)) ∈ ℧⟹H1(Ψ(κ)) ≥ 0.

Furthermore, if H1(Ψ(κ)) − h1(Ψ(κ)) ∈ ℧, where h1(Ψ(κ)) is a known polynomial such that h1(Ψ(κ)) > 0, then H1(Ψ(κ)) > 0.

Similarly, consider H2(Ψ(κ), Ψ(κ − τ)), where . If H2(Ψ(κ), Ψ(κ − τ)) − h2(Ψ(κ), Ψ(κ − τ)) ∈ ℧, where h2(Ψ(κ), Ψ(κ − τ)) is a known polynomial such that h2((Ψ(κ), Ψ(κ − τ))) > 0, then H2(Ψ(κ), Ψ(κ − τ) > 0.

Remark 2. In SOSTOOLS, the components of the vectors Ψ(κ) and Ψ(κ − τ) are exclusively represented as independent symbolic variables (SVs). For example, θ1, θ2, …, θn and θn+1, θn+2, …, θ2n are SV-representing elements of vectors Ψ(κ) and Ψ(κ − τ), respectively.

Lemma 1 (see [12].)Consider a z × z symmetric matrix , a vector ϵ containing z SV, which do not depend on Ψ(κ) and Ψ(κ − τ), then

(7)
where m(Ψ(κ), Ψ(κ − τ)) is a known positive polynomial and I is the identity matrix and has the same dimension as , which implies that
(8)

Lemma 2 (see [38].)There exist such that

(9)
where and are nonzero singular values of C.

3. Problem Formulation

Let us consider a delayed nonlinear system that is described by the following delayed polynomial model with r rules.

Plant rule i(i = 1, 2, …, r): if β1(κ) is νi1 and ⋯ and βp(κ) is νip, then
(10)
where βj(κ), j = 1, …, p, represents the measurable premise variables. νij, i = 1, …, r and j = 1 … p, represents the fuzzy sets and r is the rules’ number. In this system, Ψ(κ) is the state vector, Ψ(κ − τ) is the delayed state vector, u(κ) is the control input vector, and y(κ) is the output vector. , and is known constant real matrix. The delay τ is assumed to be both constant and known.
After the deffuzzication process of model (10), we get
(11)
where δi(β(κ)) are the membership functions in which β(κ) = [β1(κ), …, βp(κ)].
Consider the following O-BC:
(12)
where , , and represent, respectively, the estimated state, the estimated delayed state vector, and the estimated output vector, while and denote gains for the O-BC, which are to be determined.
The augmented O-BC model is written as
(13)
where
(14)
in which
(15)
(16)

In the rest, δi(β(κ)), , and are noted as δi, , and , respectively.

4. Main Results

Theorem 1. The ES of (13) is guaranteed with the convergence rate (CR) σ if there exist ∃{P, Q} ∈ ℏ such that the following conditions are satisfied:

(17)
where
(18)

Proof 1. Let us consider the following Lyapunov–Krasovskii functional (L–KF):

(19)
where
(20)
(21)

For κ > 0, we get the following CD of V1(κ) and V2(κ):

(22)

From the last two expressions, we obtain

(23)
(24)

From (19), (23), and (24), we get

(25)

The CD of V(κ) satisfies

(26)

Therefore,

(27)

Then,

(28)

Since

(29)
(30)
therefore,
(31)
where λmin(.) and λmax(.) denote the minimum and the maximum eigenvalue operators.

Our goal is to express the conditions stated in Theorem 1 in conditions which can be solved via SOSTOOLS.

Theorem 2. The ES of (13) is guaranteed with the CR σ, if there exist , such that

(32)
(33)
(34)
(35)
(36)
are satisfied, where
  • •

    P2 is written as P2 = DP22DT in which P22 has the form and is given by applying Lemma 2.

  • •

    ϵ1 and ϵ2 are vectors that are independent of .

  • •

    mi are scalars such that mi > 0, (i = 1, …, 4) and is a polynomial such that .

  • •

    , in which such that the elements of are given as follows:

(37)

In this instance, the gains of O-BC are given by
(38)
(39)
where and are given by applying Lemma 2.

Proof 2. Conditions (32)–(35) imply that P and Q are positive definite.

Inequality (17) can be rewritten as

(40)
where and
(41)
in which .

Let

(42)

By applying Lemma 2 and taking into account that P2 = DP22DT and , we get

(43)

Let , then we obtain

(44)

Substituting (42) into (40) and taking into account (44), we get

(45)

By applying Lemma 1, (36) implies and as a result, (45) are satisfied ∀i ≤ j.

Remark 3. It has been observed that (45) are bilinear functions of the following set of unknown matrices:

(46)

Therefore, SOSTOOLS cannot be used to solve it. Lemma 1 serves to transform the bilinear functions into linear functions in by introducing new SV independent of system’ SV. Nevertheless, as the number of not-free SV increases, there is a concurrent escalation in computational burden and an increase in conservatism.

The following two-step algorithm allows us to design an O-BC without using Lemma 1.

Theorem 3. The ES of (13) is guaranteed with the CR σ if there exist ∃, a solution to the following 2-step procedure:

  • •

    Step 1: we assume that all elements of Ψ are measurable, which means that , , , and . We apply Theorem 2 in this instance.

  • •

    Step 2: P1 and P2 are known matrices derived from Step 1.

There exist matrices , , and such that (34) and (35) and
(47)
are satisfied, where .

In this instance, the gains of the O-BC are given as in Theorem 2.

We employ Algorithm 1 to solve the ES of System (13), ensuring that the required S-O-S-based constraints are satisfied.

Algorithm 1.

  • •

    Step 1: by assuming that all the states are measurable and if there exist matrices , such that equations (32)–(35) and the following S-O-S-based condition is satisfied:

    (48)

  •  

    where , in which

    (49)

  •  

    Step 2: if there exist matrices {Q1, Q2} ∈ ℏ and satisfying equations (34) and (35) and the following S-O-S condition where P1 and P2 are solutions of the S-O-S conditions in Step 1:

(50)
is satisfied, where .

5. Illustrative Examples

5.1. Example 1

Consider the following CD nonlinear system with time delay:
(51)

The state matrix includes nonlinear terms sin(Ψ1)/Ψ1, −0.3Ψ2, and , providing a more general structure of conformable models compared to those in [32, 35]. In contrast, the state matrices of the conformable models presented in [32, 35] are constant.

Employing the sector nonlinearity concept, System (51) can be represented by a T–SF model consisting of eight rules, reflecting the presence of three nonlinearities. Furthermore, the states must be constrained within specific bounds. However, by utilizing PF modeling, System (51) can be described by the following two rules PF model, without imposing any bounds on the states:
(52)
where , , and the membership functions are defined as
(53)

Figure 1 shows the behavior of (52) with u = 0 for these initial states: , , , and for κ ∈ [−0.9, 0]. From this figure, we see that System (52) is unstable.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Behaviors in Ψ1(κ)–Ψ2(κ) plane (without feedback).
For simulation purposes, the resolution of Theorem 2 cannot produce a set of feasible solutions. To address this limitation, we have employed the two-step S-O-S conditions outlined in Theorem 3 to ensure the generation of feasible solutions. We noticed also that it is possible to find a feasible solution that satisfies the S-O-S conditions detailed in Theorem 3 as long as σ remains less than 1.999. In our example, we have solved the S-O-S conditions in Theorem 3, for σ = 0.9. In a first step, we start by determining the constant matrices P1 and P2, then the constant matrices Q1 and Q2 and in a second step. We obtained as a solution
(54)

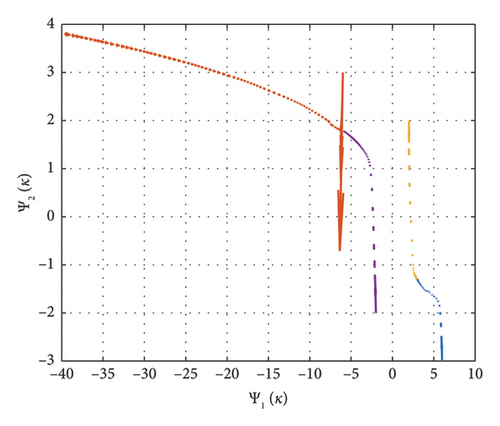
Figure 2 shows control results, for the same initial states as in Figure 1.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Behaviors in Ψ1(κ)-Ψ2(κ) plane (with feedback).

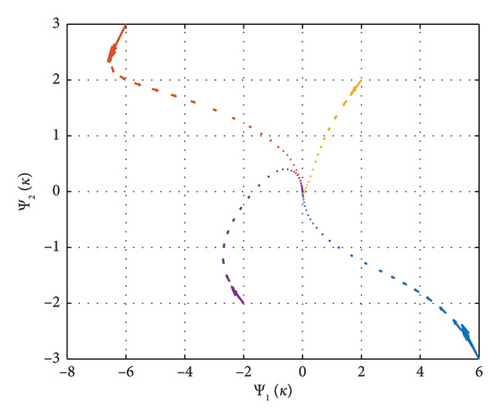
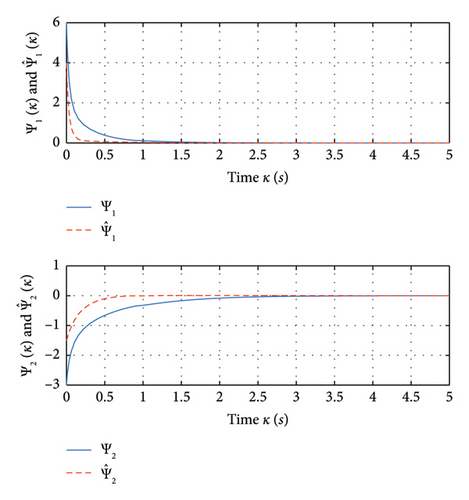
Figure 3 illustrates the temporal progression of Ψ(κ) and , from the initial states, , for κ ∈ [−0.9, 0]. It can be found that converges to Ψ(κ) during the stabilizing control. These results demonstrate the efficiency of the suggested method.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Temporal progression of Ψ(κ) and .

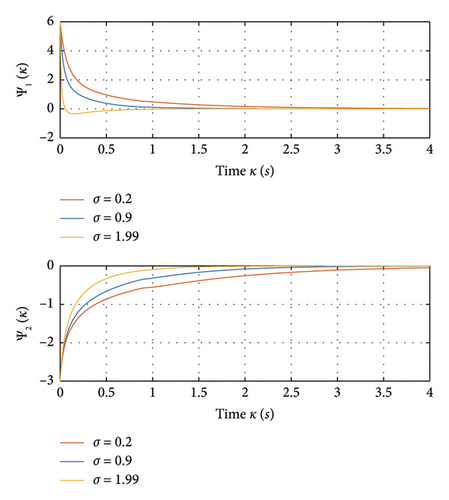
In order to test the influence of σ on the response of the system, we plotted the response of the state Ψ(κ) for different values of σ as shown in Figure 4. The results from this figure show an improvement in response time while increasing the value of σ. Hence, we can conclude that the value of σ has an influence on the system response time.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Response of the state Ψ(κ) for different values of σ.

5.2. Example 2: Application to a Mass-Spring-Damper System

The mass-spring-damper system can be described by the following model proposed in [39].
(55)
where M is the mass, Ψ1 is the displacement of the mass, Ψ2 is the velocity of the mass, and u is the input force. The parameters are M = 1, c1 = 0.003, c2 = 0.001, c3 = 0.80, and c4 = 0.1.
To highlight the significance of our results, we take into account the preceding system with CD and disturbance delay:
(56)
where ς = 0.95, τ = 0.9, and λ = 0.93.
Assume that the displacement of the mass Ψ1 is measured by a sensor with a measurement range of [−b, b]. Consequently, the output equation is represented as follows:
(57)
Given that Ψ1 ∈ [−b, b], the nonlinear model can be approximated by the following PF model:
(58)
where
(59)
By solving the S-O-S conditions in Theorem 3 for b = 1, we get
(60)

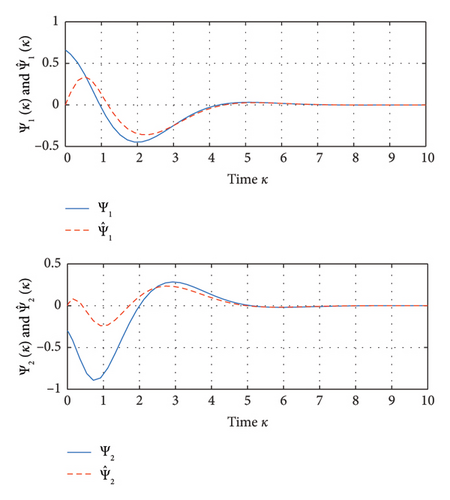
Figure 5 shows the closed-loop state Ψ(κ) and its estimated , for and , κ ∈ [−0.9, 0].

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Temporal progression of Ψ(κ) and for the mass-spring-damper system.

6. Conclusion

This paper has delved into the issue of exponential O-BC concerning conformable PF models incorporating time delay. We have examined case where polynomial matrices are contingent upon unmeasurable states. By incorporating new SV in lieu of the state, state-delay variables and their estimated, certain adequate conditions can be formulated using S-O-S. However, it has been observed that an excessive number of SV can complicate system synthesis, thereby imposing various constraints. An algorithm is suggested with the aim of decreasing the quantity of SV. Finally, two illustrative examples have been given to validate the obtained results. Our subsequent objective is to apply advanced S-O-S robust stabilization conditions to more complex CSs. This includes addressing uncertain CSs that experience external disturbances, as well as sensor and/or actuator faults.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Imen Iben Ammar: conceptualization and investigation. Hamdi Gassara: reviewing and editing and investigation. Mohamed Rhaima: investigation. Lassaad Mchiri: software and visualization. Abdellatif Ben Makhlouf: methodology and validation.

Funding

This research was funded by King Saud University in Riyadh, Saudi Arabia through researchers supporting project number (RSPD2024R683).

Acknowledgments

The authors acknowledge “Researchers Supporting Project number RSPD2024R683, King Saud University, Riyadh, Saudi Arabia.”

    Data Availability Statement

    No underlying data were collected or produced in this study.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.