Volume 2024, Issue 1 4894415

Research Article

Open Access

Symmetric Encryption Algorithms in a Polynomial Residue Number System

I. Yakymenko,

I. Yakymenko

orcid.org/0000-0003-3446-1596

Department of Cyber Security, West Ukrainian National University, Ternopil 46009, Ukraine

Search for more papers by this author

M. Karpinski,

M. Karpinski

orcid.org/0000-0002-8846-332X

Department of Cyber Security, Ternopil Ivan Puluj National Technical University, Ternopil 46001, Ukraine tntu.edu.ua

Institute of Security and Computer Science, University of the National Education Commission, 30-084 Krakow, Poland

Search for more papers by this author

R. Shevchuk,

Corresponding Author

R. Shevchuk

[email protected]

orcid.org/0000-0001-5381-9528

Department of Computer Science, West Ukrainian National University, Ternopil 46009, Ukraine

Department of Computer Science and Automatics, University of Bielsko-Biala, Bielsko-Biala 43-309, Poland bielsko.pl

Search for more papers by this author

M. Kasianchuk,

M. Kasianchuk

orcid.org/0000-0002-4469-8055

Department of Cyber Security, West Ukrainian National University, Ternopil 46009, Ukraine

Search for more papers by this author

I. Yakymenko,

I. Yakymenko

orcid.org/0000-0003-3446-1596

Department of Cyber Security, West Ukrainian National University, Ternopil 46009, Ukraine

Search for more papers by this author

M. Karpinski,

M. Karpinski

orcid.org/0000-0002-8846-332X

Department of Cyber Security, Ternopil Ivan Puluj National Technical University, Ternopil 46001, Ukraine tntu.edu.ua

Institute of Security and Computer Science, University of the National Education Commission, 30-084 Krakow, Poland

Search for more papers by this author

R. Shevchuk,

Corresponding Author

R. Shevchuk

[email protected]

orcid.org/0000-0001-5381-9528

Department of Computer Science, West Ukrainian National University, Ternopil 46009, Ukraine

Department of Computer Science and Automatics, University of Bielsko-Biala, Bielsko-Biala 43-309, Poland bielsko.pl

Search for more papers by this author

M. Kasianchuk,

M. Kasianchuk

orcid.org/0000-0002-4469-8055

Department of Cyber Security, West Ukrainian National University, Ternopil 46009, Ukraine

Search for more papers by this author

First published: 20 May 2024

https://doi.org/10.1155/2024/4894415

Citations: 5

Academic Editor: Saeid Abbasbandy

Share a link

Email
Wechat
Bluesky

Abstract

In this paper, we develop the theoretical provisions of symmetric cryptographic algorithms based on the polynomial residue number system for the first time. The main feature of the proposed approach is that when reconstructing the polynomial based on the method of undetermined coefficients, multiplication is performed not on the found base numbers but on arbitrarily selected polynomials. The latter, together with pairwise coprime residues of the residue class system, serve as the keys of the cryptographic algorithm. Schemes and examples of the implementation of the developed polynomial symmetric encryption algorithm are presented. The analytical expressions of the cryptographic strength estimation are constructed, and their graphical dependence on the number of modules and polynomial powers is presented. Our studies show that the cryptanalysis of the proposed algorithm requires combinatorial complexity, which leads to an NP-complete problem.

1. Introduction

Recently, with the growth of confidential information and the spread of computer systems, the task of ensuring information security has become increasingly important [1–3]. To minimize the risks of unauthorized access, cryptographic methods of information protection are widely used [4, 5], which are divided into symmetric and asymmetric [6, 7]. In practice, symmetric cryptographic transformations are more common for encrypting large amounts of information, as asymmetric ones are quite laborious [8, 9]. The requirements for symmetric methods have become more stringent in terms of ensuring their cryptographic strength due to the rapid development of computing tools and their increased speed. Polynomial algorithms are an alternative to modern numerical cryptoalgorithms [10–12]. In the ring Z[x], as in any other ring of polynomials, basic cryptographic operations are performed: addition, multiplication, and division with remainder [13–15]. The main idea of using polynomials in cryptography is that they can be used as plaintext, keys for encrypting and decrypting messages, building electronic digital signatures, and other cryptographic protocols [16–18].

The use of the residue number system (RNS) [19–21] in the implementation of cryptographic algorithms for information security based on polynomial arithmetic in the Z[x] ring [22, 23], by analogy with the integer RNS [24, 25], leads to parallelization of the computation process [26, 27] and reduction of the amount of data that must be processed during cryptographic operations [28–30]. In turn, it reduces the implementation time and improves the efficiency of the encryption method.

Therefore, our work is aimed at developing the concept of polynomial symmetric cryptographic algorithms based on the RNS and their practical application.

1.1. Our Contribution

In this article, our contributions are as follows:

1.
A theoretical provision for symmetric cryptographic algorithms based on the polynomial RNS was developed.
2.
Mathematical frameworks and schemes for the proposed polynomial symmetric encryption within the RNS were devised. To ascertain its resilience, a deep dive was made into constructing analytical expressions, revealing that the process of cryptanalyzing the proposed algorithm required dealing with combinatorial complexity, ultimately leading to an NP-complete problem.
3.
It was established that cryptographic strength notably improved with increasing degrees and dimensions of the Galois field p. The peak of cryptographic strength was reached when the number of modules equaled half of the potential count of irreducible polynomials with the given polynomial degrees and Galois field orders.

1.2. Related Work

Most modern symmetric cryptographic algorithms are block-based, and this feature limits the functionality of their implementation. In particular, the key size must be equal to or larger than the block size, leading to the encryption algorithm’s multiple uses for a large message. This procedure reduces the cryptographic strength of the algorithm, increases the time complexity, and, at the same time, complicates the implementation. Many authors have studied symmetric encryption algorithms in the polynomial number system. For example, Lemaire [31] proposes an 8-bit encryption algorithm based on the ideas of well-known symmetric cryptoalgorithms. The authors use divergent polynomials with variable coefficients, bitwise data operations, and two-password identification when generating pseudorandom keys. The hardware implementation of the proposed approach and comparison of the time characteristics with the AES algorithm of the 8-bit architecture based on the Arduino Uno microcontroller (ATmega328) were carried out.

A work [32] is devoted to developing and studying hardware-implemented methods of fast polynomial arithmetic for some homomorphic encryption operations based on the Karatsuba algorithm. In addition, Jayet-Griffon et al. [33] consider the possibilities of speeding up the polynomial multiplication operation for homomorphic encryption when implemented on an FPGA. In [34], a characterization of polynomial multiplication implementations for GPU-based homomorphic encryption is presented.

In [35], a highly efficient image encryption method based on permutation polynomials in finite fields was developed that is resistant to various types of attacks. In addition, the proposed encryption algorithm has no rounding errors, so encryption is lossless.

In the work [36], our effort was dedicated to developing a multifunctional architecture for the polynomial RNS within the context of cryptography. Detailed comparisons with contemporary implementations have indicated the potential utility of polynomial residue arithmetic in modular multiplication. Article [37] presents a schematic diagram of a modular pipeline multiplier, which allows for high-speed data encryption and decryption based on nonpositional polynomial RNS. The authors substantiate the efficiency of the proposed hardware design through a timing diagram. The developed pipeline device can find application in digital computing devices, particularly for high-speed data encryption based on nonpositional polynomial RNS.

In [38], a new method for constructing S-blocks of the AES algorithm is proposed based on replacing the irreducible polynomial and affine mapping. The cryptographic strength of the created S-block is evaluated by several standard tests (bijectivity, nonlinearity, strict avalanche criterion (SAC), and bit-independence criterion). It surpasses the cryptographic strength of the known S-boxes.

An article [39] proposes a method for constructing the S-block of the AES algorithm based on the smallest number of selected irreducible polynomials that meet specific criteria. There are 17 such polynomials, and their use simplifies the hardware implementation of the S-block. The SAC is studied, and it is noted that the polynomial p(x) = x⁸ + x⁷ + x⁶ + x + 1 is the best, with an outstanding value of SAC = 0.5, which indicates the cryptographic strength and reliability of the constructed S-block.

A paper [40] proposes improving the symmetric AES encryption algorithm using dynamic S-blocks whose parameters depend on the key, dynamic irreducible polynomials, and affine constants.

A paper [41] presents the most commonly used symmetric cryptosystem AES in the ring of polynomials today. The main idea is to choose an irreducible polynomial on the basis of which the encryption algorithm is built. The proposed approach was implemented in MATLAB for 30 different irreducible polynomials. As a result of the numerical experiments, it was possible to establish a negligible effect of changing irreducible polynomials on the level of the avalanche.

The authors in [42] proposed a novel method to enhance AES security against fault attacks using the polynomial RNS. The authors parallelize byte-level AES operations over GF(2⁸) by utilizing residues over smaller fields, introducing extended functionalities into AES for side-channel vulnerability analysis.

Polynomial arithmetic has also been used for asymmetric cryptosystems. In particular, in [43], modified arithmetic was developed for the RSA cryptosystem with Gauss integers and polynomials over finite fields. The analysis of the described computational procedures made it possible to determine their advantages over the classical ones. In [44], algorithmic support for the Rabin cryptosystem in the polynomial number system was proposed.

The analysis of the literary sources shows the relevance and importance of polynomial algorithms for protecting information flows. Accordingly, the development of new methods that are resistant to attacks of various types is an important direction in the development of modern cryptosystems. In particular, the combination of polynomial arithmetic and RNS in a ring of polynomials will allow parallelizing the process of performing basic operations in a ring of polynomials, which, in turn, will increase the speed of software implementation and reduce the time complexity of the algorithm, providing the required level of security.

1.3. Organization

Section 2 of this article discusses in detail the theoretical foundations for constructing symmetric cryptographic algorithms based on a polynomial RNS. Subsequently, in Section 3, the cryptographic strength of a polynomial symmetric encryption algorithm in the system of residual classes was evaluated. Finally, in Section 4, the content of this article is summarized.

2. Materials and Methods

In Subsection 2.1, the theoretical foundations for constructing symmetric cryptographic algorithms based on a polynomial RNS are proposed. Subsection 2.2 described the features of developing polynomial symmetric encryption methods in the RNS. An example of symmetric polynomial encryption in RNS presents in Subsection 2.3. In Subsection 2.4, the polynomial symmetric encryption method based on the Chinese remainder theorem (CRT) is proposed.

2.1. Theoretical Foundations of Polynomial RNS

An arbitrary polynomial N(x) in the RNS is represented as the residuals b_i(x) from dividing N(x) by each of the systems of pairwise mutually simple modulo-polynomials p_i(x) [45–47]:

(1)

The recovery of the polynomial N(x) is usually based on the CRT [48–50] in the ring of polynomials Z[x]:

(2)

where

, M_i(x) = P(x)/p_i(x), m_i(x) is sought from the expression

, and s is the number of modules. For polynomial powers, the inequality degN(x) < degP(x) must be satisfied.

2.2. Development of Polynomial Symmetric Encryption Methods in the RNS

The essence of one of the methods of polynomial symmetric encryption in RNS is that when recovering a polynomial from its residuals in the sum (2), the multiplication is not by the parameters , but by arbitrarily chosen polynomials k_i(x), mutually prime with p_i(x).

Therefore, to generate keys, both subscribers must choose module systems known only to them p_i(x) and the corresponding polynomials k_i(x), for which the following conditions are met: 1 < degk_i(x) < degp_i(x) and GCD(k_i(x), p_i(x)) = 1, where GCD denotes greatest common divisor. If p_i(x) is an irreducible polynomial, then the second condition is always met. Accordingly, both the sender and the receiver know the parameters M_i(x) and m_i(x).

For encryption, alphabetic information must be written in numerical form. The most common classical method is to replace the letter with its number in the alphabet, with the numbering starting from 0. After that, it must be represented as a polynomial with coefficients that reflect the alphabetic information, so the plaintext N(x) = a_nxⁿ + a_n−1xⁿ⁻¹ + ⋯+a₀x^o, where a_i is the sequence of digital representation of letters and

is the length of the message. Next, the plaintext block N(x) is written to the RNS according to expression (1). Encryption occurs when the number is restored to the positional number system according to the following expression:

(3)

The found polynomial is a ciphertext that is transmitted over an open communication channel from one subscriber to another.

When decrypting, the following values are first calculated:

(4)

To obtain the true residuals b_i(x), you need to perform the conversion according to the following ratio:

(5)

Accordingly, the recovery of the plaintext polynomial N(x) is carried out according to Formula (2) or the expression that follows from it can be used:

(6)

Figure 1 shows a schematic of the proposed polynomial encryption method based on the RNS.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Scheme of the proposed polynomial symmetric encryption in RNS.

The correctness of the proposed cryptosystem is established by a formal proof from the properties of congruences, taking into account the divisibility P(x) by p_i(x) and the equality

. Then, we get

(7)

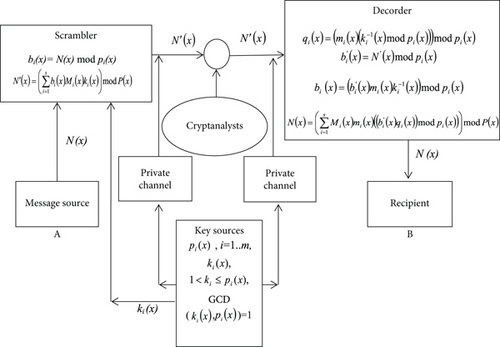
2.3. An Example of Symmetric Polynomial Encryption in RNS

Let us consider the plaintext PSMFSRD = (15181205181703), which corresponds to the polynomial N(x) = 15x⁶ + 18x⁵ + 12x⁴ + 5x³ + 18x² + 17x + 3. According to the developed polynomial symmetric cryptosystem for three modules (s = 3), p₁(x) = x² + x + 1, p₂(x) = x³ + x + 1, and p₃(x) = x² + 1 and the chosen coefficients k₁(x) = x² + 2x + 3, k₂(x) = x³ + x² + 1, and k₃(x) = x² + 3x + 2, all the parameters are calculated as follows: P(x) = p₁(x)p₂(x)p₃(x) = x⁷ + x⁶ + 3x⁵ + 3x⁴ + 4x³ + 3x² + 2x + 1, M₁(x) = P(x)/p₁(x) = (x⁷ + x⁶ + 3x⁵ + 3x⁴ + 4x³ + 3x² + 2x + 1)/(x² + x + 1) = x⁵ + 2x³ + x² + x + 1, M₂(x) = P(x)/p₂(x) = (x⁷ + x⁶ + 3x⁵ + 3x⁴ + 4x³ + 3x² + 2x + 1)/(x³ + x + 1) = x⁴ + x³ + 2x² + x + 1, and M₃(x) = P(x)/p₃(x) = (x⁷ + x⁶ + 3x⁵ + 3x⁴ + 4x³ + 3x² + 2x + 1)/(x² + 1) = x⁵ + x⁴ + 2x³ + 2x² + 2x + 1.

The search for is performed using the method of undetermined coefficients. Firstly, we look for . To do this, we write the equation (x + 2)(Ax + B)mod(x² + x + 1) = 1, and after transformations, we obtain (Ax² + (2A + B)x + 2B)mod(x² + x + 1) = (A + B)x + 2B − A = 1. From the last equation, it follows that 2B − A = 1 and B + A = 0 and takes the form A = 1/3 and B = 2/3. So, the sought-after inverse polynomial takes the form m₁(x) = (x + 2)⁻¹mod(x² + x + 1) = (1/3)x + 2/3. Similarly, the search for is carried out. We write (x² − x)(Ax² + Bx + C)mod(x³ + x + 1) = 1, where Ax² + Bx + C is the inverse polynomial modulo. We need to find the coefficients A, B, and C that satisfies the equation. After transformations (2Ax⁴ + 2Bx³ + (A + 2C)x² + Bx + C)mod(x³ + x + 1) = (C − A − B)x² + (−C − B)x + A − B = 1, we obtain 2C − A = 0, C − B − A = 0, −C − B = 0, and A − B = 1. From here, A = 2/3, B = −1/3, and C = 1/3. So, the inverse polynomial takes the following form: . Similarly, the value is computed. By applying the method of undetermined coefficients, the following transformations can be performed: (x)(Ax + B)mod(x² + 1) = (Ax² + Bx)mod(x² + 1)⇒Bx − A = 1. The last equation leads to a system of equations that allows us to compute the coefficients’ values A = −1 and B = 0 and thereby find the inverse polynomial modulo m₃(x) = −x. Thus, b₁(x) = N(x)mod p₁(x) = (15x⁶ + 18x⁵ + 12x⁴ + 5x³ + 18x² + 17x + 3)mod(x² + x + 1) = −7x − 13, b₂(x) = N(x)mod p₂(x) = (15x⁶ + 18x⁵ + 12x⁴ + 5x³ + 18x² + 17x + 3)mod(x³ + x + 1) = 3x² + 48x + 31, and b₃(x) = N(x)mod p₃(x) = (15x⁶ + 18x⁵ + 12x⁴ + 5x³ + 18x² + 17x + 3)mod(x² + 1) = 30x − 18.

Therefore, according to expression (3), the ciphertext is given by .

The parameters are computed using the method of undetermined coefficients. To find the inverse polynomial , we write (x + 2)(Ax + B)mod(x² + x + 1) = 1⇒(Ax² + (2A + B)x + 2B)mod(x² + x + 1) = (A + B)x + 2B − A = 1, where (Ax + B) is the desired value. To determine the coefficients A and B, we compute the remainder and equate the corresponding values: (A + B)x + 2B − A = 1; from here, A = −1/3, and B = 1/3. Thus, .

Similarly, we search for , where Ax² + Bx + C is the inverse polynomial modulo. After the transformation (2Ax⁴ + 2Bx³ + (A + 2C)x² + Bx + C)mod(x³ + x + 1) = (C − A − B)x² + (−C − B)x + A − B = 1, we obtain a system of three equations with three unknowns: C − B − A = 0, −C − B = 0, and A − B = 1. From here, A = 2/3, B = −1/3, and C = 1/3. Therefore, the sought inverse polynomial in Z[x] will take the following form: ; similarly, we can obtain .

In the next step, the following quantities are computed: , , and .

Additionally, for decryption, the following parameters need to be found: , , and .

Then, according to Formula (6), the original message is recovered as the plaintext: .

Accelerating the encryption and decryption process can be achieved if the participants choose parameters k_i(x) = 1. However, this will lead to a reduction in the cryptographic system’s resilience. The encryption process is simplified by using the following formula:

(8)

It should be noted that the operation of finding the inverse polynomial modulo and multiplying it in Formula (4) disappears because q_i(x) = m_i(x). The restoration of the plaintext is based on the following relationships:

(9)

For the same input parameters as in the previous example, according to Formulas (8) and (9), the following ciphertext is obtained: . To decrypt, it is necessary to compute additional parameters according to Formula (4): .

The decryption process is carried out according to Formula (9): .

This simplification reduces computational complexity by avoiding the operation of finding the parameters q_i(x) and .

2.4. Polynomial Symmetric Encryption Method Based on CRT

Another polynomial method of symmetric encryption based on the CRT involves breaking the plaintext N(x) into blocks—polynomials N_i(x) of lower order than the selected polynomial modules. These blocks will act as remainders b_i(x) modulo the chosen moduli, such that if degp_i(x) = n, then degN_i(x) ≤ n − 1; that is, N_i(x) = a_n−1xⁿ⁻¹ + a_n−2xⁿ⁻² + ⋯+a₀x⁰. After selecting the encryption parameters, the encryption is performed according to the expression (3). The ciphertext will be the value N^′(x).

Decryption is carried out using Formulas (4) and (5), which are used to find the parameters and . Concatenating the coefficients a_n−1 of the polynomials N_i(x) forms the plaintext. It should be noted that in the case of requiring fast decryption, the ciphertext can also be represented by the parameters b_i(x).

Figure 2 depicts the scheme of the polynomial symmetric encryption method in the CRT-based encryption system.

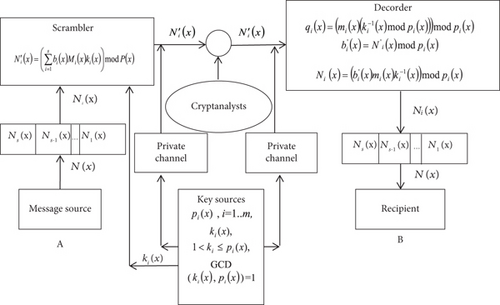
To encrypt using the aforementioned method, the chosen plaintext PSMFSRND = 1518120518171303 is divided into four blocks of two characters each: PS = 1518, MF = 1205, SR = 1817, and ND = 1303. Then, the plaintexts are formed as polynomials, N₁(x) = 15x + 18, N₂(x) = 12x + 5, N₃(x) = 18x + 17, and N₄(x) = 13x + 3, which are remainders modulo the chosen moduli p₁(x) = x² + x + 1, p₂(x) = x³ + x + 1, and p₃(x) = x² + 1, and the corresponding coefficients k₁(x) = x² + 2x + 3, k₂(x) = x³ + x² + 1, and k₃(x) = x² + 3x + 2. The ciphertext for the first block is computed based on Formula (3): .

Upon decryption using Formulas (4) and (5), the following results are obtained: , , and . The message is reconstructed based on the relation (5): .

For the second block of the input message N₂(x) = 12x + 5, the following ciphertext value is obtained: .

According to Formula (4), the remainders obtained are , , and . The restoration of the second block of the input message is done using relation (5): .

The ciphertext for the third block of the input message N₃(x) = 18x + 17 will have the following form: .

Then, according to Formula (4), the remainders obtained are , , and . The restoration is done using relation (5): . Hence, .

Therefore, the encrypted message for the fourth block, N₄(x) = 13x + 3 according to (3), will be the following polynomial: .

Then, according to Formula (4), the obtained remainders are , , and . The restoration of the fourth block is done based on expression (5): and .

The concatenation of the coefficients of the remainders corresponds to the input text PSMFSRND = 1518120518171303. According to the agreements between the participants, the ciphertext can be either the parameter N_i(x), or the remainders , where j is the block number of the message.

3. Results

In this section, we evaluate the cryptographic strength of a polynomial symmetric encryption algorithm in the system of residual classes.

The proposed polynomial symmetric encryption method based on the CRT is cryptographically strong due to the complexity of finding all possible parameter variants and cryptotransform modules. For its cryptanalysis, it is necessary to perform a complete search of all mutually prime polynomials in the ring Z[x] over a simple Galois field GF(p), where p is the prime number. The biggest challenge will be if the polynomial f(x) = a_nxⁿ + a_n−1xⁿ⁻¹ + a_n−2xⁿ⁻² + ⋯+a₀x⁰ is irreducible. Quantity S_p(n) irreducible polynomials of degree n can be calculated by the following formula [51]:

(10)

where μ(d) is the Möbius function. It is equal to 1 if d is a divisor of degree n with an even number of prime factors, −1 if d is a divisor of degree n with an odd number of prime factors, and 0 if d contains a square of a prime factor. Accordingly, the number of modules l cannot exceed S_p(n). Table 1 shows the Möbius functions for the first 64 positive integers.

Table 1. The Möbius functions for the first 64 positive integers [29].

d	1	2	3	4	5	6	7	8
μ(d)	1	−1	−1	0	−1	1	−1	0
d	9	10	11	12	13	14	15	16
μ(d)	0	1	−1	0	−1	1	1	0
d	17	18	19	20	21	22	23	24
μ(d)	−1	0	−1	0	1	1	−1	0
d	25	26	27	28	29	30	31	32
μ(d)	0	1	0	0	−1	−1	−1	0
d	33	34	35	36	37	38	39	40
μ(d)	−1	1	1	0	−1	1	1	0
d	41	42	43	44	45	46	47	48
μ(d)	−1	−1	−1	0	0	1	−1	0
d	49	50	51	52	53	54	55	56
μ(d)	0	0	1	0	−1	0	1	0
d	57	58	59	60	61	62	63	64
μ(d)	1	1	−1	0	−1	1	0	0

So, to find the number of irreducible polynomials f(x) = a_nxⁿ + a_n−1xⁿ⁻¹ + a_n−2xⁿ⁻² + ⋯+a₀x⁰ over GF(p), you need to determine all divisors of degree n, calculate the Möbius function for each of them, substitute them into Formula (10), and sum them. For example, for irreducible polynomials over GF(p) of degree n = 3 with divisors 1 (the value of the Möbius function is 1) and 3 (the value of the Möbius function is −1), their number can be found by the following formula: S_p(n) = (1/3)∑_n/dμ(d)p^n/d = (1/3)(μ(1)p^3/1 + μ(3)p^3/3) = (p³ − p)/3.

For a polynomial of degree 32 (the divisors are 1, 2, 4, 8, 16, and 32) over GF(2), according to Formula (10), the number of irreducible polynomials is as follows: S₂(32) = (1/32)∑_32/dμ(d)2^32/d = (1/32)(μ(1)2^32/1 + μ(2)2^32/2 + μ(4)2^32/4 + μ(8)2^32/8 + μ(16)2^32/16 + μ(32)2^32/32) = (1/32)(2³² − 2¹⁶) = 2²⁷ − 2¹¹ = 134215680.

Below is an example of calculating the number of irreducible polynomials for n = 32 in GF(p), where p = 3, 5, 7,11,13,17,19,23,29,31,37,43:

( )

Table 2 shows the number of irreducible polynomials for powers of n = 4, 8, 16, 32, 64, 96, and 128 and parameter p = 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, and 43.

Table 2. The number of irreducible polynomials for different powers of n and values of the parameter p.

p/n	4	8	16	32	64	96	128
2	3	30	4080	134215680	2.88 × 10¹⁷	8.25 × 10²⁶	2.66 × 10³⁶
3	18	810	2690010	5.79 × 10¹³	5.37 × 10²⁸	6.63 × 10⁴³	9.21 × 10⁵⁸
5	150	48750	9.54 × 10⁹	7.28 × 10²⁰	8.47 × 10⁴²	1.31 × 10⁶⁵	2.29 × 10⁸⁷
7	588	720300	2.08 × 10¹²	3.45 × 10²⁵	1.90 × 10⁵²	1.40 × 10⁷⁹	1.16 × 10¹⁰⁶
11	3630	26793030	2.87 × 10¹⁵	6.60 × 10³¹	6.97 × 10⁶⁴	9.80 × 10⁹⁷	1.55 × 10¹³¹
13	7098	1.02 × 10⁸	4.16 × 10¹⁶	1.38 × 10³⁴	3.06 × 10⁶⁹	9.04 × 10¹⁰⁴	3.00 × 10¹⁴⁰
17	20808	8.72 × 10⁸	3.04 × 10¹⁸	7.40 × 10³⁷	8.76 × 10⁷⁶	1.38 × 10¹¹⁶	2.46 × 10¹⁵⁵
19	32490	2.12 × 10⁹	1.8 × 10¹⁹	2.60 × 10³⁹	1.08 × 10⁸⁰	5.99 × 10¹²⁰	3.74 × 10¹⁶¹
23	69828	9.79 × 10⁹	3.83 × 10²⁰	1.18 × 10⁴²	2.21 × 10⁸⁵	5.54 × 10¹²⁸	1.56 × 10¹⁷²
29	176610	6.25 × 10¹⁰	1.56 × 10²²	1.96 × 10⁴⁵	6.12 × 10⁹¹	2.55 × 10¹³⁸	1.20 × 10¹⁸⁵
31	230640	1.07 × 10¹¹	4.55 × 10²²	1.65 × 10⁴⁶	4.37 × 10⁹³	1.54 × 10¹⁴¹	6.12 × 10¹⁸⁸
37	468198	4.39 × 10¹¹	7.71 × 10²³	4.75 × 10⁴⁸	3.62 × 10⁹⁸	3.67 × 10¹⁴⁸	4.19 × 10¹⁹⁸
41	706020	9.98 × 10¹¹	3.98 × 10²⁴	1.27 × 10⁵⁰	2.58 × 10¹⁰¹	6.99 × 10¹⁵²	2.13 × 10²⁰⁴
43	854238	1.46 × 10¹¹	8.54 × 10²⁴	5.83 × 10⁵⁰	5.44 × 10¹⁰²	6.77 × 10¹⁵⁴	9.47 × 10²⁰⁶

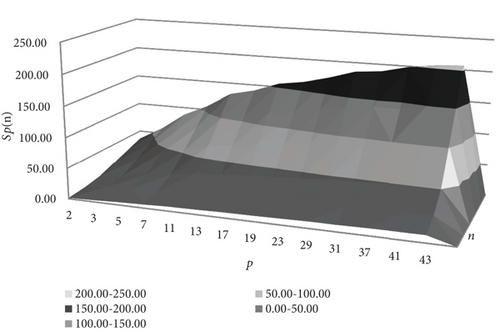
The numerical experiment shows that the number of irreducible polynomials increases with the expansion of the Galois field and the growth of the power. For the specified parameters p and n, it will lie in the following ranges: 30 ≤ S_p(8) ≤ 1.46¹², 4048 ≤ S_p(16) ≤ 8.54∗10²⁴, 1.34∗10⁸ ≤ S_p(32) ≤ 5.832∗10⁵⁰, 2.8823∗10¹⁷ ≤ S_p(64) ≤ 5.4425∗10¹⁰⁴, 8.25293∗10²⁶ ≤ S_p(96) ≤ 6.7717∗10¹⁵⁴, and 2.65846∗10³⁶ ≤ S_p(n) ≤ 9.4788∗10²⁰⁶. In addition, a given number of irreducible polynomials can be obtained either by changing the degree n or by expanding the field GF(p). For instance, S₄₃(8) ≈ S₇(16), S₄₃(16) ≈ S₇(32), S₄₃(32) ≈ S₇(64), S₄₃(64) ≈ S₇(96), and S₄₃(96) ≈ S₇(128).

Figure 3 shows the graphical dependence of the number of irreducible polynomials on these parameters on a logarithmic scale with base 10.

In general, the security of the proposed cryptosystem with l modules will be defined as the total time of complete search of all irreducible polynomials and the complexity of performing calculations with each one according to the following formula:

(11)

For instance, we can calculate the time (in clock cycles) needed to cryptanalyze the proposed encryption system with l = 5 and n = 32 in the Galois field GF(3) as follows: .

Table 3 estimates the cryptanalysis time in clock cycles for different parameter values of l, n, and S_p(n). Notably, the modern symmetric encryption algorithm AES-128 requires around 2¹²⁸ ≈ 10³⁷ clock cycles for resilience. Table 3 indicates that the proposed cryptosystem achieves a comparable level of security with the following parameters: S₃₁(4), l = 7, and n = 4; S₁₁(8), l = 5, and n = 8; S₃(16), l = 6, and n = 16; S₂(32), l = 3, and n = 32; and S₂(64), l = 2, and n = 64.

Table 3. Estimation of cryptanalysis time in clock cycles for various parameter values of l, n, and S_p(n).

l/n(S_p(n))	4(S₃₁(4))	8(S₁₁(8))	16(S₃(16))	32(S₂(32))	64(S₂(64))
2	1.5 × 10¹¹	7.9 × 10¹⁵	3.17 × 10¹⁴	5.879 × 10²⁹	5.8 × 10³⁷
3	1.7 × 10¹⁶	1.03 × 10²³	4.2 × 10²⁰	1.674 × 10⁴³	8.3 × 10⁵⁴
4	3.8 × 10²¹	2.8 × 10³⁰	1.1 × 10²⁷	9.595 × 10⁵⁶	2.4 × 10⁷²
5	2.02 × 10²⁶	1.7 × 10³⁷	6.98 × 10³²	1.29 × 10⁷⁰	1.6 × 10⁸⁹
6	8.6 × 10³¹	8.5 × 10⁴³	3.5 × 10³⁸	1.386 × 10⁸³	8.4 × 10¹⁰⁵
7	3.09 × 10³⁵	3.5 × 10⁵⁰	1.5 × 10⁴⁴	1.245 × 10⁹⁶	3.8 × 10¹²²

Table 3 shows that adding one module for parameters n = 4 and S₃₁(4) increases the strength by about 5 orders of magnitude, for n = 8 and S₁₁(8) by 7 orders of magnitude, for n = 16 and S₃(16) by 6 orders of magnitude, for n = 32 and S₂(32) by 13 orders of magnitude, and for n = 64 and S₂(64) by 17 orders of magnitude.

Figure 4 shows the graphs of cryptographic strength dependencies O(n, l) on a logarithmic scale with a base of 10 of the proposed symmetric polynomial encryption algorithm in RNS on the number of modules l for the polynomial powers n = 4 and 8 and the parameters p = 2, p = 3, p = 5, and p = 7. The horizontal line 6 corresponds to the strength of the modern symmetric encryption algorithm AES-128.

The figure shows that all graphs have the same bell-shaped character. The cryptographic strength increases significantly with increasing degree and dimension of the Galois field p and reaches its maximum at l = S_p(n)/2. This means that the cryptanalysis of the proposed algorithm requires combinatorial complexity, which leads to an NP-complete problem.

4. Conclusion

In this article, we first developed symmetric cryptographic algorithms based on the polynomial RNS. The mathematical support and schemes of the proposed polynomial symmetric encryption in the RNS are developed. To evaluate its robustness, we have studied and constructed analytical expressions that indicate that the cryptanalysis of the proposed algorithm requires combinatorial complexity, which leads to an NP-complete problem. It is established that the cryptographic strength increases significantly with the increasing degree and dimension of the Galois field p and reaches its maximum in the case when the number of modules is equal to half the possible number of irreducible polynomials with given polynomial degrees and Galois field orders. This means that finding an efficient algorithm to solve this problem requires significant computing resources and time.

We compare the strength of the proposed encryption method with the modern symmetric encryption algorithm AES-128. As a result of numerical experiments, it was found that the developed polynomial encryption methods in the RNS provide a level of resistance similar to AES-128 with the following parameters: S₃₁(4), l = 7, and n = 4; S₁₁(8), l = 5, and n = 8; S₃(16), l = 6, and n = 16; S₂(32), l = 3, and n = 32; and S₂(64), l = 2, and n = 64.

Thus, the proposed cryptographic algorithm based on the polynomial RNS can be used to ensure reliable protection of confidential information in systems with limited computing resources.

Consent

All authors have provided their consent for the publication of this research.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Conceptualization: I.Y. and M.K. (Mykhailo Kasianchuk); methodology: I.Y. and M.K. (Mykhailo Kasianchuk); validation: M.K. (Mykhailo Kasianchuk), M.K. (Mikolaj Karpinski), and R.S.; formal analysis: M.K.(Mykhailo Kasianchuk) and M.K.(Mikolaj Karpinski); investigation: I.Y., M.K. (Mykhailo Kasianchuk), M.K.(Mikolaj Karpinski), and R.S.; data curation: I.Y. and M.K.(Mykhailo Kasianchuk); writing—original draft preparation: I.Y., M.K.(Mykhailo Kasianchuk), and R.S.; writing—review and editing: I.Y., M.K.(Mykhailo Kasianchuk), and R.S. All authors have read and agreed to the published version of the article.

Funding

The authors received no specific funding for this work.

Acknowledgments

The authors express their sincere gratitude to the Armed Forces of Ukraine for providing security, which made it possible to conduct our research.

Open Research

Data Availability Statement

The authors confirm that the data supporting the findings of this study are available within the article.

References

1 Nieles M., Dempsey K., and Pillitteri V. Y., An introduction to information security, NIST Special Publication. (2017) 800, no. 12, https://doi.org/10.6028/NIST.SP.800-12r1.
10.6028/NIST.SP.800?12r1
Google Scholar
2 Milov O., Kazakova N., Milczarski P., and Korol O., Mechanisms of cyber security: the problem of conceptualization, Ukrainian Scientific Journal of Information Security. (2019) 25, no. 2, 110–116, https://doi.org/10.18372/2225-5036.25.13841.
10.18372/2225-5036.25.13841
Google Scholar
3 Alhassan M. M. and Adjei-Quaye A., Information security in an organization, International Journal of Computer (IJC). (2017) 24, no. 1, 100–116.
Google Scholar
4 Adki V. and Hatkar S., A survey on cryptography techniques, International Journal of Advanced Research in Computer Science and Software Engineering. (2016) 6, no. 6, 469–475.
Google Scholar
5 Bufalo M., Bufalo D., and Orlando G., A note on the computation of the modular inverse for cryptography, Axioms. (2021) 10, no. 2, https://doi.org/10.3390/axioms10020116.
10.3390/axioms10020116
Web of Science® Google Scholar
6 Kasianchuk M., Yakymenko I., and Nykolaychuk Y., Symmetric cryptoalgorithms in the residue number system, Cybernetics and Systems Analysis. (2021) 57, no. 2, 329–336, https://doi.org/10.1007/s10559-021-00358-6.
10.1007/s10559-021-00358-6
Web of Science® Google Scholar
7 Nykolaychuk Y., Yakymenko I., Vozna N., and Kasianchuk M., Residue number system asymmetric cryptoalgorithms, Cybernetics and Systems Analysis. (2022) 58, no. 4, 611–618, https://doi.org/10.1007/s10559-022-00494-7.
10.1007/s10559-022-00494-7
Web of Science® Google Scholar
8 Ochoa-Jimenez E., Rivera-Zamarripa L., Cruz-Cortes N., and Rodriguez-Henriquez F., Implementation of RSA signatures on GPU and CPU architectures, IEEE Access. (2020) 8, 9928–9941, https://doi.org/10.1109/ACCESS.2019.2963826.
10.1109/ACCESS.2019.2963826
Web of Science® Google Scholar
9 Biyashev R., Nyssanbayeva S., and Kapalova N., Secret Keys for Nonpositional Cryptosystems. Development, Investigation and Implementation, 2014, Lambert Academic Publishing.
Google Scholar
10 Biyashev R., Nyssanbayeva S., Kalimoldayev M., and Magzom M., Development of an encryption algorithm based on nonpositional polynomial notations, 2016 International Conference on Advanced Materials Science and Environmental Engineering, 2016, Atlantis Press, 241–243.
10.2991/amsee-16.2016.64
Google Scholar
11 Cheon J. H., Hong S., Lee C., and Son Y., Polynomial functional encryption scheme with linear ciphertext size, 2018, Cryptology ePrint Archive.
Google Scholar
12 Kapalova N. and Dyusenbayev D., Security analysis of an encryption scheme based on nonpositional polynomial notations, Open Engineering. (2016) 6, no. 1, https://doi.org/10.1515/eng-2016-0034, 2-s2.0-84990050520.
10.1515/eng-2016-0034
Google Scholar
13 Bajard J.-C., Imbert L., and Plantard T., Arithmetic operations in the polynomial modular number system, 17th IEEE Symposium on Computer Arithmetic (ARITH′05), 2005, Cape Cod, MA, USA, 206–213, https://doi.org/10.1109/ARITH.2005.11.
10.1109/ARITH.2005.11
Google Scholar
14 Didier L.-S., Dosso F.-Y., and Véron P., Efficient modular operations using the adapted modular number system, Journal of Cryptographic Engineering. (2020) 10, no. 2, 111–133, https://doi.org/10.1007/s13389-019-00221-7.
10.1007/s13389-019-00221-7
Web of Science® Google Scholar
15 Harvey D. and van Der Hoeven J., Faster polynomial multiplication over finite fields using cyclotomic coefficient rings, Journal of Complexity. (2019) 54, article 101404, https://doi.org/10.1016/j.jco.2019.03.004, 2-s2.0-85063980141.
10.1016/j.jco.2019.03.004
Web of Science® Google Scholar
16 Katz J., Sahai A., and Waters B., Predicate encryption supporting disjunctions, polynomial equations, and inner products, Advances in Cryptology–EUROCRYPT 2008: 27th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Istanbul, Turkey, April 13-17, 2008. Proceedings 27, 2008, Springer, Berlin Heidelberg, 146–162.
10.1007/978-3-540-78967-3_9
Google Scholar
17 Ashok G., Kumar A., and Kumari C., An approach of cryptosystem using polynomials and Lucas numbers, Journal of Harbin Engineering University. (2023) 44, no. 8, 25–31.
Google Scholar
18 Ashok G., Ashok K., Chaya K., and Ramakrishna M., A type of public cryptosystem using polynomials and pell sequences, Journal of Discrete Mathematical Sciences and Cryptography. (2022) 25, no. 7, 1951–1963, https://doi.org/10.1080/09720529.2022.2133237.
10.1080/09720529.2022.2133237
Web of Science® Google Scholar
19 Mohan P. V. A., Specialized residue number systems, 2016, Springer.
Google Scholar
20 Plantard T., Efficient word size modular arithmetic, IEEE Transactions on Emerging Topics in Computing. (2021) 9, no. 3, 1506–1518, https://doi.org/10.1109/TETC.2021.3073475.
10.1109/TETC.2021.3073475
Web of Science® Google Scholar
21 Omondi A. R. and Premkumar A. B., Residue Number Systems: Theory and Implementation, 2007, World Scientific.
10.1142/p523
Google Scholar
22 Bajard J.-C. and Imbert L., A full RNS implementation of RSA, IEEE Transactions on Computers. (2004) 53, no. 6, 769–774, https://doi.org/10.1109/TC.2004.2, 2-s2.0-3042531980.
10.1109/TC.2004.2
Web of Science® Google Scholar
23 Lawnik M. and Kapczy’nski A., The application of modified Chebyshev polynomials in asymmetric cryptography, Computer Science. (2019) 20, no. 3, 303–367, https://doi.org/10.7494/csci.2019.20.3.3307, 2-s2.0-85072274600.
10.7494/csci.2019.20.3.3307
Google Scholar
24 Milne J. S., Algebraic number theory (v3.08), JS Milne, 2020. http://www.jmilne.org/math/.
Google Scholar
25 Fournaris A. P., Papachristodoulou L., Batina L., and Sklavos N., Secure and efficient RNS approach for elliptic curve cryptography, In 6th Conference on Trustworthy Manufacturing and Utilization of Secure Devices (TRUDEVICE 2016), 2016, Barcelona, 121–126.
Google Scholar
26 Patel R. A., Benaissa M., and Boussakta S., Fast parallel-prefix architectures for modulo 2n-1 addition with a single representation of zero, IEEE Transactions on Computers. (2007) 56, no. 11, 1484–1492, https://doi.org/10.1109/TC.2007.70750, 2-s2.0-35148849529.
10.1109/TC.2007.70750
Web of Science® Google Scholar
27 Gao Z., Reviriego P., Pan W., Xu Z., Zhao M., Wang J., and Maestro J. A., Fault tolerant parallel filters based on error correction codes, IEEE Transactions on Very Large Scale Integration (VLSI) Systems. (2015) 23, no. 2, 384–387, https://doi.org/10.1109/TVLSI.2014.2308322, 2-s2.0-84922573170.
10.1109/TVLSI.2014.2308322
Web of Science® Google Scholar
28 Sachenko A., Hu Z., and Yatskiv V., Increasing the data transmission robustness in WSN using the modified error correction codes on residue number system, Elektronika ir Elektrotechnika. (2015) 21, no. 1, 76–81, https://doi.org/10.5755/j01.eee.21.1.6657, 2-s2.0-84922678125.
10.5755/j01.eee.21.1.6657
Web of Science® Google Scholar
29 Givaki K., Hojabr R., Najafi H., Khonsari A., Gholamrezayi M. H., Gorgin S., and Rahmati D., Using residue number systems to accelerate deterministic bit-stream multiplication, 2019 IEEE 30th International Conference on Application-specific Systems, Architectures and Processors (ASAP), 2019, New York, NY, USA, https://doi.org/10.1109/ASAP.2019.00-33, 2-s2.0-85072612141.
10.1109/ASAP.2019.00?33
Google Scholar
30 Tan W., Chiu S.-W., Wang A., Lao Y., and Parhi K. K., PaReNTT: low-latency parallel residue number system and NTT-based long polynomial modular multiplication for homomorphic encryption, 2023, https://arxiv.org/abs/2303.02237.
Google Scholar
31 Lemaire E., Pretty modular symmetric encryption (PMSE), compact algorithm for embedded cryptography with quite low computational cost, 2019, https://arxiv.org/abs/1905.08150.
Google Scholar
32 Migliore V., Real M. M., Lapotre V., Tisserand A., Fontaine C., and Gogniat G., Fast polynomial arithmetic for somewhat homomorphic encryption operations in hardware with Karatsuba algorithm, 2016 International Conference on Field-Programmable Technology (FPT), 2016, Xi′an, China, 209–212, https://doi.org/10.1109/FPT.2016.7929535, 2-s2.0-85021456210.
10.1109/FPT.2016.7929535
Google Scholar
33 Jayet-Griffon C., Cornelie M.-A., Maistri P., Elbaz-Vincent P., and Leveugle R., Polynomial multipliers for fully homomorphic encryption on FPGA, 2015 International Conference on ReConFigurable Computing and FPGAs (ReConFig), 2015, Riviera Maya, Mexico, https://doi.org/10.1109/ReConFig.2015.7393335, 2-s2.0-84964330931.
10.1109/ReConFig.2015.7393335
Google Scholar
34 Shivdikar K., Jonatan G., Mora E., Livesay N., Agrawal R., Joshi A., Abellán J. L., Kim J., and Kaeli D., Accelerating polynomial multiplication for homomorphic encryption on GPUs, 2022 IEEE International Symposium on Secure and Private Execution Environment Design (SEED), 2022, Storrs, CT, USA, 61–72, https://doi.org/10.1109/SEED55351.2022.00013.
10.1109/SEED55351.2022.00013
Google Scholar
35 Wu J., Liu H., and Zhu X., Image encryption based on permutation polynomials over finite fields, Optica Applicata. (2020) 50, no. 3, https://doi.org/10.37190/oa200303.
10.37190/oa200303
Web of Science® Google Scholar
36 Schinianakis D. and Stouraitis T., Multifunction residue architectures for cryptography, IEEE Transactions on Circuits and Systems I: Regular Papers. (2014) 61, no. 4, 1156–1169, https://doi.org/10.1109/TCSI.2013.2283674, 2-s2.0-84897962898.
10.1109/TCSI.2013.2283674
Web of Science® Google Scholar
37 Tynymbayev S., Ibraimov M., Namazbayev T., and Gnatyuk S., Development of pipelined polynomial multiplier modulo irreducible polynomials for cryptosystems, Eastern-European Journal of Enterprise Technologies. (2022) 1, no. 4.
10.15587/1729-4061.2022.251913
Google Scholar
38 Alamsyah A. B. and Adji T. B., The replacement of irreducible polynomial and affine mapping for the construction of a strong S-box, Nonlinear Dynamics. (2018) 93, no. 4, 2105–2118, https://doi.org/10.1007/s11071-018-4310-2, 2-s2.0-85047110590.
10.1007/s11071-018-4310-2
Web of Science® Google Scholar
39 Alamsyah A., A novel construction of perfect strict avalanche criterion S-box using simple irreducible polynomials, Scientific Journal of Informatics. (2020) 7, no. 1, 10–22, https://doi.org/10.15294/sji.v7i1.24006.
10.15294/sji.v7i1.24006
Google Scholar
40 Agarwal P., Singh A., and Kilicman A., Development of key-dependent dynamic S-boxes with dynamic irreducible polynomial and affine constant, Advances in Mechanical Engineering. (2018) 10, no. 7, 168781401878163, https://doi.org/10.1177/1687814018781638, 2-s2.0-85050958641.
10.1177/1687814018781638
Web of Science® Google Scholar
41 Alshammari K. F., Mostafa A., and Nashwan S., Avalanche analysis of variant polynomials for AES, Turkish Journal of Computer and Mathematics Education (TURCOMAT). (2021) 12, no. 14, 2696–2703.
Google Scholar
42 Chu J. and Benaissa M., A novel architecture of implementing error detecting AES using PRNS, 2011 14th Euromicro Conference on Digital System Design, 2011, Oulu, Finland, https://doi.org/10.1109/DSD.2011.90, 2-s2.0-80054976034.
10.1109/DSD.2011.90
Google Scholar
43 El-Kassar A. N., Haraty R., Awad Y., and Debnath N., Modified RSA in the domains of Gaussian integers and polynomials over finite fields, 2005, In CAINE.
Google Scholar
44 Yakymenko I., Kasianchuk M., Shylinska I., Shevchuk R., Yatskiv V., and Karpinski M., Polynomial Rabin cryptosystem based on the operation of addition, 2022 12th International Conference on Advanced Computer Information Technologies (ACIT), 2022, Ruzomberok, Slovakia, 345–350, https://doi.org/10.1109/ACIT54803.2022.9913089.
10.1109/ACIT54803.2022.9913089
Google Scholar
45 Turner P., Residue polynomial systems, Theoretical Computer Science. (2002) 279, no. 1-2, 29–49, https://doi.org/10.1016/S0304-3975(00)00425-4, 2-s2.0-0037188458.
10.1016/S0304-3975(00)00425-4
Web of Science® Google Scholar
46 Dosso F. Y., Berzati A., El Mrabet N., and Proy J., PMNS revisited for consistent redundancy and equality test, 2023, Cryptology ePrint Archive.
Google Scholar
47 Didier L.-S., Dosso F.-Y., El Mrabet N., Marrez J., and Véron P., Randomization of arithmetic over polynomial modular number system, 2019 IEEE 26th Symposium on Computer Arithmetic (ARITH), 2019, Kyoto, Japan, 199–206, https://doi.org/10.1109/ARITH.2019.00048.
10.1109/ARITH.2019.00048
Google Scholar
48 Karpinski M., Rajba S., Zawislak S., Warwas K., Kasianchuk M., Ivasiev S., and Yakymenko I., A method for decimal number recovery from its residues based on the addition of the product modules, 2019 10th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), 2019, Metz, France, 13–17, https://doi.org/10.1109/IDAACS.2019.8924395.
10.1109/IDAACS.2019.8924395
Google Scholar
49 Aremu A. and Gbolagade A., Redundant residue number system based multiple error detection and correction using Chinese remainder theorem (CRT), Software Engineering. (2017) 5, no. 5, 72–80, https://doi.org/10.11648/j.se.20170505.12.
10.11648/j.se.20170505.12
Google Scholar
50 Nykolaychuk Y., Kasianchuk M., and Yakymenko I., Theoretical foundations for the analytical computation of coefficients of basic numbers of Krestenson’s transformation, Cybernetics and Systems Analysis. (2014) 50, no. 5, 649–654, https://doi.org/10.1007/s10559-014-9654-0, 2-s2.0-84925483482.
10.1007/s10559-014-9654-0
Google Scholar
51 Beletsky A., Kovalchuk A., Novikov K., and Poltoratskyi D., Algorithm for the synthesis of irreducible polynomials of linear complexity, Ukrainian Information Security Research Journal. (2020) 22, no. 2, 74–87.
Google Scholar

Citing Literature

All articles

Symmetric Encryption Algorithms in a Polynomial Residue Number System

Abstract

1. Introduction

1.1. Our Contribution

1.2. Related Work

1.3. Organization

2. Materials and Methods

2.1. Theoretical Foundations of Polynomial RNS

2.2. Development of Polynomial Symmetric Encryption Methods in the RNS

2.3. An Example of Symmetric Polynomial Encryption in RNS

2.4. Polynomial Symmetric Encryption Method Based on CRT

3. Results

4. Conclusion

Consent

Conflicts of Interest

Author Contributions

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley