Discrete Dynamics in Nature and Society
Volume 2024, Issue 1 4786384
Research Article
Open Access

Limit Cycles and Local Bifurcation of Critical Periods in a Class of Switching Z2 Equivariant Quartic System

Jian Yang, 

Jian Yang

School of Mathematics and Computing Science, Guilin University of Electronic Technology, Guilin 541004, China gliet.edu.cn

Search for more papers by this author
Jukun Liu, 

Jukun Liu

Yueyang Economic and Technological Development Zone East Station Middle School, Yueyang 414022, China

Search for more papers by this author
Jingping Lu, 

Corresponding Author

Jingping Lu

School of Mathematics and Computing Science, Guilin University of Electronic Technology, Guilin 541004, China gliet.edu.cn

School of Mathematics and Statistics, Guilin University of Technology, Guilin 541004, China glut.edu.cn

Search for more papers by this author
First published: 02 May 2024
https://doi.org/10.1155/2024/4786384
Academic Editor: Chunrui Zhang

Abstract

In this paper, the limit cycles and local bifurcation of critical periods for a class of switching Z2 equivariant quartic system with two symmetric singularities are investigated. First, through the computation of Lyapunov constants, the conditions of the two singularities to become the centers are determined. Then, we prove that there are at most 18 limit cycles with a distribution pattern of 9-9 around the two symmetric singular points of the system. Numerical simulation is conducted to validate the obtained results. Furthermore, by calculating the period constants, we determine the conditions for the critical point to be a weak center of finite order. Finally, the number of local critical periods that bifurcate from the equilibrium point under the center conditions is discussed. This study presents the first example of a quartic switching smooth system with 18 limit cycles and 4 local critical periods bifurcating from two symmetric singular points.

1. Introduction

In the fields of automation, machinery, and engineering, there exist many discontinuous or nondifferentiable systems, which are called discontinuous or nonsmooth mechanical systems [1, 2]. One type of planar nonsmooth dynamical systems is known as a switching system, which is characterized by differential continuous vector fields in at least two different zones that are divided by at least one straight line or curve. The simple switching system can be described by the following equations:
(1)
where F±(x, y, μ) and G±(x, y, μ) are analytic functions in x and y. It is evident that there are two systems in system (1). As referenced in [3, 4], the system is divided into the upper system, defined in the upper half plane for y > 0, and the lower system, defined in the lower half plane for y < 0. Filippov [5] was the first to establish the fundamental qualitative theory for piecewise smooth systems. Subsequently, there has been a significant interest in the qualitative analysis of such systems. Coll et al. [6] derived the explicit expressions for the first three Lyapunov constants of pseudofocus singular points. Recently, there has been a growing interest among mathematicians in extending the second part of Hilbert’s 16th problem to planar piecewise polynomial vector fields, aiming to determine an upper bound for the maximum number of limit cycles in these systems. While it is a well-known fact that smooth linear systems cannot generate limit cycles, this is not the case for piecewise smooth systems (see [7, 8]). In the realm of piecewise smooth nonlinear systems, significant progress has been made in exploring limit cycles. Tian and Yu [9] proposed a new approach for calculating the Lyapunov constant of a planar switched system, which was subsequently utilized to analyze the bifurcation of limit cycles in the switched Bautin system. Moreover, a specific example of switching systems was presented to demonstrate the emergence of 10 small-amplitude limit cycles bifurcating from a singular point. Liu and Romanovski [10] studied a class of piecewise quadratic system with quartic perturbation, showing that 11 limit cycles could bifurcate around the double homoclinic loop. Li et al. [11] modified an existing method for computing the focal values and period constants of switching systems associated with elementary singular points. They presented a cubic switching system and demonstrated that 15 small limit cycles can bifurcate from the singular point. Li et al. [12] investigated a class of quartic piecewise smooth system and showed that 8 limit cycles can bifurcate from a weak focus of finite order.
If the above equations in (1) admit
(2)
then the switching system (1) is Z2-equivariant. Li and his collaborators have made a series of achievements in the study of dynamics such as limit cycles and integrability for Z2-equivariant planar system, as evidenced by references [13–16]. In addition, there have been notable advancements in the application research of bifurcation of limit cycles in symmetric systems. For instance, Song and Xu introduced the delayed half-center CPG oscillator and conducted an analysis of the system’s dynamical behavior with various spatiotemporal patterns [17–19]. Building upon these patterns, they developed the delayed-CPG neural system and successfully implemented locomotion control for both a snake-like robot [20] and a quadruped robot [21]. For the switching Z2-equivariant system, Guo et al. [22] constructed a class of switching Z2-equivariant cubic system to obtain 18 limit cycles from centers. Li and Yu [23] added one more switching line and used the same equations provided in [11] to construct a correct Z2-equivariant cubic system. Their analysis demonstrated that this new system can exhibit 15 limit cycles. Furthermore, Yu et al. [4] considered the bifurcation of limit cycles in a cubic switching Z2-equivariant system, revealing the emergence of 18 limit cycles bifurcating from two symmetric singular foci.

In the qualitative theory of differential equations, a crucial focus is on identifying isochronous centers and the bifurcation of critical periods within a period annulus. Similar to smooth systems, this study also aims to analyze whether the orbits near the center of system (1) have the same period. If these orbits share the same period, the origin of the system (1) is classified as an isochronous center. Alternatively, if the orbits near the center do not share the same period, it becomes essential to determine the order of the weak center and the maximum number of local critical periods that bifurcate from a finite order weak center. Chicone and Jacobs [24] introduced the theory of local bifurcation of critical periods and the definition of weak center of k-order for smooth systems. Additional relevant results for smooth systems can be found in [25–27] and references therein. However, limited research has been conducted on the investigation of isochronous centers and the bifurcation of critical periods for piecewise smooth systems. Chen et al. [28] proposed a new method for calculating the periodic constant near the center of a piecewise smooth system and discussed the problem of bifurcation of local critical periods for a switching Z2 equivariant cubic system. It was found that there are at most 5 local critical periods bifurcating from a single singular point. Huang et al. [29] investigated small-amplitude crossing limit cycles and local critical periods for some classes of piecewise smooth Kukles systems of degrees 3 and 4 and acquired new lower bounds for the local cyclicity and the criticality.

Inspired by the abovementioned work, we aim to determine a new lower bound on the maximum number of limit cycles and local critical periods for a class of quartic switching smooth systems. In this paper, we investigate the limit cycles and local bifurcation of critical periods for the following quartic switching smooth system:
(3)
where aij and bij are real parameters.

The rest of the paper is organized as follows. In the next section, we present preliminary information on the algorithm for calculating the Lyapunov constants and period constants for piecewise smooth systems, which can be easily implemented in computer algebraic software. In Section 3, we determine the necessary and sufficient condition for the equilibrium point to be a center by computing the Lyapunov constants for system (3) at the origin. In Section 4, the bifurcation of limit cycles for system (3) is investigated, demonstrating that there can be at most 18 limit cycles surrounding two symmetric equilibrium points under a suitable perturbation. In Section 5, the corresponding period constants are computed under the obtained center conditions, revealing that the equilibrium point of system (3) is not an isochronous center and that the maximum number of local critical period bifurcations from two symmetric equilibrium points is 4. Finally, conclusions are given in Section 6.

2. Preliminaries

In order to investigate the limit cycles and local bifurcation of critical periods for piecewise smooth systems, this section introduces fundamental concepts and techniques that will be utilized in subsequent sections. The approach outlined in [28, 30] is employed in this study to calculate Lyapunov constants and period constants for piecewise smooth systems, following the procedure described in the following.

The general differential system
(4)
under the polar coordinate transformation
(5)
can be rewritten as
(6)
(7)
where are polynomials of cos θ and sin θ, given by
(8)
Let
(9)
be the solutions of system (6) with the initial of r+(0, ρ) = r−(π, ρ) = ρ.
Define the positive half-return map Π+(ρ) and the negative half-return map Π−(ρ), respectively, by
(10)
where are the Taylor’s coefficients. We obtain the successor function of system (4),
(11)
where vk are the Taylor’s coefficients, as illustrated in Figure 1.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The successive function Δ(ρ).
The computation of Lyapunov constants using (11) is complex because it involves the composition of two maps Π+(ρ) and Π−(ρ) in the displacement map. Another method to calculate the Lyapunov constants was introduced by the authors of [11]. This method involves performing a change of variables (x, y, t)⟶(x, −y, −t) to transform system (4) into the following form.
(12)
According to Lemma 3 in [31], the displacement map can be calculated as
(13)
where represents the inverse map of Π−(ρ) (see Figure 2) and is the positive half-return map of system (12) (see Figure 3). The map of system (4) is equivalent to the positive half-return map of system (12). The positive half-return map of system (12) is defined as follows:
(14)
where are the Taylor’s coefficients. Consequently, a new function is derived as
(15)
where Vk is called the k th-order Lyapunov constants at the origin of system (4).
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Half-return map .
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Half-return map .

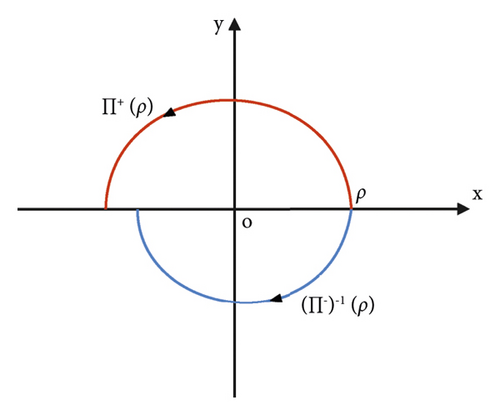
Definition 1 (see [28], [29].)The origin of system (3) is a k/2 th-order weak focus if and only if V1 = V2 = ⋯ = Vk = 0, Vk+1 ≠ 0, and the origin is called a rough focus if the order of weak focus is 0, i.e., V1 ≠ 0; the origin is a center if Vk = 0 for all k > 1.

The main issue at hand is how the order k/2 of the weak focus determines the maximum number of limit cycles that bifurcate from a finite order weak focus. In 2015, Chen, Romanovski, and Zhang provided the following result to address this question.

Proposition 2 (see [32].)Assuming that the origin is a weak focus of order k/2 in system (3) associated with the parameter value λ∗, it can be concluded that at most k limit cycles bifurcate from this weak focus at the parameter value λ∗.

To determine if there are perturbations that result in the bifurcation of exactly k limit cycles, one can refer to the following lemma as outlined in reference, Lemma 4 [9].

Lemma 3 (see [9].)If there exists λ∗ = (a1c, a2c, …, akc) such that Vi(λ∗) = 0, i = (1, 2, …, k), Vk+1(λ∗) ≠ 0 and det[∂(V1, V2, …, Vk)/∂(a1, a2, …, ak)] ≠ 0, system (3) just has k limit cycles from the origin (where λ = λ∗).

Using the computer algebra system, system (7) becomes
(16)
where are the Taylor’s coefficients.
We obtain
(17)
where is the Taylor’s coefficients.
Therefore, the periodic functions can expand as
(18)

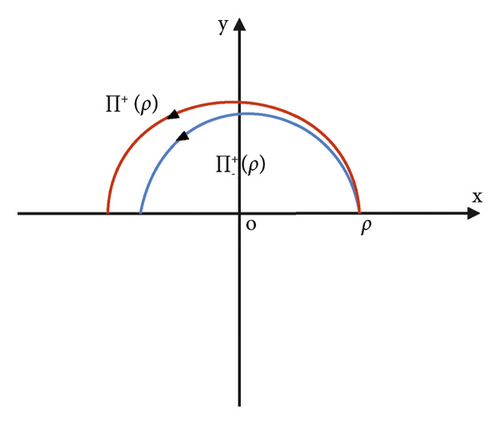
By means of transformation (x, y, t)⟶(x, −y, −t), the half-periodic functions P−(Π+(ρ)) of system (4) changes into positive half-periodic functions .

We have,
(19)
where Pk is a k th-order periodic constant.

If P1 = P2 = ⋯ = Pk = 0, Pk+1 ≠ 0, the origin of system (4) is a k − 1/2 th-order weak center. If k = 0, the origin is a strong center. If Pk = 0 for all k > 1, the origin is an isochronous center.

Similar to smooth systems, a local critical period is a period that corresponds to a critical point of the period function resulting from a bifurcation from a weak center. More precisely, the definition of k local critical periods is as follows.

Definition 4 (see [28].)Suppose that the origin is a weak center corresponding to the parameter λ∗. If there exists a λ ∈ W such that P′(ρ, λ) = 0 has k solutions in every sufficiently small neighborhood W of λ∗, then system (3) has k local critical periods bifurcating from the center.

In what follows, the key issue is how the order (k − 1)/2 of the weak focus decides the maximum number of local critical periods that bifurcate from a finite order weak center. In 2022, Huang, He, and Cai presented the following result to answer this question.

Proposition 5 (see [29].)If the origin is a weak center of order (k − 1)/2 in system (3) associated with the parameter value λ∗, then no more than k local critical periods emerge from this weak center at the parameter value λ∗.

To determine if there exist perturbations such that exactly k local critical periods are created, one can refer to the following lemma as outlined in reference [28, 33].

Lemma 6 (see [28], [33].)If there exists λ∗ = (a1c, a2c, …, akc) such that Pi(λ∗) = 0, i = (1, 2, …, k), Pk+1(λ∗) ≠ 0 and det[∂(P1, P2, …, Pk)/∂(a1, a2, …, ak)] ≠ 0, system (3) just has k critical periods bifurcating from the origin (where λ = λ∗).

In addition, we also want to know whether the origin of switching systems is a center if the first k th-order Lyapunov constants vanish. Some criteria for determining whether the equilibrium point of switching systems is a center are provided in [11].

Lemma 7 (see [11].)The necessary and sufficient conditions for the origin of system (2) to be a center if one of the following conditions are satisfied:

  • (a)

    System (3) is symmetric with the x-axis, namely, .

  • (b)

    System (3) is symmetric with the y-axis, namely, .

3. Lyapunov Constants and Center Conditions

In this section, we compute the Lyapunov constants of the corresponding equilibria and find center conditions of system (3) at the origin. First of all, it is easy to check that system (3) always has two singular point O1 = (1, 0) and O2 = (−1, 0). Due to the Z2 symmetry, we choose only O1 to analyze in detail.

By applying the transformation and introducing linear perturbations to system (3), we obtain the following system (for simplicity, we still denote by x, y, respectively):
(20)
where the singular point (1, 0) of system (3) changes into the origin of system (20).
The system (20) can be transformed into the form of system (6) under the polar coordinate transformation (5). Considering the system
(21)
the expansion of the system (21) around r = 0 can be expressed as
(22)
where Rk(θ) is a polynomial in sin θ and cos θ. Note that
(23)
Combining the above equation with (21) and (22) yields
(24)
Substituting the solution r(ρ, θ) = ∑k≥1vk(θ)ρk into (22) results in and
(25)
where Ωi,j(θ) are polynomials in vl(θ), 2 ≤ l ≤ j. Then, according to the proposition [28], Proposition 2, and (15) and using the software Mathematica (a code snippet is provided in the Appendix), we obtain the following theorems.

Theorem 8. The first ten Lyapunov constants at the origin of system (20) are given by

(26)

Case 9. a12 = 0

(27)

Case 10. a12 ≠ 0, V60 = 0 (i.e. )

(28)
where
(29)

In the above expressions of Vk, we have already set Vk−1 = 0 (k = 2, 3, …, 10).

Next, we discuss the center conditions of system (20). From Theorem 8, we obtain the following results.

Theorem 11. The first ten Lyapunov constants at the origin of system (20) are zero if and only if the following conditions are satisfied:

(30)

Proof. From the expressions of the first ten Lyapunov constants given in Theorem 8, the sufficiency of the conditions in Theorem 12 is obvious. Next, we prove that the conditions in Theorem 12 are also necessary.

Letting the second Lyapunov constant V1 = V2 = 0, we have δ = a31 = 0 and

(31)

Taking V3 = 0 yields a22 = −1/2(−8b12 − 3b13) and V4 = 8/45(20a12 − 3a13). If V4 = 0, we get a13 = 20a12/3 and . Setting V5 = 0, we obtain and

(32)

Then, solving V6 = 0 yields a12 = 0 or V60 = 0. If a12 = 0 , we have V7 = V8 = V9 = V10 = 0. This leads to the conditions a31 = 0, a22 = −4b12, a13 = 0, b13 = 0, a12 = 0. On the other hand, under the condition a12 ≠ 0, taking V60 = 0 (in particular ), we get

(33)

Taking V7 = 0, we obtain V70 = 0 (i.e., ) and

(34)

Next, we need to judge whether the equations V8 = 0, V9 = 0 and V10 = 0 have common solutions, that is, to discuss whether or not the polynomials F1, F2 and F3 have common zeros. For this purpose, we compute the Grbner basis of the ideal 〈F1, F2, F3〉 and get

(35)

This means that the polynomials F1, F2 and F3 have no common zeros. The proof of Theorem 12 is complete.

Theorem 12. The origin of system (3) is a center if and only if condition (30) is true.

Proof. When the condition (30) holds, the system (20) can be rewritten in the form

(36)

Obviously, the upper system and the lower system of system (36) are symmetric with the y-axis. Thus, the origin of system (3) is a center.

4. Bifurcation of Limit Cycles

The discussion now shifts to the maximum number of limit cycles bifurcating from the origin of system (20). To determine the highest order of the origin as a weak focus, we refer to the Proof of Theorem 12. It is established that the polynomials F1, F2 and F3 have no common root but F1 and F2 should have. Therefore, we need to solve F1 = F2 = 0 to find the solutions of a12 and b12. It can be demonstrated that the equations have 6 groups of real solutions, and we take one of them as follows:
(37)

According to the above analysis and Theorem 12, we obtain the following theorem.

Theorem 13. The origin of system (20) is a 9/2 th-order weak focus if and only if the following conditions are satisfied:

(38)

Moreover, one can directly verify that the Jacobian evaluated at the critical point equals
(39)

According to Lemma 3, the following theorem is concluded.

Theorem 14. Assume that the conditions of Theorem 14 hold, then 9 limit cycles can bifurcate from the equilibrium point of system (20) after a small perturbation. Accordingly, 18 limit cycles can exist in a small neighborhood of two symmetric equilibria (1.0) and (−1, 0) of system (3).

Theorem 15 ensures that there are 9 large-amplitude limit cycles in system (20) under small perturbations. In order to obtain 9 small-amplitude limit cycles bifurcating from the equilibrium point, it is necessary to find the exact 9 positive roots derived from solving the polynomial equation
(40)
Finding explicit parameter values to achieve a numerical realization is generally challenging. However, for our case, perturbations can be implemented sequentially, allowing for the identification of parameter values that result in 9 positive solutions for (40). It is essential to ensure that the perturbations satisfy the condition
(41)
We take perturbations in the backward order as follows: on a12 for V9, on b12 for V8, on a04 for V7, on a03 for V6, on b13 for V5, on a13 for V4, on a22 for V3, on a31 for V2, and on δ for V1. More precisely, we choose
(42)
Using the abovementioned perturbed parameter values, the resulting Lyapunov constants are
(43)
for which (40) has the following 9 positive roots:
(44)
as expected.

5. Local Bifurcation of Critical Periods

In this section, we investigate the order of a finite weak center and the number of local critical periods when the origin is a center for system (20).

When condition (30) is satisfied, using the computer algebra system Mathematica, the first three period constants of system (20) at the origin are given as follows:
(45)

For every Pk that was calculated, we already imposed that P1 = ⋯ = Pk−1 = 0, k = 2, 3. Through analysis, it was found that the equation p3 = 0 has no real root, that is, the equations P1 = 0, P2 = 0, and P3 = 0 have no common zeros. Therefore, the origin of system (20) is not an isochronous center.

Moreover, it is evident that while P1, P2 and P3 do not share any common zeros, P1 and P2 should. By solving P1 = P2 = 0, we can find the solutions for a03 and a04. Subsequently, the Jacobian determinant at the critical point is determined to be
(46)

According to the above analysis and Lemma 6, we have the following theorem.

Theorem 15. The highest order of the weak center for system (20) at the origin is 2 if the condition (30) holds, i.e., at most 2 critical periods are generated from the center of system (20). Accordingly, at most 4 critical periods can bifurcate from two symmetric equilibria (1, 0) and (−1, 0) of system (3).

6. Conclusion and Discussion

Based on an exact symbolic computation of Lyapunov constants and period constants, we have studied the center problem and determined the maximum number of limit cycles and local critical periods for a class of switching Z2 equivariant quartic system. Our findings reveal that at most 18 limit cycles and 4 local critical periods can bifurcate from two symmetric singular points. Up to our knowledge, the result of 18 limit cycles and 4 local critical periods are two new lower bounds on the maximum number of small-amplitude limit cycles and local critical periods for quartic switching smooth systems. The complexity of calculating Lyapunov constants and period constants in piecewise smooth systems increases with the degree of system (1). Compared to smooth systems, it is more challenging to improving the maximum number of limit cycles and local critical periods in these systems. Therefore, developing a more efficient method for calculating Lyapunov constants and period constants in piecewise smooth systems remains a challenging task.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (12061016) and the Basic Ability Enhancement Program for Young and Middle-Aged Teachers of Guangxi (2022KY0198 and 2022KY0254).

    Appendix

    (A.1)

    Data Availability

    A code snippet is provided in the Appendix.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.