The purpose of this paper is to introduce q-Post–Widder operators based on a new parameter and study their approximation properties. The moments and central moments are investigated. And some local approximation properties of these operators by means of modulus of continuity and Peetre’s K-functional are presented. Furthermore, the rate of convergence for these operators is obtained. Weighted approximation and the quantitative q-Voronovskaja type theorem are discussed. Finally, numerical illustrative examples have been given to show the convergence of these newly defined operators.

1. Introduction

The following form of Post–Widder operators [1, 2] are given by the following equation:

()

These operators preserve linear functions. Substituting

, we can write the operators in Equation (1) in the following way:

()

The saturation and inverse problems of the operators in Equation (2) were recently considered by May [3]. Rathore [4] introduced a generalization of the operators in Equation (2) as:

()

where p be a fixed integer. They obtained the simultaneous approximation property and established an asymptotic formula. In the special case, p = −1, the operators in Equation (3) reduce to the operators in Equation (2). In addition for the p = 0, the operators in Equation (3) were the classical Post–Widder operators defined by Widder [5] in the following equation:

()

Torun [6] constructed the Stancu type Post–Widder operators, which were a modification of the Post–Widder operators, and studied the approximation properties and the Voronovskaja type approximation theorem.

Since q-calculus has important applications in many disciplines, many researchers have recently applied the q-integers to some well-known linear positive operators and contributed to the literature by obtaining many different approximation properties of these operators. In Ünal et al. [7], the q analogue of the classical Post–Widder operators was given in the following equation:

()

The statistical approximation properties of real and complex q-Post–Widder operators were investigated. Also note that the operators in Equation (5) tend to the classical Post–Widder operators in Equation (4) as q → 1⁻. Subsequently, Aydin et al. [8] also considered a generalization of Post–Widder operators based on the q-integers and gave some approximation properties.

In recent years, the field of approximate theory has developed rapidly. Up to now, many researchers have constructed different types of positive linear operators to find the best convergence to the given function. Recently, there has been an increasing interest in the study of some operators associated with the shape parameter, one can refer to [9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]. Motivated by the above mentioned papers, the main goal of this paper is to present a kind of modified q-Post–Widder operators based on a new parameter and give local approximation by means of modulus of continuity and Peetre’s K-functional. Next, we study the rate of convergence, obtain weighted approximation, and prove quantitative q-Voronovskaja type theorems in terms of weighted modulus of continuity. Finally, with the aid of Matlab software, we present the comparison of the convergence of operators in Equation (13) to the certain functions for the different values of n, q, and α with some graphics. We also compare the convergence of operators in Equation (13) to the certain function to see the behaviour of α parameter. As a result, the α gives us more modeling in flexibility.

Before introducing the operators, we recall some concepts of q-calculus, details can be founded in [20, 21, 22, 23]. Let 0 < q < 1 and

. The q-number [k]_q is defined as:

()

Also, the q-factorial [k]_q! is defined in the following equation:

()

Further, q-power basis is defined as:

()

The q-improper integral function f is defined as:

()

The q-exponential function E_q(x) is defined as:

()

The q-gamma function is defined by the following equation:

()

which satisfies Γ_q(x + 1) = [x]_qΓ_q(x) and Γ_q(1) = 1. In particular, for any nonnegative integer k > 0, Γ_q(k + 1) = [k]_q!.

The q-derivative D_qf of f(x) with respect to x is given by the following equation:

()

and D_qf(0) = f^′(0) provided f^′(0) exists. Note that when q → 1, it reduces to the standard derivative. High-order q-derivatives are defined by

For f ∈ C[0, ∞), integer α is less than n,

, we introduce a generalized q-Post–Widder operators

based on a new parameter α as follows:

()

It is clear that as α = 1 and q → 1⁻, the operators in Equation (13) tend to the operators in Equation (1). If we take α = 0, the operators

reduce to the operators P_n,q defined by Equation (5).

2. Preliminaries

In this section, we establish some essential results, which will be useful to obtain our main results.

Lemma 1. Let e_i(t) = tⁱ, i = 0, 1, 2, …. Then, we have

()

Proof. Direct computation gives,

()

Lemma 1 is proved.

Lemma 2. For the operators defined by Equation (13), we have

()

Proof. For i = 0, . Using Equation (14) and ,

()

this completes the proof of the lemma.

Lemma 3. Let . Then,

()

Proof. From Lemma 2, we have . For i ≥ 1, using the linearity of the operators in Equation (13) and applying Equation (16), we obtain

()

Thus, we can estimate the first-, second-, and fourth-order central moments. The proof of this Lemma is completed.

Lemma 4. Let q = (q_n) be a sequence satisfying the following equation:

()

For each x ∈ [0, ∞), we can obtain

()

Proof. Using Lemma 3, we have

()

and

()

By recalling the moments of which are indicated in Lemma 3, we can write

()

where

()

Taking into account

and

()

we obtain

This proves the second formula of Equation (21). Similarly, from Equation (19), we get the last two formulas of Equation (21). Hence, the proof is completed.

Lemma 5. Let q = (q_n) be a sequence satisfying the conditions given in Equation (20). Then, for each x ∈ [0, ∞), we have

()

Proof. From Equation (8), we can easily obtain the following equation:

()

Further, we note that

are linear monotone operators. Using Cauchy–Schwarz inequality, we get

()

Similarly,

()

Thus, we have the desired results.

3. Local Approximation

In this section, we discuss direct local approximation properties of the operators

. Recall that C_B[0, ∞) is the space of all real-valued continuous bounded function f on [0, ∞), endowed with the norm

. Moreover, the first-order and second-order modulus of continuities of the function f ∈ C_B[0, ∞) are defined by the following equation:

()

The Peetre’s K-functional [24] is defined by the following equation:

()

where

. From [24, 25], there exists an absolute constant C > 0, such that

()

Now, we can prove the following approximation result.

Theorem 1. For f ∈ C_B[0, ∞), x ∈ [0, ∞) and q ∈ (0, 1), we have

()

where C₁ > 0 is a positive constant,

()

Proof. We begin by defining auxiliary operators,

()

In view of Lemma 3, the operators

are linear and preserve the linear functions:

()

Let

. Using Taylor’s expansion,

()

and Equation (37), we obtain

()

We also have,

()

Thus,

()

Taking infimum on the right-hand side over all

and using Equation (32), we get

()

This completes the proof.

Corollary 1. Let the sequence q = (q_n) satisfy the conditions given in Equation (20). For f ∈ C_B[0, ∞), we have

()

The following estimate is a local approximation theorem. Let Lip_M(γ, E) be the set of all functions f defined on [0, +∞) satisfying the condition:

()

where γ ∈ (0, 1], E ⊂ [0, +∞), and

denotes the closure of E in [0, +∞).

Theorem 2. Let 0 < γ ≤ 1 and E be any bound subset of the interval [0, +∞). If , for all x ∈ [0, ∞), then we have

()

where C₂ is a positive constant, d(x; E) is the distance between x and E defined as:

()

Proof. Considering the properties of the infimum, there is at least one point , such that d(x; E) = |t₀ − x|. Since,

()

we can write,

()

Choosing

and

and using the Hölder inequality, we have

()

which finalises the proof.

4. Rate of Convergence

We now want to consider the rate of convergence of the operators on [0, ∞). Let B₂[0, ∞) = {f : |f(x)| ≤ C_f(1 + x²)}, where C_f is a positive constant that depends only on f. C₂[0, ∞) denotes the subspace of all continuous functions in B₂[0, ∞). . The norm on is .

For f ∈ C₂[0, ∞), the weighted modulus of continuity Ω(f; δ) [26, 27] is defined as the following equation:

()

It is clear that

()

and

()

Moreover, Ω(f; δ) has the following properties [28, 29]

()

For any γ > 0, we introduce the modulus of continuity of f ∈ C(0, γ] by

In the next theorem, we present the rate of convergence for sequences of positive linear operators .

Theorem 3. If f ∈ C₂[0, ∞), θ ∈ (0, ∞), then the following holds true equation:

()

Proof. For x ∈ [0, θ] and t ∈ (θ + 1, ∞), since 1 ≤ (t − θ)² ≤ (t − x)², we have

()

For t ∈ [0, θ + 1], we can obtain

()

Using Equations (55) and (56), we get for all x ∈ [0, θ] and t ≥ 0

()

Applying Cauchy–Schwarz inequality and Lemma 3, for all x ∈ [0, θ], we get

()

By taking

, we can get the assertion of theorem.

Theorem 4. Let q = (q_n) be a sequence satisfying (20). For every , there exists a positive integer , such that for all n > N, the following inequality holds:

()

Proof. For t, x ∈ [0, ∞) and δ > 0, using the definition of Ω(f; δ) and Equation (53), we obtain

()

Since

is linear and positive,

()

In view of Equation (21), there exists a positive integer

, such that for all n > N,

()

and

()

To estimate the third term of Equation (61), utilizing Cauchy–Schwarz inequality, Equations (62) and (63), we have

()

From Equations (61), (62) and (64), we get

()

Taking

, we easily obtain Equation (59). This completes the proof.

5. Weighted Approximation and Voronovskaja Type Theorem

In this section, we derive the weighted approximation theorem as follows.

Theorem 5. Let the sequence q = (q_n) satisfy Equation (20). Then for , we have

()

Proof. Using Korovkin’s theorem [30], we need to show that:

()

Since , Equation (67) holds for k = 0. For k = 1, applying Lemma 2, we have

()

Hence,

()

Similarly, we obtain

()

Thus, it is clear that

()

Therefore, we get the desired result.

Now, we establish the quantitaitve q-Voronovskaja theorem and Voronovskaja type asymptotic formula for the operators with the help of the weighted modulus of continuity.

Theorem 6. Let q = (q_n) be a sequence such that Equation (20) is satisfied, and satisfy . For all x ∈ [0, ∞), we have

()

Proof. Considering the q-Taylor expansion formula, we get

()

where ϕ is a number between t and x and

()

By applying the operator

to the above Equation (73) and using

()

we obtain

()

Furthermore,

()

For all δ ∈ (0, 1), using Equation (53), we get

()

Therefore,

()

In the view of Lemma 5, we get

()

Now we take

, we can obtain

()

This completes the proof of theorem.

Using Theorem 6, we obtain the following Voronovskaya type result.

Corollary 2. Let q = (q_n) be a sequence such that Equation (20) is satisfied and satisfy . Then,

()

6. Graphical and Numerical Analysis

In this section, we will present some numerical illustrative examples in order to observe the approximation behavior of the newly defined operators in Equation (13). In these examples, we compare the operators in Equation (13) with its classical correspondence operators in Equation (5) with the different values of α, q, and n.

In this experiments, we consider a test function given by the following equation:

()

Let

. In Figure 1, for α = −1 and n = 30, 50, 80 respectively, we show the convergence of operators in Equation (13)

to the function f(x). In Figure 2, for α = 0 and n = 30, 50, 80 respectively, we demonstrate the convergence of operators in Equation (13)

to the function f(x). It is quite clear that, in the case of α = 0, operators

reduce to the q-Post–Widder operator operators P_n,q. For α = 1, the convergence of operators in Equation (13)

to the function f(x) for n = 30, 50, 80 is shown in Figure 3. For α = 2, n = 30, n = 50, and n = 80 respectively, we present the convergence of operators in Equation (13) to the function f(x). We can conclude from Figures 1, 2, 3, and 4 that, as the values of n increases than the convergence of operators in Equation (13) to the function f(x) becomes better.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The convergence of to f(x) for α = −1 and n = 30, 50, 80.

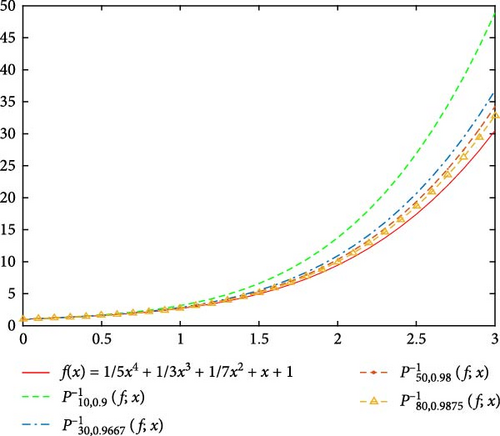
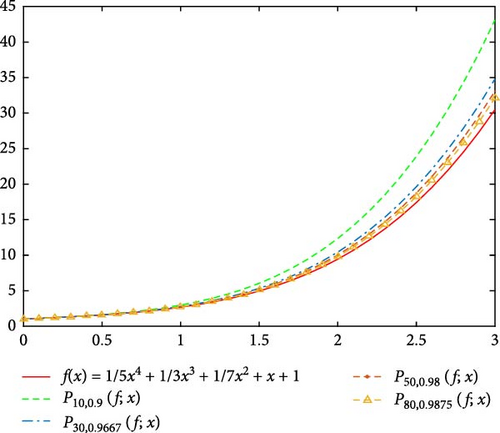
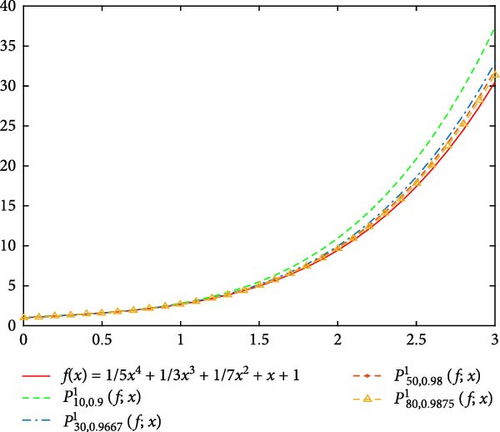
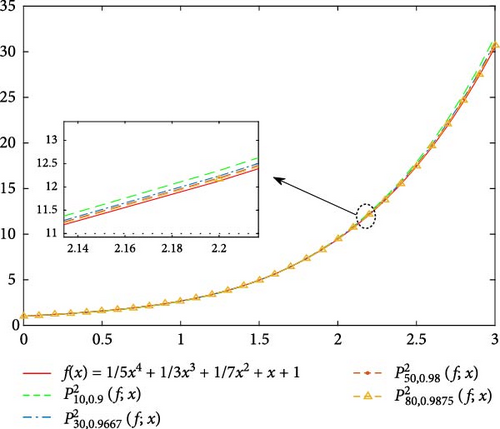
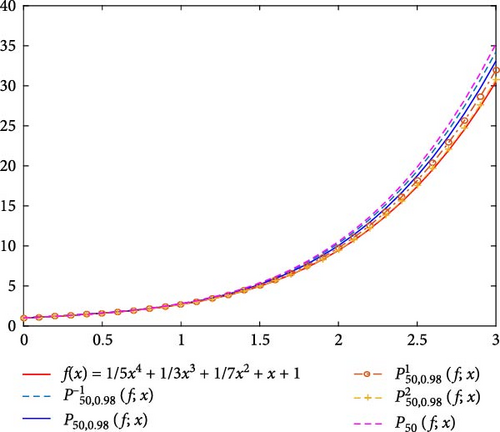
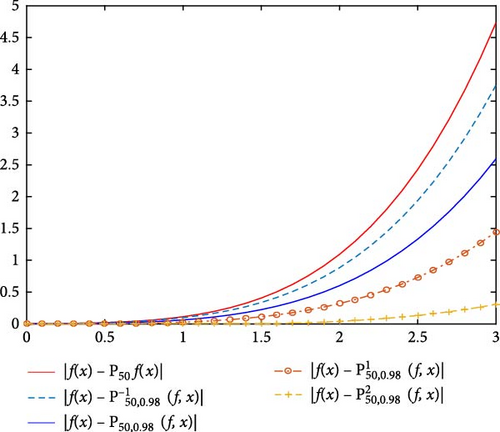
Moreover, in Figure 5, we compare the new modification of q-Post–Widder operators in Equation (13) with q-Post–Widder operators in Equation (5) and the classical Post–Widder operators in Equation (4) for the values n = 50, q = 0.98, and α = −1, 1, 2. Also, we illustrate its error of the approximation process in Figure 6. It is obvious that introduced operator in Equation (13) for α = 1 and α = 2 has better approximation than operators in Equations (4) and (5).

7. Conclusion

The new modification of q-Post–Widder operators based on the parameter α is established. The parameter α gives us more modeling flexibility. In this paper, we derive Korovkin type convergence theorem, rate of convergence, pointwise estimates, weighted approximation, and Voronovksya type theorems. Moreover, we provide some numerical experiments to verify the theoretical results.

Disclosure

It is confirmed that manuscript is not under review or published elsewhere.

Conflicts of Interest

The author declares that there is no conflicts of interest.

Acknowledgments

Qiu Lin was supported by the Research Fund for Yancheng Teachers University under 204040026.

Open Research

Data Availability

Data availability is not applicable to this article as no new data were created or analyzed in this study.

References

1 Draganov B. R. and Ivanov K. G., A characterization of weighted approximations by the Post-Widder and the Gamma operators, Journal of Approximation Theory. (2007) 146, no. 1, 3–27, https://doi.org/10.1016/j.jat.2006.09.007, 2-s2.0-34247851045.
10.1016/j.jat.2006.09.007
Web of Science® Google Scholar
2 Draganov B. R. and Ivanov K. G., A characterization of weighted approximations by the Post–Widder and the Gamma operators, II, Journal of Approximation Theory. (2010) 162, no. 10, 1805–1851, https://doi.org/10.1016/j.jat.2009.10.004, 2-s2.0-77957153491.
10.1016/j.jat.2009.10.004
Google Scholar
3 May C. P., Saturation and inverse theorems for combinations of a class of exponential-type operators, Canadian Journal of Mathematics. (1976) 28, no. 6, 1224–1250, https://doi.org/10.4153/CJM-1976-123-8.
10.4153/CJM-1976-123-8
Web of Science® Google Scholar
4 Rathore R. K. S., On convergence of derivatives of Post-Widder operators, 1980.
Google Scholar
5 Widder D. V., The Laplace Transform, (Princeton Mathematical Series, 6), 1941, Princeton University Press, Princeton.
Google Scholar
6 Torun G., On approximation properties of stancu type post-widder operators preserving exponential functions, Gazi University Journal of Science Part A: Engineering and Innovation. (2022) 9, no. 2, 173–186, https://doi.org/10.54287/gujsa.1113567.
10.54287/gujsa.1113567
Google Scholar
7 Ünal Z., Özarslan M. A., and Duman O., Approximation properties of real and complex Post-Widder operators based on q-integers, Miskolc Mathematical Notes. (2012) 13, no. 2, 581–603, https://doi.org/10.18514/MMN.2012.318.
10.18514/MMN.2012.318
Google Scholar
8 Aydin D., Aral A., and Bascanbaz-Tunca G., A generalization of Post-Widder operators based on q-integers, Analele Stiintifice ale Universitatii Al I Cuza din Iasi-Matematica. (2014) 66, no. 9-10, 1052–1062.
Google Scholar
9 Baytunç E., Aktuǧlu H., and Mahmudov N., A new generalization of Szász-Mirakjan kantorovich operators for better error estimation, Fundamental Journal of Mathematics and Applications. (2023) 6, no. 4, 194–210, https://doi.org/10.33401/fujma.1355254.
10.33401/fujma.1355254
Google Scholar
10 Aslan R., Some approximation results on λ-Szasz-Mirakjan-Kantorovich operators, Fundamental Journal of Mathematics and Applications. (2021) 4, no. 3, 150–158, https://doi.org/10.33401/fujma.903140.
10.33401/fujma.903140
Google Scholar
11 Aslan R., Approximation by Szasz-Mirakjan-Durrmeyer operators based on shape parameter λ, Communications Faculty of Sciences University of Ankara Series A1 Mathematics and Statistics. (2022) 71, no. 2, 407–421, https://doi.org/10.31801/cfsuasmas.941919.
10.31801/cfsuasmas.941919
Google Scholar
12 Usta F. and Betus Ö., A new modification of Gamma operators with a better error estimation, Linear and Multilinear Algebra. (2022) 70, no. 11, 2198–2209, https://doi.org/10.1080/03081087.2020.1791033.
10.1080/03081087.2020.1791033
Google Scholar
13 Khan T., Khan S. A., and Rao N., On approximation by bivariate Szász-Gamma type hybrid operators, Bulletin of Mathematical Analysis and Applications. (2022) 14, 11–27.
Google Scholar
14 Khan T., Rao N., Khan S. A., and Malik P., On α-Baskakov-Gamma operators with two shifted nodes, Palestine Journal of Mathematics. (2022) 11, no. 2, 457.
Google Scholar
15 Ansari K. J. and Usta F., A generalization of Szász-Mirakyan operators based on α non-negative parameter, Symmetry. (2022) 14, no. 8, https://doi.org/10.3390/sym14081596, 1596.
10.3390/sym14081596
Web of Science® Google Scholar
16 Betus Ö. and Usta F., Approximation of functions by a new type of Gamma operators, Numerical Methods for Partial Differential Equations. (2023) 39, no. 5, 3520–3531, https://doi.org/10.1002/num.22660.
10.1002/num.22660
Google Scholar
17 Su L.-T., Aslan R., Zheng F.-S., and Mursaleen M., On the Durrmeyer variant of q-Bernstein operators based on the shape parameter λ, Journal of Inequalities and Applications. (2023) 2023, no. 1, https://doi.org/10.1186/s13660-023-02965-7, 56.
10.1186/s13660-023-02965-7
Google Scholar
18 Aslan R., Rate of approximation of blending type modified univariate and bivariate λ-Schurer-Kantorovich operators, Kuwait Journal of Science. (2024) 51, no. 1, https://doi.org/10.1016/j.kjs.2023.12.007, 100168.
10.1016/j.kjs.2023.12.007
Google Scholar
19 Rao N., Yadav A. K., Mursaleen M., Sinha B. K., and Jha N. K., Szász-Beta operators via Hermite Polynomial, Journal of King Saud University-Science. (2024) 36, no. 4, https://doi.org/10.1016/j.jksus.2024.103120, 103120.
10.1016/j.jksus.2024.103120
Google Scholar
20 Aral A., Gupta V., and Agarwal R. P., Applications of q-Calculus in Operator Theory, 2013, Springer, New York.
10.1007/978-1-4614-6946-9
Google Scholar
21 De Sole A. and Kac V., On integral representations of q-gamma and q-beta functions, 2003, https://doi.org/10.48550/arXiv.math/0302032.
10.48550/arXiv.math/0302032
Google Scholar
22 Gupta V., Rassias T. M., Agrawal P. N., and Acu A. M., Recent Advances in Constructive Approximation Theory, 2018, Springer, New York.
10.1007/978-3-319-92165-5
Google Scholar
23 Kac V. G. and Cheung P., Quantum Calculus, 2002, Springer, New York.
10.1007/978-1-4613-0071-7
Google Scholar
24 DeVore R. A. and Lorentz G. G., Construtive Approximation, 1993, Springer, Berlin.
10.1007/978-3-662-02888-9
Google Scholar
25 Gupta V. and Agarwal R. P., Convergence Estimates in Approximation Theory, 2014, Springer, Cham.
10.1007/978-3-319-02765-4
Google Scholar
26 Ispir N., On modified Baskakov operators on weighted spaces, Turkish Journal of Mathematics. (2001) 25, no. 3, 355–365.
Google Scholar
27 Yuksel I. and Ispir N., Weighted approximation by a certain family of summation integral-type operators, Computers & Mathematics with Applications. (2006) 52, no. 10-11, 1463–1470, https://doi.org/10.1016/j.camwa.2006.08.031, 2-s2.0-33846860004.
10.1016/j.camwa.2006.08.031
Web of Science® Google Scholar
28 Acar T., Aral A., and Raşa I., Approximation by k-th order modifications of Szász—Mirakyan operators, Studia Scientiarum Mathematicarum Hungarica. (2016) 53, no. 3, 379–398, https://doi.org/10.1556/012.2016.53.3.1339, 2-s2.0-84987608674.
10.1556/012.2016.53.3.1339
Web of Science® Google Scholar
29 Acar T., Aral A., and Rasa I., The new forms of Voronovskaya’s theorem in weighted spaces, Positivity. (2016) 20, no. 1, 25–40, https://doi.org/10.1007/s11117-015-0338-4, 2-s2.0-84929094250.
10.1007/s11117-015-0338-4
Web of Science® Google Scholar
30 Korovkin P. P., Linear Operators and Approximation Theory, 1960, Hindustan Publishing Corporation.
Google Scholar

All articles

Approximation by q-Post-Widder Operators Based on a New Parameter

Abstract

1. Introduction

2. Preliminaries

3. Local Approximation

4. Rate of Convergence

5. Weighted Approximation and Voronovskaja Type Theorem

6. Graphical and Numerical Analysis

7. Conclusion

Disclosure

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Approximation by q-Post-Widder Operators Based on a New Parameter

Abstract

1. Introduction

2. Preliminaries

3. Local Approximation

4. Rate of Convergence

5. Weighted Approximation and Voronovskaja Type Theorem

6. Graphical and Numerical Analysis

7. Conclusion

Disclosure

Conflicts of Interest

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information