Complexity
Volume 2024, Issue 1 4369401
Research Article
Open Access

Risk Assessment for Complex Systems Based on Fuzzy Cognitive Maps: A Case of the Biopharmaceutical Industry

Hadi Abbasian, 

Hadi Abbasian

Department of Pharmacoeconomics and Pharmaceutical Administration , School of Pharmacy , Urmia University of Medical Sciences , Urmia , Iran , umsu.ac.ir

Search for more papers by this author
Reza Yousefi-Zenouz, 

Reza Yousefi-Zenouz

Lecturer in Business Analytics , Queen’s University Belfast , Belfast , UK , qub.ac.uk

Search for more papers by this author
Abdollah Amirkhani, 

Abdollah Amirkhani

Department of Electrical Engineering , School of Automotive Engineering , Iran University of Science and Technology , Tehran , Iran , iust.ac.ir

Search for more papers by this author
Masoud Shirzadeh, 

Masoud Shirzadeh

Department of Electrical Engineering , Amirkabir University of Technology (Tehran Polytechnic) , Tehran , Iran , aut.ac.ir

Search for more papers by this author
Akbar Abdollahiasl, 

Akbar Abdollahiasl

Department of Pharmacoeconomics and Pharmaceutical Administration , Faculty of Pharmacy , Tehran University of Medical Sciences , Tehran , Iran , tums.ac.ir

Search for more papers by this author
Shekoufeh Nikfar, 

Shekoufeh Nikfar

Department of Pharmacoeconomics and Pharmaceutical Administration , Faculty of Pharmacy , Tehran University of Medical Sciences , Tehran , Iran , tums.ac.ir

Search for more papers by this author
Mohammadreza Siahi-Shadabad, 

Mohammadreza Siahi-Shadabad

Department of Pharmaceutical and Food Control , Tabriz University of Medical Sciences , Tabriz , Iran , tbzmed.ac.ir

Search for more papers by this author
Abbas Kebriaeezadeh, 

Corresponding Author

Abbas Kebriaeezadeh

Department of Pharmacoeconomics and Pharmaceutical Administration , Faculty of Pharmacy , Tehran University of Medical Sciences , Tehran , Iran , tums.ac.ir

Search for more papers by this author
First published: 30 June 2024
https://doi.org/10.1155/2024/4369401
Citations: 1
Academic Editor: Roberto Natella

Abstract

Analyzing the supply chain (SC) of biopharmaceutical drugs can be challenging due to their complexity, the existence of a wide variety of risks, and the dynamics of the system. This paper presents a framework for evaluating the SC risks of Iranian biopharmaceutical companies based on cause-and-effect relationships and fuzzy cognitive maps (FCMs). We first interviewed several biopharmaceutical supply experts to learn about potential SC risks, causal relationships among FCM concepts, FCM structure, and FCM activation cycle. The most critical and relevant risks and significant elements of the SCs, such as cost, time, and quality, were identified as relevant FCM concepts. Then, we used failure mode and effects analysis (FMEA) and the FCM of the SC risks to assess the impacts of the biopharmaceutical SC risks on each other and on the crucial elements of the SCs. The Hebbian learning algorithms were then applied to train the FCM models. We tested different scenarios to evaluate the impacts of FCM concepts on the SC risks. The proposed approach can prioritize risk factors and, more importantly, predict and analyze the effect of each risk factor/risk group on other risks or the outcome of a given risk. The proposed FCM features and the knowledge gained from evaluating them can provide practical and helpful information to pharmaceutical companies to deal with their supply risks more efficiently.

1. Introduction

Biopharmaceutical products are essential in restoring health and saving lives worldwide. The biotechnology industry has made Iran a leader in the biotechnology market in the Middle East and North Africa [1]. Based on Iranian pharmaceutical statistics, domestically generated biopharmaceuticals accounted for over 11 percent of the Iranian medication market share in 2020.

When defining risk across various domains, adopting a multidisciplinary approach is imperative as it allows for the consideration of a multitude of factors, thereby facilitating a more comprehensive approach to risk analysis [2]. Multidisciplinary risk assessment frameworks that integrate techniques from fields such as operations’ research, decision science, and artificial intelligence can provide holistic insights into complex risk landscapes. Recent studies [2, 3] have demonstrated the value of combining methodologies such as fuzzy cognitive mapping, failure mode and effects analysis, and quality function deployment in enhancing risk assessments across sectors such as manufacturing, supply chains, and distribution processes. By drawing from diverse domains, these integrative approaches capture a wider range of risk factors and their intricate interdependencies, leading to more informed risk mitigation strategies. The findings demonstrate that combining multiple multicriteria decision-making (MCDM) techniques and synthesizing their outcomes enhances confidence in risk assessments and failure mode rankings, while effectively handling uncertainties and divergent expert judgments [4]. The decomposed fuzzy set (DFS) failure mode and effects analysis (FMEA) approach accounts for uncertainties and indecision in decision-makers’ evaluations by allowing them to provide assessments for risk occurrence, severity, and detectability from both optimistic and pessimistic perspectives [5].

Managing supply chain (SC) risks is a significant challenge in the field of SC management [6, 7]. Biopharmaceutical SCs face unique challenges, including supply variations [8], demand fluctuations [9], disruptive events [10], production uncertainty [11], and other factors [12, 13]. Recent advances in various biopharmaceuticals and their sensitive nature have increased the complexity of SCs for these drugs, posing new challenges for decision-makers [14]. Also, the uncertainties in the production process of biological pharmaceuticals set their SCs apart from those of chemical drugs [15, 16]. The most critical players in drug SCs are pharmaceutical manufacturers [17]. Their performance affects the efficiency of the entire process, and their significant investments in research and development and responsibility for the quality of the final products put them at higher risk than others. Therefore, drug manufacturers are in the best position to identify and manage SC risks [18].

Quality (product or service), cost, and time are the most important indicators of business performance [19]. Drug SC management aims to benefit patients and the health system by delivering high-quality products and services to end-users (patients) at the right time, cost, and location [20]. Thus, gaining a clear understanding of drug SC risks is essential to improve the efficiency of drug SCs and reduce potential risks and flaws. Prior research predominantly employed conventional quantitative/qualitative tools such as analytic hierarchy process (AHP) [21, 22]. These methods exhibit static dependencies among logical variables, lacking consideration for process variables, time, uncertainties, and human behavior [23, 24]. Consequently, they fall short in evaluating the dynamic risks inherent in these systems. Common risk analysis tools, such as failure mode and effects analysis (FMEA) [25, 26], fault tree analysis [27], analytic hierarchy process [28], and the analytic network process [29], are not able to accurately predict risk behavior and perform dynamic risk analysis. Therefore, existing tools cannot be used for an accurate assessment of the SC risks of biopharmaceutical companies.

Fuzzy cognitive maps (FCMs) serve as powerful graphical tools for modeling complex system behaviors [30, 31]. Within the framework of an FCM, nodes represent key concepts of a system, while the weights assigned to links quantify the strength of relationships between these concepts. The evolution of FCMs has seen various definitions and developments aimed at enhancing performance, interpretation, prediction, and modeling capabilities. FCMs boast advantageous features such as fuzzy reasoning, straightforward structure, high flexibility, and trainability, capturing the attention of numerous researchers [32]. The effectiveness of the FCM method is well-documented across diverse decision-making applications, as evidenced by a plethora of studies [29–33]. Particularly, noteworthy is its successful application in risk analysis within decision-making contexts. For instance, Zarrin’s evolutionary algorithm for constructing FCM models and inferring genetic causal networks showcases the method’s versatility in addressing intricate problems [33]. In the mining industry, Samadi et al. applied FCM to assess postclosure strategies, integrating evidential reasoning to contribute to sustainable mining policy [34]. FCM has also demonstrated its efficacy in tackling challenges within production processes. Jahangoshai Rezaee et al.’s study, employing FCM in conjunction with failure mode and effects analysis, successfully identified and prioritized failures in a food production process [35]. This integration of FCM with other methodologies underscores its adaptability and effectiveness in addressing real-world problems. Irannezhad et al. delved into the use of FCM to model causal relationships and assess blockchain readiness within the sphere of SC management [36]. This research exemplifies FCM’s applicability in evaluating and enhancing the resilience of SCs. Similarly, Mzougui et al. utilized FCM to organize knowledge related to human risk management, demonstrating its utility in comprehensively addressing challenges in industrial environments [37]. Furthermore, FCMs are commonly employed in risk analysis [3].

In summary, these studies collectively highlight the versatility and effectiveness of the FCM method in addressing intricate decision-making problems across diverse domains. The expansion of biopharmaceutical production in Iran, coupled with challenges in drug SCs, particularly in biopharmaceutical supply, inefficiencies in traditional risk analysis methods, and the capabilities of FCM, motivated us to leverage the FCM technique for estimating SC risks within Iranian biopharmaceutical companies. The FCM employed in this study can be refined through the use of active Hebbian learning (AHL) and nonlinear Hebbian learning (NHL) algorithms.

2. Materials and Methods

This study delves into the SC risks faced by biopharmaceutical companies in Iran, marking the first exploration of its kind. The research focuses on unraveling the cause-and-effect relationships between these risks, with the study population comprising biopharmaceutical companies registered by the Iranian Food and Drug Administration. The methodology involves a three-phase FCM-based approach for drug SC risk management.

Phase I: Identification of drug supply chain risks.

Identification of SC risks is made in 4 steps.
  • (i)

    Initial Identification. Conducting a systematic review to pinpoint SC risks.

  • (ii)

    Interviews with Experts. Engaging in semistructured interviews with industry experts, particularly those well-versed in biopharmaceuticals. Questions cover risks across different regions and phases of the biopharmaceutical SC.

  • (iii)

    Categorization. Organizing identified risks into macrorisks, supply risks, organization- and strategy-related risks, demand risks, financial risks, support risks, and regulatory risks.

  • (iv)

    Fuzzy Screening. Experts rate identified risks based on their industry significance using fuzzy numbers (FNs).

Phase II: Model design using FCM involves the following steps.
  • (i)

    Questionnaire Design. Developing a questionnaire to gather expert opinions on the mutual impact of concepts. Linguistic variables and fuzzy sets represent impact levels.

  • (ii)

    Graph FCM. Creating a specific FCM to explore causal relationships between concepts (risks and goals), treating risks and goals as nodes in the system.

  • (iii)

    Initial Weights. Calculating the arithmetic mean of expert responses for each element. The center-of-gravity defuzzification method yields nonfuzzy weights for links in the FCM graph.

Phase III: FCM inference involves the following steps.
  • (i)

    Risk Activation. Determining the initial value of risk-related concepts based on the risk priority number (RPN) from failure mode and effects analysis.

  • (ii)

    Scenario Testing. Defining various scenarios, such as simultaneous activation of all risks, group activation, and individual activation, with initial values based on risk scores.

  • (iii)

    FCM Training. Employing NHL and AHL algorithms to enhance FCM performance by iteratively updating numerical weights.

  • (iv)

    Analysis. Examining the effects of different scenarios on SC variables (time, cost, and quality) and levels of other risks.

2.1. Fuzzy Screening

According to conditions, experts are requested to rate identified risks concerning their importance to the industry. Expert opinions are organized in the form of FNs:
(1)
where XAi is the value of ith experts’ evaluation for criterion A, UA is the maximum value of all experts’ evaluation for criterion A, LA is the minimum value of all experts’ evaluation for criterion A, and MA is the geometric mean of all experts’ evaluation for criterion A.
(2)
where Ne shows the number of experts. Then, defuzzification is done, i.e., TFN is converted to a nonfuzzy (or crisp) number as follows [23]:
(3)

By implementing a threshold, we prioritize risks of higher importance over others. In line with the suggested hypothesis, factors with geometric means below the threshold were excluded. The threshold, denoted as α, was established at α = 0.8θ. In this formula, θ represents the difference between the maximum and minimum values of the non-FN. In this study, α = 0.8θ = 0.8 (4.87−1.12) = 3. Consequently, if Mc ≥ α, the risk is acknowledged as significant; otherwise, the risk is considered not very high [24].

2.2. FCM Structure

An FCM consists of a directional graph, a set of concepts, weights, expert opinions, and inferences [32]. If an FCM comprises n concepts (risks and goals according to expert opinions), the values of these concepts are represented by ci, i = 1, …, N. These numerical values are normalized in the range of [0, 1] or [−1, 1], depending on the application of the FCM and the system for which we intend to use the FCM. An FCM graph shows the existing concepts and how they are related. Weights are assigned to the graph edges, describing the severity of the causal relationships between the FCM concepts [32]. It is the experts’ responsibility to determine the numerical values of the link weights. Suppose wij is the weight of the link between the two concepts of ci and cj. If wij > 0, then ci will have a direct effect on cj; i.e., if ci increases (decreases), cj will increase (decrease) as well. The higher the weight, the stronger the influence of one concept on another. If wij < 0, then ci has an opposite effect on cj; i.e., if ci increases (decreases), cj will decrease (increase). In the case of wij = 0, the concept ci has no influence on cj. The value of a concept in the kth iteration is related to its value in the (k − 1)th iteration in the following way [31]:
(4)

Equation (4) shows an FCM inference. ci(k) denotes the value of the concept ci in the kth iteration and ci(k − 1) is its value in the (k − 1)th iteration. Also, f(⋅) represents a transfer function, the most common forms of which are the sigmoid and the hyperbolic functions [37]. Figure 1 shows an example of a hypothetical FCM with six concepts, whose transfer function is of the hyperbolic tangent type. Figure 1(a) illustrates the FCM graph, and Figure 1(b) shows the results of the FCM inference.

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
An example of a simple FCM: (a) FCM graph and (b) FCM inference results.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
An example of a simple FCM: (a) FCM graph and (b) FCM inference results.

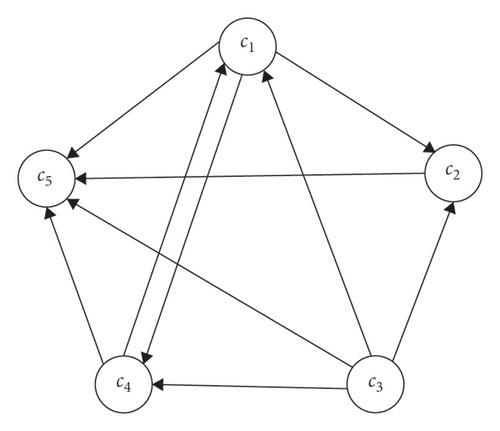
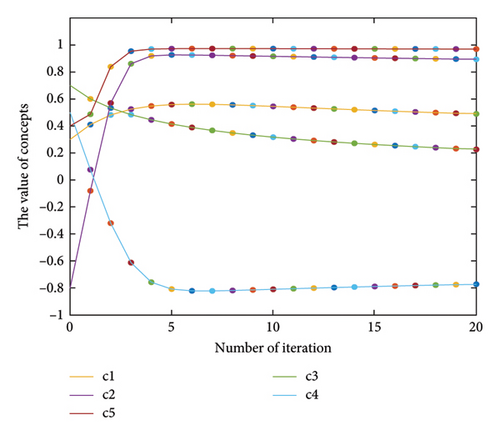
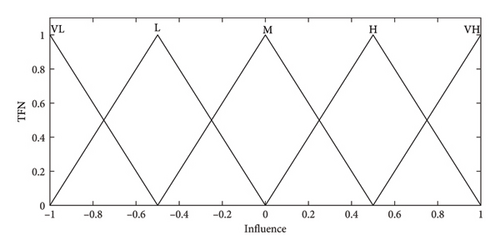
A questionnaire was designed, and experts were asked to comment on the impact of the concepts on each other using linguistic variables. The effect of concept is expressed by the linguistic variables very low (VL), low (L), moderate (M), high (H), and very high (VH) with corresponding fuzzy sets, as shown in Figure 2.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Fuzzy sets describing the impact of concepts on each other.

2.3. FCM Training and Inference

Various learning algorithms can be applied to FCM weights. These algorithms improve the performance and accuracy of the models by modifying the FCM weights. Some of these algorithms use Hebb’s rule to update the link weights. In these methods, the weights are updated and corrected during the inference phase. Therefore, the FCM inference in (5) is modified as
(5)
where wij(k − 1) is the FCM weights in the (k − 1)th iteration. The two most common types of algorithms for FCM training are the NHL and the AHL algorithms. The updated law in the NHL algorithm is expressed as
(6)
where sgn(∙) indicates a sign function and η is the learning rate [38]. The AHL algorithm considers asynchronous updates for concepts and weights. Therefore, the activated concepts and the activation sequences need to be defined. The AHL algorithm is based on the assumption that there is an activation sequence. In other words, this algorithm does not activate all the concepts at once. Figure 3 depicts a hypothetical activation cycle for the FCM, as shown in Figure 1.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
An example of an activation cycle.
In Figure 3, the concept C2 is activated first, followed by the concepts C1, C3, and C5, and finally by C4. In this case, the FCM inference is modified as
(7)
where is the activated concept in the (k − 1)th iteration. Thus, the following equation is proposed to update the weights according to the AHL algorithm.
(8)

In (8), η2 is the learning rate and η1 is the parameter of weight descent.

The arithmetic mean of all data was calculated for each element after receiving expert feedback. The resulting non-FN (using the center-of-gravity defuzzification method [39]) indicates the weight (initial weight) of the link between the two concepts in the FCM graph. The impact of activating a risk or a collection of risks on other SC risks is investigated in this step. The FCMs are inferred using equation (5), the impact of activation of a risk is investigated by the use of equation (4), and the number of risks associated with a risk being activated is inferred.

The initial value of risk-related concepts is the RPN number of activated risks. This value is obtained using the failure mode and effects analysis method. Each linguistic variable used in this questionnaire is represented by a FN, as shown in Figure 2. The content validity approach is utilized to determine the validity of the pretest questionnaires, as it was for the validation of the FCM Modeling Questionnaire. After gathering expert opinions, defuzzification is performed, exactly like the defuzzified of FCM. The risk score is calculated and normalized, and the RPN is calculated according to the following relationship [40]:
(9)

Here, D is the probability of risk detection, O is the rate of risk occurrence, CI is the impact on cost, TI is the impact on time, and QI is the impact on quality. To test the diverse scenarios and the FCM inference on these scenarios, we defined 27 scenarios, which included the simultaneous activation of all risks, the activation of risks in groups, and the activation of risks individually. The initial value of the concepts is based on the risk score obtained from the previous steps. To improve FCM performance, we train it using NHL and AHL algorithms. The numerical weights obtained in the second phase by these algorithms are updated at each FCM iteration step. For AHL, the activation cycle is determined by expert opinions. Finally, the effects of various scenarios on the three SC variables of time, cost, and quality, as well as the levels of other risks, are examined.

3. Results

After conducting a review study, 16 biopharmaceutical experts were interviewed. Based on the interviews, the coding, and synchronization of the risks, 16 different items of the risks in the review study were obtained. A total of 95 risks were identified from reviewing sources and interviewing experts. After applying fuzzy screening, 20 high-importance risks in the biopharmaceutical industry were identified. The RPN was used to determine the risk of each failure situation. This number is the product of the multiplication of the risk factors of probability, severity, and detectability, as shown in Table 1.

Table 1. RPN of biopharmaceutical manufacturers’ SC risks with prioritization.
Category Risk Ranking Risk score
Macro Sanction (R2) 1 0.381
Regulatory Lack of good governance for medicines (R16) 2 0.325
Macro MOH conflicts of interest (R1) 3 0.311
Financial Dual exchange rate (R7) 4 0.307
Regulatory Drug list limitation (R15) 5 0.305
Regulatory Lobbying risks in the decision-making process (R19) 6 0.303
Regulatory Inefficient pricing policies (R17) 7 0.298
Financial Currency fluctuation (R11) 8 0.297
Supply Defect in the domestic supply of essential raw materials (R4) 9 0.288
Financial Money transfer problem (R6) 10 0.287
Regulatory Pseudo-productivity (repacking) (R14) 11 0.280
Financial Cash flow risk (R10) 11 0.280
Financial Interest rate (R12) 12 0.231
Financial Long cash collection cycle (R9) 13 0.230
Financial Inflation rate (R8) 14 0.208
Regulatory Change in legislation and policies (R20) 15 0.205
Regulatory Banking regulation instability (R18) 16 0.204
Organization and strategies’ issues Defect of international vision (R5) 17 0.190
Macro Political instability (R3) 18 0.181
Demand Demand fluctuations (R13) 19 0.170

3.1. FCM for Dynamic Risk Assessment

Based on expert opinions and the steps taken, an FCM with 23 concepts is designed. The concepts of c1 to c20 (SC risks) are represented as R1 to R20, respectively. The concepts of c21 to c23, which represent time, cost, and quality, respectively, are represented as P1 to P3. The total number of contact vectors between nodes is 176, and on average, each node is associated with at least seven other nodes (Table 2).

Table 2. Indicators of structural analysis of the model.
Index Value
Total components 23
Total connections 176
Connection density 0.3327032
Connections per component 7.652174
Number of transmitter components 1
Number of receiver components 3
Number of ordinary components 19
Number of no connections 0
Number of self-loops 0
Complexity (R/T) 3

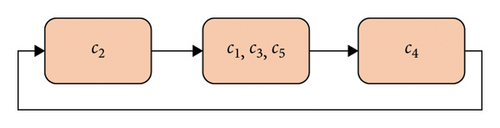
The initial weights of the communication links are obtained by defuzzifying expert opinions regarding the causal effect of concepts on each other. These values are presented in Table 3. The NHL algorithm is used to train the FCM at this stage. As suggested by the experts, the FCM activation cycle is such that the R1, R2, and R3 risks are activated first, but not all risks are activated at the same time. Then, the other risks are activated, and finally, the P1, P2, and P3 risks are activated. We also train the FCM designed for SC risks of Iranian biopharmaceutical companies using the AHL algorithm.

Table 3. Initial weights of FCM nodes.
  R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 R13 R14 R15 R16 R17 R18 R19 R20 P1 P2 P3
R1 0 0 0.23 0.1 0 0 0 0 0.27 0.24 0 0 0.14 0.22 0.35 0.37 0.35 0 0.42 0.28 0.15 0 −0.25
R2 0.6 0 0.45 0.45 0.48 0.61 0.52 0.5 0.35 0.37 0.46 0.3 0.29 0.07 0.28 0 0.25 0.35 0.2 0.23 0.46 0.41 −0.45
R3 0.13 0 0 0.29 0.31 0.18 0.18 0.19 0 0 0.27 0.13 0 0 0 0.35 0.21 0.16 0.31 0.45 0.17 0.22 −0.08
R4 0 0 0 0 0 0 0 0 0 0 0 0 0 0.22 0 0 0 0 0 0 0.42 0.35 −0.34
R5 0 0 0 0 0 0 0 0 0 0 0 0 0 0.23 0 0 0 0 0 0 0 0 −0.22
R6 0 0 0 0.25 0.12 0 0.23 0.32 0.16 0.29 0.25 0.19 0 0 0 0.14 0 0.34 0.14 0.1 0.48 0.45 −0.08
R7 0.1 0 0 0.25 0 0.38 0 0.3 0 0.24 0.35 0.18 0 0.1 0 0.19 0.26 0.17 0.16 0 0.29 0.2 −0.22
R8 0 0 0 0 0 0 0.19 0 0.22 0.33 0.33 0.39 0.18 0 0 0 0.24 0.2 0 0 0 0.35 −0.09
R9 0 0 0 0.2 0 0 0 0 0 0.51 0 0 0 0 0 0 0.09 0 0 0 0.34 0.34 −0.08
R10 0 0 0 0.24 0 0.17 0 0 0.22 0 0 0 0 0 0 0 0 0 0 0 0.27 0.38 0
R11 0 0 0.19 0.19 −0.18 0.19 0.3 0.35 0.17 0.34 0 0 0 −0.14 0 0 0.26 0.23 0 0 0.16 0.31 −0.19
R12 0 0 0 0 0 0 0 0.22 0 0.22 0 0 0 0 0 0 0 0 0 0 0 0.27 0
R13 0 0 0 0.11 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.15 0.1 0
R14 0 0 0 0.25 0.13 0 0 0 0 0 0 0 0 0 0 0.15 0.14 0 0.23 0 0 0 0
R15 0.2 0 0 0 −0.1 0 0 0 0 0 0 0 0.11 0 0 0.21 0 0 0.25 0 0 0 0
R16 0.36 0 0.14 0.25 0 0 0 0 0.1 0 0 0 0 0.34 0.26 0 0.35 0 0.48 0.32 0.21 0.23 −0.28
R17 0.1 0 0 0.26 0 0 0 0 0.19 0.25 0 0 0 0.13 0 0 0 0 0.19 0 0.16 0.26 −0.34
R18 0 0 0 0.2 0 0.32 0 0 0 0.31 0.15 0.22 0 0 0 0 0 0 0 0 0.25 0.29 0
R19 0.33 0 0 0 0 0 0 0 0 0 0 0 0 0.24 0.22 0.3 0.28 0 0 0.13 0 0 −0.31
R20 0.19 0 0 0.12 0 0 0 0 0 0 0 0 0 0 0 0.22 0 0 0 0 0.14 0 0
P1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
P2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
P3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

3.2. Result of Different Scenarios

At this stage, the inactive risks have an initial value of zero, and the initial value of the active risks is the RPN. The simulation is performed in the MATLAB software environment. The FCM-based simulation process of each scenario ends when consistency in the value of the concepts is achieved. We designed 27 different scenarios in order to assess and interpret the impact of each risk category and also each individual risk factor on the other risks, and Table 4 shows numerical results related to the scenarios, including the initial and final values of concepts and the number of iterations. Table 4 shows the untrained FCM results and the FCM results trained by the NHL.

Table 4. Initial and final values from different scenarios of SC risk activation of the BCs.
Scenario Description R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 R11 R12 R13 R14 R15 R16 R17 R18 R19 R20 P1 P2 P3
1 Activating all risks 0.311 0.381 0.181 0.288 0.190 0.287 0.307 0.208 0.230 0.280 0.297 0.231 0.170 0.280 0.305 0.325 0.298 0.204 0.303 0.205 0 0 0
NHL results (irritation 9) 0.718 0.032 0.486 0.877 0.262 0.654 0.572 0.676 0.714 0.879 0.665 0.621 0.406 0.698 0.594 0.779 0.828 0.620 0.823 0.670 0.919 0.946 −0.867
AHL results (irritation 9) 0.743 0.047 0.455 0.881 0.171 0.649 0.560 0.690 0.706 0.884 0.625 0.624 0.302 0.687 0.557 0.798 0.857 0.564 0.828 0.640 0.916 0.944 −0.865
  
2 Activating macrorisks 0.311 0.381 0.181 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
NHL results (irritation 14) 0.697 0.008 0.419 0.863 0.167 0.605 0.504 0.629 0.694 0.865 0.617 0.567 0.322 0.677 0.562 0.761 0.813 0.566 0.808 0.638 0.907 0.936 −0.853
AHL results (irritation 15) 0.652 0.011 0.341 0.824 0.113 0.503 0.398 0.526 0.629 0.818 0.496 0.460 0.231 0.627 0.490 0.716 0.779 0.442 0.770 0.565 0.880 0.913 −0.825
  
3 Activating supply risks 0 0 0 0.288 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 6) 0.004 0.000 0.001 0.015 0.001 0.000 0.000 0.000 0.002 0.003 0.000 0.000 0.000 0.010 0.003 0.006 0.006 0.000 0.008 0.004 0.016 0.014 −0.016
AHL results (irritation 6) 0.004 0.000 0.001 0.015 0.002 0.000 0.000 0.000 0.002 0.003 0.000 0.000 0.000 0.010 0.003 0.006 0.006 0.000 0.008 0.004 0.016 0.014 −0.016
  
4 Activating organization and strategies’ risks 0 0 0 0 0.190 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 6) 0.003 0 0 0 0.004 0.007 0.000 0.000 0.002 0.002 0.000 0.000 0.000 0.007 0.002 0.004 0.004 0.000 0.005 0.003 0.005 0.004 −0.009
AHL results (irritation 6) 0.003 0 0.001 0.004 0.007 0.000 0.000 0.000 0.002 0.002 0.000 0.000 0.000 0.007 0.002 0.004 0.004 0.000 0.006 0.003 0.005 0.004 −0.009
  
5 Activating financial risks 0 0 0 0 0 0.287 0.307 0.208 0.230 0.280 0.297 0.231 0 0 0 0 0 0 0 0      
NHL results (irritation 14) 0.691 0.000 0.398 0.859 0.138 0.594 0.493 0.617 0.689 0.860 0.605 0.557 0.302 0.672 0.550 0.757 0.810 0.555 0.806 0.629 0.904 0.934 −0.850
AHL results (irritation 16) 0.623 0.000 0.302 0.810 0.093 0.466 0.361 0.485 0.615 0.803 0.466 0.424 0.215 0.612 0.474 0.690 0.754 0.415 0.753 0.541 0.869 0.903 −0.812
  
6 Activating demand risks 0 0 0 0 0 0 0 0 0 0 0 0 0.170 0 0 0 0 0 0 0      
NHL results (irritation 6) 0.000 0.000 0.000 0.004 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.005 0.001 0.000 0.000 0.000 0.000 0.001 0.000 0.004 0.003 −0.002
AHL results (irritation 6) 0.000 0.000 0.000 0.004 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.005 0.001 0.000 0.001 0.001 0.000 0.001 0.000 0.004 0.003 −0.002
  
7 Activating regulatory risks 0 0 0 0 0 0 0 0 0 0 0 0 0 0.280 0.305 0.325 0.298 0.204 0.303 0.205      
NHL results (irritation 15) 0.686 0.000 0.395 0.853 0.147 0.569 0.459 0.591 0.682 0.854 0.580 0.527 0.297 0.668 0.552 0.750 0.803 0.529 0.799 0.626 0.901 0.930 −0.846
AHL results (irritation 19) 0.628 0.000 0.303 0.807 0.099 0.448 0.338 0.458 0.605 0.793 0.448 0.397 0.216 0.622 0.488 0.692 0.750 0.404 0.759 0.549 0.865 0.898 −0.810
  
8 Activating risk 1 0.311 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 25) 0.636 0.000 0.313 0.813 0.103 0.461 0.351 0.474 0.617 0.802 0.462 0.410 0.223 0.626 0.491 0.700 0.758 0.413 0.763 0.557 0.870 0.902 −0.816
AHL results (irritation 27) 0.623 0.000 0.302 0.805 0.098 0.449 0.341 0.461 0.605 0.792 0.449 0.399 0.213 0.614 0.476 0.688 0.748 0.400 0.752 0.541 0.865 0.898 −0.809
  
9 Activating risk 2 0 0.381 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 15) 0.685 0.005 0.389 0.853 0.143 0.575 0.469 0.598 0.680 0.854 0.586 0.534 0.293 0.666 0.546 0.749 0.803 0.535 0.800 0.621 0.901 0.930 −0.846
AHL results (irritation 18) 0.633 0.004 0.314 0.812 0.102 0.471 0.365 0.489 0.614 0.803 0.468 0.425 0.220 0.618 0.480 0.697 0.759 0.417 0.759 0.549 0.871 0.904 −0.815
  
10 Activating risk 3 0 0 0.181 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 27) 0.632 0.000 0.310 0.812 0.101 0.461 0.352 0.478 0.615 0.801 0.462 0.411 0.220 0.622 0.485 0.697 0.756 0.413 0.760 0.552 0.870 0.901 −0.815
AHL results (irritation 28) 0.622 0.000 0.301 0.804 0.098 0.449 0.341 0.461 0.604 0.792 0.448 0.399 0.213 0.613 0.475 0.687 0.747 0.400 0.752 0.541 0.864 0.897 −0.809
  
11 Activating risk 4 0 0 0 0.288 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 6) 0.004 0.000 0.001 0.015 0.002 0.000 0.000 0.000 0.002 0.003 0.000 0.000 0.001 0.010 0.003 0.006 0.006 0.000 0.008 0.004 0.016 0.014 −0.016
AHL results (irritation 6) 0.004 0.000 0.001 0.015 0.002 0.000 0.000 0.000 0.002 0.003 0.000 0.000 0.001 0.010 0.003 0.006 0.006 0.000 0.008 0.004 0.016 0.014 −0.016
  
12 Activating risk 5 0 0 0 0 0.190 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 6) 0.003 0.000 0.001 0.004 0.007 0.000 0.000 0.000 0.002 0.002 0.000 0.000 0.000 0.007 0.002 0.004 0.004 0.000 0.006 0.003 0.005 0.004 −0.009
AHL results (irritation 6) 0.003 0.000 0.001 0.004 0.007 0.000 0.000 0.000 0.002 0.002 0.000 0.000 0.000 0.007 0.002 0.004 0.004 0.000 0.006 0.003 0.005 0.004 −0.009
  
13 Activating risk 6 0 0 0 0 0 0.287 0 0 0 0 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 26) 0.630 0.000 0.307 0.810 0.100 0.459 0.350 0.472 0.613 0.799 0.456 0.409 0.218 0.621 0.483 0.695 0.754 0.411 0.759 0.550 0.867 0.900 −0.814
AHL results (irritation 27) 0.620 0.000 0.298 0.801 0.100 0.442 0.336 0.455 0.601 0.788 0.442 0.393 0.211 0.612 0.474 0.684 0.744 0394 0.750 0.538 0.862 0.895 −0.807
  
14 Activating risk 7 0 0 0 0 0 0 0.307 0 0 0 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 26) 0.645 0.000 0.323 0.823 0.106 0.486 0.375 0.502 0.632 0.815 0.489 0.438 0.232 0.634 0.498 0.710 0.769 0.439 0.771 0.568 0.877 0.909 −0.823
AHL results (irritation 24) 0.621 0.000 0.299 0.802 0.097 0.445 0.338 0.458 0.602 0.790 0.444 0.396 0.211 0.612 0.474 0.685 0.746 0.396 0.750 0.539 0.863 0.896 −0.807
  
15 Activating risk 8 0 0 0 0 0 0 0 0.208 0 0 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 30) 0.625 0.000 0.303 0.807 0.097 0.455 0.346 0.467 0.609 0.796 0.455 0.404 0.216 0.616 0.479 0.690 0.750 0.406 0.755 0.545 0.867 0.899 −0.811
AHL results (irritation 30) 0.620 0.000 0.299 0.802 0.097 0.445 0.337 0.456 0.602 0.789 0.444 0.395 0.212 0.612 0.474 0.685 0.745 0.396 0.750 0.539 0.863 0.896 −0.807
  
16 Activating risk 9 0 0 0 0 0 0 0 0 0.230 0 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 6) 0.003 0.000 0.001 0.020 0.001 0.005 0.002 0.003 0.016 0.018 0.003 0.002 0.000 0.008 0.002 0.005 0.008 0.003 0.007 0.003 0.029 0.031 −0.016
AHL results (irritation 6) 0.003 0.000 0.001 0.020 0.001 0.005 0.002 0.003 0.016 0.018 0.003 0.002 0.001 0.008 0.002 0.005 0.008 0.003 0.007 0.003 0.029 0.031 −0.016
  
17 Activating risk 10 0 0 0 0 0 0 0 0 0 0.280 0 0 0 0 0 0 0 0 0 0      
NHL results (irritation 6) 0.013 0.000 0.006 0.049 0.003 0.022 0.011 0.017 0.031 0.054 0.017 0.015 0.004 0.020 0.009 0.019 0.027 0.016 0.026 0.014 0.076 0.088 −0.047
AHL results (irritation 6) 0.012 0.000 0.005 0.048 0.003 0.022 0.011 0.017 0.031 0.053 0.016 0.014 0.004 0.020 0.008 0.019 0.027 0.016 0.025 0.013 0.075 0.087 −0.046
  
18 Activating risk 11 0 0 0 0 0 0 0 0 0 0 0.297 0 0 0 0 0 0 0 0 0      
NHL results (irritation 21) 0.648 0.000 0.328 0.826 0.106 0.495 0.385 0.513 0.637 0.820 0.450 0.448 0.236 0.636 0.501 0.714 0.772 0.449 0.774 0.572 0.880 0.911 −0.826
AHL results (irritation 24) 0.621 0.000 0.298 0.804 0.096 0.447 0.339 0.459 0.604 0.791 0.447 0.397 0.212 0.612 0.475 0.685 0.746 0.399 0.751 0.540 0.864 0.808 −0.826
  
19 Activating risk 12 0 0 0 0 0 0 0 0 0 0 0 0.231 0 0 0 0 0 0 0 0      
NHL results (irritation 6) 0.005 0.000 0.003 0.025 0.000 0.014 0.010 0.020 0.019 0.040 0.014 0.021 0.004 0.008 0.003 0.009 0.018 0.013 0.012 0.006 0.042 0.062 −0.025
AHL results (irritation 6) 0.005 0.000 0.003 0.024 0.000 0.014 0.010 0.020 0.019 0.040 0.015 0.021 0.004 0.008 0.003 0.008 0.018 0.013 0.012 0.006 0.041 0.062 −0.025
  
20 Activating risk 13 0 0 0 0 0 0 0 0 0 0 0 0 0.170 0 0 0 0 0 0 0      
NHL results (irritation 6) 0.000 0.000 0.000 0.004 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.005 0.001 0.000 0.001 0.001 0.000 0.001 0.000 0.004 0.003 −0.002
AHL results (irritation 6) 0.000 0.000 0.000 0.004 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.005 0.001 0.000 0.001 0.001 0.000 0.001 0.000 0.004 0.003 −0.002
  
21 Activating risk 14 0 0 0 0 0 0 0 0 0 0 0 0 0 0.280 0 0 0 0 0 0      
NHL results (irritation 6) 0.026 0.000 0.008 0.038 0.009 0.003 0.002 0.003 0.015 0.019 0.003 0.002 0.004 0.042 0.020 0.033 0.036 0.003 0.044 0.022 0.043 0.041 −0.052
AHL results (irritation 6) 0.026 0.000 0.008 0.038 0.009 0.003 0.002 0.003 0.015 0.019 0.003 0.002 0.004 0.042 0.020 0.033 0.036 0.003 0.045 0.022 0.042 0.041 −0.052
  
22 Activating risk 15 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.305 0 0 0 0 0      
NHL results (irritation 29) 0.628 0.000 0.306 0.808 0.100 0.454 0.345 0.466 0.610 0.796 0.454 0.404 0.217 0.619 0.482 0.692 0.752 0.405 0.756 0.548 0.867 0.900 −0.812
AHL results (irritation 29) 0.621 0.000 0.299 0.802 0.097 0.444 0.337 0.455 0.602 0.789 0.443 0.394 0.212 0.612 0.475 0.685 0.745 0.396 0.750 0.539 0.863 0.896 −0.807
  
23 Activating risk 16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.325 0 0 0 0      
NHL results (irritation 22) 0.650 0.000 0.329 0.824 0.111 0.482 0.371 0.497 0.633 0.815 0.485 0.432 0.236 0.638 0.507 0.714 0.770 0.435 0.773 0.575 0.878 0.909 −0.824
AHL results (irritation 24) 0.622 0.000 0.300 0.802 0.098 0.442 0.335 0.454 0.601 0.788 0.442 0.392 0.211 0.612 0.474 0.685 0.745 0.394 0.750 0.539 0.863 0.895 −0.807
  
24 Activating risk 17 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.298 0 0 0      
NHL results (irritation 31) 0.625 0.000 0.303 0.806 0.099 0.451 0.343 0.464 0.607 0.794 0.451 0.401 0.215 0.616 0.479 0.689 0.749 0.403 0.754 0.544 0.866 0.898 −0.811
AHL results (irritation 31) 0.621 0.000 0.299 0.803 0.097 0.445 0.337 0.457 0.602 0.790 0.445 0.395 0.212 0.612 0.475 0.685 0.745 0.397 0.750 0.539 0.863 0.896 −0.808
  
25 Activating risk 18 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.204 0 0      
NHL results (irritation 29) 0.624 0.000 0.302 0.806 0.098 0.451 0.342 0.463 0.607 0.794 0.451 0.401 0.214 0.616 0.478 0.689 0.749 0.403 0.754 0.543 0.865 0.898 −0.810
AHL results (irritation 30) 0.621 0.000 0.299 0.803 0.097 0.445 0.337 0.457 0.602 0.790 0.445 0.395 0.212 0.612 0.475 0.685 0.745 0.397 0.750 0.539 0.863 0.896 −0.808
  
26 Activating risk 19 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.303 0      
NHL results (irritation 24) 0.644 0.00 0.321 0.819 0.107 0.471 0.361 0.485 0.626 0.809 0.473 0.421 0.229 0.633 0.499 0.707 0.764 0.423 0.768 0.566 0.874 0.906 −0.821
AHL results (irritation 26) 0.621 0.00 0.300 0.804 0.098 0.448 0.339 0.459 0.603 0.791 0.447 0.397 0.213 0.614 0.476 0.686 0.746 0.399 0.751 0.540 0.864 0.897 −0.808
  
27 Activating risk 20 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.205      
NHL results (irritation 30) 0.624 0.000 0.301 0.804 0.099 0.447 0.339 0.459 0.605 0.792 0.447 0.397 0.214 0.615 0.478 0.688 0.748 0.399 0.753 0.543 0.865 0.897 −0.809
AHL results (irritation 27) 0.622 0.00 0.300 0.804 0.098 0.448 0.340 0.460 0.604 0.791 0.447 0.397 0.213 0.613 0.476 0.686 0.746 0.399 0.751 0.540 0.864 0.897 −0.808

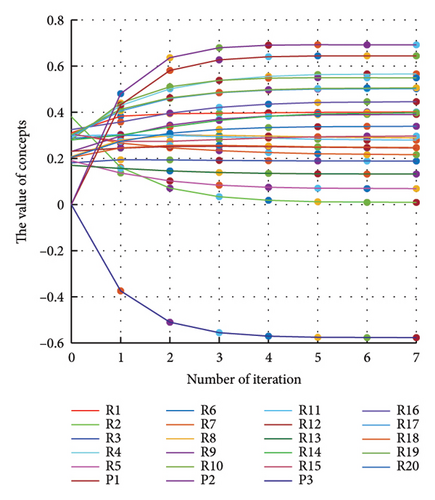
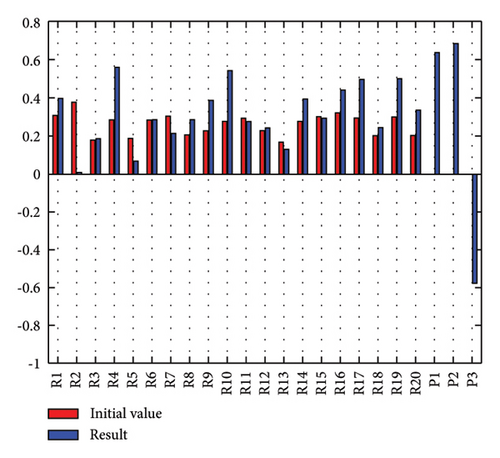
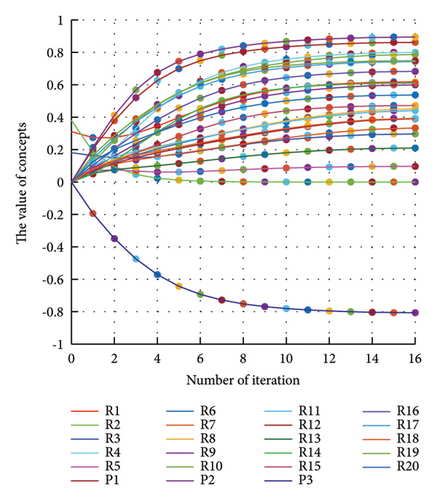
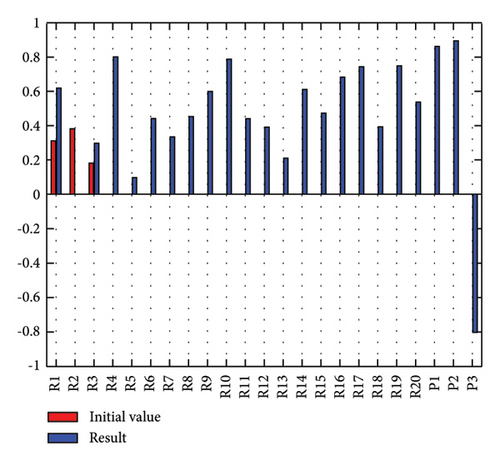
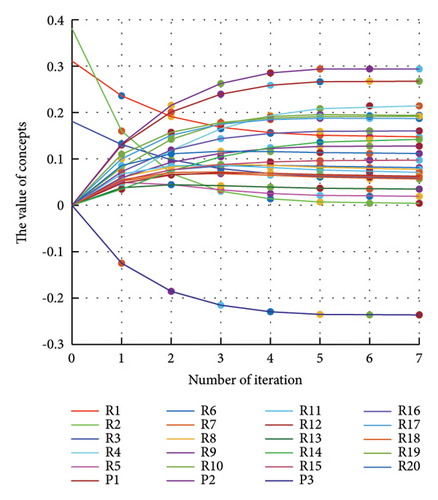
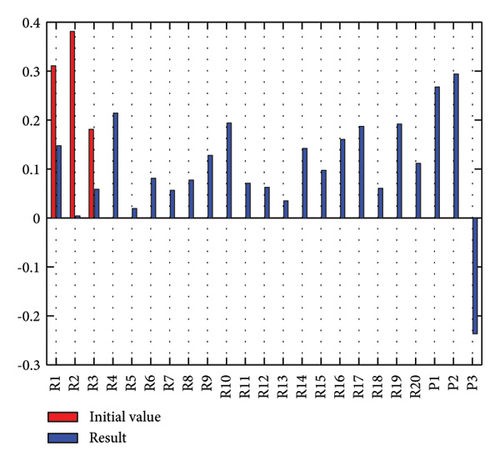
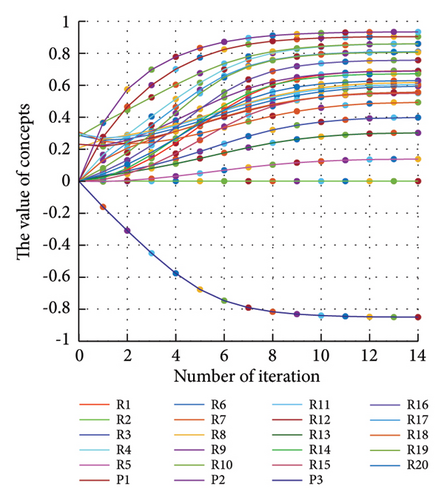
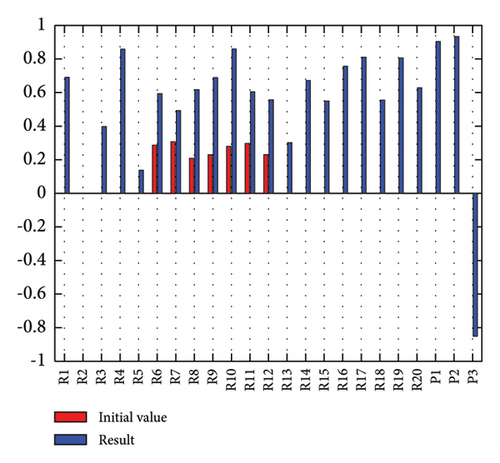
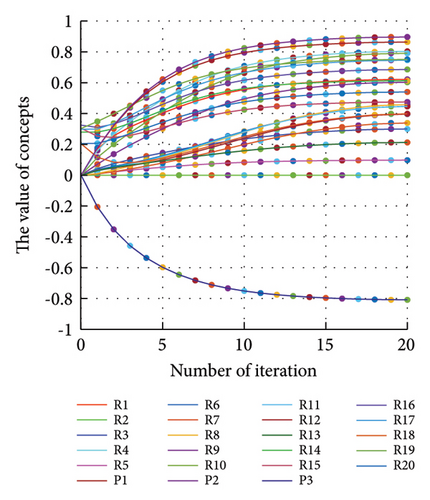
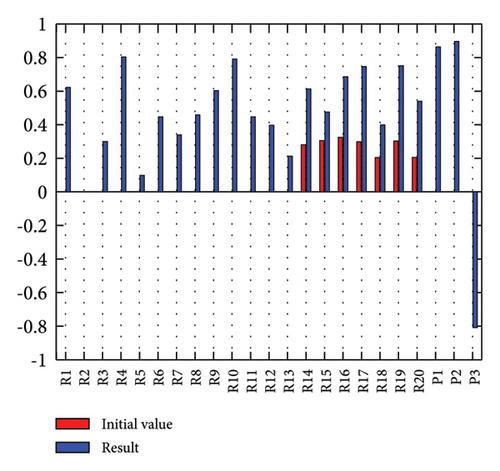
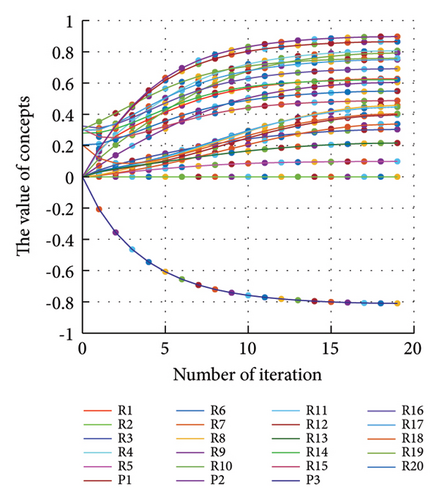
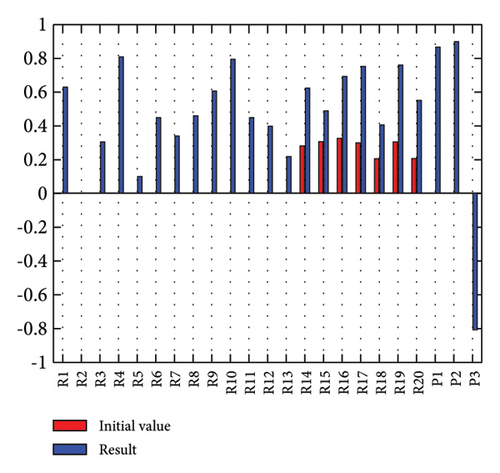
In addition to the numerical results presented in Table 4, the inference and the change of concepts during FCM iteration are presented for several scenarios in Figures 4–7 which are related to scenarios in which risks are activated as a group.

Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Scenario 1 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) initial and final vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Scenario 1 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) initial and final vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 4 (c)
Open in figure viewerPowerPoint
Scenario 1 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) initial and final vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 4 (d)
Open in figure viewerPowerPoint
Scenario 1 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) initial and final vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 4 (e)
Open in figure viewerPowerPoint
Scenario 1 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) initial and final vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 4 (f)
Open in figure viewerPowerPoint
Scenario 1 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) initial and final vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
Scenario 2 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
Scenario 2 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 5 (c)
Open in figure viewerPowerPoint
Scenario 2 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 5 (d)
Open in figure viewerPowerPoint
Scenario 2 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 5 (e)
Open in figure viewerPowerPoint
Scenario 2 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 5 (f)
Open in figure viewerPowerPoint
Scenario 2 results: (a) the initial and final state vector of concepts (without training), (b) values of concepts during the simulation process (without training), (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
Scenario 5 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
Scenario 5 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 6 (c)
Open in figure viewerPowerPoint
Scenario 5 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 6 (d)
Open in figure viewerPowerPoint
Scenario 5 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 6 (e)
Open in figure viewerPowerPoint
Scenario 5 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 6 (f)
Open in figure viewerPowerPoint
Scenario 5 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 7 (a)
Open in figure viewerPowerPoint
Scenario 7 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 7 (b)
Open in figure viewerPowerPoint
Scenario 7 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 7 (c)
Open in figure viewerPowerPoint
Scenario 7 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 7 (d)
Open in figure viewerPowerPoint
Scenario 7 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 7 (e)
Open in figure viewerPowerPoint
Scenario 7 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).
Details are in the caption following the image
Figure 7 (f)
Open in figure viewerPowerPoint
Scenario 7 results: (a) the initial and final state vector of concepts, (b) values of concepts during the simulation process, (c) the initial and final state vector of concepts (with NHL), (d) values of concepts during the simulation process (with NHL), (e) the initial and final state vector of concepts (with AHL), and (f) values of concepts during the simulation process (with AHL).

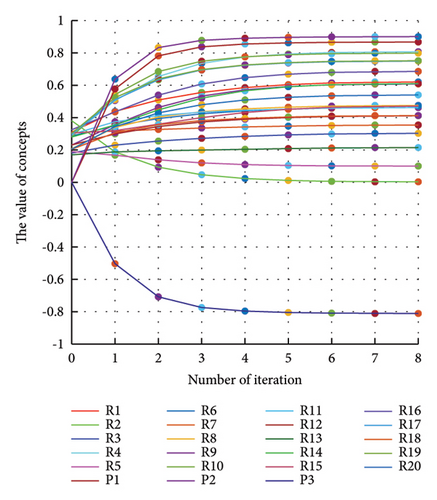
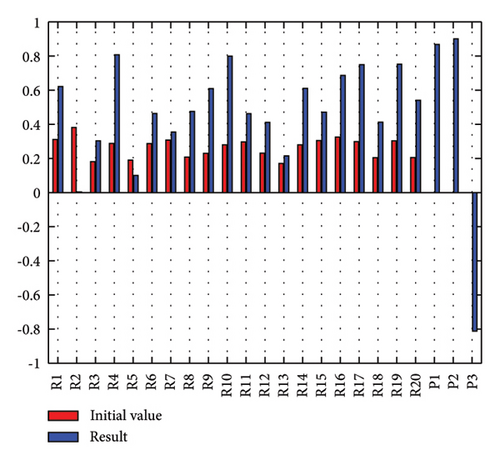
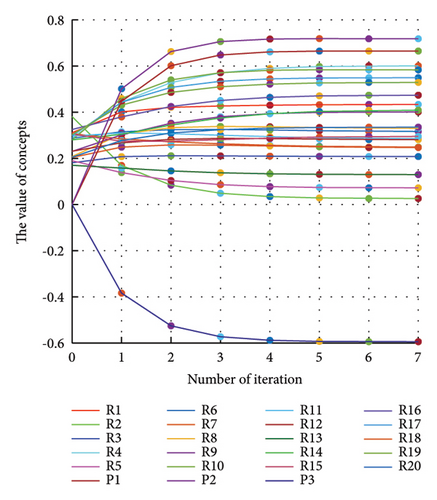
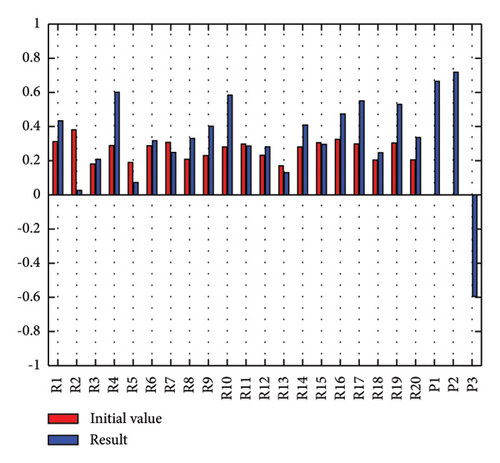
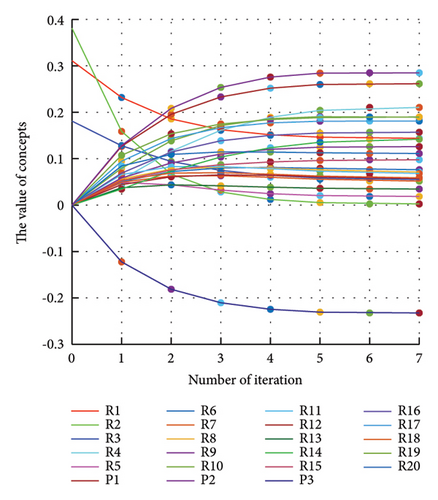
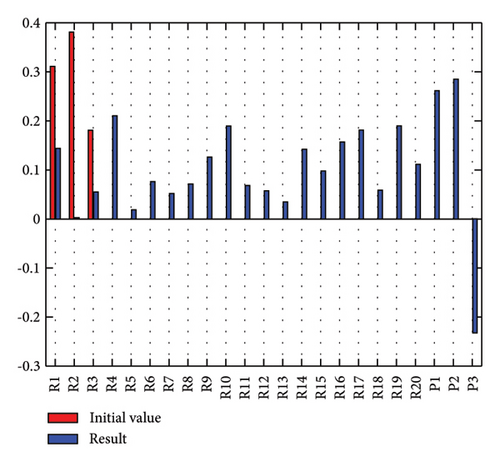
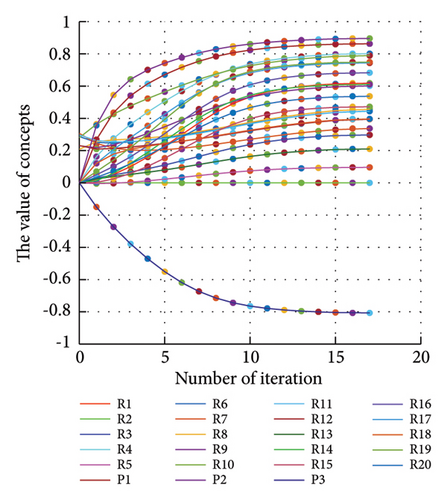
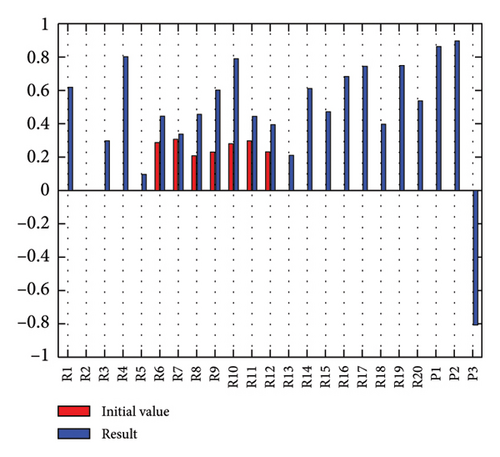
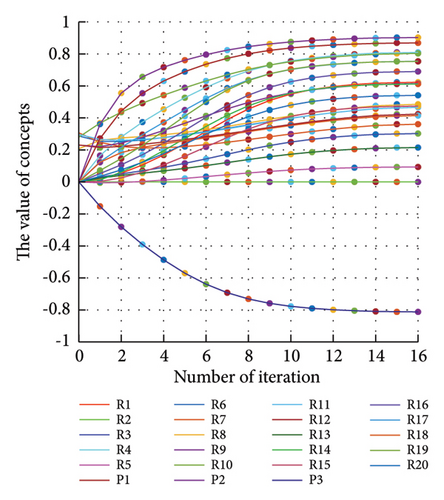
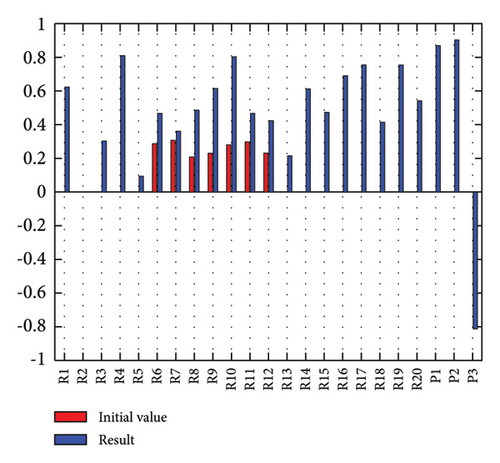
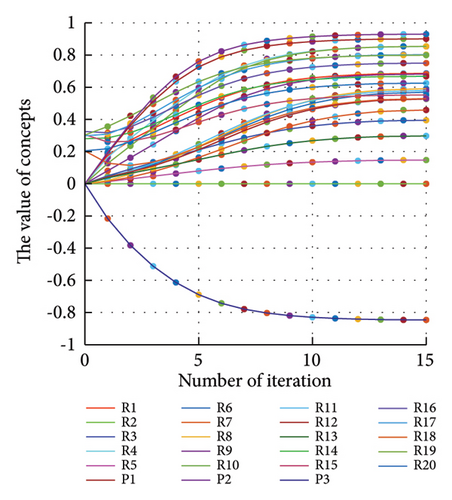
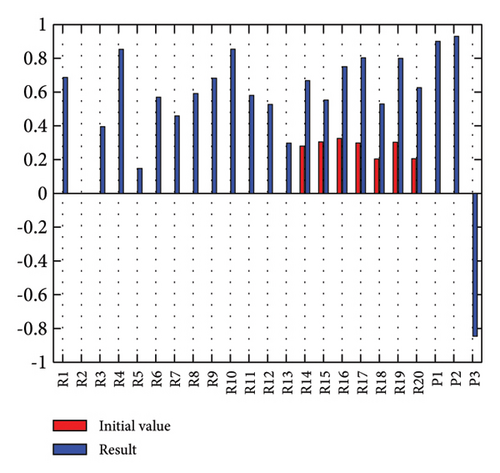
3.2.1. Scenario 1: Activation of All Risks in FCM

By activating all the risks of the model, the risk ranking differs from when the risks are considered statistically. Table 5 shows these differences.

Table 5. Difference between risk ranking concerning relationships between risks and without considering relationships.
Rank Considering the interdependency Without considering interdependency
1 Defect in the domestic supply of essential raw materials Sanction
2 Cash flow risk Lack of good governance for medicines
3 Inefficient pricing policies MOH conflicts of interest
4 Lobbying risks in the decision-making process Dual exchange rate
5 Lack of good governance for medicines Drug list limitation
6 MOH conflicts of interest Lobbying risks in the decision-making process
7 Long cash collection cycle Inefficient pricing policies
8 Pseudo-productivity (repacking) Currency fluctuation
9 Inflation rate Defect in the domestic supply of essential raw materials
10 Currency fluctuation Money transfer problem
11 Money transfer problem Cash flow risk
12 Change in legislation and policies Pseudo-productivity (repacking)
13 Banking regulation instability Interest rate
14 Interest rate Long cash collection cycle
15 Dual exchange rate Inflation rate
16 Drug list limitation Change in legislation and policies
17 Political instability Banking regulation instability
18 Demand fluctuations Defect of international vision
19 Defect of international vision Political instability
20 Sanction Demand fluctuations

Figure 4 illustrates the results of Scenario 1 and summarizes the FCM results trained by the NHL and AHL algorithms. By comparing Figures 4(a), 4(c), and 4(e), it can be observed that the trained FCM converges faster and this convergence is faster for the NHL than for the AHL.

3.2.2. Scenario 2: Activation of Macrorisks in FCM

In Scenario 2, supply and regulatory risks are more affected. In addition, costs have increased, time has increased, and quality has decreased. The model’s findings suggest that the SC of Iranian biopharmaceutical product makers, as part of the Iranian health system, is heavily influenced by Iran’s political situation, particularly at the time of the study. Figure 5 illustrates the outcomes of this scenario.

3.2.3. Scenario 5: Activation of Financial Risks in the FCM

Activation of financial risks leads to the activation of many risks in the model. Figure 6 illustrates that in this scenario, costs increase, time periods prolong, and quality decreases.

3.2.4. Scenario 7: Activation of Regulatory Risks in the FCM

The activation of regulatory risks leads to the activation of many model risks. According to Figure 7, the most affected risks are liquidity (0.854), poor supply of essential raw materials (0.853), conflicts of interest in the Ministry of Health (0.686), and long cash collection cycle (0.682). Similar to Scenario 2, in Scenario 7, costs have increased, the time has been prolonged, and quality has decreased (Figure 7).

4. Discussion

4.1. Impact of Risks on Cost, Time, and Quality

One of the most important outputs of the model is the calculation of the impact of risks on the three fundamental factors of the SC, namely, cost, time, and quality. This impact is presented in Table 6. If the influence of these three criteria is considered for risk importance and ranking, the priority of dealing with risks may shift. The ranking in Table 6 based on |P1| + |P2| + |P3| is from the highest value to the lowest value. The |⋅| symbol indicates the absolute value.

Table 6. Ranking of different risk activity scenarios in terms of influencing the three basic factors of the SC (cost, time, and quality).
Rank Description Time Cost Quality
1 Activating all risks 0.869 0.890 −0.923
2 Activating macrorisks 0.783 0.807 −0.886
3 Activating financial risks 0.774 0.799 −0.881
4 Activating sanction risks 0.769 0.795 −0.874
5 Activating regulatory risks 0.753 0.761 −0.871
6 Activating political instability risks 0.648 0.672 −0.838
7 Activating dual exchange rate risks 0.644 0.681 −0.833
8 Activating money transfer problem risks 0.652 0.686 −0.815
9 Activating currency fluctuation risks 0.663 0.693 −0.685
10 Activating lack of good governance for medicine risks 0.541 0.508 −0.803
11 Activating supply risks 0.518 0.518 −0.753
12 Activating defect in the domestic supply of essential raw material risks 0.518 0.518 −0.753
13 Activating long cash collection cycle risk 0.465 0.465 −0.699
14 Activating MOH conflicts of interest risks 0.710 0.000 −0.867
15 Activating inefficient pricing policy risk 0.384 0.368 −0.681
16 Activating inflation rate risks 0.000 0.416 −0.667
17 Activating demand risks 0.485 0.485 0.000
18 Activating demand fluctuation risks 0.485 0.485 0.000
19 Activating cash flow risks 0.465 0.465 0.000
20 Activating banking regulation instability risks 0.409 0.425 0.000
21 Activating organization and strategies’ risks 0.000 0.000 −0.799
22 Activating defect of international vision riskss 0.000 0.000 −0.799
23 Activating lobbying risks in the decision-making process risk 0.000 0.000 −0.716
24 Activating interest rate risks 0.000 0.573 0.000
25 Activating change in legislation and policies’ risks 0.515 0.000 0.000
26 Activating pseudo-productivity (repacking) risks 0.000 0.000 0.000
27 Activating drug list limitation risks 0.000 0.000 0.000

4.2. Performance Comparison Analysis

Fuzzy and FMEA represent distinct methods employed in risk assessment. In the context of FMEA, assessments delve into meticulous detail, categorizing potential failures within the system. Conversely, fuzzy methods adopt fuzzy approximation techniques to discern and classify failures [41]. Through the utilization of fuzzy rules, both systems and concerns are modeled, accounting for uncertainties and ambiguities inherent in the data. In the FMEA methodology, risks undergo evaluation and ranking based on criteria such as the probability of failure, severity of consequences, and detectability. Typically, this evaluation involves the assignment of scores, with subsequent interpretation based on the established criteria [26]. In contrast, fuzzy methods approach assessments through defuzzification and approximation, diverging from the scoring and interpretation framework utilized in FMEA. Fuzzy contrast techniques play a vital role in scrutinizing a set of values, utilizing fuzzy rules to adapt to imprecise and incomplete information. Both FMEA and the fuzzy method serve as tools for risk management. However, whereas FMEA places a stronger emphasis on quantitative- and quality-oriented evaluation, the fuzzy method has the capacity to integrate qualitative information and experiences [42]. Through the utilization of fuzzy elements and rules, the fuzzy method allows for a more elaborate modeling of risks, ambiguities, and interactions among various qualities [39]. This capability contributes to enhanced decision-making in the realm of risk management.

In contrast, opting for triangular membership functions in the fuzzy method (triangular FN (triFN)), as opposed to trapezoidal member functions (trapezoidal FN (traFN)) in FMEA, brings about a reduction in the volume of calculations. The triFN streamlines computations by minimizing complexity. Conversely, the adoption of traFN in the fuzzy method increases the number of adjustable parameters for uncertainty modeling, resulting in heightened complexity and an increased volume of calculations [43]. Both FMEA and the fuzzy method grapple with challenges inherent to fuzzy logic [44]. The implementation of the fuzzy method for risk modeling and evaluation necessitates intricate calculations, potentially leading to time-consuming and complex processes. Furthermore, dependence on expert opinions may present challenges, particularly in cases where there are divergent expert views on risk.

It is noteworthy that FCM and FMEA methods can complement each other, offering a comprehensive approach to risk management. The integration of these methods provides a robust framework for addressing various aspects of risk assessment and decision-making. The utilization of the FCM method-based FMEA, as discussed in this article, establishes a strong foundation for modeling uncertainties and ambiguities inherent in risks and processes. This approach not only integrates diverse and at times conflicting expert opinions but also stands out with its dynamic mode, allowing for agile adaptation to changes. The FCM method based on FMEA combines the strengths of both the fuzzy method and FMEA while avoiding the drawbacks associated with the conventional fuzzy method. A notable advantage of the FCM method based on FMEA lies in its ability to model intricate combinations of risks using fuzzy rules and integrating diverse criteria. This proves invaluable in addressing the multicriteria and complex nature of certain risks. Moreover, its adaptability to changes and developments over time makes it well-suited for dynamic and complex risk management scenarios. Being rooted in fuzzy logic theory, the FCM method exhibits flexibility in modeling [34, 36]. Fuzzy rules can be finely tuned to adjust weightings and relationships between factors based on varying conditions and inputs, facilitating seamless adaptation of the model to different system states. Another noteworthy strength of the FCM method based on FMEA is its versatility, being applicable to training both with and without a supervisor [38].

The implementation of sensitivity analysis provides a quantitative means of comparing different methods. To ensure the resilience of our model, a systematic approach is undertaken. Initial values of activated risks are increased by 20%, followed by running the model. Subsequently, these values are decreased by 20%, and the model is rerun. This meticulous process is replicated for the FMEA method, the fuzzy method with triFNs based on FMEA, and the fuzzy method with traFNs based on FMEA. The graphical representation of these results is presented in Figure 8.

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Performances of FMEA, fuzzy-based FMEA with triFN, fuzzy-based FMEA with traFN, and FCM-based FMEA in sensitivity analysis.

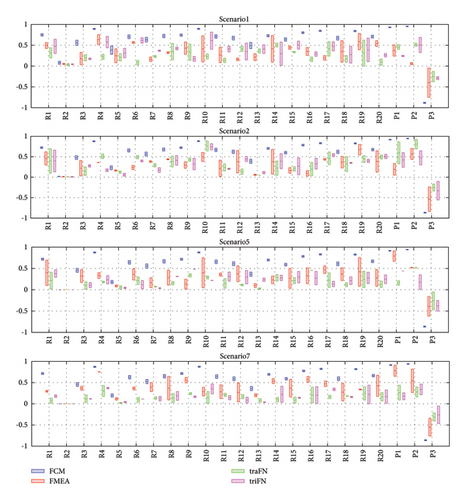
Upon meticulous examination of Figure 8, it is evident that the FCM method based on FMEA exhibits a more stable response, with less pronounced changes compared to other methods. This observation underscores the heightened robustness of the FCM method based on FMEA when subjected to variations in the initial values of activated risks.

Advantages of employing NHL and AHL algorithms in phase III for training the FCM are as follows:

Enhanced modeling capabilities: The NHL (nonlinear Hebbian learning) and AHL (active Hebbian learning) algorithms play a crucial role in augmenting the FCM’s capacity to capture intricate, nonlinear relationships among diverse risk factors and their implications. This enhancement is particularly significant within the biopharmaceutical supply chain domain, characterized by prevalent interdependencies and feedback loops.
  • (a)

    NHL empowers the FCM to depict nonlinear cause-effect associations, commonly encountered in practical supply chain dynamics, resulting in more precise system representations and enhanced predictive abilities

  • (b)

    AHL facilitates the FCM to dynamically adjust its internal weights and structure based on fresh data and feedback, thereby rendering the model more adaptable and responsive to alterations in the supply chain milieu

Enhanced convergence speed and training efficiency: Studies have demonstrated that the NHL and AHL algorithms converge at a faster rate compared to conventional FCM training methodologies, such as the standard Hebbian learning approach. This accelerated convergence facilitates more efficient training of the FCM model, enabling rapid updates and iterations to enhance the precision of risk analysis.

Enhanced scenario analysis and sensitivity testing: The flexibility and adaptability provided by NHL and AHL algorithms can enable more robust scenario analysis and sensitivity testing of the FCM. This is crucial for evaluating the impacts of different risk factors and assessing the resilience of the supply chain under various conditions.

Potential limitations and challenges in implementing the FCM-based approach are cited as follows:

Data availability and quality: The FCM-based methodology heavily depends on thorough and precise data concerning supply chain risks, their causal interconnections, and the related parameters. Acquiring such data may pose challenges within the Iranian biopharmaceutical sector, where data collection and sharing practices might not be as advanced. Potential mitigation: Establish close collaborations with industry stakeholders to enhance data collection and sharing mechanisms. Leverage expert knowledge and employ methodologies such as fuzzy set theory to handle incomplete or uncertain data effectively.

Model complexity and development effort: Building and validating a sophisticated FCM that precisely mirrors the biopharmaceutical supply chain can be a challenging and time-intensive endeavor. The incorporation of advanced algorithms such as NHL and AHL could potentially elevate the complexity of the modeling process. Potential mitigation: We implement semiautomated or knowledge-driven strategies to streamline the FCM development process. In addition, leverage modular design principles and existing domain expertise to enhance the model’s efficiency.

Organizational adoption and change management: Introducing an innovative, data-centric risk analysis approach such as the FCM-based method might encounter opposition from conventional risk management practices prevalent in Iranian pharmaceutical firms. Securing approval and support from stakeholders may necessitate substantial change management endeavors. Potential mitigation: We engage industry leaders and key decision-makers at an early stage and offer thorough training and documentation to showcase the advantages of adopting an FCM-based approach.

5. Conclusion

This paper presents a dynamic risk assessment of the Iranian biopharmaceutical supply chain (SC), which was not taken into account in earlier studies on Iranian pharmaceutical SC. The results show that the SC of biopharmaceutical and chemical drugs was not significantly different, but the impact and importance of risks in the SC can differ. During the study period, the political situation in Iran had an impact on biopharmaceutical companies and the drug SC as an essential aspect of the healthcare system. This study examined the risks that have the most significant impact on the SC of Iranian biopharmaceutical manufacturers. Analysis and modeling of SC risks of companies producing biopharmaceuticals were also presented. Given the limitations of existing risk analysis tools to accurately predict the behavior of risks and analyze them dynamically, a fuzzy cognitive map (FCM) was used. Various situations were created to investigate and acquire FCM inference; hence, the FCM was trained using the nonlinear Hebbian learning and active Hebbian learning algorithms. Finally, the results of inference, FCM simulation, and analysis were presented.

Employing FCMs, this study offers crucial insights for anticipating failure effects and causes in intricate systems. Accounting for interdependence among risk factors and consequences enhances the accuracy of risk analysis, aiding decision-makers. This approach provides robust support for managers to identify critical failures and implement effective mitigation strategies, thereby enhancing overall risk management. Furthermore, the integration of cutting-edge technologies such as edge cloud computing and deep learning underscores the synergistic capacity of amalgamating computational prowess with domain proficiency to amplify risk evaluation capabilities [45–47]. Through harnessing the distributed computational potency and swift data processing attributes of edge cloud computing, in conjunction with the feature extraction and pattern recognition proficiencies of deep learning algorithms, risk appraisal models can attain heightened sophistication and subtlety, culminating in more precise and dependable outcomes. However, the FCM method based on FMEA, while potent, is not without its limitations. Notably, it involves a higher volume of calculations compared to FMEA, posing potential challenges related to computational efficiency and time constraints. A critical consideration lies in the reliance on expert opinions to shape the structure of FCM, encompassing concepts, graph nodes, and their interrelationships. Any errors during the initial stages of risk identification, expert interviews, or risk screening may compromise the accuracy and reliability of subsequent results generated by the FCM method.

To enhance the practical applicability of the FCM method based on FMEA, it is crucial to recognize and address these limitations. Implementing rigorous validation processes, continually refining input data, and maintaining an iterative dialogue with domain experts are proactive measures that can mitigate these challenges and strengthen the overall robustness of the methodology.

Ethical Approval

The study was confirmed by the Ethics Committee of Tehran University of Medical Sciences (TUMS): IR.TUMS. VCR.REC.1397.675.

Disclosure

This study was part of Hadi Abbasian PhD thesis registered in Tehran University of Medical Sciences [48].

Conflicts of Interest

The authors declare that there are no conflicts of interest.

Data Availability

Data used to support the findings of this study are available in supplementary information files. More data will be available on request.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.