International Journal of Differential Equations

Volume 2024, Issue 1 4275850

Research Article

Open Access

Matrix and Inverse Matrix Projective Synchronization of Fractional-Order Time-Delay Chaotic Systems with Uncertainty

Vijay K. Shukla

orcid.org/0000-0002-5993-1761

Department of Mathematics , D.S.B. Campus , Kumaun University , Nainital , 263001 , Uttarakhand, India , kunainital.ac.in

Department of Mathematics , Shiv Harsh Kisan P.G. College , Basti , 272001 , India

Search for more papers by this author

Mahesh C. Joshi,

Mahesh C. Joshi

Department of Mathematics , D.S.B. Campus , Kumaun University , Nainital , 263001 , Uttarakhand, India , kunainital.ac.in

Search for more papers by this author

Prashant K. Mishra,

Prashant K. Mishra

orcid.org/0000-0002-5313-7225

Department of Mathematics , P. C. Vigyan Mahavidyalaya , Jai Prakash University , Chapra , 841301 , India , jpv.bih.nic.in

Search for more papers by this author

İbrahim Avcı,

İbrahim Avcı

orcid.org/0000-0003-0986-2195

Department of Computer Engineering , Faculty of Engineering , Final International University , Kyrenia , Northern Cyprus via Mersin 10, Türkiye , final.edu.tr

Search for more papers by this author

Sina Etemad,

Corresponding Author

Sina Etemad

[email protected]

orcid.org/0000-0002-1574-1800

Department of Mathematics , Azarbaijan Shahid Madani University , Tabriz , Iran , azaruniv.ac.ir

Mathematics in Applied Sciences and Engineering Research Group , Scientific Research Center , Al-Ayen University , Nasiriyah , 64001 , Iraq , alayen.edu.iq

Search for more papers by this author

Vijay K. Shukla,

Vijay K. Shukla

orcid.org/0000-0002-5993-1761

Department of Mathematics , D.S.B. Campus , Kumaun University , Nainital , 263001 , Uttarakhand, India , kunainital.ac.in

Department of Mathematics , Shiv Harsh Kisan P.G. College , Basti , 272001 , India

Search for more papers by this author

Mahesh C. Joshi,

Mahesh C. Joshi

Department of Mathematics , D.S.B. Campus , Kumaun University , Nainital , 263001 , Uttarakhand, India , kunainital.ac.in

Search for more papers by this author

Prashant K. Mishra,

Prashant K. Mishra

orcid.org/0000-0002-5313-7225

Department of Mathematics , P. C. Vigyan Mahavidyalaya , Jai Prakash University , Chapra , 841301 , India , jpv.bih.nic.in

Search for more papers by this author

İbrahim Avcı,

İbrahim Avcı

orcid.org/0000-0003-0986-2195

Department of Computer Engineering , Faculty of Engineering , Final International University , Kyrenia , Northern Cyprus via Mersin 10, Türkiye , final.edu.tr

Search for more papers by this author

Sina Etemad,

Corresponding Author

Sina Etemad

[email protected]

orcid.org/0000-0002-1574-1800

Department of Mathematics , Azarbaijan Shahid Madani University , Tabriz , Iran , azaruniv.ac.ir

Mathematics in Applied Sciences and Engineering Research Group , Scientific Research Center , Al-Ayen University , Nasiriyah , 64001 , Iraq , alayen.edu.iq

Search for more papers by this author

First published: 20 August 2024

https://doi.org/10.1155/2024/4275850

Academic Editor: Peiguang Wang

Share a link

Email
Wechat
Bluesky

Abstract

In the present article, the matrix projective synchronization (MPS) and the inverse matrix projective synchronization (IMPS) have been analyzed with fractional-order chaotic systems with uncertain terms. First, we theoretically discussed both types of synchronizations. To achieve both types of synchronization, several required conditions are derived. We also drew portraits of Lyapunov’s exponents and bifurcation for more analysis. Furthermore, time-delay terms are also considered, giving an elegant application in real-world problems. Finally, numerical results agreed with the theoretical hypothesis. The numerical outcomes are shown through the graphical presentation.

1. Introduction

In 1963, Lorenz [1] generated a three-dimensional system that exhibits infinite complexity and nonrepeating trajectories with certain bounds. Furthermore, this system is known as the Lorenz system. In addition, Chen and Ueta [2] produced a different chaotic system currently referred to as Chen’s chaotic system, which is the twin of the previously mentioned Lorenz system. Lu and Chen [3] developed another chaotic system that was not diffeomorphic to Lorenz and Chen systems. Chaos is a kind of unpredictable phenomenon and sensitive to the initial value and makes its long-term behavior. In the last few decades, numerous researchers have been attracted to explore chaos and synchronization. Synchronization occurs when two or more nonlinear systems interact with each other, transforming the dynamical variables of the two chaotic systems. It started a new era in the field of science and has many applications in the field of the human brain [4] and secure communication [5], etc. Furthermore, from the past to the present, numerous efficient methods have been explored for various kinds of synchronization [6, 7].

Nowadays, fractional calculus has more application in numerous branches of science and engineering [8–11]. Compared to typical integer-order systems, fractional-order chaotic systems are more precise in revealing the dynamic behavior of the original systems. In fractional calculus, the usual differentiation and integration are generalized to any noninteger order [12–14]. Chua’s chaotic system was examined by Hartley et al. [15] with fractional calculus and showed that the systems of order less than three depict chaotic behavior. In addition, Li et al. [16] and Chen et al. [17] addressed the fractional-order chaotic systems and investigated the asymptotic stability by sliding mode control.

He and Pei [18, 19] showed the application of fractional-order neural networks to improve the computational ability of neurons for information transmission in the field of security communication. They further proved that the discontinuous system easily produces complex nonlinearity. He et al. [20] also using the sliding mode technique to enhance the high security and extended the projection scaling matrix in the study of global matrix projection synchronization for the delayed fractional-order neural networks.

An integer and noninteger order 4D chaotic system was studied by Rahman et al. [21]. A fractional operator is used to study the system and to prove the existence of solution. Jiang et al. [22] examined the complex dynamic behavior of chaotic systems and discovered that the system can display chaos and Neimark–Sacker bifurcation behaviors when a cross certain critical values. Using fractal fractional operators, Han et al. [23] also investigated the chaotic systems. Chen et al. [24] analyzed a memristive cellular neural network and achieved synchronization by the sliding mode control method. Zhu et al. [25] exhibited a classifier design technique and showed that extreme learning machines are more useful for rapid learning and good capabilities.

Due to the limited speed of transmission, time delay is a common occurrence in signal transition. The presence of delay terms can exhibit various complex phenomena such as hyperchaos, bifurcation, and multistability. For practical applications, it is necessary to introduce delays into chaotic systems. Moreover, several researchers have introduced fractional calculus in time-delay chaotic systems [26–28]. Mohammadzadeh et al. [29] proposed the synchronization of fractional delay chaotic systems via robust predictive control. In the study of lag projective synchronization, Zhang et al. [30] also considered fractional delayed chaotic systems and demonstrated that the slave system can synchronize up to a scaling factor.

Since uncertainty disrupts synchronization, it takes a great deal of work to study synchronization between chaotic systems with uncertainty. In matrix and inverse matrix projective synchronization (IMPS), an arbitrary matrix plays a fundamental role in controlling the response system. Moreover, when uncertainty is taken into account for chaotic systems, matrix projective synchronization (MPS) becomes more challenging in comparison to other synchronization techniques. Several results might be obtained in the literature to analyze the behavior of MPS. MPS for chaotic systems with uncertainty and disturbances was discussed by Shukla et al. [31]. He and Chen [32] discovered the matrix synchronization, stability analysis, chaotic behavior, and chaos control of fractional Rabinovich system. Khan et al. [33] also focused their research on the MPS of chaotic system with uncertainties and external disturbances.

Further, the IMPS has been examined by Khan et al. [34] to apply in secure communication. Ouannas et al. [35] discussed IMPS for fractional-order chaotic systems and used the Lyapunov approach to study the problem. A rigorous study of generalized MPS between different networks was also investigated by Wu et al. [36]. Later, Aadhithiyan et al. [37] used the Laplace transform to study the generalized modified projective function synchronization. Furthermore, the similar synchronization between complex chaotic systems with uncertainty was studied by Sha et al. [38]. However, most of the research on projective synchronization has been done with scaling factors that are either diagonal matrices or fixed constants [39, 40]. Matrix and inverse matrix projective synchronization have a wide range of applications in several fields, including neural networks [41] and secure communication [42]. The following statement summarizes the key contribution of this present work:

(1)
This manuscript is concerned with fractional-order delayed chaotic and hyperchaotic systems with uncertainty and an effort is made to determine the existence of chaos in the mentioned systems.
(2)
Different gain matrices have been utilized for MPS and IMPS, respectively. MPS and IMPS of chaotic systems also have been attained and demonstrated graphically.
(3)
The implications of uncertainty have been shown through graphical presentations.

The delayed fractional-order nonlinear dynamical model with uncertainty is still not much more explored. So, the authors concentrate on presenting the generic method for synchronizing the fractional-order delay chaotic systems with uncertainty. To the best of the author’s knowledge, this work has not been done before. This article is structured as follows. In Section 2, basic concepts of fractional delay system and related theorems have been recalled. In Section 3, the MPS analysis between chaotic and hyperchaotic systems has been conducted in subsections 3.1 and 3.2, respectively. Section 4 deals with IMPS of the chaotic and hyperchaotic systems in subsections 4.1 and 4.2, respectively. Numerical results and discussion have been presented in Section 5. A brief conclusion of the article is given in Section 6.

2. System Description

Here, we first present a definition as a reminder and then describe the considered chaotic system.

Definition 1 (see [43].)The Caputo’s fractional derivative is expressed as

()

where 0 < γ ∈ R , m ∈ Ν , Γ(⋅) represents the Gamma function.

Lemma 2 (see [44].)Let x(t) ∈ R is a continuous and derivable for t ≥ 0, then

()

Lemma 3 (see [45].)If (d^γx(t)/dt^γ) = η x(t) and 0 < γ < 1, η ≠ 1, then for η < 0, the system is asymptotically stable.

Theorem 4 (see [46].)The system (d^γx(t)/dt^γ) = x(t) is locally asymptotically stable if all the eigenvalues of the Jacobian calculated at its equilibrium point satisfy |arg(ω)| > πγ/2.

Now, consider two fractional-order delay chaotic systems with uncertainties as

()

where

are state vectors; A and B are the m × m matrices with uncertainties ΔA and ΔB, respectively, and satisfy |ΔA| ≤ δ₁ and |ΔB| ≤ δ₂ where δ₁, δ₂ > 0, C and F represent delay terms and f, g are nonlinear parts of the systems, τ represents time delay, and η(t), ξ(t) denote the trajectories of the solutions in the past. Furthermore, U stands for the controller function.

Definition 5 (see [47].)Two systems (3) and (4) are said to have achieved the matrix projective synchronization whenever there exist a control function U(η, ξ) ∈ R^m and lim_t⟶∞‖y − κx‖ = 0, where κ is called the projective matrix.

Theorem 6. The master system (3) and slave system (4) will achieve the MPS if the controller U ∈ R^m fulfills

()

provided that (B + α) is a negative definite matrix.

Proof. In case of MPS, the derivative of error system yields

()

The Lyapunov function is defined as

()

The derivative of V along with the trajectories (3) and (4) are obtained by using Lemma 3. It can be written as

()

By choosing the value of U such that

()

when the value of the matrix (B + α) is negative definite, (d^γV/dt^γ) will be negative definite. In that case, Lemma 3 corroborates that the error system will be stable.

Definition 7 (see [47].)The systems (3) and (4) are said to achieve the IMPS if there exist a controller U ∈ R^m such that

()

where κ and e are known as the projective matrix and error value, respectively.

Theorem 8. The systems (3) and (4) will achieve the IMPS if there is a control function U ∈ R^m such that

()

Provided that (A + α) is negative definite.

Proof. For IMPS, the error system is written as

()

Now, the Lyapunov function can be expressed as

()

and its derivative along with the trajectories (3) and (4) are obtained as

()

By choosing the value of U such that

()

when (A + α) is negative definite, then (d^γV/dt^γ) is negative definite and the mentioned error system will be stable.

3. Study of Matrix Projective Synchronization

3.1. MPS between Fractional Time-Delay Chaotic Systems with Uncertainties

In this section, we consider a three-dimensional chaotic system [48] as the master system. The system with uncertainty can be expressed as

()

The system (16) represents a chaotic behavior for values γ = 0.98, τ = 0.01 at I.C. (0, 0.6, 0.6). Here,

is known as the uncertain parameter. The phase portrait of this system is given in Figure 1. With the control function, the slave system is expressed as

()

where

represents the control function and

stands for the uncertain parameter of (17). Now, the projective matrix κ is taken as

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Phase portraits of system (16) in different planes for γ = 0.98 and τ = 0.01.

Also, the coefficient matrix of the linear part of (17) is determined as

()

Furthermore, the gain matrix is chosen as follows:

()

To get the control function, Theorem 8 provides the basic platform. Putting the value of different parameters from (18), (19), and (20) in (5) of Theorem 8 and after some basic calculations, we get the controller as

()

The value of parameters and the controller being substituted, we get the error system as

()

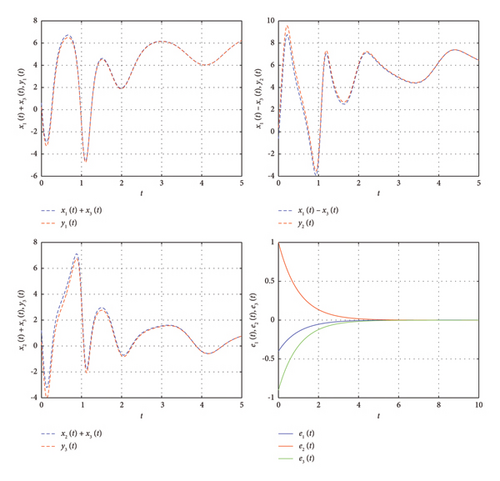
From Theorem 8, it is clear that MPS has been achieved since all the eigenvalues of the error system are negative. The phase portrait for the trajectories of the error system is depicted through Figure 2. Note that the convergence of trajectories towards zero reveals the MPS being achieved.

3.2. MPS between Fractional-Order Time-Delay Hyperchaotic Systems with Uncertainties

To show the MPS for hyperchaotic systems, we consider a 4D system [49] with the fractional order and uncertain term as the master system and it is written as

()

where the uncertain parameter is represented by

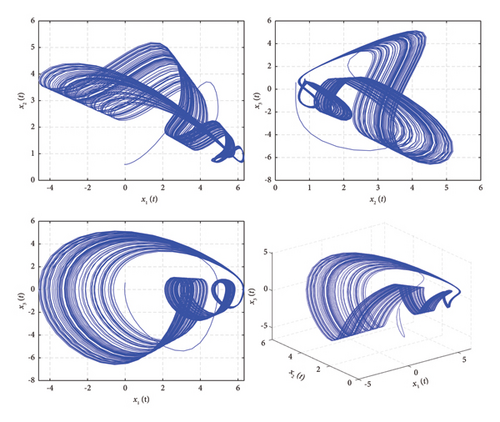
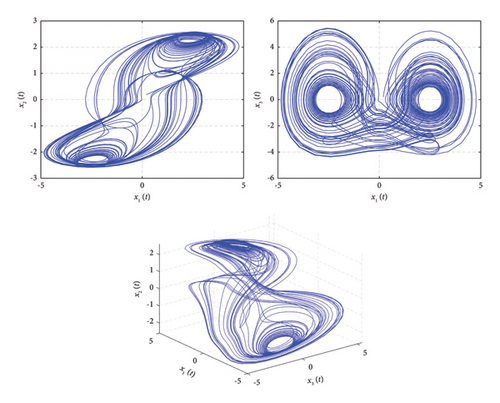
This system shows the chaotic characteristic for values a = 0.5, b = 0.5, c = 0.014 and γ = 0.98, τ = 0.01 at I.C. (0.01, 0.001, 0.001, 0.1). The phase portrait of (23) is illustrated in Figure 3.

With the control function, the slave system is expressed as

()

For system (24), the coefficient matrix for uncertainty is expressed as

()

Furthermore,

is the control function. To get the MPS, the projective matrix κ is considered as

()

Furthermore, the coefficient matrix of linear part of (24) is expressed as

()

Next, the gain matrix is considered as

()

Putting the value of κ from (26) in (5), the controller is obtained as

()

Substituting the value of controller, we get the error system

()

Since all eigenvalues are negative, we conclude that the MPS has been obtained, and the trajectories of error system also converge to zero (see Figure 4).

4. Study of Inverse Matrix Projective Synchronization

4.1. IMPS between Identical Chaotic Systems with Uncertainty

In this section, we focus on the system [50] with uncertainty as a 3D master system. This system was proposed by Sambas et al. [50] and for fractional order with delay and uncertain terms, it can be written as

()

This system represents a chaotic behavior for values γ = 0.98 and τ = 0.01 at I.C. (0.2, 0.2, 0.2).

In the next step, the slave system is introduced as

()

To determine the IMPS, we consider a matrix and its inverse matrix expressed as

()

The error is depended on the projective matrix κ and is defined as

()

Comparing equation (31) with equation (3), we obtained

()

According to the matrix A, the gain matrix is supposed as

()

Putting the values of κ, κ⁻¹, A, B, α in (11), one has

()

In IMPS, the error system is found as

()

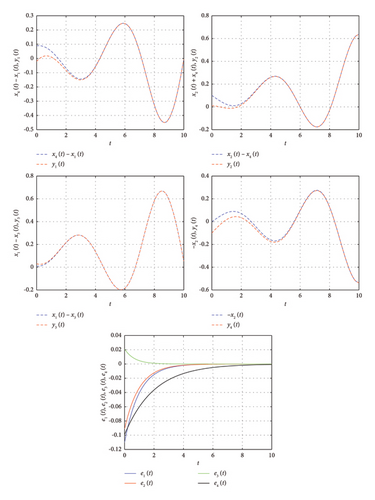
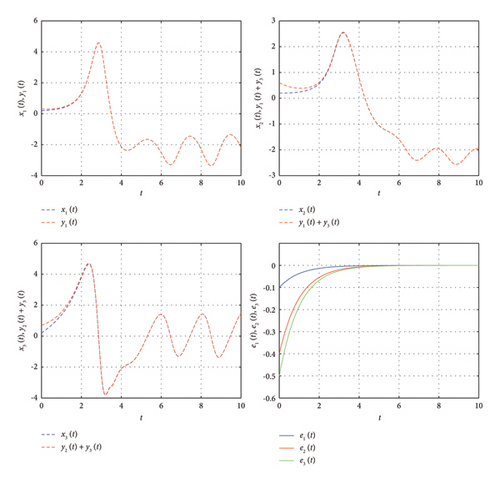
The eigenvalues of the error system are −1 , −1 , −1. It indicates that the IMPS has been achieved according to [46] because all the eigenvalues are negative. The graphical presentation of state variables of the error system is illustrated through Figure 5, which shows that the trajectories of the error system are convergent to zero, i.e., IMPS has been achieved.

4.2. IMPS between Hyperchaotic Systems with Uncertainties

In this subsection, we choose the hyperchaotic system [51] with uncertainties as

()

This system gives a chaotic behavior under the parametric values a = 20, b = 1, c = 10.6, d = 2.8, h = 0.45, k = 3.7, and τ₁ = 0.01 at I.C. (0.09, 0.4, 0.9, 0.1).

Also, the slave system is formulated as

()

Furthermore, the projective matrix along with its inverse are supposed as

()

We find the error system as

()

Comparing (16) with (3), we get

()

Furthermore, we choose the gain matrix as

()

Putting the values of κ , κ⁻¹, A, B, α in (11), we get the controller as

()

Finally, the error system is expressed as

()

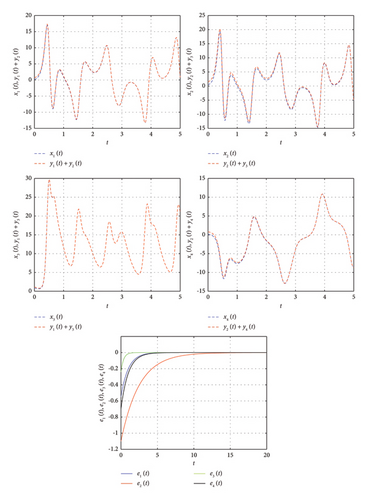
The eigenvalues of the error system are −1, − 0.4, −2.8, and − 1, which indicates that the IMPS has been achieved. The error trajectories are demonstrated in Figure 6, and the convergence of the trajectories to zero guarantees the IMPS.

5. Numerical Results and Discussion

In the present section, numerical outcomes for fractional delayed chaotic and hyperchaotic systems will be discussed. First, the initial condition 0.6, 0.6, 0.6) is chosen for MPS of the chaotic system (16) with uncertainties. The trajectories of the mentioned chaotic system (16) are illustrated through Figure 1. The MPS has been achieved between delayed fractional identical chaotic systems. The error trajectories finally converge to zero which reflect that the MPS has been done (Figure 2). Subsection 3.2 of the article deals with the MPS of delayed fractional hyperchaotic system with the initial condition (0.01, 0.001, 0.001, 0.1). The three-dimensional phase portrait of state variables of the hyperchaotic system (23) is shown through Figure 3. The error dynamics of the hyperchaotic system are portrayed in Figure 4, which reflects that the synchronization completely takes place.

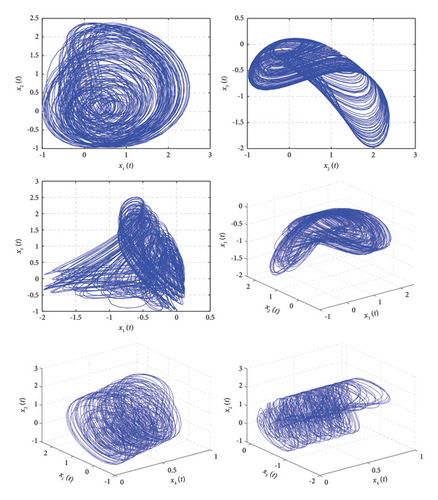
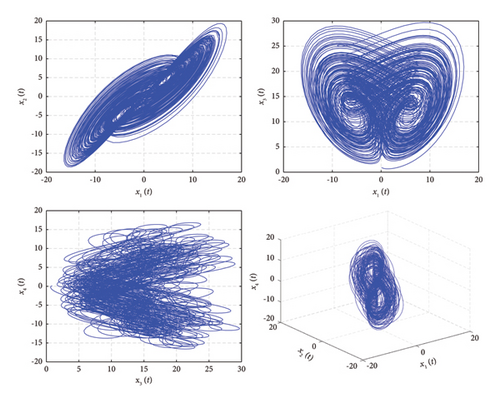
Second, IMPS has been discussed in subsections 4.1 and 4.2 for the chaotic and hyperchaotic systems, respectively. The initial condition for the system (31) was considered as (0.2, 0.2, 0.2) to achieve IMPS for identical delayed fractional chaotic systems with uncertain terms. Different delays have been considered to demonstrate the IMPS between systems (31) and (32). The phase portrait of the system (31) is shown through Figure 7 and the trajectories of the error system are observed in Figure 5. Furthermore, the parameters of the hyperchaotic system are taken as a = 20, b = 1, c = 10.6, d = 2.8, h = 0.45, and k = 3.7, with initial condition (0.09, 0.4, 0.9, 0.1) for system (39). The phase portrait of the hyperchaotic system (39) is shown through Figure 8. The time delay for hyperchaotic systems is taken as τ = 0.01. The IMPS has been achieved successfully between hyperchaotic systems (39) and (40), which finally converge to zero as depicted through Figure 6.

A chaotic system requires that at least one of the Lyapunov exponents be positive. Similarly, if a system has more than one positive Lyapunov’s exponent then this system is called a hyperchaotic system [52]. The system (16) has the Lyapunov’s exponents as λ₁ = 0.0363, λ₂ = −2.8327, and λ₃ = −2.8644. System (16) is a chaotic system. Similarly, system (23) has the value of Lyapunov’s exponents λ₁ = 0.19575, λ₂ = −0.0760, and λ₃ = −1.1197. Hence, it is also chaotic. In addition, systems (31) and (39) have the Lyapunov’s exponents as λ₁ = 0.6239, λ₂ = 0.2897, λ₃ = 0.1834, and λ₄ = 0.0269 and λ₁ = 0.8788, λ₂ = 0.0262, λ₃ = −0.2704, and λ₄ = −13.2574, respectively. Hence, both systems are hyperchaotic systems. The phase portraits of Lyapunov’s exponents of system (16), (23), (31), and (39) are shown in Figures 9, 10, 11, and 12, respectively. Numerical simulation of bifurcation diagrams is an efficient way to understand the intricate behavior of dynamical systems under parameter variation. As illustrated in Figure 9, the researchers analyze the response to changes in the parameters.

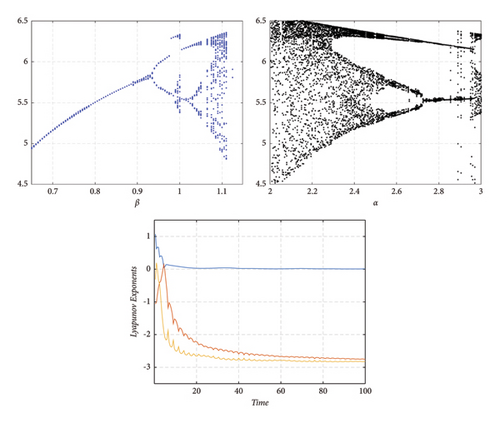
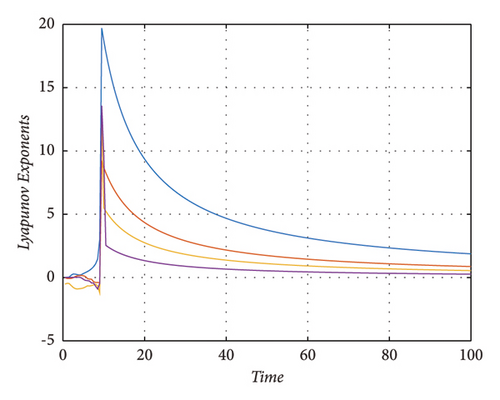
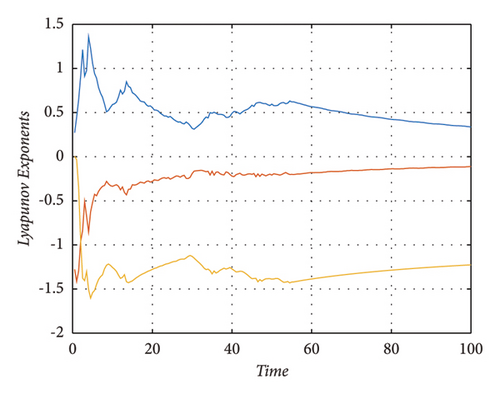
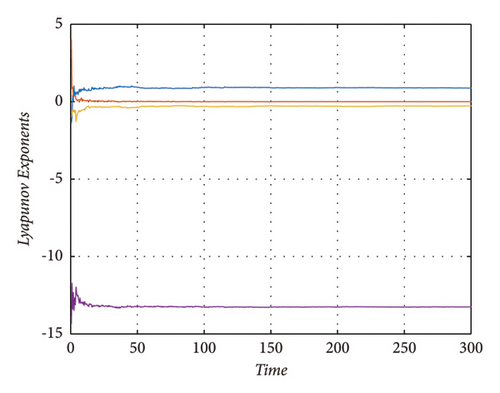
6. Conclusions

In this article, we have explored the matrix and inverse matrix projective synchronization of delayed fractional-order chaotic and hyperchaotic systems with uncertainties. First of all, the existence of chaos has been examined for chaotic and hyperchaotic systems, as shown graphically in Figures 1, 3, 7, and 8. The Lyapunov’s exponents show that these systems are chaotic and hyperchaotic in nature. The matrix and inverse matrix projective synchronization of chaotic and hyperchaotic systems have been accomplished by introducing different gain matrices. Figure 2 and 4 show the trajectories of the MPS error system, while Figures 5 and 6 show the IMPS error system. The implications of uncertainty have been shown via the graphical representations. The simulation outcomes for the synchronization of the chaotic and hyperchaotic systems showed the legitimacy of the proposed scheme. Moreover, the theoretical results agreed with the numerical outcomes.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

V.K.S., M.C.J., and P.K.M. conceptualized the study; V.K.S., M.C.J., P.K.M., I.A., and S.E. performed formal analysis and the methodology; I.A. and S.E. are responsible for software; M.C.J. and S.E. performed investigation; V.K.S., M.C.J., P.K.M., and S.E. wrote the original draft; V.K.S. and S.E. reviewed and edited the study. All the authors have read and agreed to the published version of the manuscript.

Acknowledgments

The fifth author would like to thank Azarbaijan Shahid Madani University.

Open Research

Data Availability

Data sharing is not applicable to this article as no datasets were generated nor analyzed during the current study.

References

1 Lorenz E. N., Deterministic nonperiodic flow, Journal of the Atmospheric Sciences. (1963) 20, no. 2, 130–141.
10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
Web of Science® Google Scholar
2 Chen G. and Ueta T., Yet another chaotic attractor, International Journal of Bifurcation and chaos, International Journal of Bifurcation and Chaos. (1999) 9, no. 7, 1465–1466, https://doi.org/10.1142/s0218127499001024, 2-s2.0-62249200922.
10.1142/S0218127499001024
Web of Science® Google Scholar
3 Lu J. and Chen G., A new chaotic attractor coined, International Journal of Bifurcation and chaos, International Journal of Bifurcation and Chaos. (2002) 12, no. 3, 659–661, https://doi.org/10.1142/s0218127402004620, 2-s2.0-0036011505.
10.1142/S0218127402004620
Web of Science® Google Scholar
4 Pecora L. M. and Carroll T. L., Synchronization in chaotic systems, Physical Review Letters. (1990) 64, no. 8, 821–824, https://doi.org/10.1103/physrevlett.64.821, 2-s2.0-0343689904.
10.1103/PhysRevLett.64.821
CAS PubMed Web of Science® Google Scholar
5 Schiff S. J., Jerger K., Duong D. H., Chang T., Spano M. L., and Ditto W. L., Controlling chaos in the brain, Nature. (1994) 370, no. 6491, 615–620, https://doi.org/10.1038/370615a0, 2-s2.0-0028003827.
10.1038/370615a0
CAS PubMed Web of Science® Google Scholar
6 Ojo K. S., Njah A. N., and Ogunjo S. T., Comparison of backstepping and modified active control in projective synchronization of chaos in an extended Bonhöffer–van der Pol oscillator, Pramana. (2013) 80, no. 5, 825–835, https://doi.org/10.1007/s12043-013-0526-3, 2-s2.0-84877714982.
10.1007/s12043-013-0526-3
Web of Science® Google Scholar
7 Ouannas A., Chaos synchronization approach based on new criterion of stability, Nonlinear Dynamics and Systems Theory. (2014) 14, no. 4, 395–401.
Google Scholar
8 Deressa C. T., Etemad S., and Rezapour S., On a new four-dimensional model of memristor-based chaotic circuit in the context of nonsingular Atangana-Baleanu-Caputo operators, Advances in Difference Equations. (2021) 2021, no. 1, https://doi.org/10.1186/s13662-021-03600-9.
10.1186/s13662-021-03600-9
PubMed Google Scholar
9 Baleanu D., Etemad S., and Rezapour S., A hybrid Caputo fractional modeling for thermostat with hybrid boundary value conditions, Boundary Value Problems. (2020) 2020, no. 1, https://doi.org/10.1186/s13661-020-01361-0.
10.1186/s13661-020-01361-0
PubMed Web of Science® Google Scholar
10 Rezapour S., Tellab B., Deressa C. T., Etemad S., and Nonlaopon K., H-U-type stability and numerical solutions for a nonlinear model of the coupled systems of Navier BVPs via the generalized differential transform method, Fractal and Fractional. (2021) 5, no. 4, https://doi.org/10.3390/fractalfract5040166.
10.3390/fractalfract5040166
PubMed Web of Science® Google Scholar
11 Ghala G. T., Maarof M. I. N., and Guangul F. M., Tidal and wave energy potential assessment, Clean Energy Opportunities in Tropical Countries. (2021) .
Google Scholar
12 Anatoly A. K., Srivastava H. M., and Juan J. T., Theory and Applications of Fractional Differential Equations, 2006, Elsevier, Amsterdam, Netherlands.
Google Scholar
13 Sabatier J., Agrawal O. P., and Machado J. A.T., Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering, 2007, Springer, Dordrecht, Netherlands.
10.1007/978-1-4020-6042-7
Google Scholar
14 Petráš I., Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation, 2011, Springer, Berlin, Germany.
10.1007/978-3-642-18101-6
Google Scholar
15 Hartley T. T., Lorenzo C. F., and Killory Qammer H., Chaos in a fractional order Chua’s system, IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. (1995) 42, no. 8, 485–490, https://doi.org/10.1109/81.404062, 2-s2.0-0029359880.
10.1109/81.404062
Google Scholar
16 Li C., Liao X., and Yu J., Synchronization of fractional order chaotic systems, Physical Review E. (2003) 68, no. 6, https://doi.org/10.1103/physreve.68.067203, 2-s2.0-84867523392, 067203.
10.1103/PhysRevE.68.067203
CAS PubMed Web of Science® Google Scholar
17 Chen D. Y., Liu Y. X., Ma X. Y., and Zhang R. F., Control of a class of fractional-order chaotic systems via sliding mode, Nonlinear Dynamics. (2012) 67, no. 1, 893–901, https://doi.org/10.1007/s11071-011-0002-x, 2-s2.0-82255193992.
10.1007/s11071-011-0002-x
Web of Science® Google Scholar
18 He J. M. and Pei L. J., Function matrix projection synchronization for the multi-time delayed fractional order memristor-based neural networks with parameter uncertainty, Applied Mathematics and Computation. (2023) 454, https://doi.org/10.1016/j.amc.2023.128110, 128110.
10.1016/j.amc.2023.128110
Google Scholar
19 He J. M. and Pei L. J., Function matrix projective synchronization for unknown and delayed fractional-order neural network, Neural Computing & Applications. (2023) 35, no. 24, 17941–17952, https://doi.org/10.1007/s00521-023-08641-7.
10.1007/s00521-023-08641-7
Google Scholar
20 He J. M., Lei T. F., and Chen F. Q., Global matrix projective synchronization of delayed fractional-order neural networks, Soft Computing. (2023) 27, no. 13, 8991–9000, https://doi.org/10.1007/s00500-023-07834-5.
10.1007/s00500-023-07834-5
Google Scholar
21 ur Rahman M., El-Shorbagy M. A., Alrabaiah H., Baleanu D., and Sen M. D. l., Investigating a new conservative 4-dimensional chaotic system, Results in Physics. (2023) 53, https://doi.org/10.1016/j.rinp.2023.106969, 106969.
10.1016/j.rinp.2023.106969
Google Scholar
22 Jiang X., Li J., Li B., Yin W., Sun L., and Chen X., Bifurcation, chaos, and circuit realisation of a new four-dimensional memristor system, International Journal of Nonlinear Sciences and Numerical Stimulation. (2023) 24, no. 7, 2639–2648, https://doi.org/10.1515/ijnsns-2021-0393.
10.1515/ijnsns-2021-0393
Google Scholar
23 Li P., Han L., Xu C., Peng X., Rahman M. u., and Shi S., Dynamical properties of a meminductor chaotic system with fractal–fractional power law operator, Chaos, Solitons & Fractals. (2023) 175, https://doi.org/10.1016/j.chaos.2023.114040, 114040.
10.1016/j.chaos.2023.114040
Google Scholar
24 Chen Q., Li B., Yin W., Jiang X., and Chen X., Bifurcation, chaos and fixed-time synchronization of memristor cellular neural networks, Chaos, Solitons & Fractals. (2023) 171, https://doi.org/10.1016/j.chaos.2023.113440, 113440.
10.1016/j.chaos.2023.113440
Google Scholar
25 Zhu X., Xia P., He Q., Ni Z., and Ni L., Ensemble classifier design based on perturbation binary salp swarm algorithm for classification, Computer Modeling in Engineering and Sciences. (2023) 135, no. 1, 653–671, https://doi.org/10.32604/cmes.2022.022985.
10.32604/cmes.2022.022985
Google Scholar
26 Lin L., Wang Q., He B., Chen Y., Peng X., and Mei R., Adaptive predefined-time synchronization of two different fractional-order chaotic systems with time-delay, IEEE Access. (2021) 9, 31908–31920, https://doi.org/10.1109/access.2021.3059324.
10.1109/ACCESS.2021.3059324
Web of Science® Google Scholar
27 Gokul P., Mohanrasu S. S., Kashkynbayev A., and Rakkiyappan R., Finite-time synchronization of fractional-order nonlinear systems with state-dependent delayed impulse control, International Journal of Bifurcation and Chaos. (2024) 34, no. 03, https://doi.org/10.1142/s0218127424500342, 2450034.
10.1142/S0218127424500342
Google Scholar
28 Cui X., Li H. L., Zhang L., Hu C., and Bao H., Complete synchronization for discrete-time fractional-order coupled neural networks with time delays, Chaos, Solitons & Fractals. (2023) 174, https://doi.org/10.1016/j.chaos.2023.113772, 113772.
10.1016/j.chaos.2023.113772
Google Scholar
29 Mohammadzadeh A., Ghaemi S., Kaynak O., and Mohammadi S. K., Robust predictive synchronization of uncertain fractional-order time-delayed chaotic systems, Soft Computing. (2019) 23, no. 16, 6883–6898, https://doi.org/10.1007/s00500-018-3328-1, 2-s2.0-85049058814.
10.1007/s00500-018-3328-1
Web of Science® Google Scholar
30 Zhang W., Cao J., Wu R., Alsaadi F. E., and Alsaedi A., Lag projective synchronization of fractional-order delayed chaotic systems, Journal of the Franklin Institute. (2019) 356, no. 3, 1522–1534, https://doi.org/10.1016/j.jfranklin.2018.10.024, 2-s2.0-85058475940.
10.1016/j.jfranklin.2018.10.024
Web of Science® Google Scholar
31 Shukla V. K., Mbarki L., Shukla S., Vishal K., and Mishra P. K., Matrix projective synchronization between time delay chaotic systems with disturbances and nonlinearity, International Journal of Dynamics and Control. (2023) 11, no. 4, 1926–1933, https://doi.org/10.1007/s40435-022-01099-w.
10.1007/s40435-022-01099-w
Google Scholar
32 He J. and Chen F., Dynamical analysis of a new fractional-order Rabinovich system and its fractional matrix projective synchronization, Chinese Journal of Physics. (2018) 56, no. 5, 2627–2637, https://doi.org/10.1016/j.cjph.2018.09.014, 2-s2.0-85054683978.
10.1016/j.cjph.2018.09.014
Web of Science® Google Scholar
33 Khan A., Jahanzaib L. S., Khan T., and Trikha P., Secure communication: using fractional matrix projective combination synchronization, AIP Proceedings. (2020) 2253, no. 1, 020009.
Google Scholar
34 Khan A., Jahanzaib L. S., and Trikha P., Fractional inverse matrix projective combination synchronization with application in secure communication, Proceedings of the International Conference on Artificial Intelligence and Applications, January 2021, Phuket, Thailand, 93–101, https://doi.org/10.1007/978-981-15-4992-2_10.
10.1007/978-981-15-4992-2_10
Google Scholar
35 Ouannas A., Azar A. T., Ziar and T., and Vaidyanathan S., On new fractional inverse matrix projective synchronization schemes, Fractional Order Control and Synchronization of Chaotic Systems. (2017) Springer, Berlin, Germany, 497–524.
10.1007/978-3-319-50249-6_17
Google Scholar
36 Wu Z., Xu X., Chen G., and Fu X., Generalized matrix projective synchronization of general colored networks with different-dimensional node dynamics, Journal of the Franklin Institute. (2014) 351, no. 9, 4584–4595, https://doi.org/10.1016/j.jfranklin.2014.07.008, 2-s2.0-84906305808.
10.1016/j.jfranklin.2014.07.008
Web of Science® Google Scholar
37 Aadhithiyan S., Raja R., Zhu Q., Alzabut J., Niezabitowski M., and Lim C. P., Modified projective synchronization of distributive fractional order complex dynamic networks with model uncertainty via adaptive control, Chaos, Solitons & Fractals. (2021) 147, https://doi.org/10.1016/j.chaos.2021.110853, 110853.
10.1016/j.chaos.2021.110853
Web of Science® Google Scholar
38 Sha H., Wang G., Hao T., and Wang Z., Projection synchronization of a class of complex chaotic systems with both uncertainty and disturbance, Complexity. (2020) 2020, 1–12, https://doi.org/10.1155/2020/3742876.
10.1155/2020/3742876
Google Scholar
39 Li C. L., Su K. L., and Zhang J., Amplitude control and projective synchronization of a dynamical system with exponential nonlinearity, Applied Mathematical Modelling. (2015) 39, no. 18, 5392–5398, https://doi.org/10.1016/j.apm.2015.01.012, 2-s2.0-84938549800.
10.1016/j.apm.2015.01.012
Web of Science® Google Scholar
40 Agrawal S. K. and Das S., Projective synchronization between different fractional-order hyperchaotic systems with uncertain parameters using proposed modified adaptive projective synchronization technique, Mathematical Methods in the Applied Sciences. (2014) 37, no. 14, 2164–2176, https://doi.org/10.1002/mma.2963, 2-s2.0-84905967860.
10.1002/mma.2963
Web of Science® Google Scholar
41 He J., Chen F., and Bi Q., Quasi-matrix and quasi-inverse-matrix projective synchronization for delayed and disturbed fractional order neural network, Complexity. (2019) 2019, 1–15, https://doi.org/10.1155/2019/4823709, 2-s2.0-85065660570.
10.1155/2019/4823709
Google Scholar
42 Liu F., Matrix projective synchronization of chaotic systems and the application in secure communication, Applied Mechanics and Materials. (2014) 644–650, 4216–4220, https://doi.org/10.4028/www.scientific.net/amm.644-650.4216, 2-s2.0-84915788813.
10.4028/www.scientific.net/AMM.644-650.4216
Google Scholar
43 Kilbas A. A., Srivastava H. M., and Trujillo J. J., Theory and Applications of Fractional Differential Equations, 2006, Elsevier, Amsterdam, Netherlands.
10.1016/S0304-0208(06)80001-0
Google Scholar
44 Alikhanov A. A., A priori estimates for solutions of boundary value problems for fractional-order equations, Differential Equations. (2010) 46, no. 5, 660–666, https://doi.org/10.1134/s0012266110050058, 2-s2.0-77954390264.
10.1134/S0012266110050058
Web of Science® Google Scholar
45 Čermák J., Kisela T., and Nechvátal L., Stability regions for linear fractional differential systems and their discretizations, Applied Mathematics and Computation. (2013) 219, no. 12, 7012–7022, https://doi.org/10.1016/j.amc.2012.12.019, 2-s2.0-84874100688.
10.1016/j.amc.2012.12.019
Web of Science® Google Scholar
46 Matignon D., Stability results for fractional differential equations with applications to control processing, Computational Engineering in Systems Applications. (1996) 2, no. 1, 963–968.
Google Scholar
47 Ouannas A. and Abu-Saris R., On matrix projective synchronization and inverse matrix projective synchronization for different and identical dimensional discrete-time chaotic systems, Journal of Chaos. (2016) 2016, 1–7, https://doi.org/10.1155/2016/4912520.
10.1155/2016/4912520
Google Scholar
48 Veeman D., Mehrabbeik M., Natiq H., Rajagopal K., Jafari S., and Hussain I., A new chaotic system with coexisting attractors, International Journal of Bifurcation and Chaos. (2022) 32, no. 03, https://doi.org/10.1142/s0218127422300075, 2230007.
10.1142/S0218127422300075
Web of Science® Google Scholar
49 Singh J. P. and Roy B. K., The simplest 4-D chaotic system with line of equilibria, chaotic 2-torus and 3-torus behaviour, Nonlinear Dynamics. (2017) 89, no. 3, 1845–1862, https://doi.org/10.1007/s11071-017-3556-4, 2-s2.0-85019187454.
10.1007/s11071-017-3556-4
Web of Science® Google Scholar
50 Sambas A., Vaidyanathan S., Zhang S., Zeng Y., Mohamed M. A., and Mamat M., A new double-wing chaotic system with coexisting attractors and line equilibrium: bifurcation analysis and electronic circuit simulation, IEEE Access. (2019) 7, 115454–115462, https://doi.org/10.1109/access.2019.2933456, 2-s2.0-85072292030.
10.1109/ACCESS.2019.2933456
Web of Science® Google Scholar
51 Chen J., Tang J., Zhang F., Ni H., and Tang Y., A novel digital color image encryption algorithm based on a new 4-D hyper-chaotic system and an improved S-box, International Journal of Innovative Computing, Information and Control. (2022) 18, no. 1, 73–92.
Google Scholar
52 Wolf A., Quantifying chaos with Lyapunov exponents, Chaos. (1986) 16, 285–317.
Google Scholar

All articles

Matrix and Inverse Matrix Projective Synchronization of Fractional-Order Time-Delay Chaotic Systems with Uncertainty

Abstract

1. Introduction

2. System Description

3. Study of Matrix Projective Synchronization

3.1. MPS between Fractional Time-Delay Chaotic Systems with Uncertainties

3.2. MPS between Fractional-Order Time-Delay Hyperchaotic Systems with Uncertainties

4. Study of Inverse Matrix Projective Synchronization

4.1. IMPS between Identical Chaotic Systems with Uncertainty

4.2. IMPS between Hyperchaotic Systems with Uncertainties

5. Numerical Results and Discussion

6. Conclusions

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Matrix and Inverse Matrix Projective Synchronization of Fractional-Order Time-Delay Chaotic Systems with Uncertainty

Abstract

1. Introduction

2. System Description

3. Study of Matrix Projective Synchronization

3.1. MPS between Fractional Time-Delay Chaotic Systems with Uncertainties

3.2. MPS between Fractional-Order Time-Delay Hyperchaotic Systems with Uncertainties

4. Study of Inverse Matrix Projective Synchronization

4.1. IMPS between Identical Chaotic Systems with Uncertainty

4.2. IMPS between Hyperchaotic Systems with Uncertainties

5. Numerical Results and Discussion

6. Conclusions

Conflicts of Interest

Authors’ Contributions

Acknowledgments

Open Research

Data Availability

References

Figures

References

Related

Information