This study employs the Lie symmetry technique to explore the symmetry features of the time fractional Kupershmidt equation. Specifically, we use the Lie symmetry technique to derive the symmetry generators for this equation, which incorporates a conformal fractional derivative. We use the symmetry generators to transform the fractional partial differential equation into a fractional ordinary differential equation, thereby simplifying the analysis. The obtained reduced equation is of fourth order nonlinear ordinary differential equation. To find the wave solutions, F/G-expansion process has been used to obatin different types of solutions of the time-fractional Kuperschmidt equation. The obtained wave solutions are hyperbolic and trigonometric in nature. We then use Maple software to visually depict these wave solutions for specific parameter values, providing insights into the behaviour of the system under investigation. Peak and kink wave solutions are achieved for the given problem.

1. Introduction

The Kupershmidt equation is a prominent one in the field of nonlinear dispersive waves. It entails the formation of solitary waves in a variety of nonlinear dispersive mediums. The equation is named after Boris Kupershmidt [1], who worked on developing it, and is given by

(1)

Different forms of Kupershmidt equations exist and some of them are the following:

The (2 + 1)-dimensional Broer-Kaup-Kupershmidt Equation [2] is given by

(2)

The 1 + 1-dimensional Kaup-Kupershmidt Equation [3]

(3)

The generalized Kupershmidt equation, that is, a KdV-mKdV Equation [4], is presented as

(4)

Studying problems like the Kupershmidt equation is important in many domains, including nonlinear optics, fluid dynamics, and plasma physics, where nonlinear dispersive waves play a key role.

The Kupershmidt equation has been the focus of various investigations in recent decades. Researchers have looked at several elements of this equation, including its characteristics, analytical solutions, numerical techniques for solving it, and applications in a variety of domains. Mustafa used the Adomian decomposition method (ADM) [5] to analyze the soliton solutions of the KK problem. The Cole–Hopf transformation and simplified Hirota’s approach [6] were used to solve the generalized Kaup–Kupershmidt problem. Atangana and Goufu [7] expanded the nonlinear Kaup–Kupershmidt to fractional calculus by utilizing the conventional Caputo derivative and the recently created Caputo–Fabrizio derivative, which has fractional order and no singular kernel. Several fixed-point theorem techniques, as well as the concept of Piccard L-stability, were used in the analysis to show the existence and uniqueness of the precise solution to models with both types of derivatives. Finally, several numerical simulation methodologies for both nonlinear models and graphical simulations for values of order 1.00 to 0.90 were given. The solutions were shown to behave similarly to the well-known conventional travelling wave solution for the Kaup–Kupershmidt issue. Also, Chauhan and Arora [8] used the Lie symmetry technique to generate symmetry generators for the time fractional Kupershmidt equation, using the Riemann–Liouville fractional derivative.

The bilinear technique was used to generate multisoliton solutions to the generalized fifth-order KK problem [9]. The velocity of the soliton was found to be related to the sign of the physical parameters. Iqbal et.al. [10] employed an iterative transformation strategy to provide analytical solutions, and applied an iterative transformation to provide analytical solutions for fractional-order KK equations. In 2022, three examples of the time-fractional Kaup–Kupershmidt equation were explored using the decomposition technique [11] for two types of fractional derivatives. The resulting results were compared to the solutions produced by other approaches. To analyze the solution behaviour of fuzzy-fractional–Kaup–Kupershmidt equations in both uncertain and crisp situations, a novel generalized semianalytical technique, namely, the homotopy analysis general integral transform, was used [12].

Podder et.al [13] studied the space-time fractional nonlinear evolution equation using the Bernoulli subequation function approach, and 2d and 3d plots were drawn for expressing the wave solutions. The space-time fractional CD and PKP equations [14] were solved using the G^′/G and 1/G-expansion methods to achieve the closed form wave solutions. The space-time telegraph equation and KdV equation [15] were studied using the Tanh method using conformal fractional derivatives by Arefin et al. Khatun et al [16] studied the partial differential equation (PDE), namely, the couple Boussinesq equation using the Sine–Gordan expansion method to find the wave solution using wave transformation for converting FPDE to ODE and obtained solutions were illustrated using 3d plotting. The space-time Cahn–Allen and Benjamin–Bonamahony equations [17] were solved through the extended Tanh-function method in the sense of Atangana beta derivatives. Uddin solved the space-time–modified KdV and Sine–Gordan equation [18] using a generalized G^′/G-expansion approach in order to obtain the kink wave, bell type, and periodic type solutions.

Cevikel [19] examined the Duffing equation in order to use the conformable Duffing model to discover the travelling wave solutions. With the aid of conformable fractional derivatives, nonlinear fractional differential equations were precisely solved using the modified simple equation approach [20]. Moreover, Cevikel researched the nonlinear YTSF [21] equation in order to determine the precise solutions by several methods. Conformable fractional derivatives were used to study the fractional Fitzhugh–Nagumo equation, the fractional Newell–Whitehead–Segel (NWS) equation, and the fractional Zeldovich equation in order to determine their precise solutions [22].

All the models which have the diffusion form are expressed in equilibrium stages, and the diffusion model which contains different terms can also be studied in subdiffusion stages in fractional form. Many mathematicians define fractional differential equations over time in order to represent the subdiffusion states of the system through the use of fractional derivatives. There are several ways to define these fractional derivatives, including Riemann Liouville, Caputo, and Riesz. However, one form that is utilized for solving fractional equations is the conformal derivative form.

According to the previous literature, this equation is not studied in conformable fractional form to find the wave solutions by using Lie symmetry analysis, which reduces the fractional PDEs into ordinary differential equations.

Previous literature motivated us to study the symmetry analysis and wave solution of the time fractional Kupershmidt equation [8], which is given in Equation (5).

(5)

The time fractional Kupershmidt equation, given in Equation (5), is a special case of the fifth-order KdV–mKdV equation and is called the generalized Kupershmidt equation. Here, is the conformal fractional derivative [23], u represents the wave amplitude in space x w.r.t. time t, and a, b, and β are undetermined constants. This PDE includes both dispersion and nonlinear effect, that is, u_xxx indicated third order dispersion, whereas refers to nonlinear effect. We use the Lie symmetry technique to explore the symmetry features of the time fractional Kupershmidt equation given in Equation (5) and derive the symmetry generators, which incorporate a conformal fractional derivative. We also use the F/G-expansion process as a means of generating wave solutions to the problem. We then use Maple software to visually depict these wave solutions for specific parameter values, providing insights into the behaviour of the system under investigation.

The novelty of the work is that the Lie symmetry has been applied in the Riemann–Liouville form for reduction of the Kupershmidt equation, but solutions were not obtained; but in conformal form, after applying the Lie theory, solutions have been obtained by using F/G expansion method. We then use Maple software to visually depict these wave solutions for specific parameter values, providing insights into the behaviour of the system under investigation.

This paper is constructed in the following manner: Section 2 consists of the Lie symmetry technique. Section 3 covers symmetry reductions [23]. Section 4 explains the approach for identifying wave solutions. Section 5 employs the F/G-expansion method to create travelling wave solutions. Section 6 contains three-dimensional graphs of wave solutions. The essay ends with the conclusion.

2. Lie Symmetry Technique

The time-fractional PDE is

(6a)

where w = w (x, t), H [w] is the nonlinear differential operator, and (∂^α/∂t^α) is a conformable fractional derivative.

Now, we analyze the symmetry transformation of Equation (6a) by taking invertible point transformations

(6b)

based on a continuous parameter ε and have the same form in the new variable

, which are said to be symmetry transformations. The symmetry group is a continuous group made up of H^∗ transformations. The Lie group is another name for the symmetry group H^∗. The key point in the Lie group of transformation is to deduce infinitesimal generator and determine equations.

Infinitesimal transformation of Equation (6b) be

( )

(6c)

(6d)

Here, W is the infinitesimal operator.

( )

can be computed to obtain the group transformation (6b) relating to operator (6d) and subject to initial conditions

(6e)

A surface w = w(x, t) is mapped as the group transformation, generated by W if

(6f)

Here,

satisfies to

(6g)

As the function w = w (x, t) satisfies Equation (6a), then the transformation (6b) forms a symmetry group H of Equation (6a). Extending transformation (6c) of fractional differentiation ∂^αw/∂t^α and operator of x differentiation of several order ∂^αw/∂x^k, k = 1, 2, 3, ⋯, we can find

( )

where

( )

(6h)

Here, the derivative operator D_x is defined as

(6i)

And , where extended infinitesimal associated with the conformable fractional time derivative of differentiable functions.

3. Symmetry Analysis and Reduction

The following section describes the Lie symmetry analysis [24–26] of Kupershmidt equation. Examine the infinitesimal transformations using a lie group that has only a single parameter.

(7)

The resultant infinitesimal equation is obtained by applying the extended transformation Equation (7) to Equation (5).

(8)

Alter the values of

, and replace

. By summing the various powers of the partial derivative of u, we obtain the following system of determining equations:

i.
τ_x = 0, τ_u = 0,
ii.
ξ_u = 0,
iii.
η_uu = 0,
iv.
−aη − auξ_x − 3η_xu + 3ξ_xx − βξ_x = 0,
v.
−aη_u − aξ_x = 0,
vi.
−2bβuξ_x − 2aη_x + auξ_xx + ξ_xxx − 2βη_xu − 3η_xxu − bβη + βξ_xx − t^1−αξ_t + aη_uu² − 2auη_xu − 3ξ_xau² − 2auη + au²ξ_x − au²η_u = 0,
vii.
τt^−α − t^1−ατ_t − ταt^−α + t^1−αη_u = 0,
viii.

By solving these determined equations, we obtain the following symmetries:

(9)

(10)

(11)

where H₁, H₂, H₃, and H₄ are arbitrary constants. Therefore, the symmetry group of Equation (5) is spanned by the four-vector fields.

(12)

(13)

(14)

(15)

The characteristic equation for the infinitesimal generator I₃ + I₄ is given by

(16)

This ultimately results to the similarity transformation

(17)

The following ordinary differential equation is generated by plugging Equation (17) into Equation (5).

( )

where wave solutions of the above equation exist.

4. F/G-Expansion Method

Consider a nonlinear PDE of the form

(18)

where u = u(x, t) is a function to be determined and c is a polynomial in u(x, t) with its partial derivatives including highest order derivatives and nonlinear terms. The following are the major steps of the F/G-expansion method [27, 28].

Step 1. By introducing the variable ξ = x − t^α/α, assume that

(19)

The wave variable ξ transforms Equation (18) to ODE.

(20)

Step 2. Suppose that the solution of ODE Equation (20) can be expressed by a polynomial in F/G as follows:

(21)

where G = G(ξ) and F = F(ξ) satisfy the FLODS in the form

(22)

where v₀, v₁, ⋯, v_r, λ and μ are constants for evaluation, v_w ≠ 0. By balancing the highest order derivatives and nonlinear variables in Equation (20), the positive integer w can be determined.

In cooperation with Equation (22), the following listed solutions to F(ξ) and G(ξ) can be discovered.

Case 1. If λ > 0 and μ > 0, then the following hyperbolic function solutions of Equation (22) are as follows:

(23)

Case 2. If λ < 0 and μ < 0, then the following hyperbolic function solutions of Equation (22) are as follows:

(24)

Case 3. If λ > 0 and μ < 0, then the following trigonometric function solutions of Equation (22) are as follows:

(25)

Case 4. If λ < 0 and μ > 0, then the following trigonometric function solutions of Equation (22) are as follows:

(26)

Step 3. Using Equation (21) and Equation (22) in Equation (20) severally produces a set of algebraic equations for (F/G)^q(q = 1, 2, ⋯, w). By equating the coefficients of (F/G)^q to zero, a set of nonlinear algebraic equations in v_q(q = 0, 1, 2, ⋯, w) is obtained. On solving these algebraic equations by Maple, numerous exact solutions of Equation (18) for Equations (19), (21), (23), (24), (25), and (26) will be achieved.

5. Traveling Wave Solutions

The time fractional Kupershmidt equation is given by

( )

The travelling wave transformation given by Equation (19) converts Equation (5) into ODE for u = f(ξ) in the form

(27)

On comparing the highest order derivative with the nonlinear term in Equation (27), we get w = 2. Accordingly, we get

(28)

where v₀, v₁, and v₂ are constants to be determined. With the use of Equation (28) in Equation (27) and aggregating all the terms with identical powers of F/G collectively, then L.H.S. of Equation (27) is transformed into a different polynomial in F/G. Collection of algebraic equations is acquired by comparing every coefficient of this polynomial to zero. We will solve these equations using Maple, and the following results will be obtained:

(29)

(30)

(31)

(32)

Case 1. When

a.
If λ > 0 and μ > 0, then the following hyperbolic function solutions are obtained:

(33)

where ξ = x − t^α/α and

and

are arbitrary constants.

In specific, if , , we have the solitary wave solution

(34)

b.
If λ < 0 and μ < 0, then the following hyperbolic function solutions are obtained:

(35)

where ξ = x − t^α/α and

and

are arbitrary constants.

In specific, if , , we have the solitary wave solution

(36)

c.
If λ > 0 and μ < 0, then the following trigonometric function solutions are obtained:

(37)

where ξ = x − t^α/α and

and

are arbitrary constants.

d.
If λ < 0 and μ > 0, then the following trigonometric function solutions are obtained:

(38)

where ξ = x − t^α/α and

and

are arbitrary constants.

Case 2. When

a.
If λ > 0 and μ > 0, then the following hyperbolic function solutions are obtained:

(39)

where ξ = x − t^α/α and

and

are arbitrary constants.

In specific, if , , we have the solitary wave solution

(40)

b.
If λ < 0 and μ < 0, then the following hyperbolic function solutions are obtained:

(41)

where ξ = x − t^α/α and

and

are arbitrary constants.

In specific, if , , we have the solitary wave solution

(42)

c.
If λ > 0 and μ < 0, then the following trigonometric function solutions are obtained:

(43)

where ξ = x − t^α/α and

and

are arbitrary constants.

d.
If λ < 0 and μ > 0, then the following trigonometric function solutions are obtained:

(44)

where ξ = x − t^α/α and

and

are arbitrary constants.

Case 3. When

a.
If λ > 0 and μ > 0, then the following hyperbolic function solutions are obtained:

(45)

where ξ = x − t^α/α and

and

are arbitrary constants.

In specific, if , , we have the solitary wave solution

(46)

b.
If λ < 0 and μ < 0, then the following hyperbolic function solutions are obtained:

(47)

where ξ = x − t^α/α and

and

are arbitrary constants.

In specific, if , , we have the solitary wave solution

(48)

c.
If λ > 0 and μ < 0, then the following trigonometric function solutions are obtained:

(49)

where ξ = x − t^α/α and

and

are arbitrary constants.

d.
If λ < 0 and μ > 0, then the following trigonometric function solutions are obtained:

(50)

where ξ = x − t^α/α and

and

are arbitrary constants.

Case 4. When

a.
If λ > 0 and μ > 0, then the following hyperbolic function solutions are obtained:

(51)

where ξ = x − t^α/α and

and

are arbitrary constants.

In specific, if , , we have the solitary wave solution.

(52)

b.
If λ < 0 and μ < 0, then the following hyperbolic function solutions are obtained:

(53)

where ξ = x − t^α/α and

and

are arbitrary constants.

In specific, if , , we have the solitary wave solution

(54)

c.
If λ > 0 and μ < 0, then the following trigonometric function solutions are obtained:

(55)

where ξ = x − t^α/α and

and

are arbitrary constants.

d.
If λ < 0 and μ > 0, then the following trigonometric function solutions are obtained:

(56)

where ξ = x − t^α/α and

and

are arbitrary constants.

6. Comparison Study

In this part, we present the results of the time fractional Kupershmidt equation that we got using the recommended method in order to compare them with the findings of other researchers who used alternative methodologies. It is interesting to note that while some of the solutions acquired have parallels with previously discovered methods, some findings are entirely original and creative.

i.
The generalized Kupershmidt equation was solved by Salas [6] using the Cole–Hope transformation, and hyperbolic function solutions were obtained.
ii.
KK equation was also solved by improved G’/G-expansion [29] and extended G^′/G-expansion method using local fractional derivative. The obtained results are exponential, hyperbolic, and trigonometric.
iii.
Rezazadeh et al. [30] used subequation method to obtain the exact solutions of time fractional Kaup−Kupershmidt equation using conformal fractional derivative. Trigonometric and hyperbolic function solutions are obtained.

7. Discussions

We obtained such solutions, so that arbitrary constants

may be selected in a suitable manner to replicate the physical solutions described by Equation (5). We also created graphs of solution surfaces to help us better comprehend the solutions. Figures depict the behaviour of the solution for several values of α, which helps us understand the physical prospects of Equation (5).

i.
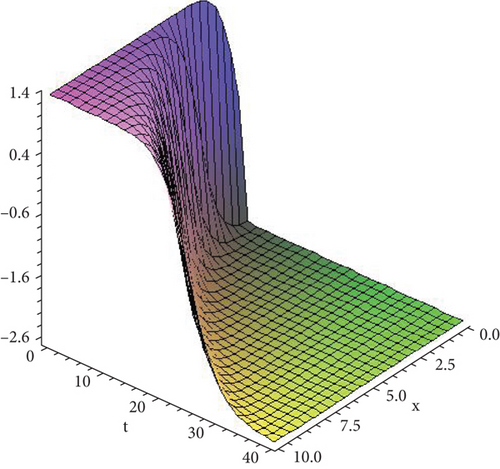
Figure 1 shows the solution given in Equation (34) with paramteric values .
ii.
Figure 2 shows the solution given in Equation (36) with parametric values .
iii.
Figure 3 shows the solution given in Equation (37) with parametric values .
iv.
Figure 4 shows the solution given in Equation (38) with parametric values .
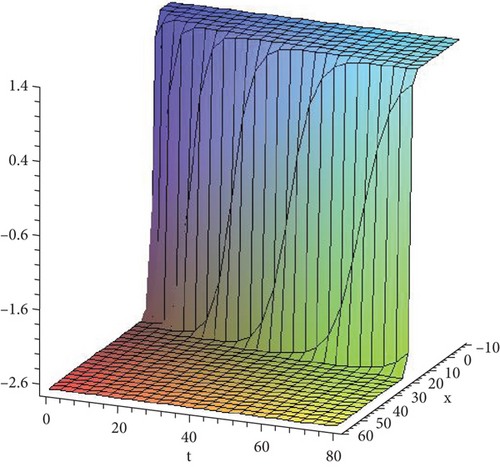
v.
Figure 5 shows the solution given in Equation (40) with parametric values .
vi.
Figure 6 shows the solution given in Equation (42) with parametric values .
vii.
Figure 7 shows the solution given in Equation (43) with parametric values .
viii.
Figure 8 shows the solution given in Equation (44) with parametric values .
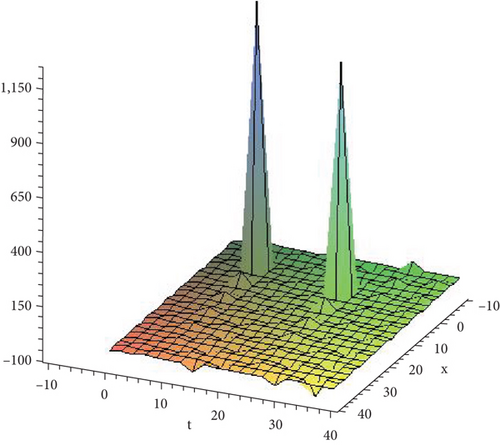
ix.
Figure 9 shows the solution given in Equation (46) with parametric values .
x.
Figure 10 shows the solution given in Equation (48) with parametric values .
xi.
Figure 11 shows the solution given in Equation (49) with parametric values .
xii.
Figure 12 shows the solution given in Equation (50) with parametric values .
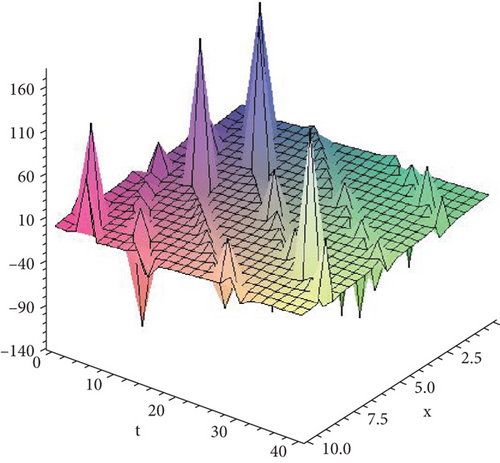
xiii.
Figure 13 shows the solution given in Equation (52) with parametric values .
xiv.
Figure 14 shows the solution given in Equation (54) with parametric values , x = −10 ⋯ 10, t = 0 ⋯ 100.
xv.
Figure 15 shows the solution given in Equation (55) with parametric values .
xvi.
Figure 16 shows the solution given in Equation (56) with parametric values .

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Graph of solution given by Equation (34) for x = 0 ⋯ 10, t = 0 ⋯ 40.

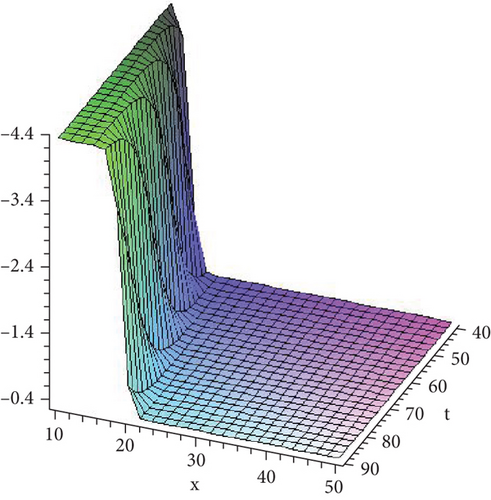
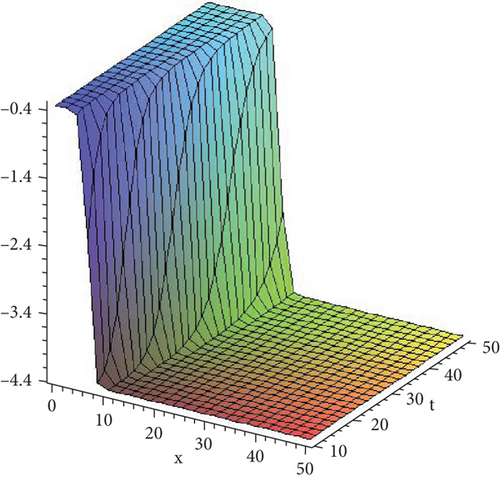
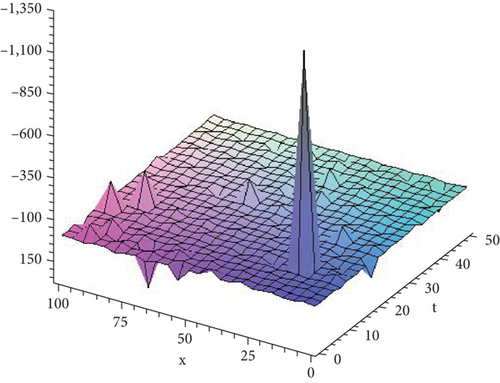
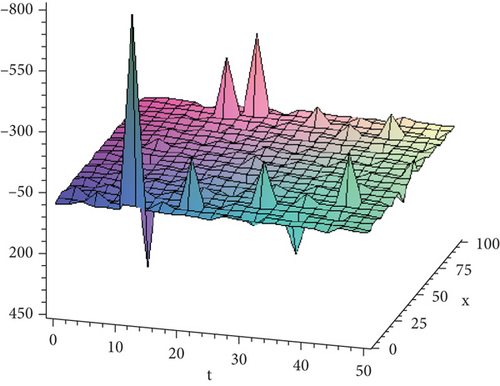
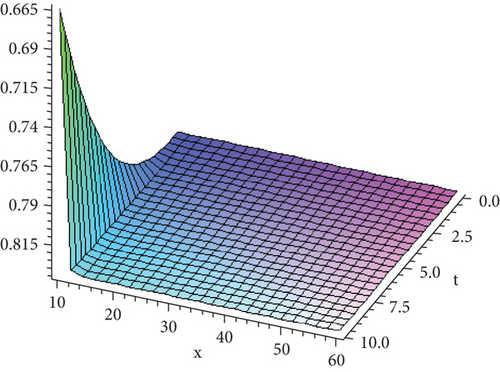
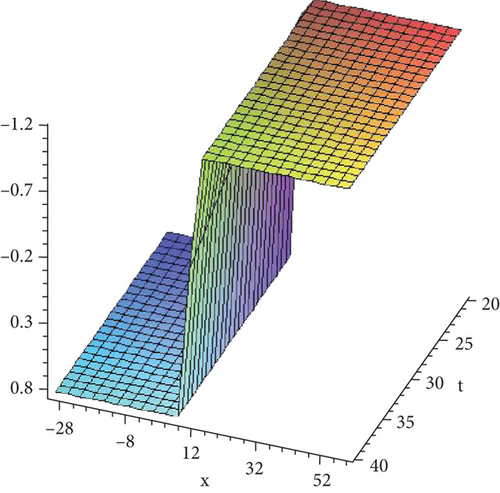
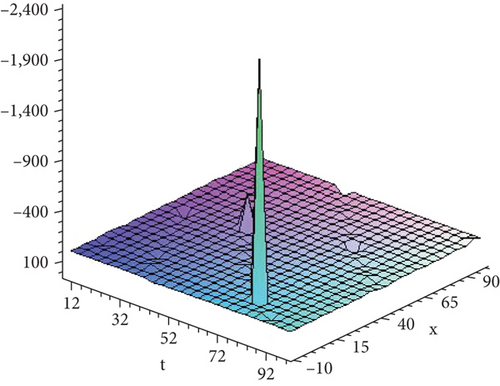
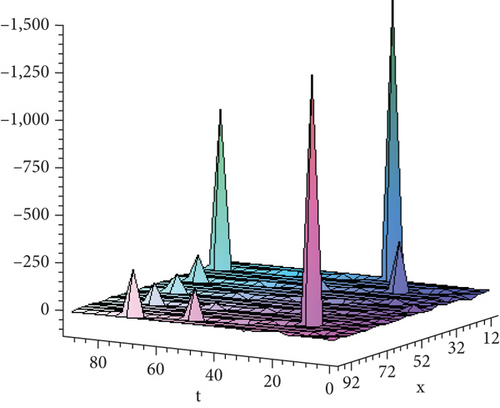
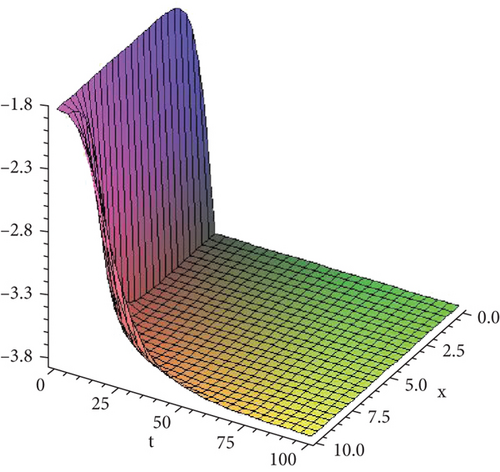
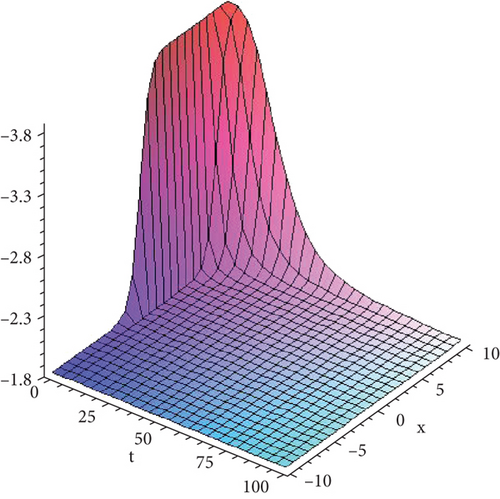
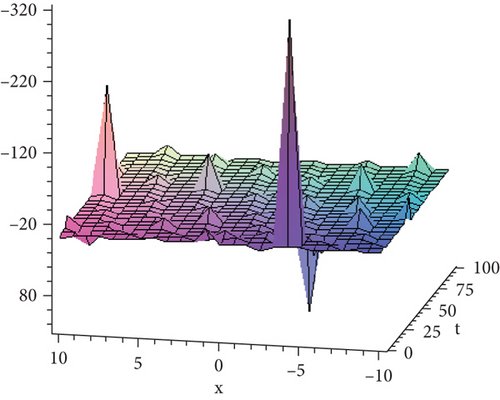
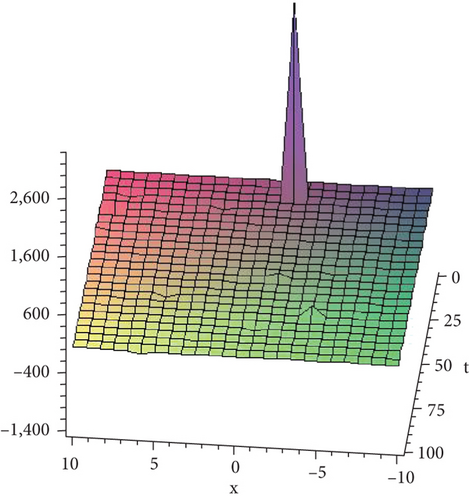
8. Conclusion

This study successfully used the fractional Lie symmetry technique to analyze the similarities between the time fractional Kupershmidt equation and the conformal fractional derivative. We have reduced the fractional PDE to the fractional ordinary differential equation via symmetry reductions. Only wave solutions exist for the reduced ordinary differential equation. The approach of F/G-expansion was applied to get more precise and general solutions to nonlinear evolution equations. In addition to producing extra travelling wave solutions with a variety of physical structures, the F/G-expansion technique also produced hyperbolic and trigonometric functions as solutions. Several travelling waves and soliton-like solutions that were previously recognised are revealed by our findings. Obtained solutions were compared to the solutions obtained by other researchers. Furthermore, as compared to current technology, the proposed solution may greatly reduce the amount of computational work. In order to give further context for each solution, graphs were also created, and peak wave and kink wave plots were produced.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The authors received no specific funding for this work.

Open Research

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author.

References

1 Gharib G., Travelling wave solutions of Kaup-Kupershmidt equation which describes pseudo spherical surfaces, Applications of Mathematics. (2015) 6, 163–172.
Google Scholar
2 Song M., Li S., and Cao J., New exact solutions for the (2 + 1)-dimensional Broer-Kaup-Kupershmidt equations, Abstract and Applied Analysis. (2010) 2010, no. 1, 652649, https://doi.org/10.1155/2010/652649, 2-s2.0-79952126829.
10.1155/2010/652649
Google Scholar
3 Charalambous K., Halder A. K., and Leach P. G. L., A note on analysis of the Kaup-Kupershmidt equation, AIP Conference Proceedings. (2019) 2153, no. 1, https://doi.org/10.1063/1.5125071, 2-s2.0-85072701559.
10.1063/1.5125071
Google Scholar
4 Zhang Y., Mei J., and Zhang X., Symmetry properties and explicit solutions of some nonlinear differential and fractional equations, Applied Mathematics and Computation. (2018) 337, 408–418, https://doi.org/10.1016/j.amc.2018.05.030, 2-s2.0-85048390222.
10.1016/j.amc.2018.05.030
Web of Science® Google Scholar
5 Inc M., On numerical soliton solution of the Kaup-Kupershmidt equation and convergence analysis of the decomposition method, Applied Mathematics and Computation. (2006) 172, no. 1, 72–85, https://doi.org/10.1016/j.amc.2005.01.120, 2-s2.0-31144467784.
10.1016/j.amc.2005.01.120
Web of Science® Google Scholar
6 Salas A. H., Solving the generalized Kaup Kupershmidt equation, Advanced Studies in Theoretical Physics. (2012) 6, 879–885.
Google Scholar
7 Atangana A. and Goufo E. F. D., Conservatory of Kaup-Kupershmidt equation to the concept of fractional derivative with and without singular kernel, Acta Math. Appl. Sin. Engl. Ser.(2018) 34, no. 2, 351–361, https://doi.org/10.1007/s10255-018-0757-7, 2-s2.0-85045969448.
10.1007/s10255-018-0757-7
Google Scholar
8 Chauhan A. and Arora R., Time fractional Kupershmidt equation: symmetry analysis and explicit series solution with convergence analysis, Communications in Mathematics. (2019) 27, no. 2, 171–185, https://doi.org/10.2478/cm-2019-0013.
10.2478/cm-2019-0013
Google Scholar
9 Wang P., Yang J. R., Chen L., Li S. X., and Qi F. H., Analytical study on the generalized fifth-order Kaup–Kupershmidt equation from the shallow water wave, Computational Mathematics and Mathematical Physics. (2020) 60, no. 9, 1480–1487, https://doi.org/10.1134/S0965542520090158.
10.1134/S0965542520090158
Google Scholar
10 Iqbal N., Yasmin H., Rezaiguia A., Kafle J., Almatroud A. O., and Hassan T. S., Analysis of the fractional-order KaupKupershmidt equation via novel transforms, Journal of Mathematics. (2021) 2021, no. 1, 2567927, https://doi.org/10.1155/2021/2567927.
10.1155/2021/2567927
Google Scholar
11 Shah N. A., Hamed Y. S., Abualnaja K. M., Chung J.-D., Shah R., and Khan A., A comparative analysis of fractional-order Kaup Kupershmidt equation within different operators, Symmetry. (2022) 14, no. 5, https://doi.org/10.3390/sym14050986.
10.3390/sym14050986
Google Scholar
12 Sartanpara P. P. and Meher R., Solution of generalised fuzzy fractional Kaup Kupershmidt equation using a robust multi parametric approach and a novel transform, Mathematics and Computers in Simulation. (2023) 205, 939–969, https://doi.org/10.1016/j.matcom.2022.10.020.
10.1016/j.matcom.2022.10.020
Google Scholar
13 Podder A., Arefin M. A., Akbar M. A., and Uddin M. H., A study of the wave dynamics of the space–time fractional nonlinear evolution equations of beta derivative using the improved Bernoulli sub-equation function approach, Scientific Reports. (2023) 13, no. 1, https://doi.org/10.1038/s41598-023-45423-6, 37993529.
10.1038/s41598-023-45423-6
PubMed Google Scholar
14 Arefin M. A., Saeed M. A., Akbar M. A., and Uddin M. H., Analytical behavior of weakly dispersive surface and internal waves in the ocean, Journal of Ocean Engineering and Science. (2022) 7, no. 4, 305–312, https://doi.org/10.1016/j.joes.2021.08.012.
10.1016/j.joes.2021.08.012
Google Scholar
15 Arefin M. A., Sadiya U., Inc M., and Uddin M. H., Adequate soliton solutions to the space–time fractional telegraph equation and modified third-order KdV equation through a reliable technique, Optical and Quantum Electronics. (2022) 54, no. 5, https://doi.org/10.1007/s11082-022-03640-9.
10.1007/s11082-022-03640-9
Google Scholar
16 Khatun M. A., Arefin M. A., Islam M. Z., Akbar M. A., and Uddin M. H., New dynamical soliton propagation of fractional type couple modified equal-width and Boussinesq equations, Alexandria Engineering Journal. (2022) 61, no. 12, 9949–9963, https://doi.org/10.1016/j.aej.2022.03.033.
10.1016/j.aej.2022.03.033
Google Scholar
17 Arefin M. A., Khatun M. A., Islam M. S., Akbar M. A., and Uddin M. H., Explicit soliton solutions to the fractional order nonlinear models through the Atangana beta derivative, International Journal of Theoretical Physics. (2023) 62, no. 6, https://doi.org/10.1007/s10773-023-05400-1.
10.1007/s10773-023-05400-1
PubMed Google Scholar
18 Uddin M. H., Zaman U. H. M., Arefin M. A., and Akbar M. A., Nonlinear dispersive wave propagation pattern in optical fiber system, Chaos, Solitons & Fractals. (2022) 164, article 112596, https://doi.org/10.1016/j.chaos.2022.112596.
10.1016/j.chaos.2022.112596
Google Scholar
19 Cevikel A. C., Traveling wave solutions of conformable Duffing model in shallow water waves, International Journal of Modern Physics B. (2022) 36, https://doi.org/10.1142/S0217979222501648.
10.1142/S0217979222501648
Google Scholar
20 Cevikel A. C. and Bekir A., Assorted hyperbolic and trigonometric function solutions of fractional equations with conformable derivative in shallow water, International Journal of Modern Physics B. (2023) 37, no. 9, https://doi.org/10.1142/S0217979223500844.
10.1142/S0217979223500844
Google Scholar
21 Cevikel A. C., Optical solutions for the (3+1)-dimensional YTSF equation, Optical and Quantum Electronics. (2023) 55, no. 6, https://doi.org/10.1007/s11082-023-04787-9.
10.1007/s11082-023-04787-9
Google Scholar
22 Cevikel A. C., Bekir A., and Guner O., Exploration of new solitons solutions for the Fitzhugh–Nagumo-type equations with conformable derivatives, International Journal of Modern Physics B. (2023) 37, no. 23, https://doi.org/10.1142/S0217979223502247.
10.1142/S0217979223502247
Google Scholar
23 Saini S., Kumar R., Deeksha A. R., and Kumar K., Symmetry analysis and wave solutions of the Fisher equation using conformal fractional derivatives, Journal of Applied Mathematics. (2023) 2023, 10, 1633450, https://doi.org/10.1155/2023/1633450.
10.1155/2023/1633450
Google Scholar
24 Kumar R., Gupta R. K., and Bhatia S. S., Lie symmetry analysis and exact solutions for a variable coefficient generalized Kuramoto–Sivashinsky equation, Romanian Reports In Physics. (2014) 66, 923–928.
Web of Science® Google Scholar
25 Bor W. C., Oduor O. M., and Rotich J. K., A lie symmetry solutions of Sawada–Kotera equation, Journal of Advances In Mathematics. (2019) 17, 1–11, https://doi.org/10.24297/jam.v17i0.8364.
10.24297/jam.v17i0.8364
Google Scholar
26 Tayyan B. A. and Sakka A. H., Lie symmetry analysis of some conformable fractional partial differential equations, Arabian Journal of Mathematics. (2020) 9, no. 1, 201–212, https://doi.org/10.1007/s40065-018-0230-8.
10.1007/s40065-018-0230-8
Web of Science® Google Scholar
27 Mortazavi M. and Gachpazan M., New F/G–expansio method and its applications to nonlinear PDE’s in mathematical physics, Journal of Mathematical Analysis and Applications. (2016) 4, 175–183.
Google Scholar
28 Celik I., The (F/G)-expansion method and travelling wave solutions of nonlinear evolution equations, International Journal of Mathematics Research. (2016) 5, no. 1, 63–74, https://doi.org/10.18488/journal.24/2016.5.1/24.1.63.74.
10.18488/journal.24/2016.5.1/24.1.63.74
Google Scholar
29 Sahoo S., Ray S. S., and Abdou M. A., New exact solutions for time-fractional Kaup-Kupershmidt equation using improved (G’/G)-expansion and extended (G’/G)-expansion methods, Alexandria Engineering Journal. (2020) 59, no. 5, 3105–3110, https://doi.org/10.1016/j.aej.2020.06.043.
10.1016/j.aej.2020.06.043
Google Scholar
30 Rezazadeh H., Kurt A., Eslami M., and Mirzazadeh M., The new sub-equation method for the general Kaup-Kupershmidt equation using capillary gravity waves with conformal fractional derivative, Asia Pacific Journal of Mathematics. (2019) 6, 1–10.
Google Scholar

All articles

Symmetry Analysis and Wave Solutions of Time Fractional Kupershmidt Equation

Abstract

1. Introduction

2. Lie Symmetry Technique

3. Symmetry Analysis and Reduction

4. F/G-Expansion Method

5. Traveling Wave Solutions

6. Comparison Study

7. Discussions

8. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Symmetry Analysis and Wave Solutions of Time Fractional Kupershmidt Equation

Abstract

1. Introduction

2. Lie Symmetry Technique

3. Symmetry Analysis and Reduction

4. F/G-Expansion Method

5. Traveling Wave Solutions

6. Comparison Study

7. Discussions

8. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information