International Journal of Aerospace Engineering

Volume 2024, Issue 1 2122895

Research Article

Open Access

Online Energy-Aware Scheduling for Deadline-Constrained Applications in Distributed Heterogeneous Systems

Yifan Liu,

Yifan Liu

orcid.org/0000-0002-2399-1076

School of Software, Northwestern Polytechnical University, Xi’an 710072, China nwpu.edu.cn

Search for more papers by this author

Chengelie Du,

Chengelie Du

School of Computer Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China nwpu.edu.cn

Search for more papers by this author

Jinchao Chen,

Corresponding Author

Jinchao Chen

[email protected]

orcid.org/0000-0001-6234-1001

School of Computer Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China nwpu.edu.cn

Search for more papers by this author

Xiaoyan Du,

Xiaoyan Du

orcid.org/0000-0002-2711-4839

School of Computer Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China nwpu.edu.cn

Search for more papers by this author

Yifan Liu,

Yifan Liu

orcid.org/0000-0002-2399-1076

School of Software, Northwestern Polytechnical University, Xi’an 710072, China nwpu.edu.cn

Search for more papers by this author

Chengelie Du,

Chengelie Du

School of Computer Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China nwpu.edu.cn

Search for more papers by this author

Jinchao Chen,

Corresponding Author

Jinchao Chen

[email protected]

orcid.org/0000-0001-6234-1001

School of Computer Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China nwpu.edu.cn

Search for more papers by this author

Xiaoyan Du,

Xiaoyan Du

orcid.org/0000-0002-2711-4839

School of Computer Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China nwpu.edu.cn

Search for more papers by this author

First published: 02 May 2024

https://doi.org/10.1155/2024/2122895

Academic Editor: Shunan Wu

Share a link

Email
Wechat
Bluesky

Abstract

In the current computing environment, the significance of distributed heterogeneous systems has gained prominence. The research on scheduling problems in distributed systems that consider energy consumption has garnered substantial attention due to its potential to enhance system stability, achieve energy savings, and contribute to environmental preservation. However, efficient scheduling in such systems necessitates not only the consideration of energy consumption but also the ability to adapt to the dynamic nature of the system. To tackle these challenges, we propose an online energy-aware scheduling algorithm for deadline-constrained applications in distributed heterogeneous systems, leveraging dynamic voltage and frequency scaling (DVFS) techniques. First, the algorithm models the continuously arriving applications and heterogeneous processors and proposes a novel task-sorting method to prioritize tasks, ensuring that more applications are completed within their respective deadlines. Second, the algorithm controls the selection range of processors based on the task’s subdeadline and assigns the task to the processor with the minimum energy consumption. Through experiments conducted with randomly generated applications, our approach consistently exhibits superior performance when compared to similar scheduling algorithms.

1. Introduction

Distributed heterogeneous systems stand out for their network of myriad computing nodes, each furnished with a unique combination of computing resources across various types and performance tiers. In the current computing landscape, the significance of such systems has gained remarkable prominence [1, 2]. These systems offer a multitude of benefits, including high-performance, efficient, and highly reliable computing capabilities, making them suitable for a wide range of application scenarios. These domains range from scientific computation, big data analytics, and artificial intelligence to cloud services, the Internet of Things, and beyond. By harnessing the diverse array of computing resources available within distributed heterogeneous systems, it becomes feasible to adeptly meet diverse application requirements [3]. Furthermore, leveraging these resources allows for enhanced system performance, improved energy utilization efficiency, and the facilitation of innovation and development across diverse fields [4]. In the orchestration of these resources, scheduling algorithms assume a pivotal role, ensuring their efficient allocation and utilization.

The issue of energy consumption poses a significant challenge in the context of distributed heterogeneous systems. Due to the varying energy consumption characteristics of different types of computing nodes within the system, it becomes imperative to devise effective approaches for managing and optimizing energy consumption. Addressing the energy consumption problem entails the development of resource allocation and task scheduling strategies that aim to minimize overall energy consumption while meeting the performance requirements of tasks. Through the utilization of energy-aware scheduling algorithms in tandem with dynamic voltage and frequency scaling (DVFS) techniques, distributed heterogeneous systems can effectively manage and control energy consumption [5]. This approach allows the system to enhance energy efficiency and sustainability by dynamically adjusting the voltage and frequency levels of computing nodes in response to workload demands.

As is widely recognized, the energy-conscious task scheduling problem is classified as an NP-hard problem [6]. Many existing algorithms primarily address static or offline scenarios, wherein all tasks are predetermined and the environment is assumed to be stable [7–10]. Despite the wealth of insightful research on static scheduling algorithms, their adaptability falls short in the face of the dynamic landscape of distributed heterogeneous systems, which are characterized by fluctuating performance levels and node availability. Consequently, the focus on online scheduling becomes critical. Through online scheduling, dynamic decisions are made concerning task distribution and scheduling by taking into account the system’s current state as well as the real-time influx of tasks, necessitating persistent surveillance of the system and resource conditions in either real time or near real time. By doing so, the system can adapt to changing conditions, allocate tasks efficiently, and optimize energy consumption in real time, thereby enhancing overall system performance and resource utilization.

Therefore, when scheduling applications in distributed heterogeneous systems, it is necessary to consider both energy consumption and online scheduling issues simultaneously. But most studies are static [11, 12] or do not consider energy consumption [13, 14]. To tackle these challenges, we propose a dynamic scheduling algorithm for randomly arrived applications, namely, online minimum energy consumption with deadline-constrained scheduling (OMECDS) algorithm. The algorithm makes informed decisions about application allocation, resource selection, and frequency scaling, which can dynamically adapt to the system’s changing conditions and optimize resource usage based on workload characteristics, energy profiles of processors, and timing constraints. The contributions are as follows:

1.
By leveraging models of complex applications and heterogeneous processors, we propose a formulation for the energy-aware application scheduling problem in heterogeneous distributed systems. This formulation revolves around a constrained optimization approach, aiming to minimize the energy consumption of applications while adhering to strict deadline constraints.
2.
We propose an OMECDS algorithm which efficiently allocates suitable processors for stochastic incoming applications with lower time complexity. Moreover, we propose a novel approach to prioritize tasks from different applications to enhance the success rate of application execution. The proposed algorithm integrates a processor selection mechanism that considers the subdeadline defined for each task, with the primary objective of minimizing energy consumption while adhering to the imposed deadline constraints.
3.
To evaluate the performance of our proposed approach, we conducted experiments using simulations with randomly generated applications. The results obtained indicate that OMECDS outperforms other existing approaches.

The remainder of this article is organized as follows. In Section 2, we provide an overview of the related work on task scheduling algorithms. Section 3 introduces the application model, energy model, and heterogeneous processor model and provides a detailed description of the problem. In Section 4, we present the algorithm proposed in this study. Section 5 presents the experimental results and provides an in-depth analysis. Lastly, in Section 6, we discuss the conclusion and further work of our research.

2. Related Work

Considerable attention has been devoted to investigating scheduling algorithms that incorporate energy consumption considerations in distributed heterogeneous systems. This research has broadly categorized existing energy-conscious scheduling strategies into two main groups: those prioritizing completion times and those driven by multiple objectives, according to their scheduling aims.

Completion time–oriented methods prioritize minimizing the overall completion time of applications in a distributed heterogeneous system, while also taking energy consumption into account. By adjusting the voltages and frequencies of system processors through techniques like DVFS, these methods are aimed at optimizing the performance-energy trade-off. Xiao et al. [15] introduced an algorithm called MSLECC, which addresses the challenge of minimizing the dispatch length of parallel applications while ensuring limited energy consumption in heterogeneous distributed systems. MSLECC incorporates an energy consumption constraint to ensure that the energy consumed during the scheduling process remains within predefined limits. By considering the energy efficiency trade-offs associated with DVFS, the algorithm strikes a balance between achieving shorter schedule lengths and maintaining energy consumption at an acceptable level. Chen et al. [11] introduced an enhanced approach to address the challenges of the MSLECC algorithm. They proposed two key strategies: an efficient task prioritization strategy and a weight-based energy distribution strategy. Building upon the genetic algorithm framework, Liu et al. [16] proposed an energy-conscious dependence task scheduling algorithm with a multiobjective fitness function to balance the makespan and energy consumption. These aforementioned studies are geared toward enhancing scheduling efficiency in distributed heterogeneous systems by transforming the multifaceted challenge of minimizing completion time and energy consumption into a singular scheduling objective. This conversion allows for the application of various optimization techniques and algorithms to find an efficient solution.

Multiple objective-oriented scheduling algorithms are designed to address scheduling problems that involve multiple conflicting objectives [17, 18]. In scheduling scenarios, multiple objectives must be simultaneously addressed, including minimizing energy consumption, lowering costs, maximizing resource utilization, and meeting deadline constraints. The multiobjective optimization scheduling algorithm endeavors to identify an optimal set of solutions, specifically the nondominated solution set, often referred to as the Pareto optimal solution set. Zhang et al. [19] focus on the combinatorial optimization problem of biobjective optimization, aiming to achieve a high level of system reliability while minimizing energy consumption in the context of parallel tasks. Li et al. [20] introduced a hybrid energy-aware multiobjective optimization algorithm that encompasses eight distinct types of neighborhood structures. In order to balance global and local search abilities, a hybrid deep exploitation and deep exploration method is employed. Khiat, Haddadi, and Bahnes [21] employed an innovative amalgamation of hybrid genetic, max–min, min–min, and random algorithms to orchestrate a harmonious equilibrium between energy consumption and overall response time. Such an equilibrium was accomplished by the judicious modulation of processor voltages and frequencies, thereby facilitating the attainment of an optimal computational solution. Rehman et al. [22] proposed an algorithm called MOGA, which was employed to address the conflicting interests of cloud stakeholders in optimization problems. This approach is aimed at minimizing the makespan while adhering to budget and deadline constraints, while also offering an energy-efficient solution through the utilization of DVFS. Additionally, a gap search algorithm was proposed in this study to optimize the resource utilization of the cloud’s available resources.

While the papers mentioned earlier primarily focused on static scheduling methods with offline task allocation processes, there is ongoing research in the field of online scheduling algorithms that can effectively handle the arrival of random tasks [23]. Zhou et al. [24] presented a multiworkflow scheduling algorithm designed to dynamically schedule concurrent workflows while adhering to user-defined deadline and budget constraints. In their approach, they use the concept of rank_u from HEFT [25] as a task priority metric. Additionally, they introduced a bifactor selection method for resources, aiming to strike an optimal balance between the budget and deadline constraints. Arabnejad, Bubendorfer, and Ng [26] involve the utilization of a central queue to manage the workflow that has arrived. In this process, the subdeadline of each task is calculated, and the algorithm employs the early deadline first strategy to prioritize and select tasks for scheduling. This strategy is aimed at improving the success number of the workflow by ensuring that tasks with earlier deadlines are scheduled first.

In the domain of task scheduling for distributed heterogeneous systems, it is crucial to take into account both energy consumption and online scheduling issues. By employing appropriate online energy consumption-aware scheduling algorithms, it enhances the overall system performance and improves energy utilization efficiency.

3. Model

In this section, we establish the heterogeneous processor model, application model, and energy model utilized in our study.

3.1. Heterogeneous Processor Model

The distributed heterogeneous system we considered consists of m diverse processors, denoted as P = {p_k|k ∈ [1, 2, ⋯, m]}, interconnected by a high-speed network. Each individual processor, p_k ∈ P, is equipped with DVFS capabilities, allowing it to switch between different frequencies, denoted as f_k. The available frequency range for processor p_k spans from the minimum value, , to the maximum value, . It is important to note that the execution time of a task decreases as the processor’s frequency increases, while the energy consumption increases. We disregard the energy impact resulting from processor frequency-state transitions. In our assumption, when a task is assigned to a processor, it is executed immediately. However, it is important to note that a processor can only execute one task at a time. This restriction ensures that the processor’s resources are effectively utilized and that tasks are processed sequentially to avoid any conflicts or resource contention [27, 28].

3.2. Application Model

A parallel application, composed of several interlinked tasks, can be depicted as a directed acyclic graph (DAG). In this representation, each node corresponds to an individual task, and each edge delineates the data dependencies among tasks. The application is submitted in a stochastic manner, but once submitted, all relevant information about the application is known. We denote the set of dynamic applications as η = {G₁, G₂, ⋯, G_w}. A specific DAG within this set, denoted as G_s, is modeled as G_s = {a^s, d^s, V^s, E^s}. In this model, a^s represents the arrival time of G_s, d^s represents the deadline of G_s, V^s is the set of nodes, where each node represents a task, and E^s is the set of edges, where each directed edge indicates the data dependency between tasks and . The communication time between tasks and is denoted as . If and are located on the same processor, we assume the communication time . A task can only be executed when all the data from its predecessors have been transferred. A task without any immediate predecessors is referred to as an entry task, symbolized as , while a task with no successors is referred to as an exit task, symbolized as . Figure 1 shows an example of a DAG-based parallel application that describes the data dependencies of eight tasks.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

An example of a DAG-based parallel application with eight tasks.

Due to the heterogeneity of processors, the execution time of a task can vary across different processors. The average execution time of task

across all processors with the maximum frequency is defined as follows:

()

where

is the execution time of task

on processor p_k with the maximum frequency. The performance of a processor is influenced by its operating frequency, which in turn can lead to varying execution times for the same task. The actual execution time of task

when allocated on processor p_k with frequency f_k,h is defined as follows:

()

where f_k,h is the actual frequency of p_k and f_k,max is the maximum frequency of p_k.

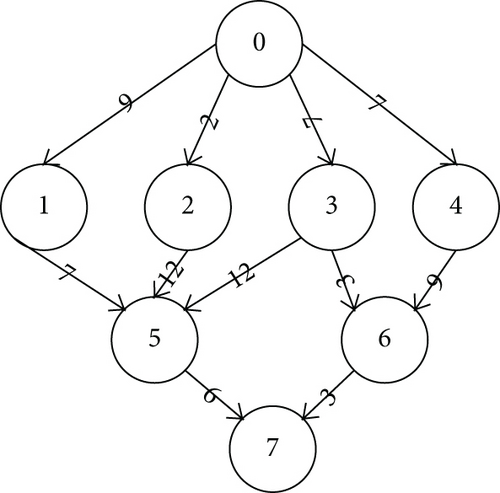
The completion of all tasks in the DAG G_s signifies the completion of G_s as a whole.

Therefore, we define makespan^s as the time it takes for G_s to be fully completed. The calculation of makespan^s can be determined by

()

where

is the actual finish time of

3.3. Energy Model

For the processor′s power model, we used the references in the existing articles [12, 29, 30]. The power consumption manifests in two forms: dynamic and static power consumption. The power consumption Power(p_k) of processor p_k with frequency f_k,h can be computed via

()

where

represents the static/leakage power consumed when the processor is turned on,

denotes the frequency-independent dynamic power,

represents the effective switching capacitance, m_k is the dynamic power exponent, and h is a Boolean coefficient indicating whether the processor is active or inactive. If a task is being executed on this processor, h = 1; otherwise, h = 0. It is assumed in this paper that the static power, which can only be eliminated by turning off the processor, is ignored. Additionally, it is assumed that the processor can only change its frequency when no task is being executed on it.

While DVFS can indeed contribute to curbing energy consumption, it is imperative to acknowledge that operating at diminished frequencies may inevitably lead to prolonged completion times for applications. Consequently, considering system-level power alone, lower frequencies may not always be the optimal choice for achieving energy savings. Thus, there exists a minimum energy-efficient frequency for processor p_k, denoted as f_k,ee [31–33], which is determined by

()

Assuming that the processor’s frequency can be adjusted continuously within the range of f_k,min and f_k,max, it is crucial for energy efficiency to limit the actual frequency f within the range of f_k,low and f_k,max (i.e., f ∈ [f_k,low, f_k,max]). f_k,low is determined as the maximum value between f_k,min and f_k,ee, which is calculated by

()

The energy consumption

of task

on the processor p_k with frequency f_k,h is calculated as

()

Therefore, the total energy consumption of application G_s can be obtained by

()

The used notations in this paper are presented in Table 1.

Table 1. The used notations in this paper.

Notation	Implication
p_k	The k-th processor in the system
m	The number of processors
G_s	The s-th DAG in the system
a^s	The arrival time of DAG G_s
d^s	The deadline of G_s
V^s	The set of tasks in G_s
E^s	The set of edges between all tasks in G_s
	The i-th task in G_s
n^s	The number of tasks in G_s
	The set of predecessors of task
	The set of successors of task
	The data transfer time between and
	The average execution time of
	The actual execution time of task on processor p_k with frequency f_k,h
	The earliest start time of
	The earliest finish time of
avail(p_k)	The earliest time that the processor p_k can execute a task
makespan_s	Schedule completion time of G_s
	The energy consumption of task on the processor p_k with frequency f_k,h

3.4. Problem Description

The primary aim of this study is to tackle the issue of allocating available processors to all tasks within incoming applications, considering the appropriate frequency settings for each task. The objective is to minimize the energy consumption of the application while simultaneously guaranteeing that the execution time of the application remains within the specified deadline constraints. The algorithm tries to find an optimal allocation strategy that achieves a balance between minimizing energy usage and meeting the application’s deadline requirements. Hence, the optimization objective is defined as follows:

()

Constraint (1) in Equation (9) states that a task cannot be executed until all of its predecessors are completed, and all data transmissions between them have been finished. The variable

represents the actual start time of task

. The

is the actual finish time of task

. The

is determined by adding the actual execution of

to the actual start time

. In Constraint (2), the binary variable

indicates whether task

is assigned to processor p_k. This assignment is defined as follows:

()

Constraint (2) ensures that each task can only be scheduled once, preventing duplication or multiple assignments. Constraint (3) states that the actual completion time of the application must satisfy its deadline requirement.

4. Proposed OMECDS Algorithm

In this section, we introduce the OMECDS algorithm, tailored for managing the scheduling of multiple applications with diverse arrival times within a heterogeneous distributed system. The main objective of the algorithm is to minimize the overall energy consumption of the system while efficiently scheduling as many applications as possible. This is accomplished through meticulous optimization of resource allocation and task scheduling, all the while adhering to the specified deadline constraints of the applications. The algorithm is divided into two main phases: the task selection phase and the processor allocation phase.

During the task selection phase, we introduce a novel approach to calculate the priority and subdeadline of each ready task derived from the incoming applications. The computation of priority and subdeadline takes into account an array of factors including task dependencies, arrival time, overarching scheduling objectives, and other pertinent considerations.

In the processor allocation phase, we map each eligible task to an available processor, taking into account the task’s subdeadline. The goal is to assign the task to a processor and select an appropriate frequency setting that ensures the subdeadline is not violated while minimizing energy consumption. This phase involves making intelligent decisions to optimize the allocation of processors and frequencies, considering the dynamic characteristics of the tasks and the available resources. The objective is to achieve efficient task execution while conserving energy resources.

4.1. Task Selection Phase

In contrast to static scheduling, online scheduling operates under the condition that the topology and data information of the application are unknown until the application is submitted. This necessitates that the algorithm must be capable of handling incoming applications, parsing their task information, and making decisions promptly. The algorithm must dynamically adapt to the evolving task requirements and efficiently make real-time scheduling decisions. It should be able to process incoming applications on the fly, adjust the task allocation, and optimize the resource utilization based on the available information. This ability to handle unknown and evolving application characteristics is essential for effective online scheduling. As the DAGs arrive, they are stored in the DAG_Pool, and their parameters are parsed during the task selection phase. In this phase, the algorithm is aimed at identifying the ready tasks, determining their priority, and allocating subdeadline for scheduling.

When a DAG is added to the DAG_Pool, the earliest start time and the last finish time of its tasks can be calculated based on the provided feature parameters. The earliest start time represents the earliest possible time for a task to be executed on a processor, which means that all tasks are finished at a minimum time. We denote the earliest start time of task

, which is defined as follows:

()

where the

is the set of the immediate predecessors of task

. The entry task’s earliest start time is its application’s arrival time. Accordingly, the earliest finish time of

is defined as

()

The latest finish time of a task represents the maximum allowable time for its completion, ensuring that the task does not exceed the specified deadline constraint. We define

as latest finish time of

, which can be calculated by

()

where

is the set of immediate successors of

To accommodate the system’s dynamics and adhere to task priority constraints, the OMECDS employs a strategy of exclusively scheduling ready tasks during each iteration. This approach prevents the scenario where the initial applications occupy a significant portion of system resources, potentially impeding the completion of subsequent applications. By prioritizing the scheduling of ready tasks, the algorithm ensures that tasks from different applications have a fair opportunity to be executed and progress toward completion according to their priorities. This approach promotes efficient utilization of system resources and facilitates the timely execution of all arriving applications.

Ready task means a task has no predecessor or its all immediate predecessors have been completed. When new DAGs arrive, all the entry tasks within the DAG are considered ready tasks and are added to the ready task list (RTL). Additionally, when the last unfinished predecessor of a task is completed, that task becomes a ready task and is also added to the RTL. As a result, the RTL consists of all tasks that are currently ready for execution. All tasks within the RTL can be executed in parallel, as they have met their dependencies and are independent of each other in terms of execution order.

Sorting the ready tasks is a crucial aspect of this work. Unlike previous studies [15, 34], which focused on a single DAG and utilized the rank_u as the tasks’ priority, this work deals with tasks from multiple DAGs that have distinct deadlines. To maximize the number of completed DAGs within their respective deadlines, we introduce the concept of

as the priority of tasks, which can be calculated by

()

The closer the task’s is to the , the more priority it has. We rank urgency of all ready tasks. This prioritization allows for the scheduling algorithm to focus on tasks that are time-critical to ensure the successful completion of the corresponding DAGs within their deadlines. When comparing priorities between two tasks and , if both urgency of and are positive or negative, the task exhibiting greater urgency is deemed to have higher priority. Conversely, if the urgency value is one positive and the other negative, the task with negative urgency is ascribed higher priority.

The process of handling newly arrived applications in OMECDS is outlined in Algorithm 1. The algorithm utilizes the RTL to manage tasks that are ready for execution. Upon the arrival of new DAGs, the algorithm calculates the earliest start time , earliest finish time , and latest finish time for all tasks in the DAG (Line 1). This information is crucial for scheduling and processor allocation. For the new DAGs, only entry tasks are considered ready tasks. The algorithm adds these entry tasks to the RTL (Line 2). Additionally, all unselected tasks are added to the TaskPool (Line 3). The TaskPool serves as a repository for tasks that are not yet ready for execution. The algorithm sorts the ready tasks in the RTL based on their values (Line 4). This prioritization ensures that tasks with higher urgency, often associated with closer deadlines or critical dependencies, are scheduled first. Finally, ready tasks in the RTL are allocated to available processor using the function ScheduleReadtTask(RTL) (Line 5). This step involves assigning suitable processors and frequencies to the tasks, while considering their timing constraints and energy efficiency objectives.

In a DAG with n tasks, the maximum number of edges e is given by ((n − 1)n)/2. In Algorithm 1, Line 1 calculates , , and for each task in order to determine their scheduling parameters. This calculation requires a time complexity of O(n²). In Line 4, the length of the RTL queue is determined by the maximum indegree of a task in G_s, denoted as n_in. Sorting tasks in the RTL queue takes a time complexity of O(n_in × log(n_in)). The calculation of urgency in the algorithm also takes a time complexity of O(n_in). Therefore, the overall time complexity of task selection for an arrival DAG G_s in the algorithm is O(n² + n_in × log(n_in)). Considering that n_in is typically small compared to n, we can simplify the time complexity to O(n²).

Algorithm 1: The preprocessing for an arrival DAG.

Require: The arrival DAG G_s = {a^s, d^s, V^s, E^s}.
Calculate , and for each tasks in V^s;
Add all entry tasks into RTL;
Add other tasks in V^s into TaskPool;
Calculate the of all tasks in RTL; and sort them in non-descending order;
Call ScheduleReadyTask(RTL; );

The process of the algorithm that handles the completed task is detailed by Algorithm 2. When a task is completed, the algorithm identifies the immediate successor tasks that become ready as a result. These ready tasks are added to the RTL to indicate that they are now eligible for execution (Lines 1–5). The values of selected tasks are calculated (Line 3). The selected tasks are then removed from the TaskPool to indicate that they have been scheduled for execution (Line 4). Tasks in the RTL are sorted based on their urgency values (Line 7). This ensures that the tasks with higher urgency, which reflects their priority, are scheduled first. Finally, the function ScheduleReadyTask(RTL) is called to allocate the resources and execute the ready tasks (Line 8).

The completion of a task indicates that its immediate successor tasks are likely to be ready for execution. By promptly identifying and scheduling ready tasks, the algorithm can potentially complete more applications within their respective deadline constraints. This dynamic handling of ready tasks enhances the overall efficiency and effectiveness of the scheduling algorithm. When a task is completed, Algorithm 2 needs to traverse each task in , which needs time O(n_out). O(n_out) is the maximum outdegree of a task among G_s. The time complexity in Line 2 is O(n_in). The length of RTL saving the ready task in is at most equal to n_out. Sorting tasks in RTL requires time O(n_outlog(n_out)). Hence, the time complexity of the processing for the finish of a task is O(n_in × n_out + n_out × log(n_out)).

Algorithm 2: The processing for the finish of a task.

Require: A completed task
For each do
If all of pred have been completed then
Calculate ;
Add task into RTL and remove from TaskPool;
Endif
Endfor
Sort all tasks in RTL by urgency in a non-descending order;
Call ScheduleReadyTask(RTL);

4.2. Processor Allocation Phase

In the processor allocation phase, the algorithm assigns appropriate processors and frequencies to the tasks in the RTL based on their priority order. The objectives are to ensure the timely completion of tasks, thereby averting any severe consequences, and to reduce the overall energy consumption of the system.

To meet the deadline constraints, we segment the overarching deadline of the application into subdeadlines, each meticulously assigned to individual tasks. The problem of matching the overall deadline of an application is transformed into the problem of matching the subdeadline of each individual task within the application. This transformation allows for a more fine-grained and task-centric approach to deadline management. The subdeadline of

can be calculated as

()

where

is the last finish time of last task in G_s and

is the earliest time of first task. It should be emphasized that the slack time

, associated with task

, must not surpass its latest finish time

. Should the calculation of

based on Equation (15) result in a value greater than

, the

is accordingly adjusted to equal

. Transforming the problem in this way enables the algorithm to schedule tasks based on their individual subdeadlines. It provides a more detailed understanding of the temporal requirements of each task and facilitates more accurate processor allocation and scheduling decisions.

The algorithm iterates through all available processors and frequencies to find the best combination for each ready task

. It considers the energy consumption

for each processor p_k and frequency f_k,h and checks if the estimated finish time

on that combination is less than the task’s subdeadline

can be calculated by

()

where avail(p_k) is the earliest time that p_k is idle.

By iterating through all possible combinations and selecting the one with the minimum energy consumption that satisfies the subdeadline constraint, the algorithm ensures that the task is allocated to the best available resources in terms of energy efficiency while meeting its timing requirements. If none of the processors can complete the task within its SD, then assign the task to the processor that completes it the fastest.

Algorithm 3: Function ScheduleReadyTask(RTL).

Require: each task in RTL.
Ensure: The schedule scheme.
For each in RTLdo
Emineft, minE⟵MAXVALUE, bestPro, bestF⟵∅;
For all processor p_kdo
For all frequency f_k,hdo
Calculate the , , and ;
If then
If then
, bestPro⟵p_k, bestF⟵f_k,h, ;
Endif
Endif
Endfor
Endfor
Schedule on bestPro with bestF;
Remove from RTL;

The pseudocode of the processor allocation phase is stated in Algorithm 3. The algorithm iterates through all available processors and frequencies to find the best combination for each ready task (Lines 1–15). The algorithm initializes related variables for every task in RTL (Line 2). Then, traverse all processors and frequencies and calculate est, eft, and E (Lines 3–5). The algorithm checks if the earliest finish time () of the task on the selected processor and frequency is less than the task’s subdeadline () (Line 6). This ensures that the allocated processor can complete the task within the specified subdeadline. The algorithm selects the processor bestPro and frequency bestF combination that results in the minimum energy consumption for the task (Lines 7 and 8). Finally, assign task to bestPro with bestF for execution and remove from RTL (Lines 13–15).

In the processor allocation phase, we only select ready tasks for scheduling, which helps improve the system’s responsiveness to dynamic events. By considering both energy consumption and subdeadline constraints, OMECDS chooses the best processor and frequency combination that minimizes energy consumption while considering the deadline constraint. The length of queue RTL is at most equal to n_in. For each task in RTL, Algorithm 3 needs to traverse all processors. The number of computing processors is m, and the maximum number of frequencies is H. Lines 1–5 in Algorithm 3 are to calculate , , and for each task and each processor, which need time . The time complexity of resource allocation is O(n_in × m × (n_in + H)).

5. Results

In this section, the performance of the proposed OMECDS algorithm is evaluated by comparing it with the LESA [11], MSLECC [15], and FCFS with rank_u algorithms. LESA addresses the challenge of energy-aware scheduling for dependent tasks on a heterogeneous multiprocessor system. It introduces a list-based algorithm to effectively determine start times and processor assignments. The approach optimizes task execution by balancing dependencies and energy constraints, strategically choosing suitable processors and speed settings for minimal completion time. MSLECC is a classic method of solving dependent task scheduling problems with the shortest schedule length while considering energy consumption constraints. It differs in task sequencing and energy allocation methods from LESA. FCFS with rank_u algorithm gives a rank for each DAG task according to the HEFT [25] and schedules DAGs according to the “first come first service.” For the online scheduling problem considered in this article, the LESA and MSLECC algorithms are repeatedly executed at each new DAG arrival to handle the scheduling. All the algorithms used in the experiments are implemented in the Java programming language. The experiments were conducted on a computer with an Intel® Core™ i7-10700H CPU operating at 2.90 GHz, 16.00 GB RAM, and a 64-bit Windows 10 operating system.

5.1. Experimental Setup

The simulated heterogeneous distributed system consists of m processors with varying processing capabilities. The processor and application parameters used in the experiments are as follows: , , , , 2.5 ≤ m_k ≤ 3.0, and f_k,max = 1 GHz (all the frequency values are discrete with an accuracy of 0.01 GHz). These parameters are set exactly by reference to existing work [3, 12, 35]. In this experiment, 20 processors are randomly generated for each experiment.

The random DAGs used in the experiment are generated using a DAG generator based on several parameters, namely, CCR, n, fat, density, regularity, and jump. The parameter settings are chosen based on a previous paper [13] to ensure a diverse set of DAG characteristics. CCR represents the ratio of communication to computation in the DAG. The available values for this parameter are {0, 1, 2}. n determines the total number of tasks in the DAG. The values used in the experiment are {10, 20, 30, 40, 50, 60, 70, 80, 90, 100}, providing a range of DAG sizes. fat influences the width and height of the DAG, thereby affecting its overall structure. The available values are {0.2, 0.4, 0.6}. density impacts the number of edges between different levels of nodes in the DAG. A higher density value indicates a larger number of edges. The values used in the experiment are {0.2, 0.4, 0.6}. regularity affects the uniformity of the number of tasks at each level of the DAG. A higher regularity value indicates a higher similarity in the number of tasks among different levels. The set of values used is {0.2, 0.4, 0.6}. jump represents the number of different levels an edge can connect. A larger jump value allows edges to connect nodes that are farther apart in the DAG. The available values for this parameter are {1, 2, 4}. Table 2 summarizes the parameter settings used in the DAG generator.

Table 2. The generator parameters of DAG.

Parameters	Value
n	= [10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
fat	= [0.2, 0.4, 0.6]
density	= [0.2, 0.4, 0.6]
regularity	= [0.2, 0.4, 0.6]
jump	= [1, 2, 4]
CCR	= [0, 1, 2]

To simulate the dynamic arrival of DAGs, an arrival time needs to be set for each DAG. The arrival time represents the time when the DAG becomes available for scheduling, which is defined as

()

where α is the parameter that can control the spacing and distribution of the DAG arrivals. The α is chosen with the values {5%, 10%, 15%, 20%, 25%, 30%}, where the default value is 15%. The arrival time interval is α multiply the deadline of the last arrived DAG. The larger the value of α, the longer the arrival interval of DAGs. The arrival time of the first DAG is 0.

The deadline of a DAG can be defined based on the calculation of a deadlineBase. deadlineBase represents the completion time of the longest path from the entry task to the exit task in the DAG, without considering the communication cost. By using the deadlineBase, we obtain the minimum overall deadline d^s for the DAG which is defined as

()

where β is selected from [2, 2.5, 3, 3.5, 4, 4.5]. The default value of β is 2. We have procedurally generated the minimum execution times for tasks on an assortment of processors, ensuring a stochastic representation of the system’s performance characteristics.

5.2. Results and Discussion

5.2.1. Planning Successful Rate (PSR) and Energy Consumption Analyses

In the experiment, the performance of the algorithms is evaluated based on two metrics: energy consumption and PSR [36]. The PSR metric represents the percentage of successfully scheduled DAGs, which is calculated as

()

where a successful schedule means that the makespan of a DAG is less than its deadline. The energy consumption metric measures the total energy consumed by the system during the execution of the scheduled DAGs. To analyze the algorithms’ performance in a dynamic environment, each algorithm is executed independently 20 times to obtain reliable and statistically significant results, and mean values are calculated. One thousand DAGs are generated using the random parameter values as a DAG pool. From this pool of DAGs, a set of 20 DAGs is randomly selected for each schedule. By running the algorithms multiple times and considering a diverse set of DAGs, the experiment is aimed at providing a comprehensive evaluation of the algorithms’ performance, taking into account different scenarios and variations in DAG characteristics.

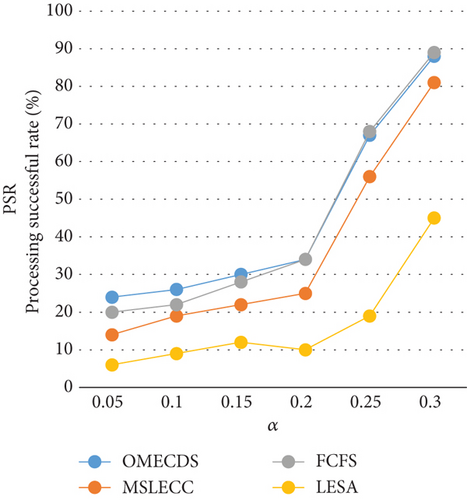
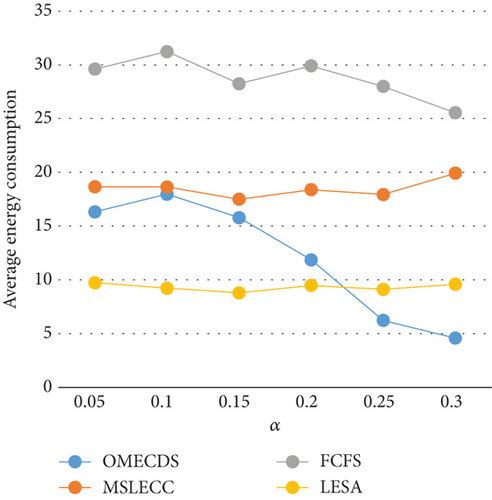
The first experiment, depicted in Figure 2, encompasses the evaluation of both PSR and average energy consumption across varying arrival time intervals. In Figure 2(a), the PSR demonstrates a discernible upward trend as the arrival time interval increases. This increase in the arrival factor, denoted by α, implies a reduction in the number of applications that the system must process within a unit of time. In the system under consideration, the number of processors is fixed. This means that the computing power of the system is limited. Consequently, the reduction of α leads to an enhancement in the successful completion rate of applications. However, it is important to note that the FCFS algorithm prioritizes minimizing the completion time of applications at the expense of significantly higher energy consumption, as illustrated in Figure 2(b). As the value of α increases, the urgency to complete applications within the specified deadline diminishes, leading to a greater emphasis on energy consumption performance, as depicted in Figure 2(b) when α exceeds 0.2. Remarkably, the OMECDS algorithm surpasses the MSLECC algorithm achieves notable energy savings and PSR improvements. In comparison to the LESA algorithm, the OMECDS algorithm exhibits a 30.55% increase in average energy consumption, but a remarkable 204.5% improvement in average PSR. When compared to the FCFS algorithm, the OMECDS algorithm achieves a 58.57% reduction in energy consumption and a 7.12% increase in average PSR.

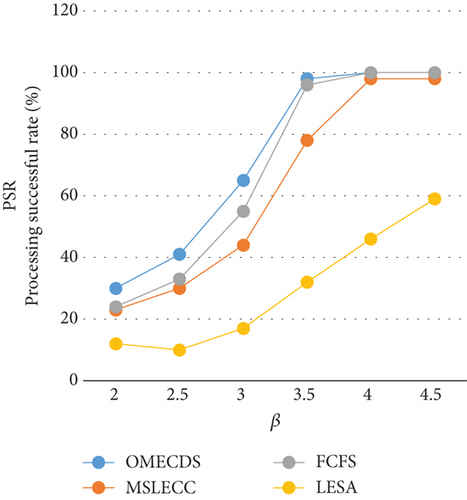
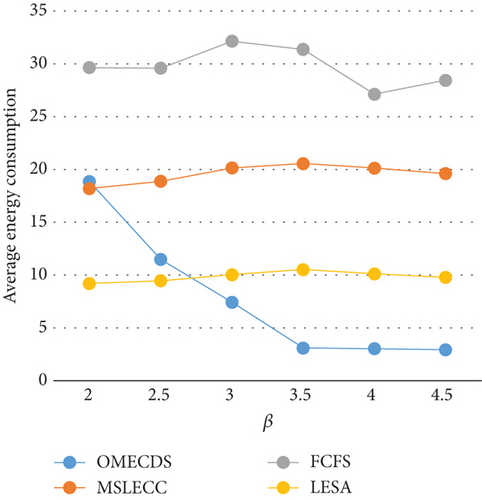
Figures 3(a) and 3(b) present the PSR and average energy consumption of the four algorithms under varying deadline factors. With an increase in the value of β, the deadlines for each application are extended, resulting in an improvement in the PSR for all algorithms. When β surpasses 3.5, OMECDS exhibits the capability to schedule all arrived applications while meeting their respective deadlines. OMECDS demonstrates a more remarkable ability to minimize energy consumption when the deadline is relaxed, as evidenced in Figure 3(b). In contrast, MSLECC and LESA algorithms allocate energy for each task, leading to similar energy consumption even under different deadline constraints, because their energy consumption constraints are fixed. Based on the experimental results, it is evident that OMECDS outperforms both FCFS and MSLECC algorithms in terms of both PSR and energy consumption across different values of β. Additionally, OMECDS surpasses LESA in terms of PSR across varying β values. Notably, when compared to LESA, in general, OMECDS still achieves a significant 18.41% reduction in average energy consumption.

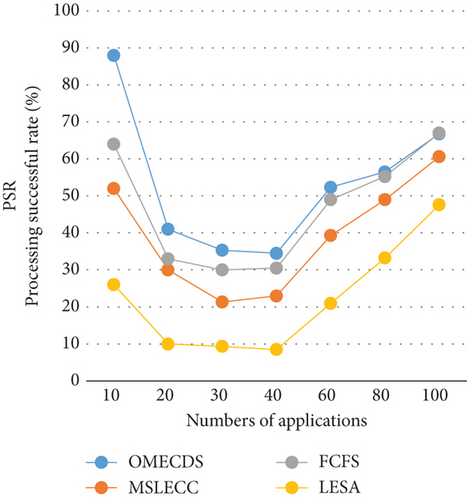
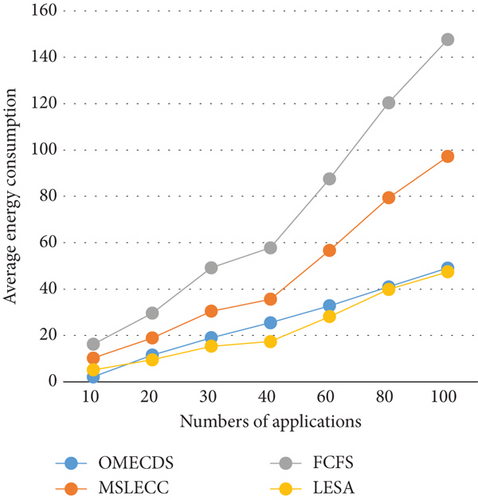
In Figure 4, we experiment with different numbers of applications. Notably, the number of tasks in an application is still randomly generated. The number of applications is 10, 20, 30, 40, 60, 80, and 100. The α is 0.15 and β is 2.5. Obviously, OMECDS exhibits superior performance compared to FCFS and MSLECC algorithms. Compared with LESA, the average energy consumption of OMECDS experiences a slight increase of 7.97%, but the PSR shows a substantial improvement of 198%.

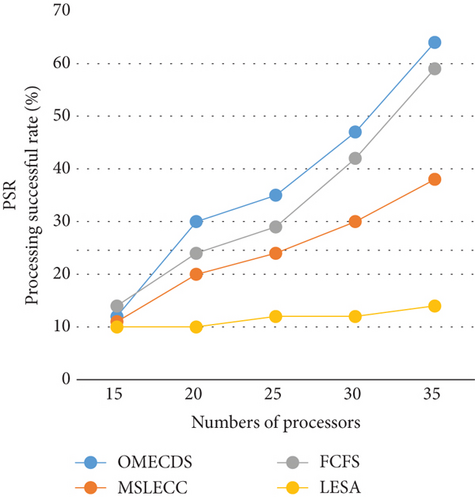
Figures 5(a) and 5(b) show the performance of the four algorithms with a varied number of processor, while keeping the number of applications fixed at 20. All processors are randomly generated. The value of α is set to 0.15 and the value of β is set to 2. As the number of processors increases, the PSR of all algorithms tends to increase. When compared to MSLECC, OMECDS achieves an average PSR improvement of 46% and reduces average energy consumption by 20.11%. In comparison to FCFS, OMECDS shows a 10.35% improvement in PSR and a 48.72% reduction in energy consumption. Compared with LESA, OMECDS experiences a 63.94% increase in energy consumption but exhibits an impressive average PSR improvement of 212.09%. Overall, when considering both the successful completion rate of applications and energy consumption, OMECDS performs better than the other algorithms.

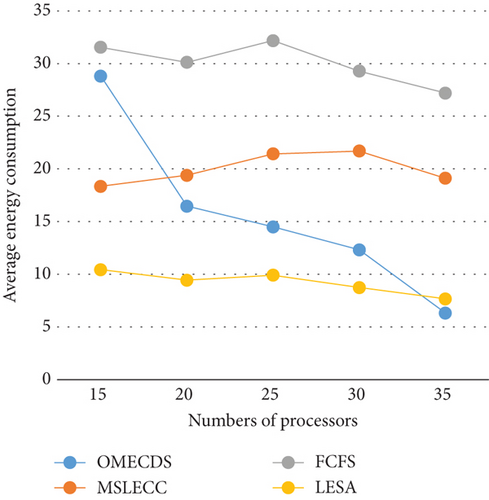
5.2.2. Runtime Analyses

This subsection is aimed at evaluating the time efficiency of the four algorithms. The running time represents the duration from the start of the algorithm to the point of finding a solution. Time performance is one of the important indicators to measure the algorithm.

In the first comparison, we analyze the average runtime of all algorithms under different deadline factors β, as illustrated in Figure 6. As mentioned previously, when the deadline constraint becomes looser, OMECDS algorithm tends to prioritize solutions with lower energy consumption. Consequently, as β increases, the running time of OMECDS experiences a slight increase. On the other hand, FCFS exhibits better time performance compared to OMECDS, LESA, and MSLECC due to its utilization of the maximum frequency for processors without dynamic adjustments. However, it is important to note that OMECDS still demonstrates better time performance compared to LESA and MSLECC. Both MSLECC and LESA are heuristic-based algorithms with low time complexity, indicating that OMECDS maintains good execution efficiency while achieving its objectives.

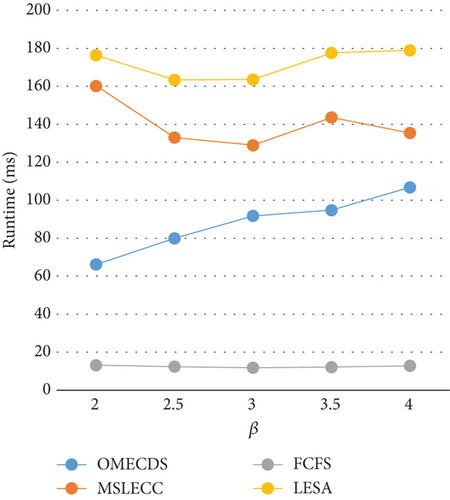
The last experiment is aimed at investigating the average running time of all algorithms under varying numbers of randomly generated applications. In Figure 7, it can be observed that as the number of applications increases, the average execution time of all algorithms also increases. However, our proposed algorithm demonstrates significantly shorter average execution times when compared to LESA and MSLECC. Although FCFS has a shorter execution time than OMECDS, it is important to highlight that OMECDS excels in application completion and energy savings. In summary, OMECDS exhibits outstanding performance in terms of execution efficiency, energy savings, and successful application scheduling.

6. Conclusions

To tackle the dynamic scheduling problem associated with parallel applications in heterogeneous distributed systems, we have introduced the OMECDS algorithm, which is aimed at minimizing energy consumption while adhering to deadline constraints. The proposed algorithm boasts a low computational complexity, making it efficient in practical implementation. Our devised task priority method effectively manages the spontaneous arrival of applications, while the formulation of subdeadlines and the selection mechanism for processors strike an optimal balance between meeting deadlines and minimizing energy consumption. Experimental results have demonstrated the superior performance of our approach compared to alternative algorithms. However, for future work, we plan to delve into distributed methods to tackle existing challenges. Centralized approaches are susceptible to single points of failure. We aspire to explore distributed solutions that can augment reliability and robustness in scheduling parallel applications.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Y.L. and J.C. designed the resource. Y.L. wrote the first draft of the paper. Y.L., X.D., J.C., and C.D. analyzed the results, read the manuscript, and approved the final version. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (No. 62106202), the Key Research and Development Program of Shaanxi (No. 2024GX-YBXM-118), the Aeronautical Science Foundation of China (No. 2023M073053003), and the Fundamental Research Funds for the Central Universities.

Open Research

Data Availability Statement

Data will be made available on request.

References

1 Chen J., Du C., Zhang Y., Han P., and Wei W., A clustering-based coverage path planning method for autonomous heterogeneous UAVs, IEEE Transactions on Intelligent Transportation Systems. (2022) 23, no. 12, 25546–25556, https://doi.org/10.1109/TITS.2021.3066240.
10.1109/TITS.2021.3066240
Web of Science® Google Scholar
2 Chen J., Zhang Y., Wu L., You T., and Ning X., An adaptive clustering-based algorithm for automatic path planning of heterogeneous UAVs, IEEE Transactions on Intelligent Transportation Systems. (2022) 23, no. 9, 16842–16853, https://doi.org/10.1109/TITS.2021.3131473.
10.1109/TITS.2021.3131473
Web of Science® Google Scholar
3 Xie G., Zeng G., Xiao X., Li R., and Li K., Energy-efficient scheduling algorithms for real-time parallel applications on heterogeneous distributed embedded systems, IEEE Transactions on Parallel and Distributed Systems. (2017) 28, no. 12, 3426–3442, https://doi.org/10.1109/TPDS.2017.2730876, 2-s2.0-85028877854.
10.1109/TPDS.2017.2730876
Web of Science® Google Scholar
4 Zhang Q., Geng S., and Cai X., Survey on task scheduling optimization strategy under multi-cloud environment, CMES-Computer Modeling in Engineering & Sciences. (2023) 135, no. 3, 1863–1900, https://doi.org/10.32604/cmes.2023.022287.
10.32604/cmes.2023.022287
Web of Science® Google Scholar
5 Zhang Y., DVFS-based energy-aware scheduling of imprecise mixed-criticality real-time tasks, Journal of Systems Architecture. (2023) 137, article 102849, https://doi.org/10.1016/j.sysarc.2023.102849.
10.1016/j.sysarc.2023.102849
Web of Science® Google Scholar
6 Tang X., Cao W., Tang H., Deng T., Mei J., Liu Y., Shi C., Xia M., and Zeng Z., Cost-efficient workflow scheduling algorithm for applications with deadline constraint on heterogeneous clouds, IEEE Transactions on Parallel and Distributed Systems. (2022) 33, no. 9, 2079–2092, https://doi.org/10.1109/TPDS.2021.3134247.
10.1109/TPDS.2021.3134247
Web of Science® Google Scholar
7 Chang S., Zhao X., Liu Z., and Deng Q., Real-time scheduling and analysis of parallel tasks on heterogeneous multi-cores, Journal of Systems Architecture. (2020) 105, article 101704, https://doi.org/10.1016/j.sysarc.2019.101704.
10.1016/j.sysarc.2019.101704
Web of Science® Google Scholar
8 Zhou J., Yan J., Cao K., Tan Y., Wei T., Chen M., Zhang G., Chen X., and Hu S., Thermal-aware correlated two-level scheduling of real-time tasks with reduced processor energy on heterogeneous MPSoCs, Journal of Systems Architecture. (2018) 82, 1–11, https://doi.org/10.1016/j.sysarc.2017.09.007, 2-s2.0-85033397789.
10.1016/j.sysarc.2017.09.007
CAS Web of Science® Google Scholar
9 Potluri S., Mohanty S., and Mohanty S., QoS-driven hybrid task scheduling algorithm in a cloud computing environment, International Journal of Grid and Utility Computing. (2023) 14, no. 4, 311–319, https://doi.org/10.1504/IJGUC.2023.132614.
10.1504/IJGUC.2023.132614
Web of Science® Google Scholar
10 Chen J., Han P., Zhang Y., You T., and Zheng P., Scheduling energy consumption-constrained workflows in heterogeneous multi-processor embedded systems, Journal of Systems Architecture. (2023) 142, article 102938, https://doi.org/10.1016/j.sysarc.2023.102938.
10.1016/j.sysarc.2023.102938
Web of Science® Google Scholar
11 Chen J., He Y., Zhang Y., Han P., and Du C., Energy-aware scheduling for dependent tasks in heterogeneous multiprocessor systems, Journal of Systems Architecture. (2022) 129, article 102598, https://doi.org/10.1016/j.sysarc.2022.102598.
10.1016/j.sysarc.2022.102598
Web of Science® Google Scholar
12 Gao N., Xu C., Peng X., Luo H., Wu W., and Xie G., Energy-efficient scheduling optimization for parallel applications on heterogeneous distributed systems, Journal of Circuits, Systems and Computers. (2020) 29, no. 13, article 2050203, https://doi.org/10.1142/S0218126620502035.
10.1142/S0218126620502035
Web of Science® Google Scholar
13 Wang G., Wang Y., Obaidat M. S., Lin C., and Guo H., Dynamic multiworkflow deadline and budget constrained scheduling in heterogeneous distributed systems, IEEE Systems Journal. (2021) 15, no. 4, 4939–4949, https://doi.org/10.1109/JSYST.2021.3087527.
10.1109/JSYST.2021.3087527
Web of Science® Google Scholar
14 Liu J., Ren J., Dai W., Zhang D., Zhou P., Zhang Y., Min G., and Najjari N., Online multi-workflow scheduling under uncertain task execution time in IaaS clouds, IEEE Transactions on Cloud Computing. (2021) 9, no. 3, 1180–1194, https://doi.org/10.1109/TCC.2019.2906300, 2-s2.0-85063365326.
10.1109/TCC.2019.2906300
Web of Science® Google Scholar
15 Xiao X., Xie G., Li R., and Li K., Minimizing schedule length of energy consumption constrained parallel applications on heterogeneous distributed systems, 2016 IEEE Trustcom/BigDataSE/ISPA, 2016, Tianjin, China, 1471–1476, https://doi.org/10.1109/TrustCom.2016.0230, 2-s2.0-85015163212.
10.1109/TrustCom.2016.0230
Google Scholar
16 Liu Y., Du C., Chen J., and Du X., Scheduling energy-conscious tasks in distributed heterogeneous computing systems, Concurrency and Computation: Practice and Experience. (2022) 34, no. 1, article e6520, https://doi.org/10.1002/cpe.6520.
10.1002/cpe.6520
Web of Science® Google Scholar
17 Chen J., Li T., Zhang Y., You T., Lu Y., Tiwari P., and Kumar N., Global-and-local attention-based reinforcement learning for cooperative behaviour control of multiple UAVs, IEEE Transactions on Vehicular Technology. (2024) 73, no. 3, 4194–4206, https://doi.org/10.1109/TVT.2023.3327571.
10.1109/TVT.2023.3327571
Web of Science® Google Scholar
18 Chen J., Ling F., Zhang Y., You T., Liu Y., and Du X., Coverage path planning of heterogeneous unmanned aerial vehicles based on ant colony system, Swarm and Evolutionary Computation. (2022) 69, article 101005, https://doi.org/10.1016/j.swevo.2021.101005.
10.1016/j.swevo.2021.101005
Web of Science® Google Scholar
19 Zhang L., Li K., Li C., and Li K., Bi-objective workflow scheduling of the energy consumption and reliability in heterogeneous computing systems, Information Sciences. (2017) 379, 241–256, https://doi.org/10.1016/j.ins.2016.08.003, 2-s2.0-85027947361.
10.1016/j.ins.2016.08.003
Web of Science® Google Scholar
20 Li J., Sang H., Han Y., Wang C., and Gao K., Efficient multi-objective optimization algorithm for hybrid flow shop scheduling problems with setup energy consumptions, Journal of Cleaner Production. (2018) 181, 584–598, https://doi.org/10.1016/j.jclepro.2018.02.004, 2-s2.0-85042369089.
10.1016/j.jclepro.2018.02.004
Web of Science® Google Scholar
21 Khiat A., Haddadi M., and Bahnes N., Genetic-based algorithm for task scheduling in fog–cloud environment, Journal of Network and Systems Management. (2024) 32, no. 1, https://doi.org/10.1007/s10922%2D023%2D09774%2D9.
10.1007/s10922-023-09774-9
Web of Science® Google Scholar
22 Rehman A., Hussain S. S., ur Rehman Z., Zia S., and Shamshirband S., Multi-objective approach of energy efficient workflow scheduling in cloud environments, Concurrency and Computation: Practice and Experience. (2019) 31, no. 8, article e4949, https://doi.org/10.1002/cpe.4949, 2-s2.0-85052810894.
10.1002/cpe.4949
PubMed Web of Science® Google Scholar
23 Liu Y., Du C., Chen J., and Du X., Online deadline-constrained scheduling of parallel applications in CPSs, 2023, https://doi.org/10.21203/rs.3.rs%2D2826816/v1.
10.21203/rs.3.rs-2826816/v1
Google Scholar
24 Zhou N., Li F., Xu K., and Qi D., Concurrent workflow budget-and deadline-constrained scheduling in heterogeneous distributed environments, Soft Computing. (2018) 22, no. 23, 7705–7718, https://doi.org/10.1007/s00500%2D018%2D3229%2D3, 2-s2.0-85048250266.
10.1007/s00500-018-3229-3
Web of Science® Google Scholar
25 Topcuoglu H., Hariri S., and Wu M., Performance-effective and low-complexity task scheduling for heterogeneous computing, IEEE Transactions on Parallel and Distributed Systems. (2002) 13, no. 3, 260–274, https://doi.org/10.1109/71.993206, 2-s2.0-0036504666.
10.1109/71.993206
Web of Science® Google Scholar
26 Arabnejad V., Bubendorfer K., and Ng B., Dynamic multi-workflow scheduling: a deadline and cost-aware approach for commercial clouds, Future Generation Computer Systems. (2019) 100, 98–108, https://doi.org/10.1016/j.future.2019.04.029, 2-s2.0-85065640401.
10.1016/j.future.2019.04.029
Web of Science® Google Scholar
27 Li L., Xu W., Tan Y., Yang Y., Yang J., and Tan D., Fluid-induced vibration evolution mechanism of multiphase free sink vortex and the multi-source vibration sensing method, Mechanical Systems and Signal Processing. (2023) 189, article 110058, https://doi.org/10.1016/j.ymssp.2022.110058.
10.1016/j.ymssp.2022.110058
Web of Science® Google Scholar
28 Li L., Li Q., Ni Y., Wang C., Tan Y., and Tan D., Critical penetrating vibration evolution behaviors of the gas-liquid coupled vortex flow, Energy. (2024) 292, article 130236, https://doi.org/10.1016/j.energy.2024.130236.
10.1016/j.energy.2024.130236
Web of Science® Google Scholar
29 Zhu D., Melhem R., and Mosse D., The effects of energy management on reliability in real-time embedded systems, IEEE/ACM International Conference on Computer Aided Design, 2004. ICCAD-2004, 2004, San Jose, CA, USA, 35–40, https://doi.org/10.1109/ICCAD.2004.1382539.
10.1109/ICCAD.2004.1382539
Google Scholar
30 Xie G., Zeng G., Jiang J., Fan C., Li R., and Li K., Energy management for multiple real-time workflows on cyber–physical cloud systems, Future Generation Computer Systems. (2020) 105, 916–931, https://doi.org/10.1016/j.future.2017.05.033, 2-s2.0-85020737168.
10.1016/j.future.2017.05.033
Web of Science® Google Scholar
31 Xie G., Zeng G., Li R., and Li K., Energy-aware processor merging algorithms for deadline constrained parallel applications in heterogeneous cloud computing, IEEE Transactions on Sustainable Computing. (2017) 2, no. 2, 62–75, https://doi.org/10.1109/TSUSC.2017.2705183.
10.1109/TSUSC.2017.2705183
Google Scholar
32 Nogues E., Pelcat M., Menard D., and Mercat A., Energy efficient scheduling of real time signal processing applications through combined DVFS and DPM, 2016 24th Euromicro International Conference on Parallel, Distributed, and Network-Based Processing (PDP), 2016, Heraklion, Greece, 622–626, https://doi.org/10.1109/PDP.2016.15, 2-s2.0-84968835132.
10.1109/PDP.2016.15
Google Scholar
33 Zhao B., Aydin H., and Zhu D., Shared recovery for energy efficiency and reliability enhancements in real-time applications with precedence constraints, ACM Transactions on Design Automation of Electronic Systems (TODAES). (2013) 18, no. 2, 1–21, https://doi.org/10.1145/2442087.2442094, 2-s2.0-84878516822.
10.1145/2500459
Web of Science® Google Scholar
34 Hu B., Cao Z., and Zhou M., Scheduling real-time parallel applications in cloud to minimize energy consumption, IEEE Transactions on Cloud Computing. (2019) 10, no. 1, 662–674, https://doi.org/10.1109/TCC.2019.2956498.
10.1109/TCC.2019.2956498
Google Scholar
35 Li J., Xie G., Li K., and Tang Z., Enhanced parallel application scheduling algorithm with energy consumption constraint in heterogeneous distributed systems, Journal of Circuits, Systems and Computers. (2019) 28, no. 11, article 1950190, https://doi.org/10.1142/S0218126619501901, 2-s2.0-85058470325.
10.1142/S0218126619501901
Web of Science® Google Scholar
36 Zheng W. and Sakellariou R., Budget-deadline constrained workflow planning for admission control, Journal of Grid Computing. (2013) 11, no. 4, 633–651, https://doi.org/10.1007/s10723%2D013%2D9257%2D4, 2-s2.0-84887451743.
10.1007/s10723-013-9257-4
Web of Science® Google Scholar

All articles

Online Energy-Aware Scheduling for Deadline-Constrained Applications in Distributed Heterogeneous Systems

Abstract

1. Introduction

2. Related Work

3. Model

3.1. Heterogeneous Processor Model

3.2. Application Model

3.3. Energy Model

3.4. Problem Description

4. Proposed OMECDS Algorithm

4.1. Task Selection Phase

4.2. Processor Allocation Phase

5. Results

5.1. Experimental Setup

5.2. Results and Discussion

5.2.1. Planning Successful Rate (PSR) and Energy Consumption Analyses

5.2.2. Runtime Analyses

6. Conclusions

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley