Abstract and Applied Analysis
Volume 2024, Issue 1 1433858
Research Article
Open Access

Efficient Numerical Method for Solving a Quadratic Riccati Differential Equation

Wendafrash Seyid Yirga, 

Wendafrash Seyid Yirga

Department of Mathematics, Dilla University, Dilla, Ethiopia du.edu.et

Search for more papers by this author
Fasika Wondimu Gelu, 

Corresponding Author

Fasika Wondimu Gelu

Department of Mathematics, Dilla University, Dilla, Ethiopia du.edu.et

Search for more papers by this author
Wondwosen Gebeyaw Melesse, 

Wondwosen Gebeyaw Melesse

Department of Mathematics, Dilla University, Dilla, Ethiopia du.edu.et

Search for more papers by this author
Gemechis File Duressa, 

Gemechis File Duressa

Department of Mathematics, Jimma University, Jimma, Ethiopia ju.edu.et

Search for more papers by this author
First published: 22 March 2024
https://doi.org/10.1155/2024/1433858
Academic Editor: Yufeng Xu

Abstract

This study presents families of the fourth-order Runge–Kutta methods for solving a quadratic Riccati differential equation. From these families, the England version is more efficient than other fourth-order Runge–Kutta methods and practically well-suited for solving initial value problems in general and quadratic Riccati differential equation in particular. The stability analysis of the present method is well-established. In order to verify the accuracy, we compared the numerical solutions obtained using the England version of fourth-order Runge–Kutta method with the recently published works reported in the literature. Several counter examples are solved using the present methods to demonstrate their reliability and efficiency.

1. Introduction

Differential equations are a popular approach to solve problems in science and engineering. The differential equation used to approximate a large number of real-world problems is difficult to solve analytically due to its complexity and nonlinearity. The challenges of finding analytical solutions to real-world problems led to the development of numerical methods.

Nonlinear ordinary differential equations are essential in many areas of both applied and pure mathematics, including engineering, applied mechanics, quantum physics, analytical chemistry, astronomy, and biology. Researchers have been interested in the analytical and numerical solutions to nonlinear ordinary differential equations. Riccati differential equation is a type of nonlinear differential equation that is particularly important in many practical scientific disciplines. For example, Riccati differential equation is closely connected to a 1D static Schrödinger equation [1]. Riccati differential equation is named after the Italian nobleman Count Jacopo Francesco Riccati [2]. These equations have applications not only in random processes, optimal control, and diffusion problems [3] but also in engineering and applied science, such as damping laws, rheology, diffusion processes, transmission line phenomena, network synthesis, financial mathematics, and stochastic realization theory problems [4].

This study is delimited to the following quadratic Riccati differential equation of the form:
()
subject to the initial condition:
()
where A(x), B(x), and C(x) are continuous functions with C(x) ≠ 0, and y0 is arbitrary constants, and y(x) is unknown function.

Many authors have proposed various numerical methods to solve Equations (1) and (2). For instance, piecewise variational iteration method in Ghorbani and Momani’s [5] study, differential transform method in Biazar and Eslami’s [4] study, cubic B-spline scaling functions and Chebyshev cardinal functions in Lakestani and Dehghan’s [6] study, application of optimal homotopy asymptotic method in Mabood et al.’s [7] study, combination of Laplace transform and new homotopy perturbation methods in Vahidi et al.’s [8] study, Legendre scaling functions in Baghchehjoughi et al.’s [9] study, Lie group method and Runge–Kutta fourth-order method in Altoum’s [10] study, fourth-order Runge–Kutta method in File and Aga’s [11] study, the Bezier curves method in Ghomanjani and Khorram’s [12] study, a weighted type of Adams–Bashforth rules in Masjed-Jamei and Shayegan’s [13] study, and the fifth order predictor corrector method in Kiltu et al.’s [14] study. The classical fourth-order Runge–Kutta method is widely used for solving quadratic Riccati differential equations. However, the accuracy is very less. Therefore, in this study, families of fourth-order Runge–Kutta methods are devised for solving quadratic Riccati differential equations. From the tables of values, one can observe that England’s version of the fourth-order Runge–Kutta method gives a more accurate numerical solution than the other Runge–Kutta methods as well as recently published works. From in this study, we therefore conclude that the England version of fourth-order Runge–Kutta method is more accurate and effective to solve a quadratic Riccati differential equation.

2. Description of the Method

To describe the present method, we write the general form of a nonlinear differential equation in Equation (1) in the following form:
()
Now, divide the interval [0, 1] into N equal subintervals of mesh size h and the mesh points xi are given by xi = x0 + ih, 1, ⋯, N, and the mesh size is given by h = 1/N. There exist general fourth-order Runge–Kutta methods with a free parameter γ, see the detail derivation in Tan and Chen’s [15] study. Therefore, the general fourth-order Runge–Kutta method with a free parameter γ can be given by the following formula:
()
where
()
Case I: Choosing γ = 2, Equation (4) reduces to the classical fourth-order Runge–Kutta method as given below:
()
where
()
Case II: Putting γ = 4 in Equation (4) gives the England version of fourth-order Runge–Kutta method [3] given by the formula as follows:
()
where
()
Case III: Plugging γ = 1 in Equation (4) yields a new formula of fourth-order Runge–Kutta method given by the following equation:
()
where
()
Case IV: Using γ = 3 in Equation (4) gives the second new formula of fourth-order Runge–Kutta method as follows:
()
where
()
Case V: For γ = 5, Equation (4) gives the third new formula of fourth-order Runge–Kutta method given by the following equation:
()
where
()

From the above families of fourth-order Runge–Kutta methods, we consider the England version of the fourth-order Runge–Kutta method given in Equation (8) to show the stability analysis.

3. Stability Analysis

Consider the Riccati differential equation at the discrete point:
()
Moreover, we consider the test differential equation [11, 16]:
()
where λ be a complex number. The analytical solution of Equation (17), at x = xi, is given as follows:
()
At (xi,  yi), from Equations (16) and (17), the function and we have the following results from the parameters of Equation (17):
()
Substituting the values k1,   k2,   k3, and k4 into Equation (8) yields the following equation:
()
Simplifying the above expression gives the following equation:
()
Further simplification yields the following first order difference equation of the form:
()
where is Taylor series approximation to eλh. We call the Runge–Kutta method absolutely stable if |E(λh)| ≤ 1 and relatively stable if |E(λh)| ≤ eλh. If λ < 0, from Equation (18), the exact solution y(xi) decreases as xi increases. From Equation (19), we find that the England version of fourth-order Runge–Kutta method is absolutely stable if and only if −2.785 < λh < 0 for real constant λ. If λ > 0, from Equation (18), the exact solution y(xi) increases with xi and we do not want |E(λh)| ≤ 1, so that the relative stability is the important condition to be satisfied. It is easy to see that the England version of fourth-order Runge-Kutta method is relatively stable since E(λh) ≤ eλh,     λ > 0. From Equation (19), the exact solution y(xi) increases for λ > 0 and decreases for λ < 0 with the factor of eλh. Moreover, the approximate solution yi increases or decreases with the factor of E(λh). Similarly, it is easy to show the stability analyses for the other cases. Now, we illustrate the theoretical findings in the previous sections in practice via numerical experiments.

4. Counter Examples

To illustrate the applicability of the proposed method, five counter examples with variable and constant coefficients of a quadratic Riccati differential equations are considered. The absolute errors (AEs) are calculated by the following formula:
()
where Yi denotes the numerical solution and y(xi) is the exact solution. The computational rate of convergence can also be obtained using the double mesh principle defined below. Let:
()
where is the numerical solution on the mesh at the mesh point xi such that xi = x0 + ih, 1, ⋯, N − 1 and where is the numerical solution at the mesh point xi on the mesh such that xi = x0 + ih/2, 1, ⋯, 2N − 1. Replacing h by h/2 and N − 1 by 2N − 1, we can define the following equation:
()
The computational rate of convergence can now be defined as follows:
()

Example 1. Consider the variable coefficient RDE [11]:

()
with condition y(0) = 1. The exact solution is y(x) = ex.

Example 2. Consider the constant coefficient RDE [11]:

()
with condition y(0) = 0. The exact solution is as follows:
()

Example 3. Consider the variable coefficient RDE [11]:

()
with condition y(0) = 1. The exact solution is .

Example 4. Consider the variable coefficient RDE:

()
with condition y(0) = 1. The exact solution is y(x) = cosx.

Example 5. Consider the variable coefficient RDE:

()
with condition y(0) = 1. The exact solution is .

5. Numerical Results and Discussions

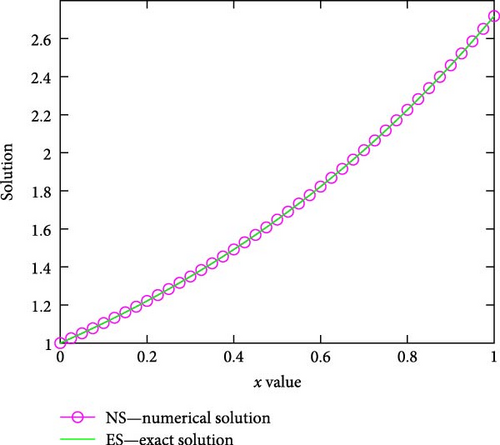
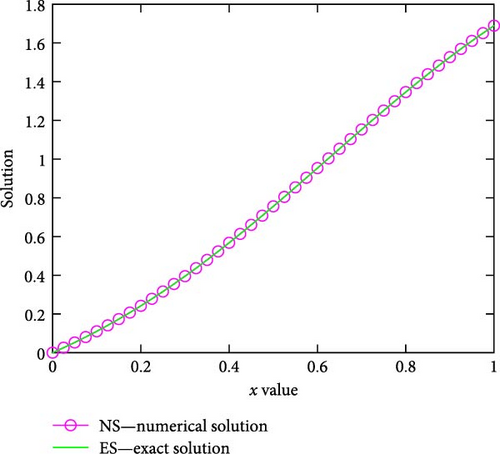
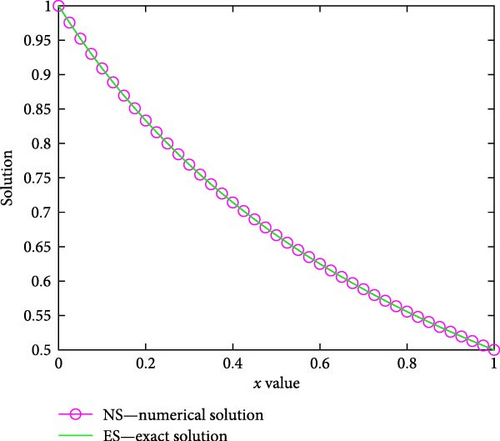
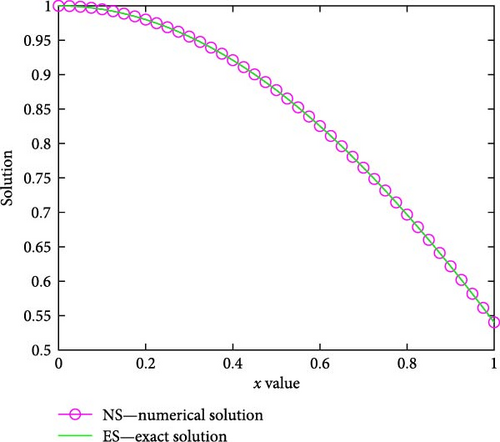
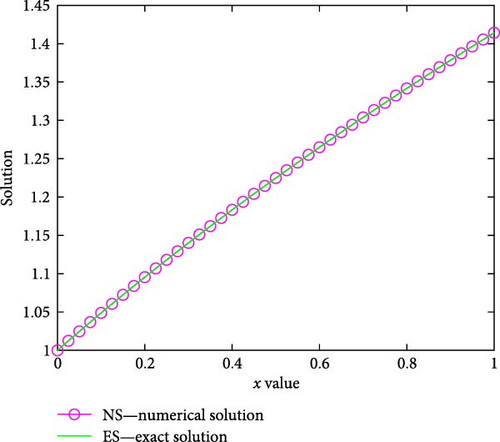
From Tables 1), (2) and (3, one can observe that England version of fourth-order Runge–Kutta method gives more accurate solution than the other versions of fourth-order Runge–Kutta methods for Examples (1) (2) and (3), respectively. For Examples (1) and (2), the numerical results using England version of fourth-order Runge–Kutta method are more accurate than those of the cubic B-spline method in Ala’yed et al.’s [17] study, the classical fourth-order Runge–Kutta method in File and Aga’s [11] study, and the BCM in Ghomanjani and Khorram’s [12] study for N = 10, as depicted in Tables 4 and 5, respectively. This implies that for the chosen N = 10, the AEs of the present method using the England version of the Runge–Kutta method are less than 10−8. The numerical results using England version of fourth-order Runge–Kutta method for Examples (4) and (5) are more accurate than in Masjed-Jamei and Shayegan’s [13] study for N = 100, as displayed in Tables 6 and 7, respectively. Table 8 demonstrates the numerical rate of convergence. In all the tables, we can observe that the AEs decrease as the number of mesh points increases. The graphs of numerical and exact solutions are sketched in Figures (1, 2)–(3) for Examples (1)–(5) for N = 40.

Table 1. The AEs of Example (1) using fourth-order Runge–Kutta (RK4) methods.
x↓ N = 10 N = 20 N = 40 N = 80 N = 160 N = 320 N = 640
Case I: classical RK4 method
0.1 1.1153e-07 7.1708e-09 4.5427e-10 2.8580e-11 1.7923e-12 1.1258e-13 7.3275e-15
0.2 2.6297e-07 1.6906e-08 1.0710e-09 6.7377e-11 4.2253e-12 2.6446e-13 1.7097e-14
0.3 4.6838e-07 3.0109e-08 1.9073e-09 1.1999e-10 7.5240e-12 4.7051e-13 3.0642e-14
0.4 7.4674e-07 4.8000e-08 3.0404e-09 1.9127e-10 1.1994e-11 7.4984e-13 4.9738e-14
0.5 1.1237e-06 7.2225e-08 4.5748e-09 2.8779e-10 1.8045e-11 1.1273e-12 7.5051e-14
0.6 1.6338e-06 1.0501e-07 6.6511e-09 4.1841e-10 2.6235e-11 1.6427e-12 1.1013e-13
0.7 2.3239e-06 1.4935e-07 9.4596e-09 5.9507e-10 3.7311e-11 2.3390e-12 1.5632e-13
0.8 3.2569e-06 2.0931e-07 1.3257e-08 8.3395e-10 5.2287e-11 3.2805e-12 2.1760e-13
0.9 4.5182e-06 2.9036e-07 1.8390e-08 1.1568e-09 7.2531e-11 4.5524e-12 2.9932e-13
1 6.2225e-06 3.9989e-07 2.5327e-08 1.5932e-09 9.9895e-11 6.2537e-12 3.8369e-13
  
Case II: England version of RK4 method
0.1 3.6077e-09 2.2755e-10 1.4254e-11 8.9129e-13 5.5733e-14 2.8866e-15 1.3323e-15
0.2 7.5843e-09 4.7887e-10 3.0005e-11 1.8767e-12 1.1746e-13 7.7716e-15 2.4425e-15
0.3 1.1965e-08 7.5640e-10 4.7408e-11 2.9652e-12 1.8630e-13 1.3101e-14 1.9984e-15
0.4 1.6788e-08 1.0628e-09 6.6638e-11 4.1682e-12 2.6201e-13 1.8208e-14 2.2204e-16
0.5 2.2093e-08 1.4011e-09 8.7883e-11 5.4976e-12 3.4595e-13 2.3981e-14 1.5543e-15
0.6 2.7922e-08 1.7744e-09 1.1135e-10 6.9678e-12 4.3876e-13 2.7534e-14 4.4409e-15
0.7 3.4318e-08 2.1862e-09 1.3728e-10 8.5918e-12 5.4046e-13 3.1086e-14 7.1054e-15
0.8 4.1327e-08 2.6404e-09 1.6592e-10 1.0387e-11 6.5414e-13 3.6415e-14 1.0214e-14
0.9 4.8992e-08 3.1410e-09 1.9756e-10 1.2370e-11 7.7893e-13 4.1744e-14 1.4655e-14
1 5.7356e-08 3.6925e-09 2.3249e-10 1.4556e-11 9.0861e-13 6.2617e-14 8.4377e-15
  
Case III: a new formula of RK4 method
0.1 3.4181e-07 2.1968e-08 1.3913e-09 8.7523e-11 5.4883e-12 3.4306e-13 2.1316e-14
0.2 8.0409e-07 5.1676e-08 3.2729e-09 2.0588e-10 1.2910e-11 8.0780e-13 4.9294e-14
0.3 1.4291e-06 9.1841e-08 5.8166e-09 3.6590e-10 2.2943e-11 1.4355e-12 8.9262e-14
0.4 2.2738e-06 1.4612e-07 9.2546e-09 5.8216e-10 3.6501e-11 2.2840e-12 1.4455e-13
0.5 3.4152e-06 2.1948e-07 1.3900e-08 8.7438e-10 5.4823e-11 3.4304e-12 2.1871e-13
0.6 4.9573e-06 3.1857e-07 2.0176e-08 1.2692e-09 7.9574e-11 4.9818e-12 3.1841e-13
0.7 7.0403e-06 4.5243e-07 2.8653e-08 1.8024e-09 1.1301e-10 7.0774e-12 4.5297e-13
0.8 9.8535e-06 6.3322e-07 4.0103e-08 2.5226e-09 1.5816e-10 9.9059e-12 6.3283e-13
0.9 1.3653e-05 8.7737e-07 5.5565e-08 3.4952e-09 2.1914e-10 1.3727e-11 8.7397e-13
1 1.8782e-05 1.2071e-06 7.6445e-08 4.8086e-09 3.0150e-10 1.8870e-11 1.1742e-12
  
Case IV: a second new formula of RK4 method
0.1 3.4772e-08 2.2386e-09 1.4192e-10 8.9324e-12 5.6022e-13 3.4861e-14 1.3323e-15
0.2 8.2602e-08 5.3161e-09 3.3699e-10 2.1208e-11 1.3303e-12 8.3045e-14 3.5527e-15
0.3 1.4815e-07 9.5322e-09 6.0415e-10 3.8020e-11 2.3841e-12 1.4855e-13 8.6597e-15
0.4 2.3772e-07 1.5291e-08 9.6905e-10 6.0980e-11 3.8232e-12 2.3848e-13 1.5321e-14
0.5 3.5983e-07 2.3141e-08 1.4663e-09 9.2267e-11 5.7845e-12 3.6016e-13 2.5757e-14
0.6 5.2599e-07 3.3820e-08 2.1428e-09 1.3482e-10 8.4523e-12 5.2913e-13 3.8414e-14
0.7 7.5175e-07 4.8327e-08 3.0617e-09 1.9263e-10 1.2077e-11 7.5939e-13 5.6399e-14
0.8 1.0581e-06 6.8011e-08 4.3084e-09 2.7106e-10 1.6994e-11 1.0703e-12 7.8604e-14
0.9 1.4734e-06 9.4694e-08 5.9983e-09 3.7736e-10 2.3660e-11 1.4921e-12 1.0791e-13
1 2.0359e-06 1.3084e-07 8.2872e-09 5.2135e-10 3.2694e-11 2.0446e-12 1.2035e-13
  
Case V: a third new formula of RK4 method
0.1 2.6635e-08 1.7072e-09 1.0796e-10 6.7855e-12 4.2544e-13 2.7089e-14 2.6645e-15
0.2 6.1696e-08 3.9559e-09 2.5020e-10 1.5727e-11 9.8588e-13 6.2617e-14 5.5511e-15
0.3 1.0803e-07 6.9295e-09 4.3835e-10 2.7556e-11 1.7273e-12 1.0969e-13 7.7716e-15
0.4 1.6949e-07 1.0875e-08 6.8805e-10 4.3256e-11 2.7112e-12 1.7164e-13 9.1038e-15
0.5 2.5125e-07 1.6126e-08 1.0204e-09 6.4155e-11 4.0221e-12 2.5424e-13 1.2434e-14
0.6 3.6027e-07 2.3131e-08 1.4638e-09 9.2041e-11 5.7707e-12 3.6171e-13 1.7097e-14
0.7 5.0596e-07 3.2494e-08 2.0567e-09 1.2932e-10 8.1086e-12 5.0493e-13 2.3981e-14
0.8 7.0098e-07 4.5031e-08 2.8505e-09 1.7925e-10 1.1239e-11 6.9855e-13 3.4639e-14
0.9 9.6242e-07 6.1842e-08 3.9151e-09 2.4621e-10 1.5439e-11 9.5746e-13 4.9294e-14
1 1.3133e-06 8.4410e-08 5.3443e-09 3.3610e-10 2.1069e-11 1.3225e-12 9.4591e-14
Table 2. The AEs of Example (2) using fourth-order Runge–Kutta (RK4) methods.
x↓ N = 10 N = 20 N = 40 N = 80 N = 160 N = 320 N = 640
Case I: classical RK4 method
0.1 2.2551e-06 1.5184e-07 9.8491e-09 6.2708e-10 3.9557e-11 2.4840e-12 1.5543e-13
0.2 4.7763e-06 3.1936e-07 2.0641e-08 1.3119e-09 8.2681e-11 5.1891e-12 3.2457e-13
0.3 7.3083e-06 4.8505e-07 3.1235e-08 1.9814e-09 1.2476e-10 7.8259e-12 4.9027e-13
0.4 9.5635e-06 6.3023e-07 4.0441e-08 2.5610e-09 1.6111e-10 1.0101e-11 6.3527e-13
0.5 1.1301e-05 7.4039e-07 4.7374e-08 2.9957e-09 1.8833e-10 1.1803e-11 7.4463e-13
0.6 1.2408e-05 8.0984e-07 5.1724e-08 3.2678e-09 2.0534e-10 1.2869e-11 8.1413e-13
0.7 1.2940e-05 8.4328e-07 5.3815e-08 3.3985e-09 2.1351e-10 1.3382e-11 8.4910e-13
0.8 1.3100e-05 8.5316e-07 5.4419e-08 3.4357e-09 2.1581e-10 1.3529e-11 8.6020e-13
0.9 1.3141e-05 8.5375e-07 5.4381e-08 3.4308e-09 2.1543e-10 1.3503e-11 8.5909e-13
1 1.3245e-05 8.5473e-07 5.4260e-08 3.4174e-09 2.1441e-10 1.3427e-11 8.3977e-13
  
Case II: England version of RK4 method
0.1 1.8238e-06 1.2286e-07 7.9738e-09 5.0789e-10 3.2046e-11 2.0125e-12 1.2590e-13
0.2 3.7840e-06 2.5339e-07 1.6397e-08 1.0428e-09 6.5747e-11 4.1272e-12 2.5807e-13
0.3 5.7022e-06 3.7952e-07 2.4483e-08 1.5547e-09 9.7944e-11 6.1453e-12 3.8519e-13
0.4 7.4121e-06 4.9044e-07 3.1547e-08 2.0004e-09 1.2593e-10 7.8977e-12 4.9760e-13
0.5 8.7887e-06 5.7860e-07 3.7126e-08 2.3512e-09 1.4792e-10 9.2731e-12 5.8653e-13
0.6 9.7606e-06 6.4011e-07 4.0995e-08 2.5937e-09 1.6310e-10 1.0225e-11 6.4893e-13
0.7 1.0321e-05 6.7501e-07 4.3170e-08 2.7294e-09 1.7158e-10 1.0757e-11 6.8523e-13
0.8 1.0545e-05 6.8794e-07 4.3938e-08 2.7761e-09 1.7445e-10 1.0938e-11 6.9811e-13
0.9 1.0585e-05 6.8771e-07 4.3828e-08 2.7662e-09 1.7373e-10 1.0892e-11 6.9567e-13
1 1.0608e-05 6.8394e-07 4.3423e-08 2.7354e-09 1.7164e-10 1.0749e-11 6.7191e-13
  
Case III: a new formula of RK4 method
0.1 3.1177e-06 2.0981e-07 1.3600e-08 8.6546e-10 5.4580e-11 3.4268e-12 2.1448e-13
0.2 6.7609e-06 4.5128e-07 2.9131e-08 1.8500e-09 1.1655e-10 7.3131e-12 4.5755e-13
0.3 1.0520e-05 6.9611e-07 4.4738e-08 2.8350e-09 1.7840e-10 1.1188e-11 7.0077e-13
0.4 1.3866e-05 9.0980e-07 5.8229e-08 3.6821e-09 2.3147e-10 1.4508e-11 9.1094e-13
0.5 1.6326e-05 1.0640e-06 6.7872e-08 4.2849e-09 2.6914e-10 1.6861e-11 1.0610e-12
0.6 1.7701e-05 1.1493e-06 7.3182e-08 4.6159e-09 2.8981e-10 1.8155e-11 1.1446e-12
0.7 1.8177e-05 1.1798e-06 7.5107e-08 4.7367e-09 2.9737e-10 1.8630e-11 1.1773e-12
0.8 1.8211e-05 1.1836e-06 7.5383e-08 4.7551e-09 2.9854e-10 1.8707e-11 1.1846e-12
0.9 1.8255e-05 1.1858e-06 7.5485e-08 4.7600e-09 2.9881e-10 1.8723e-11 1.1871e-12
1 1.8519e-05 1.1963e-06 7.5933e-08 4.7814e-09 2.9994e-10 1.8780e-11 1.1759e-12
  
Case IV: a second new formula of RK4 method
0.1 1.9675e-06 1.3252e-07 8.5989e-09 5.4762e-10 3.4549e-11 2.1696e-12 1.3577e-13
0.2 4.1148e-06 2.7538e-07 1.7812e-08 1.1325e-09 7.1392e-11 4.4811e-12 2.8008e-13
0.3 6.2376e-06 4.1469e-07 2.6734e-08 1.6969e-09 1.0688e-10 6.7053e-12 4.2016e-13
0.4 8.1292e-06 5.3704e-07 3.4512e-08 2.1872e-09 1.3766e-10 8.6320e-12 5.4312e-13
0.5 9.6262e-06 6.3253e-07 4.0542e-08 2.5660e-09 1.6139e-10 1.0116e-11 6.3882e-13
0.6 1.0643e-05 6.9669e-07 4.4571e-08 2.8184e-09 1.7718e-10 1.1107e-11 7.0366e-13
0.7 1.1194e-05 7.3110e-07 4.6718e-08 2.9525e-09 1.8555e-10 1.1633e-11 7.3919e-13
0.8 1.1397e-05 7.4302e-07 4.7432e-08 2.9960e-09 1.8824e-10 1.1801e-11 7.5162e-13
0.9 1.1437e-05 7.4305e-07 4.7346e-08 2.9877e-09 1.8763e-10 1.1762e-11 7.4984e-13
1 1.1487e-05 7.4087e-07 4.7035e-08 2.9628e-09 1.8590e-10 1.1640e-11 7.2764e-13
  
Case V: a third new formula of RK4 method
0.1 1.7375e-06 1.1706e-07 7.5988e-09 4.8405e-10 3.0543e-11 1.9182e-12 1.1996e-13
0.2 3.5855e-06 2.4020e-07 1.5548e-08 9.8900e-10 6.2360e-11 3.9146e-12 2.4469e-13
0.3 5.3810e-06 3.5841e-07 2.3133e-08 1.4693e-09 9.2579e-11 5.8089e-12 3.6421e-13
0.4 6.9818e-06 4.6248e-07 2.9769e-08 1.8882e-09 1.1889e-10 7.4570e-12 4.7018e-13
0.5 8.2862e-06 5.4624e-07 3.5076e-08 2.2222e-09 1.3984e-10 8.7679e-12 5.5511e-13
0.6 9.2312e-06 6.0616e-07 3.8849e-08 2.4589e-09 1.5466e-10 9.6974e-12 6.1595e-13
0.7 9.7971e-06 6.4135e-07 4.1041e-08 2.5956e-09 1.6319e-10 1.0233e-11 6.5215e-13
0.8 8.2862e-06 6.5490e-07 4.1841e-08 2.6442e-09 1.6618e-10 1.0421e-11 6.6547e-13
0.9 9.2312e-06 6.5450e-07 4.1718e-08 2.6333e-09 1.6539e-10 1.0371e-11 6.6280e-13
1 1.0081e-05 6.4978e-07 4.1255e-08 2.5990e-09 1.6309e-10 1.0214e-11 6.3838e-13
Table 3. The AEs of Example (3) using fourth-order Runge–Kutta (RK4) methods.
x↓ N = 10 N = 20 N = 40 N = 80 N = 160 N = 320 N = 640
Case I: classical RK4 method
0.1 3.8296e-07 2.1510e-08 1.2712e-09 7.7213e-11 4.7566e-12 2.9510e-13 1.8319e-14
0.2 5.7951e-07 3.2725e-08 1.9396e-09 1.1798e-10 7.2735e-12 4.5164e-13 2.7978e-14
0.3 6.8133e-07 3.8623e-08 2.2939e-09 1.3968e-10 8.6161e-12 5.3524e-13 3.2752e-14
0.4 7.3394e-07 4.1722e-08 2.4816e-09 1.5123e-10 9.3322e-12 5.7987e-13 3.4639e-14
0.5 7.6091e-07 4.3344e-08 2.5808e-09 1.5737e-10 9.7137e-12 6.0407e-13 3.5416e-14
0.6 7.7483e-07 4.4202e-08 2.6340e-09 1.6067e-10 9.9198e-12 6.1640e-13 3.5860e-14
0.7 7.8257e-07 4.4692e-08 2.6648e-09 1.6260e-10 1.0040e-11 6.2339e-13 3.5638e-14
0.8 7.8799e-07 4.5037e-08 2.6865e-09 1.6396e-10 1.0126e-11 6.2883e-13 3.5638e-14
0.9 7.9326e-07 4.5365e-08 2.7069e-09 1.6523e-10 1.0205e-11 6.3338e-13 3.5194e-14
1 7.9961e-07 4.5748e-08 2.7304e-09 1.6669e-10 1.0295e-11 6.4021e-13 3.7692e-14
  
Case II: England version of RK4 method
0.1 2.1401e-08 8.5002e-10 3.8238e-11 1.9329e-12 1.0647e-13 6.2172e-15 4.4409e-16
0.2 3.7105e-08 1.6162e-09 7.9370e-11 4.2936e-12 2.4736e-13 1.4988e-14 1.1102e-15
0.3 4.6667e-08 2.1219e-09 1.0802e-10 5.9908e-12 3.5072e-13 2.1538e-14 1.1102e-15
0.4 5.1839e-08 2.4094e-09 1.2480e-10 7.0011e-12 4.1289e-13 2.5757e-14 7.7716e-16
0.5 5.4295e-08 2.5521e-09 1.3332e-10 7.5204e-12 4.4509e-13 2.7978e-14 2.2204e-16
0.6 5.5228e-08 2.6096e-09 1.3685e-10 7.7387e-12 4.5852e-13 2.8200e-14 1.1102e-16
0.7 5.5412e-08 2.6231e-09 1.3773e-10 7.7948e-12 4.6207e-13 2.8089e-14 6.6613e-16
0.8 5.5315e-08 2.6185e-09 1.3748e-10 7.7798e-12 4.6108e-13 2.7534e-14 1.1102e-15
0.9 5.5215e-08 2.6116e-09 1.3702e-10 7.7501e-12 4.5897e-13 2.7200e-14 1.8874e-15
1 5.5268e-08 2.6114e-09 1.3689e-10 7.7386e-12 4.5747e-13 2.8089e-14 2.7756e-16
  
Case III: a new formula of RK4 method
0.1 1.1061e-06 6.2829e-08 3.7371e-09 2.2777e-10 1.4057e-11 8.7286e-13 5.4290e-14
0.2 1.6643e-06 9.4942e-08 5.6599e-09 3.4536e-10 2.1325e-11 1.3248e-12 8.2934e-14
0.3 1.9506e-06 1.1163e-07 6.6656e-09 4.0706e-10 2.5147e-11 1.5626e-12 9.6922e-14
0.4 2.0981e-06 1.2035e-07 7.1953e-09 4.3969e-10 2.7171e-11 1.6886e-12 1.0425e-13
0.5 2.1741e-06 1.2493e-07 7.4759e-09 4.5705e-10 2.8251e-11 1.7564e-12 1.0802e-13
0.6 2.2140e-06 1.2739e-07 7.6283e-09 4.6654e-10 2.8842e-11 1.7926e-12 1.0925e-13
0.7 2.2369e-06 1.2883e-07 7.7188e-09 4.7220e-10 2.9197e-11 1.8144e-12 1.0991e-13
0.8 2.2533e-06 1.2987e-07 7.7845e-09 4.7632e-10 2.9454e-11 1.8304e-12 1.1025e-13
0.9 2.2693e-06 1.3087e-07 7.8467e-09 4.8020e-10 2.9697e-11 1.8451e-12 1.1058e-13
1 2.2883e-06 1.3202e-07 7.9175e-09 4.8459e-10 2.9970e-11 1.8632e-12 1.1374e-13
  
Case IV: a second new formula of RK4 method
0.1 1.4192e-07 7.7366e-09 4.4923e-10 2.7026e-11 1.6567e-12 1.0247e-13 6.7724e-15
0.2 2.1791e-07 1.1986e-08 6.9943e-10 4.2190e-11 2.5897e-12 1.6087e-13 1.0547e-14
0.3 2.5822e-07 1.4289e-08 8.3663e-10 5.0555e-11 3.1062e-12 1.9318e-13 1.1879e-14
0.4 2.7921e-07 1.5514e-08 9.1041e-10 5.5078e-11 3.3863e-12 2.1050e-13 1.2212e-14
0.5 2.8983e-07 1.6149e-08 9.4916e-10 5.7469e-11 3.5351e-12 2.2005e-13 1.1990e-14
0.6 2.9509e-07 1.6474e-08 9.6923e-10 5.8717e-11 3.6128e-12 2.2415e-13 1.1879e-14
0.7 2.9780e-07 1.6646e-08 9.8007e-10 5.9396e-11 3.6553e-12 2.2615e-13 1.1435e-14
0.8 2.9954e-07 1.6758e-08 9.8715e-10 5.9840e-11 3.6833e-12 2.2760e-13 1.1102e-14
0.9 3.0123e-07 1.6863e-08 9.9365e-10 6.0244e-11 3.7086e-12 2.2859e-13 1.0547e-14
1 3.0338e-07 1.6990e-08 1.0014e-09 6.0722e-11 3.7375e-12 2.3165e-13 1.2712e-14
  
Case V: a third new formula of RK4 method
0.1 5.0912e-08 3.2819e-09 2.0836e-10 1.3123e-11 8.2334e-13 5.1736e-14 2.7756e-15
0.2 7.1376e-08 4.6056e-09 2.9267e-10 1.8444e-11 1.1573e-12 7.2387e-14 3.8858e-15
0.3 8.0264e-08 5.1784e-09 3.2915e-10 2.0747e-11 1.3018e-12 8.1379e-14 4.5519e-15
0.4 8.4581e-08 5.4532e-09 3.4657e-10 2.1845e-11 1.3706e-12 8.5598e-14 5.4401e-15
0.5 8.7029e-08 5.6062e-09 3.5619e-10 2.2449e-11 1.4083e-12 8.8041e-14 5.9952e-15
0.6 8.8691e-08 5.7088e-09 3.6258e-10 2.2848e-11 1.4331e-12 9.0150e-14 6.3283e-15
0.7 9.0020e-08 5.7907e-09 3.6768e-10 2.3166e-11 1.4526e-12 9.2037e-14 6.8834e-15
0.8 9.1220e-08 5.8652e-09 3.7233e-10 2.3456e-11 1.4706e-12 9.3481e-14 7.3275e-15
0.9 9.2394e-08 5.9391e-09 3.7696e-10 2.3747e-11 1.4888e-12 9.5257e-14 8.1046e-15
1 9.3601e-08 6.0160e-09 3.8182e-10 2.4052e-11 1.5086e-12 9.5146e-14 5.9952e-15
Table 4. Comparisons of AEs of Example (1) with the existing methods for N = 10.
x

England version of RK4

(Present method)

 Method in Ala’yed et al.’s [17] study Method in File and Aga’s [11] study Method in Ghomanjani and Khorram’s [12] study
0.1 3.6077e-09 6.5346e-8 1.1153e-7 0.00034681435605
0.3 1.1965e-08 2.0112e-7 4.6838e-7 0.00067436472882
0.5 2.2093e-08 3.6696e-7 1.1237e-6 3.8747e-10
0.7 3.4318e-08 5.6951e-7 2.3239e-6 0.00067437189321
0.9 4.8992e-08 8.1691e-7 4.5182e-6 0.00034682221170
1 5.7356e-08 9.5347e-7 6.2225e-6 0.000000000000
Table 5. Comparisons of AEs of Example (2) with the existing methods for N = 10.
x

England version of RK4

(Present method)

 Method in Ala’yed et al.’s [17] study Method in File and Aga’s [11] study Method in Ghomanjani and Khorram’s [12] study
0.1 1.8238e-06 3.3766e-6 2.2551e-6 0.000248944564121
0.3 5.7022e-06 1.0920e-5 7.3083e-6 0.0004481946615024
0.5 8.7887e-06 8.1363e-6 1.1301e-5 2.89441e-10
0.7 1.0321e-05 5.5194e-6 1.2940e-5 0.000374115023553
0.9 1.0585e-05 1.1756e-5 1.3141e-5 0.00017849475908
1 1.0608e-05 9.2686e-6 1.3245e-5 3.2516e-10
Table 6. Comparison of AEs of Example (4) with the existing method for N = 100.
x Classical RK4 method England version of RK4 method Method in Masjed-Jamei and Shayegan’s [13] study
0.04 7.3100e-12 3.2081e-12 7.3571e-10
0.12 1.9787e-11 8.0284e-12 6.4020e-10
0.20 2.9412e-11 1.0784e-11 5.5994e-10
0.28 3.6355e-11 1.1687e-11 4.9544e-10
0.36 4.0948e-11 1.1081e-11 4.4430e-10
0.44 4.3639e-11 9.3986e-12 4.0436e-10
0.52 4.4935e-11 7.1134e-12 3.7372e-10
0.60 4.5352e-11 4.6831e-12 3.5071e-10
0.68 4.5351e-11 2.5024e-12 3.3386e-10
0.76 4.5308e-11 8.6497e-13 3.2180e-10
0.84 4.5480e-11 5.7176e-14 3.1329e-10
0.92 4.6005e-11 2.1705e-13 3.0678e-10
1 4.6913e-11 3.2307e-13 3.0067e-10
Table 7. Comparison of AEs of Example (5) with the existing method for N = 100.
x Classical RK4 method England version of RK4 method Method in Masjed-Jamei and Shayegan’s [13] study
0.04 6.2454e-12 5.9921e-12 5.7760e-10
0.12 1.8305e-11 1.7579e-11 6.3606e-10
0.20 3.0242e-11 2.9066e-11 7.0280e-10
0.28 4.2489e-11 4.0871e-11 7.7828e-10
0.36 5.5411e-11 5.3341e-11 8.6407e-10
0.44 6.9339e-11 6.6796e-11 9.6195e-10
0.52 8.4599e-11 8.1547e-11 1.0741e-09
0.60 1.0152e-10 9.7917e-11 1.2030e-09
0.68 1.2048e-10 1.1626e-10 1.3518e-09
0.76 1.4185e-10 1.3695e-10 1.5242e-09
0.84 1.6611e-10 1.6043e-10 1.7245e-09
0.92 1.9377e-10 1.8721e-10 1.9582e-09
1 2.2542e-10 2.1786e-10 2.2316e-09
Table 8. Rate of convergence using England version of RK4 method for x = 0.1.
Examples N = 10 N = 20 N = 40 N = 80 N = 160 N = 320
Example (1) 3.9790 3.9948 3.9987 3.9902 3.8506 3.9476
Example (2) 3.8919 3.9456 3.9727 3.9863 3.9931 3.9986
Example (3) 4.6540 4.4744 4.3062 4.1822 4.0980 3.8073
Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Plots in terms of numerical and exact solution using England version of Runge–Kutta method for N = 40: (a) Example (1) and (b) Example (2).
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Plots in terms of numerical and exact solution using England version of Runge–Kutta method for N = 40: (a) Example (1) and (b) Example (2).
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Plots in terms of numerical and exact solution using England version of Runge–Kutta method for N = 40: (a) Example (3) and (b) Example (4).
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Plots in terms of numerical and exact solution using England version of Runge–Kutta method for N = 40: (a) Example (3) and (b) Example (4).
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Plot of Example (5) in terms of numerical and exact solutions for N = 40.

6. Conclusion

In this study, families of fourth-order Runge–Kutta methods are devised for solving quadratic Riccati differential equations. To guarantee the applicability of the present methods, five counter numerical examples are computed in terms of absolute errors. The graphs of the exact solution versus the numerical solution have been plotted. The absolute errors obtained by England’s version of the fourth-order Runge–Kutta method have been compared with the other fourth-order Runge–Kutta methods. In each table, the AEs decrease as the mesh size increases. In general, England’s version of the fourth-order Runge–Kutta method gives a more accurate numerical solution than the other Runge–Kutta methods as well as recently published works. Even though England’s version of the fourth-order Runge–Kutta method is an anomalous method, it gives a more efficient result than the other fourth-order Runge–Kutta methods to solve a quadratic Riccati differential equation. As far as future research is concerned, we will use England’s version of the fourth-order Runge–Kutta method to solve systems of initial value problems.

Conflicts of Interest

The authors declare that they have no conflicts of interest.

Authors’ Contributions

Wendafrash Seyid Yirga and Fasika Wondimu Gelu contributed to conceptualization and methodology. Fasika Wondimu Gelu, Wondwosen Gebeyaw Melesse, and Gemechis File Duressa contributed to supervision. Wendafrash Seyid Yirga, Fasika Wondimu Gelu, and Gemechis File Duressa contributed to formal analysis. Wendafrash Seyid Yirga, Fasika Wondimu Gelu, and Wondwosen Gebeyaw Melesse contributed to writing—original draft preparation.

Acknowledgments

Authors are grateful to the referees for their valuable suggestions and comments.

    Data Availability

    No data were used to support this study.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.