Maintaining good connectivity is a major concern when constructing a robust flying mesh network, known as FlyMesh. In a FlyMesh, multiple unmanned aerial vehicles (UAVs) collaborate to provide continuous network service for mobile devices on the ground. To determine the connectivity probability of the aerial link between two UAVs, the Poisson point process (PPP) is used to describe the spatial distribution of UAVs equipped with omnidirectional antennas. However, the PPP fails to reflect the fact that there is a minimum distance restriction between two neighboring UAVs. In this paper, the β-Ginibre point process (β-GPP) is adopted to model the spatial distribution of UAVs, with β representing the repulsion between nearby UAVs. Additionally, a large-scale fading method is used to model the route channel between UAVs equipped with directional antennas, allowing the monitoring of the impact of signal interference on network connectivity. Based on the β-GPP model, an analytical expression for the connectivity probability is derived. Numerical tests are conducted to demonstrate the effects of repulsion factor β, UAV intensity ρ, and beamwidth θ on network connectivity. The results indicate that an increase in UAV intensity decreases network connectivity when the repulsion factor β remains constant. These findings provide valuable insights for enhancing the service quality of the FlyMesh.

1. Introduction

Unmanned aerial vehicles (UAVs) offer numerous unique advantages for providing communication coverage to mobile devices on the ground, including a high probability of establishing line-of-sight (LoS) links and flexible deployment capabilities. UAVs act as flying base stations (FBS) and provide services to terminal equipment on the ground [1]. To enhance the coverage area, multiple UAVs can collaborate by building an aerial network called the flying mesh network, or FlyMesh for short, through aerial links between them. FlyMesh provides several benefits, including rapid deployment of networks in disaster situations, extending wireless network connectivity to sparsely populated areas, collecting and processing data from large mobile IoT devices, and improving overall network resilience [2]. FBS technology enhances wireless communication performance and offers a flexible network architecture that can adapt to real-time traffic changes to provide optimal services. It has been widely used and extensively studied in mobile edge computing [3, 4]. Due to the mobility and flexibility of UAVs [5], the topology of FlyMesh often changes [6]. To ensure a continuous service for mobile devices, maintaining a good connectivity among UAVs is critical for the FlyMesh maintainer. Therefore, it is important to build an analysis model to profile the connectivity probability among UAVs.

The essential part of building an analysis model is sculpting the spatial distribution of the UAVs, which can move at high speeds. Existing efforts typically adopt the Poisson point process (PPP) to achieve this goal [7]. In the PPP-based model, each UAV is treated as an independent point in space, and there is no connection among the positions of UAVs. However, the absence of distance restrictions in PPP model makes it challenging for existing models to account for the fact that UAVs usually maintain a distance from each other to enhance coverage and prevent collisions. Existing work often neglects the directional antennas commonly adopted by UAVs. For example, there is an exclusion (or attraction) between UAVs, which means that the actual deployed UAV location typically exhibits a more regular (or clustered) point pattern than PPP.

In this context, this paper adopts the β-Ginibre point process (β-GPP) to describe the spatial distribution of the UAVs. Compared with PPP, β-GPP restricts the minimum distance between two UAVs using parameter β. When β⟶1, UAVs are uniformly distributed in the GPP model. Thus, by adjusting β in a given environment, the distribution of UAVs can be analyzed more accurately. In other words, we can change the distance restriction in a flexible way by adjusting the value of β without modifying the analysis model. In addition, we assume that each UAV is equipped with a directional antenna to improve its connectivity. Specifically, the positions of UAVs are first modeled using β-GPP. Then, the signal-to-noise ratio (SINR) at the receiver is calculated based on the directional antenna assumption. Subsequently, the analytical expression of the connectivity probability of the wireless link between two UAVs is derived. In comparison with existing efforts, our contributions in this paper are twofold. On one hand, we use β-GPP to model the spatial distribution of UAVs and derive an analytical expression for the connectivity probability. On the other hand, we conduct a series of numerical tests based on the analytical expression to analyze the impacts of the repulsion parameter β, beamwidth θ, and UAV intensity ρ on network connectivity performance.

The rest of this paper is organized as follows: Related Work briefly introduces existing efforts. Mathematical Preliminaries provides the basic characteristics of β-GPP. System Model and Assumptions and Performance Analysis introduce the system model and analyze the network connectivity and network coverage, while Simulation and Result Analysis examines the advantages of the adopted model through experiments and data comparisons. Finally, Conclusion briefly summarizes our work.

2. Related Work

UAVs are one of the most common low-altitude platforms, considered agile, low cost, and easy to deploy [8]. These foreseeable benefits prompt academic and industry associations to recommend the use of drone base stations and evaluate their performance in various applications. For example, Arshad et al. [9] optimized the position of UAVs by utilizing their flexibility in responding to real-time device activity to minimize uplink transmission power. Mozaffari et al. [10] provided downlink services to rural areas without surface base station coverage using UAVs. Bushnaq et al. [11] considered the upstream data aggregation scenario of IoT devices from rural areas. Choi et al. [12] proposed not using a single UAV but letting the UAV collect data from the Internet of Things devices, which transmitted data as long as they were within the coverage area. Research on mobile self-organizing networks has also provided assistance. Cui et al. studied a quantum genetic-based OLSR protocol for mobile self-organizing networks, while Wei et al. analyzed the joint deployment of drones in DRL-based edge computing [13].

Stochastic geometric modeling helped to analyze the topological randomness of network geometry. PPP had been widely utilized in UAV network modeling and analysis due of its ease of handling [13–15]. Numerous theoretical results had been obtained based on the PPP model; however, PPP has certain limitations and cannot adequately describe the independence of node positions in real network deployments. Therefore, the spatial distribution of UAVs in real deployment can be better captured by considering the point process of the spatial correlation. Fang et al. [16] proposed an adaptive deployment-based solution that could effectively mitigate the excessive clustering of UAVs with negligible dispersion. Nakata and Miyoshi [17], Deng et al. [18], and Gomez et al. [19] studied and discussed the cellular network of base station deployment based on the β-GPP model. They further derived a computable integral representation of the coverage probability of typical mobile subscribers. The deterministic point process (DPP) provided a valuable model for describing spatial point pattern datasets in which nearby points repel each other [20]. In addition, they demonstrated an exclusive relationship between the location distribution and corresponding UAVs. The expressions for the DPP concerning LF and PGFL were identified. Therefore, DPP was a preferred performance analysis tool [21]. GPP is a soft-core model, which belongs to a class of DPPs. Each DPP was defined using a core matrix GPP, suitable for simulation between the communication node positions [22, 23]. GPP is more irregular than the lattice but more regular than the PPP. Herein, a more general point process called β-GPP, 0 < β ≤ 1, is introduced. The variation of the repulsion factor β reflects the interrelationship between the nodes. Notably, 1-GPP is GPP, and β-GPP weakly converges to PPP of the same strength as β⟶0. In other words, the β-GPP family generalizes GPP whereas PPP limits FlyMesh network performance. This study found that β⊆(0.2,0.4) is a good fit for rural areas, whereas β⊆(0.6,1) is a good fit for urban areas [24].

The UAVs were equipped with a directional antenna to reduce signal interference. Anisotropic radiation (directional antenna) can better connect UAVs than isotropic radiation (omnidirectional antenna), which is related to the array and design of the directional antenna. Shakhatreh et al. maximized indoor wireless coverage used using drones equipped with directional antennas [25]. Guo et al. effectively covered arbitrary two-dimensional ground areas using directional antennas to achieve efficient and scalable deployment of such flying base stations [26]. Peng et al. and Qin et al. analyzed the modeling and coverage performance of the UAVs under the directional antenna [27, 28]. Beam multiplexing techniques for directional antenna had also been widely used and intensively studied in 4G, 5G, and 6G [29].

UAVs are distributed according to β-GPP. Our study focussed on the network connectivity and coverage of interference in the β-Ginibre wireless network and the fitting of real data. Since the β-GPP family forms an intermediate class between PPP (completely random) and GPP (relatively regular), we can intuitively use β-GPP to simulate a large number of actual UAV networks by modulating the value of β.

3. Mathematical Preliminaries

In this subsection, we briefly introduce some background information on β-GPP. Consider a simple local limited point process defined on a locally compact space Ω. Next, let us examine the correlation functions λⁿ for any bounded and disjoint subsets A_n(n = 1, 2, ⋯∞) ⊂ ℝ².

(1)

where λⁿ indicates the spatial indensity of Ω. Let us consider a positive integer ∂, β = −1/∂. A Hilbert-Schmidt operator K from L²(ℝ²) into L²(ℝ²) is defined by

. K was assumed to be bounded by the symmetric operator and the spectrum of K ∈ [0, 1/β]. Here, the kernel of β-GPP is the function K. Then, when the correlation function λⁿ of Ω exist and fulfill

(2)

where det_β(A) instructs the β-determinant of a matrix

The Fredholm determinant is a generalization of the matrix determinant that defines bounded operators on the Hilbert spaces. For a kernel K and β, the Fredholm determinant can be numerically evaluated as [30]

(3)

For a β-GPP Ω with kernel K, regarding the Fredholm determinant, the hole probability can be computed as

(4)

where

is a restriction on A² and 1_A(·) is the indicator function of set A,

for

and

for

Here, for a β-GPP Ω with kernel K and a function ξ: R²⟶[0, ∞), we know that the Laplace transform is given by

(5)

where the kernel K_ξ is defined as

(6)

Therefore, there is a primary characteristics of the β-GPP. Now, we focus on β-GPP, one of the main types of β-DPPs. The observation window is set to B(O, R). For t₁ and t₂, ∈B(O, R). The formula in (5) and the cavity probability in (4) can be calculated by inserting the Ginibre kernel in (6), respectively. Given that the space Ω is the repulsive parameter β and the intensity ρ, the core matrix can be defined as

(7)

If Ω ~ DPP(K) with kernel K is used for a point process, the reduced Palm distribution

which has the kernel

coincides with another DPP [23].

(8)

The minimalist kernel of β-GPP at t_i is expressed as [23]

(9)

Let |t_i| = d_i, and t_i is assumed to be located at (d_i, 0) without loss of generality. Therefore,

can be expressed as

(10)

Let A ⊂ ℝ² and C ⊂ ℝ². Then, we can express the covariance of β-GPP with kernel K as

(11)

which contrasts to the PPP with zero covariance described above. In fact, in PPP, the position of one point does not depend on the position of the other points. In contrast to the PPP setting for the above equation, since β < 0, the number of points in the two disjoint sets is negatively correlated. Therefore, β-GPP shows more dispersion and less clustering than PPP.

4. System Model and Assumptions

4.1. Network Model

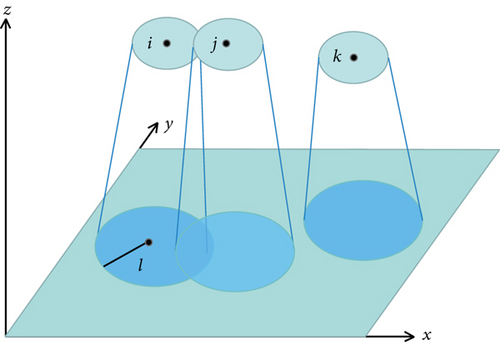
This paper considers the FlyMesh consisting of three types: flying base station (ABS), aerial mobile terminal (AMT), and ground mobile terminal (GMT), as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A flying base station mesh network.

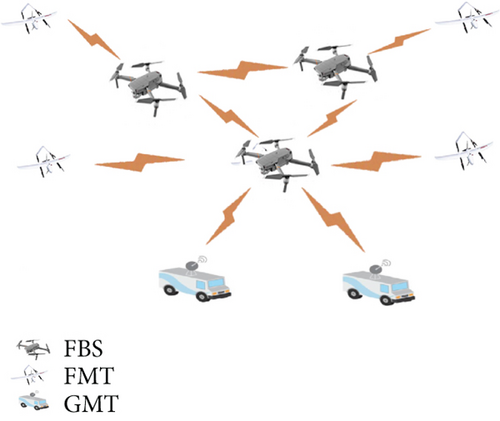
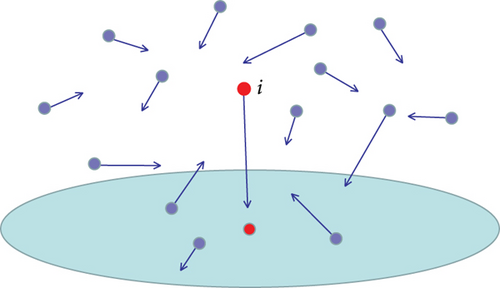
The UAV network is regarded as a FlyMesh, where the flying base stations (FBS) provide information storage and forwarding functions for mobile terminals. In complex electromagnetic environments, UAVs are equipped with directional antennas to reduce interference. The location distribution of drones in space is modeled as β-GPP model. Only the transmission between the transmitter and receiver was considered, and all other signals are considered to have interference, as shown in Figure 2. We also assumed that the receiver was deployed at the origin position of t₀(0, 0, 0). The transmitter t_i(x_i, y_i, z_i) is away from t₀.

4.2. Antenna Gain

A directional antenna is a phased array antenna. By varying the feed phase of the radiation unit in the array antenna, the direction of the antenna’s maximum range in the antenna map can be changed, thereby altering the direction and range of antenna radiation. The directional antenna is more focused in a specific direction compared to the omnidirectional antenna. It reduces interference between UAVs, improves the transmission distance, and enhances the spatial multiplexing of the channel. The schematic diagram of antenna beamforming is shown in Figure 3.

The implementation of a directional antenna significantly improves the gain of the main lobe antenna. Therefore, the antenna gain is closely related to antenna width. In this study, we mainly focus on the influence of the main valve, ignoring the side and back valves. Using a simpler model, we also describe the relationship between beam angle and antenna gain [31]. The receive antenna gain G^r and the transmission gain G^t can be expressed as described in the following equation:

(12)

(13)

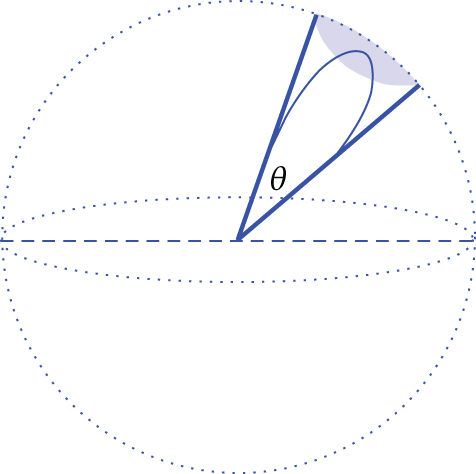
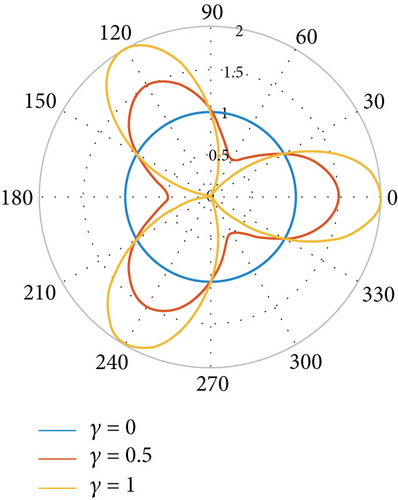
As shown in Figure 4, γ regulates the influence of the main lobe beamwidth on gain, when n represents the number of main lobes of the nodal antenna. Notably, the receive antenna gain G^r of the antenna depends only on the receiver antenna beam angle θ ∈ (0, 2π), while the transmitter gain G^t depends on its transmission antenna angle φ ∈ (0, 2π).

4.3. Path Loss and Fading

The SINR indicates the quality of communication links quantitatively. SINR depends on path loss attenuation and small-scale attenuation. In this case, small-scale fading between the transmitter and the receiver using

was modeled. SINR determines the distribution of the mean of the exponential distribution of a random variable. Since the power of the signal received by the receiving node in the far field is inversely proportional to the distance, a simple path loss attenuation function g(d) facilitates mathematical analysis.

(14)

where α is the path loss index and different values describe different communication environments. Generally, α > 2 in complex-urban environments, while α < 2 in open-field environments.

5. Performance Analysis

5.1. Network Connectivity

In this paper, the instantaneous snapshot at a specific time point is considered to simplify the model, which does not compromise generality. UAVs communicate with each other without implying any channel access protocol. The absence of channel access regulation may result in mutual interference between nearby UAVs, leading to increased packet loss rates or decreased data rates. Therefore, it is crucial to consider the SINR of transmitter i when its intended receiver locates at the origin. The received SINR of the associated receiver at t_i is expressed as

(15)

where N₀ is the average background noise power and

is the total background interference at the receiver, which we considered as shot noise. r ∈ (0, 1) represents the proportion of the desired signal affected by the interference. r = 0 means that there is no interference, and r = 1 implies that all communication nodes impact each other. P_t is the constant transmitted power of the node.

The connection probability is a fundamental quality measure for a point-to-point topological link. It can be obtained from (15) by setting a minimum reception threshold Q on SINR_i to decode the signal from the antenna transmitter i successfully. When SINR_i > Q, the network is connected. The connection probability can be expressed as

(16)

Subject to interference item (I), Equation (16) can be written as

(17)

Let

, and d_j represents the distance from the jamming node to the origin. Then, we can obtain

(18)

In space Ω with intensity ρ, the probability generating function of the inhomogeneous β-GPP model with repulsion coefficient β is

(19)

Since it is difficult to calculate the numerical result, it was solved using the quasi-Monte Carlo integral numerical method [32]. In this paper, we try to give a more manageable theoretical expression. According to the Hadamard inequality [32, 33], this is a Hermitian positive definite matrix whose determinant can be the upper bound of the product of its diagonal terms.

(20)

Due to the fact that

, connection probability (19) is approximately expressed as

(21)

Converting the rectangular coordinate system to the polar coordinate system, we can get

(22)

where θⁱ is the polar angle difference between the transmitting node and the jamming node in the polar coordinate system. We can go further:

(23)

To facilitate engineering processing, Equation (23) is approximately treated as

(24)

Here, we obtain the approximate expression of the connection probability under the β-GPP model, which can quantitatively analyze the influence of various indicators on the connection probability.

5.2. Upper and Lower Limits of UAV Intensity

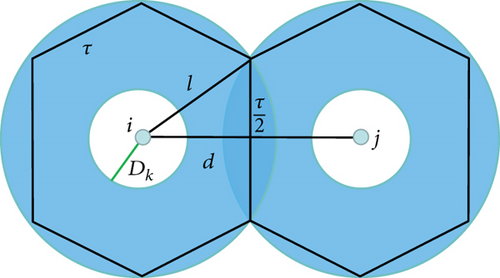
In general, FlyMesh provides network services in areas where network coverage is needed. The primary requirement is to ensure continuous and uninterrupted network coverage in the desired area. Therefore, it is crucial to design the strength of key nodes to ensure network coverage. In UAV network engineering, it is a common practice to consider a regular hexagon of circular cells.

As shown in Figure 5, we projected the beam coverage of UAV nodes i, j, and k in three-dimensional space onto a two-dimensional plane for ease of analysis. We observed beam overlap between nodes i and j, while node k remained isolated with no overlapping beams. The coverage area of each node was represented by a circle of radius l. In this study, we assumed that the beam radius between connected nodes is equal under ideal conditions. In addition, ensuring continuous coverage of desired areas is a fundamental network requirement, which implies that the range of the UAVs will overlap. Therefore, there should be no gaps. Full network coverage means that the network will cover every point in the desired area. The critical density refers to the UAV intensity where full network coverage will occur. In this context, the critical density of the covered area was determined based on the infiltration theory. Directional antenna increases the beam coverage radius in the main lobe direction. The relation between the beam coverage radius l of the UAVs and the radiated power P_i can be expressed as

(25)

where c is a constant depending on the signal gain and wavelength from the transmitter to the receiver, λ is the power threshold value, and P_i is the radiated power of the directional antenna on the main lobe. l₀ denotes the radius of the beam at the omnidirectional antenna. The relationship between gain and power is given by

(26)

where P_t is the transmitted power of the omnidirectional antenna. Gain G(dB) = G(θ). The receiver can receive the signal when the power exceeds greater than the threshold. Therefore, the closed-form solution of radius l can be obtained as

(27)

The nodal beams onto a two-dimensional plane for ease of analysis. The coverage shape of the main flap beam was a sector. When the beamwidth is θ, the beam coverage area S_t is expressed as

(28)

Since the UAVs are affected by repulsive force, the regions within the repulsive range are defined as invalid regions. This area does not transmit information to adjacent UAVs and can be expressed as

(29)

That is, the effective coverage area of the node beam is

(30)

In a limited area, the size of the network coverage area determines the network connectivity. In order to determine the maximum distance between two overlapping UAVs, we must find an approximate overlapping area. A common practice for this in cellular networks is to consider a regular hexagon. In Figure 6, we consider the UAVs to be connected in this region.

The maximum distance between two overlapped footprint is

(31)

Based on the hexagonal mosaic model, we assume that the expected coverage area is a regular hexagonal lattice, as shown in Figure 7. The area of the regular lattice hexagon differed from that of the overlapping regular hexagon. As shown in Figure 8, a hexagon is blue if it contains at least one beam coverage center. The maximum distance between two adjacent hexagons is

for two UAVs. The area covered by the hexagon is

. Studies had shown that the critical probability of seepage in the hexagonal mosaic is p_h = 0.17 [34]. The permeation condition of regular hexagonal tessellation is expressed as

(32)

(33)

(34)

To make the connectivity of the network good, the continuous coverage condition is

(35)

(36)

Therefore, by combining (34) and (36), the critical UAV intensity of the coverage is

(37)

However, repulsion forces exist between the UAV subject to interference, as shown in Figure 9. In the space of UAV intensity ρ, the distance between neighboring nodes should exceed the rejection distance.

(38)

(39)

The beamwidth affects the coverage radius of the beam. Thus, the relationship between beamwidth and UAV intensity can be given as

(40)

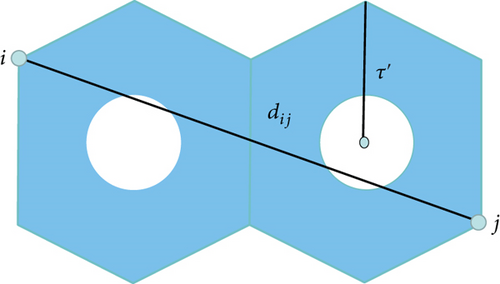
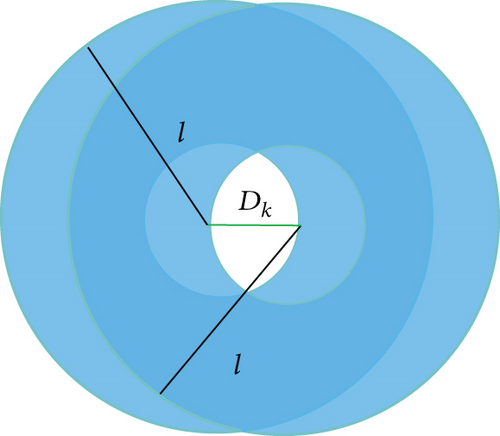
Here, we get the upper and lower limits of the UAV intensity. Within this range, the connectivity of the network coverage is guaranteed.

6. Simulation and Result Analysis

This section and numerical simulations have verified the derived theoretical results. The simulation parameters are shown in Table 1. This section is divided into three parts for simulation. To simulate an infinite domain, we used a three-dimensional hemisphere with a radius of R = 50 km and the receiving UAV was located at the center of the disk. In the simulation, the jamming transmitter was assigned a random orientation angle φ_k in [0, 2π]. Another transmitter was then placed at t_i with the orientation φ_i in [0, 2π]. The receiver orientation was θ. Channel gain was generated according to a distribution with a mean exponential distribution. The simulation was repeated 3 × 10⁴ times for different UAV positions, beamwidths, beam directions, and channel gains in Monte Carlo simulation.

Table 1. Simulation parameters.

Definition	Parameters	Values
Beamwidth of antenna	θ	Variables
Repulsion factor	β	Variables
Point intensity	β	Variables
Transmitting power	P_t	1
Beamwidth factor	γ	0.3
Noise	N₀	1
Connectivity threshold	Q	1
Power threshold	λ	1
Constant	c	1
Path attenuation factor	α	4

6.1. Antenna Gain Verification

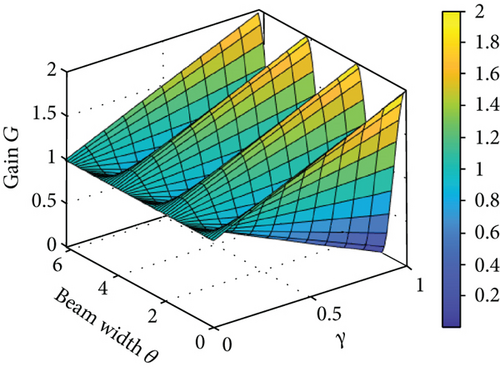
Figure 10 depicts the simulation results of the antenna gain effect under a single beam. The results demonstrate that the directionality of the antenna concentrates the radiation energy, resulting in improved gain. Additionally, the beamwidth factor determines the extent to which changes in angle affect the gain.

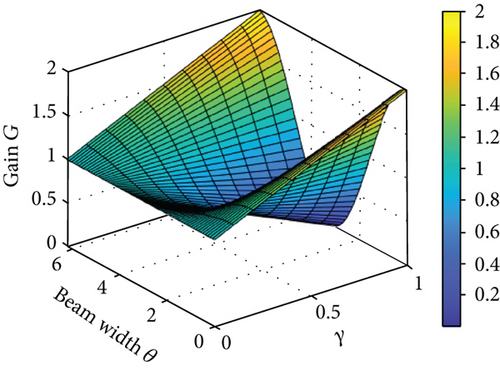
Figure 11 illustrates the simulation results of the antenna diagram with three main lobes. In this configuration, the gain reaches its maximum value in all three directions. The gain varies more rapidly with the beamwidth, while the influence of the side lobes is significantly diminished.

6.2. Verification of Approximate P_con

Figure 12 shows the relationship between connection probability and distance. As the distance increases, the connection probability decreases. Meanwhile, the rejection factor β has an impact on the connectivity probability. The magnitude of β represents the relationship between the location distribution of the drones. The connectivity probability is higher when the UAVs are deployed uniformly compared to random deployment. This is attributed to the reduced electromagnetic interference resulting from uniform deployment.

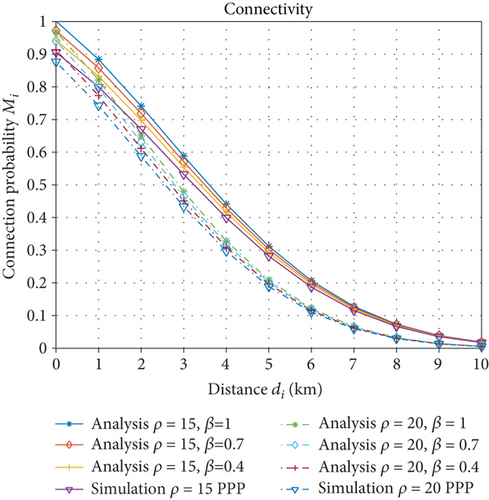
Under the same conditions as described above, Figure 13 shows the effect of different spatial intensities on the connectivity probability. In the PPP model, an increase in UAV intensity enhances the network connectivity probability. However, in the β-GPP model, the opposite effect is observed. The increase in intensity leads to a simultaneous rise in electromagnetic interference, resulting in a decrease in the connectivity probability.

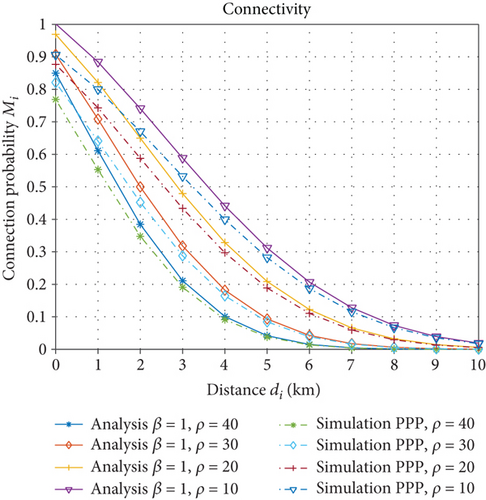
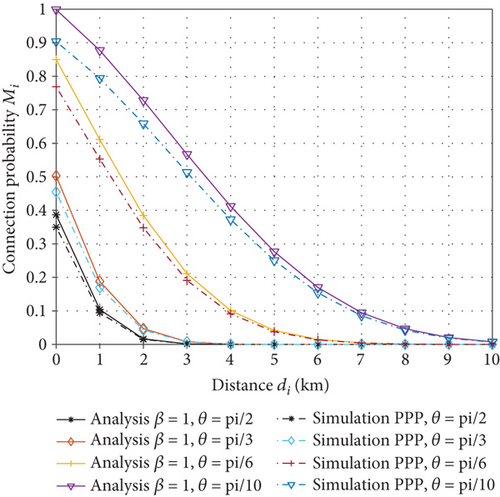
Figure 14 shows the effect of different beamwidths θ on the connectivity probability. The directionality of the antenna aids in concentrating the signal energy and minimizing energy loss during propagation. Furthermore, the narrow beam reduces electromagnetic interference in unmanned networks. Therefore, the utilization of directional antennas enhances the connectivity probability.

6.3. UAV Intensity Verification

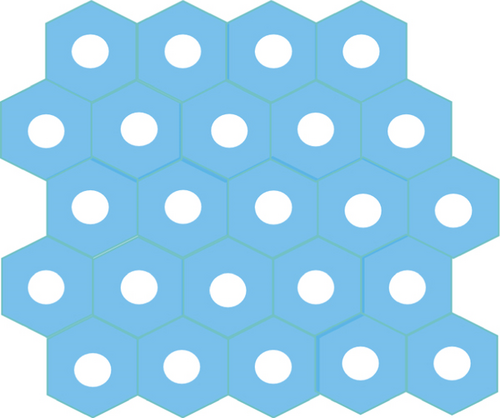
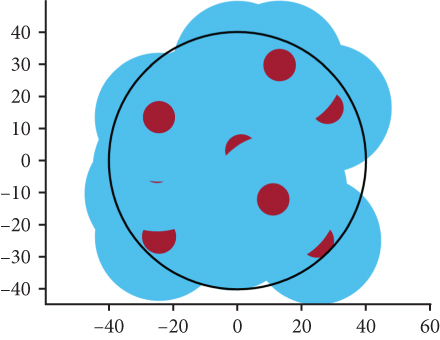
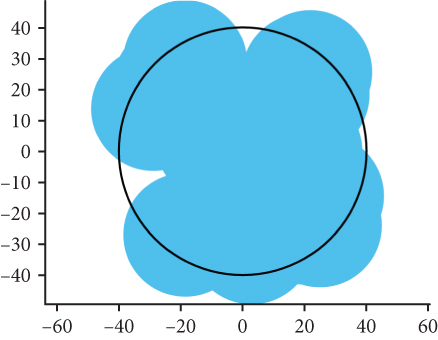
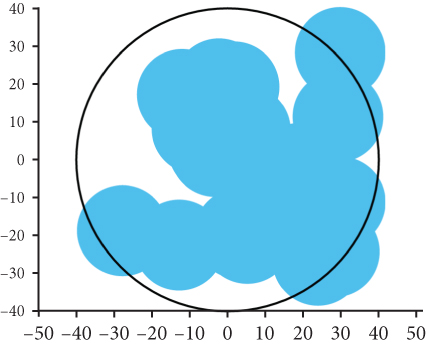
We utilized the network scenario illustrated in Figure 1 to validate our findings regarding network coverage. To simulate the network coverage scenario, we assumed that the directional antenna implemented omnidirectional scanning of 360°, and the UAVs were assumed to follow the β-GPP model. The simulation area was performed using an R = 40 km² black circle. The covered area was depicted in blue, while the uncovered area remained white. The red portion indicated an exclusion zone where UAV deployment was restricted. All UAVs in the network were initialized with the parameter values specified in Table 1.

Figure 15 shows the simulation results for the coverage effect of UAVs to 40 and comparing the network coverage of UAVs under model β-GPP and model PPP. It is evident that the network coverage effect is generally similar in both models. However, in the β-GPP model, the UAVs exhibit a certain distribution pattern with a repulsive area, effectively reducing signal interference between UAVs. At the same time, decreasing the beamwidth noticeably reduces signal interference and leads to a more regular spatial distribution of the network.

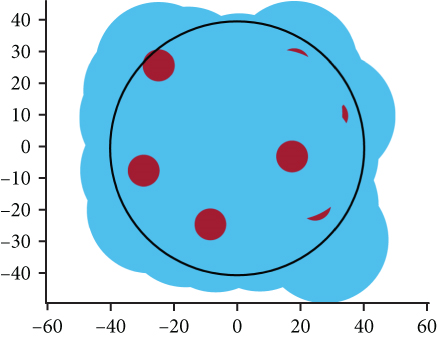
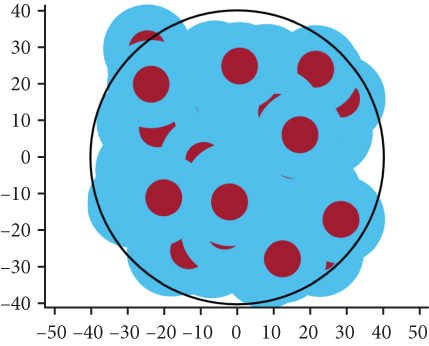
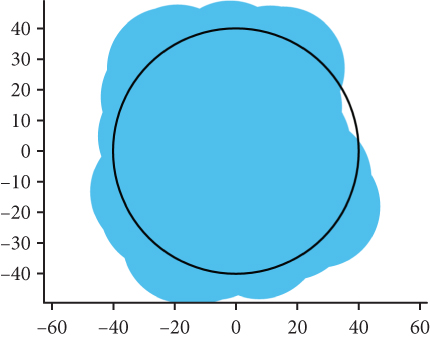
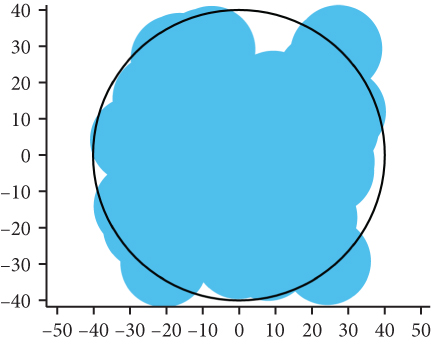
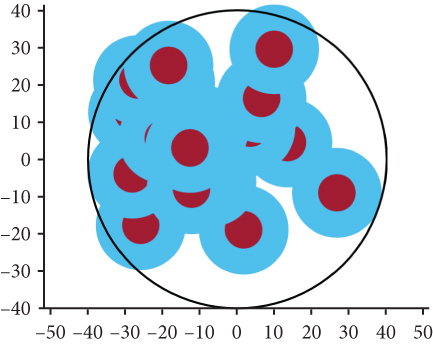
Figure 16 reduces the number of simulated UAVs to 20. As the number of UAVs decreases, the network coverage deteriorates, resulting in the network coverage deteriorates, resulting in the emergence of numerous blank areas. Notably, the network coverage of the β-GPP model exhibits a notably uniform pattern, whereas the coverage in the PPP model is more concentrated. Consequently, the distribution of UAVs in the β-GPP model is more regular compared to that in the PPP model. In this scenario, the analysis demonstrates that the β-GPP model outperforms the PPP model in terms of network coverage performance.

6.4. Discussion

This section is aimed at simulating the impact of the environmental repulsion factor β, node intensity ρ, and beamwidth θ on network connectivity. Based on the simulation results, it can be seen that regular deployment of network nodes can improve the network performance. The intensity of nodes should be within certain upper and lower limits within a finite area. The lower limit ensures network connectivity, while the upper limit helps minimize interference. Additionally, the beamwidth of the directional antenna plays a crucial role in enhancing antenna gain and maintaining stable connections between nodes. In practical applications, the environmental factor β reflects different application environments, enabling engineers to configure network node strength and antenna beamwidth accordingly to optimize network performance.

7. Conclusion

In this paper, we analyze the network performance of FlyMesh. The location distribution of FlyMesh is modeled as β-GPP to represent the spatial exclusion and correlation between these UAVs. The flexibility of the repulsion factor β enables us to adapt the FlyMesh to various engineering environments. We approximate the network model as an inhomogeneous PPP, ignoring the small fading of the wireless links, and employ stochastic geometry tools to derive approximate expressions for connectivity. By applying percolation theory, we determine the lower and upper limits of the critical node density that ensures basic network connectivity and effectively mitigates interference between nodes. Finally, the simulation results verified the correctness of the theoretical derivation and accurately described the performance of the FlyMesh. In practical deployments of FlyMesh in different environments, we optimize the system parameters based on the obtained performance metrics, which helps to improve the network performance and ensure its stability.

Conflicts of Interest

The authors declared no potential conflicts of interest concerning the research, authorship, and/or publication of this article.

Acknowledgments

The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: this work was supported by the National Natural Science Foundation of China (no. 61671471).

Open Research

Data Availability

No underlying data was collected or produced in this study.

References

1 Liu S., Zhang D., Liu X., Zhang T., and Wu H., Adaptive repair algorithm for TORA routing protocol based on flood control strategy, Computer Communications. (2020) 151, 437–448, https://doi.org/10.1016/j.comcom.2020.01.024.
10.1016/j.comcom.2020.01.024
Web of Science® Google Scholar
2 Azizi A., Parsaeefard S., Javan M. R., Mokari N., and Yanikomeroglu H., Profit maximization in 5G+ networks with heterogeneous aerial and ground base stations, IEEE Transactions on Mobile Computing. (2020) 19, no. 10, 2445–2460, https://doi.org/10.1109/tmc.2019.2926713.
10.1109/TMC.2019.2926713
Web of Science® Google Scholar
3 Zeng Y. and Zhang R., Energy-efficient UAV communication with trajectory optimization, IEEE Transactions on Wireless Communications. (2017) 16, no. 6, 3747–3760, https://doi.org/10.1109/TWC.2017.2688328, 2-s2.0-85020943053.
10.1109/TWC.2017.2688328
Web of Science® Google Scholar
4 Chen L., Zhang D. G., Zhang J., Zhang T., Wang W. J., and Cao Y. H., A novel offloading approach of IoT user perception task based on quantum behavior particle swarm optimization, Future Generation Computer Systems. (2023) 141, 577–594, https://doi.org/10.1016/j.future.2022.12.016.
10.1016/j.future.2022.12.016
Web of Science® Google Scholar
5 Khawaja W., Guvenc I., Matolak D. W., Fiebig U. C., and Schneckenburger N., A survey of air-to-ground propagation channel modeling for unmanned aerial vehicles, IEEE Communications Surveys & Tutorials. (2019) 21, no. 3, 2361–2391, https://doi.org/10.1109/COMST.2019.2915069, 2-s2.0-85068335361.
10.1109/COMST.2019.2915069
Web of Science® Google Scholar
6 Bekmezci I., Sahingoz O. K., and Temel Ş., Flying ad-hoc networks (FANETs): a survey, Ad Hoc Networks. (2013) 11, no. 3, 1254–1270, https://doi.org/10.1016/j.adhoc.2012.12.004, 2-s2.0-84875734707.
10.1016/j.adhoc.2012.12.004
Web of Science® Google Scholar
7 Qin Y. J., Kishk M. A., and Alouini M. S., Performance evaluation of UAV-enabled cellular networks with battery-limited drones, IEEE Communications Letters. (2020) 24, no. 12, 2664–2668, https://doi.org/10.1109/LCOMM.2020.3013286.
10.1109/LCOMM.2020.3013286
Web of Science® Google Scholar
8 Mei W., Wu Q., and Zhang R., Cellular-connected UAV: uplink association, power control and interference coordination, IEEE Transactions on Wireless Communications. (2019) 18, no. 11, 5380–5393, https://doi.org/10.1109/TWC.2019.2936021.
10.1109/TWC.2019.2936021
Web of Science® Google Scholar
9 Arshad R., Lampe L., ElSawy H., and Hossain M. J., Integrating UAVs into existing wireless networks: a stochastic geometry approach, 2018 IEEE Globecom Workshops (GC Wkshps), 2018, Abu Dhabi, United Arab Emirates, https://doi.org/10.1109/GLOCOMW.2018.8644504, 2-s2.0-85063448458.
10.1109/GLOCOMW.2018.8644504
Google Scholar
10 Mozaffari M., Saad W., Bennis M., and Debbah M., Unmanned aerial vehicle with underlaid device-to-device communications: performance and tradeoffs, IEEE Transactions on Wireless Communications. (2016) 15, no. 6, 3949–3963, https://doi.org/10.1109/TWC.2016.2531652, 2-s2.0-84976263049.
10.1109/TWC.2016.2531652
Web of Science® Google Scholar
11 Bushnaq O. M., Celik A., ElSawy H., Alouini M. S., and Al-Naffouri T. Y., Aeronautical data aggregation and field estimation in IoT networks: hovering and traveling time dilemma of UAVs, IEEE Transactions on Wireless Communications. (2019) 18, no. 10, 4620–4635, https://doi.org/10.1109/TWC.2019.2921955.
10.1109/TWC.2019.2921955
Web of Science® Google Scholar
12 Choi C. S., Baccelli F., and de Veciana G., Modeling and analysis of data harvesting architecture based on unmanned aerial vehicles, IEEE Transactions on Wireless Communications. (2020) 19, no. 3, 1825–1838, https://doi.org/10.1109/twc.2019.2958807.
10.1109/TWC.2019.2958807
Web of Science® Google Scholar
13 Zhou L., Yang Z., Zhou S., and Zhang W., Coverage probability analysis of UAV cellular networks in urban environments, 2018 IEEE International Conference on Communications Workshops (ICC Workshops), 2018, Kansas City, MO, USA, 1–6, https://doi.org/10.1109/ICCW.2018.8403633, 2-s2.0-85050268728.
10.1109/ICCW.2018.8403633
Google Scholar
14 Guo Y., Jia X., Cao S., and Hao Z., Analysis of downlink coverage and capacity for 3D mobile UAV networks, 2021 7th International Symposium on Mechatronics and Industrial Informatics (ISMII), 2021, Zhuhai, China, 236–239, https://doi.org/10.1109/ISMII52409.2021.00057.
10.1109/ISMII52409.2021.00057
Google Scholar
15 Lai C. C., Chen C. T., and Wang L. C., On-demand density-aware UAV base station 3D placement for arbitrarily distributed users with guaranteed data rates, IEEE Wireless Communications Letters. (2019) 8, no. 3, 913–916, https://doi.org/10.1109/LWC.2019.2899599, 2-s2.0-85066253578.
10.1109/LWC.2019.2899599
Web of Science® Google Scholar
16 Fang Y., Cheng B., Kang K., and Tan H., A self-adaptive deployment model of UAV cluster for emergency communication network, International Journal of Distributed Sensor Networks. (2021) 17, no. 10, https://doi.org/10.1177/15501477211049327, 155014772110493.
10.1177/15501477211049327
Web of Science® Google Scholar
17 Nakata I. and Miyoshi N., Spatial stochastic models for analysis of heterogeneous cellular networks with repulsively deployed base stations, Performance Evaluation. (2014) 78, 7–17, https://doi.org/10.1016/j.peva.2014.05.002, 2-s2.0-84903200151.
10.1016/j.peva.2014.05.002
Web of Science® Google Scholar
18 Deng N., Zhou W., and Haenggi M., The Ginibre point process as a model for wireless networks with repulsion, IEEE Transactions on Wireless Communications. (2015) 14, no. 1, 107–121, https://doi.org/10.1109/twc.2014.2332335, 2-s2.0-84921362362.
10.1109/TWC.2014.2332335
Web of Science® Google Scholar
19 Gomez J. S., Vasseur A., Vergne A., Martins P., Decreusefond L., and Chen W., A case study on regularity in cellular network deployment, IEEE Wireless Communications Letters. (2015) 4, no. 4, 421–424, https://doi.org/10.1109/LWC.2015.2431263, 2-s2.0-84940377676.
10.1109/LWC.2015.2431263
PubMed Web of Science® Google Scholar
20 Lavancier F., Møller J., and Rubak E., Determinantal point process models and statistical inference, Journal of the Royal Statistical Society: Series B: Statistical Methodology. (2015) 77, no. 4, 853–877, https://doi.org/10.1111/rssb.12096, 2-s2.0-84937735933.
10.1111/rssb.12096
Web of Science® Google Scholar
21 Chun Y. J., Hasna M. O., Ghrayeb A., and Di Renzo M., On modeling heterogeneous wireless networks using non-Poisson point processes, 2015, http://arxiv.org/abs/1506.06296.
Google Scholar
22 Miyoshi N. and Shirai T., A cellular network model with Ginibre configured base stations, Advances in Applied Probability. (2014) 46, no. 3, 832–845, https://doi.org/10.1239/aap/1409319562, 2-s2.0-84903219592.
10.1239/aap/1409319562
Web of Science® Google Scholar
23 Zhang C., Yu F., Wang Z., and Lyu G., Performance analysis of clustered wireless-powered ad hoc networks via β-Ginibre point processes, IEEE Transactions on Wireless Communications. (2021) 20, no. 11, 7475–7489, https://doi.org/10.1109/TWC.2021.3085247.
10.1109/TWC.2021.3085247
Web of Science® Google Scholar
24 Torrisi G. L. and Leonardi E., Large deviations of the interference in the Ginibre network model, Stochastic Systems. (2014) 4, no. 1, 173–205, https://doi.org/10.1287/13-SSY109.
10.1287/13-SSY109
Google Scholar
25 Shakhatreh H., Khreishah A., Othman N. S., and Sawalmeh A., Maximizing indoor wireless coverage using UAVs equipped with directional antennas, 2017 IEEE 13th Malaysia International Conference on Communications (MICC), 2017, Johor Bahru, Malaysia, 175–180, https://doi.org/10.1109/MICC.2017.8311754, 2-s2.0-85050643109.
10.1109/MICC.2017.8311754
Google Scholar
26 Guo J., Walk P., and Jafarkhani H., Optimal deployments of UAVs with directional antennas for a power-efficient coverage, IEEE Transactions on Communications. (2020) 68, no. 8, 5159–5174, https://doi.org/10.1109/TCOMM.2020.2992521.
10.1109/TCOMM.2020.2992521
Web of Science® Google Scholar
27 Peng J., Tang W., and Zhang H., Directional antennas modeling and coverage analysis of UAV-assisted networks, IEEE Wireless Communications Letters. (2022) 11, no. 10, 2175–2179, https://doi.org/10.1109/LWC.2022.3196227.
10.1109/LWC.2022.3196227
Web of Science® Google Scholar
28 Qin S., Peng L., Xu R., and Wang B., Enhanced connectivity of aerial 3D mesh network with directional antennas, 2022 IEEE 8th International Conference on Computer and Communications (ICCC), 2022, Chengdu, China, 1053–1057, https://doi.org/10.1109/iccc56324.2022.10065801.
10.1109/iccc56324.2022.10065801
Google Scholar
29 Chen S., Sun S., Xu G., Su X., and Cai Y., Beam-space multiplexing: practice, theory, and trends, from 4G TD-LTE, 5G, to 6G and beyond, IEEE Wireless Communications. (2020) 27, no. 2, 162–172, https://doi.org/10.1109/MWC.001.1900307.
10.1109/MWC.001.1900307
Web of Science® Google Scholar
30 Shirai T. and Takahashi Y., Random point fields associated with certain Fredholm determinants I: fermion, Poisson and boson point processes, Journal of Functional Analysis. (2003) 205, no. 2, 414–463, https://doi.org/10.1016/S0022-1236(03)00171-X, 2-s2.0-0346973069.
10.1016/S0022-1236(03)00171-X
Web of Science® Google Scholar
31 Georgiou O., Wang S., Bocus M. Z., Dettmann C. P., and Coon J. P., Directional antennas improve the link-connectivity of interference limited ad hoc networks, 2015 IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), 2015, Hong Kong, China, 1311–1316, https://doi.org/10.1109/PIMRC.2015.7343501, 2-s2.0-84958040882.
10.1109/PIMRC.2015.7343501
Google Scholar
32 Li Y., Baccelli F., Dhillon H. S., and Andrews J. G., Statistical modeling and probabilistic analysis of cellular networks with determinantal point processes, IEEE Transactions on Communications. (2015) 63, no. 9, 3405–3422, https://doi.org/10.1109/TCOMM.2015.2456016, 2-s2.0-84941201721.
10.1109/TCOMM.2015.2456016
Web of Science® Google Scholar
33 Ipsen I. C. F. and Lee D. J., Determinant approximations, 2011, http://arxiv.org/abs/1105.0437.
Google Scholar
34 Anjum M. D. N., Wang H., and Fang H., Coverage analysis of random UAV networks using percolation theory, 2020 International conference on computing, Networking and Communications (ICNC), 2020, Big Island, HI, USA, 667–673, https://doi.org/10.1109/ICNC47757.2020.9049663.
10.1109/ICNC47757.2020.9049663
Google Scholar

All articles

Modeling and Performance Analysis of Flying Mesh Network

Abstract

1. Introduction

2. Related Work

3. Mathematical Preliminaries